A Lightweight Deep Learning Model for Automatic Modulation Classification Using Dual-Path Deep Residual Shrinkage Network
Abstract
1. Introduction
- We introduce the application of a dual-path deep residual shrinkage network (DP-DRSN) for AMC.
- We create an efficient hybrid convolution neural network (CNN) and Long Short-Term Memory (LSTM) model using only 27k training parameters.
- We enhance AMC recognition accuracy by integrating a self-learnable scaling approach for signal denoising thresholds, leveraging garrote thresholding to balance denoising effectiveness, model performance, and computational complexity.
2. Related Work
2.1. Models with <5ok Tunable Parameters
2.2. Models with 50k to 100k Tunable Parameters
2.3. Models with 100k to 250k Tunable Parameters
3. Problem Statement, Hypothesis, and Research Question
3.1. Problem Statement
3.2. Hypothesis
3.3. Research Question
4. Methodology and Proposed Model
4.1. Methodology
4.2. Signal Denoising
4.3. Proposed Model
5. Experiments and Result Analysis
5.1. Dataset
5.2. Experimental Setup
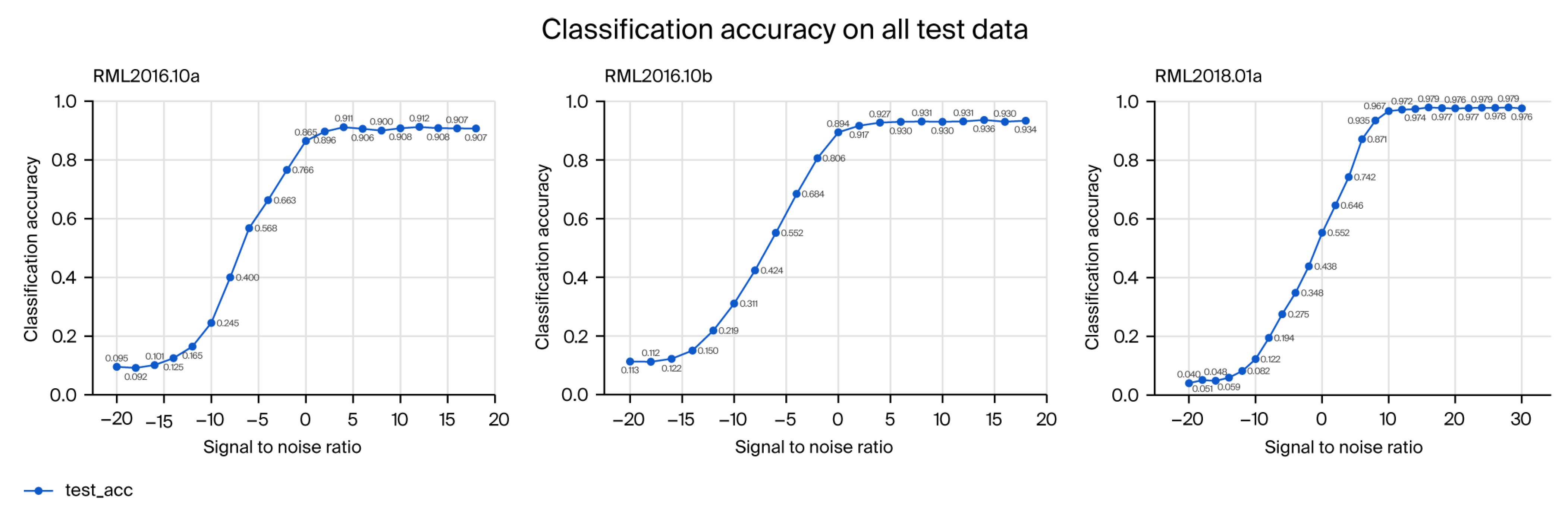
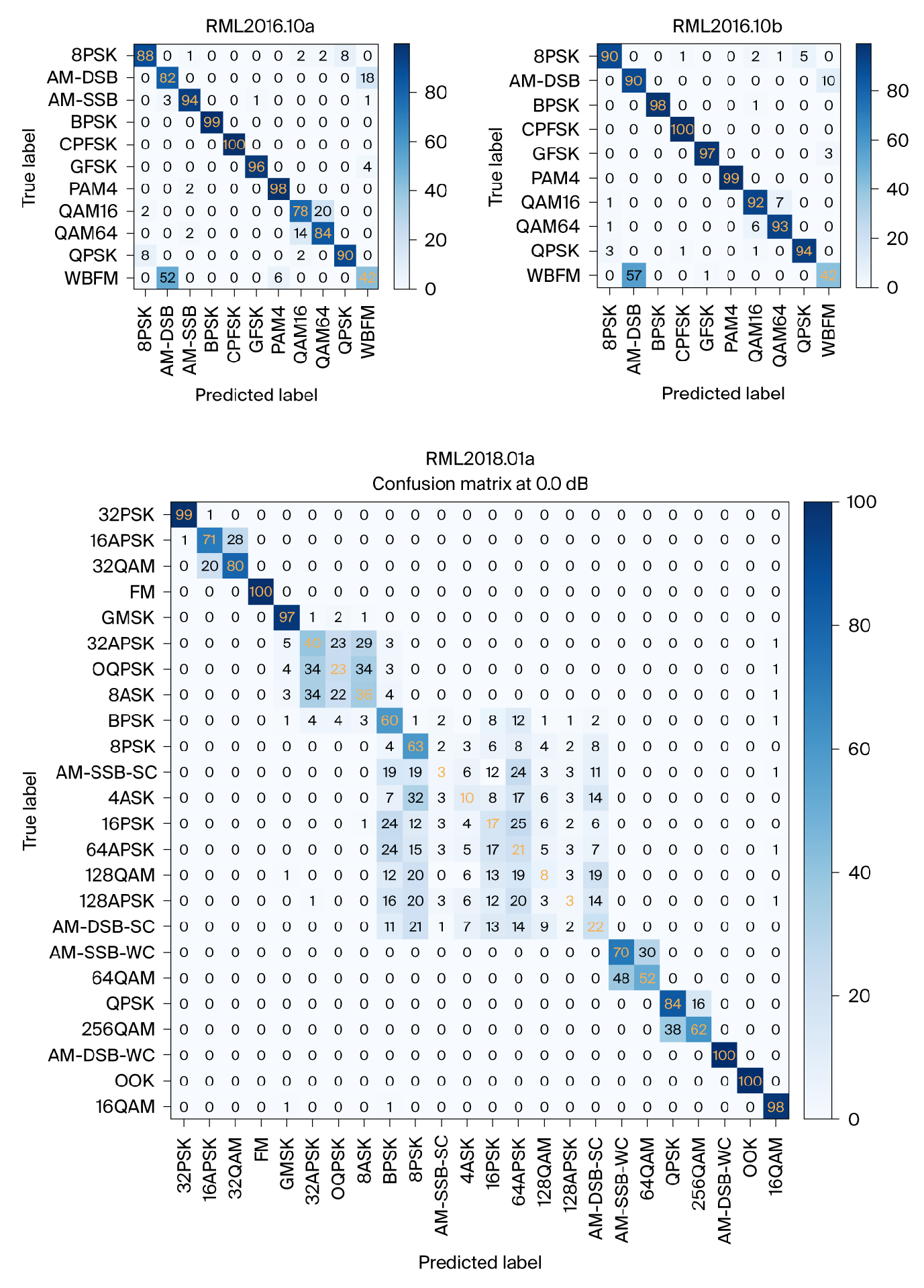
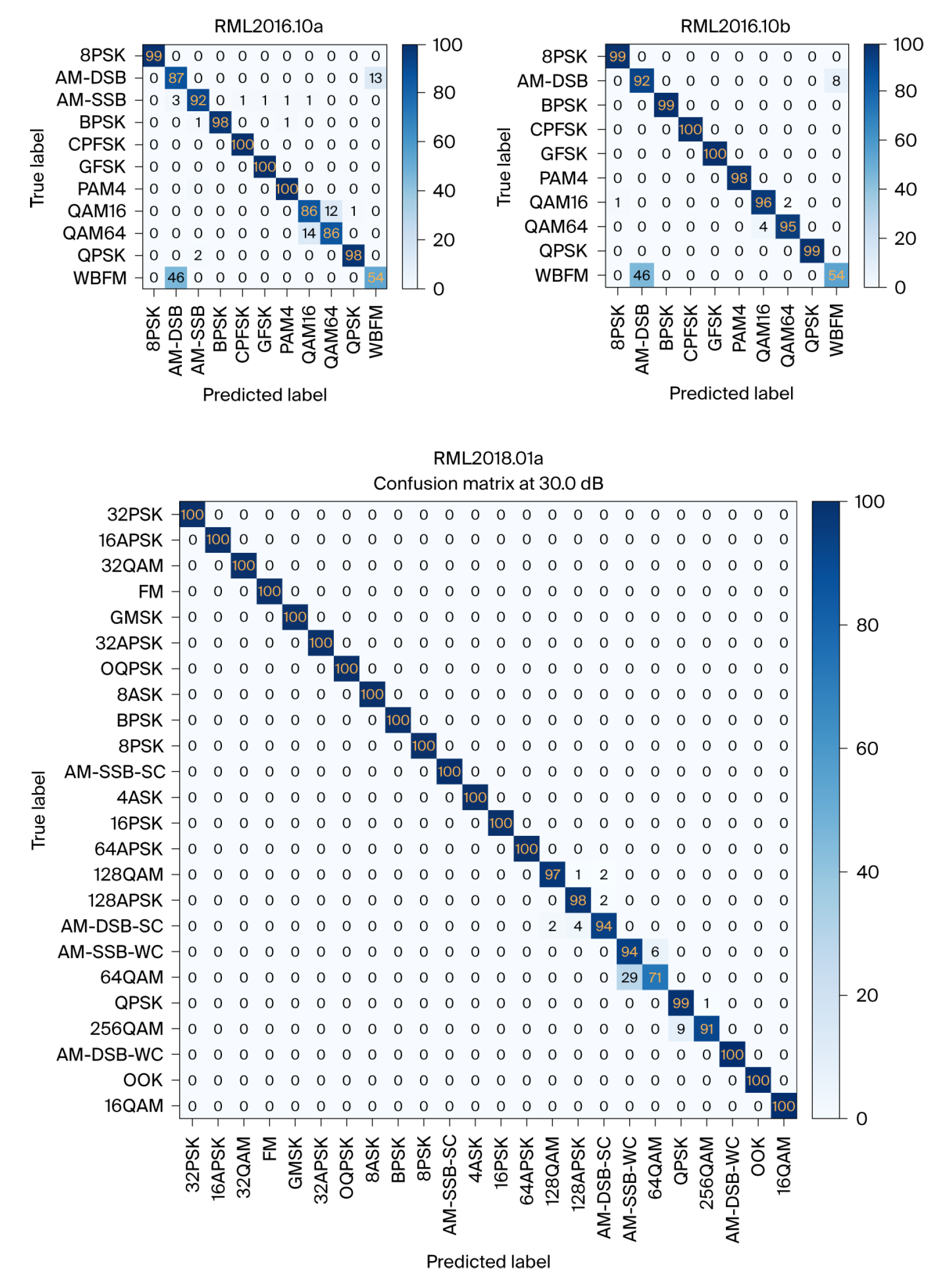
5.3. Testing and Training Results
5.4. Ablation Study
6. Discussion, Limitations, and Future Research
6.1. Discussion
6.2. Limitations
6.3. Future Research
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AMC | Automatic Modulation Classification |
| AWGN | Additive White Gaussian Noise |
| CCE | Categorical Cross-Entropy |
| CNN | Convolution Neural Network |
| CR | Cognitive Radio |
| CWT | Continuous Wavelet Transform |
| DL | Deep Learning |
| DP-DRSN | Dual-Path Deep Residual Shrinkage Network |
| DRSN | Deep Residual Shrinkage Network |
| FLOPs | Floating-point Operations per Second |
| GAP | Global Average Pooling |
| GMP | Global Max Pooling |
| LSTM | Long Short-Term Memory |
| MSE | Mean Squared Error |
| RML | Radio Machine Learning |
| ReLU | Rectified Linear Unit |
| SNR | Signal-to-Noise Ratio |
| SP-DRSN | Single-Path Deep Residual Shrinkage Network |
Appendix A
Appendix A.1. Model Design
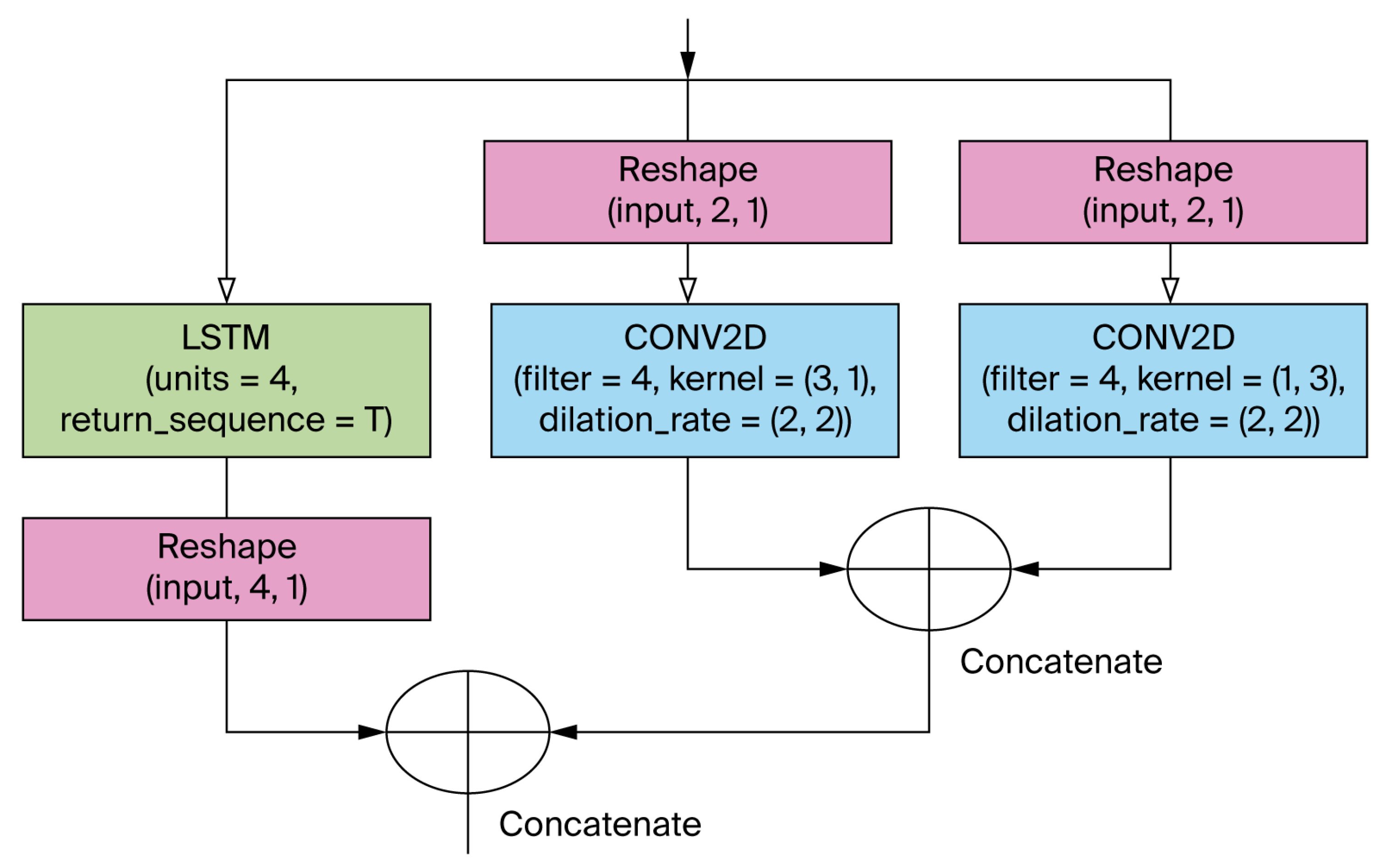


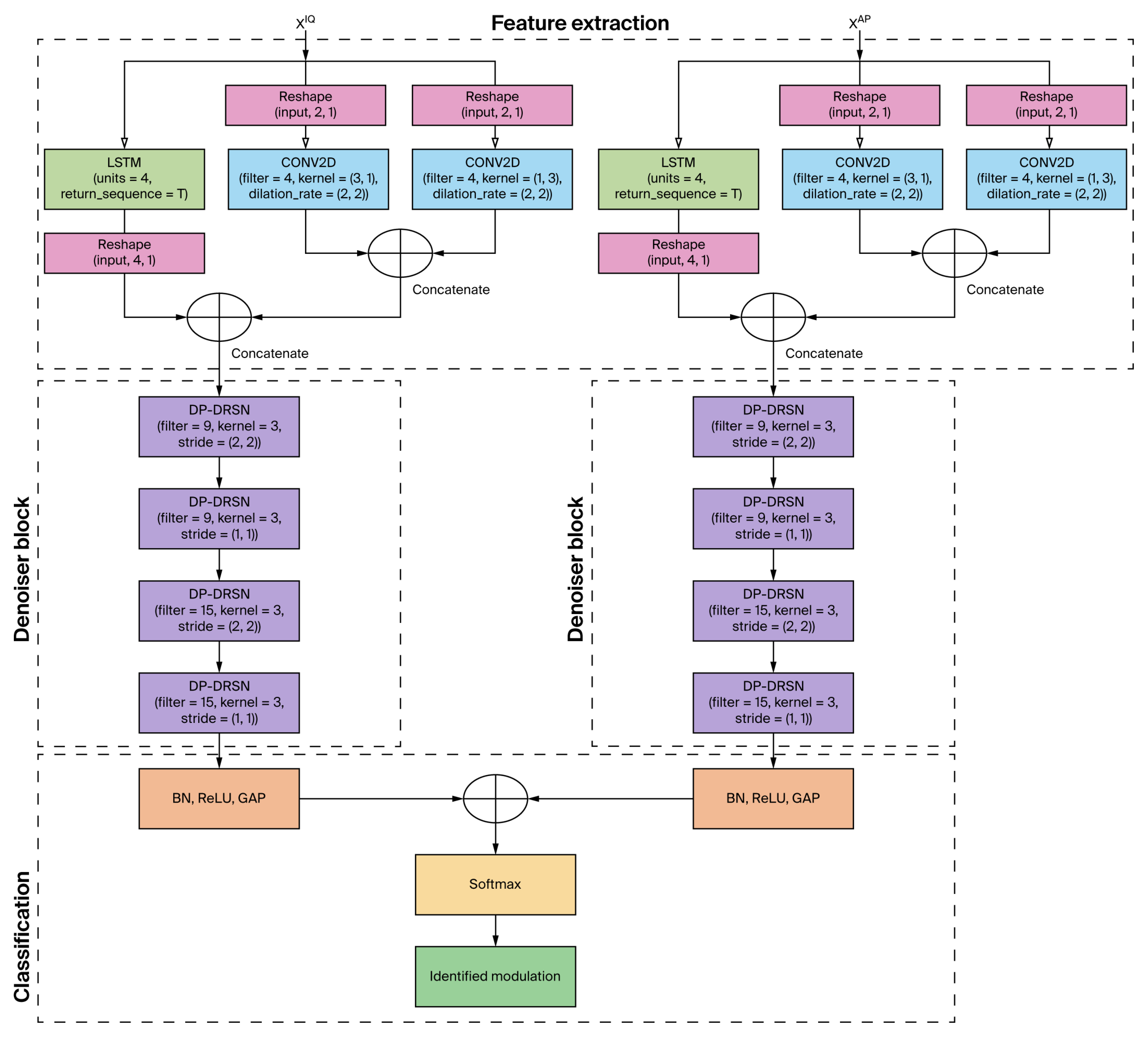
|
|
|
|
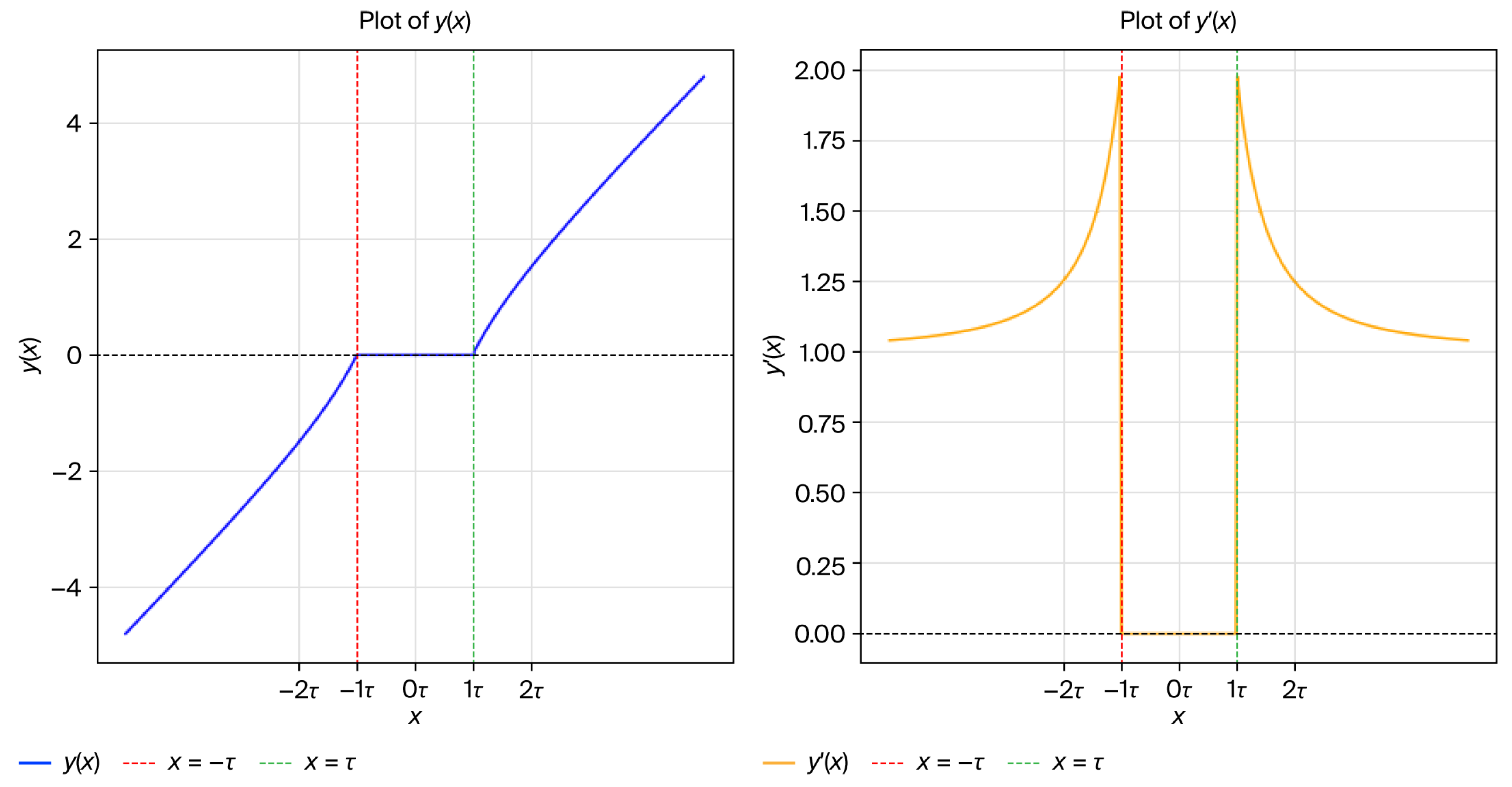
Appendix A.2. Soft Thresholding
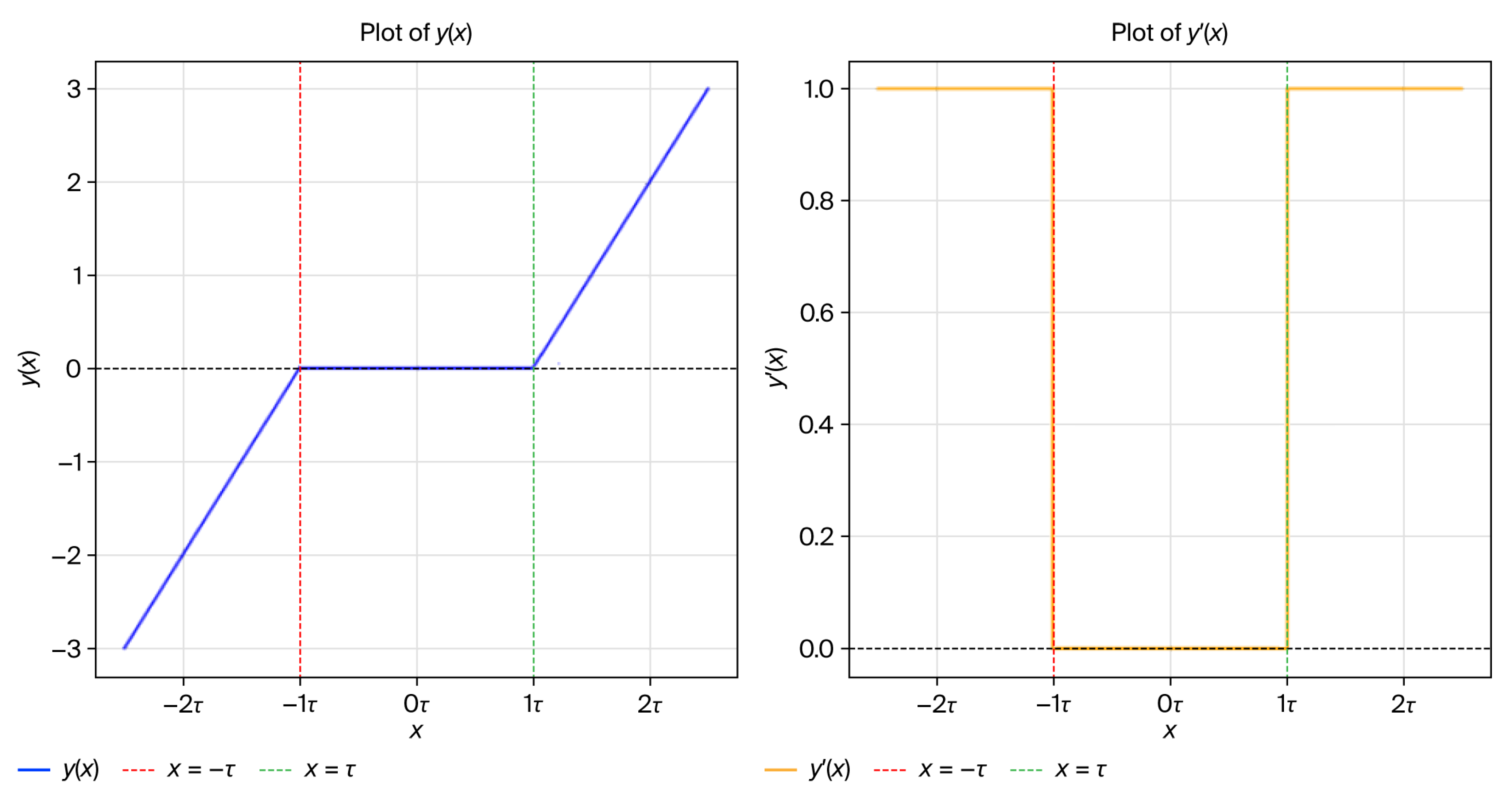
Appendix A.3. SP-DRSN Architecture

References
- Zheng, S.; Chen, S.; Qi, P.; Zhou, H.; Yang, X. Spectrum sensing based on deep learning classification for cognitive radios. China Commun. 2020, 17, 138–148. [Google Scholar] [CrossRef]
- Zheng, Q.; Tian, X.; Yu, Z.; Wang, H.; Elhanashi, A.; Saponara, S. Dl-pr: Generalized automatic modulation classification method based on deep learning with priori regularization. Eng. Appl. Artif. Intell. 2023, 122, 106082. [Google Scholar] [CrossRef]
- Guo, L.; Gao, R.; Cong, Y.; Yang, L. Robust automatic modulation classification under noise mismatch. EURASIP J. Adv. Signal Process. 2023, 2023, 73. [Google Scholar] [CrossRef]
- Lin, C.; Zhang, Z.; Wang, L.; Wang, Y.; Zhao, J.; Yang, Z.; Xiao, X. Fast and lightweight automatic modulation recognition using spiking neural network. In Proceedings of the 2024 IEEE International Symposium on Circuits and Systems (ISCAS), Singapore, 19–22 May 2024; pp. 1–5. [Google Scholar] [CrossRef]
- O’Shea, T.J.; West, N. Radio machine learning dataset generation with gnu radio. In Proceedings of the GNU Radio Conference, Boulder, CO, USA, 12–16 September 2016; Volume 1. [Google Scholar]
- O’Shea, T.J.; Roy, T.; Clancy, T.C. Over-the-air deep learning based radio signal classification. IEEE J. Sel. Top. Signal Process. 2018, 12, 168–179. [Google Scholar] [CrossRef]
- Ke, Z.; Vikalo, H. Real-time radio technology and modulation classification via an lstm auto-encoder. IEEE Trans. Wirel. Commun. 2022, 21, 370–382. [Google Scholar] [CrossRef]
- Shaik, S.; Kirthiga, S. Automatic modulation classification using densenet. In Proceedings of the 2021 5th International Conference on Computer, Communication and Signal Processing (ICCCSP), Chennai, India, 24–25 May 2021; pp. 301–305. [Google Scholar] [CrossRef]
- TianShu, C.; Zhen, H.; Dong, W.; Ruike, L. A iq correlation and long-term features neural network classifier for automatic modulation classification. In Proceedings of the 2022 IEEE 10th International Conference on Information, Communication and Networks (ICICN), Zhangye, China, 23–24 August 2022; pp. 396–400. [Google Scholar] [CrossRef]
- Shen, Y.; Yuan, H.; Zhang, P.; Li, Y.; Cai, M.; Li, J. A multi-subsampling self-attention network for unmanned aerial vehicle-to-ground automatic modulation recognition system. Drones 2023, 7, 376. [Google Scholar] [CrossRef]
- An, T.T.; Puspitasari, A.A.; Lee, B.M. Efficient automatic modulation classification for next generation wireless networks. TechRxiv 2023. [Google Scholar] [CrossRef]
- Gao, M.; Tang, X.; Pan, X.; Ren, Y.; Zhang, B.; Dai, J. Modulation recognition of communication signal with class-imbalance sample based on cnn-lstm dual channel model. In Proceedings of the 2023 IEEE International Conference on Signal Processing, Communications and Computing (ICSPCC), Zhengzhou, China, 14–17 November 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Ren, Y.; Tang, X.; Zhang, B.; Feng, J.; Gao, M. Modulation Recognition Method of Communication Signal Based on CNN-LSTM Dual Channel. In Proceedings of the 2022 5th International Conference on Information Communication and Signal Processing (ICICSP), Shenzhen, China, 16–18 September 2022; pp. 133–137. [Google Scholar] [CrossRef]
- Li, W.; Deng, W.; Wang, K.; You, L.; Huang, Z. A complex-valued transformer for automatic modulation recognition. IEEE Internet Things J. 2024, 11, 22197–22207. [Google Scholar] [CrossRef]
- Su, H.; Fan, X.; Liu, H. Robust and efficient modulation recognition with pyramid signal transformer. In Proceedings of the GLOBECOM 2022–2022 IEEE Global Communications Conference, Rio de Janeiro, Brazil, 4–8 December 2022; pp. 1868–1874. [Google Scholar] [CrossRef]
- Ding, R.; Zhou, F.; Wu, Q.; Dong, C.; Han, Z.; Dobre, O.A. Data and knowledge dual-driven automatic modulation classification for 6g wireless communications. IEEE Trans. Wirel. Commun. 2023, 23, 4228–4242. [Google Scholar] [CrossRef]
- Zhang, F.; Luo, C.; Xu, J.; Luo, Y. An efficient deep learning model for automatic modulation recognition based on parameter estimation and transformation. IEEE Commun. Lett. 2021, 25, 3287–3290. [Google Scholar] [CrossRef]
- Guo, W.; Yang, K.; Stratigopoulos, H.-G.; Aboushady, H.; Salama, K.N. An end-to-end neuromorphic radio classification system with an efficient sigma-delta-based spike encoding scheme. IEEE Trans. Artif. Intell. 2024, 5, 1869–1881. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, W.; Wang, Y.; Li, S.; Sun, X. A lightweight multi-feature fusion structure for automatic modulation classification. Phys. Commun. 2023, 61, 102170. [Google Scholar] [CrossRef]
- Zheng, Y.; Ma, Y.; Tian, C. Tmrn-glu: A transformer-based automatic classification recognition network improved by gate linear unit. Electronics 2022, 11, 1554. [Google Scholar] [CrossRef]
- Ning, M.; Zhou, F.; Wang, W.; Wang, Y.; Fei, S.; Wang, J. Automatic modulation recognition method based on multimodal i/q-frft fusion. Preprints 2024. [Google Scholar] [CrossRef]
- Shi, F.; Hu, Z.; Yue, C.; Shen, Z. Combining neural networks for modulation recognition. Digit. Signal Process. 2022, 120, 103264. [Google Scholar] [CrossRef]
- Xue, M.L.; Huang, M.; Yang, J.J.; Wu, J.D. Mlresnet: An efficient method for automatic modulation classification based on residual neural network. In Proceedings of the 2021 2nd International Symposium on Computer Engineering and Intelligent Communications (ISCEIC), Nanjing, China, 6–8 August 2021; pp. 122–126. [Google Scholar] [CrossRef]
- Riddhi, S.; Parmar, A.; Captain, K.; Ka, D.; Chouhan, A.; Patel, J. A dual-stream convolution-gru-attention network for automatic modulation classification. In Proceedings of the 2024 16th International Conference on COMmunication Systems & NETworkS (COMSNETS), Bengaluru, India, 3–7 January 2024; pp. 720–724. [Google Scholar] [CrossRef]
- Parmar, A.; Ka, D.; Chouhan, A.; Captain, K. Dual-stream cnn-bilstm model with attention layer for automatic modulation classification. In Proceedings of the 2023 15th International Conference on COMmunication Systems & NETworkS (COMSNETS), Bangalore, India, 3–8 January 2023; pp. 603–608. [Google Scholar] [CrossRef]
- Parmar, A.; Chouhan, A.; Captain, K.; Patel, J. Deep multilevel architecture for automatic modulation classification. Phys. Commun. 2024, 64, 102361. [Google Scholar] [CrossRef]
- Chang, S.; Yang, Z.; He, J.; Li, R.; Huang, S.; Feng, Z. A fast multi-loss learning deep neural network for automatic modulation classification. IEEE Trans. Cogn. Commun. Netw. 2023, 9, 1503–1518. [Google Scholar] [CrossRef]
- Chang, S.; Huang, S.; Zhang, R.; Feng, Z.; Liu, L. Multitask-learning-based deep neural network for automatic modulation classification. IEEE Internet Things J. 2022, 9, 2192–2206. [Google Scholar] [CrossRef]
- Luo, Z.; Xiao, W.; Zhang, X.; Zhu, L.; Xiong, X. Rlitnn: A multi-channel modulation recognition model combining multi-modal features. IEEE Trans. Wirel. Commun. 2024, 23, 19083–19097. [Google Scholar] [CrossRef]
- Harper, C.; Thornton, M.A.; Larson, E.C. Learnable statistical moments pooling for automatic modulation classification. In Proceedings of the ICASSP 2024—2024 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Seoul, Republic of Korea, 14–19 April 2024; pp. 8981–8985. [Google Scholar] [CrossRef]
- Harper, C.A.; Thornton, M.A.; Larson, E.C. Automatic modulation classification with deep neural networks. Electronics 2023, 12, 3962. [Google Scholar] [CrossRef]
- Huynh-The, T.; Hua, C.-H.; Pham, Q.-V.; Kim, D.-S. Mcnet: An efficient cnn architecture for robust automatic modulation classification. IEEE Commun. Lett. 2020, 24, 811–815. [Google Scholar] [CrossRef]
- Sun, S.; Wang, Y. A novel deep learning automatic modulation classifier with fusion of multichannel information using gru. EURASIP J. Wirel. Commun. Netw. 2023, 2023, 66. [Google Scholar] [CrossRef]
- Nisar, M.Z.; Ibrahim, M.S.; Usman, M.; Jeong-A, L. A lightweight deep learning model for automatic modulation classification using residual learning and squeeze–excitation blocks. Appl. Sci. 2023, 13, 5145. [Google Scholar] [CrossRef]
- Nguyen, T.-V.; Nguyen, T.T.; Ruby, R.; Zeng, M.; Kim, D.-S. Automatic modulation classification: A deep architecture survey. IEEE Access 2021, 9, 142950–142971. [Google Scholar] [CrossRef]
- Luo, R.; Sun, J.; Guo, Y. Deep learning-based modulation recognition for imbalanced classification. In Proceedings of the 2023 4th International Conference on Machine Learning and Computer Application, Association for Computing Machinery, Hangzhou, China, 27–29 October 2023; pp. 531–535. [Google Scholar] [CrossRef]
- Tekbıyık, K.; Ekti, A.R.; Görçin, A.; Kurt, G.K.; Keçeci, C. Robust and fast automatic modulation classification with cnn under multipath fading channels. In Proceedings of the 2020 IEEE 91st Vehicular Technology Conference (VTC2020-Spring), Antwerp, Belgium, 25–28 May 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Cheng, R.; Chen, Q.; Huang, M. Automatic modulation recognition using deep cvcnn-lstm architecture. Alex. Eng. J. 2024, 104, 162–170. [Google Scholar] [CrossRef]
- Rajendran, S.; Meert, W.; Giustiniano, D.; Lenders, V.; Pollin, S. Deep learning models for wireless signal classification with distributed low-cost spectrum sensors. IEEE Trans. Cogn. Commun. Netw. 2018, 4, 433–445. [Google Scholar] [CrossRef]
- Xu, J.; Luo, C.; Parr, G.; Luo, Y. A Spatiotemporal Multi-Channel Learning Framework for Automatic Modulation Recognition. IEEE Wirel. Commun. Lett. 2020, 9, 1629–1632. [Google Scholar] [CrossRef]
- Xiao, C.; Yang, S.; Feng, Z. Complex-valued depthwise separable convolutional neural network for automatic modulation classification. IEEE Trans. Instrum. Meas. 2023, 72, 1–10. [Google Scholar] [CrossRef]
- Syed, S.N.; Lazaridis, P.I.; Khan, F.A.; Ahmed, Q.Z.; Hafeez, M.; Ivanov, A.; Poulkov, V.; Zaharis, Z.D. Deep neural networks for spectrum sensing: A review. IEEE Access 2023, 11, 89591–89615. [Google Scholar] [CrossRef]
- Zhang, F.; Luo, C.; Xu, J.; Luo, Y.; Zheng, F.-C. Deep learning based automatic modulation recognition: Models, datasets, and challenges. Digit. Signal Process. 2022, 129, 103650. [Google Scholar] [CrossRef]
- Chen, G.; Xie, W.; Zhao, Y. Wavelet-based denoising: A brief review. In Proceedings of the 2013 Fourth International Conference on Intelligent Control and Information Processing (ICICIP), Beijing, China, 9–11 June 2013; pp. 570–574. [Google Scholar] [CrossRef]
- Donoho, D.L. De-noising by soft-thresholding. IEEE Trans. Inf. Theory 1995, 41, 613–627. [Google Scholar] [CrossRef]
- Zhao, M.; Zhong, S.; Fu, X.; Tang, B.; Pecht, M. Deep residual shrinkage networks for fault diagnosis. IEEE Trans. Ind. Inform. 2020, 16, 4681–4690. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar] [CrossRef]
- Salimy, A.; Mitiche, I.; Boreham, P.; Nesbitt, A.; Morison, G. Dynamic Noise Reduction with Deep Residual Shrinkage Networks for Online Fault Classification. Sensors 2022, 22, 515. [Google Scholar] [CrossRef] [PubMed]
- Ruan, F.; Dang, L.; Ge, Q.; Zhang, Q.; Qiao, B.; Zuo, X. Dual-path residual “shrinkage” network for side-scan sonar image classification. Comput. Intell. Neurosci. 2022, 2022, 6962838. [Google Scholar] [CrossRef]
- Gao, H.-Y. Wavelet shrinkage denoising using the non-negative garrote. J. Comput. Graph. Stat. 1998, 7, 469–488. [Google Scholar] [CrossRef]
- Marino, R.; Macris, N. Solving non-linear kolmogorov equations in large dimensions by using deep learning: A numerical comparison of discretization schemes. J. Sci. Comput. 2023, 94, 8. [Google Scholar] [CrossRef]
- An, T.T.; Lee, B.M. Robust automatic modulation classification in low signal to noise ratio. IEEE Access 2023, 11, 7860–7872. [Google Scholar] [CrossRef]
- Hu, J.; Shen, L.; Sun, G. Squeeze-and-excitation networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 7132–7141. [Google Scholar]


| Author | Year | Model Name | DL Architecture | Trainable Parameters | Dataset | Avg Accuracy | Max Accuracy |
|---|---|---|---|---|---|---|---|
| Lin et al. [4] | 2024 | LSM | 7k | A | 36.39% | ||
| B | 39.74% | ||||||
| C | 53.79% | ||||||
| Ke and Vikalo [7] | 2022 | DAE | LSTM | 14k | C | 58.74% | 97.91% |
| Shaik and Kirthiga [8] | 2021 | DenseNet | 19k | C | 55% | ||
| TianShu et al. [9] | 2022 | IQCLNet | CNN, LSTM | 29k | A | 59.73% | |
| Shen et al. [10] | 2023 | MSSA | CNN | 36k to 218k | C | 55.25% to 60.90% | |
| An et al. [11] | 2023 | TDRNN | CNN, GRU | 41k | A | 63.5% [−8 dB to18 dB] | |
| Gao et al. [12] | 2023 | CNN, LSTM | 43k | A | 66.7% [5 Modulations] | ||
| Li et al. [14] | 2024 | CV-TRN | Complex-Value Transformer | 44k | A | 63.74% | 93.76% |
| C | 64.13% | 98.95% | |||||
| Su et al. [15] | 2022 | SigFormer | Transformer | 44k | A | 63.71% | 93.60% |
| 44k | B | 65.77% | 94.80% | ||||
| 158k | C | 63.96% | 97.50% | ||||
| Ding et al. [16] | 2023 | CNN, BiGRU | 69k | C | 34% (−10 dB) [−10 dB to 2 dB] | ||
| Zhang et al. [17] | 2021 | PET-CGDNN | CNN, GRU | 71k to 75k | A | 60.44% | |
| B | 63.82% | ||||||
| C | 63.00% | ||||||
| Guo et al. [18] | 2024 | SNN | 84k–627k, 83k–542k | A | 56.69% | ||
| C | 64.29% | ||||||
| Li et al. [19] | 2023 | LightMFFS | CNN | 95k | A | 63.44% | |
| B | 65.44% | ||||||
| Zheng et al. [20] | 2022 | TMRN-GLU (small/large) | Transformer | 25k (Small) 106k (Large) | B | 61.7% (Small) 65.7% (Large) | 93.70% |
| Ning et al. [21] | 2024 | MAMR | Transformer | 110k | B | 61.50% | |
| Shi et al. [22] | 2022 | CNN, SE block | 113k | C | 98.70% | ||
| Xue et al. [23] | 2021 | MLResNet | CNN, LSTM | 115k | C | 96.6% (18 dB) | |
| Riddhi et al. [24] | 2024 | CNN, GRU | 145k | B | 68.23% [Digital Mod] | ||
| Parmar et al. [25] | 2023 | CNN, BiLSTM | 146k | B | 68.23% | ||
| Parmar et al. [26] | 2024 | CNN, LSTM | 155k | B | 63% | ||
| Chang et al. [27] | 2023 | FastMLDNN | CNN, Transformer | 159k | A | 63.24% | |
| Luo et al. [29] | 2024 | RLITNN | CNN, LSTM, Transformer | 181k | A | 63.84% | |
| B | 65.32% | ||||||
| Harper et al. [30] | 2024 | CNN, SE Block | 200k | C | 63.15% | ||
| Harper et al. [31] | 2023 | CNN, SE Block | 203k | C | 63.70% | 98.90% | |
| Huynh-The et al. [32] | 2020 | MCNet | CNN | 220k | C | 93% (20 dB) | |
| Sun & Wang [33] | 2023 | FGDNN | CNN, GRU | 253k | C | 90% (8 dB) | |
| Nisar et al. [34] | 2023 | CNN, SE Block | 253k | A | 81% (18 dB) | ||
| Proposed Model | CNN, LSTM, DP-DRSN | 27k | A | 61.20% | 91.23% | ||
| B | 63.78% | 93.64% | |||||
| C | 62.13% | 97.94% |
| Dataset | Signal Dimension | SNR Range | Train/ Validation/ Test Sample Size | Modulation Classes |
|---|---|---|---|---|
| RML2016.10a | 2 × 128 | −20 dB to 18 dB | 132k/44k/44k | 11 |
| RML2016.10b | 2 × 128 | −20 dB to 18 dB | 720k/240k/240k | 10 |
| RML2018.01a | 2 × 1024 | −20 dB to 30 dB | 1M/200k/200k | 24 |
| Dataset | Trainable Parameter | FLOPs | Avg Acc. | Max. Acc. |
|---|---|---|---|---|
| RML2016.10a | 26,638 | 2.36 M | 61.20% | 91.23% |
| RML2016.10b | 26,638 | 2.36 M | 63.78% | 93.64% |
| RML2018.01a | 27,072 | 18.82 M | 62.13% | 97.94% |
| Dataset | Memory Usage (GB) | Inference Time/Sample (ms) | Energy Usage/Sample (mJ) |
|---|---|---|---|
| RML2016.10a | 10.47 | 0.14 | 3.31 |
| RML2016.10b | 10.58 | 0.25 | 3.85 |
| RML2018.01a | 10.58 | 1.04 | 31.49 |
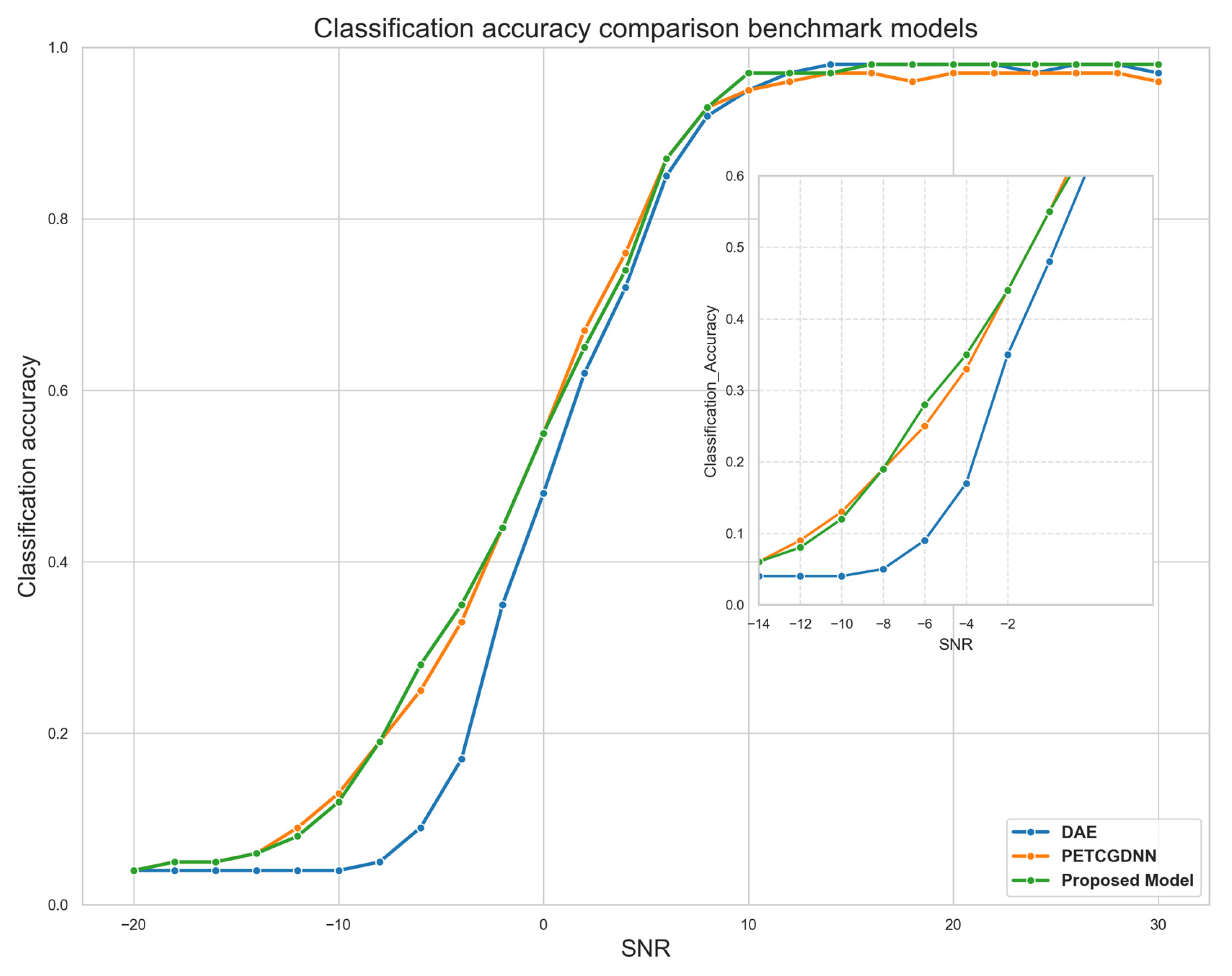
| Model | Avg. Acc. | Max. Acc. | FLOPs (M) | Inference Time/Sample (ms) | Param. (K) |
|---|---|---|---|---|---|
| ResNet [6] | 59.29% | 94.12% | 12.18 | 5.40 | 163.22 |
| DAE [7] | 58.74% | 98.91% | 2.89 | 0.43 | 14.88 |
| LSTM [39] | 61.78% | 97.92% | 206.6 | 38.52 | 202.78 |
| MCLDNN [40] | 61.08% | 96.84% | 443.36 | 42.41 | 427.88 |
| PET-CGDNN [17] | 61.76% | 96.93% | 71.92 | 20.63 | 75.34 |
| CDSCNN [41] | 62.52% | 98.01% | 74.11 | 6.80 | 322.62 |
| CV-TRN [14] | 64.13% | 98.85% | 6.42 | 6.81 | 44.79 |
| Proposed Model | 62.13% | 97.94% | 18.82 | 1.04 | 27.07 |
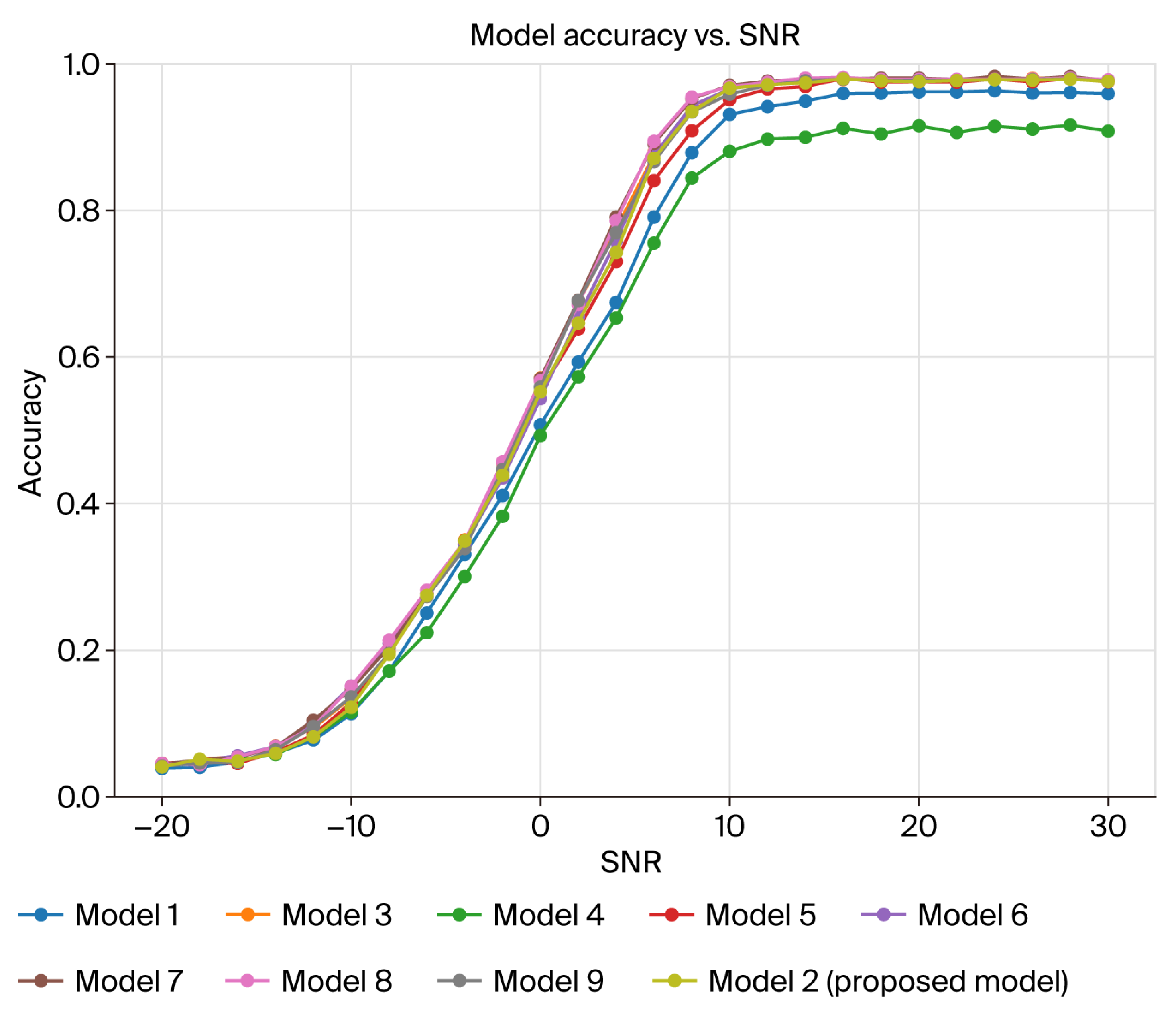
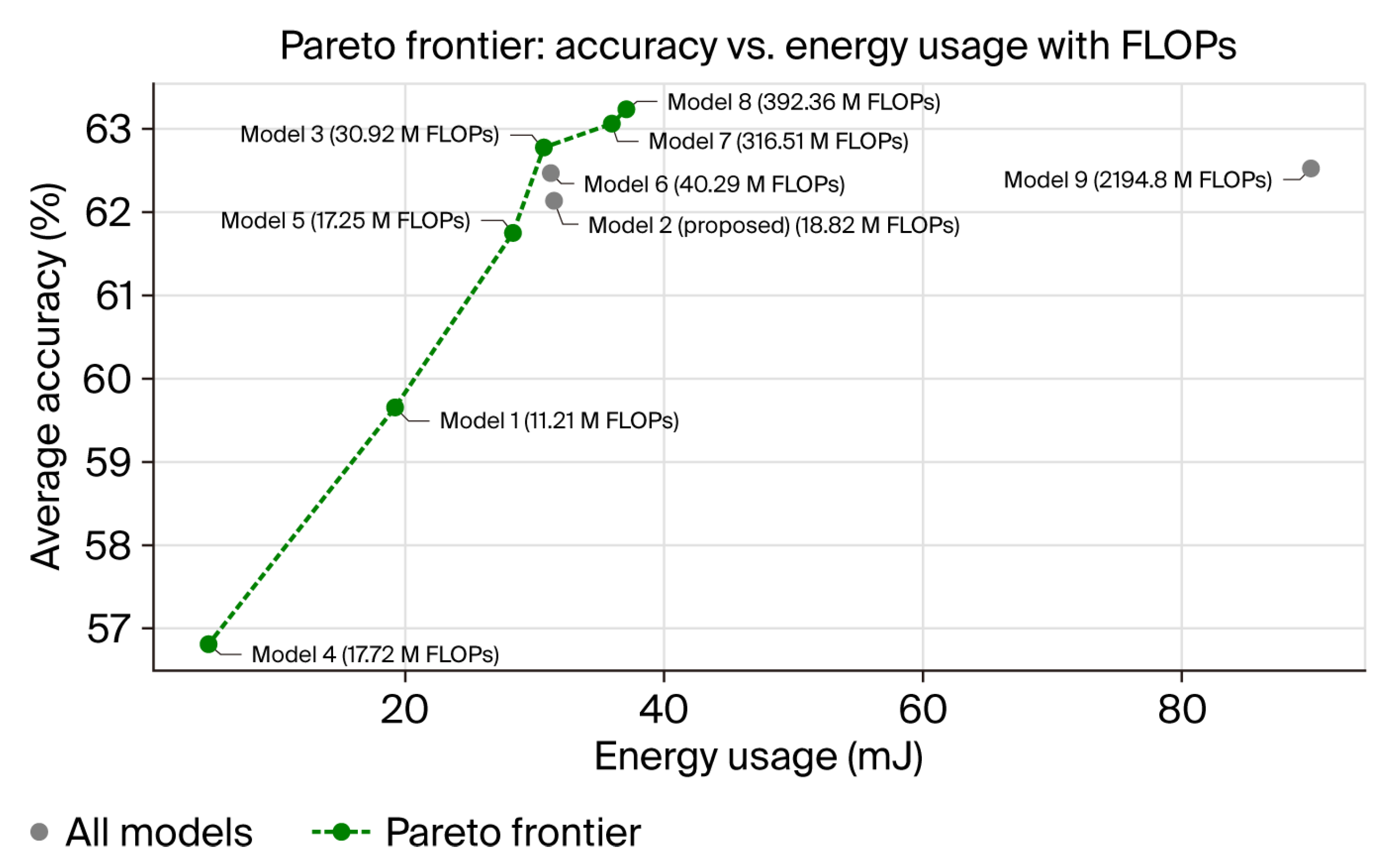
| Feature Extraction | Denoising Blocks (Garrote Thresholding) | Model Performance Results | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Model | LSTM | CNN | DP-DRSN Blocks | Denoising Parameters | Trainable Param | FLOPs (M) | Memory Usage (GB) | Inference Time (ms) | Energy Usage (mJ) | Avg Acc. | Max Acc. |
| Denoising Block Size 2, 4, 6 | |||||||||||
| Model 1 | Unit = 4 | Filter = 4 | 2 | Filter = 9, Stride = (2, 2); Filter = 9, Stride = (1, 1); | 7756 | 11.21 | 10.58 | 0.91 | 19.21 | 59.65% | 96.12% |
| Model 2 (Proposed Model) | Unit = 4 | Filter = 4 | 4 | Filter = 9, Stride = (2, 2); Filter = 9, Stride = (1, 1); Filter = 15, Stride = (2, 2); Filter = 15, Stride = (1, 1) | 27,072 | 18.82 | 10.58 | 1.04 | 31.49 | 62.13% | 97.94% |
| Model 3 | Unit = 4 | Filter = 4 | 6 | Filter = 9, Stride = (2, 2); Filter = 9, Stride = (1, 1); Filter = 15, Stride = (2, 2); Filter = 15, Stride = (1, 1); Filter = 27, Stride = (2, 2); Filter = 27, Stride = (1, 1) | 87,488 | 30.92 | 10.58 | 1.04 | 30.71 | 62.77% | 98.24% |
| Feature Extraction: LSTM only and CNN only | |||||||||||
| Model 4 | X | Filter = 4 | 4 | Filter = 9, Stride = (2, 2); Filter = 9, Stride = (1, 1); Filter = 15, Stride = (2, 2); Filter = 15, Stride = (1, 1) | 27,512 | 17.72 | 10.47 | 0.16 | 4.81 | 56.81% | 91.63% |
| Model 5 | Unit = 4 | X | 4 | Filter = 9, Stride = (2, 2); Filter = 9, Stride = (1, 1); Filter = 15, Stride = (2, 2); Filter = 15, Stride = (1, 1) | 26,344 | 17.25 | 10.58 | 1.03 | 28.33 | 61.75% | 97.93% |
| Feature Extraction: increasing LSTM unit, CNN Filter Size, and Denoising Blocks | |||||||||||
| Model 6 | Unit = 8 | Filter = 8 | 4 | Filter = 9, Stride = (2, 2); Filter = 9, Stride = (1, 1); Filter = 15, Stride = (2, 2); Filter = 15, Stride = (1, 1) | 28,280 | 40.29 | 10.58 | 1.05 | 31.23 | 62.46% | 98.12% |
| Model 7 | Unit = 16 | Filter = 16 | 4 | Filter = 17, Stride = (2, 2); Filter = 17, Stride = (1, 1); Filter = 33, Stride = (2, 2); Filter = 33, Stride = (1, 1) | 118,940 | 316.51 | 10.58 | 1.24 | 35.94 | 63.06% | 98.24% |
| Model 8 | Unit = 16 | Filter = 16 | 6 | Filter = 17, Stride = (2, 2); Filter = 17, Stride = (1, 1); Filter = 33, Stride = (2, 2); Filter = 33, Stride = (1, 1); Filter = 47, Stride = (2, 2); Filter = 47, Stride = (1, 1) | 304,800 | 392.36 | 10.58 | 1.22 | 37.07 | 63.23% | 98.24% |
| Model 9 | Unit = 32 | Filter = 32 | 6 | Filter = 33, Stride = (2, 2); Filter = 33, Stride = (1, 1); Filter = 47, Stride = (2, 2); Filter = 47, Stride = (1, 1); Filter = 65, Stride = (2, 2); Filter = 65, Stride = (1, 1) | 650,012 | 2194.8 | 10.58 | 3.21 | 90.03 | 62.52% | 98.03% |
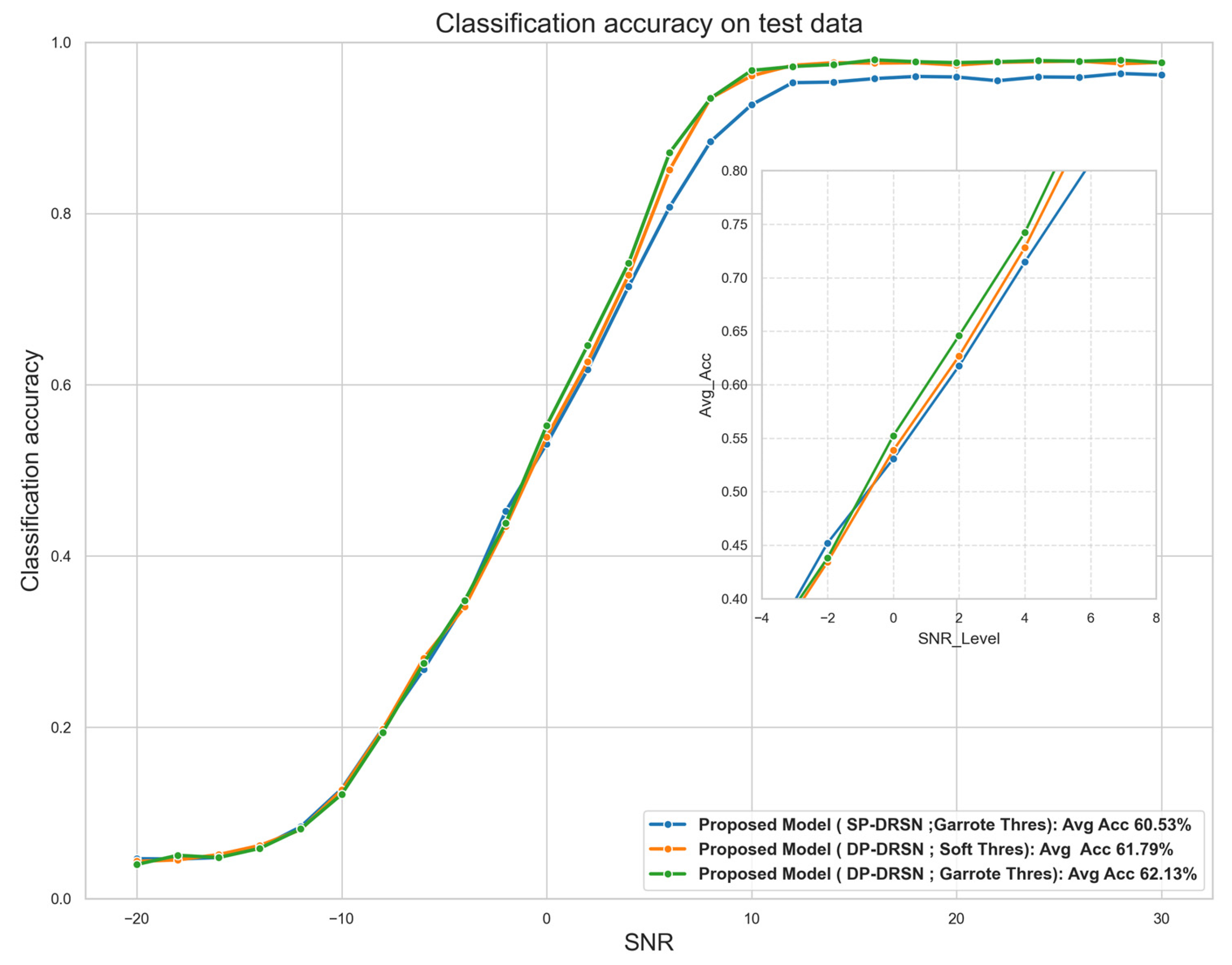
| SNR Levels | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Model | −20 | −18 | −16 | −14 | −12 | −10 | −8 | −6 | −4 | −2 | 0 | 2 | 4 |
| SP-DRSN; Garrote Thres: Avg Acc 60.53% | 4.68% | 4.63% | 4.81% | 5.96% | 8.40% | 12.82% | 19.88% | 26.78% | 34.41% | 45.21% | 53.08% | 61.76% | 71.47% |
| DP-DRSN; Soft Thres: Avg Acc 61.79% | 4.37% | 4.53% | 5.16% | 6.22% | 8.06% | 12.69% | 19.79% | 28.07% | 34.07% | 43.45% | 53.87% | 62.68% | 72.81% |
| DP-DRSN; Garrote Thres: Avg Acc 62.13% | 4.00% | 5.07% | 4.81% | 5.88% | 8.15% | 12.19% | 19.41% | 27.50% | 34.80% | 43.83% | 55.23% | 64.59% | 74.22% |
| Model | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 | 24 | 26 | 28 | 30 |
| SP-DRSN; Garrote Thres: Avg Acc 60.53% | 80.76% | 88.41% | 92.70% | 95.29% | 95.36% | 95.76% | 96.01% | 95.95% | 95.51% | 95.95% | 95.92% | 96.36% | 96.19% |
| DP-DRSN; Soft Thres: Avg Acc 61.79% | 85.11% | 93.48% | 96.09% | 97.31% | 97.62% | 97.57% | 97.62% | 97.34% | 97.66% | 97.74% | 97.81% | 97.49% | 97.66% |
| DP-DRSN; Garrote Thres: Avg Acc 62.13% | 87.10% | 93.47% | 96.71% | 97.17% | 97.40% | 97.95% | 97.74% | 97.62% | 97.73% | 97.86% | 97.79% | 97.94% | 97.61% |
| Comparison | t-Statistic | p-Value | Significance (Alpha = 0.05) |
|---|---|---|---|
| SP-DRSN (Garrote Thres) vs. DP-DRSN (Soft Thres) | −4.2 | 0.0003 | Significant |
| SP-DRSN (Garrote Thres) vs. DP-DRSN (Garrote Thres) | −4.35 | 0.0002 | Significant |
| DP-DRSN (Soft Thres) vs. DP-DRSN (Garrote Thres) | −2.1 | 0.046 | Significant |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Suman, P.; Qu, Y. A Lightweight Deep Learning Model for Automatic Modulation Classification Using Dual-Path Deep Residual Shrinkage Network. AI 2025, 6, 195. https://doi.org/10.3390/ai6080195
Suman P, Qu Y. A Lightweight Deep Learning Model for Automatic Modulation Classification Using Dual-Path Deep Residual Shrinkage Network. AI. 2025; 6(8):195. https://doi.org/10.3390/ai6080195
Chicago/Turabian StyleSuman, Prakash, and Yanzhen Qu. 2025. "A Lightweight Deep Learning Model for Automatic Modulation Classification Using Dual-Path Deep Residual Shrinkage Network" AI 6, no. 8: 195. https://doi.org/10.3390/ai6080195
APA StyleSuman, P., & Qu, Y. (2025). A Lightweight Deep Learning Model for Automatic Modulation Classification Using Dual-Path Deep Residual Shrinkage Network. AI, 6(8), 195. https://doi.org/10.3390/ai6080195






