Breast Cancer Classification via a High-Precision Hybrid IGWO–SOA Optimized Deep Learning Framework
Abstract
1. Introduction
2. Literature Review
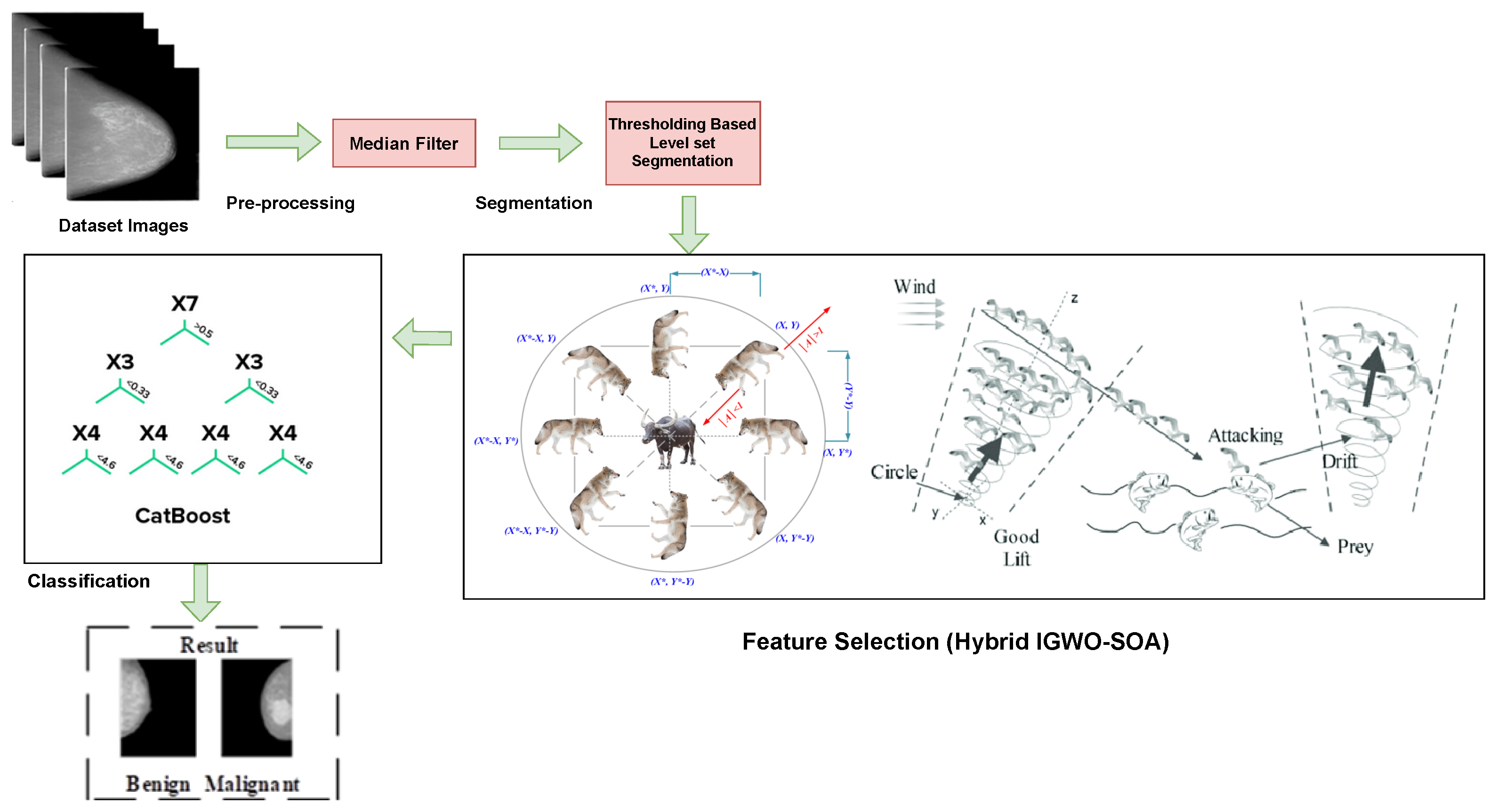
3. Proposed Methodology
3.1. Pre-Processing
3.2. Integration of Thresholding-Based Level Set Segmentation
3.3. Mammogram Image Feature Selection Using Hybrid Meta-Heuristic Algorithm (IGWO–SOA Optimization)
3.3.1. Social Hierarchy
3.3.2. Encircling Prey
3.3.3. Hunting
3.3.4. Attacking Prey
3.3.5. Search Prey
3.4. BRCA Classification System Using Proposed DL Algorithm
3.4.1. System Architecture
3.4.2. Hyper-Parameter Tuning Using LWO
4. Results and Discussions
4.1. Dataset Description: CBIS-DDSM
4.2. Evaluation Metrics
4.3. Experimental Setup
- 1.
- Test accuracy;
- 2.
- Test loss;
- 3.
- Generalization gap;
- 4.
- The difference in accuracy between the training and testing sets.
- Batch size (BS) = 32;
- Learning rate (LR) = ;
- L2-Regularization (l2-Reg.) = ;
- Number of Iteration = 100;
- Number of Epoch = 50;
- Population Size = 30.
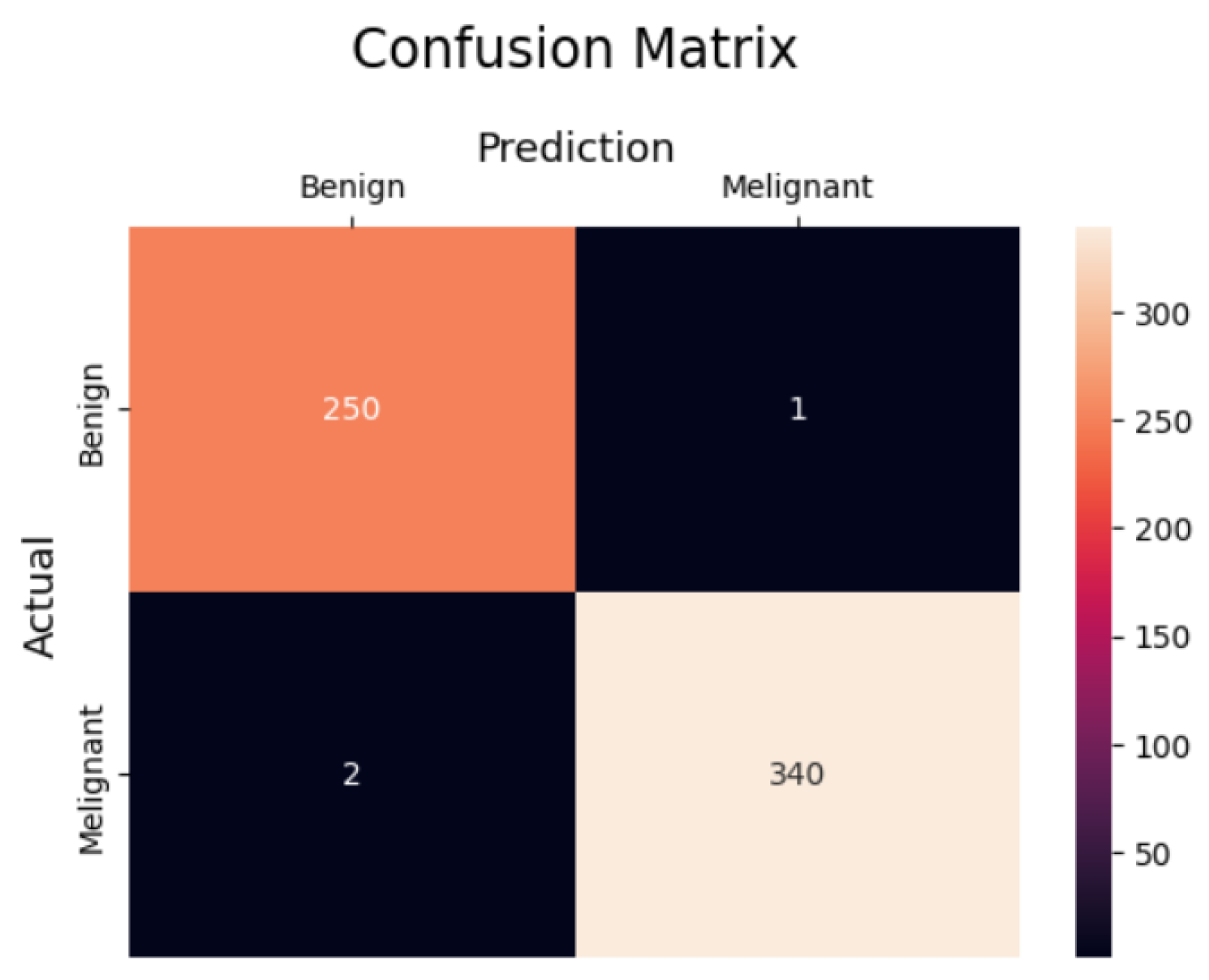
4.4. Experimental Results
4.4.1. Performance of the Classifier Without and with Feature Selection
4.4.2. 5-Fold Cross-Validation Analysis
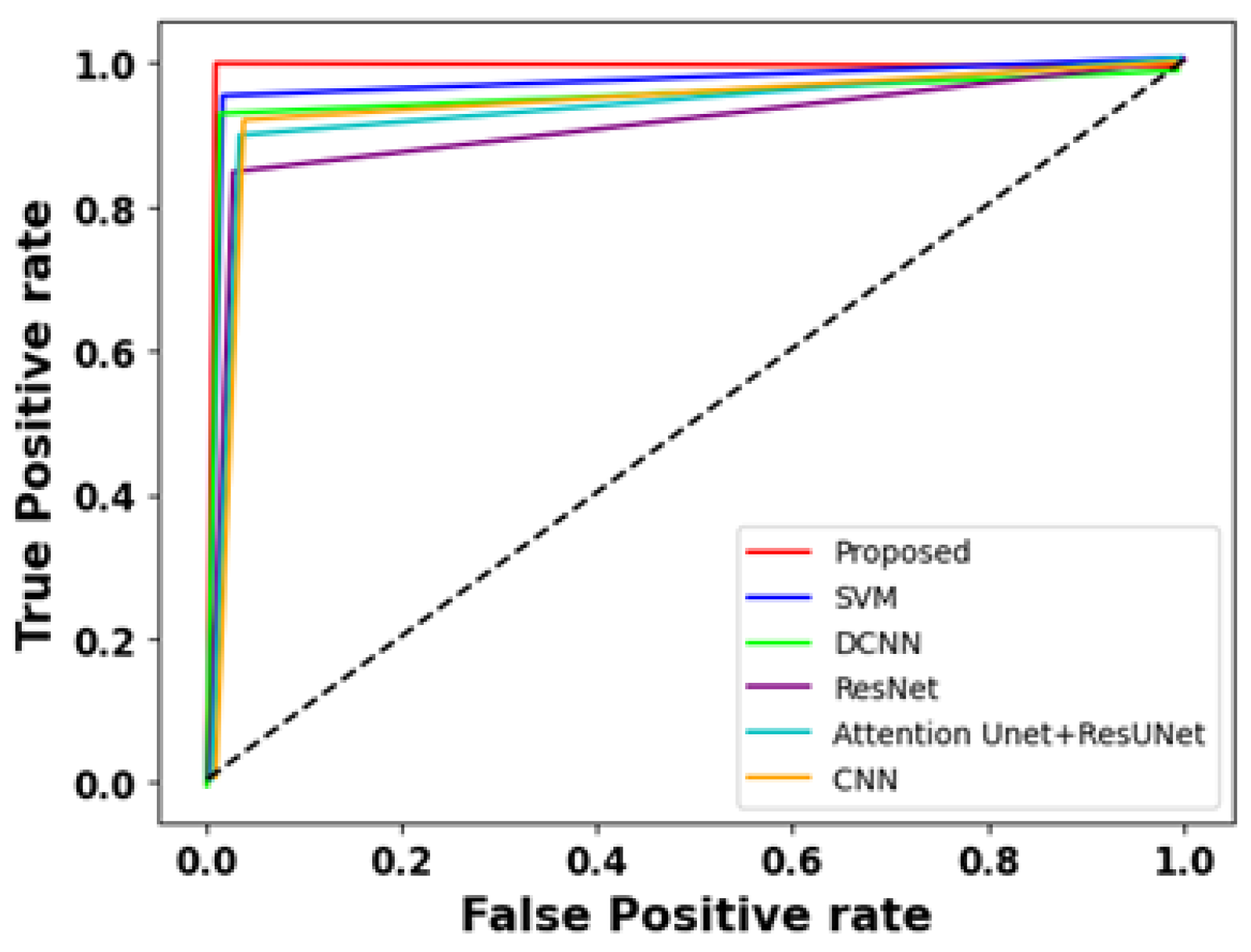
4.4.3. Comparison Results
4.4.4. ROC Analysis
4.4.5. Limitations
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, L.; Zhu, F.; Xie, L.; Wang, C.; Wang, J.; Chen, R.; Jia, P.; Guan, H.Q.; Peng, L.; Chen, Y. Clinical characteristics of COVID-19-infected cancer patients: A retrospective case study in three hospitals within Wuhan, China. Ann. Oncol. 2020, 31, 894–901. [Google Scholar] [CrossRef] [PubMed]
- Hameed, Z.; Zahia, S.; Garcia-Zapirain, B.; Javier Aguirre, J.; María Vanegas, A. Breast cancer histopathology image classification using an ensemble of DL models. Sensors 2020, 20, 4373. [Google Scholar] [CrossRef] [PubMed]
- Fang, Y.; Zhao, J.; Hu, L.; Ying, X.; Pan, Y.; Wang, X. Image classification toward breast cancer using deeply-learned quality features. J. Vis. Commun. Image Represent. 2019, 64, 102609. [Google Scholar] [CrossRef]
- Zheng, J.; Lin, D.; Gao, Z.; Wang, S.; He, M.; Fan, J. Deep learning assisted efficient AdaBoost algorithm for breast cancer detection and early diagnosis. IEEE Access 2020, 8, 96946–96954. [Google Scholar] [CrossRef]
- Titoriya, A.; Sachdeva, S. Breast cancer histopathology image classification using AlexNet. In Proceedings of the 2019 4th International Conference on Information Systems and Computer Networks (ISCON), Mathura, India, 21–22 November 2019; pp. 708–712. [Google Scholar]
- Mittal, S.; Wrobel, T.P.; Walsh, M.; Kajdacsy-Balla, A.; Bhargava, R. Breast cancer histopathology using infrared spectroscopic imaging: The impact of instrumental configurations. Clin. Spectrosc. 2021, 3, 100006. [Google Scholar] [CrossRef]
- Mahbod, A.; Ellinger, I.; Ecker, R.; Smedby, Ö.; Wang, C. Breast cancer histological image classification using fine-tuned deep network fusion. In Proceedings of the International Conference on Image Analysis and Recognition, Póvoa de Varzim, Portugal, 27–29 June 2018; Springer: Cham, Switzerland, 2018; pp. 754–762. [Google Scholar]
- Yao, H.; Zhang, X.; Zhou, X.; Liu, S. Parallel structure deep neural network using CNN and RNN with an attention mechanism for breast cancer histology image classification. Cancers 2019, 11, 1901. [Google Scholar] [CrossRef] [PubMed]
- Farrokh, A.; Goldmann, G.; Meyer-Johann, U.; Hille-Betz, U.; Hillemanns, P.; Bader, W.; Wojcinski, S. Clinical differences between invasive lobular breast cancer and invasive carcinoma of no special type in the German mammography-screening-program. Women Health 2022, 62, 144–156. [Google Scholar] [CrossRef] [PubMed]
- Hu, Q.; Liu, Y.; Chen, C.; Kang, S.; Sun, Z.; Wang, Y.; Xiang, M.; Guan, H.; Xia, L. Application of computer-aided detection (CAD) software to automatically detect nodules under SDCT and LDCT scans with different parameters. Comput. Biol. Med. 2022, 146, 105538. [Google Scholar] [CrossRef] [PubMed]
- Kumar, A.; Singh, S.K.; Saxena, S.; Lakshmanan, K.; Sangaiah, A.K.; Chauhan, H.; Shrivastava, S.; Singh, R.K. Deep feature learning for histopathological image classification of canine mammary tumors and human breast cancer. Inf. Sci. 2020, 508, 405–421. [Google Scholar] [CrossRef]
- Alirezazadeh, P.; Hejrati, B.; Monsef-Esfahani, A.; Fathi, A. Representation learning-based unsupervised domain adaptation for classification of breast cancer histopathology images. Biocybern. Biomed. Eng. 2018, 38, 671–683. [Google Scholar] [CrossRef]
- Budak, Ü.; Cömert, Z.; Rashid, Z.N.; Şengür, A.; Çıbuk, M. Computer-aided diagnosis system combining FCN and Bi-LSTM model for efficient breast cancer detection from histopathological images. Appl. Soft Comput. 2019, 85, 105765. [Google Scholar] [CrossRef]
- Singla, S.; Ghosh, P.; Kumari, U. Breast cancer detection using genetic algorithm with correlation-based feature selection: Experiment on different datasets. Int. J. Comp. Sci. Eng. 2019, 7, 406–410. [Google Scholar] [CrossRef]
- George, K.; Faziludeen, S.; Sankaran, P. Breast cancer detection from biopsy images using nucleus-guided transfer learning and belief-based fusion. Comput. Biol. Med. 2020, 124, 103954. [Google Scholar] [CrossRef] [PubMed]
- Singh, R.; Ahmed, T.; Kumar, A.; Singh, A.K.; Pandey, A.K.; Singh, S.K. Imbalanced breast cancer classification using transfer learning. IEEE/ACM Trans. Comput. Biol. Bioinform. 2020, 18, 83–93. [Google Scholar] [CrossRef] [PubMed]
- Hirra, I.; Ahmad, M.; Hussain, A.; Ashraf, M.U.; Saeed, I.A.; Qadri, S.F.; Alghamdi, A.M.; Alfakeeh, A.S. Breast Cancer Classification from Histopathological Images Using Patch-Based Deep Learning Modeling. IEEE Access 2021, 9, 24273–24287. [Google Scholar] [CrossRef]
- Li, G.; Li, C.; Wu, G.; Ji, D.; Zhang, H. Multi-view Attention-Guided Multiple Instance Detection Network for Interpretable Breast Cancer Histopathological Image Diagnosis. IEEE Access 2021, 9, 79671–79684. [Google Scholar] [CrossRef]
- Das, A.; Mohanty, M.N.; Mallick, P.K.; Tiwari, P.; Muhammad, K.; Zhu, H. Breast cancer detection using an ensemble deep learning method. Biomed. Signal Process. Control 2021, 70, 103009. [Google Scholar] [CrossRef]
- Gupta, V.; Vasudev, M.; Doeger, A.; Sambyal, N. Breast cancer detection from histopathology images using modified residual neural networks. Biocybern. Biomed. Eng. 2021, 41, 1272–1287. [Google Scholar] [CrossRef]
- Mohiuddin, N.; Dar, R.A.; Rasool, M.; Assad, A. Breast cancer detection using deep learning: Datasets, methods, and challenges ahead. Comput. Biol. Med. 2022, 149, 106073. [Google Scholar] [CrossRef] [PubMed]
- Khalid, A.; Mehmood, A.; Alabrah, A.; Alkhamees, B.F.; Amin, F.; AlSalman, H.; Choi, G.S. Breast Cancer Detection and Prevention Using Machine Learning. Diagnostics 2023, 13, 3113. [Google Scholar] [CrossRef] [PubMed]
- Sharafaddini, A.M.; Esfahani, K.K.; Mansouri, N. Deep learning approaches to detect breast cancer: A comprehensive review. Multimed. Tools Appl. 2024, 84, 24079–24190. [Google Scholar] [CrossRef]
- Nassih, R.; Berrado, A. Breast Cancer Classification Using an Adapted Bump-Hunting Algorithm. Algorithms 2025, 18, 136. [Google Scholar] [CrossRef]
- Erkan, U.; Gökrem, L.; Enginoğlu, S. Different applied median filter in salt and pepper noise. Comput. Electr. Eng. 2018, 70, 789–798. [Google Scholar] [CrossRef]
- Sathiyabhama, B.; Kumar, S.U.; Jayanthi, J.; Sathiya, T.; Ilavarasi, A.K.; Yuvarajan, V.; Gopikrishna, K. A novel feature selection framework based on grey wolf optimizer for mammogram image analysis. Neural Comput. Appl. 2021, 33, 14583. [Google Scholar] [CrossRef]
- Dhiman, G.; Kumar, V. Seagull optimization algorithm: Theory and its applications for large-scale industrial engineering problems. Knowl.-Based Syst. 2019, 165, 169–196. [Google Scholar] [CrossRef]
- Faris, H.; Aljarah, I.; Al-Betar, M.A.; Mirjalili, S. Grey wolf optimizer: A review of recent variants and applications. Neural Comput. Appl. 2018, 30, 413–435. [Google Scholar] [CrossRef]
- Kumar, A.; Zhou, Y.; Gandhi, C.P.; Kumar, R.; Xiang, J. Bearing defect size assessment using wavelet transform-based Deep Convolutional Neural Network (DCNN). Alex. Eng. J. 2020, 59, 999–1012. [Google Scholar] [CrossRef]
- Falconi, L.G.; Pérez, M.; Aguilar, W.G.; Conci, A. Transfer learning and fine tuning in breast mammogram abnormalities classification on CBIS-DDSM database. Adv. Sci. Technol. Eng. Syst. 2020, 5, 154–165. [Google Scholar] [CrossRef]
- Sejuti, Z.A.; Islam, M.S. A hybrid CNN–KNN approach for identification of COVID-19 with 5-fold cross-validation. Sens. Int. 2023, 4, 100229. [Google Scholar] [CrossRef] [PubMed]
- Lbachir, I.A.; Daoudi, I.; Tallal, S. Automatic computer-aided diagnosis system for mass detection and classification in mammography. Multimed. Tools Appl. 2021, 80, 9493–9525. [Google Scholar] [CrossRef]
- Ragab, D.A.; Sharkas, M.; Marshall, S.; Ren, J. Breast cancer detection using deep convolutional neural networks and support vector machines. PeerJ 2019, 7, e6201. [Google Scholar] [CrossRef] [PubMed]
- Baccouche, A.; Garcia-Zapirain, B.; Elmaghraby, A.S. An integrated framework for breast mass classification and diagnosis using stacked ensemble of residual neural networks. Sci. Rep. 2022, 12, 12259. [Google Scholar] [CrossRef] [PubMed]
- Baccouche, A.; Garcia-Zapirain, B.; Castillo Olea, C.; Elmaghraby, A.S. Connected-UNets: A deep learning architecture for breast mass segmentation. NPJ Breast Cancer 2021, 7, 151. [Google Scholar] [CrossRef] [PubMed]
- Tsochatzidis, L.; Koutla, P.; Costaridou, L.; Pratikakis, I. Integrating segmentation information into CNN for breast cancer diagnosis of mammographic masses. Comput. Methods Programs Biomed. 2021, 200, 105913. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Quan, H.; Wang, C.; Yang, G. Pyramid-based self-supervised learning for histopathological image classification. Comput. Biol. Med. 2024, 165, 107336. [Google Scholar] [CrossRef] [PubMed]
- Huang, P.W.; Ouyang, H.; Hsu, B.Y.; Chang, Y.R.; Lin, Y.C.; Chen, Y.A.; Hsieh, Y.H.; Fu, C.C.; Li, C.F.; Lin, C.H.; et al. Deep-learning based breast cancer detection for cross-staining histopathology images. Heliyon 2024, 9, e13171. [Google Scholar] [CrossRef] [PubMed]
- Khan, M.; Su’ud, M.M.; Alam, M.M.; Karimullah, S.; Shaik, F.; Subhan, F. Enhancing Breast Cancer Detection Through Optimized Thermal Image Analysis Using PRMS-Net Deep Learning Approach. J. Imaging Inform. Med. 2025. [Google Scholar] [CrossRef] [PubMed]

| IGWO–SOA Algorithm Pseudocode |
|---|
| Randomly initiate the grey wolf population within the designated search area. |
| Initialize the maximum number of iterations, population size, and other control parameters. |
| Initialize the self-organizing architecture parameters. |
| Initialize the best solution and set its fitness to infinity. |
| Continue iterating until the maximum number of cycles has been reached: |
| Evaluate the fitness of each grey wolf in the population. |
| Update the best solution if a better solution is found. |
| Apply the self-organizing architecture to adjust the positions of grey wolves: |
| For each grey wolf: |
| Update the position based on the grey wolf’s current position, the best solution, |
| and the self-organizing architecture parameters. |
| Apply boundary constraints to ensure the new position remains within the search space. |
| Apply the self-organizing architecture to adjust the population size: |
| For each grey wolf: |
| Determine the fitness ratio of every individual grey wolf. |
| Sort the grey wolves based on their fitness ratio. |
| Determine the new population size based on the self-organizing architecture parameters and the current iteration. |
| Remove the lowest-ranking grey wolves from the population until the desired population size is achieved. |
| Perform optional local search or other refinement techniques. |
| Update the convergence curve or other performance metrics. |
| Return the best solution found. |
| Layer Count | Layer | Type | Output Shape | Parameters |
|---|---|---|---|---|
| 1 | Conv2d-28 | Conv2D | 222 × 222 × 32 | 896 |
| 2 | Activation-36 | Activation | 24 × 24 × 256 | 0 |
| 3 | Max-pooling2d-25 | Max-Pooling | 112 × 112 × 64 | 0 |
| 4 | Conv2d-29 | Conv2D | 109 × 109 × 64 | 18,496 |
| 5 | Max-pooling2d-29 | Max-Pooling | 5 × 5 × 512 | 0 |
| 6 | Activation-40 | Activation | 54 × 54 × 64 | 0 |
| 7 | Conv2d-32 | Conv2D | 10 × 10 × 512 | 73,856 |
| 8 | Max-pooling2d-28 | Activation | 24 × 24 × 256 | 0 |
| 9 | Max-pooling2d-27 | Max-Pooling | 26 × 26 × 128 | 0 |
| 10 | Conv2d-31 | Conv2D | 24 × 24 × 256 | 295,168 |
| 11 | Activation-39 | Activation | 52 × 52 × 128 | 0 |
| 12 | Activation-38 | Max-Pooling | 12 × 12 × 256 | 0 |
| 13 | Conv2d-30 | Conv2D | 52 × 52 × 128 | 1,180,160 |
| 14 | Max-pooling2d-26 | Max-Pooling | 54 × 54 × 64 | 0 |
| 15 | Activation-37 | Activation | 109 × 109 × 64 | 0 |
| Flow of Hybrid IGWO–SOA for Tuning Parameters | |
|---|---|
| Start | |
| • Randomly begin the grey wolf population in the search area. | |
| • Initialize the maximum number of iterations and other control parameters. | |
| • Initialize the self-organizing architecture parameters. | |
| • Determine each population’s grey wolves’ level of fitness. | |
| • Set the best solution as the grey wolf with the highest fitness. | |
| • Continue until the maximum number of iterations has been completed: | |
| • Apply the self-organizing architecture to adjust the positions of grey wolves based on their fitness values and the current iteration. | |
| • Apply the self-organizing architecture to adjust the population size based on the current iteration. | |
| • Perform optional local search or other refinement techniques. | |
| • Update the convergence curve or other performance metrics. | |
| • Determine each population’s level of fitness for grey wolves. | |
| • Update the best solution if a better solution is found. | |
| • Return the best solution found. | |
| End | |
| Metrics | With Feature Selection | Without Feature Selection |
|---|---|---|
| Accuracy | 99.4% | 96.5% |
| Precision | 99.2% | 96.2% |
| Recall | 99.1% | 97% |
| F1-Score | 99.0% | 96.4% |
| Specificity | 99.1% | 96% |
| Fold Test | Accuracy | Precision | Recall | F1-Score | Specificity |
|---|---|---|---|---|---|
| 1st fold | 96.7 | 97.1 | 98 | 95.9 | 97.1 |
| 2nd fold | 95.6 | 95.5 | 95.1 | 96.9 | 95.0 |
| 3rd fold | 97.5 | 96.5 | 94 | 97.0 | 95.4 |
| 4th fold | 95.5 | 95.5 | 96.2 | 97.2 | 96.2 |
| 5th fold | 97.0 | 97.6 | 95.5 | 96.5 | 97.4 |
| Average | 96.46 | 96.44 | 95.76 | 96.7 | 96.22 |
| Fold Test | Accuracy | Precision | Recall | F-Score | Specificity |
|---|---|---|---|---|---|
| 1st fold | 99.7 | 99.1 | 99 | 98.9 | 99.1 |
| 2nd fold | 99.6 | 99.5 | 99.1 | 98.9 | 99 |
| 3rd fold | 99.5 | 99.5 | 99 | 99 | 99 |
| 4th fold | 99.5 | 99.5 | 99.2 | 99 | 99.2 |
| 5th fold | 99 | 98.6 | 99.5 | 99.2 | 99.4 |
| Average | 99.46 | 99.24 | 99.16 | 99 | 99.14 |
| Technique | Accuracy (%) | Precision (%) | Recall (%) | F1-Score (%) | Specificity (%) |
|---|---|---|---|---|---|
| Proposed Technique | 99.4% | 99.2% | 99.1% | 99.0% | 99.1% |
| PTr (Pyramid Transformer + SAM) [37] | 99.3% | 99.1% | 98.9% | 98.8% | 99.0% |
| CBAM-EfficientNetV2 [38] | 99.1% | 98.6% | 98.4% | 98.3% | 98.7% |
| PRMS-Net [39] | 99.2% | 99.0% | 98.8% | 98.9% | 98.7% |
| SVM [32] | 98.4% | 97.5% | 98.0% | 97.5% | 96.5% |
| DCNN [33] | 95.4% | 94.2% | 94.3% | 95.0% | 95.2% |
| ResNet [34] | 96.5% | 96.4% | 96.2% | 95.4% | 95.0% |
| Attention Unet | |||||
| +ResUNet [35] | 96.8% | 95.4% | 92.5% | 93.5% | 94.5% |
| CNN [33] | 97.5% | 96.3% | 96.0% | 96.8% | 97.0% |
| Metrics | Results |
|---|---|
| FDR | 0.54 |
| FNR | 0.001 |
| FPR | 0.002 |
| MCC | 0.987 |
| NPV | 0.997 |
| Optimization Technique | Accuracy (%) | Precision (%) | Recall (%) | F1-Score (%) | Specificity (%) |
|---|---|---|---|---|---|
| IGWO | 97.8% | 97.5% | 97.3% | 97.4% | 97.0% |
| SOA | 97.1% | 96.8% | 96.5% | 96.6% | 96.2% |
| IGWO–SOA (Proposed Method) | 99.4% | 99.2% | 99.1% | 99.0% | 99.1% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deka, A.; Misra, D.D.; Das, A.; Saikia, M.J. Breast Cancer Classification via a High-Precision Hybrid IGWO–SOA Optimized Deep Learning Framework. AI 2025, 6, 167. https://doi.org/10.3390/ai6080167
Deka A, Misra DD, Das A, Saikia MJ. Breast Cancer Classification via a High-Precision Hybrid IGWO–SOA Optimized Deep Learning Framework. AI. 2025; 6(8):167. https://doi.org/10.3390/ai6080167
Chicago/Turabian StyleDeka, Aniruddha, Debashis Dev Misra, Anindita Das, and Manob Jyoti Saikia. 2025. "Breast Cancer Classification via a High-Precision Hybrid IGWO–SOA Optimized Deep Learning Framework" AI 6, no. 8: 167. https://doi.org/10.3390/ai6080167
APA StyleDeka, A., Misra, D. D., Das, A., & Saikia, M. J. (2025). Breast Cancer Classification via a High-Precision Hybrid IGWO–SOA Optimized Deep Learning Framework. AI, 6(8), 167. https://doi.org/10.3390/ai6080167








