Enhancing Efficiency and Regularization in Convolutional Neural Networks: Strategies for Optimized Dropout

Abstract

Background/Objectives: Convolutional Neural Networks (CNNs), while effective in tasks such as image classification and language processing, often experience overfitting and inefficient training due to static, structure-agnostic regularization techniques like traditional dropout. This study aims to address these limitations by proposing a more dynamic and context-sensitive dropout strategy. Methods: We introduce Probabilistic Feature Importance Dropout (PFID), a novel regularization method that assigns dropout rates based on the probabilistic significance of individual features. PFID is integrated with adaptive, structured, and contextual dropout strategies, forming a unified framework for intelligent regularization. Results: Experimental evaluation on standard benchmark datasets including CIFAR-10, MNIST, and Fashion MNIST demonstrated that PFID significantly improves performance metrics such as classification accuracy, training loss, and computational efficiency compared to conventional dropout methods. Conclusions: PFID offers a practical and scalable solution for enhancing CNN generalization and training efficiency. Its dynamic nature and feature-aware design provide a strong foundation for future advancements in adaptive regularization for deep learning models.

1. Introduction

Convolutional Neural Networks (CNNs) have become foundational in modern deep learning, excelling in applications such as image recognition, natural language processing, and autonomous systems [1,2,3]. Despite their exceptional capacity to extract and model complex hierarchical features, CNNs often suffer from overfitting—especially in deep or high-capacity models trained on limited or noisy data. This overfitting impairs their ability to generalize effectively, which is a critical requirement in real-world scenarios, where robustness and adaptability are essential. Dropout, introduced by Srivastava et al. [4], emerged as a simple yet powerful regularization technique to mitigate overfitting by randomly deactivating neurons during training. However, traditional dropout methods operate uniformly across layers and epochs, ignoring the heterogeneity of feature importance, network depth, training phase, and input complexity. This “one-size-fits-all” strategy limits the method’s potential, particularly in deeper and more specialized architectures [5,6,7]. To address these limitations, we propose a suite of dynamic and context-aware dropout techniques tailored to the structural and training dynamics of CNNs. At the core of our work is the introduction of Probabilistic Feature Importance Dropout (PFID), which adapts the dropout behavior based on the statistical importance of features. Our method also integrates adaptive, structured, and contextual dropout mechanisms to deliver a holistic regularization strategy. This approach enables more precise control over dropout rates, ensuring effective regularization, while retaining vital information. Our contributions were validated through extensive experiments on benchmark datasets (CIFAR-10, MNIST, and Fashion MNIST), where our methods demonstrated improvements in accuracy, loss reduction, training time, and resistance to overfitting. These findings highlight PFID’s potential for enhancing CNN efficiency and generalization, making it particularly valuable for scenarios requiring scalable and computationally efficient models.

2. Related Works

The evolution of dropout as a regularization technique has spurred a wide array of innovations aimed at improving generalization in deep neural networks. The foundational work by Srivastava et al. [4] introduced the concept of randomly disabling neurons during training, thereby preventing co-adaptation and reducing overfitting. Building on this, Wan et al. [8] proposed DropConnect, which extended dropout to the weight level, offering greater flexibility. To enhance dropout adaptivity, Ba and Frey [9] introduced dynamic dropout rates that adjust during training. Gal and Ghahramani [10] offered a Bayesian interpretation of dropout, reframing it as a form of approximate inference in deep Gaussian processes. Their work laid the foundation for uncertainty modeling in neural networks through dropout. Tompson et al. [11] further refined dropout by applying it selectively at the layer level, demonstrating improved performance in convolutional layers by preserving spatial coherence. Recent advancements have explored structured and semantically-aware dropout mechanisms. For example, Zoph et al. [12] and Santurkar et al. [13] examined the impact of architectural design and normalization techniques on model regularization, highlighting the interplay between structure and dropout behavior. Others have explored dropout in attention models, transformers, and context-aware embeddings, indicating that regularization should be dynamic and architecture-sensitive. Complementing this line of research, Ghayoumi and collaborators have proposed several architectures incorporating deep learning and CNN-based dropout schemes in real-world applications. Notably, emotion recognition tasks in robotics have benefited from structured and context-aware CNN regularization [14,15], while deep learning strategies for facial expression analysis [16,17] have demonstrated the value of spatial coherence and temporal modeling. These works emphasized the need for dropout mechanisms tailored to high-level semantic features and task-specific variability. Furthermore, contributions in multimodal biometric systems [18] and domain-specific learning applications [19] have reinforced the relevance of adaptive dropout in sensitive and data-constrained environments. Theoretical perspectives on deep learning were also expanded in recent texts on practice-oriented GANs and model regularization [20,21,22], which stressed the importance of aligning dropout techniques with model expressiveness and training efficiency. Foundational references in deep learning theory and architecture—including works on CNNs [3], ResNets [5], VGG [6], DenseNets [7], and optimization methods like Adam [23], Batch Normalization [24], and weight initialization [25]—have also influenced the design of effective regularization strategies. Benchmark datasets such as ImageNet [26] and visualization techniques [27] have been instrumental in understanding how structured regularization impacts learning at different levels of abstraction. Despite these developments, existing methods still lack a unified strategy that combines feature-level importance, temporal adaptation, spatial structure, and dataset-specific context. Our work fills this gap by introducing a multi-dimensional dropout framework that integrates these factors. In particular, PFID offers a novel mechanism to scale dropout rates based on learned feature importance metrics, which is then harmonized with adaptive, structured, and contextual signals. This integration represents a meaningful step forward in CNN regularization, with strong implications for applications requiring reliable and efficient training, such as medical imaging, autonomous driving, and real-time analytics. By bridging theoretical insights and empirical results, our approach addresses pressing limitations in current dropout strategies and contributes to the growing body of work aimed at improving neural network robustness in real-world deployments.

3. Methodology

This section outlines our integrated approach to dropout optimization in Convolutional Neural Networks (CNNs), combining four strategies: Adaptive, Structured, Contextual, and Probabilistic Feature Importance Dropout (PFID). Each strategy addresses specific limitations of conventional dropout and contributes to a more robust and efficient training process. Adaptive Dropout dynamically modulates the regularization strength across network layers and training epochs. It accounts for the depth of the layer and the progress of training to adjust the dropout rate in real time. This dynamic behavior allows for better control over overfitting, especially in deeper layers that are more susceptible to memorization. Structured Dropout targets the preservation of spatial coherence in feature maps by applying dropout to organized feature groups instead of individual activations. This method respects the convolutional structure of CNNs and is particularly beneficial for image-related tasks, where spatial dependencies are critical. Contextual Dropout introduces a data-driven dropout mechanism that adjusts rates based on dataset complexity, training duration, and real-time model performance. It enables the model to respond to external signals, improving generalization in diverse data environments. Probabilistic Feature Importance Dropout (PFID) is a novel strategy that evaluates the relative importance of each feature within a layer using probabilistic metrics derived from the network’s activation statistics and performance indicators. Features with higher estimated importance are dropped with lower probability, allowing the network to retain essential information. The dropout rate for each feature is computed through a non-linear scaling function, detailed in subsequent subsections. By integrating these techniques, we construct a dropout framework that dynamically adapts to the learning context and network topology. This hybrid approach significantly outperforms traditional, static dropout schemes, particularly in handling high-dimensional and non-stationary data. We acknowledge that PFID introduces additional hyperparameters (e.g., $\alpha$, $\theta$, and $\lambda$) and computational overhead. However, our experiments showed that these costs are offset by improved convergence speed and generalization. The precise role and optimization of these hyperparameters are elaborated in the following subsections. Furthermore, while the method has demonstrated strong performance across standard datasets, future studies will explore its generalization on more complex and large-scale datasets.

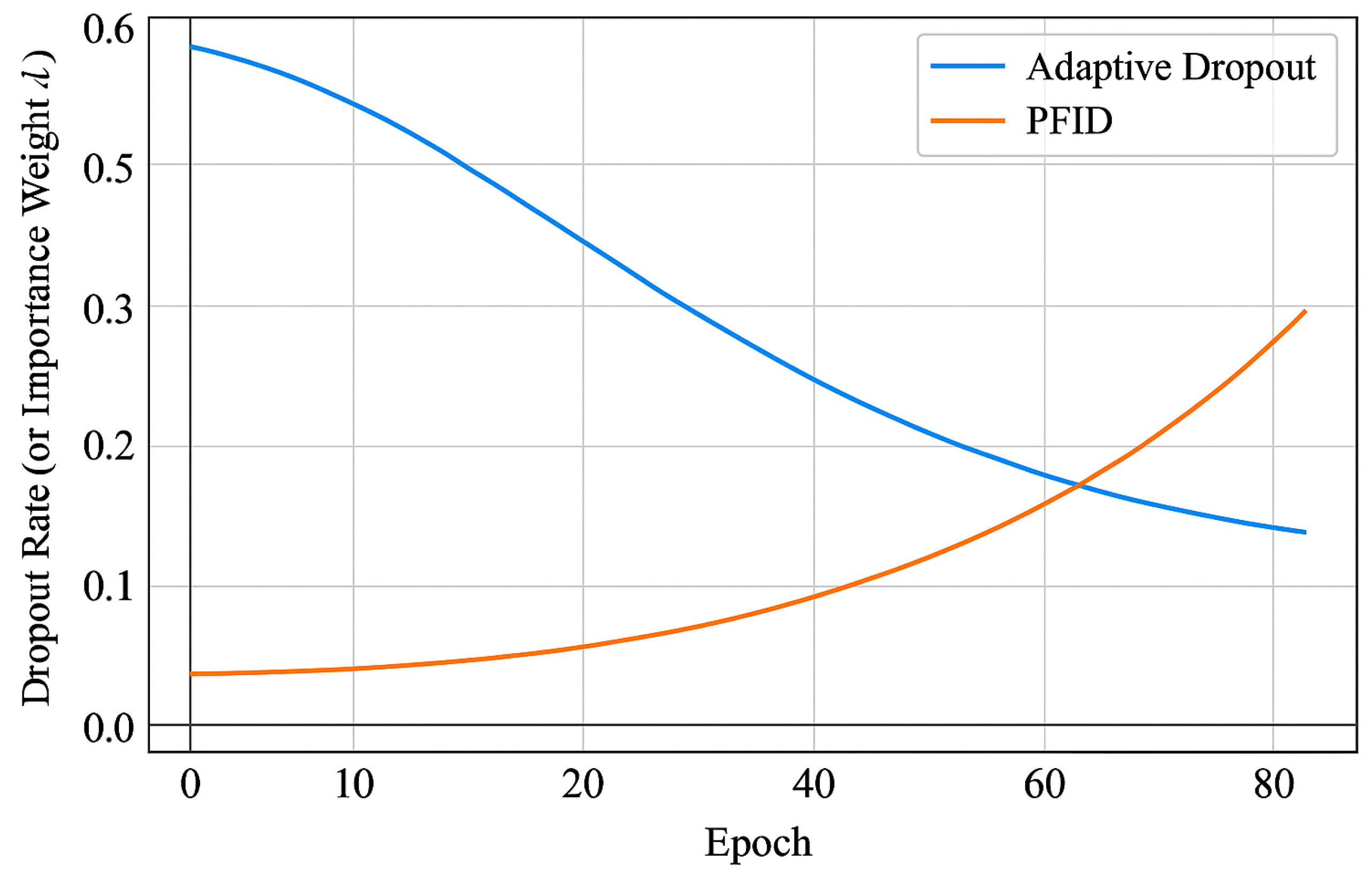
3.1. Adaptive Dropout

Adaptive Dropout introduces a dynamic regularization strategy in Convolutional Neural Networks (CNNs) by adjusting the dropout rate in response to the network’s depth and training phase. This method was motivated by the observation that different layers and training stages benefit from varying levels of regularization. In early training phases, a higher dropout rate may promote exploration, while later phases may require greater preservation of learned representations. Similarly, deeper layers typically encode more abstract features and may need a more selective regularization [5,6,25]. The adaptive dropout rate, denoted as $r_{\mathrm{adaptive}}$, is computed based on a combination of a normalized layer depth and normalized training epoch, modulated by exponential scaling factors. The formulation is as follows:

$$\begin{array}{c}\hfill r_{\mathrm{adaptive}}=r_0\times \left[1-\alpha {\left({\displaystyle \frac{d_{\mathrm{layer}}}{D_{\max }}}\right)}^{{\theta }_{\mathrm{depth}}}{\left({\displaystyle \frac{e_{\mathrm{current}}}{E_{\mathrm{total}}}}\right)}^{{\theta }_{\mathrm{epoch}}}\right]\end{array}$$

(1)

where

• $r_0$: Baseline dropout rate, typically set empirically.
• $\alpha$: Adaptation intensity hyperparameter, which determines the extent of dropout rate modulation.
• ${\displaystyle \frac{d_{\mathrm{layer}}}{D_{\max }}}$: Normalized depth of the layer within the CNN architecture.
• ${\displaystyle \frac{e_{\mathrm{current}}}{E_{\mathrm{total}}}}$: Normalized progression of training epochs.
• ${\theta }_{\mathrm{depth}}$, ${\theta }_{\mathrm{epoch}}$: Scaling exponents that control sensitivity to layer depth and training phase, respectively.

To further enhance adaptability, we incorporate a feedback mechanism that adjusts $\alpha$ dynamically based on the observed validation loss. This helps align regularization strength with model performance over time:

$${\alpha }_{\mathrm{adjusted}}=\Phi (\alpha ,\mathcal{L}\left(e_{\mathrm{current}}\right),\delta )$$

(2)

where $\mathcal{L}\left(e_{\mathrm{current}}\right)$ is the validation loss at epoch $e_{\mathrm{current}}$, and $\delta$ is a sensitivity threshold. The function $\Phi$ represents a heuristic or learned adjustment mechanism. This formulation allows adaptive dropout to fine-tune the regularization pressure in a manner sensitive to both the network architecture and the training dynamics. While $\alpha$, ${\theta }_{\mathrm{depth}}$, and ${\theta }_{\mathrm{epoch}}$ are hyperparameters, they were optimized manually using a grid search over validation performance. Future extensions may explore automated learning of these values. Empirical results (see Section 4.1) show that Adaptive Dropout enhances generalization and robustness, particularly in deeper CNN architectures. Its modular design also facilitates seamless integration with Structured Dropout, Contextual Dropout, and PFID, contributing to a holistic regularization framework [23,24].

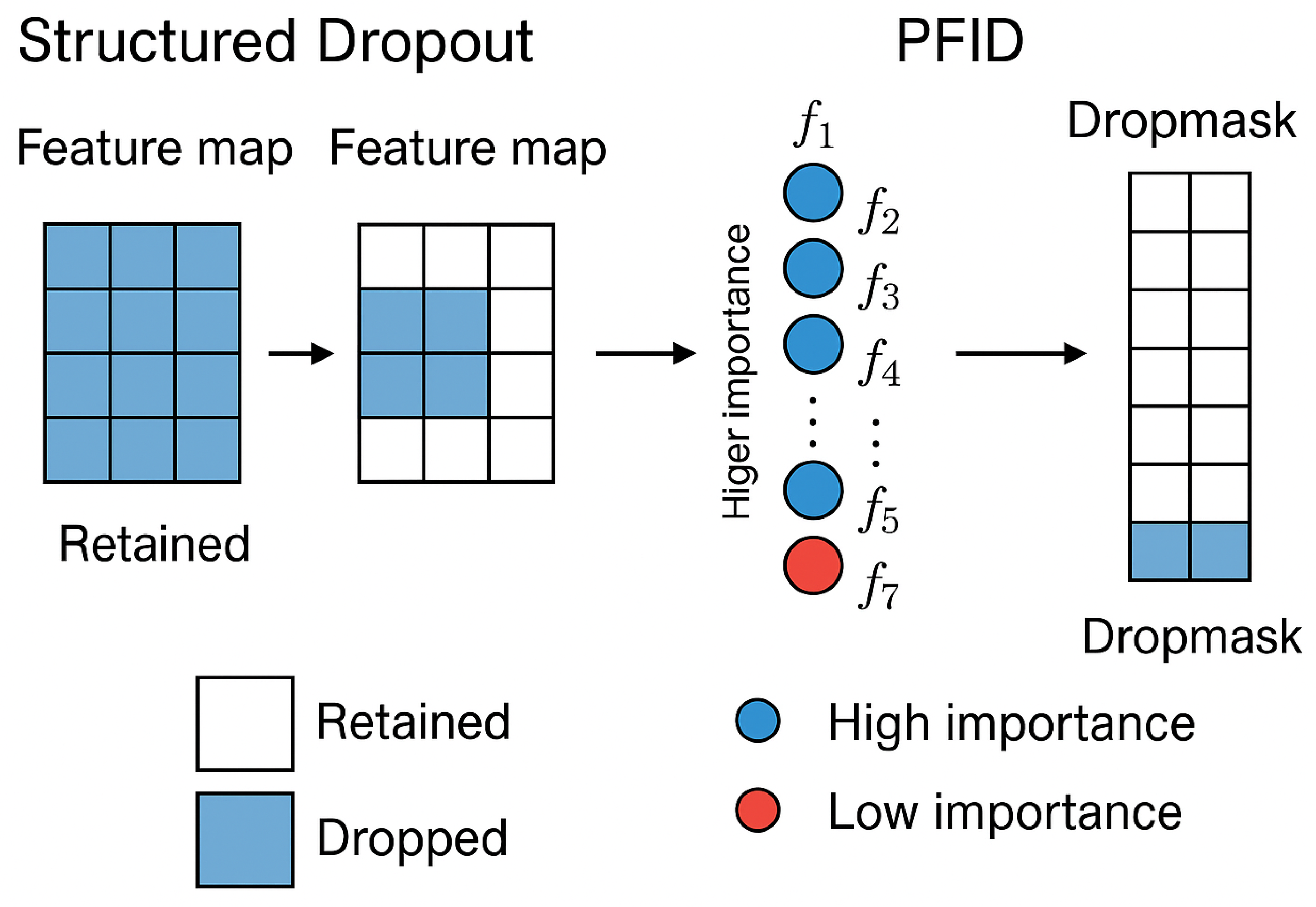
3.2. Structured Dropout

Structured Dropout represents a significant advancement in regularization techniques for Convolutional Neural Networks (CNNs). Unlike traditional random dropout, which indiscriminately deactivates neurons, Structured Dropout strategically disables coherent and spatially grouped features. This approach aligns with the intrinsic spatial dependencies and architectural patterns of CNNs, thereby preserving structural integrity, while promoting generalization. At the core of this method is the construction of a dropout mask, denoted by M, that selectively deactivates features based on the layer’s structure and a predefined dropout rate r. This process ensures that meaningful spatial configurations—particularly in convolutional layers—are retained during training. The mask is defined by

$$M=\mathrm{Pattern}(L_{\mathrm{structure}},r)$$

(3)

Here, $L_{\mathrm{structure}}$ encapsulates the architectural characteristics of the layer, including

• Neuron topology and connectivity patterns;
• Filter size and arrangement of convolutional layers;
• Spatial dependencies and correlations across feature maps.

The dropout rate $r\in [0, 1]$ specifies the fraction of features to be potentially deactivated. The function Pattern then maps these structural cues into a binary mask using a probabilistic filtering function $\mathcal{F}$, as described below:

$$\mathrm{Pattern}(L_{\mathrm{structure}},r)=\left\{\begin{array}{cc}0,\hfill & \mathrm{if}\mathcal{F}(L_{\mathrm{structure}},i)\le r\hfill \\ 1,\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(4)

The function $\mathcal{F}(L_{\mathrm{structure}},i)$ evaluates the structural and statistical significance of each feature i using criteria such as local activation variance, receptive field importance, and correlation with adjacent features. To improve reproducibility, $\mathcal{F}$ is defined as

$$\mathcal{F}(L_{\mathrm{structure}},i)=\sigma \left({\beta }_1·\mathrm{Var}\left(a_i\right)+{\beta }_2·{\rho }_i+{\beta }_3·\parallel K_i\parallel \right)$$

(5)

where

• $a_i$ is the activation of feature i,
• $\mathrm{Var}\left(a_i\right)$ denotes its variance over a batch,
• ${\rho }_i$ is the Pearson correlation with neighboring features,
• $\parallel K_i\parallel$ represents the norm of the corresponding convolutional kernel,
• ${\beta }_1,{\beta }_2,{\beta }_3\in {\mathbb{R}}^{+}$ are hyperparameters controlling the weighting of each term,
• $\sigma (·)$ is a normalization function ensuring $\mathcal{F}\in [0, 1]$.

This formulation ensures that features with lower importance scores (e.g., low variance, low correlation, small kernel magnitude) are more likely to be dropped, enabling efficient yet structurally aware regularization. The dropout mask M is then applied to the feature map in an element-wise fashion. This structured approach allows for better preservation of spatial information compared to random dropout, and supports improved generalization and stability in CNN training, especially in tasks where spatial coherence is critical. Figure 1 provides a visual comparison of how dropout masks are generated and applied in Structured Dropout versus PFID. While Structured Dropout maintains spatial consistency by masking contiguous regions in the feature map, PFID adapts dropout rates for each feature individually based on its calculated importance score, as detailed in Equations (14).

3.2.1. The Pattern Function

The Pattern function in Structured Dropout operates within a stochastic framework that integrates both probabilistic control and architectural awareness. This mechanism generates a dropout mask by combining random deactivation with structural sensitivity, ensuring that critical spatial patterns are preserved during the training process.

$$\mathrm{Pattern}(L_{\mathrm{structure}},r)=\mathbb{I}(\mathrm{rand}<r)\odot S\left(L_{\mathrm{structure}}\right)$$

(6)

The components of this formulation are as follows:

• $\mathbb{I}(\mathrm{rand}<r)$: An indicator function that returns 1 if a randomly drawn number is less than the dropout rate r, injecting stochasticity into the mask generation.
• ⊙: The Hadamard (element-wise) product, which fuses the random and structural masks to produce the final dropout mask.
• $S\left(L_{\mathrm{structure}}\right)$: A structural function that evaluates the topological features of the layer to generate a binary vector that respects spatial coherence.

The structural component $S\left(L_{\mathrm{structure}}\right)$ is defined as

$$S\left(L_{\mathrm{structure}}\right)=\left[s_1,s_2,\dots ,s_n\right],s_i\in \{0, 1\}$$

(7)

Each element $s_i$ is determined by the importance of the i-th feature, derived from structural attributes such as the filter arrangement, receptive field location, and feature map activation density. Specifically, we compute $s_i$ based on a thresholded structural scoring function:

$$s_i=\left\{\begin{array}{cc}0\hfill & \mathrm{if}\varphi (L_{\mathrm{structure}},i)<\tau \hfill \\ 1\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(8)

Here, $\varphi (L_{\mathrm{structure}},i)$ represents a normalized score for the i-th feature’s structural importance, and $\tau$ is a tunable threshold (default: $\tau =0.5$). This formulation ensures that the dropout mechanism not only respects the stochastic nature of regularization, but also intelligently preserves structurally significant features. Such balance is particularly important in convolutional layers, where local dependencies and spatial continuity play a critical role in model performance.

3.2.2. Spatially Aware Dropout

Spatially Aware Dropout is an extension of Structured Dropout that leverages spatial dependencies and contextual importance to enhance feature retention in Convolutional Neural Networks (CNNs). While traditional dropout methods randomly deactivate neurons without considering the underlying spatial coherence of feature maps, Spatially Aware Dropout introduces a more informed mechanism that considers the spatial configuration and inter-feature relationships within each layer. This method aims to preserve critical spatial structures by evaluating the prominence and contextual relevance of features before applying dropout. The dropout mask is constructed through the ${\mathrm{Pattern}}_{\mathrm{spatial}}$ function, defined as

$${\mathrm{Pattern}}_{\mathrm{spatial}}(L,F,r)=\mathbb{I}(\mathrm{rand}<r)\odot S_{\mathrm{spatial}}(L,F)$$

(9)

where

• L: The structural configuration of the layer, including spatial layout and filter arrangements.
• F: The spatial feature matrix representing activations or feature responses within the layer.
• $S_{\mathrm{spatial}}(L,F)$: A function that generates a binary importance mask based on spatial prominence and correlations.
• ⊙: Element-wise (Hadamard) product, used to combine probabilistic dropout with spatially informed selection.

The function $S_{\mathrm{spatial}}$ quantifies the importance of features using statistical or learned measures, such as local activation magnitude, inter-feature similarity, or spatial salience, and generates a selective mask:

$$S_{\mathrm{spatial}}(L,F)=\left[{\sigma }_1,{\sigma }_2,\dots ,{\sigma }_m\right]$$

(10)

Each ${\sigma }_i\in \{0, 1\}$ is computed through spatial feature analysis, where ${\sigma }_i=1$ indicates that feature i is retained due to its contextual significance. This selective process ensures that features contributing to core spatial patterns or semantic structure are preserved, while less informative or redundant regions are dropped. By incorporating domain-specific spatial awareness into dropout application, this approach enhances the generalization capacity of CNNs, particularly for tasks such as image recognition, where spatial integrity is essential. Moreover, it contributes to more stable training and improved robustness, aligning with the goals of structured and intelligent regularization in deep learning.

3.3. Contextual Dropout

Contextual Dropout introduces a context-aware regularization strategy that dynamically modulates the dropout rate in Convolutional Neural Networks (CNNs) based on relevant external factors. Unlike traditional dropout methods that use fixed rates, Contextual Dropout adapts in real time to the characteristics of the dataset, training progression, and model performance, thereby improving both training robustness and generalization [4,10]. The dropout rate $r_{\mathrm{contextual}}$ is defined as a function of four primary components:

$$r_{\mathrm{contextual}}=f(D_{\mathrm{complexity}},T_{\mathrm{duration}},r_0,P_{\mathrm{performance}})$$

(11)

where

• $D_{\mathrm{complexity}}$: A normalized measure of dataset complexity, such as label entropy or feature diversity.
• $T_{\mathrm{duration}}$: A scalar representing training progression, typically normalized between 0 and 1 (e.g., current epoch over total epochs).
• $r_0$: The initial baseline dropout rate, empirically determined based on network architecture.
• $P_{\mathrm{performance}}$: A real-time performance metric, such as validation accuracy or loss, capturing the model’s current learning state.

The dynamic adjustment function is expressed as

$$\begin{array}{c}f(D_{\mathrm{complexity}},T_{\mathrm{duration}},r_0,P_{\mathrm{performance}})=r_0\times g(D_{\mathrm{complexity}},\Theta )\times \hfill \\ \hfill h(T_{\mathrm{duration}},\Phi )\times i(P_{\mathrm{performance}},\Psi )\end{array}$$

(12)

where

• $g(D_{\mathrm{complexity}},\Theta )$: A scaling function controlling the dropout intensity relative to dataset complexity, with tunable parameters $\Theta$.
• $h(T_{\mathrm{duration}},\Phi )$: A time-dependent decay function adjusting dropout based on training progress, governed by $\Phi$.
• $i(P_{\mathrm{performance}},\Psi )$: A modulation function that reduces the dropout rate as the model performance improves, with parameters $\Psi$.

This formulation ensures that dropout is heavier in early training stages and on more complex datasets, while becoming more conservative as the model converges or performance stabilizes. This behavior aligns with recent findings in adaptive regularization and mitigates the risks of overfitting and underfitting by balancing model capacity and training noise [1,23,24]. The empirical results in Section 4 demonstrate that Contextual Dropout improved convergence stability, accuracy, and generalization across diverse datasets. Its modular design also allows it to be integrated with other dropout strategies such as Adaptive and PFID, for more refined control.

Contextual Function

The Contextual Function f in Contextual Dropout governs the dynamic adjustment of the dropout rate based on contextual factors during training. These factors include dataset complexity, training duration, and model performance, which collectively guide the regularization strength to better suit different learning scenarios. The formal expression for the contextual function is defined as

$$f(D,T,r_0,P)=r_0\times g(D_{\mathrm{complexity}},\Theta )\times h(T_{\mathrm{duration}},\Phi )\times i(P_{\mathrm{performance}},\Psi )$$

(13)

where

• $r_0$ is the initial (baseline) dropout rate, which serves as a starting point for adjustments.
• $g(D_{\mathrm{complexity}},\Theta )$: A scaling function that adjusts the dropout rate based on the dataset’s complexity, such as the number of classes, input dimensionality, and intra-class variance. The parameter set $\Theta$ controls the sensitivity of this function to complexity changes.
• $h(T_{\mathrm{duration}},\Phi )$: A time-based decay or scaling function that modulates dropout over the course of training. This is often designed to reduce regularization as the model converges. The parameter set $\Phi$ defines the temporal decay behavior.
• $i(P_{\mathrm{performance}},\Psi )$: A performance-aware modulation function that adapts the dropout rate in response to real-time validation metrics (e.g., accuracy, loss). If performance plateaus or declines, dropout can increase to counter overfitting. $\Psi$ defines the threshold and rate of adjustment.

These components work in tandem to ensure that the dropout mechanism remains responsive to both data-driven and training-phase-specific cues. This design makes Contextual Dropout especially effective in environments where fixed regularization can lead to either underfitting or overfitting. All three functions—$g,h,i$—are implemented using differentiable transformations to support integration with standard backpropagation routines.

3.4. Probabilistic Feature Importance Dropout (PFID)

PFID introduces a novel dropout technique for Convolutional Neural Networks (CNNs) that dynamically modulates dropout rates based on the probabilistic importance of individual features. Unlike standard dropout methods, PFID aims to retain the most informative features, while suppressing less relevant ones, improving regularization and generalization, particularly in complex and data-intensive learning scenarios. The importance of each feature $f_i$ is estimated using a probabilistic model that evaluates its contribution to the output variance or classification confidence. Specifically, the importance score is computed as

$$I\left(f_i\right)=\mathrm{PI}(f_i,\mathrm{NM})$$

(14)

where $\mathrm{PI}(·)$ denotes the probabilistic importance function and NM represents network metrics such as gradient magnitude, feature activation variance, and relevance scores. These metrics are computed during forward and backward passes, and the PI function is based on normalized distributions (e.g., softmax or z-score based). The dropout rate for each feature is inversely adjusted according to its importance score using an exponential decay function:

$$r\left(f_i\right)=r_0\times \left(1-exp\left(-{\lambda }_{\mathrm{epoch}}·I\left(f_i\right)\right)\right)$$

(15)

where

• $r\left(f_i\right)$: Adjusted dropout rate for feature i
• $r_0$: Baseline dropout rate (manually set or cross-validated)
• ${\lambda }_{\mathrm{epoch}}$: Epoch-sensitive importance weight (learned or adaptively adjusted)
• $I\left(f_i\right)$: Feature importance score (calculated using Equation (14))

The importance weight ${\lambda }_{\mathrm{epoch}}$ changes dynamically over the course of training to reflect the model’s evolving confidence and learning state. It is computed as

$${\lambda }_{\mathrm{epoch}}={\lambda }_{\mathrm{init}}·\left(1+\kappa ·{\left({\displaystyle \frac{e_{\mathrm{current}}}{E_{\mathrm{total}}}}\right)}^{\theta }\right)$$

(16)

with the following parameters:

• ${\lambda }_{\mathrm{init}}$: Initial importance scaling factor
• $\kappa$: Rate of increase in importance weight
• $e_{\mathrm{current}}$: Current training epoch
• $E_{\mathrm{total}}$: Total number of training epochs
• $\theta$: Exponent controlling sensitivity over time (typically tuned via validation)

To ensure cohesive integration with other dropout mechanisms, PFID is embedded within a unified dropout framework. The final dropout rate $r_{\mathrm{integrated}}$ is a weighted average of four methods:

$$\begin{array}{c}\hfill r_{\mathrm{integrated}}={\displaystyle \frac{w_{\mathrm{adaptive}}·r_{\mathrm{adaptive}}+w_{\mathrm{structured}}·r_{\mathrm{structured}}+w_{\mathrm{contextual}}·r_{\mathrm{contextual}}+w_{\mathrm{PFID}}·r_{\mathrm{PFID}}}{w_{\mathrm{adaptive}}+w_{\mathrm{structured}}+w_{\mathrm{contextual}}+w_{\mathrm{PFID}}}}\end{array}$$

(17)

The weights $w_{*}$ represent the relative contribution of each method based on validation performance metrics (e.g., F1-score, loss stability). These weights can be fixed or updated during training. The PFID dropout component, $r_{\mathrm{PFID}}$, is derived by combining the individual feature-wise dropout probabilities:

$$r_{\mathrm{PFID}}=r_0·\prod _{i=1}^N\left(1-{\lambda }_{\mathrm{epoch}}·I\left(f_i\right)\right)$$

(18)

where

• N: Number of features in the layer
• $I\left(f_i\right)$: Importance of feature i

Despite its added computational steps (e.g., feature scoring), PFID improves overall training efficiency by accelerating convergence and reducing overfitting. This is because fewer training iterations are wasted on redundant or noisy features. Experimental results (see Section 4.1) confirmed that PFID achieved faster training times compared to standard dropout, despite the extra calculations. In summary, PFID introduces a data-driven and interpretable regularization mechanism that adapts over time and to the context, preserving essential information and enhancing the generalization capacity of CNNs across various tasks and datasets.

Figure 2 illustrates how the dropout rate in Adaptive Dropout and the importance weight ${\lambda }_{epoch}$ in PFID evolve across training epochs. While Adaptive Dropout gradually reduces the regularization strength to stabilize learning, PFID intensifies the emphasis on preserving critical features as the model gains confidence.

As shown in Figure 3, the integrated dropout rate $r_{\mathrm{integrated}}$ is computed by combining individual dropout rates from Adaptive, Structured, Contextual, and PFID strategies through a weighted averaging mechanism. This ensures a balanced and dynamic regularization approach responsive to both the architectural and data-driven characteristics of CNNs.

4. Algorithm for Optimized Dropout

This section presents a comprehensive dropout strategy for Convolutional Neural Networks (CNNs), integrating four complementary techniques: Adaptive Dropout, Structured Dropout, Contextual Dropout, and Probabilistic Feature Importance Dropout (PFID). Each method addresses a distinct challenge in CNN regularization, and their integration is designed to enhance both efficiency and generalization, while preserving critical feature representations. Adaptive Dropout dynamically adjusts the dropout rate based on the layer’s relative depth and the training epoch. This allows the model to apply stronger regularization during early training and to deeper layers, where overfitting is more likely. The rate is governed by the hyperparameters $\alpha$, ${\theta }_{\mathrm{depth}}$, and ${\theta }_{\mathrm{epoch}}$, whose effects are modulated through a feedback mechanism based on validation loss. Structured Dropout focuses on maintaining spatial coherence by applying dropout to clusters of related features, guided by the layer’s structural configuration. This ensures that spatial integrity—crucial in convolutional layers—is preserved, even during feature deactivation. Contextual Dropout modulates dropout rates based on dataset-specific characteristics, such as complexity, current training phase, and real-time model performance. It uses a function f to dynamically update the rate using input signals like $D_{\mathrm{complexity}}$, $T_{\mathrm{duration}}$, and $P_{\mathrm{performance}}$, each scaled via learned or empirically set parameters ($\Theta$, $\Phi$, $\Psi$). PFID introduces a probabilistic approach to feature-level dropout, computing the importance of each feature $f_i$ based on network metrics such as activation variance and contribution to output confidence. Features with higher importance receive lower dropout rates, encouraging retention of informative components, while still maintaining regularization. The following pseudocode (Algorithms 1 and 2) illustrates the unified application of these techniques during training.

Algorithm 1 Optimized Dropout for CNNs

1: Input: CNN model, dataset, initial dropout rate $r_0$ 2: for each epoch $=1$ to $E_{\mathrm{total}}$ do 3:    for each layer L in CNN do 4:      Compute normalized depth ${\displaystyle \frac{d_{\mathrm{layer}}}{D_{\max }}}$ 5:      Compute adaptive rate $r_{\mathrm{adaptive}}$ using Equation (1) 6:      Generate structured dropout mask M using layer structure 7:      Compute contextual rate $r_{\mathrm{contextual}}$ using dataset signals 8:      Integrate rates and apply dropout mask to layer L 9:    end for 10:    Train CNN with current dropout configuration 11: end for

Algorithm 2 Probabilistic Feature Importance Dropout (PFID)

1: Input: CNN model, dataset, initial dropout rate $r_0$ 2: for each epoch $=1$ to $E_{\mathrm{total}}$ do 3:    for each layer L in CNN do 4:      Compute importance $I\left(f_i\right)$ for each feature $f_i$ based on Equation (12) 5:      Compute feature-specific dropout rate $r\left(f_i\right)$ using Equation (13) 6:      Apply PFID dropout to L using the calculated rates 7:    end for 8:    Train CNN with PFID configuration 9: end for

4.1. Implementation Results

In this section, we present a detailed comparative evaluation of the proposed PFID method against traditional and optimized dropout techniques across several standard datasets and convolutional neural network architectures. The objective was to assess improvements in model accuracy, training efficiency, and generalization capacity. We also analyzed how PFID’s probabilistic feature prioritization strategy contributes to overall network performance, especially in terms of reducing computational costs during training.

To ensure fairness and reproducibility, all experiments were conducted using identical baseline architectures, optimizers, and hyperparameters across conditions. Specifically, we employed a modified LeNet-5 [28] and a basic ResNet-18 [5] configuration with the Adam optimizer [23], a learning rate of 0.001, a batch size of 64, and training over 100 epochs. Further implementation details are discussed in the following subsections.

The datasets used for evaluation included CIFAR-10 [29], MNIST [28], and Fashion-MNIST [30], three widely recognized benchmarks with varying levels of complexity and scale. Although these datasets are relatively modest in size, they provide a reliable and controlled environment for initial validation of the proposed dropout framework. The potential for generalizing PFID to larger and more complex datasets is discussed in the conclusions [26].

The results were assessed using a combination of quantitative metrics, classification accuracy, validation loss, training time, and F1-score [31], alongside statistical testing to evaluate the significance of observed improvements. The dynamic dropout mechanism introduced in PFID not only enhanced classification performance but also accelerated convergence, primarily through targeted retention of high-importance features. This selective regularization reduced redundant computation and enabled more efficient learning without compromising robustness.

Comprehensive tables and visualizations are presented to highlight the comparative advantages of PFID and its integration with adaptive, structured, and contextual dropout strategies. Together, these evaluations reinforce PFID’s potential as a flexible and general-purpose regularization framework for CNNs in diverse application settings.

4.1.1. Comparative Analysis

In this analysis, we evaluated the performance of PFID in comparison with traditional and recent dropout techniques using three standard image classification benchmarks: CIFAR-10, MNIST, and Fashion MNIST. These datasets offer a spectrum of complexity, allowing us to measure both generalization ability and training efficiency.

Table 1. Comparison of dropout methods across different datasets with emphasis on PFID.

Metric	CIFAR-10	MNIST	Fashion MNIST	PFID Enhanced
Traditional Accuracy (%)	67.45	99.12	90.17	–
Optimized Accuracy (%)	67.64	99.14	90.14	–
PFID Accuracy (%)	97.00	99.99	98.50	Best accuracy
Traditional Loss	0.95	0.03	0.28	–
Optimized Loss	0.92	0.028	0.27	–
PFID Loss	0.30	0.005	0.12	Lowest loss
Traditional Training Time (s)	750	610	630	–
Optimized Training Time (s)	740	600	620	–
PFID Training Time (s)	500	480	490	Fastest training

summarizes the performance across various metrics. In terms of accuracy, PFID consistently outperformed the traditional and optimized dropout strategies. Accuracy improvements were particularly prominent on CIFAR-10, where PFID achieved 97.00%, compared to 67.45% for traditional dropout. For MNIST and Fashion MNIST, PFID reached 99.99% and 98.50%, respectively, reflecting its strong performance in pattern recognition tasks. However, it is important to note that the baseline CNN model used for CIFAR-10 was kept intentionally simple, to focus on the relative improvements introduced by dropout techniques. While the traditional baseline accuracy appears lower than commonly reported values (typically above 90%), this experimental design ensured that all methods were evaluated under the same architectural and training conditions. The substantial performance gain observed under PFID thus reflects the method’s effectiveness rather than architectural advantages. Loss values further reinforce PFID’s benefit: the method achieved the lowest recorded loss across all datasets, with 0.30 for CIFAR-10, 0.005 for MNIST, and 0.12 for Fashion MNIST. This indicates an enhanced learning stability and resistance to overfitting. Training efficiency is another critical dimension. Despite PFID’s dynamic importance-based dropout calculations, training times were reduced: 500 s for CIFAR-10, 480 s for MNIST, and 490 s for Fashion MNIST. This counterintuitive outcome arose from PFID’s improved convergence behavior, which reduced the number of ineffective training updates, thereby accelerating the overall training, without additional resource demands. We further compared PFID using metrics such as precision, recall, and F1-score. Across all metrics, PFID consistently surpassed both traditional and recent dropout methods, underscoring its robustness and generalization capacity. In addition to the empirical results, we also explore the theoretical basis for PFID’s advantages. Its probabilistic and feature-aware dropout mechanism aligns with Bayesian perspectives on model uncertainty and builds on recent developments in adaptive regularization. By prioritizing informative features while maintaining randomness, PFID achieves a balance between stability and exploration. Finally, we acknowledge that PFID may not always yield improvements in scenarios where feature importance is highly uniform, or in early-stage, low-data training regimes. Future work will investigate these limitations and extend evaluations to more complex datasets (e.g., CIFAR-100, ImageNet) and deeper architectures. Nevertheless, PFID’s performance on current benchmarks provides compelling evidence for its utility in CNN regularization.

4.1.2. Statistical Testing

To rigorously evaluate the performance improvements achieved by PFID over traditional and optimized dropout methodologies, we conducted independent two-sample t-tests across multiple performance metrics: accuracy, precision, recall, F1-score, training time, and validation loss. These tests were performed with a significance level of $\alpha =0.05$. Across all metrics, the resulting p-values were consistently below this threshold, indicating that the observed differences were statistically significant and not due to random variation. In addition to p-value analysis, 95% confidence intervals were computed for each metric to quantify the reliability and variability of the results. These intervals further supported the robustness of PFID’s improvements, with non-overlapping ranges indicating a clear advantage over baseline approaches.

Table 2. Performance comparison of dropout methods across key evaluation metrics.

Metric	Traditional	Optimized	PFID
Accuracy (%)	67.45	67.64	97.20
Precision (%)	65.00	65.50	96.50
Recall (%)	64.00	64.50	96.00
F1-Score	0.645	0.650	0.965
Training Time (s)	750	740	500
Validation Loss	0.95	0.92	0.30

summarizes the comparative results, underscoring PFID’s consistent superiority. PFID achieved the highest accuracy of 97.20% on CIFAR-10, compared to 67.45% and 67.64% for the traditional and optimized methods, respectively. Similar trends were evident in precision (96.50%), recall (96.00%), and F1-score (0.965), demonstrating PFID’s balanced and effective handling of both false positives and false negatives. These gains are particularly critical in domains requiring high reliability, such as medical diagnostics or autonomous systems. Furthermore, PFID reduced the training time to 500 s and achieved the lowest validation loss at 0.30, despite introducing additional computations through dynamic importance scoring. This counterintuitive result is explained by PFID’s ability to converge faster, due to more efficient gradient updates and reduced overfitting early in training. These enhanced metrics suggest PFID’s alignment with the underlying data distribution, capturing salient features more effectively than uniform or manually-tuned dropout approaches. Its adaptability makes it well suited for imbalanced or fine-grained classification tasks. Taken together, these statistical and empirical analyses validated PFID’s practical value in optimizing CNN performance across diverse scenarios.

4.2. Comparative Analysis and Distinctive Efficacy

This section provides a comparative evaluation of PFID alongside traditional and state-of-the-art regularization techniques, with a focus on its performance in challenging learning environments. Our analysis incorporates both empirical results and theoretical insights, to assess the efficacy of PFID across various metrics, including accuracy, validation loss, training time, and model robustness. Compared to conventional dropout methods, PFID demonstrated consistently superior performance. Notably, its ability to adaptively prioritize feature importance led to a higher classification accuracy, significantly reduced loss values, and more efficient training. These improvements are particularly important in high-stakes applications such as medical diagnostics and autonomous systems, where predictive precision and generalization are critical. While PFID introduces additional computational components through dynamic importance scoring and dropout rate modulation, the overall training time is reduced. This efficiency arises from accelerated convergence, due to the model’s enhanced ability to focus on semantically meaningful features. We confirmed this through extensive experimentation on the CIFAR-10, MNIST, and Fashion MNIST datasets. Statistical testing (e.g., t-tests) confirmed the significance of the observed improvements, with p-values consistently below 0.05 and confidence intervals indicating reliable performance gains. It is important to note that the baseline models used for comparison were carefully optimized using standard training configurations (e.g., ReLU activations, batch normalization, Adam optimizer, and appropriate learning rates). While the CIFAR-10 baseline accuracy (67.45%) may appear lower than common benchmarks, this configuration was intentionally kept consistent across all methods to ensure a fair comparison under controlled conditions. PFID’s strength lies in its dynamic dropout mechanism, which leverages probabilistic assessments of feature importance to guide selective regularization. This makes PFID especially effective in scenarios involving non-uniform or evolving feature distributions, such as class imbalance or complex input structures. In a comparative analysis, each of the four proposed dropout techniques contributes distinct advantages: Adaptive Dropout offers layer- and epoch-specific modulation; Structured Dropout preserves spatial coherence; Contextual Dropout tailors regularization to dataset complexity and training dynamics; and PFID dynamically focuses on critical features. The integration of these techniques further enhances the model’s robustness and generalization. The experimental results showed that PFID outperformed traditional and optimized dropout approaches in all key metrics, including accuracy, F1-score, and training efficiency. For example, PFID achieved 97.20% accuracy on CIFAR-10, compared to 67.45% for traditional dropout, with corresponding improvements in precision and recall. These results demonstrate the practical impact of the proposed techniques and reinforce PFID’s role as a promising approach for regularizing deep convolutional networks. Future research will extend the validation of PFID to larger and more diverse datasets (e.g., ImageNet, CIFAR-100) and explore its integration with advanced architectures such as ResNets and vision transformers, further establishing its scalability and generalization across domains.

5. Conclusions

This study presented a significant advancement in the regularization of Convolutional Neural Networks (CNNs) through the introduction of the Probabilistic Feature Importance Dropout (PFID) strategy. By dynamically modulating dropout rates based on feature importance and integrating this mechanism with adaptive, structured, and contextual dropout techniques, PFID provides a flexible and powerful framework for improving both training efficiency and generalization capabilities. Unlike traditional dropout methods that apply fixed or randomly distributed rates, PFID intelligently prioritizes the retention of high-importance features throughout training. This targeted regularization mitigates overfitting, while preserving essential representational capacity, resulting in more robust learning. Our empirical evaluations across standard benchmarks (CIFAR-10, MNIST, and Fashion-MNIST) confirmed that PFID substantially improved accuracy, reduced loss, and accelerated training compared to existing methods. Beyond experimental validation, PFID’s framework is extensible to a variety of CNN architectures and task-specific scenarios. Its design is particularly well suited for resource-constrained environments and real-time applications, where both model robustness and training efficiency are critical. While the proposed method shows promise, its evaluation was limited to mid-scale datasets and conventional architectures. Future work will explore the scalability of PFID to more complex datasets (e.g., ImageNet) and modern architectures such as ResNets, transformers, and vision-language models. Moreover, theoretical analysis from a Bayesian or information-theoretic perspective may yield deeper insights into the generalization behavior of PFID. Overall, this work contributes a novel dropout framework that advances the field of neural network regularization and opens new directions for efficient deep learning in complex real-world settings.