LineMVGNN: Anti-Money Laundering with Line-Graph-Assisted Multi-View Graph Neural Networks
Abstract
1. Introduction
- MVGNN is introduced as a lightweight yet effective model within the Dir-GNN framework due to its genericness. It supports edge features and considers both in- and out-neighbors in an attributed digraph, such as a transaction graph.
- LineMVGNN is proposed, extending MVGNN by utilizing the line graph view of the original graph for the effective propagation of transaction information (edge features in the original graph).
- Extensive experiments are conducted on the Ethereum phishing transaction network and the financial payment transaction (FPT) dataset.
2. Related Work
2.1. GNNs for Digraphs
2.1.1. Spectral Methods
2.1.2. Spatial Methods
2.2. Edge Feature Learning and Line Graphs
3. Proposed Method
3.1. Problem Statement
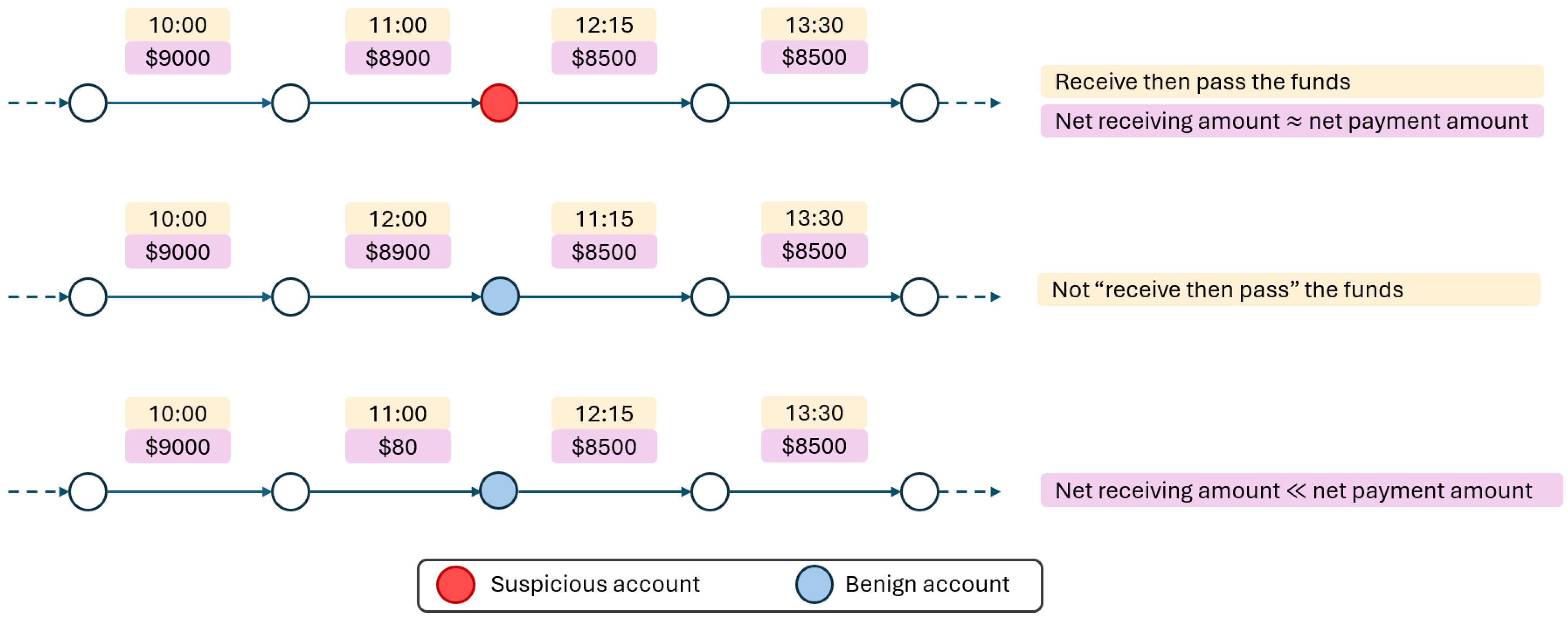
3.2. Two-Way Message Passing
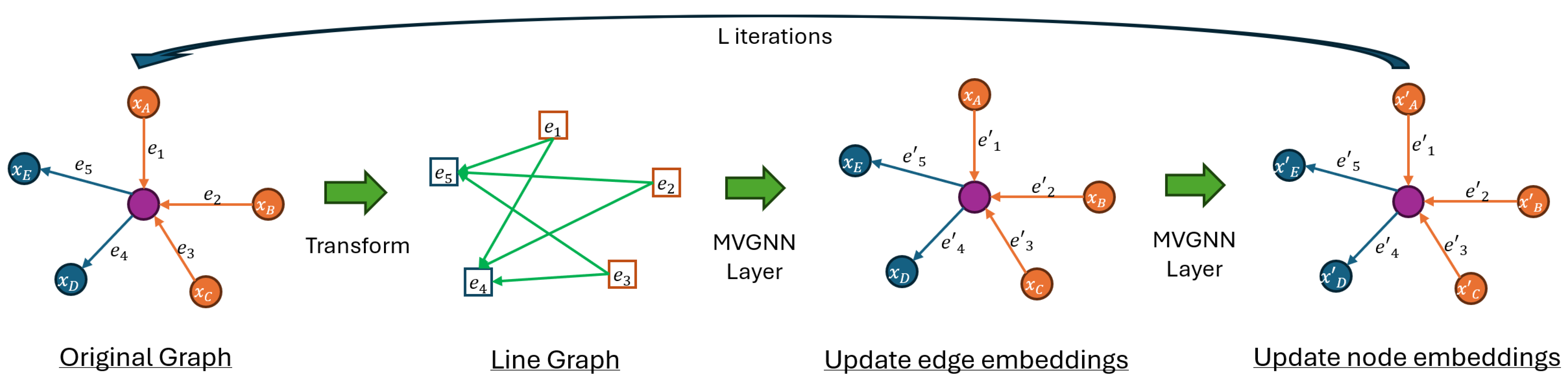
3.3. Line Graph View
| Algorithm 1 LineMVGNN |
| Input: Graph ; input node features ; input edge features ; model depth L Parameter: Output: Vector |
3.4. Computational Complexity
| Algorithm 2 Refined LineMVGNN (Without Explicit Line Graph Construction) |
| Input: Graph ; input node features ; input edge features ; model depth L Parameter: Output: Vector |
4. Experiments
4.1. Datasets
4.1.1. Ethereum (ETH) Datasets
4.1.2. Financial Payment Transaction (FPT) Dataset
4.2. Compared Methods and Evaluation Metrics
4.3. Results
4.4. Discussion
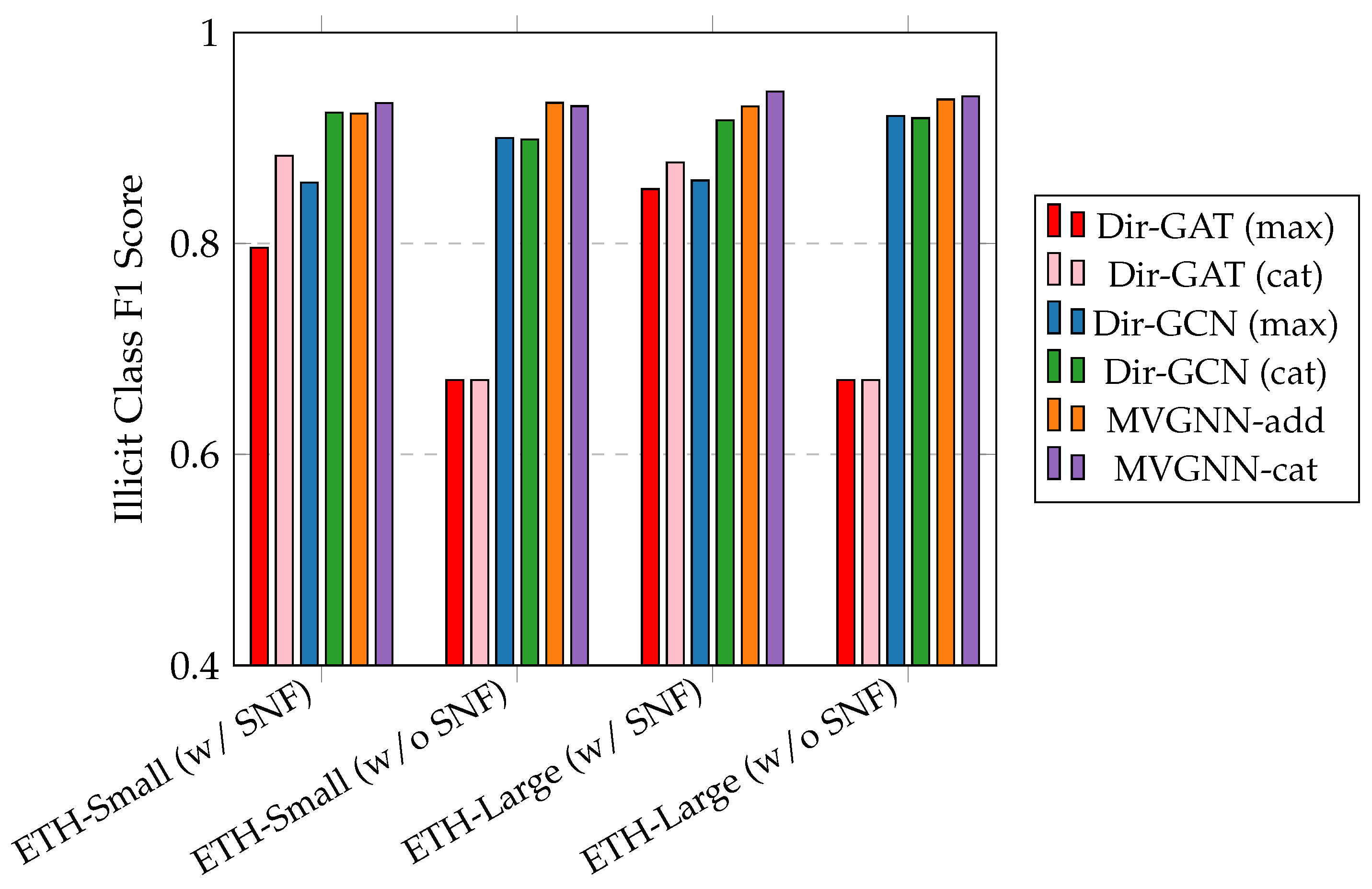
4.4.1. Effect of Different Views
4.4.2. Effect of SNF
4.4.3. Effect of Parameter Sharing
4.4.4. Effect of Learning Rate
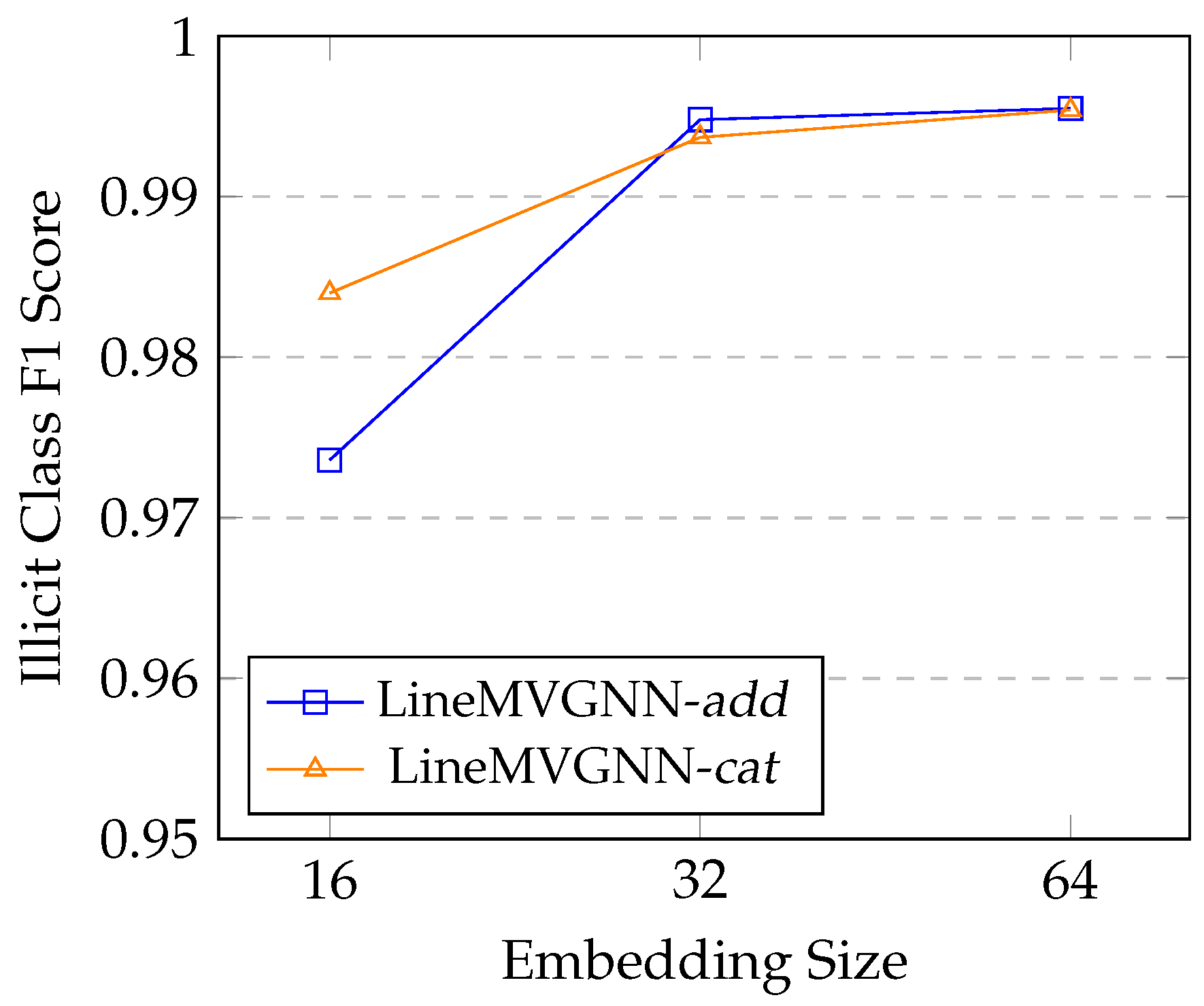
4.4.5. Effect of Embedding Size
4.4.6. Qualitative Discussion
5. Limitations and Future Work
5.1. Scalability
5.2. Adversarial Robustness
5.3. Regulatory Considerations
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| SOTA | State-of-the-Art |
| AML | Anti-Money Laundering |
| GNN | Graph Neural Network |
| ETH | Ethereum |
| FPT | Financial Payment Transaction |
| SNF | Structural Node Feature |
| MPNN | Message Passing Neural Network |
| Dir-GNN | Directed Graph Neural Network |
| MVGNN | Multi-View Graph Neural Network |
| LineMVGNN | Line-Graph-Assisted Multi-View Graph Neural Network |
| GCN | Graph Convolutional Network |
| GraphSAGE | Graph SAmple and aggreGatE |
| GIN | Graph Isomorphism Network |
| PNA | Principal Neighborhood Aggregation |
| EGAT | Graph Attention Network with Edge Features |
| DiGCN | Digraph Inception Convolutional Networks |
| Dir-GCN | Directed Graph Convolutional Network |
| Dir-GAT | Directed Graph Attention Network |
| MagNet | Digraph GNN Based on the Magnetic Laplacian |
| SigMaNet | Digraph GNN Based on the Sign-Magnetic Laplacian |
| FaberNet | Spectral Digraph GNN Using Faber Polynomials |
| OOM | Out of Memory |
| TWMP | Two-Way Message Passing |
| LGV | Line Graph View |
| eq | equation |
| w/ | with |
| w/o | without |
Appendix A. FPT Dataset
| Set | Day | Number of Nodes | Number of Edges |
|---|---|---|---|
| Train | 1 | 1,116,969 | 1,160,635 |
| 2 | 1,013,391 | 1,039,540 | |
| 3 | 1,259,733 | 1,294,309 | |
| 4 | 1,175,766 | 1,208,983 | |
| 5 | 1,165,737 | 1,217,110 | |
| 6 | 1,101,062 | 1,141,048 | |
| 7 | 1,137,598 | 1,185,835 | |
| 8 | 911,029 | 955,756 | |
| 9 | 924,847 | 976,963 | |
| 10 | 1,117,958 | 1,167,333 | |
| 11 | 997,538 | 1,037,538 | |
| 12 | 1,036,556 | 1,094,068 | |
| 13 | 970,965 | 1,008,168 | |
| 14 | 976,630 | 1,012,067 | |
| 15 | 888,321 | 920,889 | |
| 16 | 875,318 | 925,757 | |
| 17 | 1,029,538 | 1,070,001 | |
| 18 | 975,762 | 1,012,953 | |
| 19 | 1,024,562 | 1,077,209 | |
| Validation | 20 | 1,024,570 | 1,061,908 |
| 21 | 982,044 | 1,025,592 | |
| 22 | 843,878 | 879,405 | |
| 23 | 848,317 | 902,103 | |
| 24 | 1,044,676 | 1,094,133 | |
| 25 | 1,057,020 | 1,097,454 | |
| Test | 26 | 1,117,969 | 1,176,023 |
| 27 | 1,173,160 | 1,221,627 | |
| 28 | 1,265,930 | 1,314,902 | |
| 29 | 1,022,037 | 1,064,851 | |
| 30 | 1,001,363 | 1,060,849 | |
| 31 | 1,423,624 | 1,474,741 |
- Randomly select a pattern from path, cycle, clique, multipartite graph.
- Generate the pattern with n nodes (and e edges).
- Randomly select e rows of transaction data from the FPT dataset.
- Assign each row of transaction attribute values to each edge and the corresponding end nodes. (To simulate a flow of money in paths and cycles, the selected rows of transaction data are sorted and assigned, such that for each node the transaction timestamp of incoming edges is earlier than that of the outgoing edges except one edge in each cycle pattern. Similarly, in multipartite graphs, the selected transaction data are sorted and assigned such that transaction timestamps in all edges in the first layer are earlier than those in the second layer. Also, in each path and cycle, transaction amounts of edges within a given anomaly are set by randomly choosing from one out of e rows of selected transaction data).
- Insert the anomaly into the transaction graph.
- Repeat the steps above until a desired number of synthetic nodes has been reached.

Appendix B. Compared Methods
- GCN [25] leverages spectral graph convolutions to capture neighborhood information and perform various tasks, such as node classification. Since it does not naturally support multi-dimensional edge features, we concatenate in-node features with in-edge features during message passing.
- GraphSAGE [26] utilizes neighborhood sampling and aggregation for inductive learning on large graphs. We choose the pooling aggregator and full neighbor sampling as the baseline model setting. Since it does not naturally support multi-dimensional edge features, we concatenate in-node features with in-edge features during message passing.
- MPNN [14] is a framework for processing graph structured data. It enables the exchange of messages between nodes iteratively, allowing for information aggregation and updates. Specifically, it proposes the message function to be a matrix multiplication between the source node embeddings and a matrix, which is mapped by the edge feature vectors with a neural network.
- GIN [27] is designed to achieve maximum discriminative power among WL-test equivalent graphs. It uses sum aggregation and MLPs to process node features and neighborhood information. Since it does not naturally support multi-dimensional edge features, we concatenate in-node features with in-edge features during message passing. Although [39] extends GIN by summing up node features and edge features, we find it inappropriate for our datasets because of (1) the considerable context difference between node and edge features and (2) the difference in feature sizes.
- PNA [36] enhances GNNs by employing multiple aggregators and degree scalars. For aggregators, we picked mean, max, min, and sum; for degree scalars, amplification, attenuation, and identity are used.
- EGAT [37] extends graph attention networks, GAT, by incorporating edge features into the attention mechanism. The unnormalized attention score is computed with a concatenated vector of node and edge features. In this work, we use three attention heads by default.
- DiGCN [7] extends graph convolutional networks to digraphs. It utilizes digraph convolution and kth-order proximity to achieve larger receptive fields and learn multi-scale features in digraphs. As suggested in the paper, we compute the approximate digraph Laplacian, which alters node connections, during data preprocessing because of considerable computation time. Since it does not naturally support multi-dimensional edge features and performs edge manipulation (such as adding/removing edges), we aggregate all features from in-edges by summation and update node features by concatenating with the aggregated edge features.
- MagNet [6] is a spectral GNN for digraphs that utilizes a complex Hermitian matrix called the magnetic Laplacian to encode both undirected structure and directional information. We set the phase parameter to be learnable and initialize it as 0.125. Unless otherwise specified, other model parameters are set to default values from PyTorch Geometric Signed Directed (version 0.22.0) [40]. Since it does not naturally support multi-dimensional edge features and performs edge manipulation (such as adding/removing edges), we aggregate all features from in-edges by summation and update node features by concatenating with the aggregated edge features.
- SigMaNet [5] is a generalized graph convolutional network that unifies the treatment of undirected and directed graphs with arbitrary edge weights. It introduces the Sign-Magnetic Laplacian which extends spectral GCN theory to graphs with positive and negative weights. Since it does not naturally support multi-dimensional edge features and performs edge manipulation (such as adding/removing edges), we aggregate all features from in-edges by summation and update node features by concatenating with the aggregated edge features.
- FaberNet [4] leverages Faber Polynomials and advanced tools from complex analysis to extend spectral convolutional networks to digraphs. It achieves superior results in heterophilic node classification. Unless specified, default parameters in that paper are used. We experimented with two different jumping knowledge options (“cat” and “max”), producing variant models FaberNet (cat) and FaberNet (cat), respectively. We use real FaberNets because [4] proves that the expressive power of real FaberNets is higher than complex ones given the same number of real parameters. Since it does not naturally support multi-dimensional edge features, we concatenate in-node features with in-edge features during message passing.
- Dir-GCN and Dir-GAT [11] are instance models under the proposed Dir-GNN framework for digraph learning. It extends message passing neural networks by performing separate message aggregations from in- and out-neighbors. We experimented on the base models, GCN and GAT, respectively, with two different jumping knowledge options (“max” and “cat”) with learnable combination coefficient , producing four variant models, namely Dir-GCN (cat), Dir-GCN (max), Dir-GAT (max), and Dir-GAT (cat). For details about jumping knowledge, readers can refer to [38].
Appendix C. Implementation Details
References
- Chen, Z.; Khoa, L.D.; Teoh, E.N.; Nazir, A.; Karuppiah, E.K.; Lam, K.S. Machine learning techniques for anti-money laundering (AML) solutions in suspicious transaction detection: A review. Knowl. Inf. Syst. 2018, 57, 245–285. [Google Scholar] [CrossRef]
- Hilal, W.; Gadsden, S.A.; Yawney, J. Financial Fraud: A Review of Anomaly Detection Techniques and Recent Advances. Expert Syst. Appl. 2022, 193, 116429. [Google Scholar] [CrossRef]
- Motie, S.; Raahemi, B. Financial fraud detection using graph neural networks: A systematic review. Expert Syst. Appl. 2024, 240, 122156. [Google Scholar] [CrossRef]
- Koke, C.; Cremers, D. HoloNets: Spectral Convolutions do extend to Directed Graphs. In Proceedings of the Twelfth International Conference on Learning Representations, ICLR 2024, Vienna, Austria, 7–11 May 2024. [Google Scholar]
- Fiorini, S.; Coniglio, S.; Ciavotta, M.; Messina, E. SigMaNet: One laplacian to rule them all. In Proceedings of the Thirty-Seventh AAAI Conference on Artificial Intelligence and Thirty-Fifth Conference on Innovative Applications of Artificial Intelligence and Thirteenth Symposium on Educational Advances in Artificial Intelligence, AAAI’23/IAAI’23/EAAI’23, Washington, DC, USA, 7–14 February 2023; AAAI Press: Washington, DC, USA, 2023. [Google Scholar] [CrossRef]
- Zhang, X.; He, Y.; Brugnone, N.; Perlmutter, M.; Hirn, M.J. MagNet: A Neural Network for Directed Graphs. In Proceedings of the NeurIPS, Online, 6–14 December 2021; Ranzato, M., Beygelzimer, A., Dauphin, Y.N., Liang, P., Vaughan, J.W., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2021; pp. 27003–27015. [Google Scholar]
- Tong, Z.; Liang, Y.; Sun, C.; Li, X.; Rosenblum, D.S.; Lim, A. Digraph Inception Convolutional Networks. In Proceedings of the Advances in Neural Information Processing Systems 33: Annual Conference on Neural Information Processing Systems 2020, NeurIPS 2020, Virtual, 6–12 December 2020; Larochelle, H., Ranzato, M., Hadsell, R., Balcan, M., Lin, H., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2020. [Google Scholar]
- Tong, Z.; Liang, Y.; Sun, C.; Rosenblum, D.S.; Lim, A. Directed Graph Convolutional Network. arXiv 2020, arXiv:2004.13970. [Google Scholar]
- Ma, Y.; Hao, J.; Yang, Y.; Li, H.; Jin, J.; Chen, G. Spectral-based Graph Convolutional Network for Directed Graphs. arXiv 2019, arXiv:1907.08990. [Google Scholar]
- Monti, F.; Otness, K.; Bronstein, M.M. MotifNet: A motif-based Graph Convolutional Network for directed graphs. arXiv 2018, arXiv:1802.01572. [Google Scholar]
- Rossi, E.; Charpentier, B.; Giovanni, F.D.; Frasca, F.; Günnemann, S.; Bronstein, M.M. Edge Directionality Improves Learning on Heterophilic Graphs. In Proceedings of the LoG, PMLR, Virtual, 27–30 November 2023; Villar, S., Chamberlain, B., Eds.; PMLR: London, UK, 2023; Volume 231, p. 25. [Google Scholar]
- Thost, V.; Chen, J. Directed Acyclic Graph Neural Networks. In Proceedings of the 9th International Conference on Learning Representations, ICLR 2021, Virtual, Austria, 3–7 May 2021. [Google Scholar]
- Li, Y.; Tarlow, D.; Brockschmidt, M.; Zemel, R.S. Gated Graph Sequence Neural Networks. In Proceedings of the 4th International Conference on Learning Representations, ICLR 2016, San Juan, PR, USA, 2–4 May 2016. [Google Scholar]
- Gilmer, J.; Schoenholz, S.S.; Riley, P.F.; Vinyals, O.; Dahl, G.E. Neural Message Passing for Quantum Chemistry. In Proceedings of the 34th International Conference on Machine Learning, ICML 2017, Sydney, NSW, Australia, 6–11 August 2017; Precup, D., Teh, Y.W., Eds.; PMLR: London, UK, 2017; Volume 70, pp. 1263–1272. [Google Scholar]
- Scarselli, F.; Gori, M.; Tsoi, A.C.; Hagenbuchner, M.; Monfardini, G. The Graph Neural Network Model. IEEE Trans. Neural Netw. 2009, 20, 61–80. [Google Scholar] [CrossRef] [PubMed]
- Joint Financial Intelligence Unit. Screen the Account for Suspicious Indicators: Recognition of a Suspicious Activity Indicator or Indicators. 2024. Available online: https://www.jfiu.gov.hk/en/str_screen.html (accessed on 10 August 2024).
- Bahmani, B.; Chowdhury, A.; Goel, A. Fast incremental and personalized PageRank. Proc. VLDB Endow. 2010, 4, 173–184. [Google Scholar] [CrossRef]
- Velickovic, P.; Cucurull, G.; Casanova, A.; Romero, A.; Liò, P.; Bengio, Y. Graph Attention Networks. In Proceedings of the 6th International Conference on Learning Representations, ICLR 2018, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Chen, Z.; Li, L.; Bruna, J. Supervised Community Detection with Line Graph Neural Networks. In Proceedings of the 7th International Conference on Learning Representations, ICLR 2019, New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Liang, J.; Pu, C. Line Graph Neural Networks for Link Weight Prediction. arXiv 2023, arXiv:2309.15728. [Google Scholar]
- Morshed, M.G.; Sultana, T.; Lee, Y.K. LeL-GNN: Learnable Edge Sampling and Line Based Graph Neural Network for Link Prediction. IEEE Access 2023, 11, 56083–56097. [Google Scholar] [CrossRef]
- Zhang, H.; Xia, J.; Zhang, G.; Xu, M. Learning Graph Representations Through Learning and Propagating Edge Features. IEEE Trans. Neural Netw. Learn. Syst. 2024, 35, 8429–8440. [Google Scholar] [CrossRef] [PubMed]
- Jiang, X.; Ji, P.; Li, S. CensNet: Convolution with Edge-Node Switching in Graph Neural Networks. In Proceedings of the IJCAI, Macao, 10–16 August 2019; Kraus, S., Ed.; AAAI Press: Washington, DC, USA, 2019; pp. 2656–2662. [Google Scholar]
- Li, M.; Meng, L.; Ye, Z.; Xiao, Y.; Cao, S.; Zhao, H. Line graph contrastive learning for node classification. J. King Saud Univ. Comput. Inf. Sci. 2024, 36, 102011. [Google Scholar] [CrossRef]
- Kipf, T.N.; Welling, M. Semi-Supervised Classification with Graph Convolutional Networks. In Proceedings of the 5th International Conference on Learning Representations, ICLR 2017, Toulon, France, 24–26 April 2017. [Google Scholar]
- Hamilton, W.L.; Ying, Z.; Leskovec, J. Inductive Representation Learning on Large Graphs. In Proceedings of the NIPS, Long Beach, CA, USA, 4–9 December 2017; Guyon, I., von Luxburg, U., Bengio, S., Wallach, H.M., Fergus, R., Vishwanathan, S.V.N., Garnett, R., Eds.; Curran Associates Inc.: Red Hook, NY, USA, 2017; pp. 1024–1034. [Google Scholar]
- Xu, K.; Hu, W.; Leskovec, J.; Jegelka, S. How Powerful are Graph Neural Networks? In Proceedings of the 7th International Conference on Learning Representations, ICLR 2019, New Orleans, LA, USA, 6–9 May 2019.
- Gong, Z.; Wang, G.; Sun, Y.; Liu, Q.; Ning, Y.; Xiong, H.; Peng, J. Beyond Homophily: Robust Graph Anomaly Detection via Neural Sparsification. In Proceedings of the IJCAI, Macao, 19–25 August 2023; pp. 2104–2113. [Google Scholar]
- Chien, E.; Peng, J.; Li, P.; Milenkovic, O. Adaptive Universal Generalized PageRank Graph Neural Network. In Proceedings of the 9th International Conference on Learning Representations, ICLR 2021, Virtual, Austria, 3–7 May 2021. [Google Scholar]
- Cardoso, M.; Saleiro, P.; Bizarro, P. LaundroGraph: Self-Supervised Graph Representation Learning for Anti-Money Laundering. In Proceedings of the Third ACM International Conference on AI in Finance, ICAIF ’22, New York, NY, USA, 2–4 November 2022; pp. 130–138. [Google Scholar] [CrossRef]
- Misra, I.; Shrivastava, A.; Gupta, A.; Hebert, M. Cross-Stitch Networks for Multi-task Learning. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2016, Las Vegas, NV, USA, 27–30 June 2016; IEEE Computer Society: Piscataway, NJ, USA, 2016; pp. 3994–4003. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2016, Las Vegas, NV, USA, 27–30 June 2016; IEEE Computer Society: Piscataway, NJ, USA, 2016; pp. 770–778. [Google Scholar] [CrossRef]
- Kanezashi, H.; Suzumura, T.; Liu, X.; Hirofuchi, T. Ethereum Fraud Detection with Heterogeneous Graph Neural Networks. arXiv 2022, arXiv:2203.12363. [Google Scholar]
- Wu, J.; Yuan, Q.; Lin, D.; You, W.; Chen, W.; Chen, C.; Zheng, Z. Who Are the Phishers? Phishing Scam Detection on Ethereum via Network Embedding. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 1156–1166. [Google Scholar] [CrossRef]
- Elliott, A.; Cucuringu, M.; Luaces, M.M.; Reidy, P.; Reinert, G. Anomaly Detection in Networks with Application to Financial Transaction Networks. arXiv 2019, arXiv:1901.00402. [Google Scholar]
- Corso, G.; Cavalleri, L.; Beaini, D.; Liò, P.; Velickovic, P. Principal Neighbourhood Aggregation for Graph Nets. In Proceedings of the Advances in Neural Information Processing Systems 33: Annual Conference on Neural Information Processing Systems 2020, NeurIPS 2020, Virtual, 6–12 December 2020; Larochelle, H., Ranzato, M., Hadsell, R., Balcan, M., Lin, H., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2020. [Google Scholar]
- Kamiński, K.; Ludwiczak, J.; Jasiński, M.; Bukala, A.; Madaj, R.; Szczepaniak, K.; Dunin-Horkawicz, S. Rossmann-toolbox: A deep learning-based protocol for the prediction and design of cofactor specificity in Rossmann fold proteins. Brief. Bioinform. 2021, 23, bbab371. [Google Scholar] [CrossRef] [PubMed]
- Xu, K.; Li, C.; Tian, Y.; Sonobe, T.; Kawarabayashi, K.; Jegelka, S. Representation Learning on Graphs with Jumping Knowledge Networks. In Proceedings of the 35th International Conference on Machine Learning, ICML 2018, PMLR, Stockholm, Sweden, 10–15 July 2018; Dy, J.G., Krause, A., Eds.; PMLR: London, UK, 2018; Volume 80, pp. 5449–5458. [Google Scholar]
- Hu, W.; Liu, B.; Gomes, J.; Zitnik, M.; Liang, P.; Pande, V.S.; Leskovec, J. Strategies for Pre-training Graph Neural Networks. In Proceedings of the 8th International Conference on Learning Representations, ICLR 2020, Addis Ababa, Ethiopia, 26–30 April 2020. [Google Scholar]
- He, Y.; Zhang, X.; Huang, J.; Rozemberczki, B.; Cucuringu, M.; Reinert, G. PyTorch Geometric Signed Directed: A Software Package on Graph Neural Networks for Signed and Directed Graphs. In Proceedings of the Second Learning on Graphs Conference (LoG 2023), PMLR 231, Virtual, New Orleans, LA, USA, 27–30 November 2023. [Google Scholar]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. PyTorch: An Imperative Style, High-Performance Deep Learning Library. In Proceedings of the Advances in Neural Information Processing Systems 32: Annual Conference on Neural Information Processing Systems 2019, NeurIPS 2019, Vancouver, BC, Canada, 8–14 December 2019; Wallach, H.M., Larochelle, H., Beygelzimer, A., d’Alché-Buc, F., Fox, E.B., Garnett, R., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2019; pp. 8024–8035. [Google Scholar]
- Wang, M.; Zheng, D.; Ye, Z.; Gan, Q.; Li, M.; Song, X.; Zhou, J.; Ma, C.; Yu, L.; Gai, Y.; et al. Deep Graph Library: A Graph-Centric, Highly-Performant Package for Graph Neural Networks. arXiv 2019, arXiv:1909.01315. [Google Scholar]
- Fey, M.; Lenssen, J.E. Fast Graph Representation Learning with PyTorch Geometric. arXiv 2019, arXiv:1903.02428. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. In Proceedings of the 3rd International Conference on Learning Representations, ICLR 2015, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Loshchilov, I.; Hutter, F. SGDR: Stochastic Gradient Descent with Warm Restarts. In Proceedings of the 5th International Conference on Learning Representations, ICLR 2017, Toulon, France, 24–26 April 2017. [Google Scholar]




| Category | Methods | ETH-Small | ETH-Large | FPT | ||
|---|---|---|---|---|---|---|
| w/ SNF | w/o SNF | w/ SNF | w/o SNF | w/o SNF | ||
| Non-Digraph GNNs | GCN | 0.8770 | 0.8998 | 0.9068 | 0.9072 | 0.8817 |
| GraphSAGE | 0.8752 | 0.6705 | 0.8984 | 0.6705 | 0.8802 | |
| MPNN | 0.7857 | 0.8912 | 0.8854 | 0.9087 | OOM | |
| GIN | 0.9055 | 0.8954 | 0.9117 | 0.8950 | 0.8802 | |
| PNA | 0.9352 | 0.9105 | 0.9130 | 0.9249 | OOM | |
| EGAT | 0.8916 | 0.6705 | 0.9195 | 0.6705 | OOM | |
| Digraph GNNs | DiGCN | 0.8192 | 0.8055 | 0.8650 | 0.8290 | OOM |
| MagNet | 0.9009 | 0.9012 | 0.9330 | 0.9354 | 0.9616 | |
| SigMaNet | 0.8072 | 0.8319 | 0.8018 | 0.8300 | 0.5033 | |
| FaberNet (cat) | 0.9352 | 0.9393 | 0.9476 | 0.9451 | 0.9934 | |
| FaberNet (max) | 0.9336 | 0.9376 | 0.9381 | 0.9460 | 0.9945 | |
| Dir-GCN (cat) | 0.9240 | 0.8987 | 0.9168 | 0.9188 | 0.6402 | |
| Dir-GCN (max) | 0.8577 | 0.9000 | 0.8598 | 0.9207 | 0.6402 | |
| Dir-GAT (cat) | 0.8831 | 0.6705 | 0.8769 | 0.6705 | 0.9768 | |
| Dir-GAT (max) | 0.7958 | 0.6705 | 0.8515 | 0.6705 | 0.9908 | |
| Our Digraph GNNs | MVGNN-add | 0.9231 | 0.9333 | 0.9300 | 0.9365 | 0.9821 |
| MVGNN-cat | 0.9331 | 0.9301 | 0.9439 | 0.9394 | 0.9858 | |
| LineMVGNN-add | 0.9362 | 0.9407 | 0.9598 | 0.9048 | 0.9905 | |
| LineMVGNN-cat | 0.9441 | 0.9455 | 0.9394 | 0.9565 | 0.9954 | |
| Method | Components | ETH-Small | ETH-Large | FPT | ||
|---|---|---|---|---|---|---|
| w/ SNF | w/o SNF | w/ SNF | w/o SNF | w/o SNF | ||
| LineMVGNN-cat | TWMP + LGV | 0.9441 | 0.9455 | 0.9394 | 0.9565 | 0.9954 |
| - LGV | 0.9331 | 0.9301 | 0.9439 | 0.9394 | 0.9858 | |
| - TWMP | 0.9009 | 0.8922 | 0.9042 | 0.9031 | 0.8188 | |
| LineMVGNN-add | TWMP + LGV | 0.9362 | 0.9407 | 0.9598 | 0.9048 | 0.9905 |
| - LGV | 0.9231 | 0.9333 | 0.9300 | 0.9365 | 0.9821 | |
| - TWMP | 0.9009 | 0.8922 | 0.9042 | 0.9031 | 0.8188 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Poon, C.-H.; Kwok, J.; Chow, C.; Choi, J.-H. LineMVGNN: Anti-Money Laundering with Line-Graph-Assisted Multi-View Graph Neural Networks. AI 2025, 6, 69. https://doi.org/10.3390/ai6040069
Poon C-H, Kwok J, Chow C, Choi J-H. LineMVGNN: Anti-Money Laundering with Line-Graph-Assisted Multi-View Graph Neural Networks. AI. 2025; 6(4):69. https://doi.org/10.3390/ai6040069
Chicago/Turabian StylePoon, Chung-Hoo, James Kwok, Calvin Chow, and Jang-Hyeon Choi. 2025. "LineMVGNN: Anti-Money Laundering with Line-Graph-Assisted Multi-View Graph Neural Networks" AI 6, no. 4: 69. https://doi.org/10.3390/ai6040069
APA StylePoon, C.-H., Kwok, J., Chow, C., & Choi, J.-H. (2025). LineMVGNN: Anti-Money Laundering with Line-Graph-Assisted Multi-View Graph Neural Networks. AI, 6(4), 69. https://doi.org/10.3390/ai6040069


_Zheng.png)



