Abstract
Introduction: The Earth’s growing population is increasing resource consumption, heavily pressuring agriculture, which, currently, uses 70% of the world’s freshwater from rivers and lakes, which, themselves, comprise only 1% of the Earth’s water reserves. Combined with climate change, the situation is alarming. These challenges drive Agriculture 4.0, which is focused on sustainable agricultural processes to optimise water use. Objective: Given this context, this study proposes a model, based on Artificial Intelligence (AI) techniques to predict topsoil moisture in a study area located in the south of the Iberian Peninsula, primarily an agricultural region facing recurrent droughts and water scarcity. Methods: To develop the model, a comparison between Artificial Neural Networks (ANNs) and Gradient Booster Regressors (GBRs) was conducted, and topsoil moisture data from seven probes distributed over the study area were used, in addition to several variables (temperature, relative humidity, solar radiation, wind speed, precipitation and evapotranspiration) from a selection of weather stations and ensemble forecasts from meteorological models. Results: The final GBR model, with a 0.01 learning rate, 5 max depth, and 350 estimators, predicted topsoil moisture with an average mean squared error (MSE) of 0.027 and a maximum difference between observed and predicted data of 20.09% in a two-year series (May 2022–June 2024).
1. Introduction
The significant and continuous growth of the global population has led to an ever-increasing demand for natural resources, particularly raw materials, intensifying pressure on production systems. Furthermore, the rising need for food places substantial challenges on ecosystems and agriculture [1,2].
Intense anthropogenic activities affect the quality of natural resources and also contribute to the acceleration of climate change, favouring complex, non-linear processes that put terrestrial ecosystems at risk of major changes in their composition and structure.
A remarkable example was observed during the COVID-19 pandemic, when the significant reduction in anthropogenic activities on a global scale led to a notable decrease in environmental pressure. During this period, a significant direct relationship was observed between the decrease in human activity and the increase in air quality, associated with a decrease in observed concentrations of gases from the burning of fossil fuels [3] as well as an improvement in water quality, specifically in the reduction of suspended particulate matter observed in Vembanad, India’s largest freshwater lake [4].
Among the natural resources most impacted by anthropogenic activities and climate change, water stands out as one of the most essential and vulnerable. Vital for life, this resource is under increasing pressure due to intensive consumption, particularly in agriculture, which accounts for approximately 70% of the planet’s available freshwater—this is primarily drawn from rivers and lakes, which make up only 1% of the Earth’s total water resources [5,6]. The intensification of climate change exacerbate this already precarious situation, with extreme events such as more frequent and severe droughts posing a serious threat to water availability [7,8], underscoring the urgency of adopting sustainable management practices.
The increasing frequency and severity of droughts further intensify the challenges faced by agricultural producers who rely heavily on these limited resources [9,10], particularly in semi-arid regions where agricultural demands are already high [11]. One such region is the semi-arid Mediterranean, which frequently experiences droughts that severely impact water resources by depleting groundwater levels and reducing water stored in dams and reservoirs [12]. These conditions compromise agricultural production and threaten the survival of agroecosystems during dry summers [13].
Moreover, rising global temperatures are projected to further reduce water availability, complicating the water management strategies required for sustainable agriculture [14].
A report released by the United Nations indicates that by the year 2050, global food production must increase by 50% to meet population demands [5]. However, limited water availability, unsustainable agricultural practices, and inefficient irrigation threaten the ability to meet these needs, especially in already water-stressed regions such as the Middle East [15], parts of Africa [16,17], southeastern Spain [18], and South Asia [19].
The Mediterranean stands out as one of the regions with the highest socio-economic vulnerability to droughts, the severity of which is expected to increase due to climate change [20]. Moreover, the uneven distribution of its water resources exacerbates this vulnerability, leading to international and supranational conflicts, particularly in transboundary basins and regions dependent on inter-basin water transfers. These conflicts are exacerbated by recurrent droughts and changes in the provision of ecosystem services [21,22].
In this context, understanding and managing surface soil moisture (SSM) is becoming a critical factor in addressing agricultural water challenges. Recognised as an Essential Climate Variable (ECV) by the European Union in 2010 [23], SSM refers to the water content of the top layer of soil. This factor plays a key role in hydrological processes, influencing the exchange of water and energy between the land and the atmosphere.
In addition, SSM directly affects plant growth and agricultural yields by determining the availability of water for crops [24]. It is also a key variable in hydrological models, influencing streamflow generation and ecosystem health [25]. Understanding and monitoring SSM is therefore essential for intelligent water resource management, improving agricultural productivity and formulating climate adaptation strategies.
To address these challenges, advanced tools such as machine learning algorithms, including Artificial Neural Networks (ANNs) and Gradient Boosting Regressors (GBRs) have proven effective in analysing moisture data and improving predictive accuracy for resource management.
Due to these growing issues, effective agricultural water management practices—such as improving irrigation efficiency and enhancing drought preparedness—are essential to mitigating the impacts of climate change and ensuring global food security [14,26].
This study focuses on comparing GBR and ANN methodologies for predicting surface soil moisture using weather station data and meteorological forecasts, providing a robust approach to support smarter water resource management and foster more sustainable agricultural practices.
2. Related Works
A recent investigation in the prediction of SSM utilised sophisticated methodologies, including machine learning, which effectively capture spatial and temporal patterns in soil moisture data, achieving high predictive accuracy [27]. Furthermore, other studies have also highlighted the importance of certain machine learning techniques for soil moisture prediction. For example, recent studies [28,29] have experimented with Random Forest in conjunction with data from the Global Navigation Satellite System (GNSS) to enhance soil moisture retrieval accuracy. Its effectiveness has also been tested in sensitive ecosystems such as peatlands [30], and, in general, in estimating vertical soil moisture profiles [31]. Other studied techniques include Long Short-Term Memory (LSTM) networks, which have been combined with the attention mechanism for predicting soil moisture and temperature [32], and with residual learning [33]; these networks have also been used in hybrid models with wavelet decomposition or particle swarm optimisation [34] and Convolutional Neural Networks (CNN) [35]. In this section, we present a literature review of various studies that have explored soil moisture estimation using neural networks, especially ANNs and GBRs, highlighting their methodologies, advantages, and limitations, as these models have proved to be effective in this field of study, as detailed in the following two subsections. Moreover, these models do not consume an excessive amount of computational resources, unlike more complex models such as LSTMs. Additionally, focusing on these two specific techniques allowed for a more in-depth and exhaustive exploration of their capabilities.
2.1. Neural Networks
Neural networks have emerged as powerful tools for predicting topsoil moisture, leveraging various data sources and methodologies. Recent studies highlight their effectiveness in integrating remote sensing data and machine learning techniques to enhance prediction accuracy, as demonstrated in [36,37]. Other approaches combined ANNs with physical models and equations, such as Richards’ equation, demonstrating the potential of integrating physical principles with machine learning [38,39]. Moreover, a fully connected feed-forward ANN model was developed in [40], which outperformed ten other machine learning algorithms.
In addition to these advancements, high-resolution aerial imagery has been explored as a valuable input for soil moisture estimation. For instance, a study in [41] developed an ANN model that leverages spectral images from the AggieAir™ UAV platform to estimate surface soil moisture.
Therefore, as highlighted by the provided studies, ANNs exhibits several strengths in predicting soil moisture, with one of these primary strengths being their ability to handle complex, multi-scale data inputs, such as satellite and in situ data, which allows for high-resolution soil moisture predictions. For instance, in [42] a multi-scale deep learning model achieved a median correlation of 0.901 and a root mean square error of 0.034 m3/m3, outperforming traditional land surface models and satellite products. Moreover, as stated before, ANNs can integrate physics-based principles, such as the water balance principle, to enhance prediction accuracy by capturing the underlying physical processes, while reducing the need for extensive datasets and training time [43]. However, ANNs also face limitations, including challenges in processing structurally diverse characteristics and meteorological influences, which complicate the development of optimal computational formulas for soil moisture predictions [44].
On the other hand, and with the aim to address some of the issues of the ANNs, such as a lack of spatial autocorrelation and vague feature representation, which can hinder model performance, further studies demonstrate that Long Short-Term Memory (LSTM) networks effectively capture soil moisture dynamics across different scales, utilising extensive in situ data to enhance predictive accuracy [45,46,47]. Moreover, incorporating attention in models like CONV1D+Attention has improved the ability to handle complex time series data, achieving significant predictive performance [48]. Lastly, optimised models, such as a GRU recurrent neural network, have shown high accuracy in short-term predictions [49].
2.2. Gradient Boosting Models and Ensemble Techniques
Gradient boosting regressors effectively predict surface soil moisture by leveraging atmospheric and soil factors, enhancing prediction accuracy through advanced modelling techniques [50,51]. Particularly, Extreme Gradient Boosting (XGBoost) has been highlighted for its superior performance in predicting soil moisture, achieving high correlation coefficients and low RMSE values in provincial-level studies [52,53]. In a multi-sensor data approach, the XGBR-GA model outperformed other models like Random Forest and Support Vector Machines, as stated in [54].
Furthermore, ensemble methods, including stacking and Boruta-GBDT, have been shown to enhance prediction accuracy by combining multiple algorithms and integrating various machine learning techniques, leading to improved RMSE and correlation metrics, as well as proving effective in managing the spatial variability of soil moisture [55,56,57].
Similarly to ANNs, GBR models also present notable strengths and some limitations in soil moisture prediction. One significant advantage is their high accuracy and robustness, as demonstrated by the GBR-RF algorithm, which outperformed traditional methods with R2 values reaching 0.8838 [58]. In addition, these models effectively integrate various data sources, such as satellite imagery, enhancing predictive capabilities through multi-band data combinations [58]. Furthermore, its ability to handle missing data through imputation techniques enhances overall model performance [59]. Nonetheless, regarding limitations, they include the requirement for extensive data preprocessing and feature engineering to ensure model reliability, as well as potential overfitting if the hyperparameters are not optimally tuned [60,61]. Furthermore, while gradient boosting models outperform traditional methods, they may still struggle with extreme outlier conditions or when faced with highly variable soil types [52,61].
Therefore, and as a general conclusion of this section, it is worth mentioning that recent advancements in soil moisture prediction have demonstrated the effectiveness of both neural networks (NNs) and GBRs in integrating diverse data sources, such as remote sensing, in situ measurements, and multi-scale atmospheric variables. NNs, particularly ANNs and LSTMs, have shown strong capabilities in handling complex, multi-temporal inputs, achieving high predictive accuracy by incorporating physics-based principles and deep learning architectures. Meanwhile, GBR models, including XGBoost and ensemble techniques, have proven robust in capturing spatial variability, efficiently integrating heterogeneous data, and delivering competitive results with minimal computational costs.
The study presented in this paper builds upon the work presented in [36], expanding the scope and refining the prediction model for surface soil moisture, incorporating a comparison between ANNs and GBRs. Additionally, the new model utilises a more comprehensive dataset, spanning (daily) from May 2022 to June 2024 (unlike the previous study, which considered data solely from the year 2023), since it is the maximum period of time available for the moisture data collected by the seven installed probes, and integrates additional variables from selected weather stations and the ensemble of numerical weather forecasting models, enhancing the robustness of the predictions.
In this section, we have reviewed recent studies utilising neural networks and gradient boosting techniques to predict surface soil moisture, demonstrating their effectiveness in capturing spatial and temporal patterns and improving predictive accuracy. The rest of the paper is structured as follows: Section 3 is divided in two subsections, with Section 3.1 describing the data used, including probe measurements and meteorological variables, as well as statistical analysis methods and model development; Section 3.2 details the study area, dataset construction, and the development and cross-validation of neural network and gradient boosting models. Furthermore, Section 4 presents and discusses the obtained results, comparing model accuracy and analysing performance in different scenarios; finally, Section 5 summarises the main findings of the study, discusses implications for water management in agriculture, and suggests possible future research directions.
3. Materials and Methods
3.1. Background
3.1.1. Probes’ Data
Currently, the installation of probes in crop fields is becoming increasingly popular and widely used. The reason lies in different key aspects. First of all, probes provide real-time data on several soil variables, allowing farmers to make informed decisions immediately, optimising the use of resources such as water and fertilisers, and therefore reducing the costs and the environmental impact. Moreover, they can detect anomalous changes in the soil, helping in identifying potential problems before they become severe, thereby allowing for early intervention.
Furthermore, the data measured by probes are of paramount importance for training AI models, as they provide large volumes of historical real, precise, and accurate data on specific variables for specific study areas, allowing AI models to make more reliable predictions, and reducing the human error that can be committed making manual measurements. Moreover, probes can be installed in multiple locations within a field, providing a detailed spatial coverage through a granular view of the crop or area of interest.
Seven Drill & Drop SDI-12 probes, which are Sentek Technologies products [62], have been used for this study, the same ones employed in [36]. Although this type of probe collects different parameters, thanks to the integration of multiple sensors, only measurements taken for surface soil moisture have been used for this research. These measurements have a precision of ±0.03% vol and a resolution of 1:10,000, demonstrating that the probes are capable of detecting small changes in soil moisture. The distribution of the probes employed in the study area is shown in Figure 1, where the white rectangle defines the ROI and each yellow pin represents a probe.
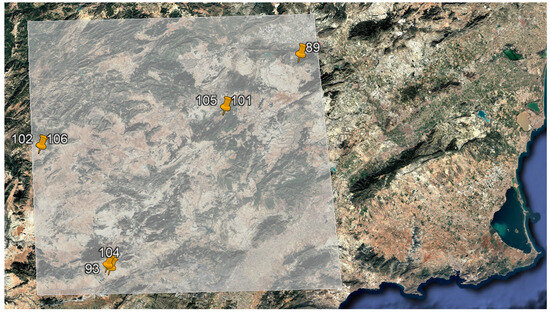
Figure 1.
Distribution on the study area of the seven probes employed for the research.
3.1.2. Weather Stations Data
Weather stations offer similar advantages to probes, but they are applied to environmental variables. For this study, four meteorological stations were selected, distributed throughout the study area and located at points closest to each of the seven probes used. Since the defined basin of interest spans several provinces, stations from different public and open networks were used, depending on the location of the probes. For the three probes situated within the Region of Murcia, data were sourced from the stations of the Agrometeorological Network of IMIDA (Murcian Institute for Agricultural and Environmental Research and Development), which were accessed through the SIAM (Agricultural Information System of Murcia) online platform [63]. Specifically, two stations from this network, positioned in Cieza and Cehegín, were utilised. In the case of the two probes located in the province of Almería, a meteorological station established in the municipality of Chirivel, part of the METEO Network, was employed. Access to the data from this station was facilitated by the web portal [64] of the FrostSE project, which was developed by the Department of Geography at the University of Murcia [65]. For the probes installed in Granada, a meteorological station situated in Puebla de Don Fadrique, designated with the code GR02, and operated by the Andalusian Institute of Agricultural and Fisheries Research and Training (IFAPA), was utilised. To retrieve the environmental information documented by this station, the web portal of the Agroclimatic Information Network of Andalusia (RIA) [66] was referenced.
Figure 2 shows the distribution of the meteorological stations used, marked with red pins, in relation to the probes in the study area.
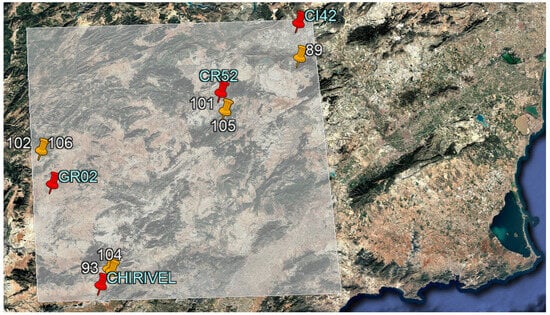
Figure 2.
Distribution of the meteorological stations used in the study area.
Daily data on maximum, minimum, and average temperatures; maximum, minimum, and average relative humidity; average wind speed; precipitation; and average solar radiation were collected from the stations.
3.1.3. Meteorological Models’ Forecasts
Weather forecast models allow future weather conditions to be estimated based on initial and contour data, providing forecasts up to 15 days ahead.
Although they are not as accurate as observed data, such as that from meteorological stations or in situ probes, which collect data in near real time, they provide one of the inputs needed for artificial intelligence models, such as the one developed in this study, to be able to make predictions of the variable of interest. In this research, the Visual Crossing (VC) API [67] has been used, as it offers a free limited version from which data can be accessed. From its API, two types of data can be retrieved:
- -
- Historical data: these data are retrieved from multiple sources, such as weather stations, satellites, and radars. Normally, to collect historical records from a concrete latitude and longitude, three weather stations in a range of 50 km around the latitude and longitude specified are used [68,69]. Due to this low spatial resolution, the data retrieved are less accurate and reliable than those obtained from the weather stations mentioned in Section 3.1.2.
- -
- Weather forecast: current data are combined with mathematical and physics algorithms to obtain weather forecasts using meteorological models; in this case, these are the models of ECMWF (European Centre for Medium-Range Weather Forecasts), GFS (Global Forecast System), ICON (Icosahedral Nonhydrostatic Model from the German Meteorological Office), NAM (North American Mesoscale Model), and HRRR (High-Resolution Rapid Refresh). The models are continuously adjusted with new data to improve accuracy, through the calibration and validation of the generated data using real data to ensure their precision and coincidence with the real conditions [69,70].
Daily data on maximum, minimum, and average temperatures; maximum, minimum, and average relative humidity; average wind speed; precipitation; and average solar radiation were collected from Visual Crossing.
3.1.4. Evapotranspiration
Evapotranspiration (ET) is the process by which water is transferred from land to the atmosphere through evaporation and plant transpiration. The Penman–Monteith Equation (1), which has been employed in this study, is a widely used method for calculating reference evapotranspiration (ETo), integrating several meteorological parameters to provide accurate estimates. This equation combines energy balance and mass transfer principles, requiring inputs such as temperature, solar radiation, humidity, and wind speed [71]. It is particularly effective for estimating ETo under standard conditions, as demonstrated in [72], which utilised local weather data to validate its accuracy. Moreover, the equation accounts for stomatal conductance and the vapor pressure deficit, which are crucial for understanding plant water use [71].
3.1.5. Artificial Neural Networks
Artificial Neural Networks (ANNs) are computational models inspired by the human brain, designed to recognise patterns and make predictions from large datasets. These networks consist of layers of interconnected nodes (neurons) that process input data and adjust their connections based on errors, thereby improving predictions over time [73].
ANNs are particularly valuable in predicting soil properties due to their ability to handle the complex, non-linear relationships inherent in soil data. They have been effectively applied in various soil science domains, including predicting soil–water characteristics, assessing soil quality, and estimating compressive strength in geotechnical engineering [74,75,76,77]. Their capacity to learn from extensive datasets enables accurate predictions of soil characteristics such as pH, organic carbon concentration, and moisture content, which are crucial for land use planning and sustainable agriculture [78]. Additionally, ANNs can quantify uncertainty in predictions, enhancing the reliability of soil assessments, especially in areas with limited data [74].
3.1.6. Gradient Boosting Regressors
Gradient Boosting Regressors are a class of machine learning algorithms that build predictive models by combining multiple weak learners, typically decision trees, in a sequential manner [79]. The process begins with an initial model, and subsequent models are trained to correct the errors made by the previous ones, effectively minimising a loss function through gradient descent techniques. This approach allows for the creation of a robust model that can handle complex data patterns and improve accuracy over time [80]. The adaptability of gradient boosting to stochastic data streams allows it to efficiently process varying soil moisture conditions, making it suitable for real-time applications [81].
3.2. Proposed Solution
The methodology is structured into subsections that constitute the main steps taken to obtain the solution.
3.2.1. Area of Study
The geographical area of interest for this study, depicted in Figure 1, was primarily identified based on the spatial distribution of the seven probes available for in situ soil moisture assessment. This area is located in the southeastern part of the Iberian Peninsula, encompassing regions within the provinces of Murcia, Almería, Albacete, and Granada. The terrain covers a total area of approximately 7539 km² and is defined by two specific vertices with the following coordinates:
- -
- Vertex 1: Latitude: 38°19′58.65″ N—Longitude: 2°26′12.26″ W;
- -
- Vertex 2: Latitude: 37°33′52.96″ N—Longitude: 1°23′4.54″ W.
The study area is characterised by a semi-arid subtropical Mediterranean climate, which features elevated summer temperatures and relatively mild winter conditions. In terms of thermal measurements, it is noteworthy that the mean annual temperature hovers around 19 °C, with pronounced climatic variances observed between coastal and inland regions, where altitude significantly influences these differences, complemented by an average annual sunshine duration that surpasses 3014.3 h [82]. Conversely, precipitation is limited and erratic, exhibiting a propensity for torrential occurrences that can result in flooding, predominantly during the autumn and spring seasons [83]. Furthermore, in light of the region’s topographical characteristics, nearly 27% of the area is composed of mountainous terrains, 35% consists of plains and plateaus, while the remaining 38% encompasses intramountain depressions and valleys. The median elevation is approximately 645 m [84]. Additionally, in the province of Murcia alone, 47.44% of the total land area is allocated for agricultural purposes [82]. Given that nearly half of the province’s area is committed to agriculture, it is imperative to monitor soil moisture, as it represents one of the most significant determinants of plant growth and development.
3.2.2. Dataset Construction
Although the detailed creation of the datasets used in this study will be explained throughout this section, a flowchart is presented first in Figure 3 to visually provide an initial overview of the main steps followed.
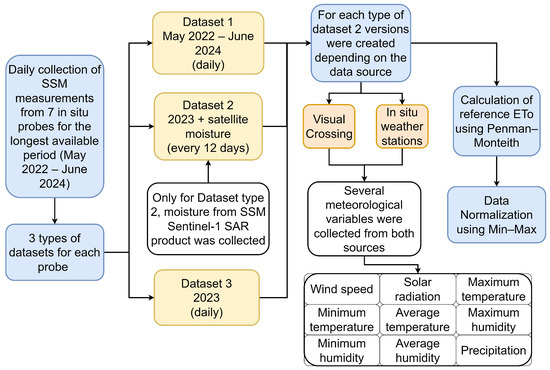
Figure 3.
Flowchart illustrating the main steps followed in the creation of the three datasets used in this study. This visual representation provides an initial overview before delving into the detailed explanations presented in this section.
First of all, the longest possible time series of SMM measurements, recorded by each of the seven probes, was obtained, covering, daily, the period from May 2022 to June 2024. The rest of the data were retrieved according to these time limits. After this, two types of data were collected:
- -
- Real data from the closest weather stations to each of the probes: from each weather station, daily data were collected for nine variables: minimum temperature, average temperature, maximum temperature, minimum relative humidity, average relative humidity, maximum relative humidity, average wind speed, accumulated precipitation, and average solar radiation.
- -
- Historical data from Visual Crossing: using the limited free access API, daily data from seven variables were obtained: minimum temperature, maximum temperature, minimum relative humidity, maximum relative humidity, average wind speed, accumulated precipitation, and average solar radiation.
Both of these variables are essential for the Penman–Monteith formula, which is used to calculate evapotranspiration. Although precipitation is not required in the Penman–Monteith formula, it is important to use it to better estimate the water balance, where, in a simplified way, precipitation represents the contribution of water, some of which infiltrates into the soil and contributes to an increase in soil surface moisture, and evapotranspiration represents the loss of water to the atmosphere, where it contributes to a decrease in soil moisture.
Moreover, data from the SSM Sentinel-1 SAR product, derived from Sentinel-1 SAR, were collected for the year 2023. These data have a temporal limitation, as they only fully cover the selected study area every 12 days.
Once all the data were obtained, three datasets were created for each type of data and probe, where the different environmental variables were the independent variables that would be used for predicting the SSM measured by the probe (the dependent variable):
- -
- The first dataset covers data from May 2022 to June 2024 and takes into account all the environmental variables (minimum temperature, average temperature, maximum temperature, minimum relative humidity, average relative humidity, maximum relative humidity, average wind speed, accumulated precipitation, and average solar radiation), either from Visual Crossing or from weather stations.
- -
- The second dataset covers the entire year 2023 in 12 day intervals and, in addition to the environmental variables, also includes satellite moisture.
- -
- The third dataset also covers the year 2023, but with records for each day of the year. In this case, only the environmental variables are included, without the satellite moisture. This third dataset is constructed as an intermediate degree between the previous two.
The aim of this division was twofold. On one hand, the aim was to compare the results obtained by the different models on each of the datasets, in order to determine, especially, the impact of satellite data on the dependent variable. The goal was to elucidate what was better: to use a longer time series of data or to renounce having a ‘large’ amount of data in favour of having a variable that offers a broader satellite perspective on soil moisture. On the other hand, the objective was to compare which models offer better and more accurate results: those trained with real data measured by the weather station closest to each probe, or those trained with the historical data from Visual Crossing, which offers measurements with a lower spatial resolution.
Once all the datasets were constructed, the different environmental variables were used to calculate the evapotranspiration (ETo) associated with each daily record. To carry this out, the Penman–Monteith formula was programmed in Python (version 3.12.6, with libraries Pandas (2.2.2) and NumPy (1.26.4)), and the calculation of this variable was automated for each record in each dataset.
After incorporating this final variable, all datasets were normalised using Min–Max normalisation. This method is advantageous when variables do not follow a normal distribution (as is the case here, which will be elaborated on in the statistical analysis section), as it preserves the original data distribution while scaling all values within a fixed range [0, 1] [85]. Additionally, Min–Max normalisation prevents data structure distortion that other techniques, such as Z-score normalisation, might introduce when dealing with skewed or heavy-tailed distributions. Furthermore, it enhances feature weighting by emphasising features with strong correlations to the target variable, thereby improving classification performance across various machine learning classifiers [86]. It is also worth noting that the global maximums and minimums of each variable (i.e., the maximum and minimum values of each variable across all datasets) were used, ensuring a more robust and general normalisation for the entire study area.
Furthermore, applying normalisation is crucial for the performance of the models (the ANN and the GBR) that will be trained on these data. In the case of ANNs, normalisation helps to prevent issues related to different scales among input variables, improving convergence speed and stability during training by avoiding saturation in activation functions [85,87,88,89]. For GBR, while tree-based models are generally less sensitive to feature scaling than gradient-based methods, normalisation can still be beneficial when dealing with heterogeneous data distributions, ensuring a more balanced contribution of features to the model and improving accuracy [90].
Finally, each dataset was divided into two parts: training (constituting 80%), and the validation (the remaining 20%) of the different models that were developed.
3.2.3. Statistical Analysis and Comparison Between Visual Crossing Data and Weather Stations Data
With the aim of deciding which environmental variables were the most significant for predicting topsoil moisture, a statistical analysis and comparison between Visual Crossing and weather stations data was conducted. Several steps were followed.
- -
- First of all, an exploratory data analysis was conducted. For this, the mean, median, standard deviation, and interquartile range of the data were calculated, and outliers were identified using box plots. For both types of data, and generally for all probes, the results were very similar.Next, the distributions followed by the different variables for each probe were analysed, which again, were very similar both for all probes and between the VC data and the station data. It is noteworthy in this case that none of the variables, in any data or probe, followed a normal distribution, as demonstrated by the Shapiro–Wilk test. This statistical test determines, for a small or medium number of records, as is the case here, whether the distribution followed by a variable is normal or not, based on whether a certain threshold (having a p-value greater than 0.05) is exceeded.
- -
- The next phase involved conducting a correlation analysis. Given that the previous step demonstrated that the variables did not follow normal distributions, Spearman’s correlation was employed. This method measures the statistical dependence between the ranks of two variables and is particularly useful when the relationships between variables are not linear but follow a monotonic trend. In most cases, a significant correlation was observed between the different variables and the moisture recorded by the probes, notably highlighting the inverse relationship between humidity and either ETo or solar radiation. It is also noteworthy that precipitation data obtained from Visual Crossing did not show a clear correlation with the dependent variable, unlike the data recorded by most of the stations. This discrepancy is due to the low resolution of the VC data, which averages data from three stations within a 50-km range, whereas the manually selected weather station is, at worst, less than 10 km away from its respective probe. These results are partially illustrated in Figure 4 and Figure 5. These figures represent average correlation matrices, showing the mean of all correlations between the different independent variables and the dependent variable ‘’. Thus, the values presented provide a general representation of each particular correlation matrix, which may be influenced by outlier correlation values from some of the probes.
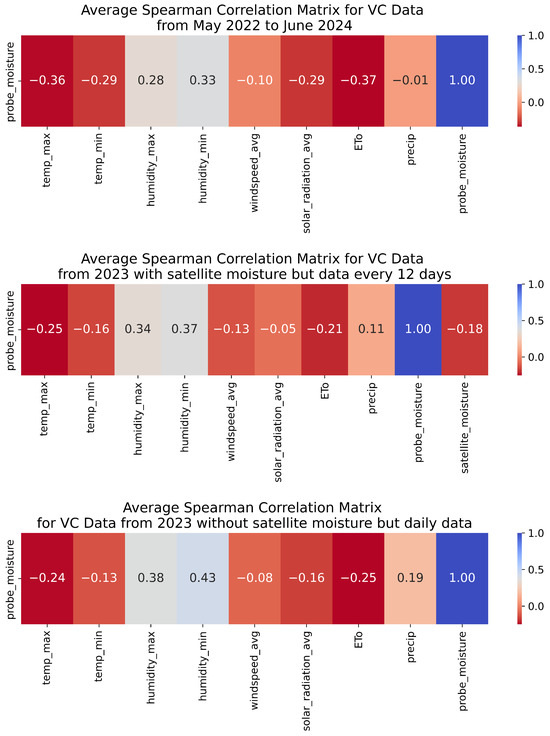 Figure 4. Spearman correlation of the different environmental variables (minimum temperature, average temperature, maximum temperature, minimum relative humidity, average relative humidity, maximum relative humidity, average wind speed, accumulated precipitation, and average solar radiation) collected in each of the three datasets (dataset from May 2022 to June 2024 with daily but without satellite soil moisture measurements, dataset from the year 2023 in 12-day intervals with satellite soil moisture measurements, and dataset from the year 2023 with daily data and without the satellite soil moisture measurements) for VC data, with respect to the dependent variable .
Figure 4. Spearman correlation of the different environmental variables (minimum temperature, average temperature, maximum temperature, minimum relative humidity, average relative humidity, maximum relative humidity, average wind speed, accumulated precipitation, and average solar radiation) collected in each of the three datasets (dataset from May 2022 to June 2024 with daily but without satellite soil moisture measurements, dataset from the year 2023 in 12-day intervals with satellite soil moisture measurements, and dataset from the year 2023 with daily data and without the satellite soil moisture measurements) for VC data, with respect to the dependent variable .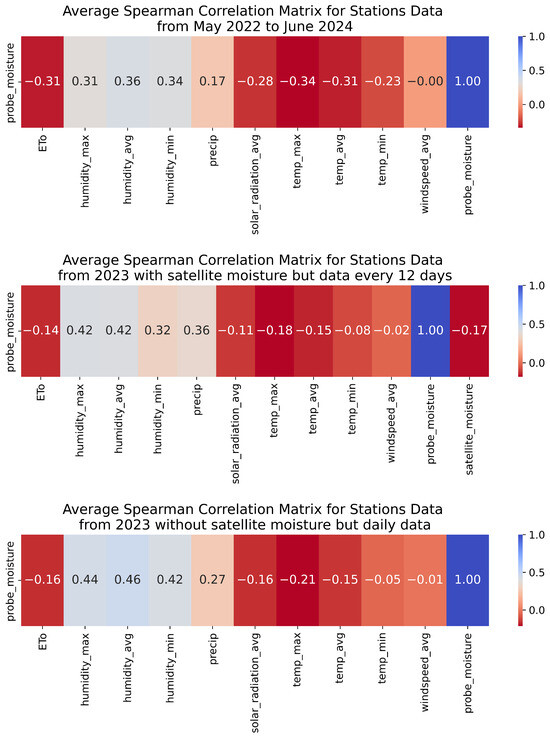 Figure 5. Spearman correlation of the different environmental variables collected (minimum temperature, average temperature, maximum temperature, minimum relative humidity, average relative humidity, maximum relative humidity, average wind speed, accumulated precipitation, and average solar radiation) in each of the three datasets (dataset from May 2022 to June 2024 with daily but without satellite soil moisture measurements, dataset from the year 2023 in 12-day intervals with satellite soil moisture measurements, and dataset from the year 2023 with daily data and without the satellite soil moisture measurements) for weather stations data, with respect to the dependent variable .
Figure 5. Spearman correlation of the different environmental variables collected (minimum temperature, average temperature, maximum temperature, minimum relative humidity, average relative humidity, maximum relative humidity, average wind speed, accumulated precipitation, and average solar radiation) in each of the three datasets (dataset from May 2022 to June 2024 with daily but without satellite soil moisture measurements, dataset from the year 2023 in 12-day intervals with satellite soil moisture measurements, and dataset from the year 2023 with daily data and without the satellite soil moisture measurements) for weather stations data, with respect to the dependent variable . - -
- The final phase consisted of detecting systematic errors in the data. This was carried out in three steps. First, a bias analysis was conducted by calculating the difference between the means of the station data and those calculated by VC. In this initial step, it was discovered that VC tended to slightly overestimate ETo, precipitation, and minimum temperature, and notably overestimate average wind speed and minimum relative humidity. Conversely, it perceptibly underestimated maximum relative humidity. The next step involved performing a residual analysis, which is the difference between the VC values and the station values, where the results obtained in the previous bias analysis were reaffirmed. Finally, Bland–Altman plots were used, which serve to visually compare two measurement techniques and to assess the agreement between two data sets.
3.2.4. Statistical Analysis of the Influence of the Satellite Moisture on the Dependent Variable
This analysis is an extension of the previous one, although it is specifically focused on determining the impact of satellite moisture on the moisture recorded by the probes. The most notable phases of this analysis are presented below:
- -
- Firstly, a Spearman correlation test was conducted (it was previously verified that satellite moisture also did not follow a normal distribution). Here, it was observed that the data covering the period from 2022 to 2024 showed a slightly higher correlation with the dependent variable than the data covering the year 2023 daily, and that the latter had a higher correlation than the datasets covering 2023 in 12-day intervals. Additionally, it was found that the correlation of satellite moisture with the moisture measured by the probes was null or even significantly inverse. Nevertheless, it was retained in the second type of dataset explained in Section 3.2.2 to ensure that models trained using this additional variable performed worse than those using the other two types of datasets also explained in Section 3.2.2. These results are shown in the Figure 4 and Figure 5.
- -
- Next, a regression analysis was performed, as a good way to understand how the independent variables affect the dependent variable is to fit a multiple regression model and interpret the obtained coefficients, evaluating their statistical significance through p-values. The most notable observations from this analysis are, firstly, that as the time series of the data is reduced, the p-value associated with each variable increases significantly, making them less significant in the predictions. It is noteworthy that the average p-value associated with satellite moisture in the different regression models trained, both for VC and station data, is above 0.3. However, as the data time series is reduced, the R2 coefficient of the models increases. This could be explained by considering that we are using linear models to obtain an initial idea of the influences of the independent variables on the probe moisture, when the relationships between these variables do not have to be linear, especially as the volume of data increases, since these models are too simple and the relationships between the variables are complex.
- -
- Lastly, and especially since ETo was calculated from the other variables using the Penman–Monteith formula, a collinearity analysis was conducted using the Variance Inflation Factor (VIF), where it was observed that all datasets had variables with very high collinearity indices. To address this, Principal Component Analysis (PCA) was employed to extract the principal components that explained 95% of the variance of the dependent variable. However, after applying PCA, the linear models were repeated, resulting in a significant decrease in the R2 coefficient in all linear models, especially those trained on the 2023 dataset with satellite moisture. Therefore, all variables (except for satellite moisture) were left in the final datasets.
More details on the following two phases are given in Section 4, where the results are presented.
3.2.5. Development and Cross-Validation of the ANNs
The following flowchart in Figure 6 summarises the key aspects of the neural network development and cross-validation process. Although detailed explanations are provided throughout this section, this visual representation offers an initial overview of the main steps involved.
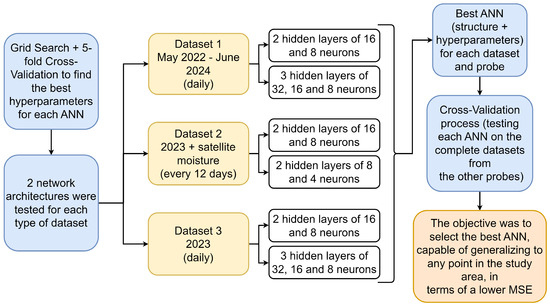
Figure 6.
Flowchart summarising the key aspects of the neural network development and cross-validation process.
The first type of model trained was the ANNs. For each of the three datasets, within each type of data, several ANNs were trained (i.e., with different structures, number of layers, and neurons), using the Grid Search technique with a wide grid of hyperparameters with 90 combinations. The hyperparameters varied primarily included the batch size, number of epochs, and optimiser. Specifically, the batch sizes tested were 1, 4, and 8; the number of epochs tested were 50, 100, 200, 300, 400, and 500; and the optimisers tested included Adam, Nadam, SGD, RMSprop, and AdamW. The batch size was varied to balance between computational efficiency and model performance, the number of epochs was adjusted to ensure sufficient training without overfitting, and different optimisers were tested to find the most effective one for each dataset. A fivefold cross-validation was used to find the best combination of these hyperparameters, a method extensively recognised and employed in the literature [91,92,93]. In this cross-validation, the corresponding training data were divided into five folds, with each fold containing temporally contiguous data. Each model was then trained five times, using four folds for training and validating on the remaining fold each time.
Moreover, for all datasets, a base structure was tested, consisting of two hidden layers, the first with 16 neurons and the second with 8. This base structure was chosen as a starting point due to its simplicity and effectiveness in initial tests. Additionally, for the datasets comprising data from 2022 to 2024, and 2023 daily, a more complex neural network structure was also tested, consisting of three hidden layers with 32, 16, and 8 neurons, respectively. This more complex structure was expected to capture more intricate patterns in the data. For the datasets covering only 2023 in 12-day intervals, a slightly simpler structure was tested, consisting of two hidden layers with eight and four neurons, as the preliminary results indicated that a simpler model was sufficient for this dataset.
Over all the trained neural networks, a cross-validation process was carried out. In this case, cross-validation means testing each neural network on the complete datasets from the other probes. As an example, the two neural network models created for probe 89 with data from 2022 to 2024 were used to predict the datasets of the same type (from 2022 to 2024) from the other six probes. It is worth noting that this process was carried out only on the neural networks trained with data extracted from weather stations since they obtained the best results, as will be discussed in Section 4. The objective of this cross-validation is to select the best neural network, capable of generalising to any point in the study area, in terms of a lower MSE.
3.2.6. Development and Cross-Validation of the GBRs
Once the development, training, and validation of the neural networks were completed, GBRs were developed solely for the station’s data, as they demonstrated better results in almost all the previous analyses and models. Similar to the ANNs, an extensive grid of hyperparameters was used to find the best configuration for each dataset and each probe. In this case, the grid consisted of 420 combinations, varying primarily between the number of estimators, learning rate, and maximum depth. Specifically, the number of estimators tested were 5, 10, 15, 20, 25, 50, 75, 100, 150, 200, 250, 300, 350, and 400; the learning rates tested were 0.1, 0.01, 0.001, and 0.0001; and the maximum depths tested were 3, 5, 10, 20, 50, and 75. The number of estimators was varied to control the number of trees in the ensemble, the learning rate was adjusted to balance the speed of learning and the risk of overfitting, and the maximum depth was tested to determine the complexity of the individual trees.
The same process of cross-validation employed to find the ANN that best generalised for the entire study area was also applied to the GBRs.
4. Results and Discussion
4.1. Main Results from the Statistical Analysis of the Data
First, analysing the results obtained from the statistical analysis of the data, the following key points can be highlighted:
- -
- The data collected by the weather stations showed a higher correlation with the SSM recorded by the probes, especially in the case of precipitation and average wind speed. This is due to the higher spatial resolution of the data taken by the weather stations and their closer proximity to the probes. The VC data consist of an average of the data collected by three weather stations in an area of 50 km around the point where the probe is located, and therefore, the data are more biased and inaccurate, as changes in the value of the environmental variables can be lost in the averaging process; the data collected by the manually-selected weather stations are never more than 10 kilometres away from the point where the probe is located, enhancing the accuracy of the data.
- -
- Regarding the influence of the satellite data on the dependent variable, it is worth noting that it was null and even inverse in terms of correlation; this seems to be due to the differences in depth and spatial resolution. While the satellite data cover wide regions of a square kilometre, probe data are collected locally, which are highly accurate but less general. Moreover, satellite data comprise the soil moisture in a vertical column that is 5 cm deep, while probes collect the soil moisture at a concrete point at 10 cm deep. Moreover, the temporal restrictions imposed by including this variable in the data significantly reduce the time series, and, therefore, the models’ ability to extract a better behaviour pattern in topsoil moisture, since it requires records every 12 days (due to spatial coverage restrictions) instead of making daily measurements. Furthermore, it was demonstrated that the data showed a higher correlation with the dependent variable the longer that the chosen time series was.
4.2. Model Performance Comparison
According to the results obtained in the development and cross-validation of the ANNs, it is worth noting that the best neural network, in terms of the lowest MSE reached in the cross-validation process, was the one trained with the data from the weather station closest to probe 93 that covered the period from May 2022 to June 2024. The MSE reached by this model in the respective cross-validation process was 0.041591 (denormalised it is 6.67%). This ANN consists of two hidden layers with 16 and 8 neurons, respectively, and the HeNormal kernel initialiser. It was trained with a batch size of 1 and the RMSprop optimiser, during 50 epochs.
Furthermore, regarding the results in the development and cross-validation of the GBRs, the model trained with the same data as the best ANN once again stood out as the best model developed with this machine learning technique. In fact, this model outperformed the best neural network, showing an average MSE of 0.027231 (denormalised it is 6.05%) in the cross-validation process. This model was trained with a learning rate of 0.01, a max depth of 5, and with 350 estimators (decision trees).
The reason why GBRs outperform ANNs in predicting surface soil moisture can be attributed to their ability to effectively manage bias and variance through the aggregation of multiple predictors. Moreover, as the GBR technique specifically enhances model performance by sequentially correcting errors from previous simpler models, it allows for a more robust prediction in complex environments like soil moisture estimation. In contrast, ANNs can be sensitive to overfitting, especially when the training data are limited or noisy, leading to less reliable predictions.
4.2.1. Implications of Feature Importance
Furthermore, to better understand the reasons behind the models’ performance and the variables that most influence their predictions, the feature importance graphs of the two best models, the ANN and the GBR, are presented in Figure 7 and Figure 8, respectively. In these Figures, the differences in how each model calculates feature importance become evident:
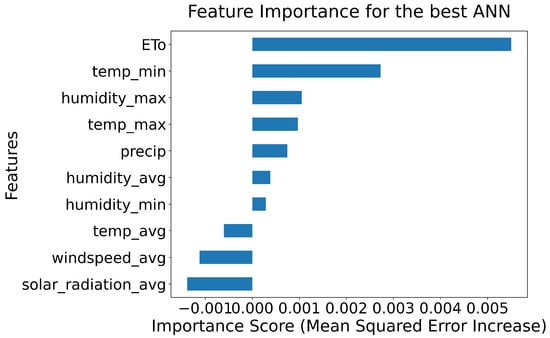
Figure 7.
Feature importance of the ANN, derived using permutation importance. Positive values indicate features that improve model performance, while negative values suggest noisy or irrelevant features.
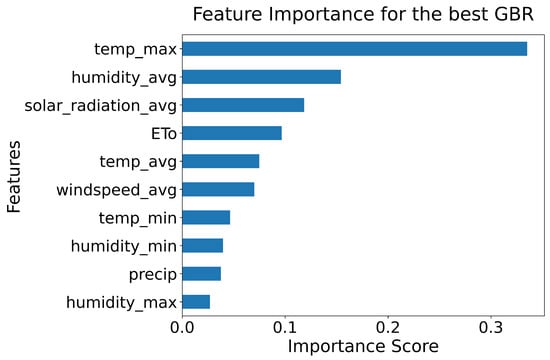
Figure 8.
Feature importance of the GBR, based on reduction in the loss function. Positive values indicate features that directly contribute to prediction accuracy, with maximum temperature being particularly important.
- -
- For the ANN, feature importance is derived using permutation importance, where each feature is randomly shuffled to measure the degradation (or improvement) in model performance. This method can result in both positive and negative importance values. Positive values, as in evapotranspiration, minimum and maximum temperature, precipitation, and maximum, minimum, and average humidity, indicate that the features contribute positively to the model’s accuracy (i.e., by using these features, the model performance improves), while negative values (in average temperature, windspeed and solar radiation) suggest that permuting the feature paradoxically improves performance. These negative values are likely because the feature is noisy or irrelevant (especially in the case of average windspeed, as shown in Figure 4 and Figure 5, where the correlation of this variable with the soil moisture was null) or because the model might be overfitting on that feature.
- -
- In contrast, the GBR calculates feature importance based on the reduction in the loss function achieved when a feature is used to split data in its decision trees. This method inherently produces only positive values, as it aggregates the contributions of features to reducing the overall error, and, therefore, it primarily reflects direct contributions to prediction. In this case, Figure 8 shows that features in the GBR, such as maximum temperature or average humidity that were not as relevant for the ANN, are of great importance. This is due to the way GBR prioritises features that create effective splits in the data, capturing linear and monotonic relationships more effectively, being, therefore, contrary to the ANN, which is better in detecting complex, non-linear interactions.
4.2.2. Data Source Evaluation: Weather Station Data vs. Visual Crossing Data
The two best final models were used to estimate the difference in predicting soil surface moisture using data from weather stations and Visual Crossing. The maximum difference obtained by the best ANN was 32.35%, while the best GBR showed a maximum difference of 20.09% between using Visual Crossing data and weather station data.
Figure 9 presents a bar chart comparing the MSE values obtained by the two best models (GBR and ANN), both in the Visual Crossing and in the meteorological station datasets from May 2022 to June 2024 of each of the seven probes. It can be seen, that, in general, the GBR obtained lower MSEs for all the probes’ data, demonstrating, once again, to outperform the ANN.
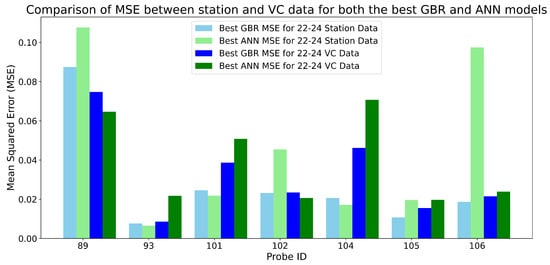
Figure 9.
Comparison of the mean squared error obtained between weather station and Visual Crossing data for both the best Gradient Boosting Regressor and Artificial Neural Network models in a cross-validation using all the probes’ data.
As demonstrated, the GBR model trained with weather station data and probe 93 data achieves superior results, evidenced by the lowest average MSE in the cross-validation process and the lowest maximum absolute difference in predicting surface moisture using data from weather stations and Visual Crossing. Figure 10 illustrates the performance of the best model for predicting topsoil moisture over a reserved test period from 23 August 2023 to 22 January 2024. The predictions are based on data from Visual Crossing and the nearest weather station to probe 93. Additionally, the graph includes a line representing the 10-day moving average for the actual topsoil moisture during this period. It can be concluded from this graph that both predictions made by the model (using Visual Crossing weather data and the nearest weather station data) generally follow the trend of the actual moisture. However, both predictions exhibit more fluctuations but tend to remain within a relatively stable range, unlike the actual moisture, which shows abrupt peaks on specific days (e.g., during a very punctual torrential rain). The predictions based on Visual Crossing weather data tend to be higher than those based on the weather station data, although they are very close to each other. Additionally, except for periods of abrupt peaks in actual moisture, both types of predictions tend to slightly overestimate topsoil moisture.
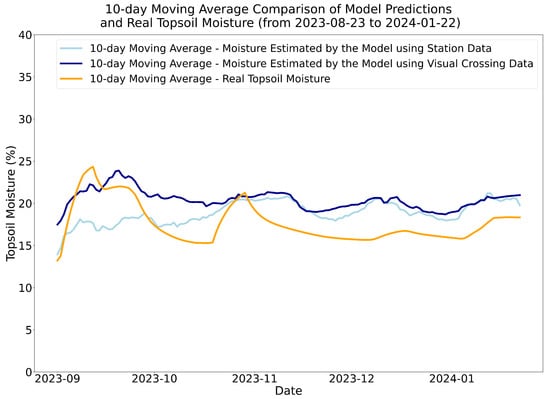
Figure 10.
Comparison of the 10-day moving average for model predictions and real topsoil moisture from 23 August 2023 to 22 January 2024. The plot shows the 10-day moving average for the moisture estimated by the model using station data and Visual Crossing data, along with the real topsoil moisture.
4.3. Surface Soil Moisture Prediction: Comparison of Forecasted and Actual Data
Furthermore, to demonstrate the model’s capability to accurately predict topsoil moisture with a certain lead time, two maps were created. The first map, shown in Figure 11, displays the surface soil moisture predicted by the model using forecast data retrieved from Visual Crossing for the period from 30 November 2024 to 9 December 2024, inclusively. Due to the limitations of the free version of the Visual Crossing API, only 10 days of weather forecast data could be collected. These data had to be gathered all at once to avoid any alterations, resulting in a large volume of requests for all points in the study area. Conversely, Figure 12 shows a map with the moisture predictions made by the model using actual data collected from Visual Crossing’s historical records after the same 10-day period. Both maps represent average values, calculated by taking the daily moisture predictions made by the model for each latitude and longitude and averaging them over the entire period. In both maps, bluer shades correspond to areas with higher moisture, while redder shades indicate areas with lower moisture.

Figure 11.
The map shows the surface soil moisture predicted by the best GBR using forecast data from Visual Crossing for the period from 30 November 2024 to 9 December 2024. Bluer shades indicate higher moisture levels, while redder shades indicate lower moisture levels.

Figure 12.
The map displays the surface soil moisture predictions made by the best GBR using actual data collected from Visual Crossing’s historical records for the same period from 30 November 2024 to 9 December 2024. Bluer shades represent areas with higher moisture, and redder shades represent areas with lower moisture.
Based on the comparison of both maps, it can be observed that there is little visual difference between the soil moisture predictions made by the model using forecast data from Visual Crossing and the predictions made using actual data from Visual Crossing for the same period. Specifically, it is worth noting that using forecast data, the model tends to overestimate the soil moisture. In fact, the maximum difference between the soil moisture map predicted by the model using forecast data and the map with moisture estimates using actual data is 2.96%, demonstrating that the model is capable of predicting surface soil moisture with a certain lead time. This small discrepancy highlights the model’s accuracy and reliability in predicting soil moisture levels, even when using forecast data instead of real-time measurements. It is also noteworthy that, given that the study area has a very similar climate throughout and the period comprises only 10 days, the differences between the maximum and minimum moisture estimated by the model are not very high.
4.4. Discussion
Among the studies most similar to this one, we analysed the results of [94], which presented a multiple linear regression model with an MSE of 0.14 for soil moisture forecasts one day ahead. In the same context, our study obtained a lower average MSE of 0.027 for the Gradient Boosting Regressor (GBR) during cross-validation, where the model was evaluated on complete datasets, spanning two years of data, from all probes, also making one-day-ahead predictions. Moreover, in [95], a root mean squared error (RMSE) of 4.6% was reported for their Random Forest model, which translates to an RMSE of approximately 21.16%. However, the GBR model developed in this study performed with an average RMSE of 6.05% (which is equivalent to 0.027 but denormalised) during the same cross-validation process.
Furthermore, after an extensive literature review, no previous study was found that specifically compared the results of soil moisture prediction using observed meteorological data and predicted meteorological data. The difference over a 10-day period found in this study was 2.96%, demonstrating the validity and feasibility of using a machine learning model on forecasted meteorological data, even when trained on observed meteorological data, and also highlighting the accuracy of meteorological predictions and their proximity to actual values. Additionally, the study not only analysed and evaluated the impact of using forecasted versus observed meteorological data on soil moisture predictions, but also assessed and compared the effects of using meteorological data obtained directly from weather stations located near the soil moisture probes versus data obtained from third-party services such as Visual Crossing. While third-party services offer more convenient and universal data access without requiring researchers to set up their own weather stations, their spatial resolution is often lower, as the weather stations they rely on may not be near the regions of interest.
Beyond these methodological contributions, the practical implications of this study are particularly relevant for real-time irrigation management systems. The high accuracy and low latency of the GBR model make it a strong candidate for integration into smart agriculture platforms.
Notably, integrating GBR involves real-time data assimilation from meteorological forecasts and soil moisture sensors, enabling dynamic irrigation recommendations tailored to specific field conditions. This approach supports sustainable water management by preventing over-irrigation and ensuring that crops receive the necessary moisture based on future conditions rather than reactive responses to soil dryness.
5. Conclusions
The study concluded that data from weather stations had a higher correlation with soil moisture measured by the probes, primarily due to their higher resolution and proximity compared to Visual Crossing data, which averaged data from three stations located 50 km away. In contrast, satellite data did not show a significant correlation with the dependent variable, mainly because of differences in depth and spatial resolution, as well as temporal constraints that limit the data series. Among the models tested, the best neural network (ANN) was trained with data from the weather station closest to probe 93, achieving a mean squared error (MSE) of 0.041591 in cross-validation. However, the Gradient Boosting Regressor (GBR) model trained with the same data outperformed the ANN, with an average MSE of 0.027231, demonstrating superior predictive capability in estimating soil surface moisture. Additionally, the maximum absolute difference in predicting soil surface moisture using Visual Crossing data versus weather station data was 32.35% for the best ANN and 20.09% for the best GBR, indicating that GBR models exhibit less variation in this aspect. This comprehensive analysis underscores the importance of selecting appropriate data sources and models for accurate soil moisture prediction. Lastly, the comparison between the predicted soil moisture map using forecast data and the map using actual data showed a maximum difference of only 2.96%. This small difference demonstrates the model’s ability to accurately predict soil moisture with a certain lead time, confirming its reliability and effectiveness.
These findings hold significant implications for agriculture in semi-arid regions, where efficient water resource management is crucial for ensuring sustainable crop production. The ability of the GBR model to provide more accurate and stable predictions of soil moisture can help to optimise irrigation practices, reduce water waste, and improve crop yields. Moreover, ongoing efforts are focused on integrating the final GBR model into a smart agriculture platform specifically designed for the southern region of the Iberian Peninsula, characterised by a semi-arid climate and increasing water resource stress. Therefore, our model will help to mitigate the risks associated with drought and water scarcity by utilising the on-field sensor data provided by the platform, allowing farmers to monitor soil moisture levels and receive irrigation recommendations tailored to their specific location and crop type.
It is worth noting that this study is affected by some limitations. In particular, it should be highlighted that the models have been trained with data recorded for the selected basin, thus being limited to the dry climate of this southern Mediterranean region of the Iberian Peninsula. This means that they will not perform well in areas with humid climates, where storms are much more frequent. Although this limitation stands as the main future direction of this research, it is worth noting that the developed model can be recalibrated with data from different regions since the main variables related to the processes of water accumulation and loss in the soil are included in the model. This would allow the methodology and input variables to be correctly generalised to other climatic regions. Nonetheless, another approach to address this limitation is to develop specific models for several regions with different climate types, installing probes in each of these regions to collect in situ soil moisture measurements to be used as references for training and testing the models. Then, each specific model can be integrated into a larger model capable of selecting the appropriate prediction based on the latitude and longitude of the desired geographic area by the user.
Author Contributions
M.Z.M.: Conceptualisation, methodology, software, formal analysis, investigation, resources, data curation, writing—original draft, writing—review and editing, visualisation. L.H.M.d.S.: Conceptualisation, methodology, formal analysis, investigation, resources, data curation, writing—original draft, writing—review and editing, visualisation, supervision. R.M.-P.: Writing—review and editing, supervision, project administration, funding acquisition. A.F.S.G.: Writing—review and editing, supervision, project administration, funding acquisition. All authors have read and agreed to the published version of the manuscript.
Funding
This paper has been supported by the EU Commission under the following projects: NEPHELE (GA 101070487) and HYPER-AI (GA 101135982). This paper was also supported by the Innovation Spanish Agency under the following projects: EDEN (Reference CPP2021-009146), OPEN2CLOSE (Reference CPP2021-008538), PROMETEO (Reference TSI-064200-2022-003), GEMINI (Reference TED2021-129767B-I00), and Agro6GSense (Reference TSI-064200-2023-8).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original data presented in the study are openly available in GitHub at https://github.com/miriozzy/Development_and_Comparison_of_ANNs_and_GBRs_for_Predicting_Topsoil_Moisture_Using_Forecast_Data (accessed on 16 February 2025), commit: a6bce44db885cb533767636147dffee3e8dfd1ff.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Lianos, T.P. Population and Environment. In Capitalism, Degrowth and the Steady State Economy: Debating Future Economic Models; Springer: Berlin/Heidelberg, Germany, 2024; pp. 45–56. [Google Scholar] [CrossRef]
- Wang, J.; Azam, W. Natural resource scarcity, fossil fuel energy consumption, and total greenhouse gas emissions in top emitting countries. Geosci. Front. 2024, 15, 101757. [Google Scholar] [CrossRef]
- da Silveira, L.H.M.; Cataldi, M.; de Farias, W.C.M. Development of multi-scale indices of human mobility restriction during the COVID-19 based on air quality from local and global NO2 concentration. iScience 2023, 26, 107599. [Google Scholar] [CrossRef]
- Yunus, A.P.; Masago, Y.; Hijioka, Y. COVID-19 and surface water quality: Improved lake water quality during the lockdown. Sci. Total Environ. 2020, 731, 139012. [Google Scholar] [CrossRef] [PubMed]
- Programme, U.W.W.A.; Koncagül, E.; Connor, R.; Abete, V. The United Nations World Water Development Report 2024: Water for Prosperity and Peace; Facts, Figures and Action Examples; UNESCO Publishing: Paris, France, 2024. [Google Scholar]
- Tolba, M.K. Recursos de agua dulce y calidad del agua. In Salvemos El Planeta: Problemas y Esperanzas; Springer: Dordrecht, The Netherlands, 1992; pp. 45–56. [Google Scholar] [CrossRef]
- Eze, J.N.; Salihu, B.Z.; Isong, A.; Aliyu, U.; Ibrahim, P.A.; Gbanguba, A.U.; Ayanniyi, N.N.; Alfa, N.; Alfa, M.; Aremu, P.A.; et al. Climate Change Impact on Agriculture and Water Resources—A Review. Badeggi J. Agric. Res. Environ. 2022, 4, 43–53. [Google Scholar] [CrossRef]
- Augusto Getirana, R.L.; Cataldi, M. Brazil is in water crisis—It needs a drought plan. Nature 2021, 600, 218–220. [Google Scholar] [CrossRef]
- Srivastav, A.L.; Dhyani, R.; Ranjan, M.; Madhav, S.; Sillanpää, M. Climate-resilient strategies for sustainable management of water resources and agriculture. Environ. Sci. Pollut. Res. 2021, 28, 41576–41595. [Google Scholar] [CrossRef] [PubMed]
- Singh, V.P.; Mishra, A.K.; Chowdhary, H.; Khedun, C.P. Climate change and its impact on water resources. In Modern Water Resources Engineering; Humana Press: Totowa, NJ, USA, 2013; pp. 525–569. [Google Scholar] [CrossRef]
- Kanae, S. Global warming and the water crisis. J. Health Sci. 2009, 55, 860–864. [Google Scholar] [CrossRef][Green Version]
- Lorenzo-Lacruz, J.; Garcia, C.; Morán-Tejeda, E. Groundwater level responses to precipitation variability in Mediterranean insular aquifers. J. Hydrol. 2017, 552, 516–531. [Google Scholar] [CrossRef]
- Guerrero-Baena, M.; Gómez-Limón, J. Insuring Water Supply in Irrigated Agriculture: A Proposal for Hydrological Drought Index-Based Insurance in Spain. Water 2019, 11, 686. [Google Scholar] [CrossRef]
- O’Neill, M.P.; Michael, D.P. Water and agriculture in a changing climate. HortScience 2011, 46, 155–157. [Google Scholar] [CrossRef]
- Sraïri, M. IWater uses in sustainable agriculture practices: Reconsidering the priorities in water scarce areas. Adv. Plants Agric. Res. 2018, 8, 333–334. [Google Scholar] [CrossRef]
- Du Plessis, A.; du Plessis, A. Current and future water scarcity and stress. In Water as an Inescapable Risk: Current Global Water Availability, Quality and Risks with a Specific Focus on South Africa; Springer: Cham, Switzerland, 2018; pp. 13–25. [Google Scholar] [CrossRef]
- Kotze, H.C.; Qotoyi, M.S.; Bahta, Y.T.; Jordaan, H.; Monteiro, M.A. A Systematic Review and Meta-Analysis of Factors Influencing Water Use Behaviour and the Efficiency of Agricultural Production in South Africa. Resources 2024, 13, 94. [Google Scholar] [CrossRef]
- Martínez-Alvarez, V.; González-Ortega, M.; Martin-Gorriz, B.; Soto-García, M.; Maestre-Valero, J. The use of desalinated seawater for crop irrigation in the Segura River Basin (south-eastern Spain). Desalination 2017, 422, 153–164. [Google Scholar] [CrossRef]
- Mehta, P.; Siebert, S.; Kummu, M.; Deng, Q.; Ali, T.; Marston, L.; Xie, W.; Davis, K.F. Half of twenty-first century global irrigation expansion has been in water-stressed regions. Nat. Water 2024, 2, 254–261. [Google Scholar] [CrossRef]
- Gu, L.; Chen, J.; Yin, J.; Sullivan, S.C.; Wang, H.; Guo, S.; Zhang, L.; Kim, J. Projected increases in magnitude and socioeconomic exposure of global droughts in 1.5 and 2 °C warmer climates. Hydrol. Earth Syst. Sci. 2020, 24, 451–472. [Google Scholar] [CrossRef]
- Schleussner, C.; Lissner, T.K.; Fischer, E.M.; Wohland, J.; Perrette, M.; Golly, A.; Rogelj, J.; Childers, K.; Schewe, J.; Frieler, K.; et al. Differential climate impacts for policy-relevant limits to global warming: The case of 1.5 °C and 2 °C. Earth Syst. Dyn. 2016, 7, 327–351. [Google Scholar] [CrossRef]
- Cramer, W.; Guiot, J.; Fader, M.; Garrabou, J.; Gattuso, J.; Iglesias, A.; Lange, M.A.; Lionello, P.; Llasat, M.C.; Paz, S.; et al. Climate change and interconnected risks to sustainable development in the Mediterranean. Nat. Clim. Change 2018, 8, 972–980. [Google Scholar] [CrossRef]
- Wagner, W.; Dorigo, W.; de Jeu, R.; Fernandez, D.; Benveniste, J.; Haas, E.; Ertl, M. Fusion of Active and Passive Microwave Observations to Create an Essential Climate Variable Data Record on Soil Moisture. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2012, I-7, 315–321. [Google Scholar] [CrossRef]
- Stańczyk, T.; Kasperska-Wołowicz, W.; Szatyłowicz, J.; Gnatowski, T.; Papierowska, E. Surface Soil Moisture Determination of Irrigated and Drained Agricultural Lands with the OPTRAM Method and Sentinel-2 Observations. Remote Sens. 2023, 15, 5576. [Google Scholar] [CrossRef]
- World Meteorological Organization. State of Global Water Resources 2022; United Nations: New York, NY, USA, 2023; pp. 14–15. [Google Scholar] [CrossRef]
- de Fraiture, C.; Smakhtin, V.; Bossio, D.; McCornick, P.; Hoanh, C.; Noble, A.; Molden, D.; Gichuki, F.; Giordano, M.; Finlayson, M.; et al. Facing climate change by securing water for food, livelihoods and ecosystems. J. Semi-Arid Trop. Agric. Res. 2007, 4, 21. [Google Scholar]
- ElSaadani, M.; Habib, E.; Abdelhameed, A.M.; Bayoumi, M. Assessment of a spatiotemporal deep learning approach for soil moisture prediction and filling the gaps in between soil moisture observations. Front. Artif. Intell. 2021, 4, 636234. [Google Scholar] [CrossRef] [PubMed]
- Jiang, Y.; Zhang, R.; Sun, B.; Wang, T.; Zhang, B.; Tu, J.; Nie, S.; Jiang, H.; Chen, K. GNSS-IR Soil Moisture Retrieval Using Multi-Satellite Data Fusion Based on Random Forest. Remote Sens. 2024, 16, 3428. [Google Scholar] [CrossRef]
- Wilson, M.; Datta, R.; Savarimuthu, S.; Moller, D.; Ruf, C. Prediction of Soil Moisture From Near-Global Cygnss Gnss-Reflectometry Using a Random Forest Machine Learning Model. In Proceedings of the IGARSS 2024—2024 IEEE International Geoscience and Remote Sensing Symposium, Athens, Greece, 7–12 July 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 4465–4471. [Google Scholar] [CrossRef]
- Taihuttu, H.Y.; Sitanggang, I.S.; Syaufina, L. Soil Moisture Prediction Model in Peatland Using Random Forest Regressor. BAREKENG J. Ilmu Mat. Dan Terap. 2024, 18, 2505–2516. [Google Scholar] [CrossRef]
- Brakhasi, F.; Walker, J.P.; Judge, J.; Liu, P.W.; Shen, X.; Ye, N.; Wu, X.; Yeo, I.Y.; Prajapati, R.; Kim, E.; et al. Multi-Layer Soil Moisture Estimation Using Combined L-and P-Band Radiometry: An Application of Machine Learning Algorithms. In Proceedings of the IGARSS 2024—2024 IEEE International Geoscience and Remote Sensing Symposium, Athens, Greece, 7–12 July 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 4411–4415. [Google Scholar] [CrossRef]
- Li, Q.; Zhu, Y.; Shangguan, W.; Wang, X.; Li, L.; Yu, F. An attention-aware LSTM model for soil moisture and soil temperature prediction. Geoderma 2022, 409, 115651. [Google Scholar] [CrossRef]
- Li, X.; Zhang, Z.; Li, Q.; Zhu, J. Enhancing Soil Moisture Forecasting Accuracy with REDF-LSTM: Integrating Residual En-Decoding and Feature Attention Mechanisms. Water 2024, 16, 1376. [Google Scholar] [CrossRef]
- Jayasinghe, W.; Deo, R.C.; Raj, N.; Ghimire, S.; Yaseen, Z.M.; Nguyen-Huy, T.; Ghahramani, A. Forecasting Multi-Step Soil Moisture with Three-Phase Hybrid Wavelet-Least Absolute Shrinkage Selection Operator-Long Short-Term Memory Network (moDWT-Lasso-LSTM) Model. Water 2024, 16, 3133. [Google Scholar] [CrossRef]
- Zhou, G.; Li, G. Forecasting Soil Moisture Using PSO-CNN-LSTM Model. In Proceedings of the 2024 IEEE Congress on Evolutionary Computation (CEC), Yokohama, Japan, 30 June–5 July 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 1–7. [Google Scholar] [CrossRef]
- Martínez, M.Z.; Da Silveira, L.H.M.; Marin-Perez, R.; Gomez, A.F.S. Development of a Neural Network System for Predicting Topsoil Moisture Using Remote Sensing and Rainfall Forecast Data. In Proceedings of the 2024 4th International Conference on Embedded & Distributed Systems (EDiS), Bechar, Algeria, 3–5 November 2024; pp. 249–254. [Google Scholar] [CrossRef]
- Hrushikesh, R.; Pathak, A.A.; Punithraj, G. Quantifying Surface Soil Moisture Variability Through Synergistic Applications of SAR and Machine Learning Techniques. In Proceedings of the 2023 IEEE India Geoscience and Remote Sensing Symposium (InGARSS), Bangalore, India, 10–13 December 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 1–4. [Google Scholar] [CrossRef]
- Singh, A.; Gaurav, K. A physics-informed machine learning approach to estimate surface soil moisture. In Proceedings of the EGU General Assembly Conference Abstracts, Vienna, Austria, 24–28 April 2023. [Google Scholar] [CrossRef]
- Guan, J.; Bragdon, S.; Clausen, J. Predicting Soil Moisture Content Using Physics-Informed Neural Networks (PINNs); Engineer Research and Development Center: Vicksburg, MS, USA, 2024. [Google Scholar] [CrossRef]
- Singh, A.; Gaurav, K. Deep learning and data fusion to estimate surface soil moisture from multi-sensor satellite images. Sci. Rep. 2023, 13, 2251. [Google Scholar] [CrossRef] [PubMed]
- Hassan-Esfahani, L.; Torres-Rua, A.; Jensen, A.; McKee, M. Assessment of surface soil moisture using high-resolution multi-spectral imagery and artificial neural networks. Remote Sens. 2015, 7, 2627–2646. [Google Scholar] [CrossRef]
- Liu, J.; Shen, C.; Rahmani, F.; Lawson, K. A multiscale deep learning model integrating satellite-based and in-situ data for high-resolution soil moisture predictions. In Proceedings of the EGU General Assembly Conference Abstracts, Vienna, Austria, 23–28 April 2023. [Google Scholar] [CrossRef]
- Ma, Z.; Wu, B.; Chang, S.; Yan, N.; Zhu, W. Developing a physics-guided neural network to predict soil moisture with remote sensing evapotranspiration and weather forecasting. In Proceedings of the EGU General Assembly Conference Abstracts, Vienna, Austria, 24–28 April 2023. [Google Scholar] [CrossRef]
- Meenakshi, M.; Naresh, R. Prediction of soil moisture root zone health in Artificial Neural Network. In Proceedings of the 2021 4th International Conference on Recent Trends in Computer Science and Technology (ICRTCST), Jamshedpur, India, 11–12 February 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1–5. [Google Scholar] [CrossRef]
- Bischof, B.; Zehe, E.; Loritz, R. Using neural networks for predicting soil water storage based in situ soil moisture observations. techreport. In Proceedings of the Copernicus Meetings, Vienna, Austria, 14–19 April 2024. [Google Scholar] [CrossRef]
- Wang, Y.; Shi, L.; Hu, Y.; Hu, X.; Song, W.; Wang, L. A comprehensive study of deep learning for soil moisture prediction. Hydrol. Earth Syst. Sci. 2024, 28, 917–943. [Google Scholar] [CrossRef]
- Li, L.; Dai, Y.; Shangguan, W.; Wei, N.; Wei, Z.; Gupta, S. Multistep forecasting of soil moisture using spatiotemporal deep encoder–decoder networks. J. Hydrometeorol. 2022, 23, 337–350. [Google Scholar] [CrossRef]
- Grubišić, V.; Vasić, D.; Ljubić, H.; Rozić, R.; Volarić, T. Soil Moisture Prediction with Attention-Enhanced Models: A Deep Learning Approach. Authorea Prepr. 2024. [Google Scholar] [CrossRef]
- Wang, G.; Wei, C.; Yan, L.; Li, J. Soil Moisture Prediction Model Based on Improved GRU Recurrent Neural Network. Strateg. Plan. Energy Environ. 2024, 43, 381–400. [Google Scholar] [CrossRef]
- Islam, M.N.; Logofatu, D.; Haque, M.Z. A Comparative Study on Machine Learning Methods Through Evaluating the Impact of Contributing Factors on The Accuracy of Soil Moisture Prediction. In Proceedings of the 2023 International Conference on Innovations in Intelligent Systems and Applications (INISTA), Hammamet, Tunisia, 20–23 September 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Divya, A.; Josphineleela, R.; Sheela, L.J. A machine learning based approach for prediction and interpretation of soil properties from soil spectral data. J. Environ. Biol. 2024, 45, 96–105. [Google Scholar] [CrossRef]
- Ren, Y.; Ling, F.; Wang, Y. Research on Provincial-Level Soil Moisture Prediction Based on Extreme Gradient Boosting Model. Agriculture 2023, 13, 927. [Google Scholar] [CrossRef]
- Zhu, Y.; Jing, X.; Ding, A. Prediction of soil moisture in Inner Mongolia’s League based on machine learning. In Proceedings of the Fourth International Conference on Signal Processing and Computer Science (SPCS 2023), Guilin, China, 25–27 August 2023; SPIE: Bellingham, WA, USA, 2023; Volume 12970, pp. 17–20. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Ngo, H.H.; Guo, W.; Chang, S.W.; Nguyen, D.D.; Nguyen, C.T.; Zhang, J.; Liang, S.; Bui, X.T.; Hoang, N.B. A low-cost approach for soil moisture prediction using multi-sensor data and machine learning algorithm. Sci. Total Environ. 2022, 833, 155066. [Google Scholar] [CrossRef]
- Jamei, M.; Ali, M.; Karbasi, M.; Sharma, E.; Jamei, M.; Chu, X.; Yaseen, Z.M. A high dimensional features-based cascaded forward neural network coupled with MVMD and Boruta-GBDT for multi-step ahead forecasting of surface soil moisture. Eng. Appl. Artif. Intell. 2023, 120, 105895. [Google Scholar] [CrossRef]
- Cheng, Y.; Li, Y.; Wu, H.; Li, F.; Li, Y.; He, L. Soil Moisture Retrieval Using Stacked Generalization: An Ensemble Machine Learning Method. In Proceedings of the 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS, Brussels, Belgium, 11–16 July 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 6984–6987. [Google Scholar] [CrossRef]
- Han, Q.; Zeng, Y.; Zhang, L.; Cira, C.I.; Prikaziuk, E.; Duan, T.; Wang, C.; Szabó, B.; Manfreda, S.; Zhuang, R.; et al. Ensemble of optimised machine learning algorithms for predicting surface soil moisture content at a global scale. Geosci. Model Dev. 2023, 16, 5825–5845. [Google Scholar] [CrossRef]
- Li, X.; Wu, J.; Yu, J.; Zhou, Z.; Wang, Q.; Zhao, W.; Hu, L. Inversion of Soil Moisture Content in Cotton Fields Using GBR-RF Algorithm Combined with Sentinel-2 Satellite Spectral Data. Agronomy 2024, 14, 784. [Google Scholar] [CrossRef]
- Sharma, S.; Singh, G. Cultivating Precision: Integrating XGBoost Imputation with Random Forest Regression for Accurate Soil Moisture Prediction. In Proceedings of the 2024 10th International Conference on Advanced Computing and Communication Systems (ICACCS), Coimbatore, India, 14–15 March 2024; IEEE: Piscataway, NJ, USA, 2024; Volume 1, pp. 156–161. [Google Scholar] [CrossRef]
- Kumar, A.; Kaushik, K.; Singh, G. Predicting Soil Moisture Levels Using Ensemble Machine Learning Methods. In Proceedings of the 2024 10th International Conference on Advanced Computing and Communication Systems (ICACCS), Coimbatore, India, 14–15 March 2024; IEEE: Piscataway, NJ, USA, 2024; Volume 1, pp. 127–132. [Google Scholar] [CrossRef]
- Acharya, U.; Daigh, A.L.; Oduor, P.G. Machine learning for predicting field soil moisture using soil, crop, and nearby weather station data in the Red River Valley of the North. Soil Syst. 2021, 5, 57. [Google Scholar] [CrossRef]
- Technologies, S. Sentek SDI-12 Series II Manual (Ver 1.1). 2022. Available online: https://www.sentektechnologies.com/manuals/sdi-12-series-ii (accessed on 27 March 2024).
- IMIDA. Informe Agrometeorológico Personalizado. 2024. Available online: http://siam.imida.es/apex/f?p=101:46:344545242704833::::: (accessed on 25 March 2024).
- Department of Geography of the University of Murcia. SUREMET. 2024. Available online: https://suremet.es/index.php (accessed on 25 March 2024).
- Department of Geography of the University of Murcia. Proyecto FrostSE. 2021. Available online: https://frostsureste.wordpress.com/proyecto (accessed on 25 March 2024).
- IFAPA. Datos de la Estación|Instituto de Investigación y Formación Agraria y Pesquera (IFAPA). 2024. Available online: https://www.juntadeandalucia.es/agriculturaypesca/ifapa/riaweb/web/estacion/18/2 (accessed on 25 March 2024).
- Visual Crossing. Visual Crossing Weather API. 2020. Available online: https://www.visualcrossing.com/weather-api (accessed on 16 February 2025).
- Visual Crossing. FAQs for Visual Crossing Weather Data. 2020. Available online: https://www.visualcrossing.com/resources/documentation/weather-data/frequently-asked-questions-faq-for-visual-crossing-weather-data/ (accessed on 16 February 2025).
- Visual Crossing. Available Data for Visual Crossing Weather. 2020. Available online: https://www.visualcrossing.com/resources/documentation/weather-data/available-data-for-visual-crossing-weather-updated-january-2020/ (accessed on 16 February 2025).
- Visual Crossing. Weather Data Documentation for Visual Crossing. 2023. Available online: https://www.visualcrossing.com/resources/documentation/weather-data/weather-data-documentation/ (accessed on 16 February 2025).
- Han, Y.; Calabrese, S.; Du, H.; Yin, J. Evaluating biases in Penman and Penman–Monteith evapotranspiration rates at different timescales. J. Hydrol. 2024, 638, 131534. [Google Scholar] [CrossRef]
- Cárdenas, O.L.; Gastélum, R.D.E.; Campos, M.N.; Galaviz, R.E.P.; Serrano, L.A.G.; Montoya, J.M. Penman–Monteith Reference Evapotranspiration Estimation Models, Using Latitude–Temperature Data, in the State of Sinaloa, Mexico. Preprints 2024. [Google Scholar] [CrossRef]
- Wang, S.C. Artificial neural network. Interdiscip. Comput. Java Program. 2003, 743, 81–100. [Google Scholar] [CrossRef]
- Rau, K.; Eggensperger, K.; Schneider, F.; Hennig, P.; Scholten, T. How can we quantify, explain, and apply the uncertainty of complex soil maps predicted with neural networks? Sci. Total Environ. 2024, 944, 173720. [Google Scholar] [CrossRef] [PubMed]
- Acharjee, P.; Souliman, M.; Isied, M. Artificial neural network-based prediction model for soil-water characteristics curve coefficients from soil index properties. In Bituminous Mixtures and Pavements VIII; CRC Press: Boca Raton, FL, USA, 2024; p. 129. [Google Scholar] [CrossRef]
- Pacci, S.; Dengiz, O.; Alaboz, P.; Saygın, F. Artificial neural networks in soil quality prediction: Significance for sustainable tea cultivation. Sci. Total Environ. 2024, 947, 174447. [Google Scholar] [CrossRef] [PubMed]
- Uzer, A.U. Efficient prediction of compressive strength in geotechnical engineering using artificial neural networks. Turk. J. Eng. 2024, 8, 457–468. [Google Scholar] [CrossRef]
- Elakiya, N.; Keerthana, G. Application of Artificial Neural Networks in Soil Science Research. Arch. Curr. Res. Int. 2024, 24, 1–15. [Google Scholar] [CrossRef]
- Natekin, A.; Knoll, A. Gradient boosting machines, a tutorial. Front. Neurorobot. 2013, 7, 21. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Hu, H.; Sun, W.; Venkatraman, A.; Hebert, M.; Bagnell, A. Gradient boosting on stochastic data streams. In Proceedings of the Artificial Intelligence and Statistics, Ft. Lauderdale, FL, USA, 20–22 April 2017; Singh, A., Zhu, J., Eds.; PMLR, Proceedings of Machine Learning Research. pp. 595–603. [Google Scholar]
- CARM. Data of the Region of Murcia. 2024. Available online: https://www.carm.es/web/pagina?IDCONTENIDO=1619&IDTIPO=100&RASTRO=c$m25987,127,1604 (accessed on 21 February 2024).
- CARM. Geographic Data of the Region of Murcia. 2024. Available online: https://www.carm.es/web/pagina?IDCONTENIDO=1613&IDTIPO=100&RASTRO=c\protect\T1\textdollarm25987,127,1604 (accessed on 17 February 2024).
- topographic map.com. Topographic Map of the Region of Murcia, Altitude, Relief. 2024. Available online: https://es-es.topographic-map.com/map-7lkf3/Regi%C3%B3n-de-Murcia (accessed on 9 October 2024).
- Chepino, B.G.; Yacoub, R.R.; Aula, A.; Saleh, M.; Sanjaya, B.W. Effect of MinMax Normalization on ORB Data for Improved ANN Accuracy. J. Electr. Eng. Energy Inf. Technol. (J3EIT) 2023, 11, 29–35. [Google Scholar] [CrossRef]
- Shantal, M.; Othman, Z.; Bakar, A.A. A novel approach for data feature weighting using correlation coefficients and min–max normalization. Symmetry 2023, 15, 2185. [Google Scholar] [CrossRef]
- Huang, L. Motivation and Overview of Normalization in DNNs. In Normalization Techniques in Deep Learning; Springer: Cham, Switzerland, 2022; pp. 11–18. [Google Scholar] [CrossRef]
- Nawi, N.M.; Atomi, W.H.; Rehman, M.Z. The effect of data pre-processing on optimized training of artificial neural networks. Procedia Technol. 2013, 11, 32–39. [Google Scholar] [CrossRef]
- Liew, S.S.; Khalil-Hani, M.; Bakhteri, R. Bounded activation functions for enhanced training stability of deep neural networks on visual pattern recognition problems. Neurocomputing 2016, 216, 718–734. [Google Scholar] [CrossRef]
- Upadhyay, D.; Manero, J.; Zaman, M.; Sampalli, S. Gradient boosting feature selection with machine learning classifiers for intrusion detection on power grids. IEEE Trans. Netw. Serv. Manag. 2020, 18, 1104–1116. [Google Scholar] [CrossRef]
- Shekar, B.; Dagnew, G. Grid search-based hyperparameter tuning and classification of microarray cancer data. In Proceedings of the 2019 Second International Conference on Advanced Computational and Communication Paradigms (ICACCP), Gangtok, India, 25–28 February 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–8. [Google Scholar] [CrossRef]
- Abas, M.A.H.; Ismail, N.; Ali, N.; Tajuddin, S.; Tahir, N.M. Agarwood oil quality classification using support vector classifier and grid search cross validation hyperparameter tuning. Int. J. Emerg. Trends Eng. Res. 2020, 8, 2551–2556. [Google Scholar] [CrossRef]
- Sah, S.; Surendiran, B.; Dhanalakshmi, R.; Yamin, M. COVID-19 cases prediction using SARIMAX Model by tuning hyperparameter through grid search cross-validation approach. Expert Syst. 2023, 40, e13086. [Google Scholar] [CrossRef] [PubMed]
- Prakash, S.; Sharma, A.; Sahu, S.S. Soil moisture prediction using machine learning. In Proceedings of the 2018 Second International Conference on Inventive Communication and Computational Technologies (ICICCT), Coimbatore, India, 20–21 April 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Adab, H.; Morbidelli, R.; Saltalippi, C.; Moradian, M.; Ghalhari, G.A.F. Machine learning to estimate surface soil moisture from remote sensing data. Water 2020, 12, 3223. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).