Super-Resolution Reconstruction Approach for MRI Images Based on Transformer Network
Abstract
1. Introduction
2. Theoretical Basis
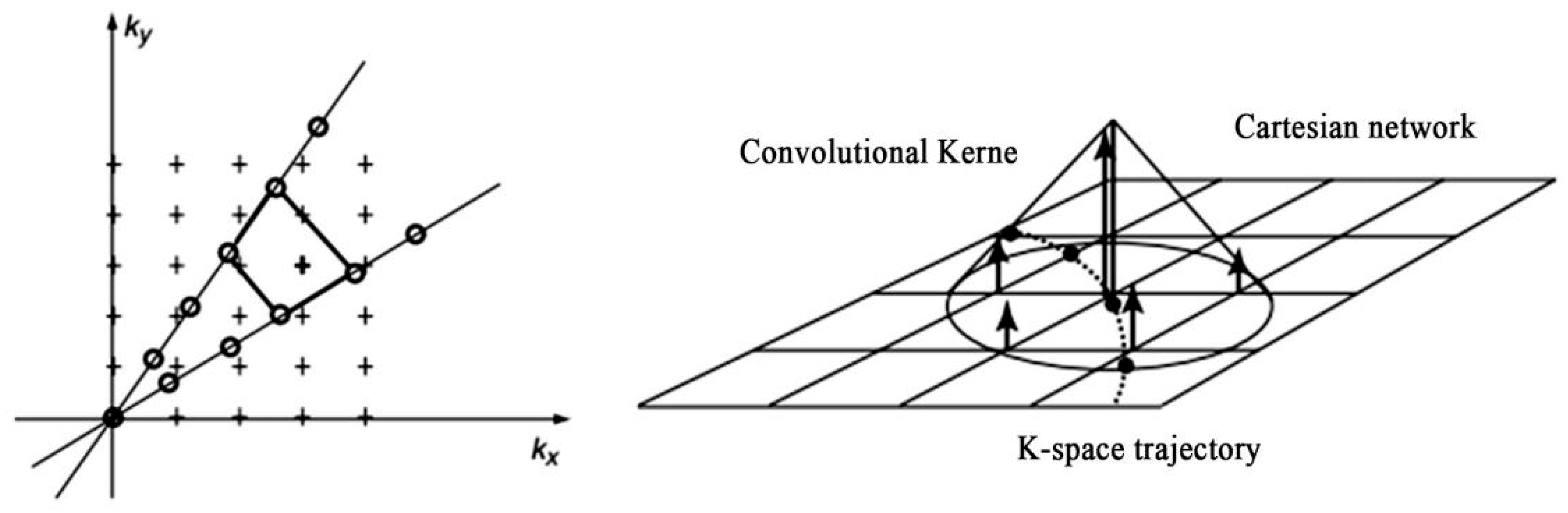
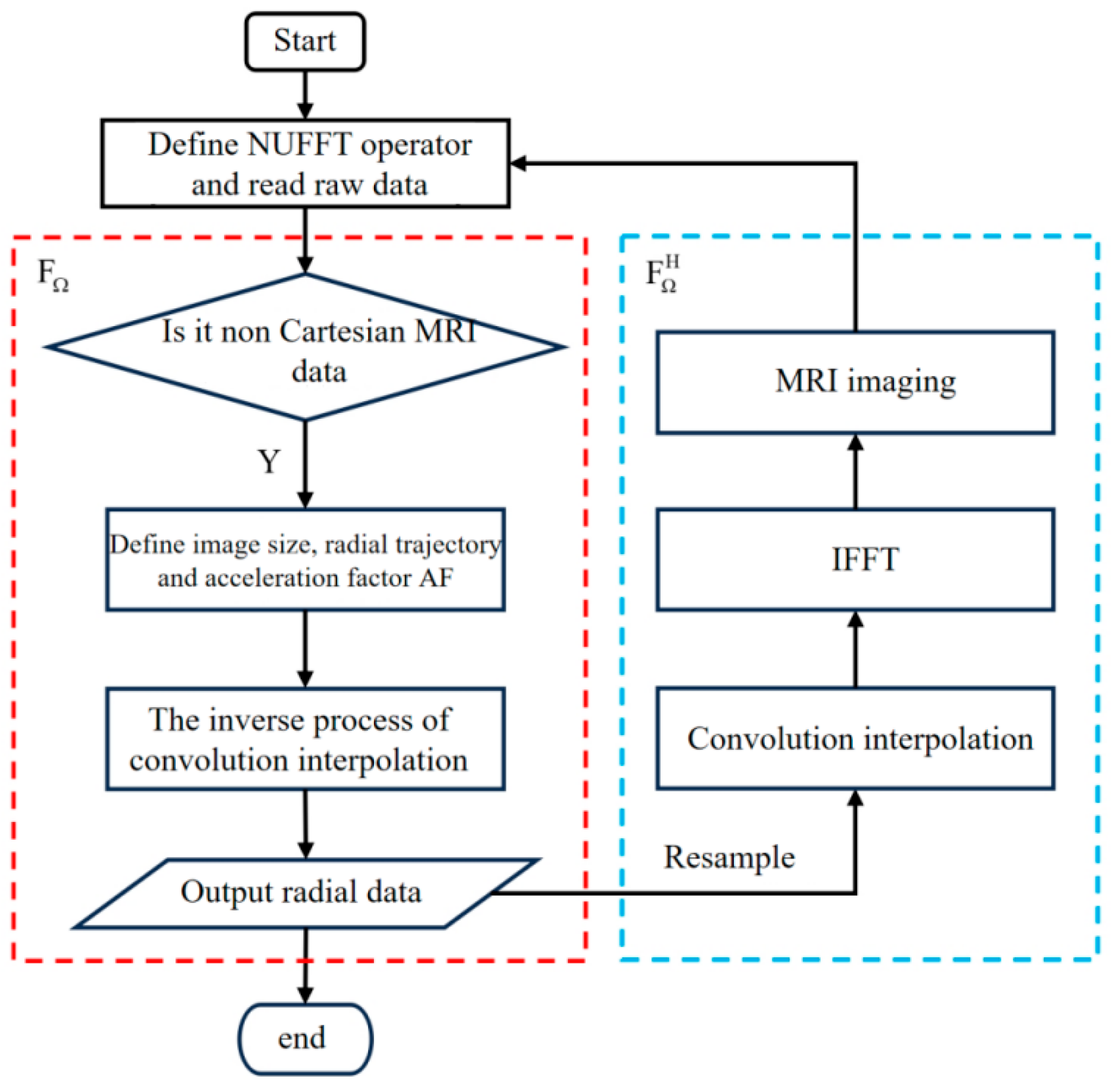
2.1. Principle of NUFFT Image Reconstruction
2.2. Principle of Transformer Network
3. Design of Image Super Resolution Reconstruction Network
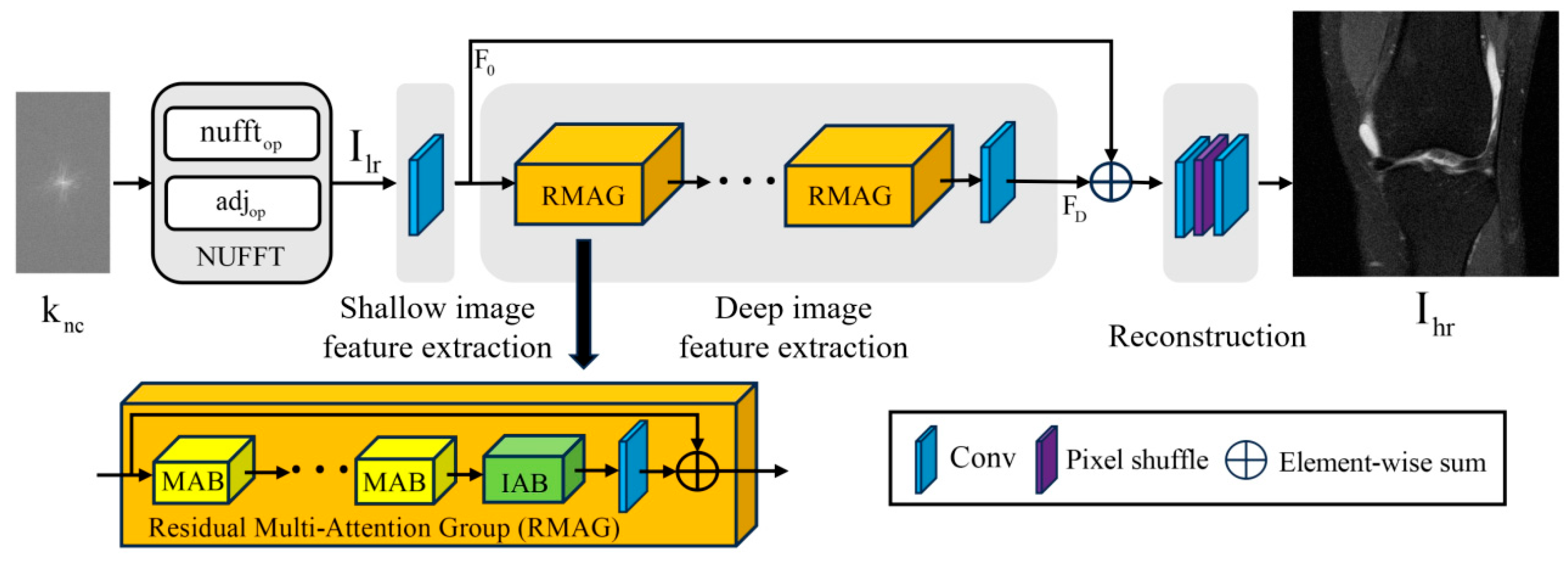
3.1. Overall Network Structure Design
3.2. The Main Modules of the Network
3.2.1. Adaptive Density Compensated NUFFT Module
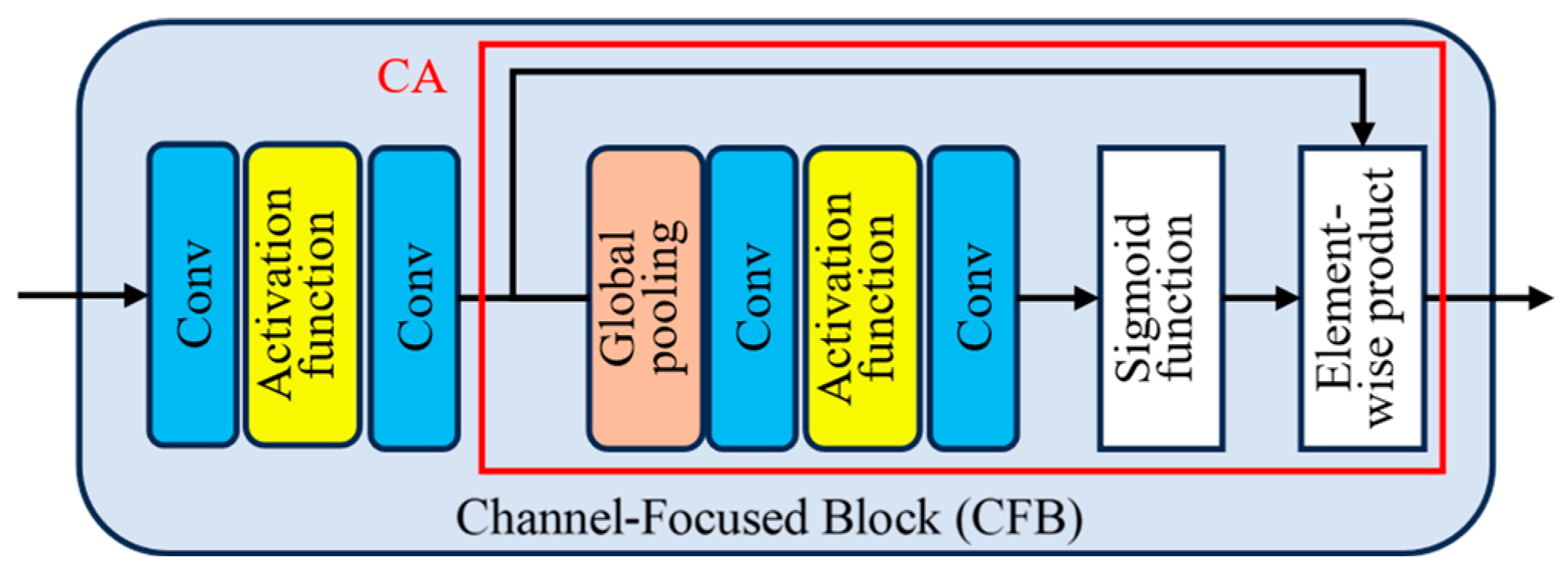
3.2.2. Mixed Attention Module MAB
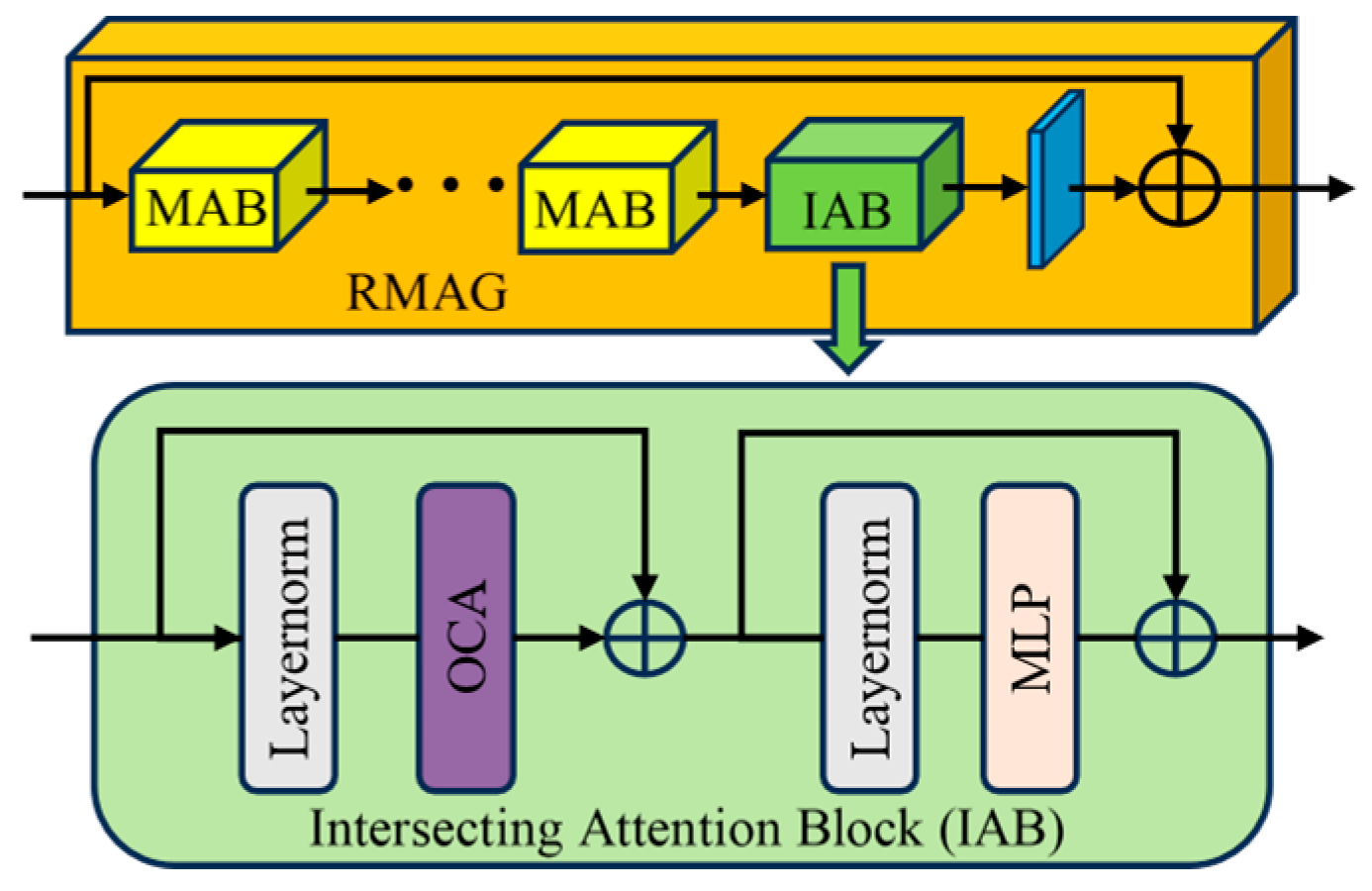
3.2.3. Cross Attention Module IAB
3.2.4. Image Reconstruction Module and Loss Function
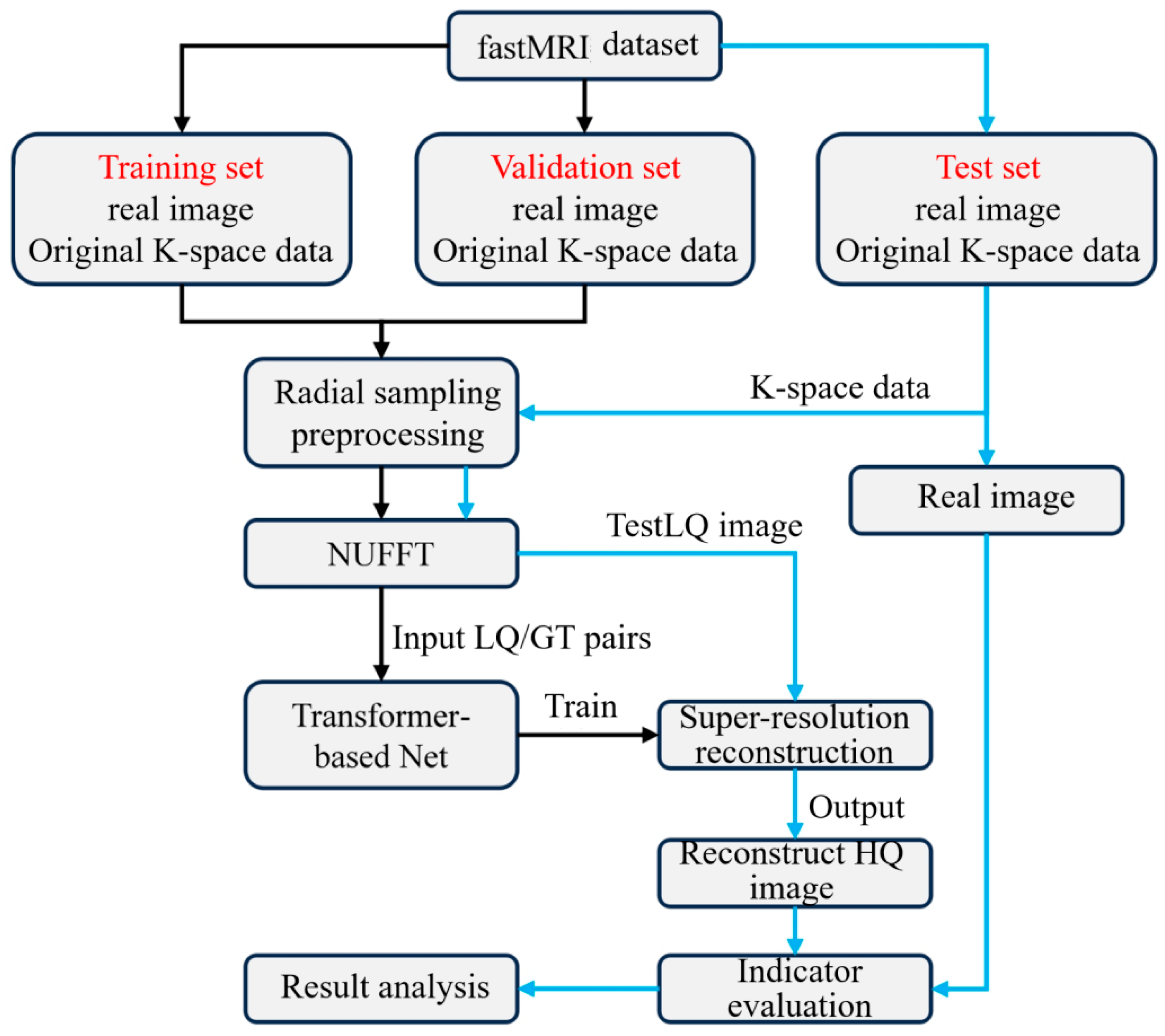
4. Experimental Research
4.1. Data Sets and Evaluation Indicators
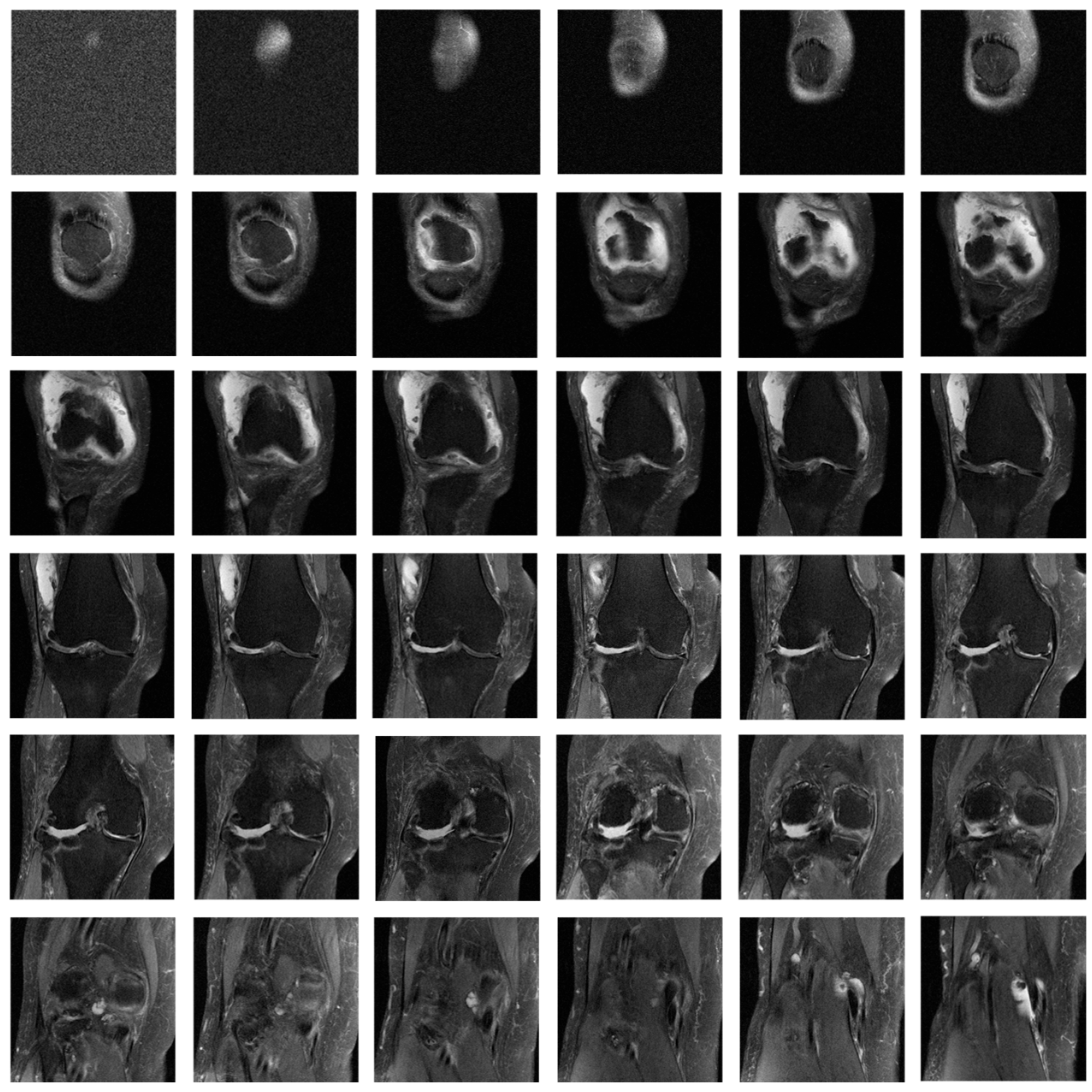
4.1.1. Experimental Data Set
- Raw Data Extraction: Retrieve fully-sampled k-space data from .h5 files and discard all invalid slices dominated by noise or devoid of meaningful signals;
- Data Normalization: Normalize each slice’s k-space magnitude spectrum to a maximum amplitude of 1;
- Radial Sampling Emulation: Generate radial undersampling trajectories via golden-angle non-uniform spacing and resample the fully-sampled k-space data accordingly;
- Data Augmentation: Enhance model robustness and generalization by applying random ±10° rotations and ±10% scaling transformations to images during training;
- Low-Resolution Synthesis: Crop the 320 × 320 ground-truth images into overlapping patches through downsampling for network training.
4.1.2. Evaluating Indicator
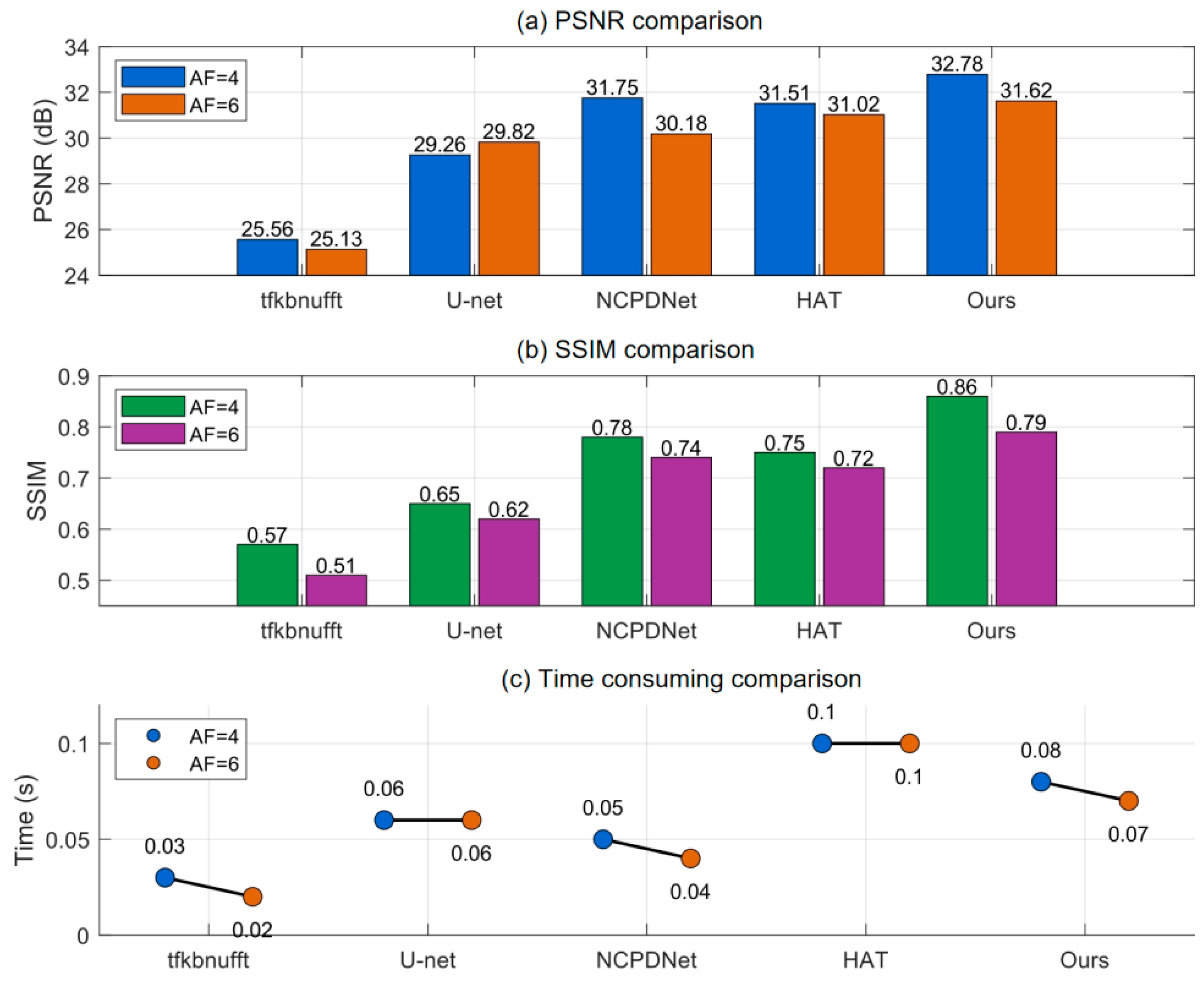
4.2. Experimental Results and Analysiss
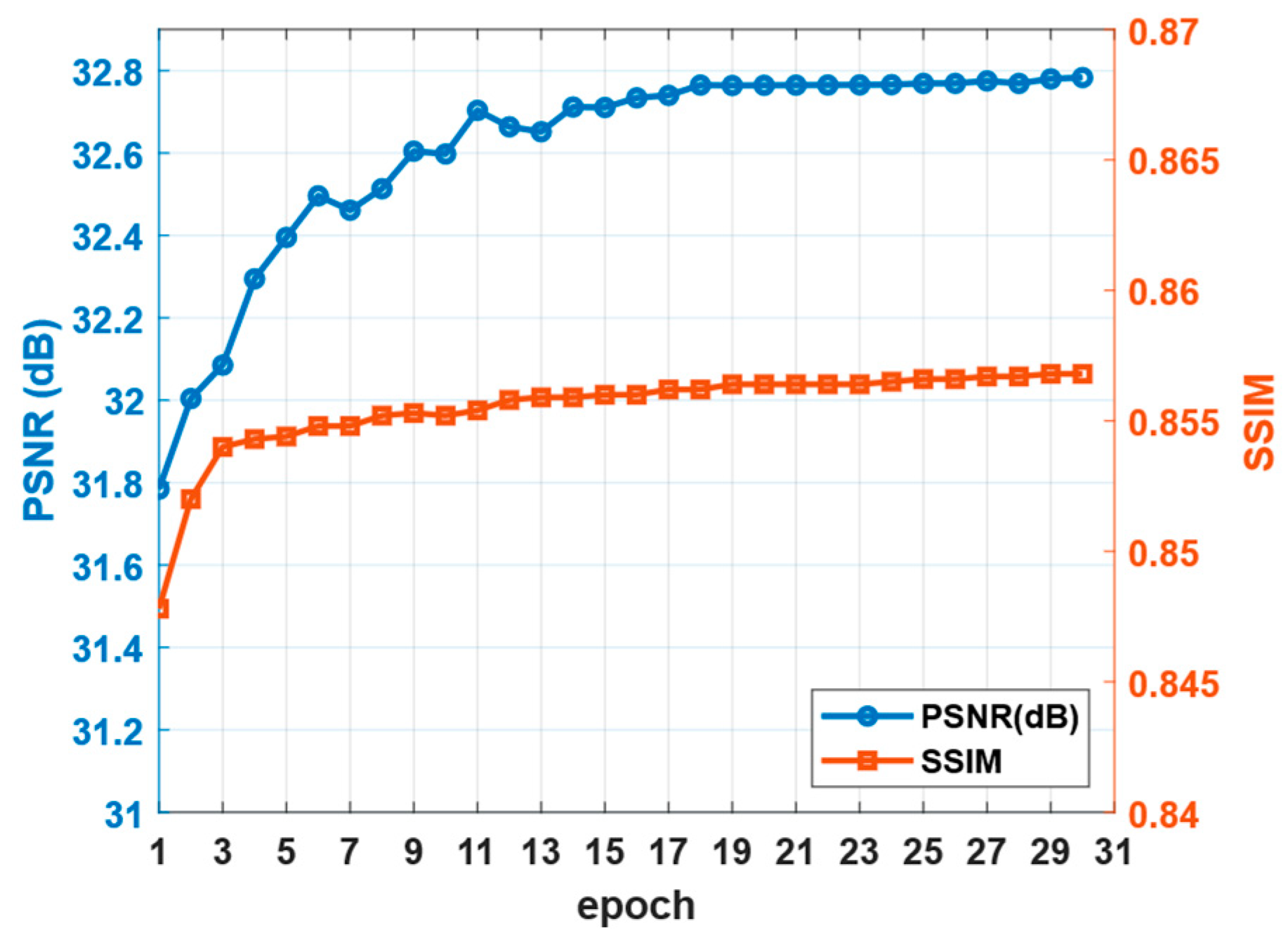
4.2.1. Model Parameters and Training Settings
4.2.2. Ablation Experiment
- (1)
- The Effect of Window Size in MAB
- (2)
- Effectiveness of CFB and IAB Modules
- (3)
- The influence of CFB weighting factor and IAB overlap rate
- (4)
- Comparison of Model Sizes
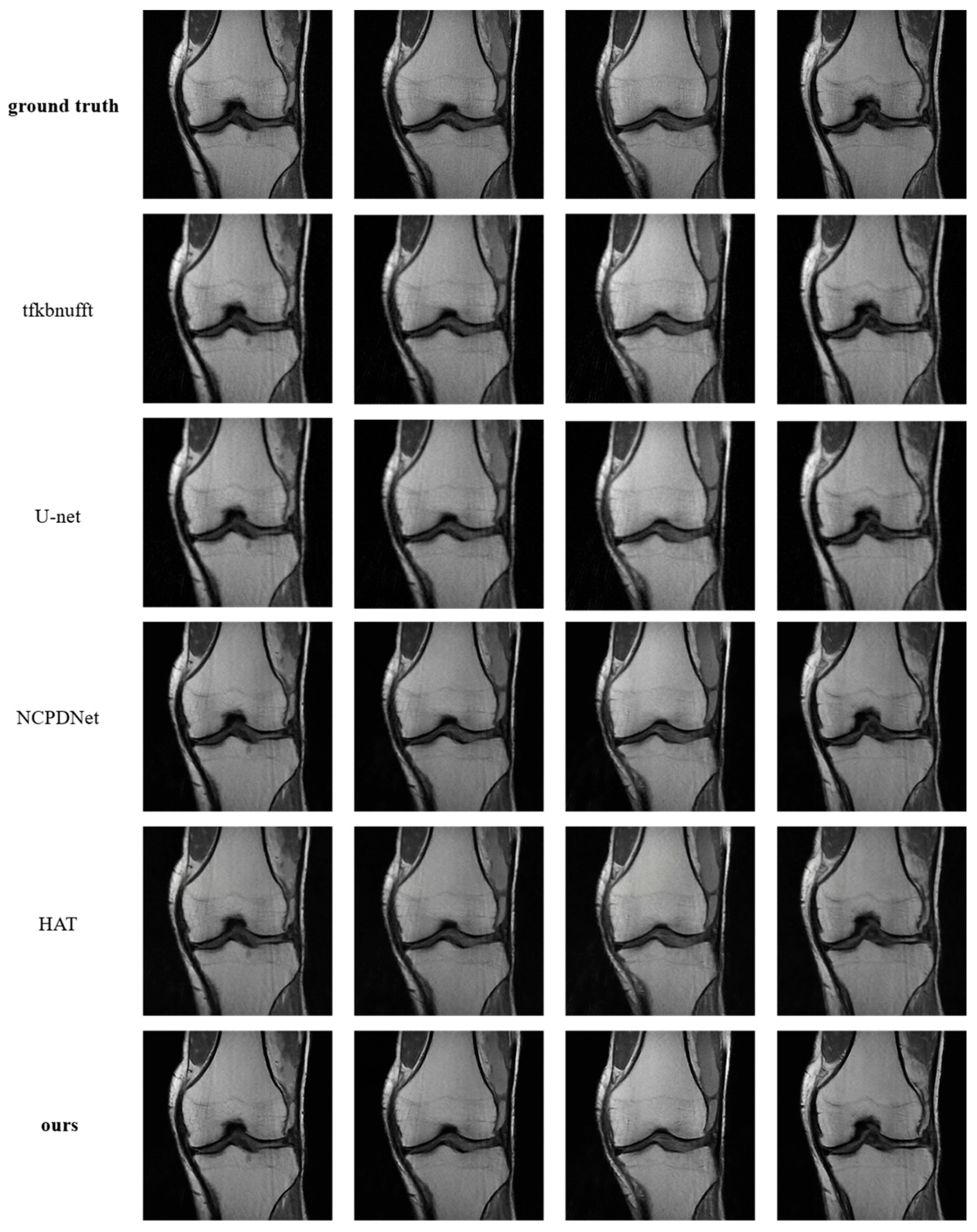
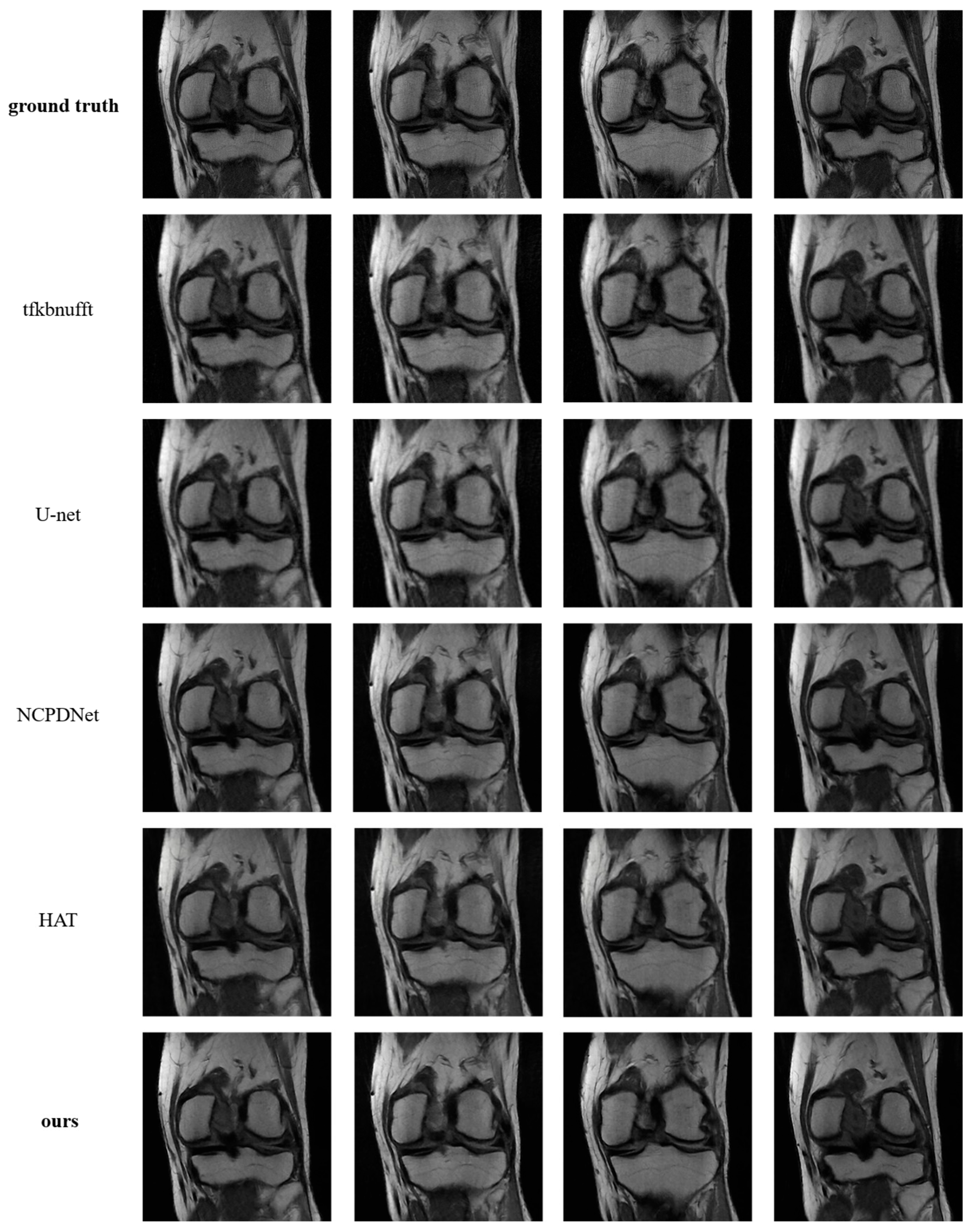
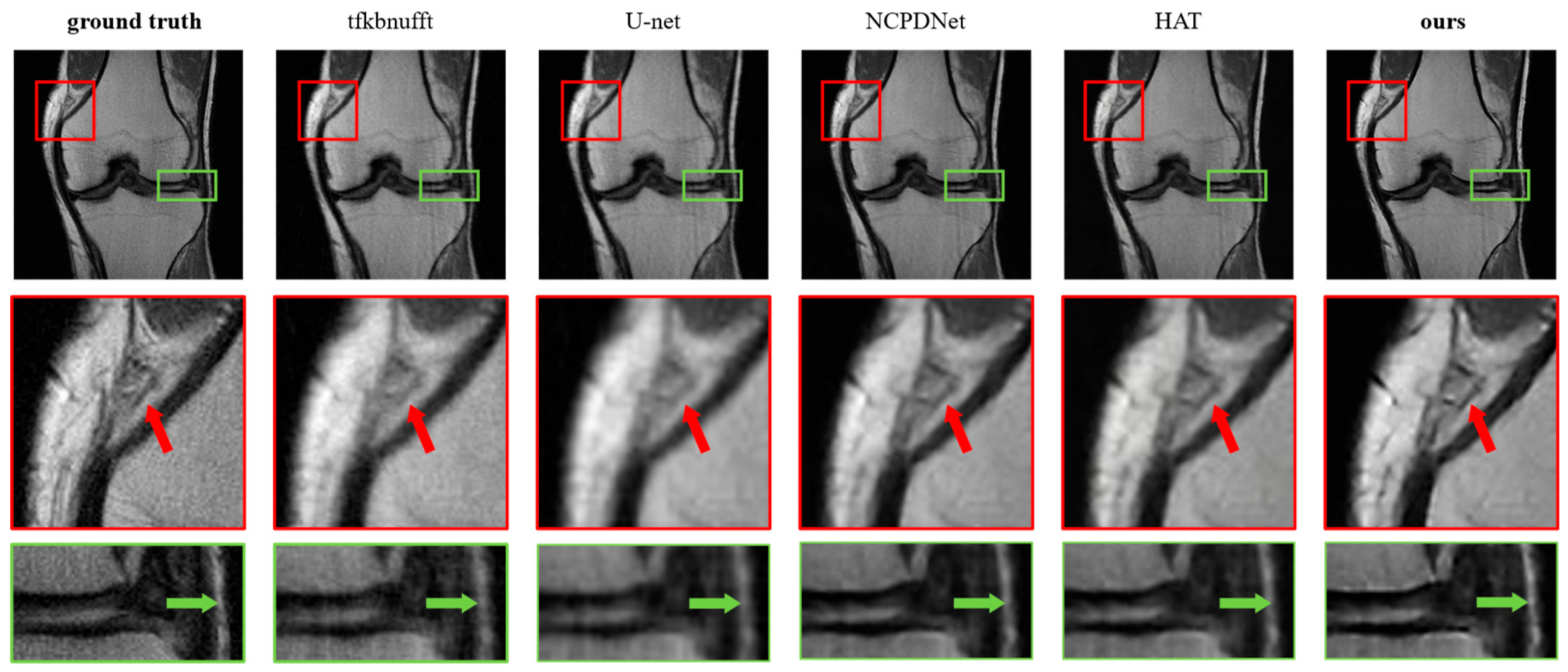
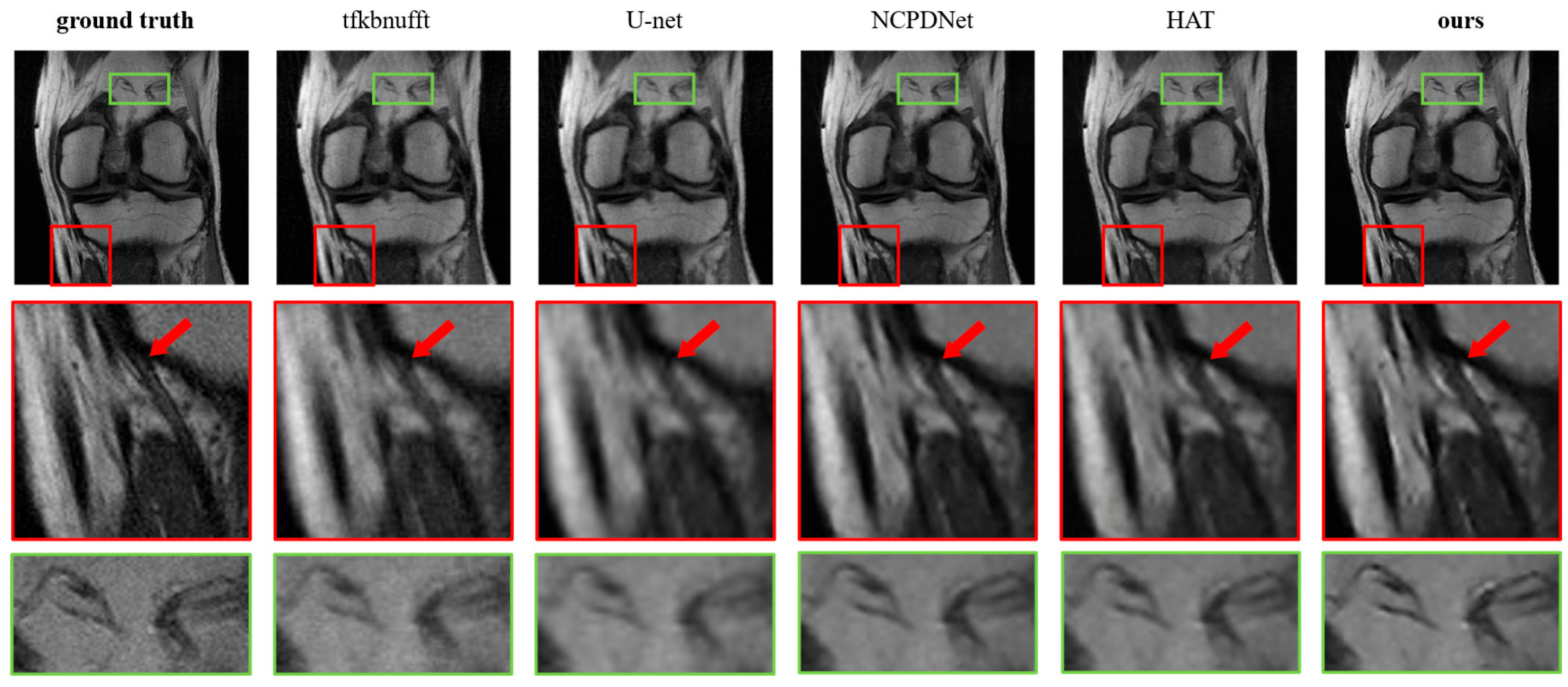
4.2.3. Contrast Experiment
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yu, X.; Zhou, N.; Zheng, J.; Liang, M.; Qiu, L.; Xu, Q. Mixture density knowledge distillation in super-resolution reconstruction of mri medical images. Med. Eng. Phys. 2025, 139, 104330. [Google Scholar] [CrossRef]
- Rahman, T.; Bilgin, A.; Cabrera, S.D. Multi-channel MRI reconstruction using cascaded Swinμ transformers with overlapped attention. Phys. Med. Biol. 2025, 70, 075002. [Google Scholar] [CrossRef]
- Cui, C.; Jung, K.J.; Al-Masni, M.A.; Kim, J.-H.; Kim, S.-Y.; Park, M.; Huang, S.Y.; Chun, S.Y.; Kim, D.-H. Deep Network Regularization for Phase-Based Magnetic Resonance Electrical Properties Tomography With Stein’s Unbiased Risk Estimator. IEEE Trans. Biomed. Eng. 2025, 72, 43–55. [Google Scholar] [CrossRef] [PubMed]
- Yadav, S.; Kumar, U. A Hybrid Dehazing and Illumination Based Approach for Preprocessing, Enhancement and Segmentation of Lung Images Using Deep Learning. Trait. Du Signal 2025, 42, 1161. [Google Scholar] [CrossRef]
- Wu, T.; Liu, S.; Zhang, H.; Zeng, T. Estimation-Denoising Integration Network Architecture With Updated Parameter for MRI Reconstruction. IEEE Trans. Comput. Imaging 2025, 11, 142–153. [Google Scholar] [CrossRef]
- Zhang, D.; Lin, L.; Deng, C. Advanced Imaging Strategies Based on Intelligent Micro/Nanomotors. Cyborg Bionic Syst. 2025, 6, 0384. [Google Scholar] [CrossRef]
- Plummer, J.W.; Hussain, R.; Bdaiwi, A.S.; Soderlund, S.A.; Hoyos, X.; Lanier, J.M.; Garrison, W.J.; Parra-Robles, J.; Willmering, M.M.; Niedbalski, P.J. A decay-modeled compressed sensing reconstruction approach for non-Cartesian hyperpolarized 129Xe MRI. Magn. Reson. Med. 2024, 92, 13. [Google Scholar] [CrossRef] [PubMed]
- Jurgita, I.; Justina, I.; Farnaz, L.S. A New Methodology for Evaluation of Large Vestibular Aqueduct in CT and MRI Images. Otol. Neurotol. 2024, 45, 440–446. [Google Scholar] [CrossRef]
- Cai, X.; Hou, X.; Sun, S.N.S. Accelerating image reconstruction for multi-contrast MRI based on Y-Net3+. J. X-Ray Sci. Technol. 2023, 31, 797–810. [Google Scholar] [CrossRef]
- Almansour, H.; Herrmann, J.; Gassenmaier, S.; Afat, S.; Jacoby, J.; Koerzdoerfer, G.; Nickel, D.; Mostapha, M.; Nadar, M.; Othman, A.E. Deep Learning Reconstruction for Accelerated Spine MRI: Prospective Analysis of Interchangeability. Radiology 2023, 306, 8. [Google Scholar] [CrossRef]
- Dane, B.; Bagga, B.; Bansal, B.; Beier, S.; Kim, S.; Reddy, A.; Fenty, F.; Keerthivasan, M.; Chandarana, H. Accelerated T2-weighted MRI of the Bowel at 3T Using a Single-shot Technique with Deep Learning-based Image Reconstruction: Impact on Image Quality and Disease Detection. Acad. Radiol. 2025, 32, 210–217. [Google Scholar] [CrossRef]
- Li, J.; Xia, Y.; Zhou, T.; Dong, Q.; Lin, X.; Gu, L.; Jiang, S.; Xu, M.; Wan, X.; Duan, G.; et al. Accelerated Spine MRI with Deep Learning Based Image Reconstruction: A Prospective Comparison with Standard MRI. Acad. Radiol. 2025, 32, 2121–2132. [Google Scholar] [CrossRef]
- Choi, Y.; Ko, J.S.; Park, J.E.; Jeong, G.; Seo, M.; Jun, Y.; Fujita, S.; Bilgic, B. Beyond the Conventional Structural MRI: Clinical Application of Deep Learning Image Reconstruction and Synthetic MRI of the Brain. Investig. Radiol. 2025, 60, 16. [Google Scholar] [CrossRef]
- Li, Y.; Qi, H.; Hu, Z.; Sun, H.; Li, G.; Zhang, Z.; Liu, Y.; Guo, H.; Chen, H. Deep Convolutional Neural Network Enhanced Non-uniform Fast Fourier Transform for Undersampled MRI Reconstruction. Int. J. Comput. Vis. 2025, 133, 4158–4176. [Google Scholar] [CrossRef]
- Khatami, H.R.; Riahi, M.A.; Abedi, M.M.; Dehkhargani, A.A. A comparative study over improved fast iterative shrinkage-thresholding algorithms: An application to seismic data reconstruction. Stud. Geophys. Geod. 2024, 68, 61. [Google Scholar] [CrossRef]
- Zumbo, S.; Mandija, S.; Meliadò, E.F.; Stijnman, P.; Meerbothe, T.G.; Berg, C.A.v.D.; Isernia, T.; Bevacqua, M.T. Unrolled Optimization via Physics-Assisted Convolutional Neural Network for MR-Based Electrical Properties Tomography: A Numerical Investigation. IEEE Open J. Eng. Med. Biol. 2024, 5, 505–513. [Google Scholar] [CrossRef] [PubMed]
- Pham, T.V.; Vu, T.N.; Le, H.M.Q.; Pham, V.-T.; Tran, T.-T. CapNet: An Automatic Attention-Based with Mixer Model for Cardiovascular Magnetic Resonance Image Segmentation. J. Digit. Imaging 2025, 38, 94–123. [Google Scholar] [CrossRef]
- Davarani, M.N.; Darestani, A.A.; Caas, V.G.; Harirchian, M.H.; Zarei, A.; Havadaragh, S.H.; Hashemi, H. Enhanced Segmentation of Active and Nonactive Multiple Sclerosis Plaques in T1 and FLAIR MRI Images Using Transformer-Based Encoders. Int. J. Imaging Syst. Technol. 2025, 35, 1–14. [Google Scholar] [CrossRef]
- Touvron, H.; Cord, M.; Douze, M.; Massa, F.; Sablayrolles, A.; Jegou, H. Training data-efficient image transformers & distillation through attention. In Proceedings of the 38th International Conference on Machine Learning, PMLR, Virtual, 18–24 July 2021; Volume 139, pp. 10347–10357. [Google Scholar]
- Feng, C.M.; Yan, Y.; Fu, H.; Chen, L.; Xu, Y. Task transformer network for joint MRI reconstruction and super-resolution. In Proceedings of the Medical Image Computing and Computer Assisted Intervention–MICCAI 2021: 24th International Conference, Strasbourg, France, 27 September–1 October 2021; Part VI 24. Springer International Publishing: Cham, Switzerland, 2021; pp. 307–317. [Google Scholar]
- Liang, J.; Cao, J.; Sun, G.; Zhang, K.; Van Gool, L.; Timofte, R. Swinir: Image restoration using swin transformer. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 1833–1844. [Google Scholar]
- Tanabene, A.; Radhakrishna, C.G.; Massire, A.; Nadar, M.S.; Ciuciu, P. Benchmarking 3D multi-coil NC-PDNet MRI reconstruction. In Proceedings of the IEEE 22nd International Symposium on Biomedical Imaging (ISBI), Houston, TX, USA, 14–17 April 2025. [Google Scholar]
- Guo, P.; Mei, Y.; Zhou, J.; Jiang, S.; Patel, V.M. ReconFormer: Accelerated MRI Reconstruction Using Recurrent Transformer. IEEE Trans. Med. Imaging 2024, 43, 12. [Google Scholar] [CrossRef]
- Xu, S.; Früh Marcel Hammernik, K.; Lingg, A.; Kübler, J.; Krumm, P.; Rueckert, D.; Gatidis, S.; Küstner, T. Self-supervised feature learning for cardiac Cine MR image reconstruction. IEEE Trans. Med. Imaging 2025, 44, 3858–3869. [Google Scholar] [CrossRef]
- Zbontar, J.; Knoll, F.; Sriram, A.; Murrell, T.; Huang, Z.; Muckley, M.J.; Defazio, A.; Stern, R.; Johnson, P.; Bruno, M. fastMRI: An open dataset and benchmarks for accelerated MRI. arXiv 2018, arXiv:1811.08839. [Google Scholar]
- Muckley, M.J.; Stern, R.; Murrell, T.; Knoll, F. TorchKbNufft: A high-level, hardware-agnostic non-uniform fast Fourier transform. In Proceedings of the ISMRM Workshop on Data Sampling & Image Reconstruction, Sedona, AZ, USA, 26–29 January 2020; p. 22. [Google Scholar]
- Ramzi, Z.; Ciuciu, P.; Starck, J.L. XPDNet for MRI reconstruction: An application to the fastMRI 2020 brain challenge. arXiv 2020, arXiv:2010.07290. [Google Scholar]
- Chen, X.; Wang, X.; Zhou, J.; Qiao, Y.; Dong, C. Activating more pixels in image super-resolution transformer. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 18–22 June 2023; pp. 22367–22377. [Google Scholar]




| fastMRI Datasets | Volumes | Slices | ||
|---|---|---|---|---|
| Multi-Coil | Single-Coil | Multi-Coil | Single-Coil | |
| training | 973 | 973 | 34,742 | 34,742 |
| validation | 199 | 199 | 7135 | 7135 |
| test | 118 | 108 | 4092 | 3903 |
| Datasets | Column Properties | Size | Introduce |
|---|---|---|---|
| Trainingsets | Kspace | (number of slices, height, width) | Simulate single coil K space data |
| reconstruction_rss | (number of slices, 320, 320) | The reconstruction of the single coil K-space cut to the central region is summed | |
| reconstruction_esc | (number of slices, 320, 320) | The ground truth of the real reconstructed image data is cropped to the central region | |
| Validationsets | Kspace | (number of slices, height, width) | Simulate single coil K space data |
| reconstruction_rss | (number of slices, 320, 320) | The reconstruction of the single coil K-space cut to the central region is summed | |
| reconstruction_esc | (number of slices, 320, 320) | The ground truth of the real reconstructed image data is cropped to the central region | |
| Testsets | Kspace | (number of slices, height, width) | Simulate single coil K space data |
| Mask | (width, 1) | The Cartesian undersampling mask |
| Radial Sampling | Number of Sampling Points | Sampling Length L | Number of Sampling Lines N |
|---|---|---|---|
| accelerating factor AF = 4 | 64,000 | 640 | 100 |
| accelerating factor AF = 6 | 42,240 | 640 | 66 |
| Parameter | Value |
|---|---|
| scale_factor | |
| oversampling_factor | |
| image_size | (640,400) |
| width | 2.34 |
| Window Size | Set5 Datasets | Set14 Datasets | fastMRI Datasets |
|---|---|---|---|
| 8 × 8 | 32.88 | 29.09 | 27.53 |
| 16 × 16 | 32.97 | 29.12 | 27.68 |
| 24 × 24 | 33.04 | 29.16 | 27.71 |
| 32 × 32 | 33.11 | 29.18 | 27.66 |
| Module | Different Combinations of Modules | |||
|---|---|---|---|---|
| CFB | ✗ | ✓ | ✗ | ✓ |
| IAB | ✗ | ✗ | ✓ | ✓ |
| PSNR (dB) | 34.14 | 34.19 | 34.21 | 34.25 |
| 0 | 0.01 | 0.1 | 1 | |
|---|---|---|---|---|
| PSNR(dB) | 27.81 | 27.97 | 27.90 | 27.86 |
| 0 | 0.25 | 0.50 | 0.75 | |
| PSNR(dB) | 27.85 | 27.81 | 27.91 | 27.86 |
| RMAGs | MABs | PSNR(dB) | SSIM |
|---|---|---|---|
| 1 | 1 | 32.1254 | 0.8512 |
| 2 | 32.3182 | 0.8526 | |
| 3 | 32.5846 | 0.8557 | |
| 2 | 1 | 32.469 | 0.8555 |
| 2 | 32.7404 | 0.8566 | |
| 3 | 32.7832 | 0.8579 | |
| 3 | 1 | 32.6585 | 0.8559 |
| 2 | 32.6597 | 0.8563 | |
| 3 | 32.7128 | 0.8574 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Huang, C.; Meng, J.; Chen, Q.; Ji, W.; Wang, Q. Super-Resolution Reconstruction Approach for MRI Images Based on Transformer Network. AI 2025, 6, 291. https://doi.org/10.3390/ai6110291
Liu X, Huang C, Meng J, Chen Q, Ji W, Wang Q. Super-Resolution Reconstruction Approach for MRI Images Based on Transformer Network. AI. 2025; 6(11):291. https://doi.org/10.3390/ai6110291
Chicago/Turabian StyleLiu, Xin, Chuangxin Huang, Jianli Meng, Qi Chen, Wuzheng Ji, and Qiuliang Wang. 2025. "Super-Resolution Reconstruction Approach for MRI Images Based on Transformer Network" AI 6, no. 11: 291. https://doi.org/10.3390/ai6110291
APA StyleLiu, X., Huang, C., Meng, J., Chen, Q., Ji, W., & Wang, Q. (2025). Super-Resolution Reconstruction Approach for MRI Images Based on Transformer Network. AI, 6(11), 291. https://doi.org/10.3390/ai6110291






