Abstract
Nowadays, online examination (exam in short) platforms are becoming more popular, demanding strong security measures for digital learning environments. This includes addressing key challenges such as head pose detection and estimation, which are integral for applications like automatic face recognition, advanced surveillance systems, intuitive human–computer interfaces, and enhancing driving safety measures. The proposed work holds significant potential in enhancing the security and reliability of online exam platforms. It achieves this by accurately classifying students’ attentiveness based on distinct head poses, a novel approach that leverages advanced techniques like federated learning and deep learning models. The proposed work aims to classify students’ attentiveness with the help of different head poses. In this work, we considered five head poses: front face, down face, right face, up face, and left face. A federated learning (FL) framework with a pre-trained deep learning model (ResNet50) was used to accomplish the classification task. To classify students’ activity (behavior) in an online exam environment using the FL framework’s local client device, we considered the ResNet50 model. However, identifying the best hyperparameters in the local client ResNet50 model is challenging. Hence, in this study, we proposed two hybrid bio-inspired optimized methods, namely, Particle Swarm Optimization with Genetic Algorithm (PSOGA) and Particle Swarm Optimization with Elitist Genetic Algorithm (PSOEGA), to fine-tune the hyperparameters of the ResNet50 model. The bio-inspired optimized methods employed in the ResNet50 model will train and classify the students’ behavior in an online exam environment. The FL framework trains the client model locally and sends the updated weights to the server model. The proposed hybrid bio-inspired algorithms outperform the GA and PSO when independently used. The proposed PSOGA not only outperforms the proposed PSOEGA but also outperforms the benchmark algorithms considered for performance evaluation by giving an accuracy of 95.97%.
1. Introduction
Incorporating the latest technology has been increasingly important in molding the educational experience in today’s quickly changing educational environment [1,2]. Teachers must work harder than ever to keep their students interested and paying attention when they learn online. Leveraging current technology is crucial for improving online learning and maintaining students’ engagement in today’s ever-changing educational environment. Addressing the challenging issue of monitoring and enhancing students’ engagement in online learning environments, this study aims to classify students’ activities based on head positions during examinations. This proposed work aims to contribute to the educational field by using modern technology to classify students’ activity based on distinct head positions. Opportunities and challenges abound as more and more schools embrace digital transformation, meaning that conventional classrooms give way to online learning. A significant obstacle is measuring and improving students’ engagement, essential for successful learning outcomes [3,4]. Online environments may need to be more conducive to using tried-and-true techniques for measuring focus, such as direct observation.
Federated learning (FL) allows numerous users to work together, while physically located at different places, by sharing data to train an incrementally better deep learning (DL) model [5,6]. Each client downloads a pre-trained model from a cloud data center. Confidential data are used to train the model, which can be subsequently summarized and encrypted [7,8]. In order to include the model updates in the centralized model, these updates will be transmitted to the cloud, decrypted, and averaged. Until the model is thoroughly trained, collaborative training continues iteration after iteration [9,10].
The federation of a central server and individual clients solves FL tasks. Unlike classical DL, FL has global and individual models [11,12]. In federated networks, validation data are distributed between devices, limiting access to the complete dataset. Instead, a central server may access a limited number of devices per communication cycle for local training and validation. The number of communication rounds is the traditional complexity measure in FL, so computing validation metrics significantly increases the cost. Since two equally essential parts perform the procedure, it is better to handle both simultaneously. FL needs more hyperparameters than the DL model to perform well [13,14]. FL hyperparameters significantly impact training overhead regarding computation and transmission load [15,16]. FL is a distributed ML paradigm in which several clients train models without centralizing data. In FL, hyperparameter selection influences the client’s local optimization and server aggregation operation, which is similar to typical ML. Manual selection of FL hyperparameters is burdensome for practitioners, as different applications have distinct training preferences [17,18,19].
The proposed work analyzes and classifies students’ head postures to assess their attentiveness during online exams within an FL environment. Several domains, including security monitoring and human–computer interaction, have begun to highlight head position analysis. Still, its potential in the classroom is yet to be thoroughly investigated, especially in measuring students’ attentiveness during online activity. This study offers a detailed knowledge of students’ involvement during virtual learning sessions by focusing on five head poses: front face, down face, right face, up face, and left face.
The biggest problem with the pre-trained DL model (ResNet50) is that its architecture and hyperparameter settings are task-specific and depend on the dataset [20,21,22]. Identifying and finding the best possible hyperparameters within the search space is an essential pre-training phase of the ResNet50 model. A bio-inspired optimization method is needed to identify the best possible hyperparameters in the ResNet50 model, thus achieving the highest accuracy by fine-tuning the identified best possible hyperparameters.
The deployment of meta-heuristic approaches for solving various problems has grown exponentially [23,24]. These methods outperform the conventional approaches to solving optimization problems of a very high degree of complexity. Further, they outperform standard optimization methods in terms of speed and ease of implementation.
Different categories of bio-inspired optimization approaches draw inspiration from Evolutionary Algorithms (EAs), Swarm Intelligence (SI), etc. The first type of algorithm, called EA, derives its motivation from attempts to model fundamental genetic processes like selection, crossover, and mutation. The second type of algorithm, the Swarm Intelligence (SI) technique, acts out a scenario similar to how swarms in the wild approach foraging for food. The Multi-Verse Optimizer (MVO), Particle Swarm Optimization (PSO), Salp Swarm Algorithm (SSA), and Whale Optimization Algorithm (WOA) are the most widely used techniques among these algorithms [25,26].
The key contributions of this paper are as follows:
- (1)
- Designing novel hybrid bio-inspired optimization methods for fine-tuning the hyperparameters of the ResNet50 model: PSOGA (Particle Swarm Optimization (PSO) with Genetic Algorithm (GA)) and PSOEGA (PSO with Elitist GA).
- (2)
- Recognizing students’ activity by classifying head poses during online exams using FL with the fine-tuned ResNet50 model and hybrid bio-inspired techniques.
2. Related Works
The COVID-19 pandemic has significantly contributed to the recent global surge in the popularity of online education [27]. Atom et al. [28] developed a model capable of identifying cheating activities during online exams using a webcam, wearable camera, and microphone. The results concluded that automated proctoring is adequate and accurate for conducting exams in an online environment. Ganidi et al. [29] proposed a model using deep learning techniques for face recognition in online exams. However, they become inoperative under poor lighting conditions and when specific postures are not recognized. Ashwin et al. [30] developed a proctoring algorithm utilizing transfer learning for deep learning, thus detecting anomalies: impersonation, using fraudulent objects/gadgets for cheating, and students’ abnormal gaze patterns. Song et al. [31] considered the YOLOv3 model for identifying individual sheep faces. Experimental results demonstrated that the YOLOv3 model has a higher detection edge than YOLOv1 and YOLOv2. Prathish et al. [32] considered features including point extraction and yaw angle detection to assist instructors in monitoring students during online exams. Hassan et al. [33] developed algorithms for extracting features from sensor signals and conducting human activity classification using machine learning models. Hussain et al. [34] proposed e-learning systems incorporating hybrid deep learning for automatic learning style identification. Their model outperforms existing works in detecting learning styles, thus enhancing the quality of customized content delivery.
FL is a collaborative, decentralized ML technique that enables training algorithms on edge devices [35,36]. In traditional ML techniques, the data from local devices are shared with the server for computation [37,38]. However, FL is applicable when devices do not want to share the data with the server. Roth et al. [39] proposed a federated learning approach for medical imaging classification, and based on the experimental results, federated learning in real-world scenarios can improve local model accuracy. McMahan et al. [40] demonstrated that FedAvg can train high-quality models with only limited communication rounds across different model architectures. Zhu et al. [41] proposed the federated deep reinforcement learning framework, designed to address issues related to small feature spaces in states and limited training data. Additionally, transfer learning methods within deep reinforcement learning were proposed to improve model performance. In federated learning, the working nodes are the participating users who own their local data and operate independently of the server. A key advantage of federated learning is its ability to preserve data privacy and security [42]. Rai et al. [43] presented an FL approach addressing client selection for balanced and unbalanced data and found that distributing data equally among clients can enhance its performance.
Table 1 highlights the outcomes of the literature survey. It is observed that task-specific architecture and hyperparameter choices depend on the dataset, which is a major issue of the ResNet50 model. Choosing the correct hyperparameters is a crucial task before training ResNet50. Finding the optimum hyperparameters requires an optimal searching space. The bio-inspired optimization methods employed in the ResNet50 model are used to train and classify students’ behavior in an online exam environment. Therefore, in this work, we consider the bio-inspired optimization methods essential for fine-tuning the hyperparameters of the ResNet50 model in order to achieve maximum accuracy.

Table 1.
Summary of key existing related works.
3. Proposed Methodology
3.1. Pre-trained Deep Learning Model (ResNet50)
In the proposed work using the FL framework, the learning models are trained in local client devices using the pre-trained ResNet50 model to train the data. To fine-tune hyperparameters in the ResNet50 model, we proposed the PSOGA and PSOEGA optimization methods as shown in Figure 1. ResNet50 has two types of mapping: identity mapping, which refers to the curved line, and residual mapping, which refers to everything other than the curved line, leading to the ultimate output of . Residual mapping, , refers to the difference between two points: y and x. In contrast, identity mapping, x, refers to itself, represented by x in the formula. ResNet-50 accomplishes the classification tasks after a convolution operation, three residual blocks, and an entire connection operation on the ResNet50 network, which includes 50 Conv2D layers, followed by the fully connected (FC) layer and the last layer (output layer) of the ResNet50 network. Consider the first two layers of convolution and pooling as feature engineering, local amplification, and feature extraction and the third and fourth layers of the FC layer as feature weighting. The flattened data, transformed into column vectors, are then fed to the feed-forward neural network to prepare the image for a multi-layer perceptron. These flattened data are used in each training iteration. The model’s ability to differentiate the primary and low-level image components and their classification are enhanced by the ReLU activation function, as shown in Figure 2.
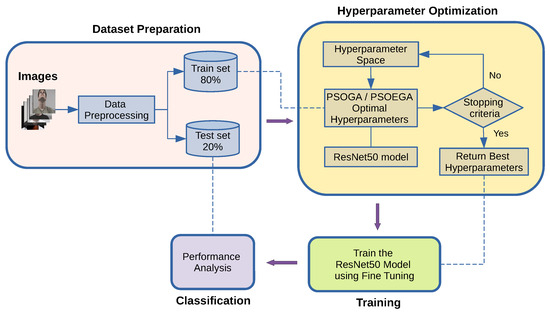
Figure 1.
Proposed PSOGA and PSOEGA optimization method in ResNet50 model.
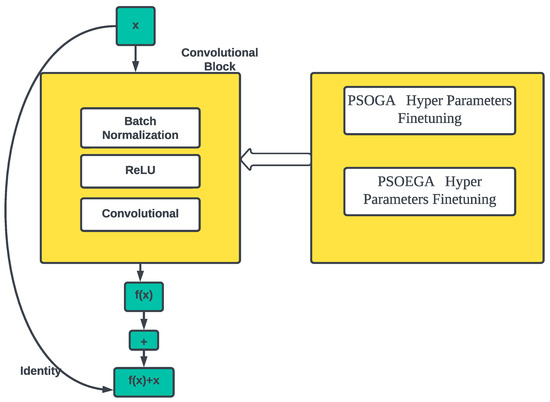
Figure 2.
Convolutional block in ResNet50.
3.2. Deployment of Deep Learning ResNet50 Model in Federated Learning Framework
FL facilitates collaboration among multiple parties for model development without explicitly sharing their data. The method involves training the model on a decentralized network, where data remain with the local client devices or servers at different locations. In the proposed work in the FL environment, the model is initialized on a central server and then distributed to the client devices that generate the data. Each client device trains the model using the locally available data and thus returns the updated model parameters to the central server. Hence, in our proposed FL approach with local client devices, we integrate the ResNet50 model to classify head poses during online exams. This proposed work mainly contributes to fine-tuning the best possible hyperparameters in local client devices for better accuracy. Therefore, we propose two hybrid bio-inspired methods, namely, Particle Swarm Optimization with Genetic Algorithm (PSOGA) and Particle Swarm Optimization with Elitist Genetic Algorithm (PSOEGA), to fine-tune the hyperparameters of the ResNet50 model as illustrated in Figure 3.
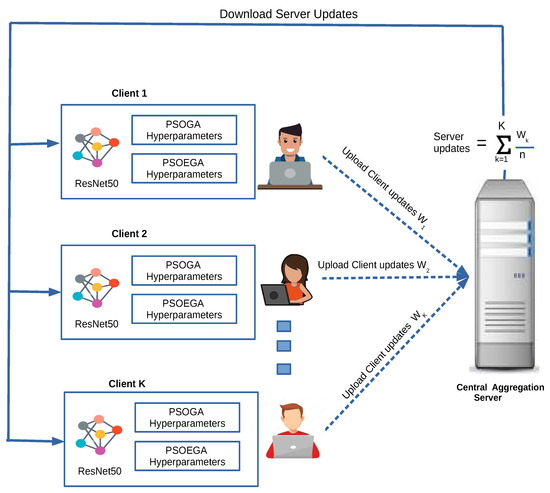
Figure 3.
ResNet50 model in federated learning framework.
The central server aggregates the updated parameters received from each device to update the global model. This updating process is iterative and will continue until the model achieves satisfactory performance and accuracy.
The client-side training of the FL model is described here. The LocalUpdate class trains the neural network on the local dataset for a given client. It takes as input the arguments, the dataset, and the indices of the samples that should be used for training. The class is initialized with a loss function, a list of selected clients, and a data loader that loads the local datasets. The training method of the LocalUpdate class takes a ResNet50 model as input and trains it on the local dataset using stochastic gradient descent. It initializes the optimizer and loss function and trains the model for a fixed number of epochs. During each round of FL, the local updates are performed by client devices using their local datasets with the help of the LocalUpdate class. The local clients send their updated model weights to the server after training so that the server can aggregate the weights across all local clients and update the global model. This updating process will be repeated for multiple rounds until it converges.
This section describes the FL model’s client-side aggregation. In contrast, in server-side aggregation, the server collects and aggregates the updated parameters received from each client and generates a global model. After the local clients complete the training, the clients’ updated parameters will be sent to the server for aggregation. Our proposed online proctoring system using the FL model performs the aggregation process on the server using the Federated Averaging algorithm. The server can start the training to enable each local client device to receive an initial global update. Then, each client can train this global model locally using the available data, and the clients’ updated parameters will be sent to the server, creating a new global model. This updating process is repeated until the accuracy and loss functions converge.
3.3. Hyperparameter Tuning of ResNet50 Model in Federated Learning Framework
The technique of hyperparameter tuning involves choosing the best hyperparameters for maximizing the performance of the ResNet50 model. The optimization process frequently comprises looking through a predetermined space or range of potential values for each hyperparameter. Therefore, in this work, we considered the GA, PSO, PSOGA, and PSOEGA methods to fine-tune the hyperparameters of the ResNet50 model.
3.4. Particle Swarm Optimization
Particle Swarm Optimization (PSO) uses m-dimensional real-number vectors to represent each particle in the population. The PSO method evolves by considering each particle swarm as a potential solution obtained within a finite search space [48].
PSO randomly initializes a particle population. After initializing the PSO population, an evolution procedure is run for several generations [49]. Each particle (individual) changes direction based on the position and velocity of their previous best experience (best) and the previous best experience of swarm particles (best) to find the optimal solution. Each particle’s current location and performance score would be computed after initializing its position and velocity. The following iteration would involve changing the particle’s new position after computing its velocity using both its current local position and its global position. Equation (1) calculates the updated velocity for particle i in iteration within the context of Particle Swarm Optimization (PSO). This velocity is computed as the sum of three terms: the inertia term w multiplied by the previous velocity , the cognitive term multiplied by a random factor , representing cognitive learning, and the difference between the particle’s current position and its personal best position . Additionally, it includes the social term multiplied by another random factor , representing social learning and the difference between the global best position and the particle’s current position .
Equation (2) updates the particle’s position from its current position at iteration k to its new position at iteration by incorporating its updated velocity .
3.5. Genetic Algorithm
Natural selection and evolution influence a meta-heuristic optimization technique called the Genetic Algorithm (GA). The GA acts on a population of candidate solutions in the context of hyperparameter tuning, where each candidate solution corresponds to a set of hyperparameters for a machine learning model. The GA searches for the ideal set of hyperparameters by applying genetic operations to the population, including selection, crossover, and mutation. Initialization selects search space candidates randomly [50]. In this investigation, we define search space size as an input from the hyperparameter set. We also utilize a uniform distribution to ensure the randomness of the search space candidates. Each hyperparameter has a defined range within which the gene can assume values, restricting the GA’s search space [51]. At population initialization, hyperparameters are set, and a random value is selected within the predefined interval for chromosome encoding. We include dropout, learning rate, and momentum coefficient for chromosomal encoding in an array. Each chromosome contains three genes, each encoding an accurate value for its hyperparameter.
Fitness finds selection, with the fittest chromosomes participating in reproduction. Current-generation chromosomes with the highest fitness levels are most likely to spawn the future population in this operator. This study utilized linear ranking and tournament selection.
Linear ranking classifies persons based on fitness, with selection probability exclusively based on fitness. The worst individual receives a rating of 1, and the second worst receives a grade of 2. This process continues until the top individual obtains a rating of N, which reflects the population’s chromosomal count. Each individual has a probability p of being selected from a population of N individuals based on their rating as defined by Equation (3). Here, p represents the probability or normalized score assigned to a particular rank and Rank is the rank position of an individual or item, typically starting from 1 for the highest rank, and N is the total number of individuals.
Elitist Genetic Algorithm
The Elitist Genetic Algorithm (EGA) is an elitism mechanism to ensure that the best solutions (individuals) from one generation are carried over to the next generation without any alteration. This approach prevents the loss of the best-found solutions due to the stochastic nature of genetic operations like crossover and mutation. The EGA is a strategy used in hyperparameter tuning to enhance optimization efficiency by preserving the best solutions across generations. In this approach, a Genetic Algorithm is employed to optimize hyperparameters, where a population of potential hyperparameter sets is evolved over multiple generations. Each set’s performance is evaluated using accuracy as a fitness function. The top-performing sets, identified through their fitness scores, are directly copied to the next generation to retain their high-quality attributes. The rest of the population is generated via selection, crossover, and mutation processes, introducing variability and enabling exploration. This strategy ensures that the best hyperparameter configurations are not lost, accelerating convergence toward an optimal solution while maintaining diversity within the population to avoid premature convergence.
3.6. Particle Swarm Optimization with Genetic Algorithm (PSOGA)
In the context of hyperparameter tuning, we combine these two algorithms to utilize both advantages and obtain global optimum results with fast convergence. First, we initialize the population swarm. PSO treats each particle as a potential solution (a set of hyperparameters) and follows the same steps discussed previously for PSO and mimics the particles’ movement in a search space to find the optimal hyperparameter configuration. To find the best local and global positions, the cognitive and social components are calculated. Velocity is updated using the inertia weight, cognitive component, and social component. The position is updated by adding the velocity to the current position and finally checks for the termination condition. If the condition is false, it will follow the GA approach and randomly select parents from the population. After that, mutation is performed to change the genetic material (hyperparameter values) of the offspring individuals. Then, the parents, along with the children, are added to the new population. The swarm is updated with a new population, and the process repeats until the termination condition. The worst-case time complexity of the proposed PSOGA is , where G is the number of generations, N is the number of particles in PSO or individuals in the GA, d is the number of dimensions (hyperparameters), and T is the time for computing the fitness function. Algorithm 1 shows the working principle of PSOGA.

3.7. Particle Swarm Optimization with Elitist Genetic Algorithm (PSOEGA)
PSOEGA uses a genetic method to refine the particle population further. Only a selection of particles, usually the best performers, are chosen for the genetic manipulations [52]. Crossover is used to make the elite individuals behave like genetic recombinants. Hyperparameter sets are traded between two top particles to create new solutions that take on the traits of both parents. When selected elite people undergo mutation, their hyperparameter settings undergo random modifications. So, instead of being stuck in local optima, the solution space can be explored more thoroughly. Because of processes like mutation and crossover, new generations will replace some members of the original population. Therefore, each iteration will have a new set of hyperparameter values. The ResNet50 model is trained to find how fit the newly generated people are. This phase determines whether the alterations introduced through genetic operations improve or worsen the model’s performance.
PSO and the EGA cooperate to fine-tune the ResNet50 model’s hyperparameters. As PSO directs the search in the solution space, the EGA uses genetic operations to fine-tune the best-performing solutions. The first step in optimization is starting with a population of particles with different ResNet50 hyperparameter sets. PSO continuously updates the particle locations and velocities per the fitness function when a stopping requirement is satisfied. Particles with the best performance, as determined by PSO, are chosen as the elite individuals to be used in the Genetic Algorithm. Elite individuals undergo genetic operations such as mutation and crossover to produce new sets of hyperparameters. By training the ResNet50 model, we can assess the fitness of the newly generated solutions. The combined PSO and EGA process stops after a certain number of iterations or when a convergence requirement is satisfied. The worst-case time complexity of the proposed PSOEGA is the same as that of PSOGA. The details of PSOEGA are shown in Algorithm 2.

4. Results Analysis
The dataset used for the project consists of publicly available head poses of 250 people from a research paper by Gourier et al. [53]. We also added images from the web to increase the dataset’s size and include various images with different backgrounds, ethnicities, and genders. The dataset contains instances of individuals with varying skin colors and with or without reading glasses. We filtered out the poses of the head as left, right, up, down, and front. A total of 1786 images were taken into account for conducting this experiment, consisting of five labels: front face, down face, right face, up face, and left face. Figure 4 shows the sample dataset used for our experimental study.

Figure 4.
Sample of dataset used. (a) Front face; (b) down face; (c) right face; (d) left face; (e) up face.
We consider three clients, a batch size of 32, and a training learning rate of 0.001 to perform our experiment. The input images are scaled to a size of 224 × 224 pixels. The model uses Stochastic Gradient Descent (SGD) as the optimizer. The dataset is partitioned into three parts, and we consider three clients for this experiment. We train the model with 596 images for each client. The dataset on each client is divided into training and testing sets with a ratio of 80:20. Table 2 shows the tools and technologies used for our work.

Table 2.
Tools and technologies used.
4.1. Parameters of Hyperparameter Tuning
The parameters considered for hyperparameter tuning are the learning rate and local epoch. Table 3 shows a list of parameters used in the experiment.

Table 3.
Hyperparameters used for the experiment.
4.2. Results of Centralized Deep Learning Models
Table 4 shows the results of running the centralized ResNet50 model for ten epochs with a learning rate of 0.01.

Table 4.
Results of centralized DL model.
4.3. Results of Decentralized Deep Learning Models
We executed the decentralized ResNet50 model on the dataset for ten epochs with a learning rate of 0.001. Table 5 shows the evaluation results of FL models on the dataset. Comparing this result to the centralized one, we observe that the performance of the decentralized DL models degrades by 3.7% when we run the models on the same settings as those of the centralized approach. This may be the result of overhead in communication or additional latency delays.

Table 5.
Results of decentralized DL model.
4.4. Results of Genetic Algorithm
In this approach, we run the ResNet-50 model on the Genetic Algorithm, as discussed in Section 3.5. We run the algorithm for different iterations, such as 10, 20, and 40 epochs. Table 6 shows the evaluation results of the GA on FL models. Here, we observe a fluctuation of 1 to 20 iterations. After that, it converges in the next 20 and 40 generations to an accuracy of 91.28%. with hyperparameters tuned to [0.01, 7]. For the next 20 and 40 generations, we got the same accuracy with the hyperparameters [0.01, 7]. For this experiment, we considered a population size of 20 and a mutation rate of 0.1. Figure 5 shows the trends of the accuracy and loss of the GA when we run it for 40 iterations.

Table 6.
Results of genetic algorithm.
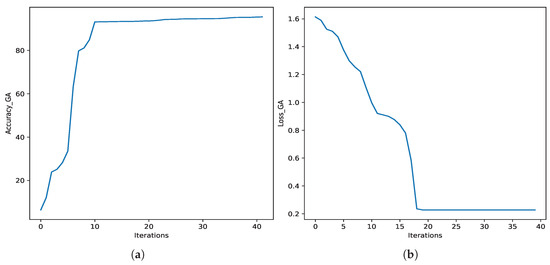
Figure 5.
Accuracy and loss. (a) Accuracy for GA; (b) loss graph for GA.
4.5. Results for Particle Swarm Optimization Algorithm
In this approach, we run the ResNet-50 model on the PSO algorithm, as discussed in Section 3.4. We run the algorithm for different iterations, such as 10, 20, and 40. Table 7 shows the evaluation results of PSO on FL models. Here, we observed that we achieved local optima in 10 iterations with an accuracy of 92.63%. and the global optima in 20 generations with an accuracy of 94.96%. After running the model for the next 20 and 40 generations, we obtained the same accuracy with the hyperparameter [0.01, 5]. We considered the following parameters for the PSO algorithm: swarm size 20, inertia weight is 0.9, Cognitive weight is 2.0, and Social weight is 2.0. Figure 6 show the trend of accuracy and loss of PSO when we run it for 40 iterations.

Table 7.
Results of PSO algorithm.
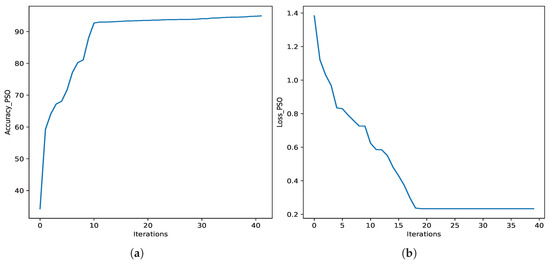
Figure 6.
Accuracy and loss. (a) Accuracy for PSO; (b) loss graph for PSO.
4.6. Results for Hybrid Bio-Inspired PSOGA Algorithm
We run the ResNet-50 model using the hybrid PSOGA algorithm, as discussed in Section 3.6. We run the algorithm for different iterations, such as 10, 20, and 40. Table 8 shows the evaluation results of PSOGA on FL models. We observe that the experimentation generates local optima in 10 iterations with an accuracy of 93.63%, and a global optimum is generated in 20 generations with an accuracy of 95.97%. We achieved the same accuracy for the next 20 and 40 generations with the hyperparameter [0.01, 7]. We considered the following parameters for the PSOGA method: a swarm size of 20, inertia weight of 0.9, cognitive weight of 2.0, social weight of 2.0, and mutation rate of 0.1.

Table 8.
Results of hybrid PSOGA algorithm.
Figure 7 shows the trends of accuracy and loss of PSOGA when we run it for 40 iterations.
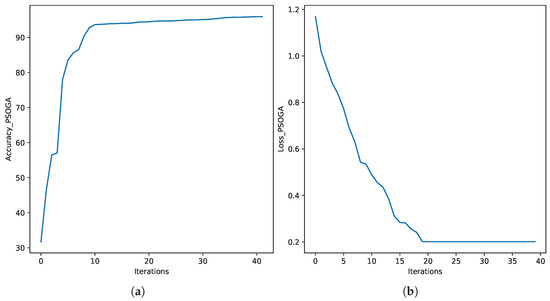
Figure 7.
Accuracy and loss. (a) Accuracy for PSOGA; (b) loss graph for PSOGA.
4.7. Results of Hybrid Bio-Inspired PSOEGA Algorithm
In this approach, we run the ResNet-50 model using the hybrid PSOEGA algorithm, as discussed in Section 3.7. We run the algorithm for different iterations, such as 10, 20, and 40. Table 9 shows the evaluation results of the GA on FL models. Here, we can observe that we obtain local optima in 10 iterations with an accuracy of 94.30% and global optima in 20 generations with an accuracy of 94.97%. After running it for the next 20 to 40 generations, we obtained the same accuracy using the hyperparameters [0.01, 5]. We considered the following parameters for the PSOEGA algorithm: swarm size is 20, inertia weight is 0.9, cognitive weight is 2.0, social weight is 2.0, and mutation rate is 0.1.

Table 9.
Results of PSOEGA algorithm.
Figure 8 shows the trends of accuracy and loss of PSOEGA when we run it for 40 iterations.
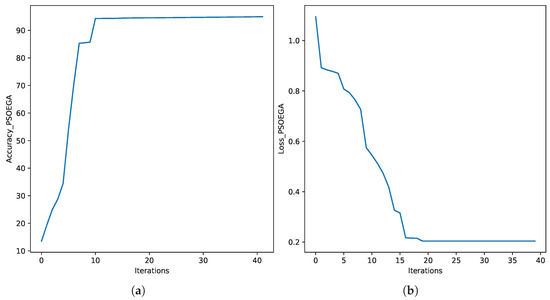
Figure 8.
Accuracy and loss. (a) Accuracy for PSOEGA; (b) loss graph for PSOEGA.
Table 10 demonstrates a comparison of our proposed approach to PSOGA, and PSOEGA with individual bio-optimized techniques is considered as the baseline. It is observed in Table 10 that the decentralized model has a lower accuracy compared to the centralized model. This is because the dataset is distributed across different clients, resulting in communication overhead between clients and the server model. Consequently, this overhead led to a 3.69% reduction in accuracy. After performing the hyperparameter tuning of the ResNet50 model in FL, we observed that from our proposed hybrid algorithms (PSOGA and PSOEGA), PSOGA gives slightly higher accuracy than PSOEGA. We considered the top 3%, which restricts our exploration capacity, resulting in comparatively less accuracy for PSOEGA than PSOGA.

Table 10.
Comparison of proposed algorithm with other methods.
Based on the experimental results, we conclude that the proposed decentralized DL model with PSOGA outperforms the other models, with an accuracy of 95.97%. This algorithm outperforms the DL with GA and the centralized DL models, which also achieved respectable results but were marginally behind in accuracy and precision. The proposed DL with PSOEGA similarly demonstrates impressive performance, matching the centralized DL model in accuracy at 94.97%. In contrast to the conventional models developed by Potluri et al. [54], Verma et al. [55], and Khaireddin et al. [56], which exhibit significantly lower accuracy and incomplete metric data, the suggested approaches efficiently and robustly balance high accuracy and comprehensive metric performance. Combining DL with optimization methods like Genetic and Particle Swarm Algorithms effectively manages server storage and load while significantly improving recognition capabilities.
The proposed method for tuning hyperparameters in a DL model using the hybrid PSOGA and PSOEGA in FL demonstrates superior performance. While the decentralized technique is often less efficient than the centralized approach due to communication overhead, our hybrid PSOGA method surpasses PSOEGA in terms of accuracy. The enhanced performance can be attributed to hybrid PSOGA’s exceptional exploration capabilities, which randomly select parents from half the population. This allows for different crossover and mutation operations. On the other hand, the hybrid PSOEGA, which chooses parents based on the highest three fitness values, restricts the process of exploration and, as a result, produces lesser levels of accuracy. Although PSOEGA exhibits faster convergence because it utilizes elite parents to generate new individuals, its limited exploration leads to inferior performance compared to PSOGA.
5. Conclusions
We proposed a novel method to tune the hyperparameters of a DL model using the hybrid PSOGA and PSOEGA in FL. Compared to other methods, the proposed DL with the PSOGA method achieves the best accuracy rate of 95.97%, making it the most effective of the proposed algorithms. In addition, the F1-score, recall, and precision are also competitive at 0.92, 0.91, and 0.93, respectively. While DL with GA is 95.64%, it is as accurate as the Centralised DL Model, with F1-scores of 0.93. Our study finds that the result of the decentralized approach is less than that of the centralized approach due to the overhead of communication rounds. We proposed two hybrid approaches, PSOGA and PSOEGA, in which hybrid PSOGA gave higher accuracy than PSOEGA. Hybrid PSOGA has high exploration, as we randomly selected parents from half of the population and performed crossover and mutation operations. Meanwhile, in hybrid PSOEGA, we selected parents from the top three fitness values, which restricts our exploration capacity and results in comparatively less accuracy than PSOGA. In hybrid PSOEGA, we observed a faster convergence as we utilized elite parents to create new individuals for future iterations. These proposed models have some limitations. Further, the optimization process may require running the ResNet50 model many times, resulting in high computational costs for large datasets, and this makes it hard to test very complex cases.
Bio-inspired optimization methods will be used to handle more complex scenarios and improve model performance. Other frameworks can be explored to reduce the overhead of communication rounds between distributed nodes. Future advancements in fine-tuning hyperparameters can consider integrating other meta-heuristics or optimization techniques to develop hybrid bio-inspired approaches. These hybrid bio-inspired approaches can leverage the strengths of multiple algorithms and provide more effective and efficient hyperparameter optimization.
Author Contributions
R.S.: Conceptualization of this study, Methodology, Software, Writing original draft. N.P.: Conceptualization of this study, Methodology, Software, Writing original draft. R.M.R.G.: Conceptualization, Supervision, Writing—review and editing. B.R.M.: Supervision, Writing—review and editing. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data used are publicly available and their citation is provided in the manuscript.
Acknowledgments
We would like to express our gratitude to Ravi Ranjan Kumar for his assistance in the successful completion of this project.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| FL | federated learning |
| PSOGA | Particle Swarm Optimization with Genetic Algorithm |
| PSOEGA | Particle Swarm Optimization with Elite Genetic Algorithm |
| PSO | Particle Swarm Optimization |
| CNN | convolutional neural network |
| ML | machine learning |
| GA | Genetic Algorithm |
| SGD | Stochastic Gradient Descent |
| DL | deep learning |
References
- Pabba, C.; Kumar, P. A vision-based multi-cues approach for individual students’ and overall class engagement monitoring in smart classroom environments. Multimed. Tools Appl. 2023, 83, 1–32. [Google Scholar] [CrossRef]
- Kolar Rajagopal, A.; Subramanian, R.; Ricci, E.; Vieriu, R.L.; Lanz, O.; Kalpathi R, R.; Sebe, N. Exploring transfer learning approaches for head pose classification from multi-view surveillance images. Int. J. Comput. Vis. 2014, 109, 146–167. [Google Scholar] [CrossRef]
- Afroze, S.; Hoque, M.M. Head pose classification based on deep convolution networks. In Proceedings of the International Conference on Internet of Things and Connected Technologies, Patna, India, 3–5 July 2020; Springer: Berlin/Heidelberg, Germany, 2020; pp. 458–469. [Google Scholar]
- Malek, S.; Rossi, S. Head pose estimation using facial-landmarks classification for children rehabilitation games. Pattern Recognit. Lett. 2021, 152, 406–412. [Google Scholar] [CrossRef]
- Niu, Y.; Deng, W. Federated learning for face recognition with gradient correction. In Proceedings of the AAAI Conference on Artificial Intelligence, Online, 22 February–1 March 2022; Volume 36, pp. 1999–2007. [Google Scholar]
- Butt, M.A.; Qayyum, A.; Ali, H.; Al-Fuqaha, A.; Qadir, J. Towards secure private and trustworthy human-centric embedded machine learning: An emotion-aware facial recognition case study. Comput. Secur. 2023, 125, 103058. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, Y.; Wang, Y.; Wei, S.; Xu, Y.; Shang, X. Federated learning-outcome prediction with multi-layer privacy protection. Front. Comput. Sci. 2024, 18, 186604. [Google Scholar] [CrossRef]
- Simić, N.; Suzić, S.; Milošević, N.; Stanojev, V.; Nosek, T.; Popović, B.; Bajović, D. Enhancing Emotion Recognition through Federated Learning: A Multimodal Approach with Convolutional Neural Networks. Appl. Sci. 2024, 14, 1325. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, Y.; Wei, S.; Wang, Y.; Li, Y.; Shang, X. Doubly contrastive representation learning for federated image recognition. Pattern Recognit. 2023, 139, 109507. [Google Scholar] [CrossRef]
- Wen, J.; Zhang, Z.; Lan, Y.; Cui, Z.; Cai, J.; Zhang, W. A survey on federated learning: Challenges and applications. Int. J. Mach. Learn. Cybern. 2023, 14, 513–535. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Li, H.; Zhang, M. Hyper-parameter tuning of federated learning based on particle swarm optimization. In Proceedings of the 2021 IEEE 7th International Conference on Cloud Computing and Intelligent Systems (CCIS), Xi’an, China, 7–8 November 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 99–103. [Google Scholar]
- Parra-Ullauri, J.; Zhang, X.; Bravalheri, A.; Nejabati, R.; Simeonidou, D. Federated Hyperparameter Optimisation with Flower and Optuna. In Proceedings of the 38th ACM/SIGAPP Symposium on Applied Computing, Tallinn, Estonia, 27–31 March 2023; pp. 1209–1216. [Google Scholar]
- Khodak, M.; Tu, R.; Li, T.; Li, L.; Balcan, M.F.F.; Smith, V.; Talwalkar, A. Federated hyperparameter tuning: Challenges, baselines, and connections to weight-sharing. Adv. Neural Inf. Process. Syst. 2021, 34, 19184–19197. [Google Scholar]
- Zhou, Y.; Ram, P.; Salonidis, T.; Baracaldo, N.; Samulowitz, H.; Ludwig, H. Single-shot general hyper-parameter optimization for federated learning. In Proceedings of the Eleventh International Conference on Learning Representations, Virtual Event, 25–29 April 2022. [Google Scholar]
- Zhang, H.; Zhang, M.; Liu, X.; Mohapatra, P.; DeLucia, M. Fedtune: Automatic tuning of federated learning hyper-parameters from system perspective. In Proceedings of the MILCOM 2022–2022 IEEE Military Communications Conference (MILCOM), Rockville, ML, USA, 1–2 December 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 478–483. [Google Scholar]
- Kundroo, M.; Kim, T. Federated learning with hyper-parameter optimization. J. King Saud-Univ.-Comput. Inf. Sci. 2023, 35, 101740. [Google Scholar] [CrossRef]
- Kundroo, M.; Kim, T. Efficient Federated Learning with Adaptive Client-Side Hyper-Parameter Optimization. In Proceedings of the 2023 IEEE 43rd International Conference on Distributed Computing Systems (ICDCS), Hong Kong, China, 18–21 July 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 973–974. [Google Scholar]
- Chen, H.; Krompass, D.; Gu, J.; Tresp, V. FedPop: Federated Population-based Hyperparameter Tuning. arXiv 2023, arXiv:2308.08634. [Google Scholar]
- Srivinay; Manujakshi, B.C.; Kabadi, M.G.; Naik, N. A Hybrid Stock Price Prediction Model Based on PRE and Deep Neural Network. Data 2022, 7, 51. [Google Scholar] [CrossRef]
- Ibrahim, R.; Ghnemat, R.; Abu Al-Haija, Q. Improving Alzheimer’s Disease and Brain Tumor Detection Using Deep Learning with Particle Swarm Optimization. AI 2023, 4, 551–573. [Google Scholar] [CrossRef]
- Yang, J.; Wang, Z.; Huang, B.; Xiao, J.; Liang, C.; Han, Z.; Zou, H. HeadPose-Softmax: Head pose adaptive curriculum learning loss for deep face recognition. Pattern Recognit. 2023, 140, 109552. [Google Scholar] [CrossRef]
- Chao, Y.; Liu, T.; Shen, L.M. Method of recognizing sleep postures based on air pressure sensor and convolutional neural network: For an air spring mattress. Eng. Appl. Artif. Intell. 2023, 121, 106009. [Google Scholar] [CrossRef]
- Golnoori, F.; Boroujeni, F.Z.; Monadjemi, A. Metaheuristic algorithm based hyper-parameters optimization for skin lesion classification. Multimed. Tools Appl. 2023, 82, 1–33. [Google Scholar] [CrossRef]
- Kaveh, M.; Mesgari, M.S. Application of meta-heuristic algorithms for training neural networks and deep learning architectures: A comprehensive review. Neural Process. Lett. 2023, 55, 4519–4622. [Google Scholar] [CrossRef] [PubMed]
- Mostafa, R.R.; El-Attar, N.E.; Sabbeh, S.F.; Vidyarthi, A.; Hashim, F.A. ST-AL: A hybridized search based metaheuristic computational algorithm towards optimization of high dimensional industrial datasets. Soft Comput. 2023, 27, 13553–13581. [Google Scholar] [CrossRef] [PubMed]
- Liu, W.; Liu, Z.; Xiong, S.; Wang, M. Comparative prediction performance of the strength of a new type of Ti tailings cemented backfilling body using PSO-RF, SSA-RF, and WOA-RF models. Case Stud. Constr. Mater. 2024, 20, e02766. [Google Scholar] [CrossRef]
- Muzaffar, A.W.; Tahir, M.; Anwar, M.W.; Chaudry, Q.; Mir, S.R.; Rasheed, Y. A systematic review of online exams solutions in e-learning: Techniques, tools, and global adoption. IEEE Access 2021, 9, 32689–32712. [Google Scholar] [CrossRef]
- Atoum, Y.; Chen, L.; Liu, A.X.; Hsu, S.D.; Liu, X. Automated online exam proctoring. IEEE Trans. Multimed. 2017, 19, 1609–1624. [Google Scholar] [CrossRef]
- Ganidisastra, A.H.S.; Bandung, Y. An incremental training on deep learning face recognition for m-learning online exam proctoring. In Proceedings of the 2021 IEEE Asia Pacific Conference on Wireless and Mobile (APWiMob), Bandung, Indonesia, 8–9 April 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 213–219. [Google Scholar]
- Ashwinkumar, J.; Kumaran, H.S.; Sivakarthikeyan, U.; Rajesh, K.P.; Lavanya, R. Deep Learning based Approach for Facilitating Online Proctoring using Transfer Learning. In Proceedings of the 2021 5th International Conference on Computer, Communication and Signal Processing (ICCCSP), Chennai, India, 24–25 May 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 306–312. [Google Scholar]
- Song, S.; Liu, T.; Wang, H.; Hasi, B.; Yuan, C.; Gao, F.; Shi, H. Using Pruning-Based YOLOv3 Deep Learning Algorithm for Accurate Detection of Sheep Face. Animals 2022, 12, 1465. [Google Scholar] [CrossRef] [PubMed]
- Prathish, S.; Athi Narayanan, S.; Bijlani, K. An intelligent system for online exam monitoring. In Proceedings of the 2016 International Conference on Information Science (ICIS), Kochi, India, 12–13 August 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 138–143. [Google Scholar]
- Hassan, M.M.; Uddin, M.Z.; Mohamed, A.; Almogren, A. A robust human activity recognition system using smartphone sensors and deep learning. Future Gener. Comput. Syst. 2018, 81, 307–313. [Google Scholar] [CrossRef]
- Hussain, T.; Yu, L.; Asim, M.; Ahmed, A.; Wani, M.A. Enhancing E-Learning Adaptability with Automated Learning Style Identification and Sentiment Analysis: A Hybrid Deep Learning Approach for Smart Education. Information 2024, 15, 277. [Google Scholar] [CrossRef]
- Wahab, O.A.; Mourad, A.; Otrok, H.; Taleb, T. Federated machine learning: Survey, multi-level classification, desirable criteria and future directions in communication and networking systems. IEEE Commun. Surv. Tutor. 2021, 23, 1342–1397. [Google Scholar] [CrossRef]
- Ekmefjord, M.; Ait-Mlouk, A.; Alawadi, S.; Åkesson, M.; Stoyanova, D.; Spjuth, O.; Toor, S.; Hellander, A. Scalable federated machine learning with FEDn. arXiv 2021, arXiv:2103.00148. [Google Scholar]
- Verbraeken, J.; Wolting, M.; Katzy, J.; Kloppenburg, J.; Verbelen, T.; Rellermeyer, J.S. A survey on distributed machine learning. ACM Comput. Surv. (Csur) 2020, 53, 1–33. [Google Scholar] [CrossRef]
- Drainakis, G.; Katsaros, K.V.; Pantazopoulos, P.; Sourlas, V.; Amditis, A. Federated vs. centralized machine learning under privacy-elastic users: A comparative analysis. In Proceedings of the 2020 IEEE 19th International Symposium on Network Computing and Applications (NCA), Cambridge, MA, USA, 24–27 November 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1–8. [Google Scholar]
- Roth, H.R.; Chang, K.; Singh, P.; Neumark, N.; Li, W.; Gupta, V.; Gupta, S.; Qu, L.; Ihsani, A.; Bizzo, B.C.; et al. Federated learning for breast density classification: A real-world implementation. In Domain Adaptation and Representation Transfer, and Distributed and Collaborative Learning; Springer: Berlin/Heidelberg, Germany, 2020; pp. 181–191. [Google Scholar]
- McMahan, B.; Moore, E.; Ramage, D.; Hampson, S.; y Arcas, B.A. Communication-efficient learning of deep networks from decentralized data. In Proceedings of the 20th International Conference on Artificial Intelligence and Statistics, Fort Lauderdale, FL, USA, 20–22 April 2017. [Google Scholar]
- Zhu, H.; Jin, Y. Multi-objective evolutionary federated learning. IEEE Trans. Neural Netw. Learn. Syst. 2019, 31, 1310–1322. [Google Scholar] [CrossRef]
- Li, Q.; Wen, Z.; Wu, Z.; Hu, S.; Wang, N.; Li, Y.; Liu, X.; He, B. A survey on federated learning systems: Vision, hype and reality for data privacy and protection. IEEE Trans. Knowl. Data Eng. 2021, 35, 3347–3366. [Google Scholar] [CrossRef]
- Rai, S.; Kumari, A.; Prasad, D.K. Client Selection in Federated Learning under Imperfections in Environment. AI 2022, 3, 124–145. [Google Scholar] [CrossRef]
- Cao, L.; Wang, Y.; Zhang, B.; Jin, Q.; Vasilakos, A.V. GCHAR: An efficient Group-based Context—Aware human activity recognition on smartphone. J. Parallel Distrib. Comput. 2018, 118, 67–80. [Google Scholar] [CrossRef]
- Reyes-Ortiz, J.L.; Oneto, L.; Sama, A.; Parra, X.; Anguita, D. Transition-aware human activity recognition using smartphones. Neurocomputing 2016, 171, 754–767. [Google Scholar] [CrossRef]
- San-Segundo, R.; Blunck, H.; Moreno-Pimentel, J.; Stisen, A.; Gil-Martín, M. Robust Human Activity Recognition using smartwatches and smartphones. Eng. Appl. Artif. Intell. 2018, 72, 190–202. [Google Scholar] [CrossRef]
- Ronao, C.A.; Cho, S.B. Human activity recognition with smartphone sensors using deep learning neural networks. Expert Syst. Appl. 2016, 59, 235–244. [Google Scholar] [CrossRef]
- Aguerchi, K.; Jabrane, Y.; Habba, M.; El Hassani, A.H. A CNN Hyperparameters Optimization Based on Particle Swarm Optimization for Mammography Breast Cancer Classification. J. Imaging 2024, 10, 30. [Google Scholar] [CrossRef] [PubMed]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; IEEE: Piscataway, NJ, USA, 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Holland, J.H. Genetic algorithms. Sci. Am. 1992, 267, 66–73. [Google Scholar] [CrossRef]
- Ayan, E. Genetic algorithm-based hyperparameter optimization for convolutional neural networks in the classification of crop pests. Arab. J. Sci. Eng. 2024, 49, 3079–3093. [Google Scholar] [CrossRef]
- Yang, Q.; Guo, X.; Gao, X.D.; Xu, D.D.; Lu, Z.Y. Differential elite learning particle swarm optimization for global numerical optimization. Mathematics 2022, 10, 1261. [Google Scholar] [CrossRef]
- Gourier, N.; Hall, D.; Crowley, J.L. Estimating Face orientation from Robust Detection of Salient Facial Structures. In FG Net Workshop on Visual Observation of Deictic Gestures; Cambridge, UK, 2004; Available online: https://www.semanticscholar.org/paper/Estimating-Face-orientation-from-Robust-Detection-Gourier-Hall/bbb3e9cdfd89711939ce2e8ed7afb3ff264f02ce (accessed on 16 January 2024).
- Potluri, T.; Venkata, K.K.K. An automated online proctoring system using attentive-net to assess student mischievous behavior. Multimed. Tools Appl. 2023, 82, 30375–30404. [Google Scholar] [CrossRef]
- Verma, P.; Malhotra, N.; Suri, R.; Kumar, R. Automated smart artificial intelligence-based proctoring system using deep learning. Soft Comput. 2024, 28, 3479–3489. [Google Scholar] [CrossRef]
- Khaireddin, Y.; Chen, Z. Facial emotion recognition: State of the art performance on FER2013. arXiv 2021, arXiv:2105.03588. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).