Enhancing Thermo-Acoustic Waste Heat Recovery through Machine Learning: A Comparative Analysis of Artificial Neural Network–Particle Swarm Optimization, Adaptive Neuro Fuzzy Inference System, and Artificial Neural Network Models
Abstract
1. Introduction
2. Literature Review
3. Motivation of the Study
4. Proposed Approaches
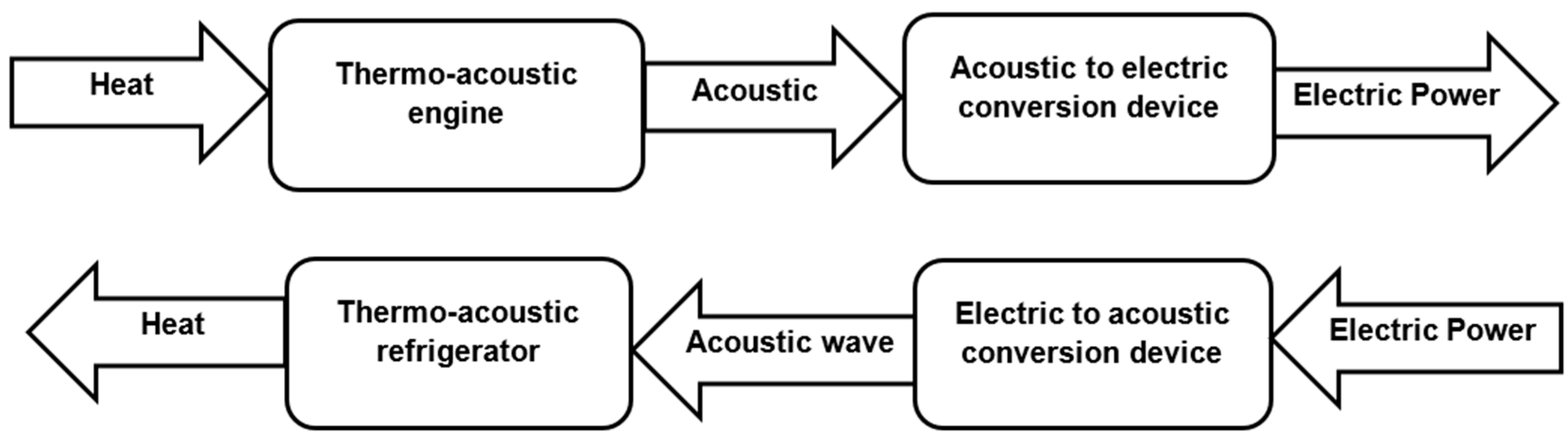
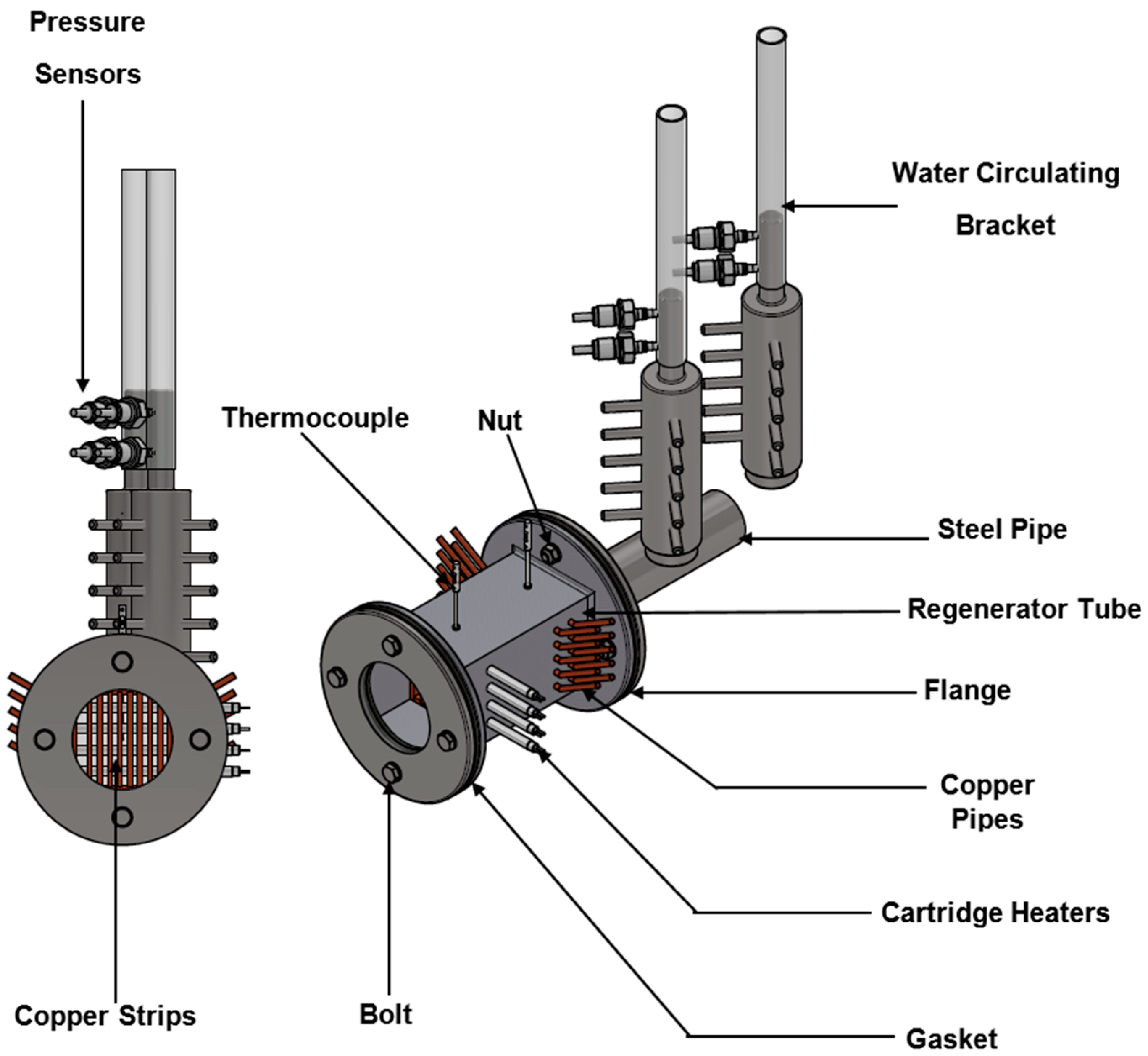
4.1. Design of a Thermo-Acoustic Generator
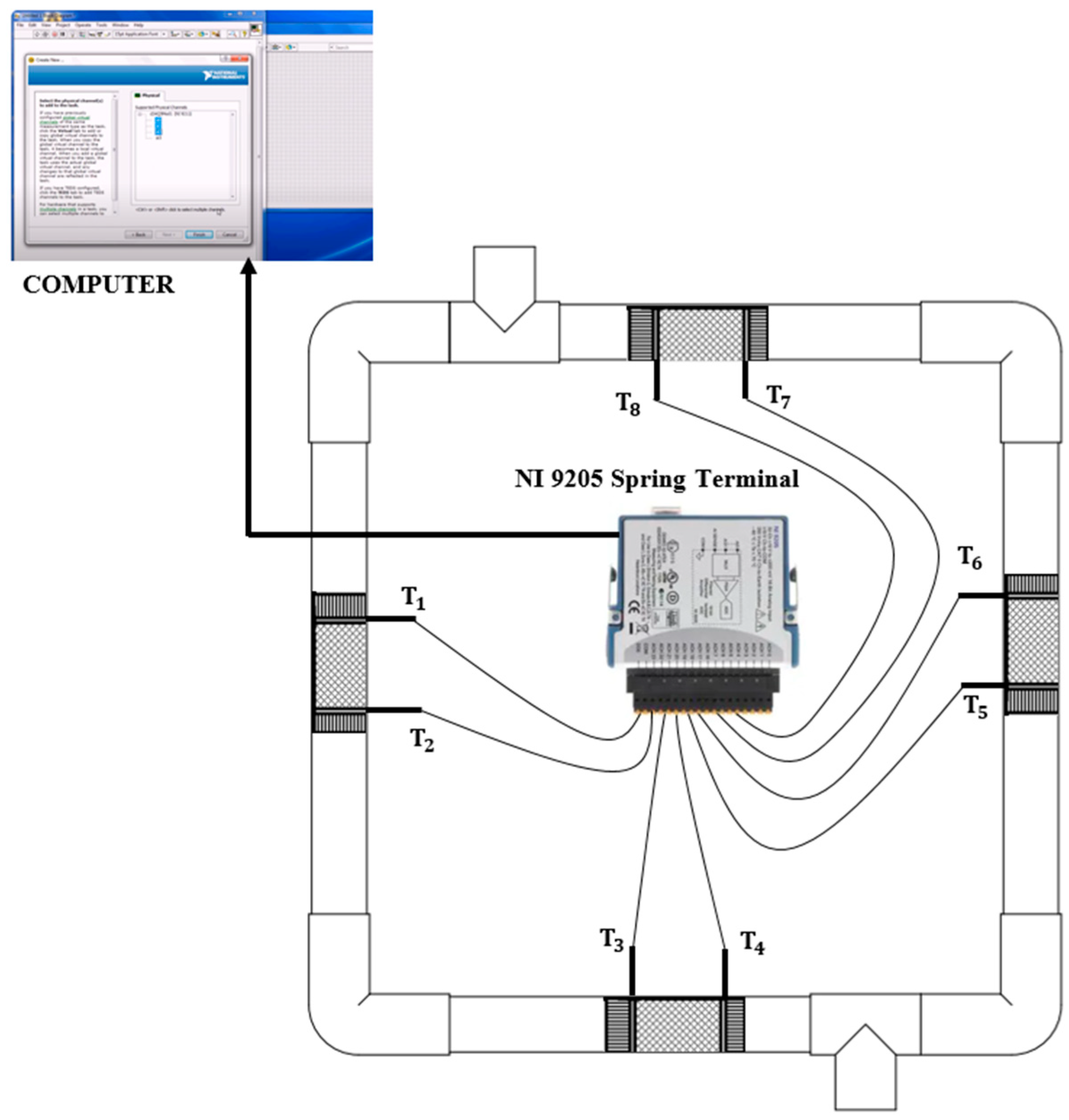
4.2. Temperature Measurements
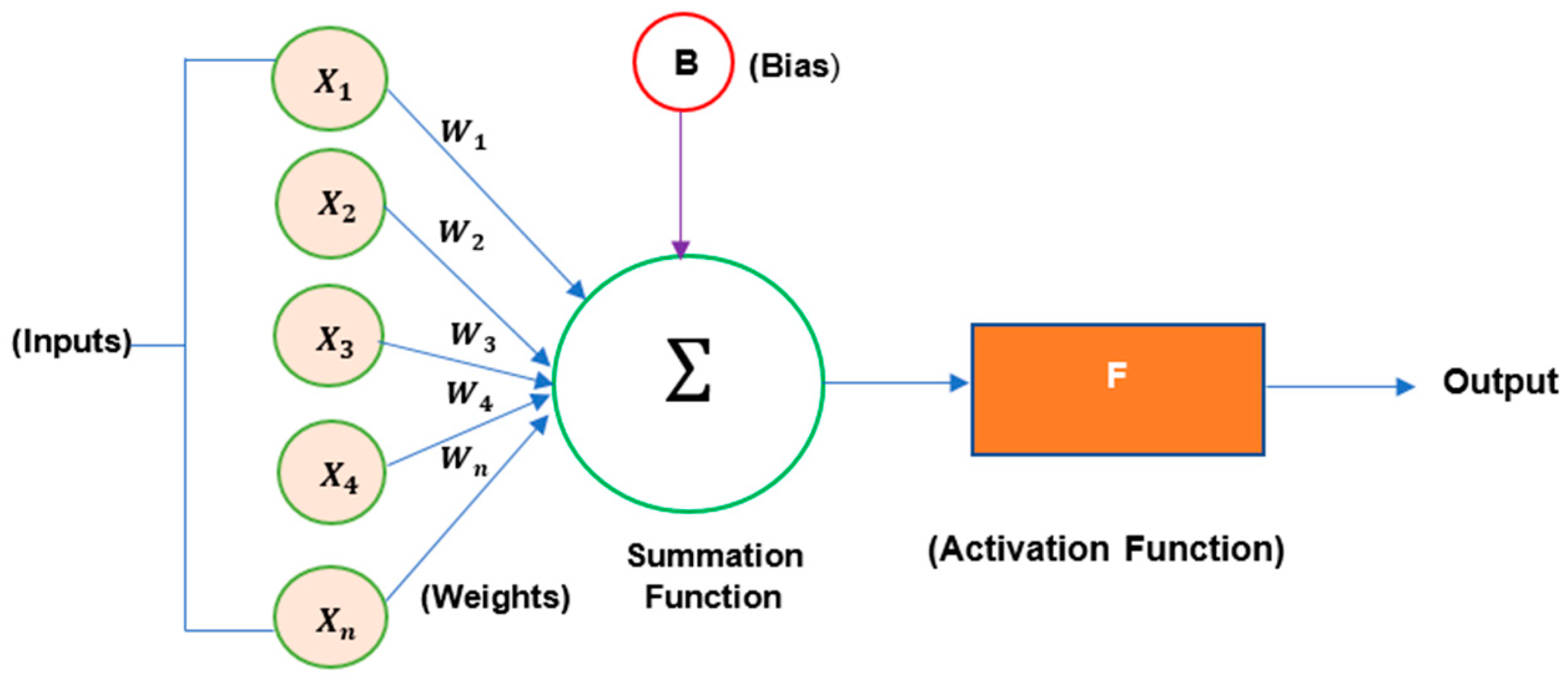
4.3. Artificial Neural Network (ANN)
4.4. Adaptive Neuro Fuzzy-Inference System (ANFIS)
4.5. Hybrid ANN-PSO
5. Results and Discussion
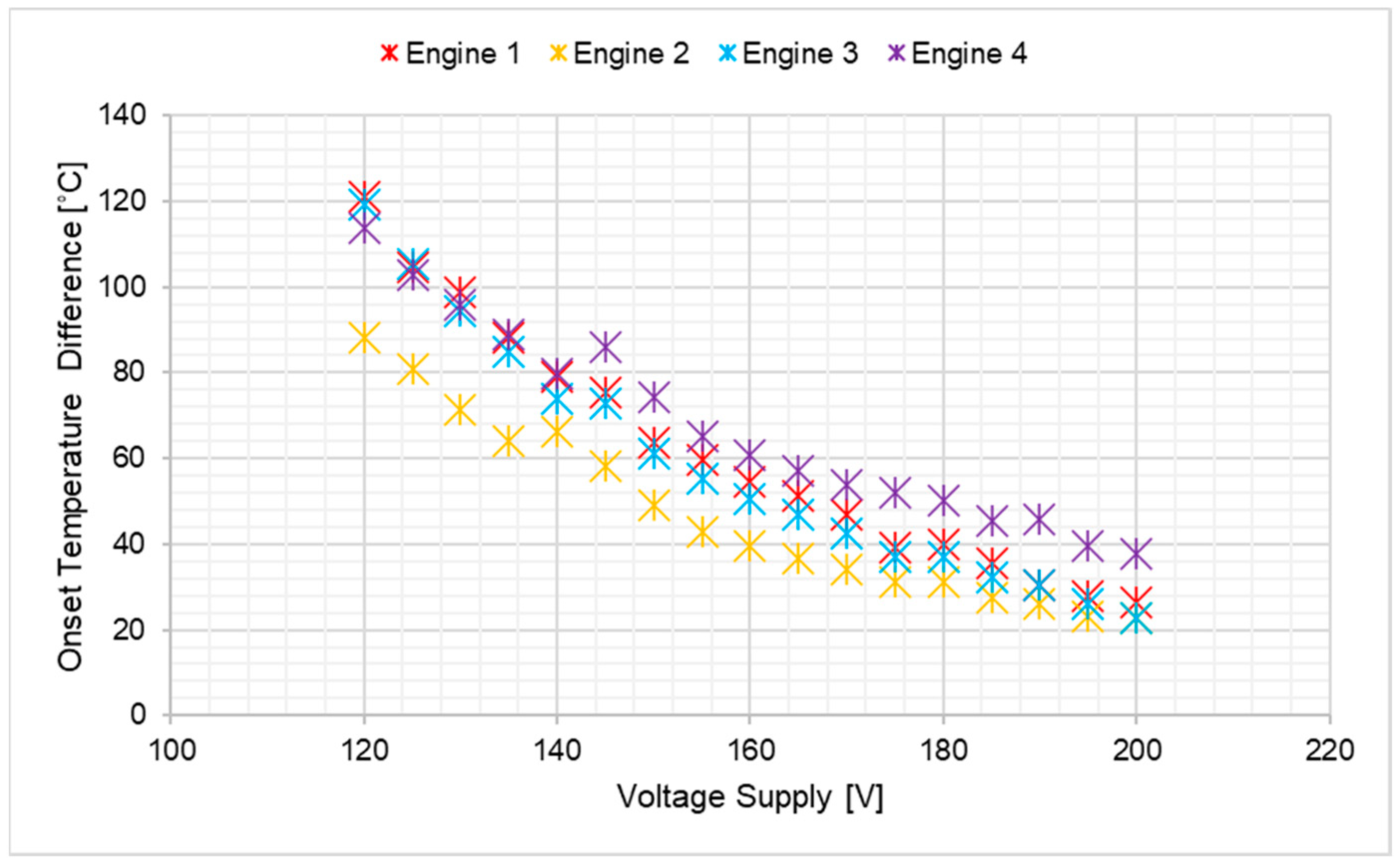
5.1. Comparison of a Temperature Difference of a Four-Stage Configuration
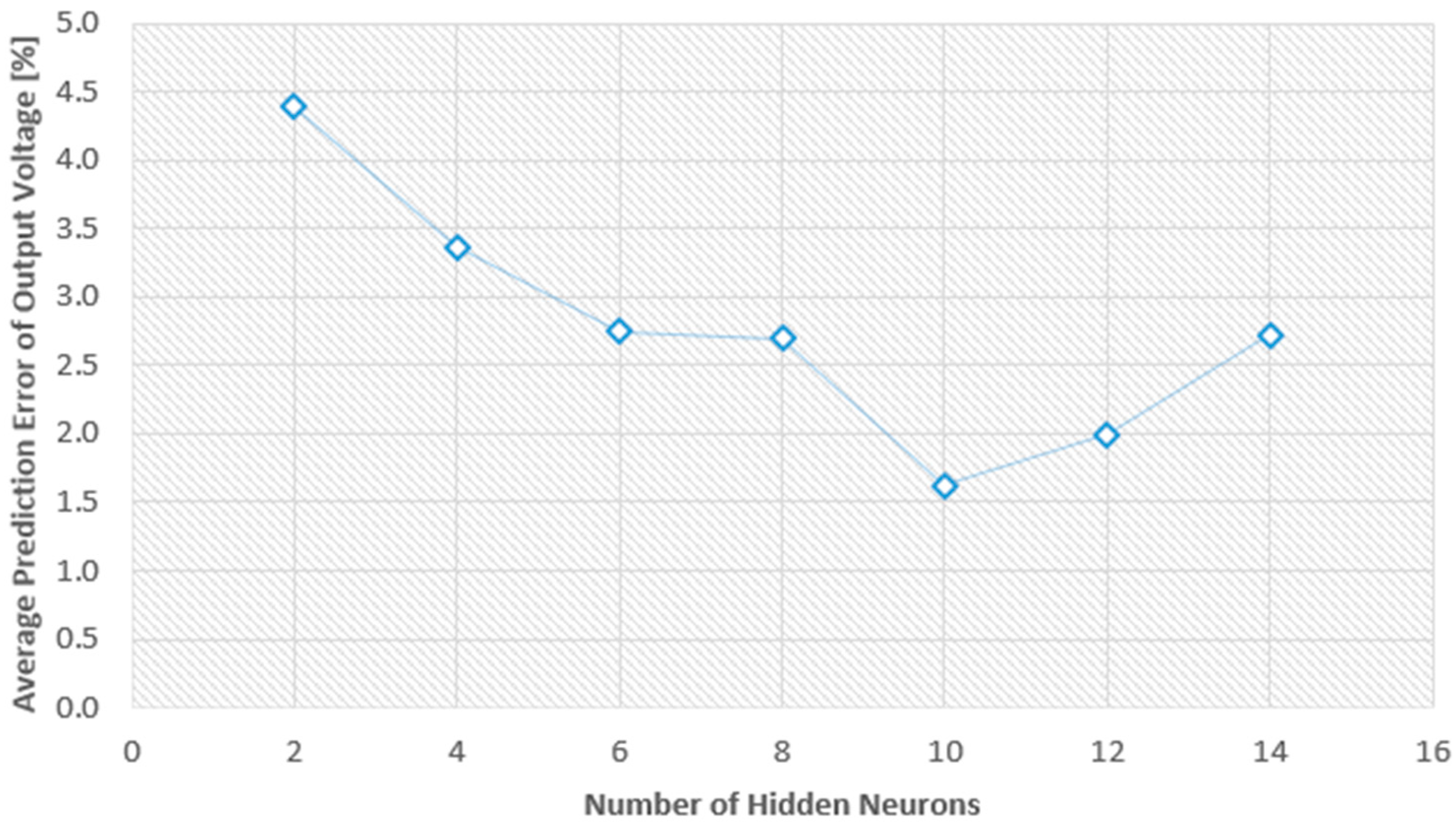
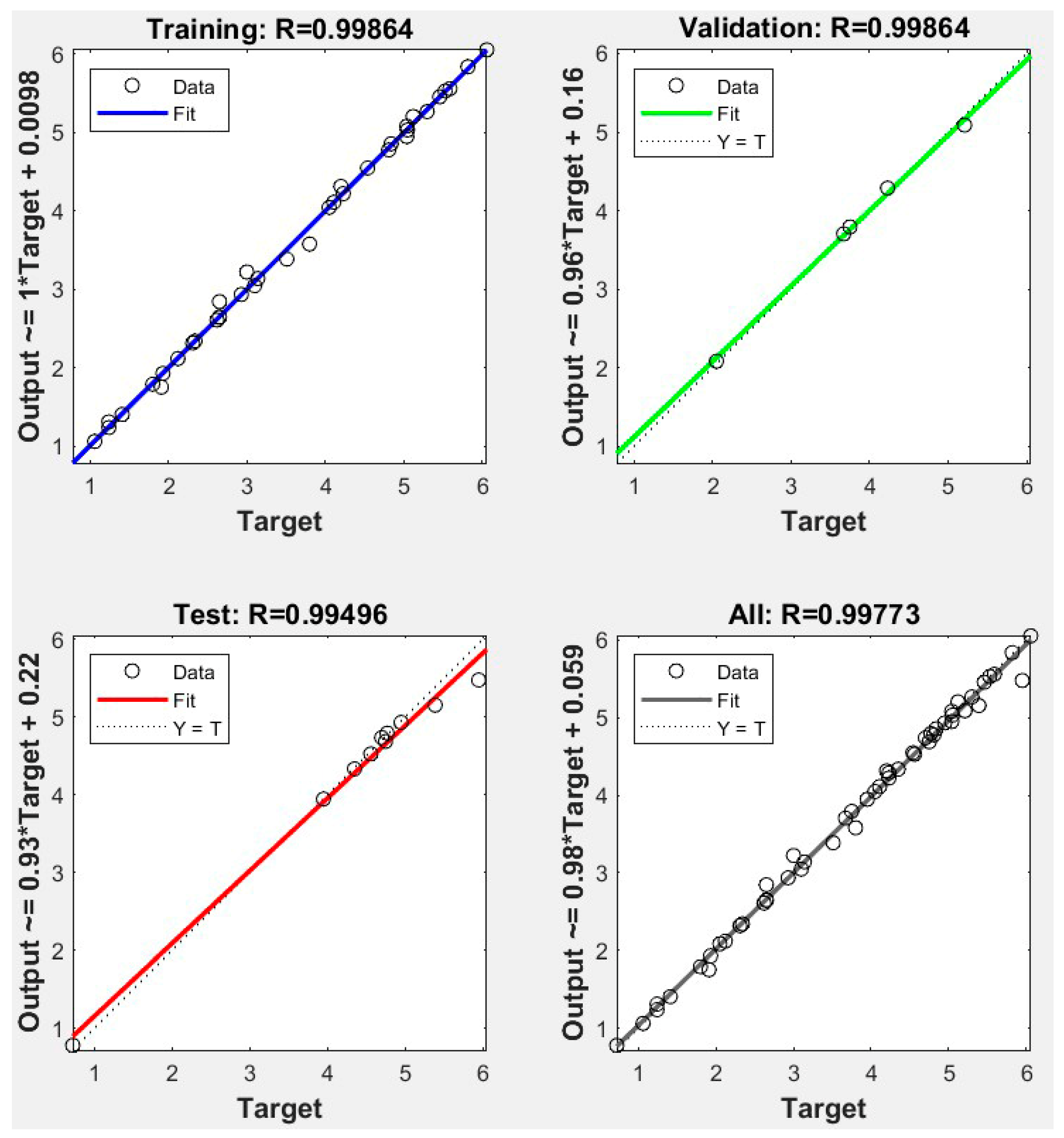
5.2. ANN Model Prediction
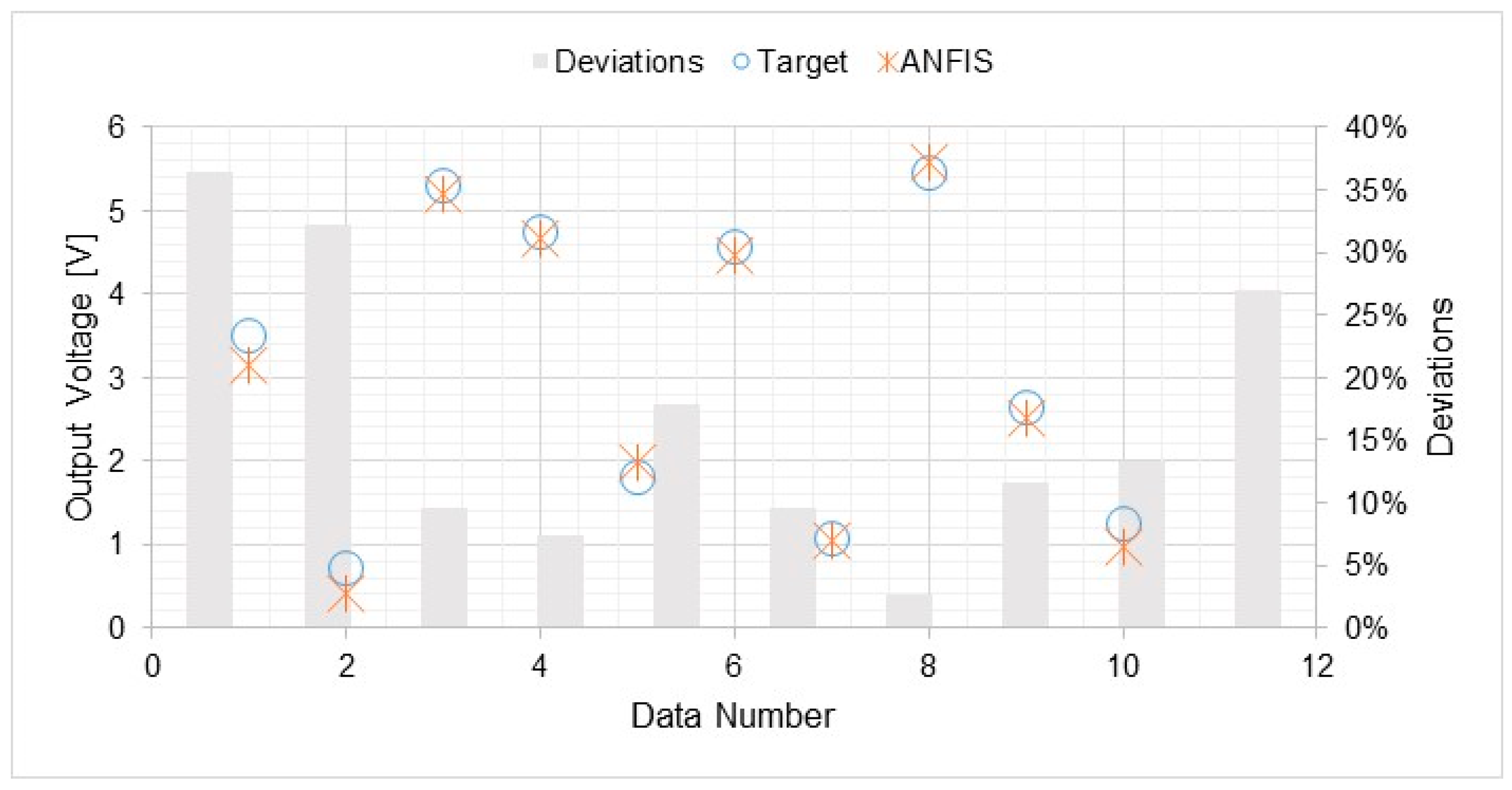
5.3. ANFIS Model Prediction
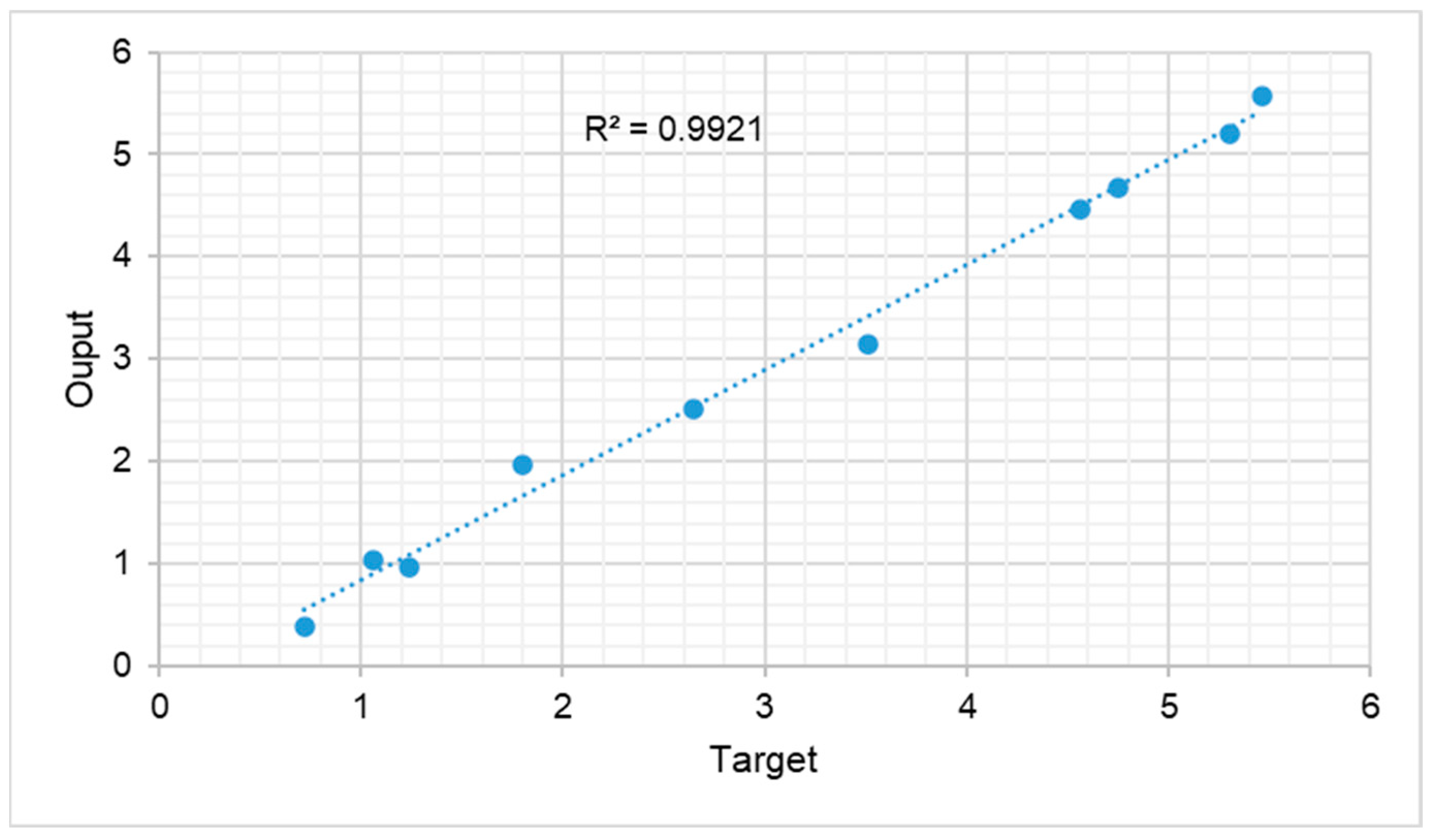
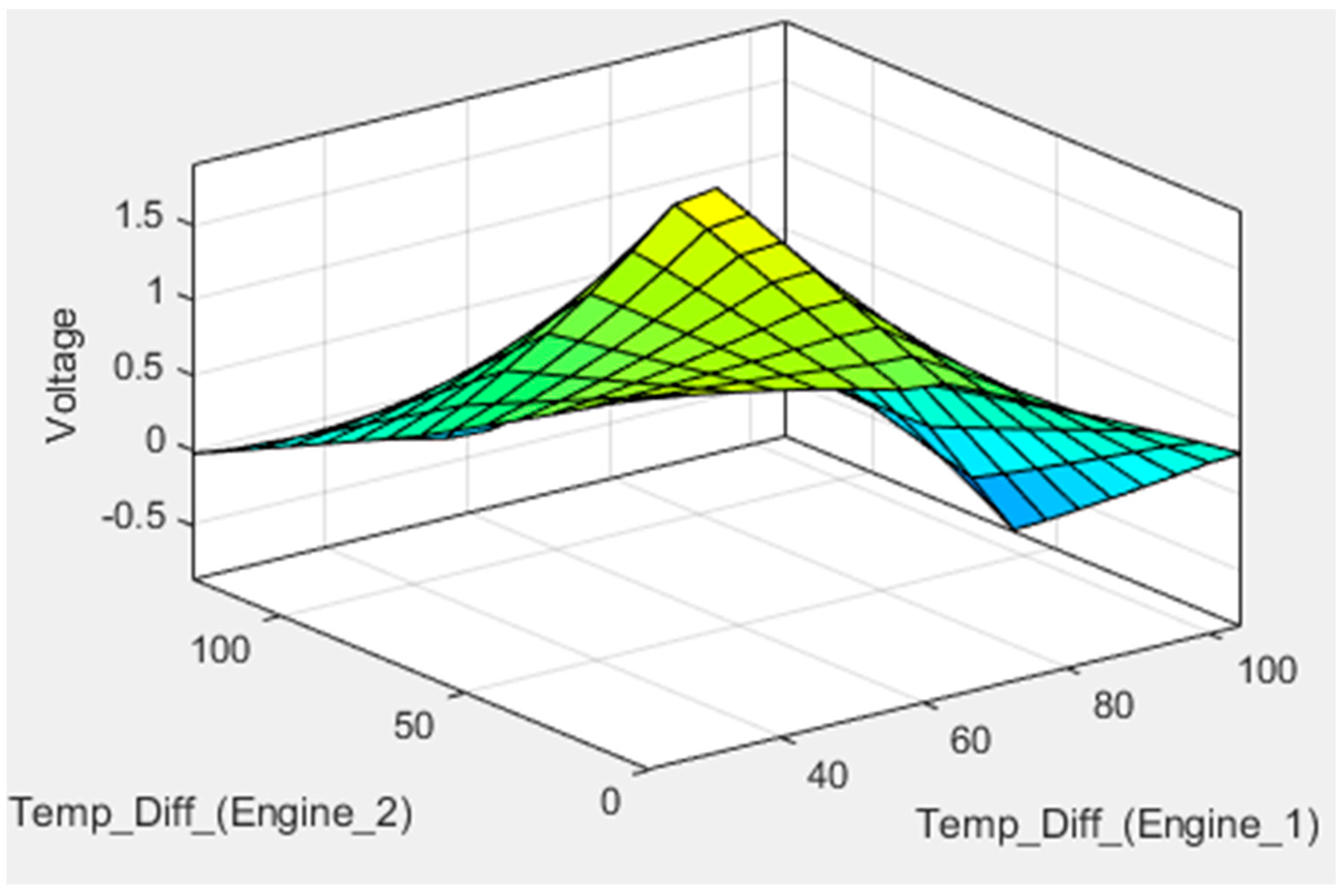
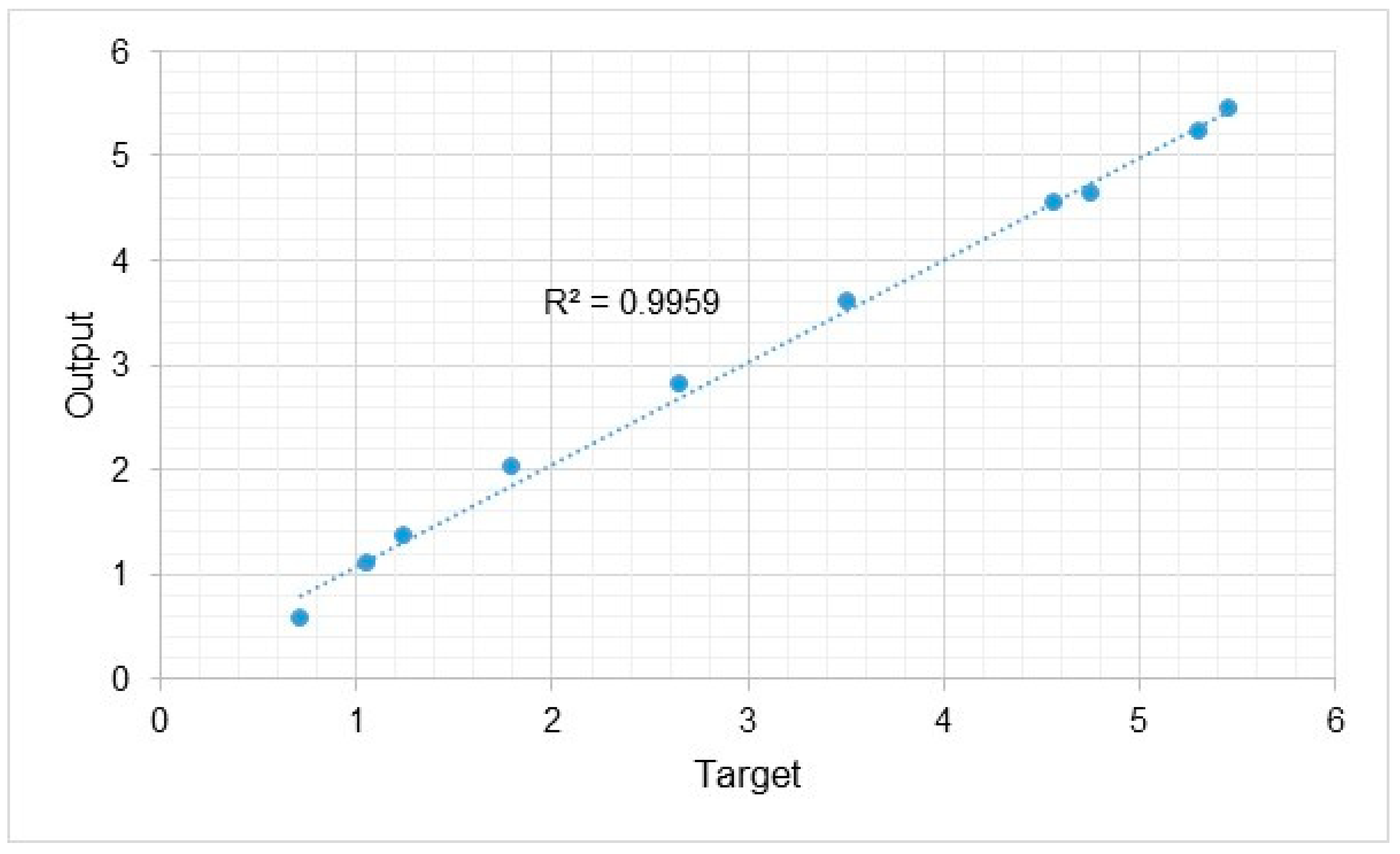
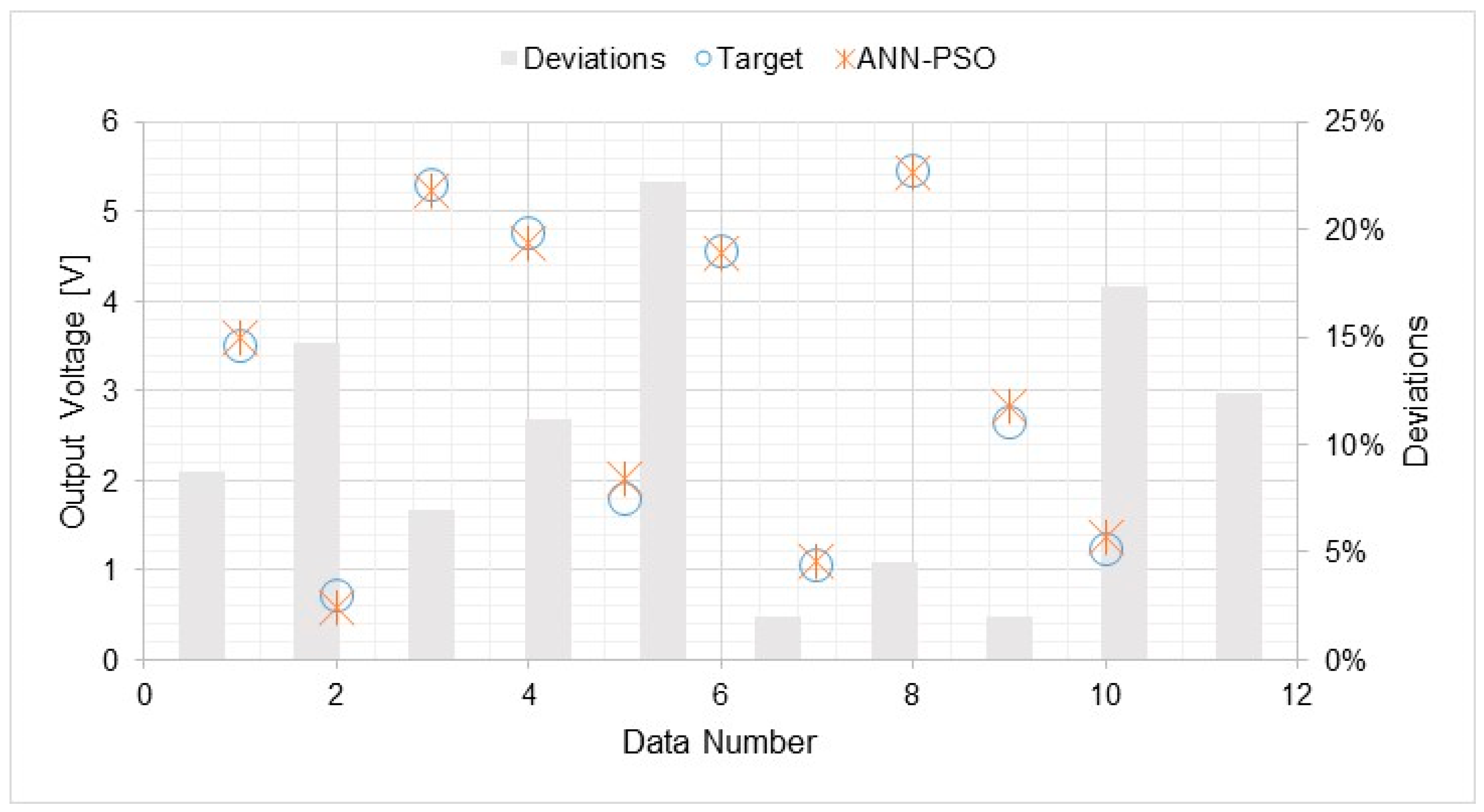
5.4. Analysis of ANN-PSO Models
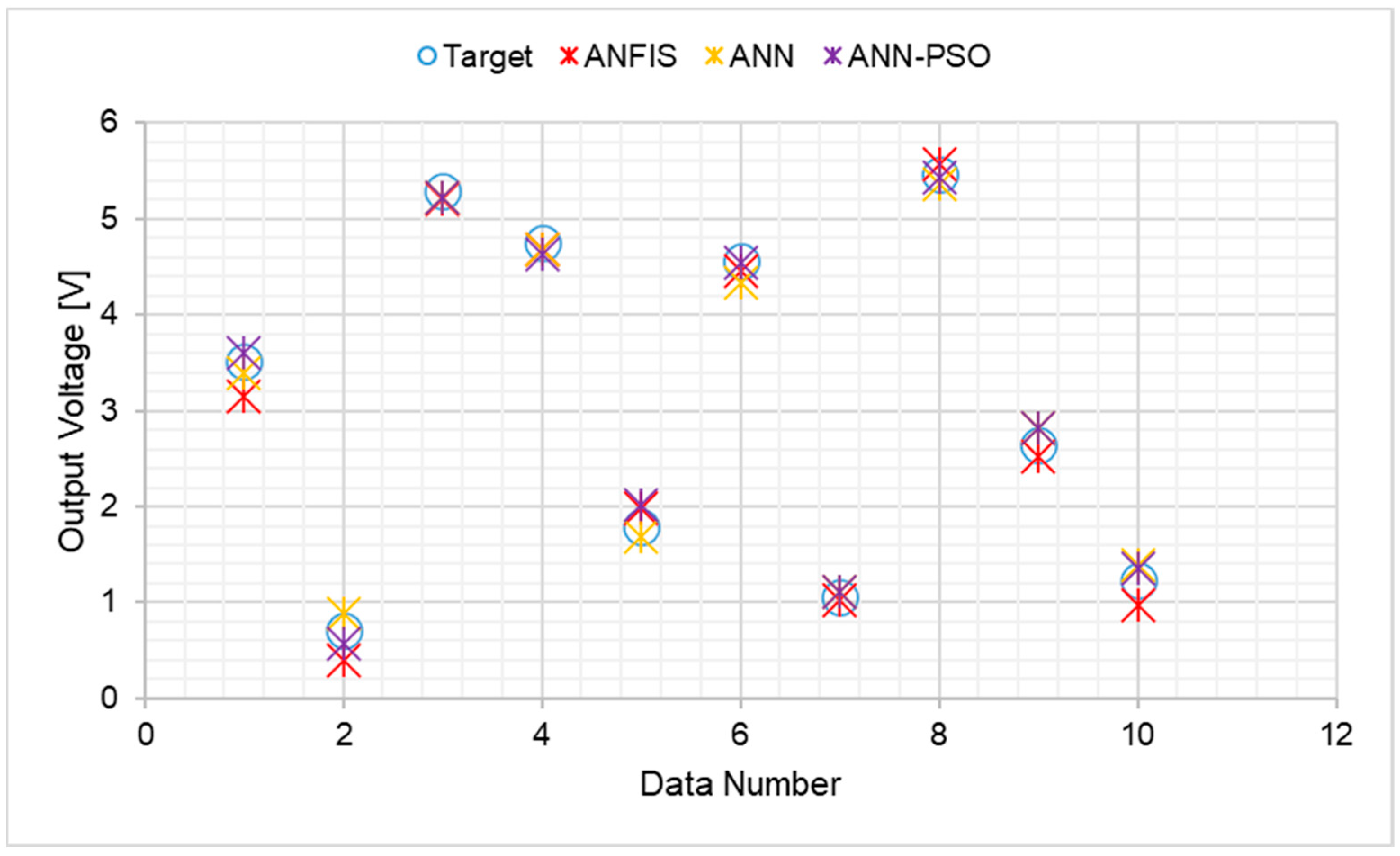
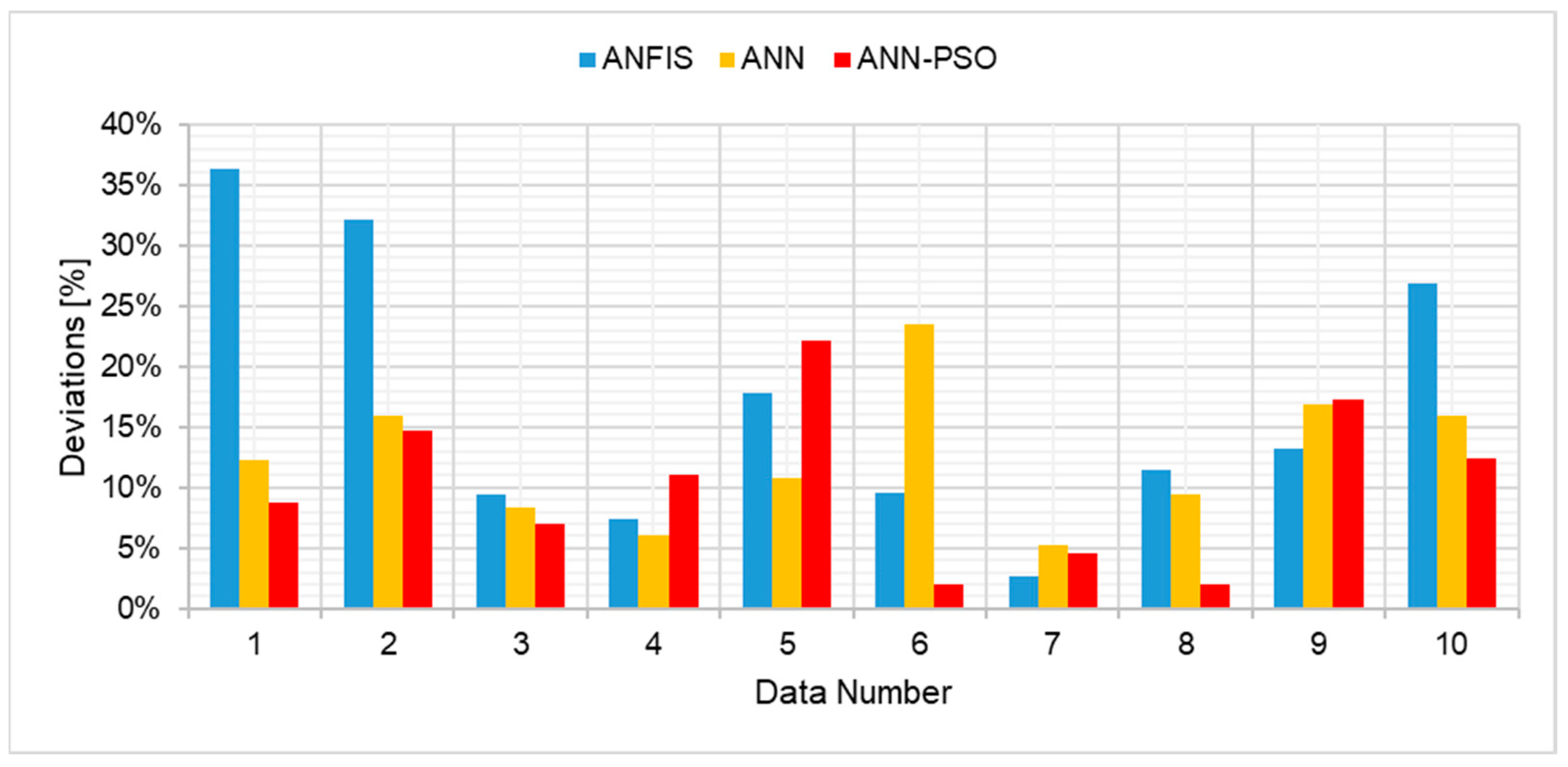
5.5. Comparison of Results for ANN-PSO, ANFIS, and ANN
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Belu, R. Artificial intelligence techniques for solar energy and photovoltaic applications. In Handbook of Research on Solar Energy Systems and Technologies; IGI Global: Hershey, PA, USA, 2014; pp. 1661–1720. [Google Scholar] [CrossRef]
- Fausett, L.V. Fundamentals of Neural Networks. Architectures, Algorithms, and Application, 1st ed.; Pearson: London, UK, 1993; pp. 9–20. ISBN -10: 0133341860. [Google Scholar]
- Rahman, A.A.; Zhang, X. Prediction of acoustic-wave parameters of thermo-acoustic prime mover through Artificial Neural Network technique: Practical approach for thermo-acoustics. J. Therm. Sci. Eng. Prog. 2018, 8, 257–268. [Google Scholar] [CrossRef]
- Fadlallah, S.O.; Anderson, T.N.; Nates, R.J. Artificial neural network–particle swarm optimization (ANN-PSO) approach for behaviour prediction and structural optimization of lightweight sandwich composite heliostats. Arab. J. Sci. Eng. 2021, 46, 12721–12742. [Google Scholar] [CrossRef]
- Tarno, A.; Rusgiyono, A. Sugito Adaptive Neuro Fuzzy Inference System (ANFIS) approach for modeling paddy production data in Central Java. J. Phys. Conf. Ser. 2019, 1217, 012083. [Google Scholar] [CrossRef]
- Zare, S.; Tavakolpour-Saleh, A.; Aghahosseini, A.; Sangdani, M.; Mirshekari, R. Design and Optimization of Stirling Engines Using Soft Computing Methods: A review. Appl. Energy 2021, 283, 116258. [Google Scholar] [CrossRef]
- Tijani, M.E.H.; Zeegers, J.C.H.; De Waele, A.T.A.M. The optimal stack spacing for thermoacoustic refrigeration. J. Acoust. Soc. Am. 2002, 112, 128–133. [Google Scholar] [CrossRef]
- Kisha, W.; Riley, P.; McKechnie, J.; Hann, D. Asymmetrically heated multi-stage travelling-wave thermoacoustic electricity generator. Energy 2021, 235, 121312. [Google Scholar] [CrossRef]
- Bi, T.; Wu, Z.; Zhang, L.; Yu, G.; Luo, E.; Dai, W. Development of a 5 kW traveling-wave thermoacoustic electric generator. Appl. Energy 2016, 185, 1355–1361. [Google Scholar] [CrossRef]
- Wu, Z.; Zhang, L.; Dai, W.; Luo, E. Investigation on a 1 kW traveling-wave thermoacoustic electrical generator. Appl. Energy 2014, 124, 140–147. [Google Scholar] [CrossRef]
- Wu, Z.; Dai, W.; Man, M.; Luo, E. A solar-powered traveling-wave thermoacoustic electricity generator. Sol. Energy 2012, 86, 2376–2382. [Google Scholar] [CrossRef]
- Alrwashdeh, S.S.; Ammari, H.; Madanat, M.A.; Al-Falahat, A.M. The Effect of Heat Exchanger Design on Heat transfer Rate and Temperature Distribution. Emerg. Sci. J. 2022, 6, 128–137. [Google Scholar] [CrossRef]
- Hamood, A.; Jaworski, A.J.; Blunt, L.; Townsend, A. The application of additive manufacturing to heat exchangers for oscillatory flow: A case study. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2023. [Google Scholar] [CrossRef]
- Rosle, N.D.A.; Saat, F.A.Z.M.; Othman, R.N.F.K.R.; Abd Rahim, I.; Saechan, P. Investigation on Standing Wave Thermoacoustic Generator Using DeltaEC. J. Adv. Res. Fluid Mech. Therm. Sci. 2022, 96, 51–64. [Google Scholar]
- McGaughy, M.; Wang, C.; Boessneck, E.; Salem, T.; Wagner, J. A Traveling wave thermoacoustic engine—Design and test. ASME Lett. Dyn. Syst. Control 2021, 1, 031006. [Google Scholar] [CrossRef]
- Xiao, L.; Luo, K.; Zhao, D.; Chen, G.; Bi, T.; Xu, J.; Luo, E. Time-domain acoustic-electrical analogy investigation on a high-power traveling-wave thermoacoustic electric generator. Energy 2023, 263, 126088. [Google Scholar] [CrossRef]
- Machesa, M.; Tartibu, L.; Okwu, M. Prediction of the oscillatory heat transfer coefficient in thermoacoustic refrigerators. Sustainability 2021, 13, 9509. [Google Scholar] [CrossRef]
- Toghyani, S.; Ahmadi, M.H.; Kasaeian, A.; Mohammadi, A.H. Artificial neural network, ANN-PSO and ANN-ICA for modelling the Stirling engine. Int. J. Ambient Energy 2016, 37, 456–468. [Google Scholar] [CrossRef]
- Duan, C.; Wang, X.; Shu, S.; Jing, C.; Chang, H. Thermodynamic Design of Stirling Engine Using Multi-Objective Particle Swarm Optimization Algorithm. Energy Convers. Manag. 2014, 84, 88–96. [Google Scholar] [CrossRef]
- Rahman, A.A.; Zhang, X. Prediction of temperature difference across thermoacoustic stack through artificial neural network technique. Future 2021, 3, 2314–7237. [Google Scholar]
- Wildemans, R.; Kornilov, V.; de Goey, P.; Arteaga, I.L. Nonlinear dynamics of pure intrinsic thermo-acoustic modes. Combust. Flame 2023, 251, 112703. [Google Scholar] [CrossRef]
- Alamir, M.A. An artificial neural network model for predicting the performance of thermoacoustic refrigerators. Int. J. Heat Mass Transf. 2021, 164, 120551. [Google Scholar] [CrossRef]
- Machesa, M.G.K.; Tartibu, L.K.; Okwu, M.O. Performance analysis of stirling engine using computational intelligence techniques (ANN Fuzzy Mamdani Model) and hybrid algorithms (ANN-PSO ANFIS). Neural Comput. Appl. 2023, 35, 1225–1245. [Google Scholar] [CrossRef]
- Tijani, M.E.H.; Zeegers, J.C.H.; De Waele, A.T.A.M. Design of thermoacoustic refrigerators. Cryogenics 2002, 42, 49–57. [Google Scholar] [CrossRef]
- RS Component Thermocouples and Sensors. RS PRO Type K Thermocouple 150 mm Length, 6 mm Diameter. Available online: https://docs.rsonline.com/bd9d/A700000007350778.pdf (accessed on 6 May 2023).

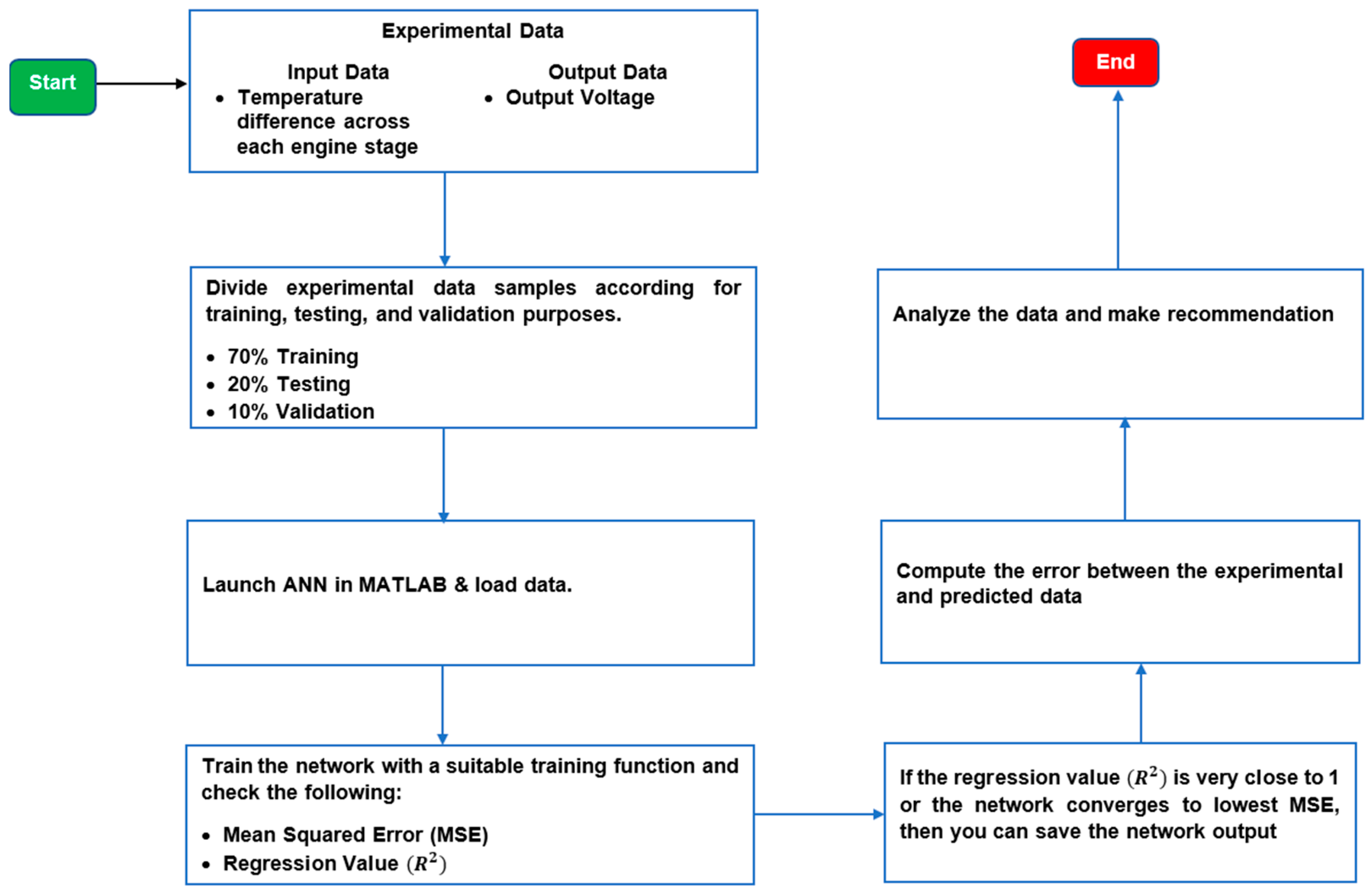
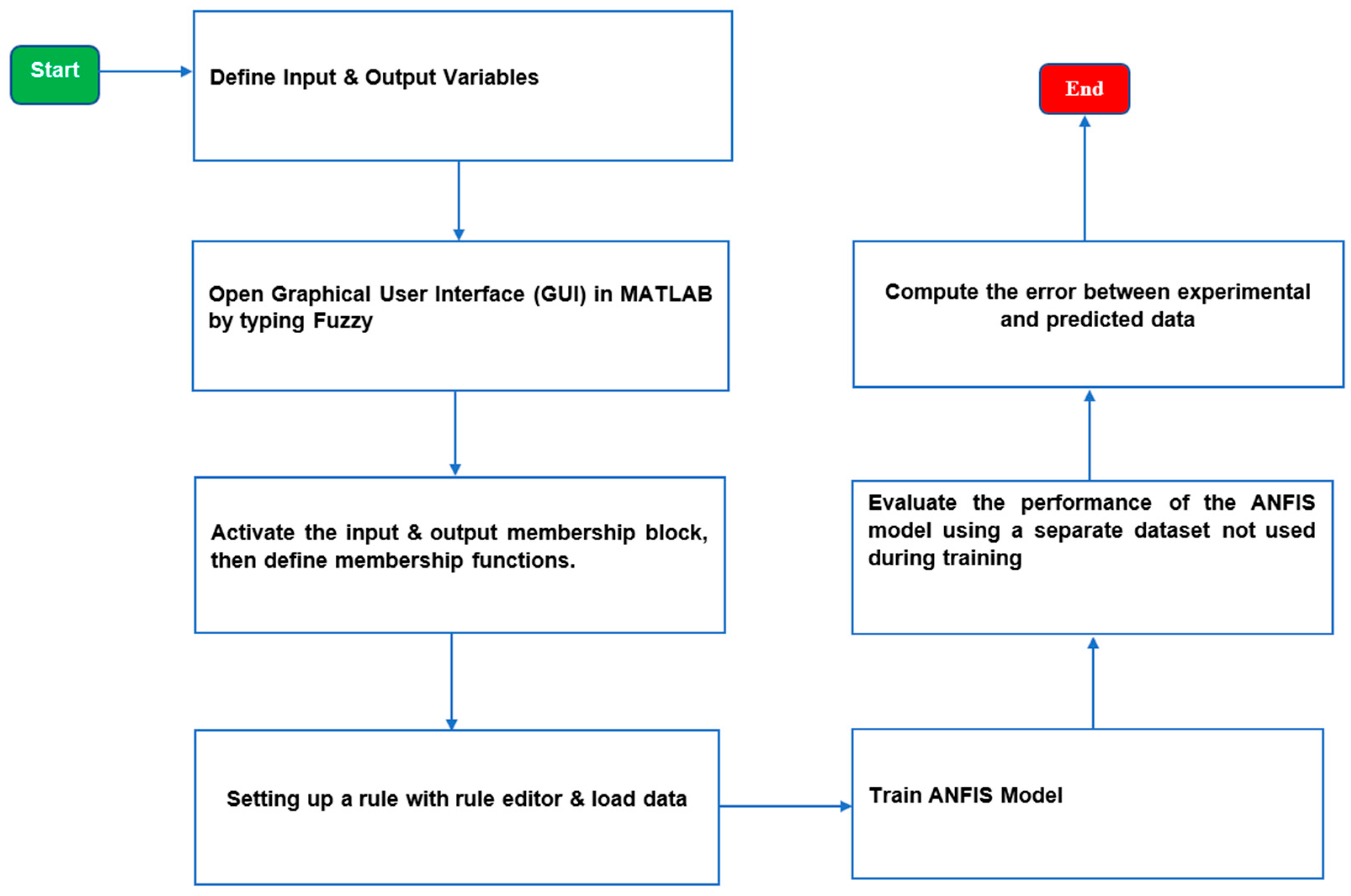
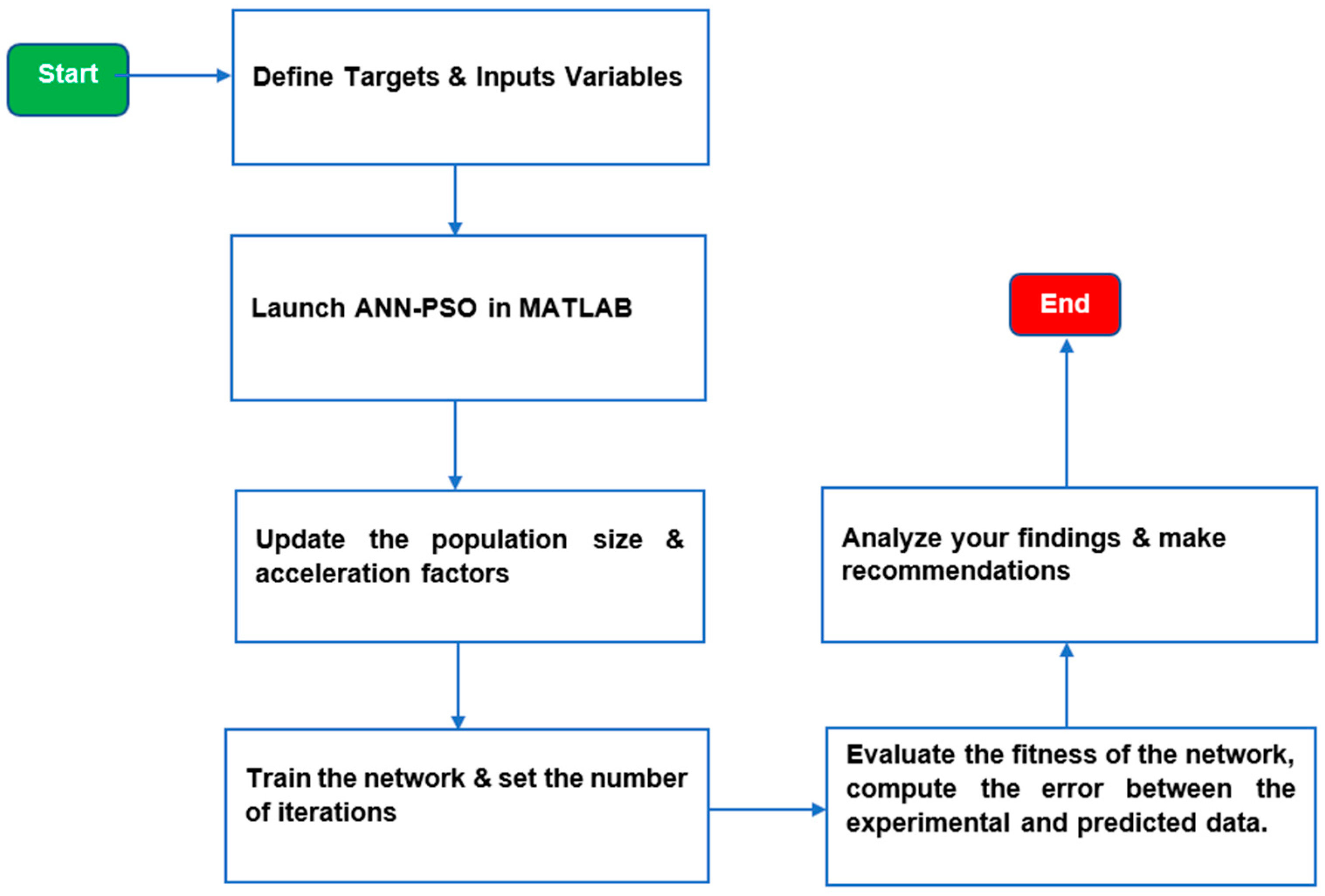


| ML Technique | Advantages | Disadvantages |
|---|---|---|
| ANN | ANNs can model complex, nonlinear relationships in data, making them suitable for tasks in which traditional linear models might fail. | Training large ANNs can be computationally expensive and time-consuming, especially for deep architectures with many layers and parameters. |
| ANFIS | ANFIS excels in capturing intricate, nonlinear relationships between input and output variables, making it ideal for systems with complex patterns. Its adaptability to changing environments is notable, as it dynamically adjusts parameters during the learning phase to enhance performance. | ANFIS performance hinges on the quality and quantity of training data. Inadequate or biased data can yield inaccurate models. Training ANFIS is computationally demanding, particularly with large datasets or intricate rule bases, leading to extended training times and increased resource demands. |
| ANN-PSO | The combination of ANN and PSO (ANN-PSO) helps us to find global optima for complex optimization problems and also enhances the ability to fine-tune the parameters of the neural network for improved performance. Finally, it allows for better adaptation of the network’s weights and biases to capture intricate patterns in the data. | The utilization of the combined ANN and PSO approach poses significant computational demands, particularly when applied to extensive datasets or large-scale problems. The training of neural networks and the optimization of PSO parameters necessitate substantial computational resources. Moreover, this technique is notably sensitive to the selection of hyperparameters for both the neural network and the PSO algorithm. Achieving the optimal set of parameters proves to be a challenging task, requiring additional fine-tuning efforts. |
| Stage 1 Onset Temp Diff | Stage 2 Onset Temp Diff | Stage 3 Onset Temp Diff | Stage 4 Onset Temp Diff | No of Engine Stages | Output Voltage |
|---|---|---|---|---|---|
| [V] | |||||
| 36.37 | 0 | 0 | 0 | 1 | 3.51 |
| 39.09 | 0 | 0 | 0 | 1 | 2.65 |
| 46.92 | 0 | 0 | 0 | 1 | 1.91 |
| 51.56 | 0 | 0 | 0 | 1 | 1.24 |
| 58.24 | 0 | 0 | 0 | 1 | 0.72 |
| 21.47 | 18.85 | 0 | 0 | 2 | 5.3 |
| 21.18 | 20.17 | 0 | 0 | 2 | 5.12 |
| 24.27 | 24.03 | 0 | 0 | 2 | 5.04 |
| 27.38 | 23.36 | 0 | 0 | 2 | 4.95 |
| 27.93 | 26.99 | 0 | 0 | 2 | 4.7 |
| 30.25 | 27.25 | 0 | 0 | 2 | 4.75 |
| 35.78 | 34.78 | 0 | 0 | 2 | 4.23 |
| 35.76 | 32.97 | 0 | 0 | 2 | 4.2 |
| 41.88 | 38.4 | 0 | 0 | 2 | 3.95 |
| 48.95 | 43.34 | 0 | 0 | 2 | 3.8 |
| 54.56 | 54.8 | 0 | 0 | 2 | 3.1 |
| 54.23 | 49.3 | 0 | 0 | 2 | 3 |
| 64.19 | 59.41 | 0 | 0 | 2 | 2.65 |
| 73.35 | 60.98 | 0 | 0 | 2 | 1.8 |
| 29.71 | 29.09 | 39.18 | 0 | 3 | 5.95 |
| 31.27 | 30.36 | 44.48 | 0 | 3 | 5.53 |
| 33.64 | 35.58 | 52.64 | 0 | 3 | 5.39 |
| 36.4 | 38.87 | 56.51 | 0 | 3 | 5.05 |
| 37.93 | 41.81 | 58.6 | 0 | 3 | 4.84 |
| 41.86 | 46.23 | 61.32 | 0 | 3 | 4.77 |
| 45.3 | 51.73 | 66.14 | 0 | 3 | 4.56 |
| 47.95 | 56.34 | 70.47 | 0 | 3 | 4.23 |
| 51.77 | 61.81 | 75.42 | 0 | 3 | 4.05 |
| 58.25 | 67.41 | 81.78 | 0 | 3 | 3.75 |
| 59.92 | 74.6 | 87.45 | 0 | 3 | 2.93 |
| 66.42 | 81.23 | 91.63 | 0 | 3 | 2.62 |
| 75.54 | 92.04 | 99.36 | 0 | 3 | 2.31 |
| 91.47 | 107.33 | 111.72 | 0 | 3 | 2.05 |
| 98.28 | 123.41 | 118.25 | 0 | 3 | 1.41 |
| 111.55 | 141.72 | 130.25 | 0 | 3 | 1.06 |
| 26.29 | 22.62 | 22.66 | 37.61 | 4 | 6.06 |
| 27.85 | 23.07 | 26.21 | 39.72 | 4 | 5.82 |
| 30.4 | 26.21 | 30.39 | 45.68 | 4 | 5.59 |
| 35.62 | 27.52 | 32.11 | 45.33 | 4 | 5.46 |
| 39.92 | 31.14 | 37.03 | 50.35 | 4 | 5.21 |
| 39.23 | 31.18 | 36.98 | 51.86 | 4 | 5.04 |
| 46.79 | 34.15 | 42.68 | 53.81 | 4 | 4.81 |
| 51.13 | 36.7 | 47.05 | 57.08 | 4 | 4.54 |
| 54.55 | 39.53 | 50.59 | 60.83 | 4 | 4.35 |
| 59.5 | 42.91 | 55.22 | 65.14 | 4 | 4.11 |
| 63.66 | 49.04 | 60.98 | 74.44 | 4 | 3.67 |
| 75.49 | 58.25 | 72.85 | 85.92 | 4 | 3.14 |
| 79.06 | 66.16 | 73.96 | 79.91 | 4 | 2.65 |
| 88.12 | 64.06 | 84.78 | 88.83 | 4 | 2.34 |
| 98.61 | 71.28 | 94.54 | 95.82 | 4 | 2.12 |
| 104.81 | 80.76 | 105.31 | 102.96 | 4 | 1.93 |
| 121.23 | 88.21 | 119.23 | 113.8 | 4 | 1.24 |
| Number of Neurons | Swarm Population Size | Acceleration Factors | MSE | |||
|---|---|---|---|---|---|---|
| 5 | 10 | 2.25 | 2 | 0.98675 | 0.0459 | 0.9124 |
| 5 | 20 | 2.25 | 2 | 0.99070 | 0.0323 | 0.8843 |
| 5 | 50 | 1.5 | 2.25 | 0.99456 | 0.0189 | 0.9439 |
| 5 | 100 | 1 | 2.75 | 0.99519 | 0.0167 | 0.9481 |
| 5 | 200 | 1.5 | 2 | 0.99599 | 0.0139 | 0.9840 |
| 5 | 400 | 1.5 | 2 | 0.99590 | 0.0142 | 0.9714 |
| 6 | 10 | 1 | 3 | 0.99553 | 0.0155 | 0.9232 |
| 6 | 20 | 2 | 2.25 | 0.98119 | 0.0663 | 0.9190 |
| 6 | 50 | 1 | 2.5 | 0.99587 | 0.0143 | 0.9743 |
| 6 | 100 | 1 | 2.5 | 0.99633 | 0.0128 | 0.8290 |
| 6 | 200 | 1 | 2.75 | 0.99617 | 0.0133 | 0.9200 |
| 6 | 400 | 1 | 2.25 | 0.99505 | 0.0172 | 0.9661 |
| 7 | 10 | 1.5 | 2.5 | 0.99522 | 0.0166 | 0.9478 |
| 7 | 20 | 1 | 2.75 | 0.99563 | 0.0152 | 0.9544 |
| 7 | 50 | 1 | 2.5 | 0.99519 | 0.0167 | 0.9640 |
| 7 | 100 | 1 | 2.5 | 0.99386 | 0.0213 | 0.9566 |
| 7 | 200 | 1.5 | 2.25 | 0.99365 | 0.0220 | 0.9811 |
| 7 | 400 | 2 | 2 | 0.99442 | 0.0194 | 0.9497 |
| 8 | 10 | 1 | 2.75 | 0.99499 | 0.0174 | 0.9871 |
| 8 | 20 | 1 | 2.5 | 0.99563 | 0.0152 | 0.9391 |
| 8 | 50 | 1.5 | 2.25 | 0.99551 | 0.0156 | 0.9630 |
| 8 | 100 | 1 | 2.5 | 0.99741 | 0.0090 | 0.9740 |
| 8 | 200 | 1 | 2.75 | 0.99762 | 0.0083 | 0.9844 |
| 8 | 400 | 1 | 2.25 | 0.99522 | 0.0026 | 0.9959 |
| 9 | 10 | 1 | 2.75 | 0.98904 | 0.0380 | 0.8716 |
| 9 | 20 | 1 | 3 | 0.99618 | 0.0133 | 0.9667 |
| 9 | 50 | 1.5 | 2.25 | 0.99408 | 0.0206 | 0.9697 |
| 9 | 100 | 2 | 2 | 0.99362 | 0.0222 | 0.9559 |
| 9 | 200 | 1.5 | 2.25 | 0.99533 | 0.0162 | 0.9593 |
| 9 | 400 | 1 | 2.5 | 0.99704 | 0.0103 | 0.9796 |
| 10 | 10 | 1 | 2.75 | 0.99485 | 0.0179 | 0.9406 |
| 10 | 20 | 1.5 | 2.5 | 0.99470 | 0.0184 | 0.9480 |
| 10 | 50 | 1.5 | 2.5 | 0.99656 | 0.0120 | 0.9555 |
| 10 | 100 | 1 | 2.75 | 0.99645 | 0.0123 | 0.9459 |
| 10 | 200 | 1 | 2.75 | 0.99764 | 0.0082 | 0.9717 |
| 10 | 400 | 1.5 | 2.5 | 0.99419 | 0.0202 | 0.9738 |
| Output Voltage | ||
|---|---|---|
| (Training or Testing) | MSE (Training or Testing) | |
| ANN-PSO | 0.99764/0.9959 | 0.0026/- |
| ANN | 0.99864/0.99496 | 5.89257 × 10−3/2.87704 × 10−2 |
| ANFIS | 0.9981/0.9921 | 0.0574524/0.0574534 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ngcukayitobi, M.; Tartibu, L.K.; Bannwart, F. Enhancing Thermo-Acoustic Waste Heat Recovery through Machine Learning: A Comparative Analysis of Artificial Neural Network–Particle Swarm Optimization, Adaptive Neuro Fuzzy Inference System, and Artificial Neural Network Models. AI 2024, 5, 237-258. https://doi.org/10.3390/ai5010013
Ngcukayitobi M, Tartibu LK, Bannwart F. Enhancing Thermo-Acoustic Waste Heat Recovery through Machine Learning: A Comparative Analysis of Artificial Neural Network–Particle Swarm Optimization, Adaptive Neuro Fuzzy Inference System, and Artificial Neural Network Models. AI. 2024; 5(1):237-258. https://doi.org/10.3390/ai5010013
Chicago/Turabian StyleNgcukayitobi, Miniyenkosi, Lagouge Kwanda Tartibu, and Flávio Bannwart. 2024. "Enhancing Thermo-Acoustic Waste Heat Recovery through Machine Learning: A Comparative Analysis of Artificial Neural Network–Particle Swarm Optimization, Adaptive Neuro Fuzzy Inference System, and Artificial Neural Network Models" AI 5, no. 1: 237-258. https://doi.org/10.3390/ai5010013
APA StyleNgcukayitobi, M., Tartibu, L. K., & Bannwart, F. (2024). Enhancing Thermo-Acoustic Waste Heat Recovery through Machine Learning: A Comparative Analysis of Artificial Neural Network–Particle Swarm Optimization, Adaptive Neuro Fuzzy Inference System, and Artificial Neural Network Models. AI, 5(1), 237-258. https://doi.org/10.3390/ai5010013







