FatNet: High-Resolution Kernels for Classification Using Fully Convolutional Optical Neural Networks

Abstract

This paper describes the transformation of a traditional in silico classification network into an optical fully convolutional neural network with high-resolution feature maps and kernels. When using the free-space 4f system to accelerate the inference speed of neural networks, higher resolutions of feature maps and kernels can be used without the loss in frame rate. We present FatNet for the classification of images, which is more compatible with free-space acceleration than standard convolutional classifiers. It neglects the standard combination of convolutional feature extraction and classifier dense layers by performing both in one fully convolutional network. This approach takes full advantage of the parallelism in the 4f free-space system and performs fewer conversions between electronics and optics by reducing the number of channels and increasing the resolution, making this network faster in optics than off-the-shelf networks. To demonstrate the capabilities of FatNet, it was trained with the CIFAR100 dataset on GPU and the simulator of the 4f system. A comparison of the results against ResNet-18 shows 8.2 times fewer convolution operations at the cost of only 6% lower accuracy. This demonstrates that the optical implementation of FatNet results in significantly faster inference than the optical implementation of the original ResNet-18. These are promising results for the approach of training deep learning with high-resolution kernels in the direction toward the upcoming optics era.

1. Introduction

One of the major problems of the modern deep learning approach is the speed of training and inference of architectures where there are a very large number of parameters to train. Computer vision, which can involve a large number of images with very slight differences, is considered to be one of the most complex problem areas for AI. Within the deep learning approaches, convolutional neural networks (CNNs) have become a standard approach for various computer vision problems. Recently, CNNs have been successfully applied to image classification [1], object detection [2], localization [3], and segmentation [4], among many other applications. CNNs are suitable for computer vision tasks because neurons in CNNs are only connected to the pixels of their receptive field, rather than to every single neuron of the next layer as in fully connected networks. This approach reduces the number of trainable parameters, which accelerates the inference and makes the neural network more immune to overfitting. Although CNNs are computationally less expensive than fully connected neural networks, accelerating CNNs is also an important task, especially with the ever growing number of images and videos that are captured.

There are many techniques to accelerate deep learning training, e.g., using shallow networks, pruning redundant weights, or using lower quantization levels [5]. In addition, hardware accelerators can be used to speed up the training and inference of neural networks, for example, in application-specific integrated circuits (ASICs), which can outperform standard CPUs and GPUs [6]. Large tech companies are actively working on their AI accelerators, such as Google’s TPU [7], Intel’s Loihi [8], and IBM’s TrueNorth [9]. Unfortunately, these accelerators are starting to face limitations in the post Moore’s law era, since the computational power of the processors is not improving at the same pace as before [10].

Optical processors are an interesting alternative to processing data with silicon chips. Optical computing uses photons of light, instead of electrons, as the information carrier for data processing [11]. Since Moore’s law does not affect optical computing, optical accelerators can be used for deep learning, offering advantages such as the high bandwidth of the light beam, high speed, zero resistance, lower energy consumption, and immunity to overheating [12]. There are two main approaches to optical neural networks: free space using spatial light modulators (SLM) [13,14] or silicon photonics approach using Mach–Zehnder interferometers (MZI) [15,16]. Unlike the silicon photonics approach, free-space optics uses wireless light propagation through a medium which can be air, outer space or vacuum. Although the silicon photonics approach is faster, as its clock speed can reach several GHz, it is inferior to the free-space system in parallelism [17].

This research is focused on the 4f free-space approach as described in Li et al. [13], which takes advantage of the parallelism of free-space optics. The 4f free-space optical system can be used to perform convolution operations faster than traditional electronic processors.

The Fourier transform is a well-known mathematical operation that decomposes a signal into its fundamental sinusoids in the frequency domain that, when combined, form the original function [18]. A Fourier transform is initially defined over one dimension, and can be extended to two or more dimensions [19]. The computational complexity of this process increases with the dimensions of the data, and even with fast methods such as the fast Fourier transform [20], transforming large data can take considerable resources with complexity in the order of $O\left(n^{2}log\left(n\right)\right)$, where $n^2$ is the number of pixels of an image [21]. On the other hand, performing a 2D Fourier transform in free-space optics can be easily achieved by passing the light through the convex lens, where the light only has to travel two focal distances (f) from the lens [22].

Taking the convolution theorem into account, the convolution of two signals can be represented as the inverse Fourier transform of the pointwise product of their Fourier transforms [18]. The 4f correlator is based on the Fourier transform properties of the convex lenses [23] and performs the convolution operation based on the convolution theorem. Any convex lens projects a Fourier transform of the input object located on the front focal plane onto the back focal plane [23], where it can be pointwise multiplied by the kernel in the Fourier domain. After passing through the second lens, it can be converted back into the space domain. The system is called 4f because the light in the 4f system travels four focal distances of the lens. Hence, the 4f approach can accelerate convolutional neural networks by performing the Fourier transforms at the speed of light. The parallelism advantage of the 4f system comes from the theoretically infinite resolution that is bounded in reality by the resolution of the modulators and the camera.

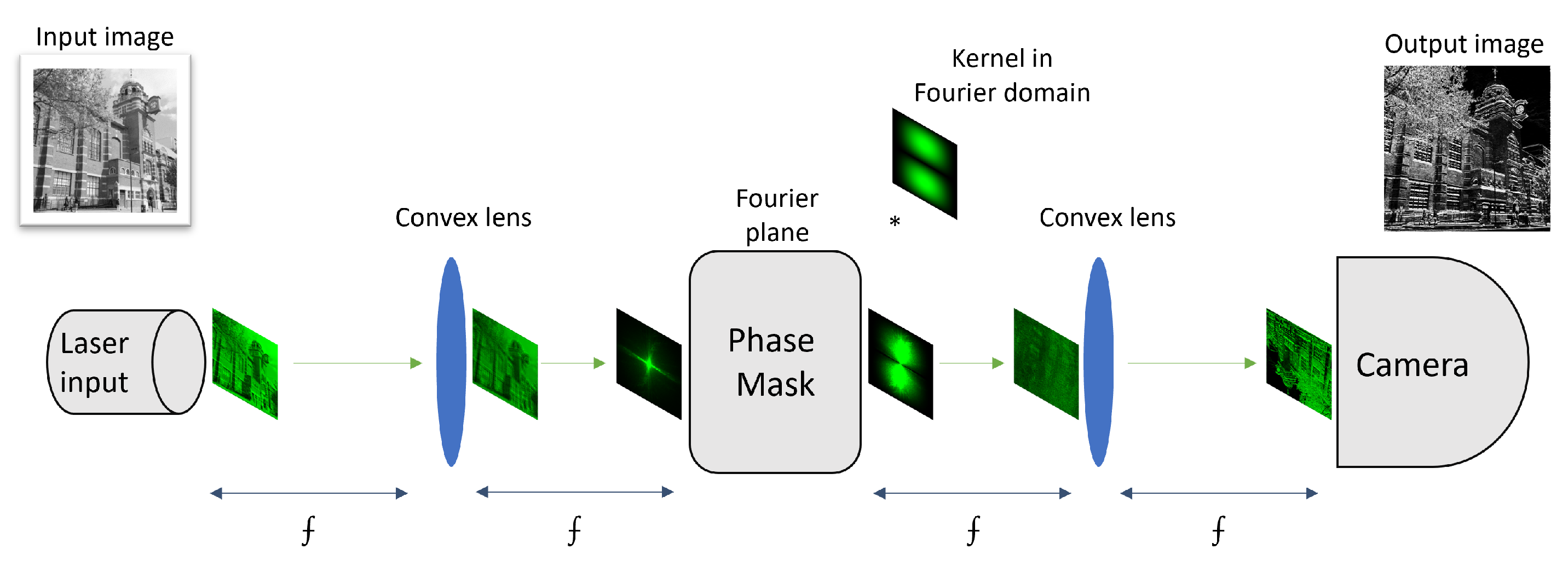
The first optical convolution technique with the 4f system was described by Weaver and Goodman [24] in 1966. It was not used for the acceleration of neural networks until neural networks started gaining popularity in the 21st century [25]. A standard 4f optical system consists of an input source, two convex lenses, two light modulators, and a sensor (see Figure 1). The input source is the laser emitting the light modulated right in the beginning with the input image by altering the light intensity. The modulated light passes through the first convex lens after travelling the focal distance of the lens and is projected onto the focal plane, where the Fourier transform of the input is formed. On the focal plane using another modulator, the input is element-wise multiplied with the kernel in the frequency domain. After the multiplication in the Fourier domain, the light passes through the second lens to perform the inverse Fourier transform and is captured by the camera or the array of photodetectors. In some cases, instead of the modulator, the fixed phase mask is used to perform the multiplication in the Fourier plane, as demonstrated in Chang et al. [14].

The 4f system is used in combination with the electronic compound, called an optical–electronic hybrid system [14]. This system is used only for inference, and training is performed using the simulator. The networks were trained using the simulator, and the phase mask of the trained kernels of the first layer was fabricated. Those fabricated kernels were used only for the inference of the pre-trained first layer. Hence, the inference of the first convolutional layer is optically computed, and the output of the electronic network is then fitted into the electronic portion of the network. This allows the multiplication to be performed passively, i.e., without energy consumption or latency. It also enables high speed-up, since the first layer of the network is usually the heaviest due to the high resolutions, which the free-space optics can handle for free. Since the optical–electronic hybrid system uses kernel tiling, this system can perform several convolution operations of the first layer in parallel without losing frame rate and power. However, a passive architecture such as this lacks flexibility and can only be used with one set of kernels, meaning it cannot be reused for all network layers. This is the reason for considering only active 4f architecture in our approach, allowing the device to perform all convolutional layers of the network by altering the kernel on the Fourier plane.

Unlike standard neural networks, optical neural networks involve various bottlenecks and constraints. Since the read-out camera captures the intensity of light, which is the square of the amplitude, it is impossible to perform the computations with negative values. One of the possible ways for getting around this problem is the non-negative constraint, which can significantly affect the accuracy. One way around this constraint is called pseudo-negativity, which can address the restriction to positive values by doubling the number of filters [14]. This method only uses positive values for the kernel by labeling half of the kernels as positive and the other half negative. After the read-out, the results of ‘positive’ convolutions are subtracted from the ‘negative’ results, thus providing the correct outcome for the convolution operation. Another bottleneck is the resolution of the modulator and the camera. Although modern cameras can capture up to 4K resolution, this limit does not allow many channels to be tiled and high-resolution feature maps to be used in combination with tiling.

Despite the many advantages of 4f systems, they have not been popular among the modern AI accelerators. The main problem lies in the very slow cameras and light modulators used in the system. However, there is the possibility to gain acceleration using parallelism and through simultaneously performing several convolution operations. For example, Li et al. [13] proposed kernel, channel, and mixed tiling approaches to better utilize the resolution of the 4f system. Their approaches enable all convolution operations for specific output channels and sum them using one inference through the 4f system. In a technique used by [13], zero-padding is applied to the input channels, which are tiled into one big input block, while their corresponding kernels are tiled in the same manner, forming a kernel block. This method takes advantage of the massive parallelism of free-space optics. It performs all convolutions of each output channel of the convolutional layer, including the channel summation via one optical inference. By optically convolving the input block and the kernel, the summation of all convolutions of those particular input channels with output channels appears in the middle of the output tensor. This significantly reduces the number of conversions between optics and electronics. That is why it is essential to use the high-resolution capabilities of the 4f system.

Tiny kernel resolutions have become one of the nuances of building CNN architectures. Kernel sizes of 3 × 3 or 5 × 5 are now the standard for CNNs [1]. Although sometimes in ResNet architectures, a large kernel size can be seen in the first layer of the networks [26]. Theoretically, having a small kernel size has a range of advantages. The reduction of kernel size not only increases the computational efficiency during training but also decreases the number of trainable parameters, thereby increasing the robustness of the network against overfitting [27,28]. Modern neural networks are all trained on CPU/GPU, whose training time depends on the number of parameters. This led to the development of architectures with a very small resolution of kernels. For the same reason, all classifier architectures were developed in the cone shape, where the image is pooled down at every layer, making it faster for the CPU/GPU process. However, this works entirely differently for optical neural networks. Due to the nature of free-space optics, the use of large kernels in 4f system-based neural networks will not affect the inference time. Unfortunately, almost all the attempts to train the convolutional neural networks on the 4f system are based on the standard convolutional cone-shaped architectures.

To overcome underutilization of the 4f system, we propose FatNet, which takes advantage of the high-resolution capabilities of the 4f system by using fewer channels and larger input/kernel resolution in CNNs. Since the resolution does not affect the speed of inference in the 4f system, increasing the resolution and reducing the number of channels results in the network performing fewer convolution operations. This means fewer translations from optics to electronics, since the main bottleneck of the system is based on optics–electronics conversions. Our approach does not require pooling between most layers, which speeds up the inference even more for the small cost of a loss in accuracy.

2. Materials

We trained our network with the CIFAR-100 dataset (see Figure 2) and chose ResNet-18 as the backbone network. The CIFAR-100 (Canadian Institute For Advanced Research) dataset consists of 60,000 images of 32 × 32 resolution. It is split into 20 superclasses sub-grouped into 100 classes, with 600 images per class [29]. Only 50,000 images are used for training, and the other 10,000 data samples are in the test set. The similarity of classes under the same superclass in CIFAR-100 makes it harder to train.

Shah et al. [30] managed to train CIFAR-100 using different ResNet models, including their variation, where ELU (exponential linear unit) [31] was used as an activation function. Their test error on standard ResNet-101 achieved 27.23%. For this reason, we decided to use residual networks in our experiments. In our research, we have limited our focus to serial networks that do not contain branching structures. Therefore, networks that use depthwise convolutions, such as the highly accurate EfficientNet-B0 [32] with an accuracy rate of 88.1%, are outside the scope of our analysis.

ResNet-18 is a CNN, one of five networks introduced in He et al. [26] for the ImageNet dataset [33]. The feature distinguishing these networks from others is the residual connections between layers. Formally, He et al. [26] noted the blocks of the networks as:

$$y=F(x,\left\{W_i\right\})+x$$

(1)

where x and y are the input and the output of the residual block, and $F(x,\left\{W_i\right\})$ represents the building block of the residual layer, which can contain one or several weight layers.

Residual connections are the connections in which one or more layers are skipped. In ResNet, those connections perform identity mapping, and the outputs of these connections are added to the output of the stacked layers. This configuration allows the use of deeper networks by avoiding vanishing/exploding gradient problems.

PyTorch was used to train all our networks [34]. PyTorch is an open source machine learning framework originally developed by Meta AI. We used PyTorch for its flexibility and ease in creating custom neural network layers. One example is the simulation of our optical layer, which we also built using PyTorch. PyTorch was also used by Miscuglio [35] to precisely simulate an actual 4f system.

3. Methods

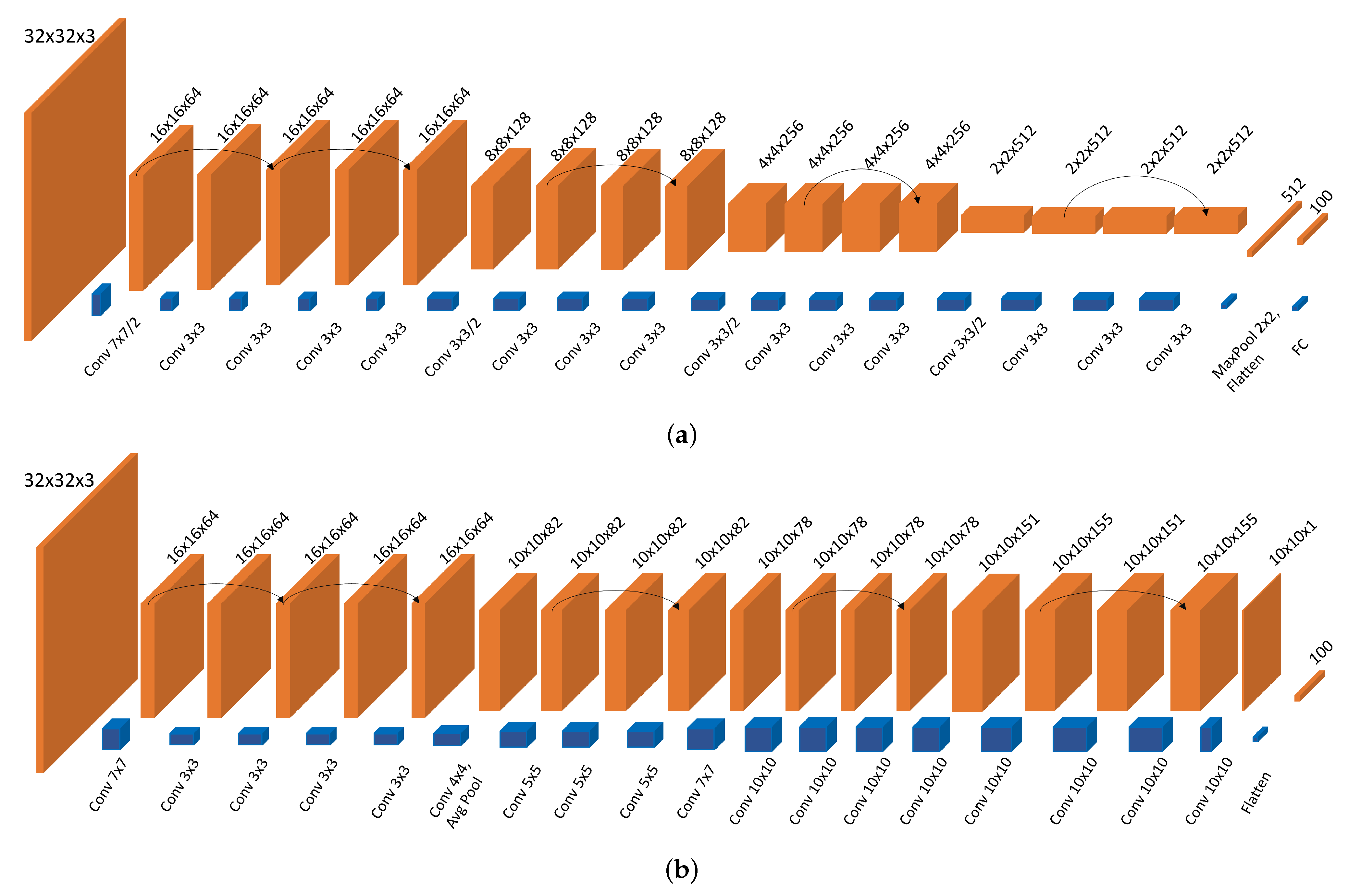
Nearly all classifier CNNs are cone-shaped and use either strides or pooling layers to reduce the resolution of the feature map [28]. This architecture has several advantages. The main advantage is the training speed, since the network gets simpler after each feature extraction and ends up with very low-resolution feature maps, which are flattened and passed to the fully connected layers for further classification. However, this kind of structure became standard only due to the dominance of electronic computing. Unlike in electronics, having larger resolutions for inputs and kernels in the 4f system does not affect the speed of inference, which makes it essential to explore new architectures that are compatible with optics. Our approach is called FatNet, due to its barrel shaped structure and most of the kernels having the same resolution as the feature maps (see Figure 3b).

By having larger feature maps and kernel sizes in the classifier CNN, we can ensure full utilization of the free-space optics. Although higher resolutions come with the problem of overfitting, our approach uses the same number of trainable parameters as the standard approach. Essentially, we have created the following rules for turning any classifier into a FatNet:

• The FatNet should preserve the same number of layers as the original network to keep the same number of non-linear activation functions.
• The FatNet should keep precisely the same architecture as the original network on the shallow layers until the shape of the feature maps pools down to the shape where the number of elements of the feature map is less than or equal to the number of classes.
• FatNet has the same total number of pixels of the feature maps at the output of each layer as the original networks. Hence, since the feature maps’ shape stays constant and does not use pooling, the new number of output channels needs to be calculated, which will be less than for the original network.
• FatNet has the same number of trainable parameters per layer as the original network. Since we have reduced the number of output channels based on the third rule, the number of trainable parameters has also been reduced. Hence, a new kernel size needs to be calculated based on the number of output channels.

It is also important to remember that FatNet is more efficient when the number of classes is significant; for example, ImageNET contains 20,000 classes. We chose ResNet-18 as the backbone network for proof of concept and trained the network with the CIFAR-100 dataset. We chose CIFAR-100 over CIFAR-10 due to the larger number of classes and the ability to keep the feature maps in the square shape of 10 × 10. It is essential to know that one of the limitations of the 4f-based convolution is the failure to perform the convolutions with the stride. Since most off-the-shelf networks contain stridden convolutions, this can be a potential problem. However, we can get around the problem by replacing the stridden convolutions with the combination of standard convolution and pooling. Because we do not want to reduce the resolution of our feature maps, we decided to ignore the strides in our ResNet-18 architecture and use 2 × 2 MaxPooling after the first layer.

No modification of the first five layers is carried out, since they all have 16 × 16 resolution. For the following layers, we have calculated the number of pixels in each feature map and measured how many channels the layers should contain if all layers’ feature maps remain 10 × 10. We then calculated the number of trainable parameters in the original network (excluding bias). Based on the number of trainable parameters and the new number of channels, we have calculated the new kernel resolutions as shown in

Table 1. Construction of FatNet from ResNet-18.

Layer	Number of Weights	Feature Pixels	FatNet Layer
64 × 128, k = (3 × 3)	73,728	8192	64 × 82, k = (4 × 4)
128 × 128, k = (3 × 3)	147,456	8192	82 × 82, k = (5 × 5)
128 × 128, k = (3 × 3)	147,456	82,192	82 × 82, k = (5 × 5)
128 × 128, k = (3 × 3)	147,456	82,192	82 × 82, k = (5 × 5)
128 × 256, k = (3 × 3)	294,912	4096	82 × 41, k = (9 × 9)
256 × 256, k = (3 × 3)	589,824	4096	41 × 41, k = (19 × 19)
256 × 256, k = (3 × 3)	589,824	4096	41, 41, k = (19 × 19)
256 × 256, k = (3 × 3)	589,824	4096	41, 41, k = (19 × 19)
256 × 512, k = (3 × 3)	1,179,648	2048	41 × 21, k = (37 × 37)
512 × 512, k = (3 × 3)	2,359,296	2048	21 × 21, k = (73 × 73)
512 × 512, k = (3 × 3)	2,359,296	2048	21 × 21, k = (73 × 73)
512 × 512, k = (3 × 3)	2,359,296	2048	21 × 21, k = (73 × 73)
FC (512, 100)	51,200	100	21 × 1, k = (49 × 49)

.

Unfortunately, kernels larger than the input features in the last layer cause a problem. The main problem is that the convolutions are the same padding type, meaning that the input and output resolutions are the same 10 × 10 in our case. This means the outer regions of the kernels larger than 10 × 10 are redundant and will not be trained. This restricts us to the convolutions of the kernel with a maximum resolution of 10 × 10. Therefore, we reduced the kernel size by increasing the number of channels in those layers, which violates the third rule of the FatNet construction (see Figure 3). However, this is the better solution, since the network may underfit if the number of trainable parameters is reduced.

Usually, the image classifier neural networks are based on the convolutional layers for the feature extraction and dense layers for the classification. Sometimes, fully convolution networks end up with a convolutional layer with a 1 × 1 shape and the number of output channels equal to the number of classes. The FatNet’s output layer is a convolutional layer with one channel and each pixel representing the probability of the class in the classification network. In our case with CIFAR-100 training, the output shape is 10 × 10 with one output channel. The main advantage of FatNet and its suitability for free-space optical training is that FatNet uses fewer output channels but larger resolution feature maps and kernels. Moreover, it is a fully convolutional network, which makes it fully compatible with the 4f accelerator.

As part of this work, we developed an application called FatSpitter to convert any sequential network into a FatNet model. FatSpitter accepts a PyTorch neural network object as an input and outputs a refined FatNet model that ensures that the size of the kernel never exceeds the input size of the corresponding convolutional layer. It follows an algorithm similar to that described above. Initially, a construction table, as demonstrated in Table 1, is established. Upon obtaining the construction table and determining the index of the layer at which FatNet has to start, the implementation begins by substituting original convolutional layers with the new “Fat” convolutional layer, which features altered kernel sizes and output channels. If the kernel size is larger than the input, the kernel size is adjusted to match the input, and the number of output channels is recalculated. It is important to remember that if the number of input channels in the original convolutional layer is equal to the output channels, this equality must also be maintained in FatNet. If this is not considered, the number of output channels will keep rising and falling in the network, making it impossible to train.

To validate our results, we developed a simulator as the custom layer on top of PyTorch called OptConv2d. OptConv2d replaces the convolution operation of the standard convolutional layer with the simulation of 4f inference. In order to achieve this, we had to simulate the propagation of the amplitude-modulated light using the angular spectrum of plane waves (ASPW) method. According to the angular spectrum method, if the initial wavefront is $U_1(x,y)$, the next wavefront is calculated as:

$$U_2(x,y)=F^{-1}\left[F\left[U_1(x,y)\right]H(f_x,f_y)\right]$$

(2)

where $H(f_x,f_y)$ is the transmittance function for free space.

The transmittance function of free-space propagation comes from the Fresnel diffraction transfer function:

$$H_F(f_x,f_y)=exp\left[jkz-j\pi \lambda z(f_x^2+f_y^2)\right]$$

(3)

where $k=\frac{2\pi }{\lambda }$, z is the distance travelled by light, and $\lambda$ is the wavelength [36,37].

Since the 4f system contains two lenses, the transmittance function of each lens is:

$$t_A(x,y)=P(x,y)exp\left[-j\frac{k}{2f}(x^2+y^2)\right]$$

(4)

where f is the focal length of the lens, and $P(x,y)$ is the pupil function [37].

The distance at which the angular spectrum method calculates the next wavefront depends on the pixel scale and is calculated as:

$$z=\frac{N{(\Delta x)}^2}{\lambda }$$

(5)

where $\Delta x$ is the pixel scale, N is the number of pixels, and $\lambda$ is the wavelength. In case when the propagation distance needs to be longer than the above formula for the distance, the propagation can be calculated in several iterations. We chose such a pixel scale for each propagation, so z becomes equal to the focal distance of the lens. In this case, we have to do only one iteration for each focal distance propagation in the 4f system.

The simulator uses pseudo-negativity, so each convolution is run twice to avoid negative values for the kernels in optics. Moreover, due to the laws of geometrical optics, the output of the 4f device is always rotated 180 degrees. Luckily, this is not a problem for convolutional neural networks, since they can continue extracting the future values from the rotated feature maps.

Experiments

The main goal of FatNet is not to gain accuracy but to demonstrate that the network with its prescribed architecture can maintain accuracy by being accelerated using free-space optics while performing fewer inferences through the 4f system than the original network. Hence, our experiments aimed at testing and comparing the original network and FatNet.

We recreated the modified version of ResNet-18, converted it to the FatNet, and trained both networks. To validate the accuracy of the FatNet in the optical device, we trained the network in the simulator. In the real 4f system, we would have taken advantage of the parallelism of the network by tiling the batches. However, batches were not tiled in the simulator, since the matrices are represented in PyTorch’s tensor format. All operations were performed without unwrapping the tensor, and the Fourier transforms and multiplications were performed directly on the 4-dimensional tensors. We chose this approach since the simulator-based training of the network was much slower than the standard PyTorch network. Each epoch of the optical simulation of FatNet takes 67 min, while the epoch in the standard FatNet with Conv2d layer of PyTorch is 15 s only.

The wavelength of the laser was set to 532 nm (green), and convex lenses with a 5 mm diameter and focal distance of 10 mm were assumed. It should also be noted that we have not taken the device’s quantization and noise into account and used type float32.

We split our training set into training and validation sets according to a 80–20% ratio, respectively, resulting in 40,000 for training and 10,000 images for validation. The dataset was normalized using the mean and standard derivation of the CIFAR-100 at all channels. Moreover, we have applied augmentation methods, including the horizontal flip and random crop with the padding of four. All networks were trained with the SGD optimizer, 0.9 for the momentum, and the starting learning rate of 0.01, updating every 50 steps by 0.2. The last layers of all networks were passed through the 20% dropout layer. We trained all the networks using 2× NVIDIA A100 40 GB GPUs.

ResNet-18 and FatNet were trained with a batch size of 64 (32 per GPU). However, the optical simulation of FatNet had to be trained with a batch size of 16 (8 per GPU) due to the high memory requirement of the simulator, as the optical simulation enhances the computational graph and number of gradients. Although we have not simulated the parallelism of the 4f system, to gain acceleration, the 4f system needs to take advantage of high resolution. FatNet’s best acceleration can be achieved if batch tiling is performed. In order to use batch tiling, all the inputs of the same batch have to be tiled in one input block, and the kernel has to be padded to the same size as the input block. Before tiling the inputs, they must be individually padded to $M+N-1$, where M × M is the input size, and N × N is the kernel size. According to this method, the number of possible batch sizes can be calculated as follows:

$$n={\lfloor \frac{R}{M+N-1}\rfloor }^2$$

(6)

where R is the resolution of the 4f system and $\lfloor ·\rfloor$ is the floor function.

4. Results

Based on the configurations described above, our implementation of ResNet-18 achieved an accuracy of 66%. In comparison, FatNet’s implementations, both with GPU and simulation of optics, lagged in accuracy with a result of 60% (see

Table 2. Comparison of the test accuracy and number of convolution operations used in each tested network.

Architecture	Test Accuracy	Number of Conv Operations	Number of Conv Operations
	mean±std		Ratio to Baseline
ResNet-18	$66\pm 1.4\%$	1,220,800	1 (baseline)
FatNet	$60\pm 1.4\%$	148,637	0.12
Optical simulation FatNet	60%	148,637	0.12

). However, FatNet implementation performs 8.2 times fewer convolution operations to reach this level of accuracy and does not require any dense layers for classification.

The same can be said about the training process. Since it may take more epochs for the FatNet to reach the desired accuracy, this architecture is only beneficial if accelerated with the 4f system.

The measured and calculated inference time for FatNet and ResNet-18 with optics and GPU were obtained and observed (see

Table 3. Inference time in seconds per input for ResNet-18 and FatNet with optics and GPU with batch sizes of 64 and 3136 for cases when the 4k resolution of the 4f device is fully utilized. The frame rate of the 4f device is approximated at 2 MHz [13].

Architecture	Batch 64	Batch 3136
ResNet-18 (GPU)	$1.350\times {10}^{-4}$	$1.167\times {10}^{-4}$
FatNet (GPU)	$4.565\times {10}^{-4}$	$7.942\times {10}^{-4}$
ResNet-18 (Optics)	$3.815\times {10}^{-2}$	$7.786\times {10}^{-4}$
FatNet (Optics)	$4.645\times {10}^{-3}$	$9.479\times {10}^{-5}$

). The observations were conducted based on the batch size of 64, such as in our experiments, and 3136 maximum utilization of 4f system with 4k resolution modulators and camera.

5. Discussion

Although FatNet does not converge as well as ResNet-18, it is still 8.2 times faster, if both are trained with optics. CIFAR-100 is an extended dataset of CIFAR-10, but unlike CIFAR-10, CIFAR-100 is much harder to train. Numerous researchers have tried different augmentation and regularization methods to improve the classification performance of the CIFAR-100. For instance, Mizusawa [38] tried the interlayer regularization method and improved the accuracy of the classification of CIFAR-100 in ResNet-20 from an average of 64.09% to 65.59%. Shah [30] used ELU activation layers to improve the CIFAR-100 accuracy from 72.77% to 73.45%. Our modification of ResNet-18 achieved an average test accuracy of 66%, which is comparable to Mizusawa but lower than Shah. Then, our tests of FatNet showed that by sacrificing only 6% of test accuracy, we could perform 8.3 times fewer convolutions in optics, which will mean fewer conversions from optics to electronics and vice versa. During the training process of the original FatNet on GPU, three trials were conducted, achieving accuracies of 59%, 59%, and 62%. These results suggest that it may be possible to achieve a smaller loss with FatNet through further optimization efforts.

In contrast to our approach of reducing the number of convolution operations to improve speed and adapt the network to optical implementation, other research has focused on accelerating networks by accepting a small sacrifice in performance when run on CPU/GPU. For example, Luo et al. [39] accelerated the neural networks by discarding redundant weights. One of their implementations, ThiNet-Tiny, accelerated the forward and backward timing of VGG-16 by 6.4 and 7.3 times, respectively, at the cost of a 9% reduction in top-1 accuracy. Moreover, Rastegari et al. [5] achieved an acceleration of approximately 58 times by binarizing the inputs and weights of convolutional operations and estimating convolutions using XNOR and bit counting operations. However, when testing ImageNet trained on ResNet-18 with this method, they observed a loss of 18.1% in accuracy.

The training accuracy graph in Figure 4 shows that the network trained with the optical simulation trains slower than in other experiments. When simulating the 4f system, PyTorch uses the simulation of light propagation as part of the computation graph of the neural network, which vastly increases the computation graph. This causes a slowdown in network training. From the point of view of validation accuracy, the FatNet trained with GPU, and its optical simulation, are not altered much, especially after the first learning rate step on epoch 50. Although the validation accuracy of FatNet and optical simulation of FatNet did not exceed 57% and 58%, respectively, the test accuracy reached 60% in both cases. This difference is caused by the augmentation applied only to the validation and training sets and not to the test set.

However, it should be noted that the acceleration in a 4f system with FatNet is only possible if the parallelism of the 4f system is utilized not with the channel or kernel tiling but with batch tiling. The increase in resolution and reduction of the number of channels will not change the performance much if channel tiling is used. Unfortunately, due to the high latency of modern light modulators and cameras, it is almost impossible to get an acceptable acceleration over GPU with 4f, with the efficiency batch size shown in Table 3. However, the 4f system’s acceleration is almost equalized to the GPU in comparison with non-GPU inference (see Table 3). If we fully utilize the 4K resolution of the 4f system, the batch size of 3136 can be used, and the acceleration of the 4f system over GPU becomes obvious. Moreover, it can be seen that the use of FatNet improves the speed of the inference in optics and works in a completely opposite way with the GPU, regardless of the batch size. However, enormous batch sizes such as this are not efficient and will lead to overfitting.

Moreover, it should be mentioned that in our experiments, we have not tested the network with the different quantization levels and noise that can occur in the system. Low-precision training can potentially affect the test accuracy of the network, but there have been many successful attempts to train the neural networks with low precision to save on memory or accelerate the inference. On the other hand, noise can be used as a regularization method, since random and unpredictable noise can be a sort of augmentation method for our dataset. If we use a smaller bit depth, the noise may not affect the accuracy, since the changes in resulting light intensity will be low.

Another issue that is important to consider is the alignment of the optical elements. One of the main disadvantages of the 4f system compared with the silicon photonics approach is the alignment of optical elements. A slight alteration in the alignment of the elements of the 4f system can lead to entirely wrong results and to the inability to correctly keep track of the graph. Unfortunately, our simulator is not designed to consider alignment problems. In practice, optical cage systems can be used to keep elements fixed and aligned.

The FatSpitter algorithm, used to convert ResNet to FatNet, follows the rules we have established but only takes into account serial networks. Hence, it cannot be applied to networks that use depth-wise separable convolutions. It is possible to integrate branching into the algorithm for future implementation, but the most significant challenge remains the implementation of 1 × 1 convolutions. These convolutions can be executed in a 4f device as normal convolutions, but the question remains whether they need to be converted into fat layers. The main purpose of 1 × 1 convolutions is to reduce the dimensionality, so it makes sense not to convert them into FatNet and keep them as they are. On the other hand, converting 1 × 1 convolutions into FatNet would lead to a further reduction in the number of channels, which may not be necessary.

The design of the FatNet makes it more suitable for datasets with a large number of classes, such as 100 in our case, but it can also potentially work with images of a higher resolution. Unfortunately, the simulation of light propagation takes a large amount of GPU memory, which is the reason for not using ImageNet in our experiments when it seemed the most obvious choice for FatNet.

6. Conclusions

In this research, we looked at a new way of fully utilizing the high-resolution capabilities of the 4f system for classification. We introduced a transformation method, which makes the regular neural network designed for the CPU/GPU training more compatible with the free-space optical device. After testing FatNet with the CIFAR-100 dataset, using ResNet-18 as the backbone network and the optical simulation of the FatNet using the angular spectrum method, we reached a test accuracy of 66% with ResNet and 60% with FatNet. Eventually, it was demonstrated that FatNet performs 8.2 times fewer convolution operations than ResNet-18 without a loss in frame rate when both were implemented in optics. Compared with the standard ResNet-18, FatNet is always faster than ResNet-18 when run with the optical device and also than ResNet-18 run with GPU when the batch size is as large as 3136. Moreover, our research demonstrates the importance of using high-resolution kernels in CNN, especially in the future, when the speed of cameras and light modulators improves.