Estimation of Clinch Joint Characteristics Based on Limited Input Data Using Pre-Trained Metamodels
Abstract
:1. Introduction
2. Related Work
3. Research Questions
4. Method
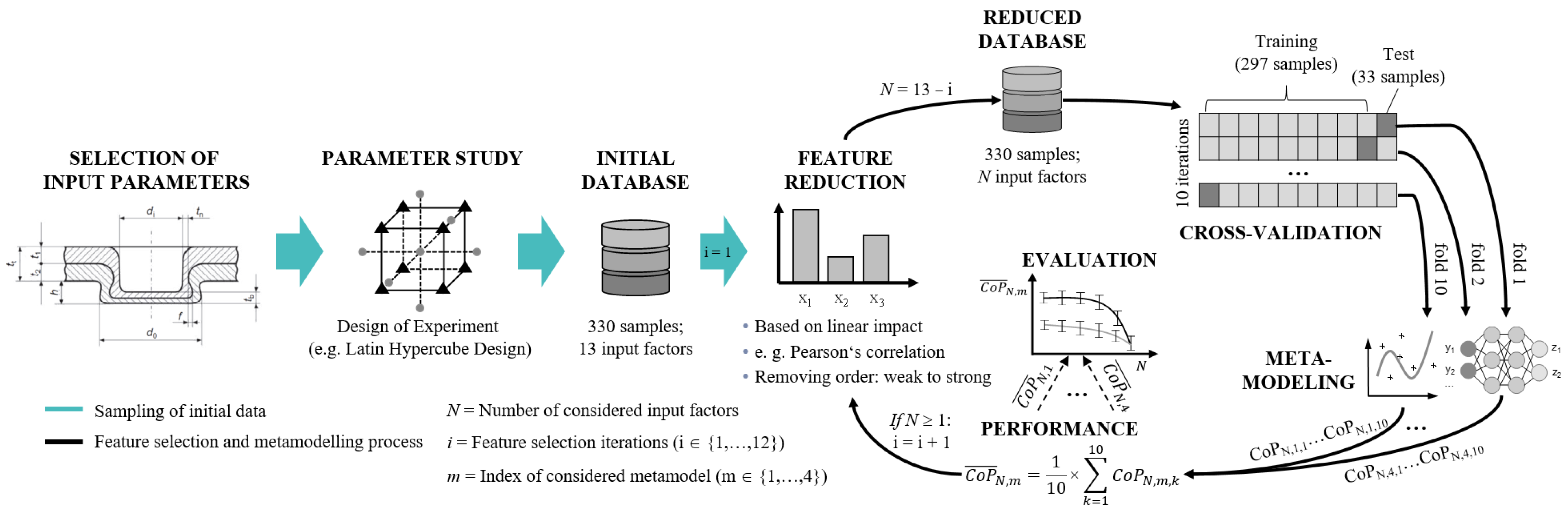
4.1. General Approach
4.2. Numerical Clinching Process
4.3. Design of Experiments
4.4. Metamodeling
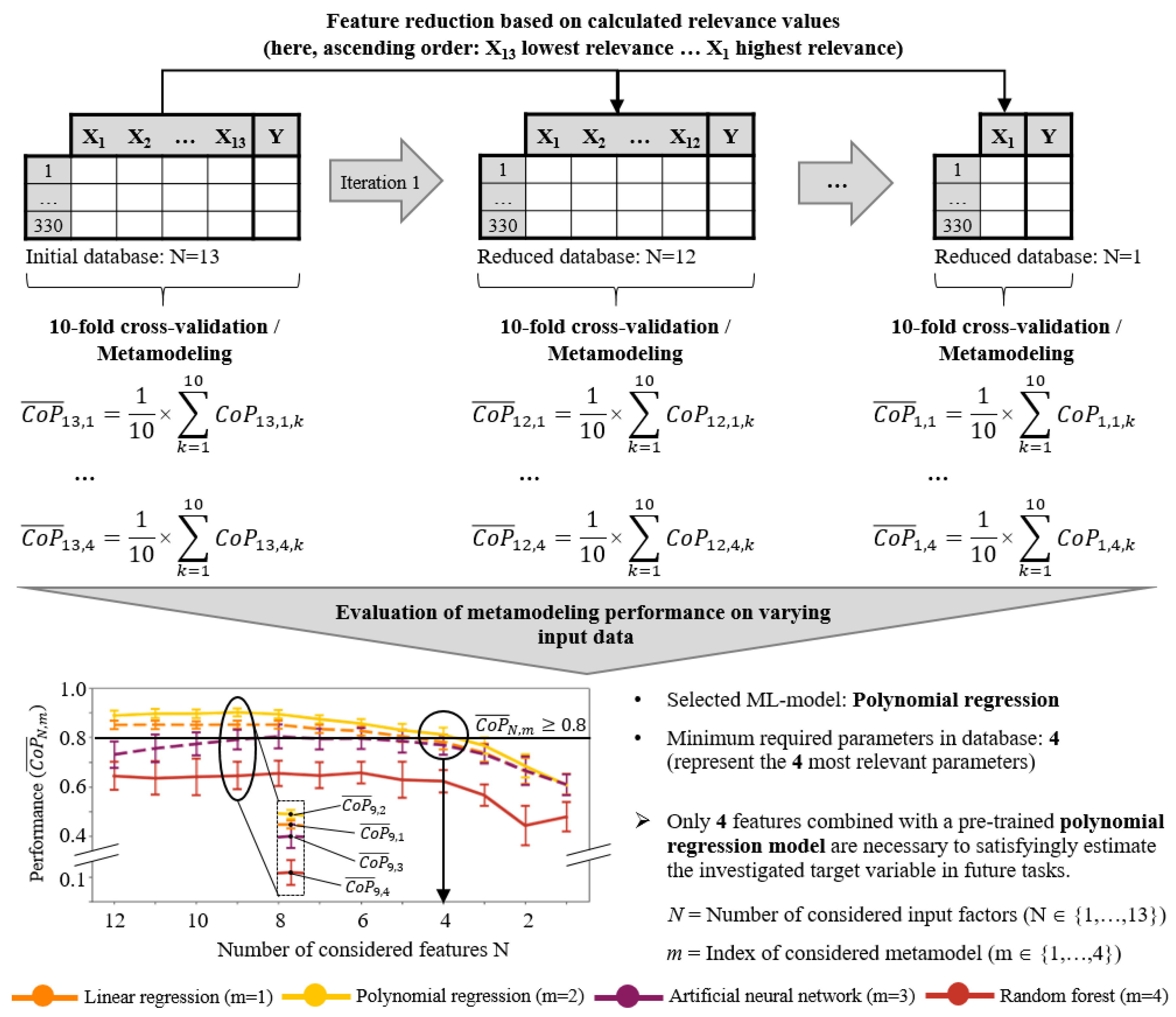
4.5. Feature Selection
5. Results
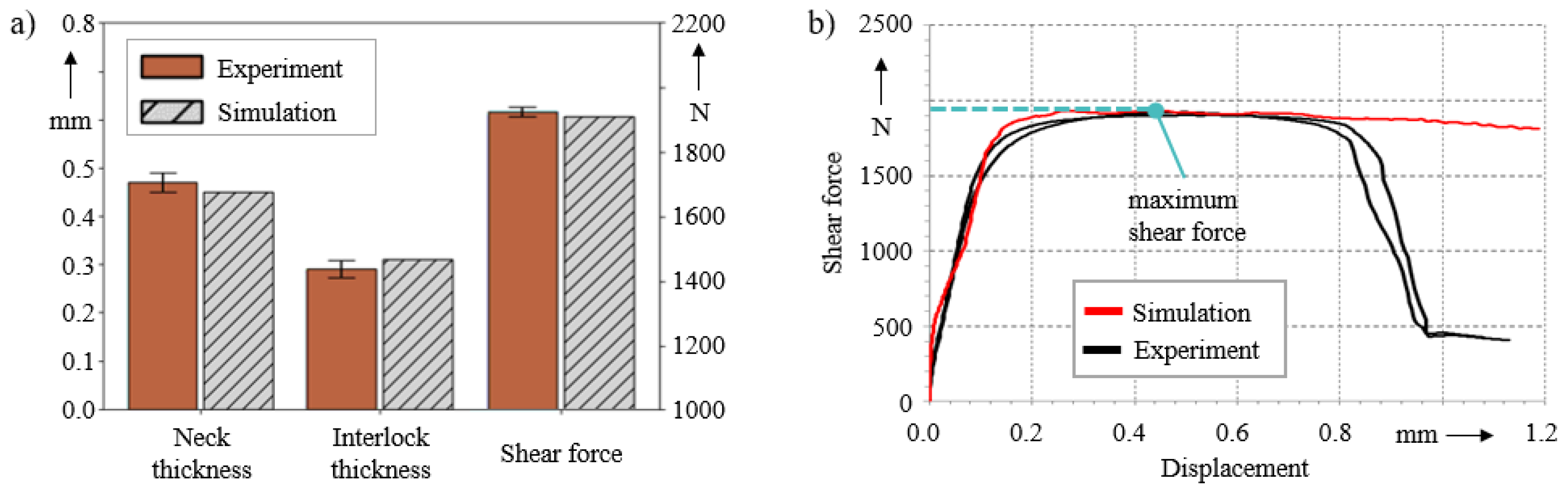
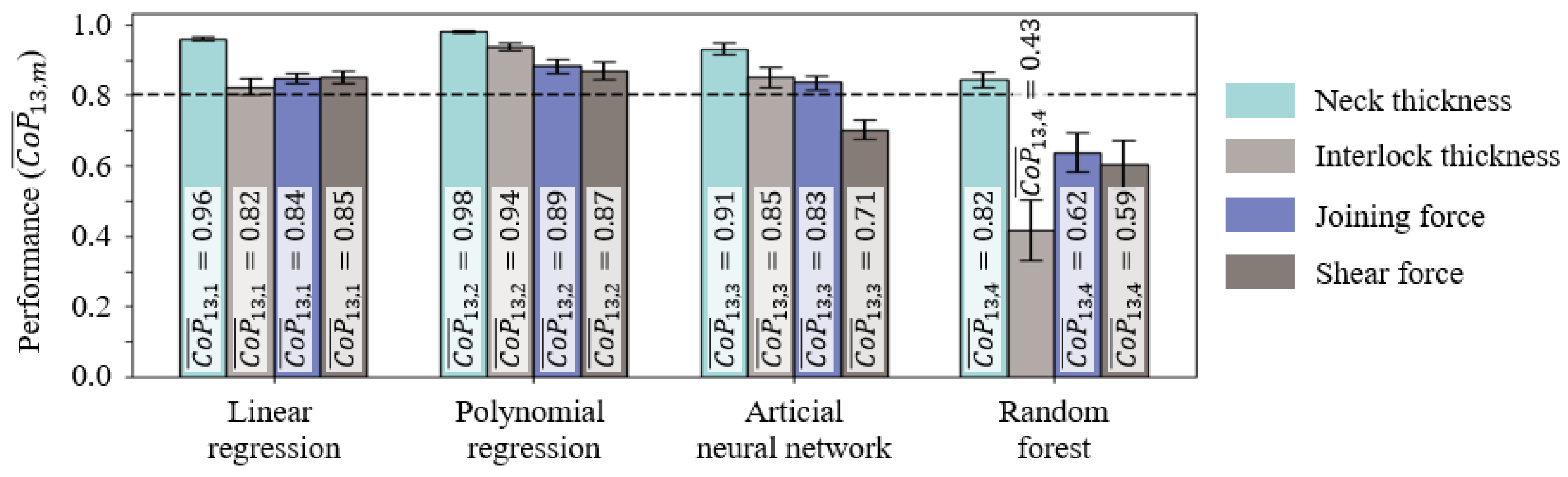
5.1. Performance of Machine Learning Algorithms on a Comprehensive Database
5.2. Correlation Analysis
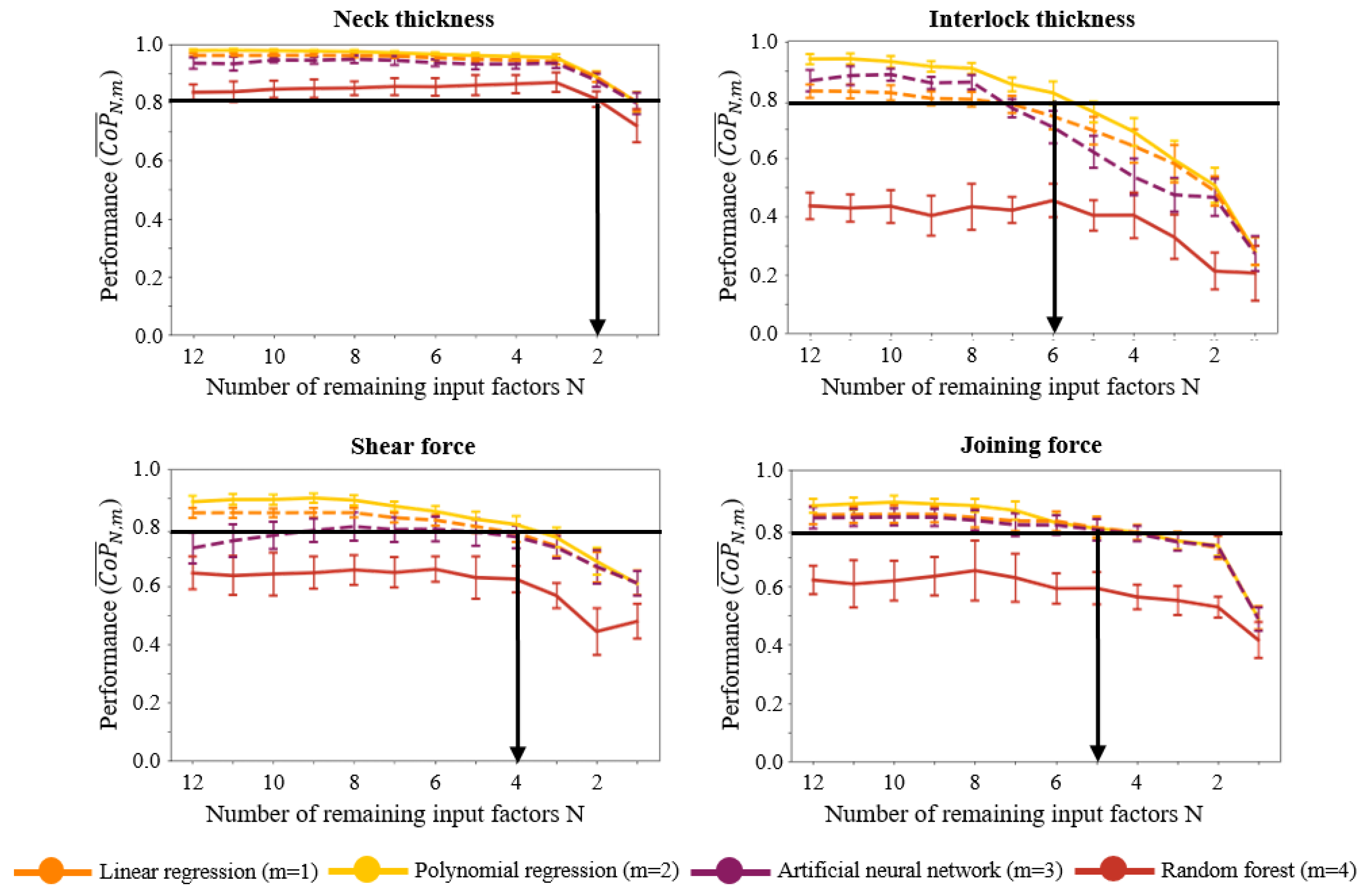
5.3. Performance of Machine Learning Algorithms on Varying Input Data
5.4. Design Equations
6. Discussion
7. Conclusions
- •
- The linear and polynomial regression models achieved the highest ability to predict the investigated clinch joint properties considering comprehensive and even limited input data.
- •
- The application of a correlation-based feature-selection method enabled the significant decrease of the model complexity based on a systematic reduction of the database. For instance, the accurate estimation of the neck thickness can be achieved by only considering a linear regression model and data regarding the applied die depth and die bottom diameter.
- •
- The experimental evaluation of the generated results confirm a high applicability of the simplified models and design equations for the prediction of clinch joint characteristics even if only a limited number of features are available. Thus, besides the reduction of computational and modeling effort, the results can pave the way to a more versatile application of pretrained regression models on varying tool configurations for a given joining task.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ANN | Artificial Neural Network |
| CoP | Coefficient of Prognosis |
| DoE | Design of Experiment |
| FE | Finite Element |
| GA | Genetic Algorithm |
| MLS | Moving Least-Square |
| NSGA-II | Non-Dominated Sorting Genetic Algorithm |
| PCA | Principal Component Analysis |
| RQ | Research Questions |
References
- Kaščák, L.; Spišák, E.; Majerníková, J. Clinching and Clinch-Riveting as a Green Alternative to Resistance Spot Welding. In Proceedings of the 2019 International Council on Technologies of Environmental Protection (ICTEP), Stary Smokovec, Slovakia, 23–25 October 2019; pp. 138–142. [Google Scholar] [CrossRef]
- Shi, C.; Li, H.; Chen, C.; Ouyang, Y.; Qin, D. Experimental investigation of the flat clinch–rivet process. Thin-Walled Struct. 2022, 171, 108612. [Google Scholar] [CrossRef]
- Ran, X.; Chen, C.; Zhang, H.; Ouyang, Y. Investigation of the clinching process with rectangle punch. Thin-Walled Struct. 2021, 166, 108034. [Google Scholar] [CrossRef]
- Zhang, X.; Chen, C.; Peng, H. Recent development of clinching tools and machines. Int. J. Adv. Manuf. Technol. 2022, 121, 2867–2899. [Google Scholar] [CrossRef]
- DVS-EFB 3470:2017-02; Mechanisches Fügen—Konstruktion und Auslegung—Grundlagen/Überblick. DVS Media GmbH: Düsseldorf, Germany, 2017.
- DVS-EFB 3420; Clinchen—Überblick—Clinching—Basics. DVS Media GmbH: Düsseldorf, Germany, 2012.
- Neugebauer, R.; Riedel, F.; Marx, R. Entwicklung eines Konstruktionssystems für den Rechnerischen Festigkeitsnachweis von Punktförmig Mechanisch gefüGten Bauteilen; EFB-FB Nr. 323; Europäische Forschungsgesellschaft für Blechverarbeitung e.V.: Hannover, Germany, 2010; ISBN 978-3-86776-359-2. [Google Scholar]
- Zirngibl, C.; Schleich, B.; Wartzack, S. Potentiale datengestützter Methoden zur Gestaltung und Optimierung mechanischer Fügeverbindungen. Proc. Symp. DfX 2020, 31, 71–80. [Google Scholar] [CrossRef]
- Oudjene, M.; Ben-Ayed, L. On the parametrical study of clinch joining of metallic sheets using the Taguchi method. Eng. Struct. 2008, 30, 1782–1788. [Google Scholar] [CrossRef]
- Oudjene, M.; Ben-Ayed, L.; Delamézière, A.; Batoz, J.-L. Shape optimization of clinching tools using the response surface methodology with moving least-square approximation. J. Mater. Process Technol. 2009, 209, 289–296. [Google Scholar] [CrossRef]
- Lebaal, N.; Oudjene, M.; Roth, S. The optimal design of sheet metal forming processes: Application to the clinching of thin sheets. Int. J. Comput. Appl. Technol. 2012, 43, 110–116. [Google Scholar] [CrossRef]
- Roux, E.; Bouchard, P.-O. Kriging metamodel global optimization of clinching joining processes accounting for ductile damage. J. Mater. Process Technol. 2013, 213, 1038–1047. [Google Scholar] [CrossRef]
- Lambiase, F.; Di Ilio, A. Optimization of the clinching tools by means of integrated FE modeling and artificial intelligence techniques. Procedia CIRP 2013, 12, 163–168. [Google Scholar] [CrossRef]
- Eshtayeh, M.; Hrairi, M. Multi objective optimization of clinching joints quality using grey-based taguchi method. Int. J. Adv. Manuf. Technol. 2016, 87, 1–17. [Google Scholar] [CrossRef]
- Wang, M.; Xiao, G.; Li, Z.; Wang, J. Shape optimization methodology of clinching tools based on Bezier curve. Int. J. Adv. Manuf. Technol. 2017, 24, 2267–2280. [Google Scholar] [CrossRef]
- Wang, X.; Li, X.; Shen, Z.; Ma, Y.; Liu, H. Finite element simulation on ivestigations, modeling, and multiobjective optimization for linch joining process design accounting for process paramteres and design constraints. Int. J. Adv. Manuf. Technol. 2018, 96, 3481–3501. [Google Scholar] [CrossRef]
- Schwarz, C.; Kropp, T.; Kraus, C.; Drossel, W.-G. Optimization of thick sheet clinching tools using principal component analysis. Int. J. Adv. Manuf. Technol. 2020, 106, 471–479. [Google Scholar] [CrossRef]
- Bielak, C.R.; Böhnke, M.; Beck, R.; Bobbert, M.; Meschut, G. Numerical analysis of the robustness of clinching process considering the pre-forming of the parts. J. Adv. Join. Process. 2021, 3, 100038. [Google Scholar] [CrossRef]
- Martin, S.; Bielak, C.R.; Bobbert, M.; Tröster, T.; Meschut, G. Numerical investigation of the clinched joint loadings considering the initial pre-strain in the joining area. Prod. Eng. 2022, 16, 261–273. [Google Scholar] [CrossRef]
- Zirngibl, C.; Dworschak, F.; Schleich, B.; Wartzack, S. Application of reinforcement learning for the optimization of clinch joint characteristics. Prod. Eng. 2022, 16, 315–325. [Google Scholar] [CrossRef]
- Bielak, C.R.; Böhnke, M.; Bobbert, M.; Meschut, G. Further Development of a Numerical Method for Analyzing the Load Capacity of Clinched Joints in Versatile Process Chains. Paper Presented at ESAFORM 2021. In Proceedings of the 24th International Conference on Material Forming, Liège, Belgium, 14–16 April 2021. [Google Scholar] [CrossRef]
- Zirngibl, C.; Schleich, B.; Wartzack, S. Approach for the automated and data-based design of mechanical joints. Proc. Des. Soc. 2021, 1, 521–530. [Google Scholar] [CrossRef]
- Zirngibl, C.; Schleich, B. Approach for the Automated Analysis of Geometrical Clinch Joint Characteristics. Key Eng. Mater. 2020, 883, 105–110. [Google Scholar] [CrossRef]
- Siebertz, K.; van Bebber, D.; Hochkirchen, T. Statistische Versuchsplanung—Design of Experiments (DoE); Springer: Wiesbaden, Germany, 2017. [Google Scholar] [CrossRef]
- Witten, I.H.; Frank, E.; Hall, M.A. Data Mining: Practical Machine Learning Tools and Techniques, 3rd ed.; Morgan Kaufmann: Burlington, MA, USA, 2011. [Google Scholar]
- Most, T.; Will, J. Metamodel of Optimal Prognosis—An automatic approach for variable reduction and optimal metamodel selection. Proc. Weimar. Optim. Stochastiktage 2008, 5, 20–21. [Google Scholar]
- Lambiase, F. Influence of process parameters in mechanical clinching with extensible dies. Int. J. Adv. Manuf. Technol. 2013, 66, 2123–2131. [Google Scholar] [CrossRef]
- Drossel, W.-G.; Falk, T.; Israel, M.; Jesche, F. Unerring Planning of Clinching Processes through the use of Mathematical Methods. Key Eng. Mater. 2014, 611–612, 1437–1444. [Google Scholar] [CrossRef]
- Drossel, W.-G.; Israel, M.; Falk, T. Robustness evaluation and tool optimization in forming applications. In Proceedings of the 9th Weimar Optimization and Stochastic Days, Weimar, Germany, 29–30 November 2012. [Google Scholar]
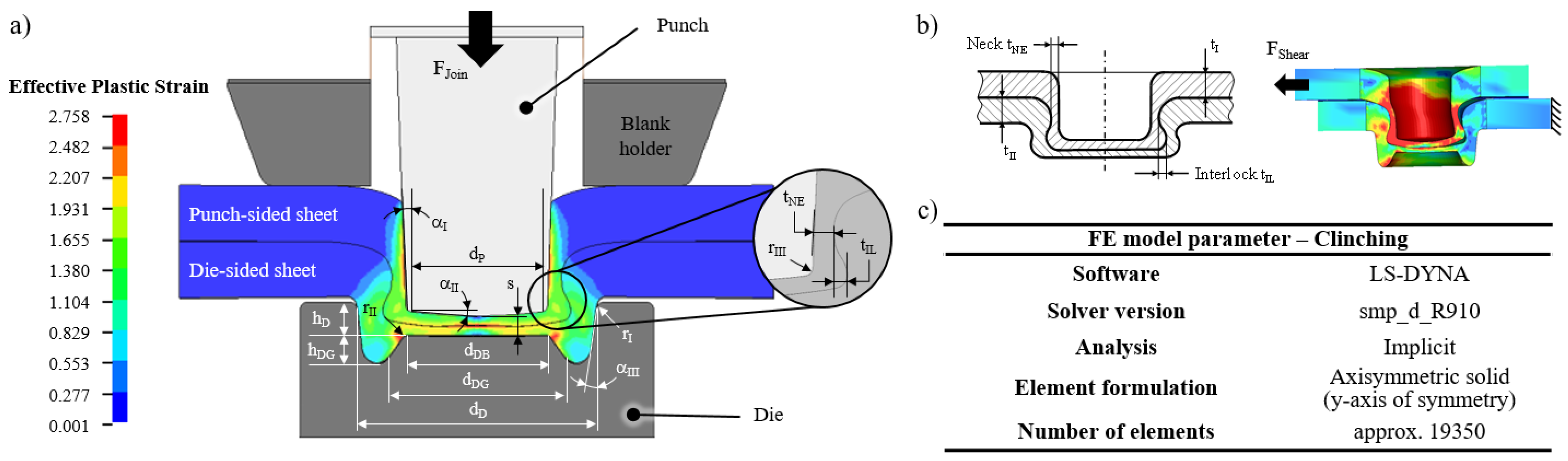

| Input Parameter | Unit | Min.–Max. | Input Parameter | Unit | Min.–Max. |
|---|---|---|---|---|---|
| Punch | Die | ||||
| Diameter d | mm | 4.5–6.0 | Diameter d | mm | 7.5–8.5 |
| Radius r | mm | 0.1–0.6 | Depth h | mm | 0.8–1.8 |
| Side draft angle | deg | 0.0–4.0 | Groove depth h | mm | 0.5–1.3 |
| Face draft angle | deg | 3.0–8.0 | Bottom diameter d | mm | 3.5–4.8 |
| Process | Groove diameter d | mm | 5.6–7.0 | ||
| Punch penetration s | % | 70–90 * | Corner radius I r | mm | 0.1–0.4 |
| Joining velocity | mm s−1 | 2 (const.) | Corner radius II r | mm | 0.1–0.4 |
| Blank holder | Side draft angle | deg | 0.0–8.0 | ||
| Force | N | 785 (const.) | |||
| Tool dimensions | const. |
| Removed Input Parameter in Each Feature Selection Iteration | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 13 * (1 **) | 12 (2) | 11 (3) | 10 (4) | 9 (5) | 8 (6) | 7 (7) | 6 (8) | 5 (9) | 4 (10) | 3 (11) | 2 (12) | 1 – | |
| s | |||||||||||||
| s | |||||||||||||
| s | |||||||||||||
| s *** | |||||||||||||
| Input Data: 330 Samples, 13 Features | Input Data: 330 Samples, N Features | ||||
|---|---|---|---|---|---|
| Target Variables | Metamodel | Remaining Features N | |||
| Neck | → | Linear regression | 2 (, ) | ||
| Interlock | → | Poly. regression | 6 (, , , , , s) | ||
| Joining force | → | Linear regression | 5 (, , , s, ) | ||
| Shear force | → | Poly. regression | 4 (, , , ) | ||
| Regression Functions | Prediction | Exp. Study * | ||
|---|---|---|---|---|
| = | 0.46 mm | [0.45–0.49] mm | ||
| = | 0.34 mm | [0.28–0.32] mm | ||
| = | 29.2 kN | [31.5–35.7] kN | ||
| = | 1895 N | [1902–1946] N | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zirngibl, C.; Schleich, B.; Wartzack, S. Estimation of Clinch Joint Characteristics Based on Limited Input Data Using Pre-Trained Metamodels. AI 2022, 3, 990-1006. https://doi.org/10.3390/ai3040059
Zirngibl C, Schleich B, Wartzack S. Estimation of Clinch Joint Characteristics Based on Limited Input Data Using Pre-Trained Metamodels. AI. 2022; 3(4):990-1006. https://doi.org/10.3390/ai3040059
Chicago/Turabian StyleZirngibl, Christoph, Benjamin Schleich, and Sandro Wartzack. 2022. "Estimation of Clinch Joint Characteristics Based on Limited Input Data Using Pre-Trained Metamodels" AI 3, no. 4: 990-1006. https://doi.org/10.3390/ai3040059
APA StyleZirngibl, C., Schleich, B., & Wartzack, S. (2022). Estimation of Clinch Joint Characteristics Based on Limited Input Data Using Pre-Trained Metamodels. AI, 3(4), 990-1006. https://doi.org/10.3390/ai3040059







