Gamma Ray Source Localization for Time Projection Chamber Telescopes Using Convolutional Neural Networks
Abstract
1. Introduction
2. Related Work
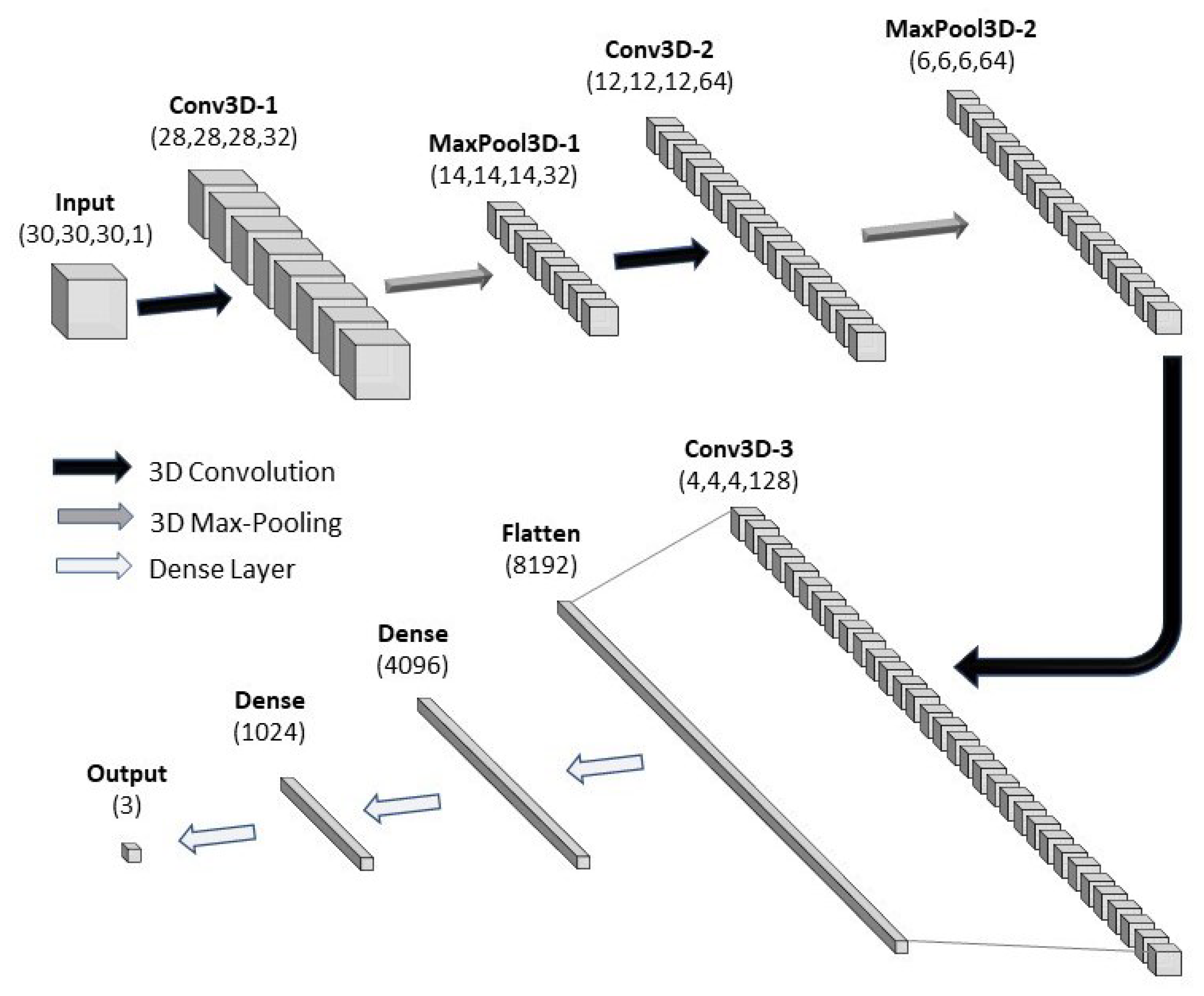
3. Methods
4. Model Results for Separated Energy and Drift Distance Data
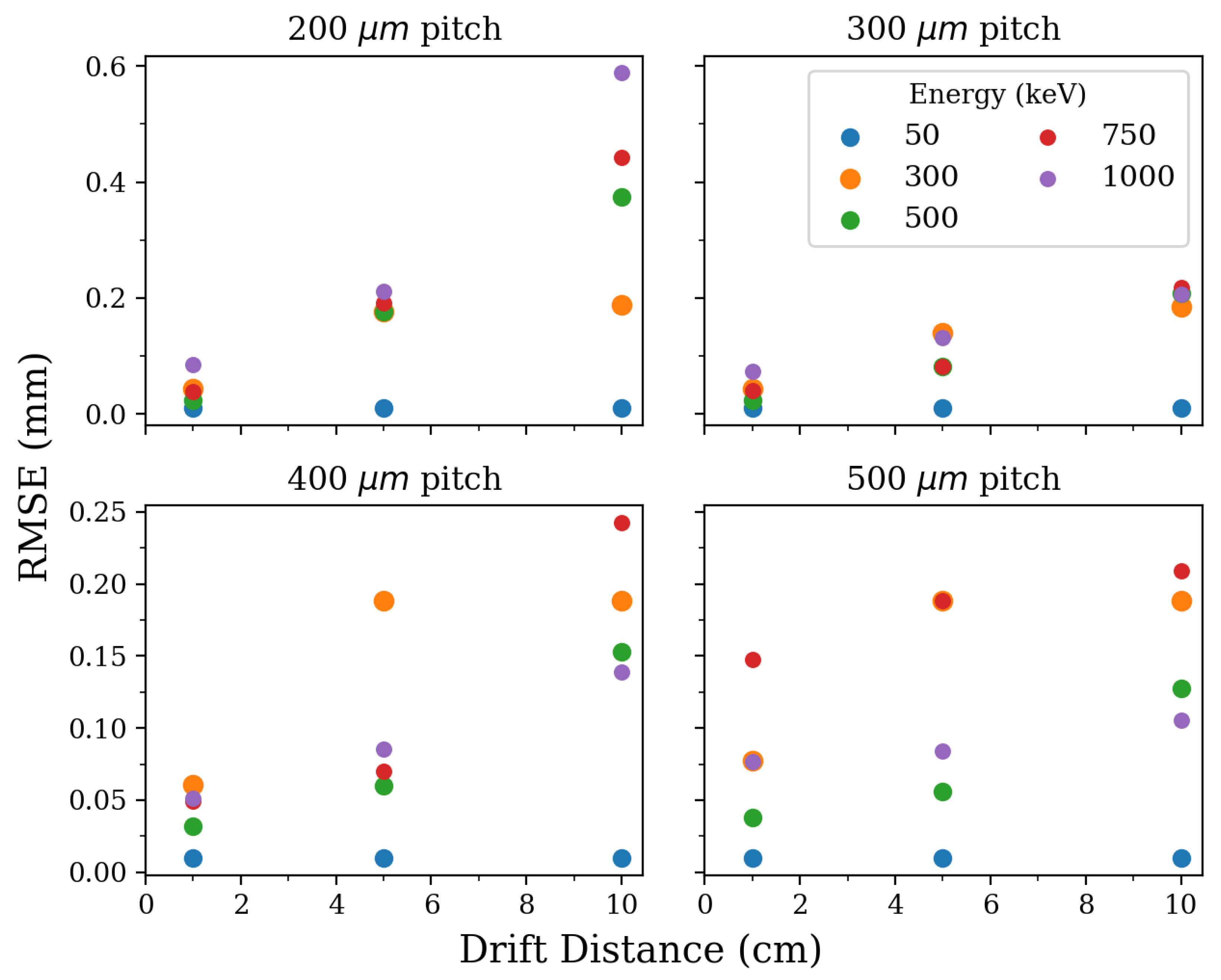
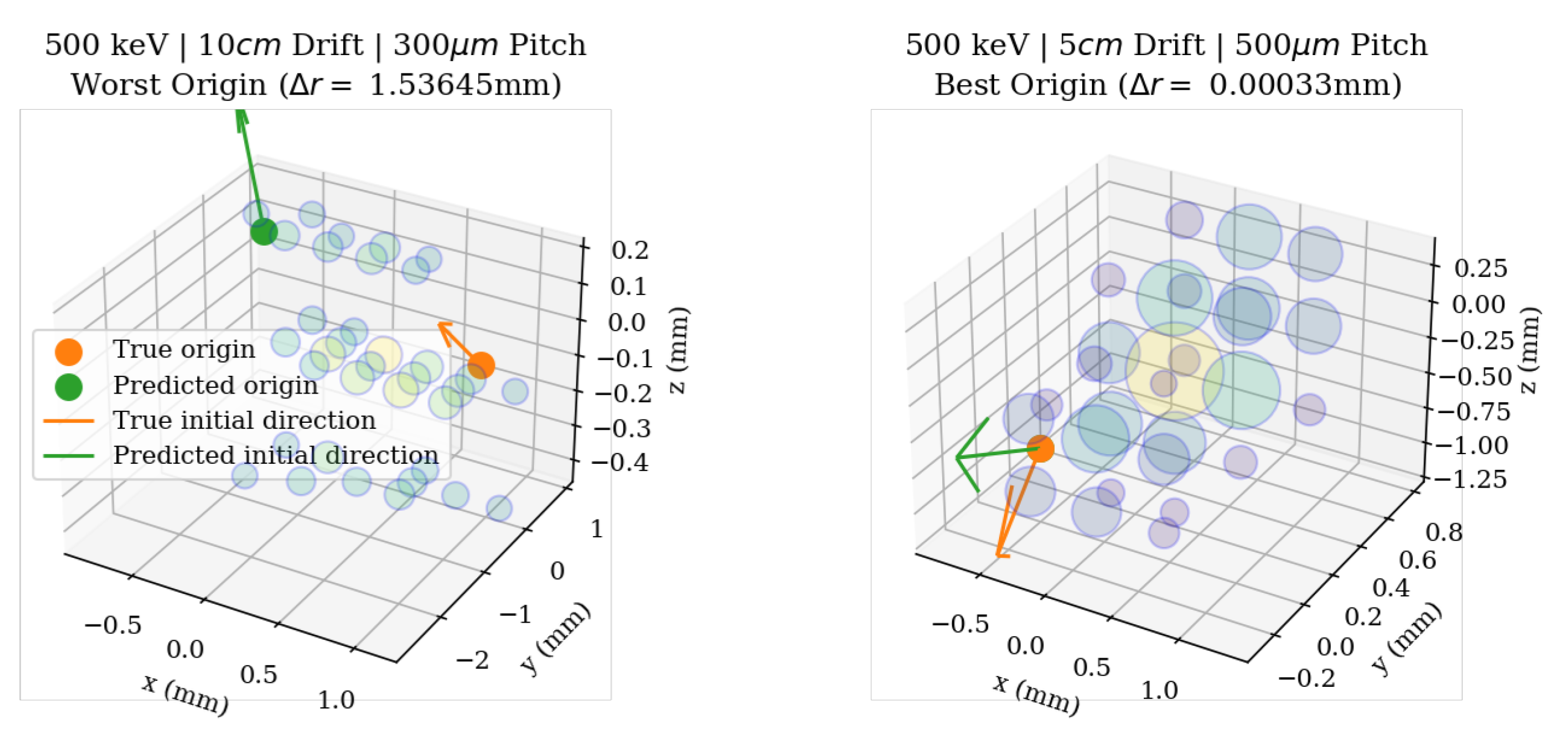
4.1. Track Origin Predictions
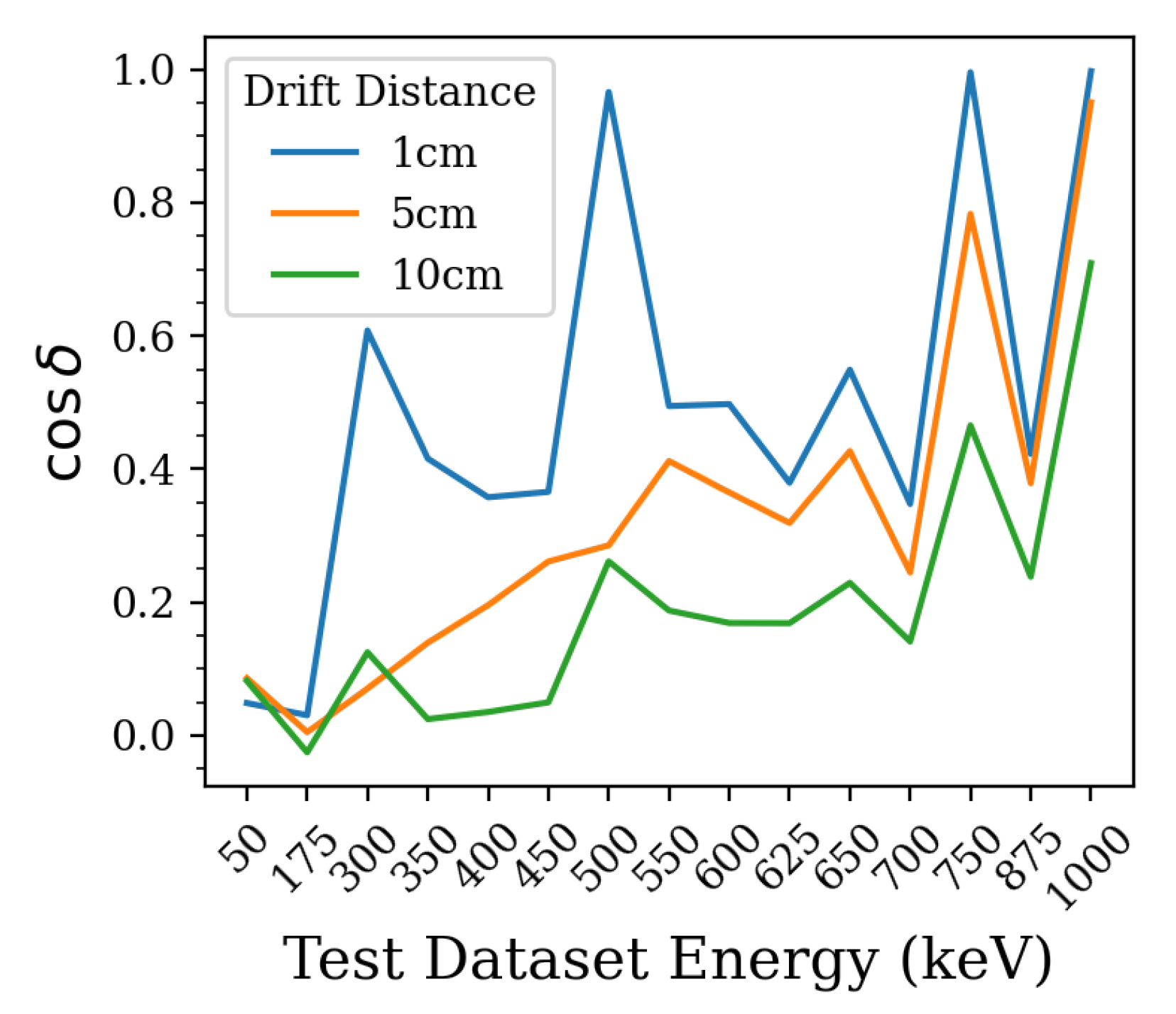
4.2. Initial Direction Predictions
4.3. Visualization of Selected Electron Tracks
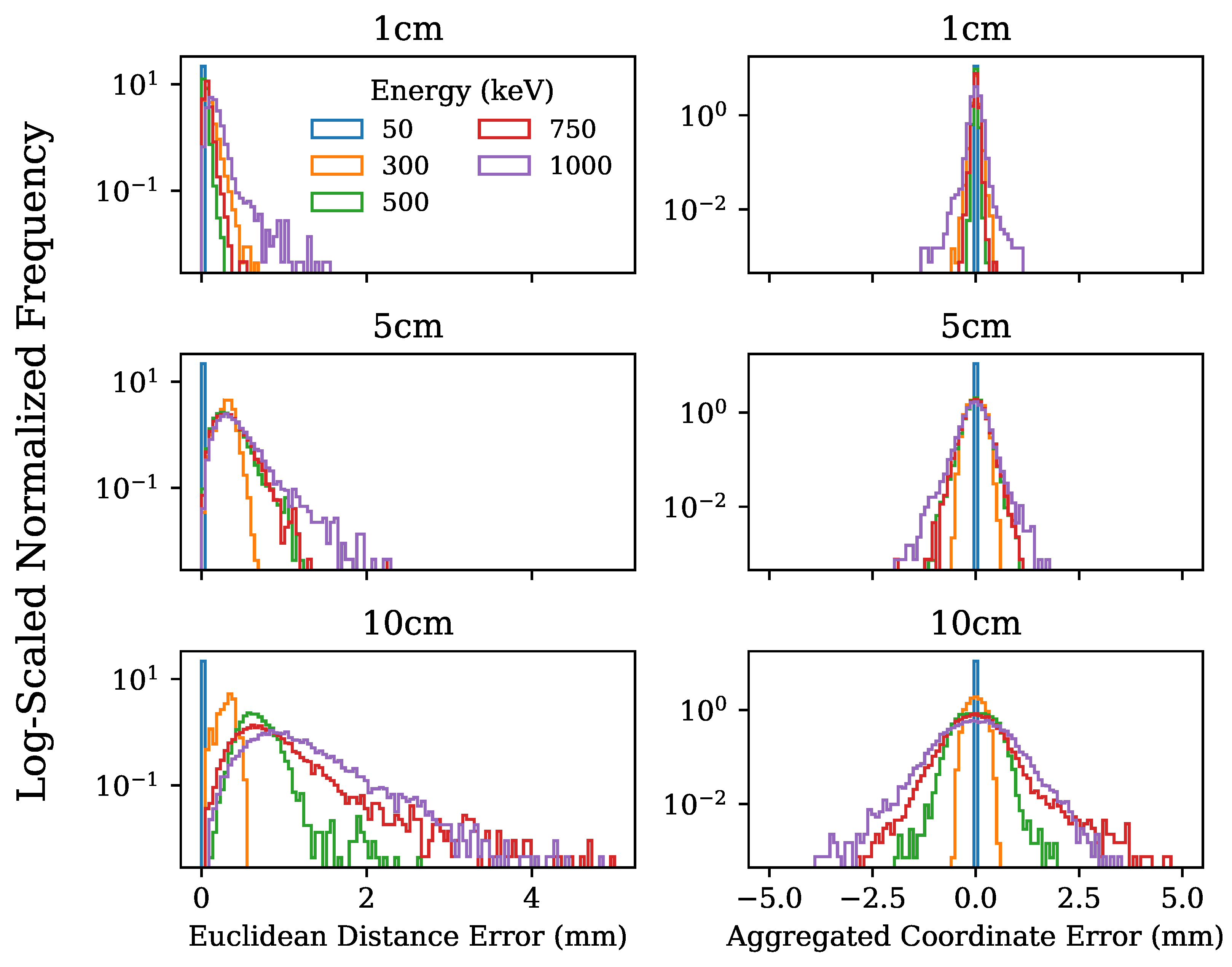
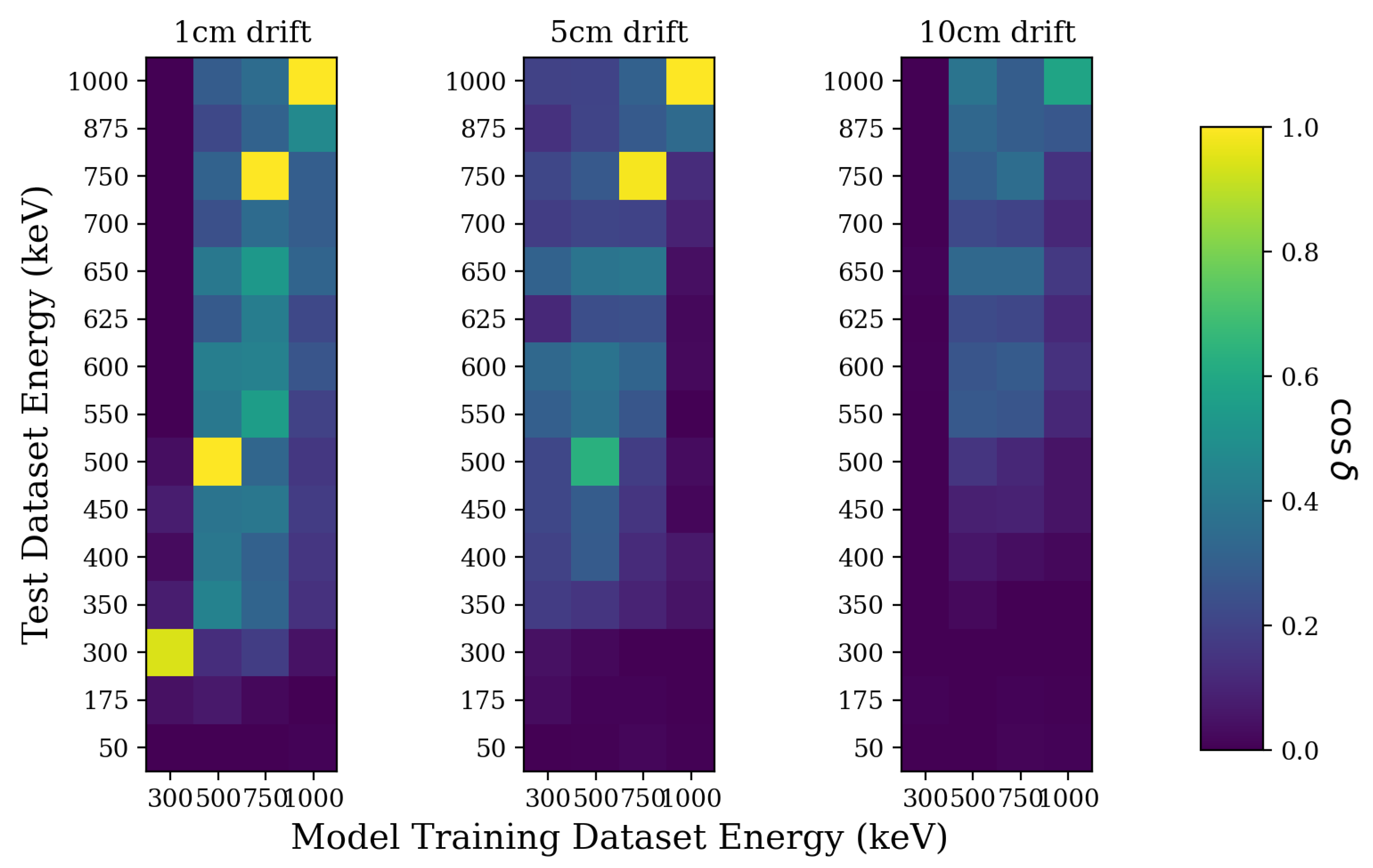
5. Model Results for Aggregated Energy and Drift Distance Data
5.1. Track Origin Predictions
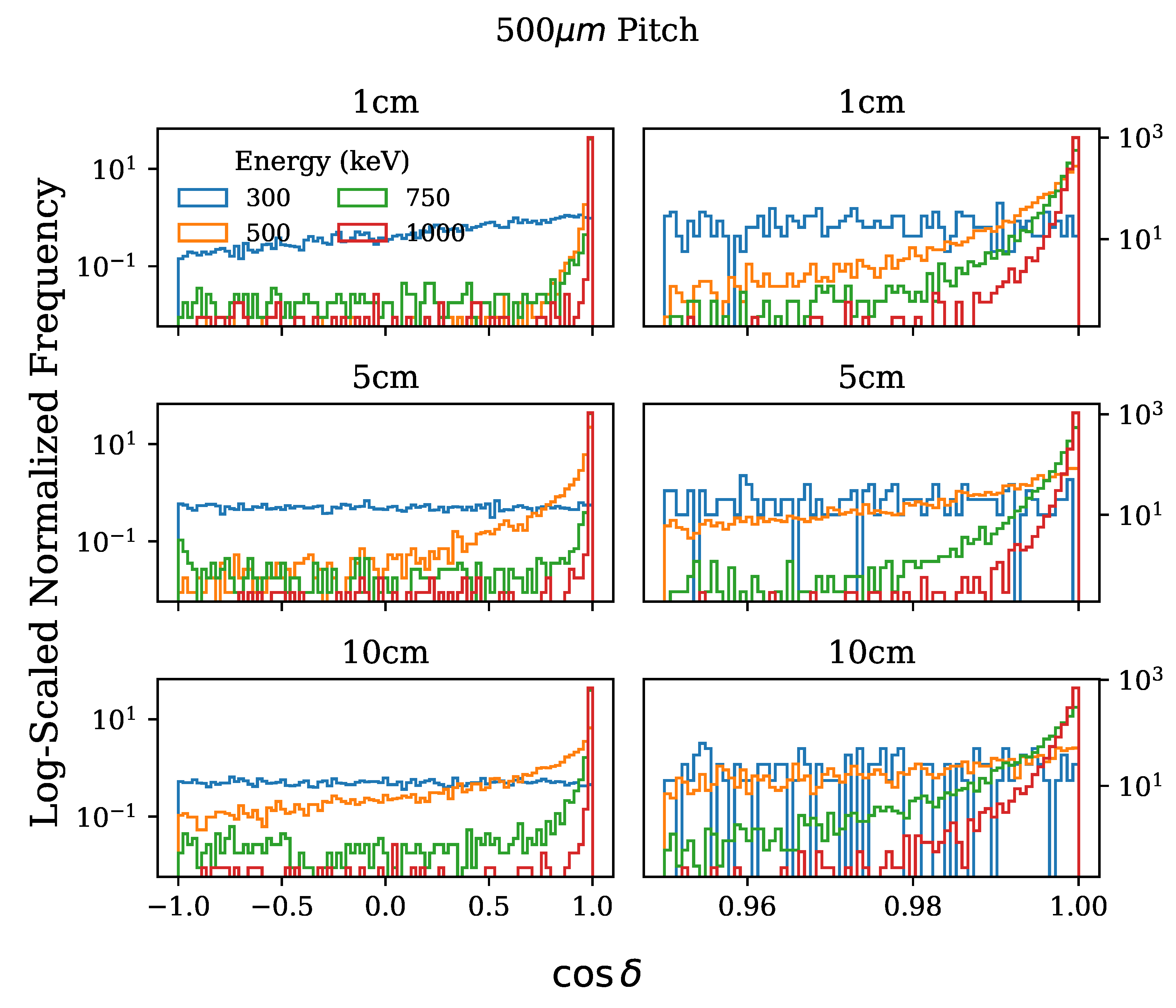
5.2. Initial Direction Predictions
6. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| LAr | Liquid Argon |
| TPC | Time Projection Chamber |
| WIMP | Weakly Interacting Massive Particle |
| COMPTEL | Compton Telescope |
| OSSE | Oriented Scintillation Spectrometer Experiment |
| CNN | Convolutional Neural Network |
| ML | Machine Learning |
| MSE | Mean Squared Error |
| VGG | Visual Geometry Group |
| PIC | Pixel Chamber |
| ResNet | Residual Neural Network |
References
- McEnery, J.; Barrio, J.A.; Agudo, I.; Ajello, M.; Álvarez, J.; Ansoldi, S.; Anton, S.; Auricchio, N.; Stephen, J.B.; Baldini, L.; et al. All-sky Medium Energy Gamma-ray Observatory: Exploring the Extreme Multimessenger Universe. arXiv 2019, arXiv:1907.07558. [Google Scholar]
- Cembranos, J.A.; Strigari, L.E. Diffuse MeV gamma rays and galactic 511 keV line from decaying WIMP dark matter. Phys. Rev. D 2008, 77, 123519. [Google Scholar] [CrossRef]
- Lawson, K.; Zhitnitsky, A.R. Diffuse cosmic gamma rays at 1–20 MeV: A trace of the dark matter? J. Cosmol. Astropart. Phys. 2008, 2008, 022. [Google Scholar] [CrossRef]
- Tomsick, J.; Zoglauer, A.; Sleator, C.; Lazar, H.; Beechert, J.; Boggs, S.; Roberts, J.; Siegert, T.; Lowell, A.; Wulf, E.; et al. The compton spectrometer and imager. Bull. Am. Astron. Soc. 2019, 51, 98. [Google Scholar]
- Shutt, T. Development of a Novel Readout System for a Liquid Argon Time Projection Chamber MeV Gamma-Ray Telescope. In Proceedings of the SnowMass 2021 Meeting, Seattle, WA, USA, 4 November 2021. [Google Scholar]
- Aramaki, T.; Boezio, M.; Buckley, J.; Bulbul, E.; von Doetinchem, P.; Donato, F.; Harding, J.P.; Karwin, C.; Kumar, J.; Leane, R.K.; et al. Snowmass2021 Cosmic Frontier: The landscape of cosmic-ray and high-energy photon probes of particle dark matter. arXiv 2022, arXiv:2203.06894. [Google Scholar]
- Cooper, M.; Mijnarends, P.; Shiotani, N.; Sakai, N.; Bansil, A. X-ray Compton Scattering; OXford University Press: Oxford, UK, 2004; Volume 5. [Google Scholar]
- Bellazzini, R.; Angelini, F.; Baldini, L.; Brez, A.; Costa, E.; Di Persio, G.; Latronico, L.; Massai, M.M.; Omodei, N.; Pacciani, L.; et al. Novel gaseous X-ray polarimeter: Data analysis and simulation. In Proceedings of the Astronomical Telescopes and Instrumentation, Waikoloa, HI, USA, 22–28 August 2002; Volume 4843, pp. 383–393. [Google Scholar]
- Li, T.; Zeng, M.; Feng, H.; Cang, J.; Li, H.; Zhang, H.; Zeng, Z.; Cheng, J.; Ma, H.; Liu, Y. Electron track reconstruction and improved modulation for photoelectric X-ray polarimetry. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectr. Detect. Assoc. Equip. 2017, 858, 62–68. [Google Scholar] [CrossRef]
- Yoneda, H.; Saito, S.; Watanabe, S.; Ikeda, H.; Takahashi, T. Development of Si-CMOS hybrid detectors towards electron tracking based Compton imaging in semiconductor detectors. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectr. Detect. Assoc. Equip. 2018, 912, 269–273. [Google Scholar] [CrossRef]
- Bernard, D.; Hunter, S.D.; Tanimori, T. Time projection chambers for gamma-ray astronomy. arXiv 2022, arXiv:2206.08676. [Google Scholar]
- Ikeda, T.; Takada, A.; Abe, M.; Yoshikawa, K.; Tsuda, M.; Ogio, S.; Sonoda, S.; Mizumura, Y.; Yoshida, Y.; Tanimori, T. Development of convolutional neural networks for an electron-tracking Compton camera. Prog. Theor. Exp. Phys. 2021, 2021, 083F01. [Google Scholar] [CrossRef]
- Takada, A.; Takemura, T.; Yoshikawa, K.; Mizumura, Y.; Ikeda, T.; Nakamura, Y.; Onozaka, K.; Abe, M.; Hamaguchi, K.; Kubo, H.; et al. First Observation of the MeV Gamma-Ray Universe with Bijective Imaging Spectroscopy Using the Electron-tracking Compton Telescope on Board SMILE-2+. Astrophys. J. 2022, 930, 6. [Google Scholar] [CrossRef]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. arXiv 2015, arXiv:1505.04597. [Google Scholar]
- Peirson, A.; Romani, R.; Marshall, H.; Steiner, J.; Baldini, L. Deep ensemble analysis for Imaging X-ray Polarimetry. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectr. Detect. Assoc. Equip. 2021, 986, 164740. [Google Scholar] [CrossRef]
- Peirson, A.; Romani, R. A deep ensemble approach to X-ray polarimetry. arXiv 2021, arXiv:2111.03047. [Google Scholar]
- Peirson, A.; Romani, R.W. Toward optimal signal extraction for imaging x-ray polarimetry. Astrophys. J. 2021, 920, 40. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Agency, N.E. PENELOPE 2018: A Code System for Monte Carlo Simulation of Electron and Photon Transport; Nuclear Energy Agency: Paris, France, 2019; p. 420. [Google Scholar] [CrossRef]
- Bronstein, M.M.; Bruna, J.; Cohen, T.; Veličković, P. Geometric deep learning: Grids, groups, graphs, geodesics, and gauges. arXiv 2021, arXiv:2104.13478. [Google Scholar]
- Karniadakis, G.E.; Kevrekidis, I.G.; Lu, L.; Perdikaris, P.; Wang, S.; Yang, L. Physics-informed machine learning. Nat. Rev. Phys. 2021, 3, 422–440. [Google Scholar] [CrossRef]
- Kauderer-Abrams, E. Quantifying translation-invariance in convolutional neural networks. arXiv 2017, arXiv:1801.01450. [Google Scholar]
- Ihme, M.; Chung, W.T.; Mishra, A.A. Combustion machine learning: Principles, progress and prospects. Prog. Energy Combust. Sci. 2022, 91, 101010. [Google Scholar]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Tompson, J.; Goroshin, R.; Jain, A.; LeCun, Y.; Bregler, C. Efficient object localization using convolutional networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 648–656. [Google Scholar]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Ioffe, S.; Szegedy, C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. In Proceedings of the International Conference on Machine Learning, Lille, France, 6–11 July 2015; pp. 448–456. [Google Scholar]
- Buuck, M.; Mishra, A.; Charles, E.; Di Lalla, N.; Hitchcock, O.; Monzani, M.E.; Omodei, N.; Shutt, T. Low-Energy Electron-Track Imaging for a Liquid Argon Time-Projection-Chamber Telescope Concept using Probabilistic Deep Learning. arXiv 2022, arXiv:2207.07805. [Google Scholar]
- Daxberger, E.; Kristiadi, A.; Immer, A.; Eschenhagen, R.; Bauer, M.; Hennig, P. Laplace redux-effortless bayesian deep learning. Adv. Neural Inf. Process. Syst. 2021, 34, 20089–20103. [Google Scholar]

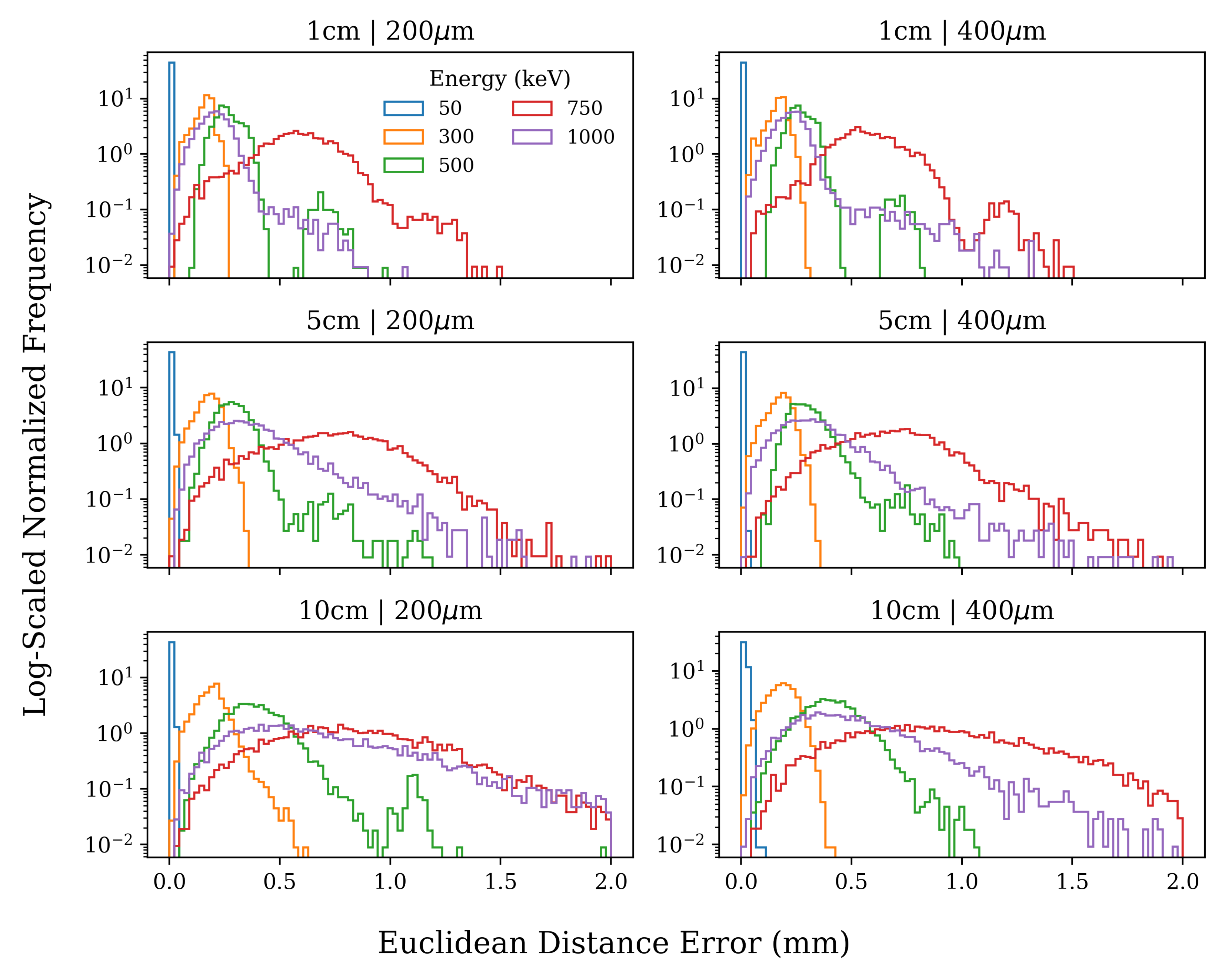
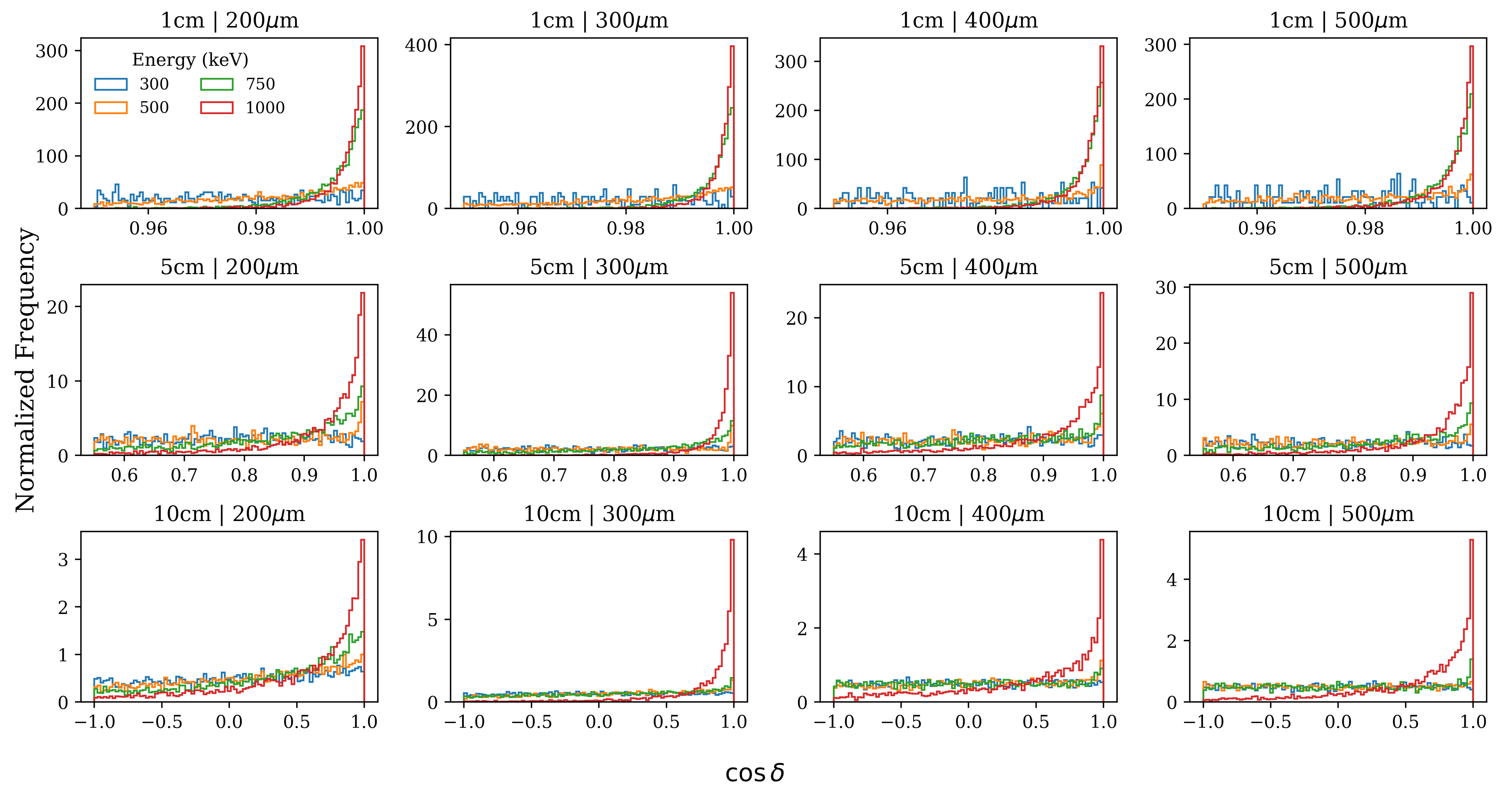
| Pixel Pitch (m) | |||||
|---|---|---|---|---|---|
| 200 | 300 | 400 | 500 | ||
| Drift Distance (cm) | 1 | 0.05664 | 0.05621 | 0.06626 | 0.10167 |
| 5 | 0.28113 | 0.15146 | 0.12109 | 0.15662 | |
| 10 | 0.51667 | 0.30343 | 0.26007 | 0.22308 | |
| Pixel Pitch (m) | |||||
|---|---|---|---|---|---|
| 200 | 300 | 400 | 500 | ||
| Drift Distance (cm) | 1 | 2.0336 | 2.0443 | 3.067 | 3.572 |
| 5 | 24.660 | 7.4337 | 5.0245 | 5.3518 | |
| 10 | 72.978 | 29.078 | 17.206 | 11.117 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khek, B.; Mishra, A.; Buuck, M.; Shutt, T. Gamma Ray Source Localization for Time Projection Chamber Telescopes Using Convolutional Neural Networks. AI 2022, 3, 975-989. https://doi.org/10.3390/ai3040058
Khek B, Mishra A, Buuck M, Shutt T. Gamma Ray Source Localization for Time Projection Chamber Telescopes Using Convolutional Neural Networks. AI. 2022; 3(4):975-989. https://doi.org/10.3390/ai3040058
Chicago/Turabian StyleKhek, Brandon, Aashwin Mishra, Micah Buuck, and Tom Shutt. 2022. "Gamma Ray Source Localization for Time Projection Chamber Telescopes Using Convolutional Neural Networks" AI 3, no. 4: 975-989. https://doi.org/10.3390/ai3040058
APA StyleKhek, B., Mishra, A., Buuck, M., & Shutt, T. (2022). Gamma Ray Source Localization for Time Projection Chamber Telescopes Using Convolutional Neural Networks. AI, 3(4), 975-989. https://doi.org/10.3390/ai3040058







