The Form in Formal Thought Disorder: A Model of Dyssyntax in Semantic Networking
Abstract
:1. Introduction
2. Semantic Networking
2.1. Semantic Networks
2.2. The Syntax–Semantics Interface, Set Theory, and Logic
3. Formal Thought Disorder
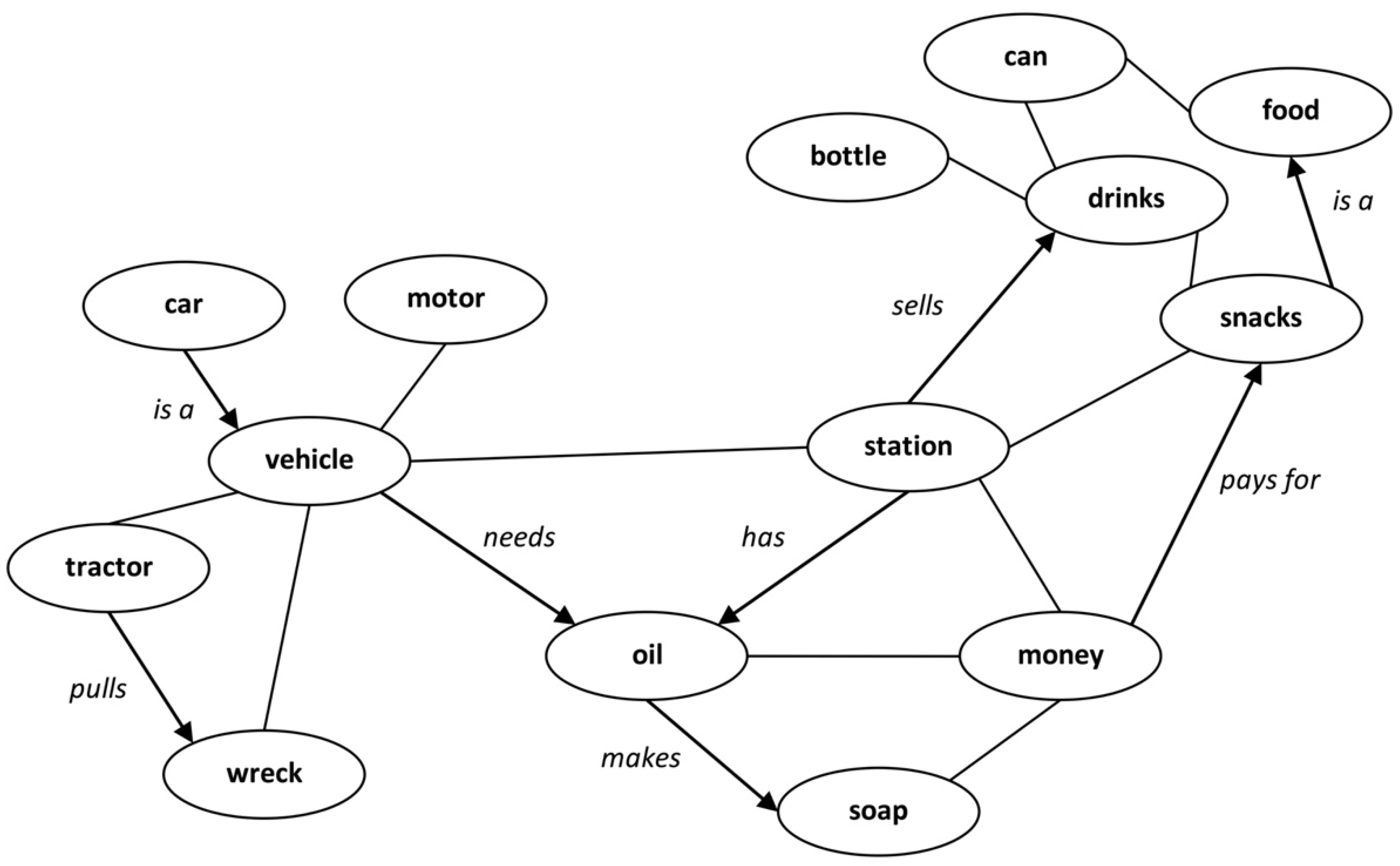
“They’re destroying too many cattle and oil just to make soap. If we need soap when you can jump into a pool of water, and then when you go to buy your gasoline, my folks always thought they should, get pop but the best thing to get, is motor oil, and, money. May may as well go there and, trade in some, pop caps and, uh, tires, and tractors to grup, car garages, so they can pull cars away from wrecks, is what I believe in. So I didn’t go there to get no more pop when my folks said it. I just went there to get a ice-cream cone, and some pop, in cans, or we can go over there to get a cigarette.”
4. The Dyssyntax Model
4.1. Logical Form
Well, er… not quite the same as, er… don’t know quite how to say it. It isn’t the same, being in hospital as, er… working. Er… the job isn’t quite the same, er… very much the same but, of course, it isn’t exactly the same.([17], p. 10)
4.2. Description Logic
- 1.
- The interpretation of some atomic concept A is equivalent to AI, so that we have (A)I = AI ∈ ∆I.
- 2.
- The interpretation of some atomic role r is equivalent to rI, so that we have (r)I = rI ⊆ ∆I × ∆I.
- 3.
- The interpretation of the top concept (⊤) is equivalent to ∆I. This means that the logical concept <Truth> expresses the validity of the interpretation of all members of the interpretation domain.
- 4.
- The interpretation of the bottom concept (⊥) is equivalent to Ø. This means that the logical concept <Falsity> expresses the fact that the interpretations of all members of the interpretation domain are invalid (i.e., meaningless).
- 5.
- The interpretation of the concept conjunction A1 ⊓ A2, or (A1 ⊓ A2)I, is equivalent to A1I ∩ A2I.
- 6.
- The interpretation of the concept disjunction A1 ⊔ A2, or (A1 ⊔ A2)I, is equivalent to A1I ∪ A2I.
- 7.
- The interpretation of the concept negation ¬A, or (¬A)I, is equivalent to ∆I\AI. More precisely, those elements of the interpretation domain (which do not exist within the concept description A) are interpreted as the constructors of the concept negation ¬A.
- 8.
- The interpretation of the concept subsumption A1 ⊑ A2 is equivalent to A1I ⊆ A2I.
- 9.
- The interpretation of the role subsumption r1 ⊑ r2 is equivalent to r1I ⊆ r2I.
- 10.
- The interpretation of the concept equivalence A1 ≡ A2 is equivalent to A1I = A2I.
- 11.
- The interpretation of the role equivalence r1 ≡ r2 is equivalent to r1I = r2I.
- 12.
- The existence of the concept assertion A(a) expresses the fact that individual a is interpreted to be an instance of concept A, i.e., aI∈ AI.
- 13.
- The existence of the role assertion r(a, b) expresses the property that the individuals a and b are interpreted to be related together by means of role r, i.e., (aI, bI) ∈ rI.
4.3. Conception Language
Conception Categorization and Association in Thought Processes in CL
- Singular ::= Marycow and atomic conception ::= <MaryCow>. More specifically, Marycow expresses Mary’s conception of some individual “cow” in the world. Additionally, the atomic conception <MaryCow> expresses Mary’s conception of her constructed concept <Cow>. In Mary’s view, any cow is an instance of <Cow>.
- Singular ::= Marybull, atomic conception ::= <MaryBull>.
- Singular ::= Maryleather, atomic conception ::= <MaryLeather>.
- Singular ::= MarykilledCow and atomic conception ::= <MaryKilledCow>. More specifically, MarykilledCow is equivalent to Mary’s conception of some individual “killed-cow”. Additionally, the atomic conception <MaryKilledCow> expresses Mary’s conception of her constructed concept <KilledCow>. In Mary’s view, any individual killedCow is an instance of her constructed concept <KilledCow>.
- Singular ::= MarykilledBull and atomic conception ::= <MaryKilledBull>.
- Singular ::= MaryproducedLeather and atomic conception ::= <MaryProducedLeather>.
4.4. Diagnosing FTD with CL
“Oh, it was superb, you know, the trains broke, and the pond fell in the front doorway.”
- ($)
- I got so angry I picked up a dish and threw it at the geshinker.
- (&)
- So I sort of bawked the whole thing up.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Collins, A.M.; Loftus, E.F. A spreading activation theory of semantic processing. Psychol. Rev. 1975, 82, 407–428. [Google Scholar] [CrossRef]
- Collins, A.M.; Quillian, M.R. Retrieval time from semantic memory. J. Verbal Learn. Verbal Behav. 1969, 8, 240–248. [Google Scholar] [CrossRef]
- Quillian, M.R. Word concepts: A theory and simulation of some basic semantic capabilities. Behav. Sci. 1967, 12, 410–439. [Google Scholar] [CrossRef]
- Quillian, M.R. Semantic networks. In Semantic Information Processing; Minsky, M.L., Ed.; MIT Press: Cambridge, MA, USA, 1968; pp. 227–270. [Google Scholar]
- Quillian, M.R. The Teachable Language Comprehender: A simulation program and theory of language. Commun. ACM 1969, 12, 459–476. [Google Scholar] [CrossRef]
- Johnson-Laird, P.N.; Herrmann, D.J.; Chaffin, R. Only connections: A critique of semantic networks. Psychol. Bull. 1984, 96, 292–315. [Google Scholar] [CrossRef]
- Augusto, L.M.; Badie, F. Formal thought disorder and logical form: A symbolic computational model of terminological knowledge. J. Knowl. Struct. Syst. forthcoming.
- Badie, F. On logical characterisation of human concept learning based on terminological systems. Log. Log. Philos. 2018, 27, 545–566. [Google Scholar] [CrossRef] [Green Version]
- Badie, F. A description logic based knowledge representation model for concept understanding. In Agents and Artificial Intelligence; van den Herik, J., Rocha, A., Filipe, J., Eds.; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2018; Volume 10839. [Google Scholar]
- Badie, F. A formal ontology for conception representation in terminological systems. In Reasoning: Logic, Cognition, and Games; Urbanski, M., Skura, T., Lupkowski, P., Eds.; College Publications: London, UK, 2020; pp. 137–157. [Google Scholar]
- Badie, F. Logic and constructivism: A model of terminological knowledge. J. Knowl. Struct. Syst. 2020, 1, 23–39. [Google Scholar]
- Badie, F. Towards contingent world descriptions in description logics. Log. Log. Philos. 2020, 29, 115–141. [Google Scholar] [CrossRef]
- Minsky, M. A Framework for Representing Knowledge (AIM-306); MIT Artificial Intelligence Laboratory: Cambridge, MA, USA, 1974. [Google Scholar]
- Minsky, M. A framework for representing knowledge. In The Psychology of Computer Vision; Wiston, P., Ed.; McGraw Hill: New York, NY, USA, 1975; pp. 211–277. [Google Scholar]
- Baader, F.; McGuiness, D.L.; Nardi, D.; Patel-Schneider, P.F. (Eds.) The Description Logic Handbook: Theory, Implementation and Applications; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Baader, F.; Horrocks, I.; Lutz, C.; Sattler, U. An Introduction to Description Logic; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar]
- McKenna, P.; Oh, T. Schizophrenic Speech. Making Sense of Bathroots and Ponds That Fall in Doorways; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Harnad, S. To cognize is to categorize: Cognition is categorization. In Handbook of Categorization in Cognitive Science; Cohen, H., Lefebvre, C., Eds.; Elsevier: Amsterdam, The Netherlands, 2005; pp. 20–43. [Google Scholar]
- Briganti, G.; Le Moine, O. Artificial Intelligence in medicine: Today and tomorrow. Front. Med. 2020, 7, 27. [Google Scholar] [CrossRef]
- Aceto, G.; Persico, V.; Pescapé, A. Big data, and cloud computing for Healthcare 4.0. J. Ind. Inf. Integr. 2020, 18, 100129. [Google Scholar]
- Massaro, A.; Maritati, V.; Savino, N.; Galiano, A.M. Neural networks for automated smart health platforms oriented on heart predictive diagnostic big data systems. In Proceedings of the 2018 AEIT International Annual Conference, Bari, Italy, 3–5 October 2018; pp. 1–5. [Google Scholar]
- Massaro, A.; Ricci, G.; Selicato, S.; Raminelli, S.; Galiano, A.M. Decisional support system with Artificial Intelligence oriented on health prediction using a wearable device and big data. In Proceedings of the 2020 IEEE International Workshop on Metrology for Industry 4.0 & IoT, Roma, Italy, 3–5 June 2020; pp. 718–723. [Google Scholar]
- El-Sherif, D.M.; Abouzid, M.; Elzarif, M.T.; Ahmed, A.A.; Albakri, A.; Alshehri, M.M. Telehealth and Artificial Intelligence insights into healthcare during the COVID-19 pandemic. Healthcare 2022, 10, 385. [Google Scholar] [CrossRef] [PubMed]
- Zhou, X.; Edirippulige, S.; Bai, X.; Bambling, M. Are online mental health interventions for youth effective? A systematic review. J. Telemed. Telecare 2021, 27, 638–666. [Google Scholar] [CrossRef] [PubMed]
- Adams, R.A.; Huys, Q.J.M.; Roiser, J.P. Computational psychiatry: Towards a mathematically informed understanding of mental illness. J. Neurol. Neurosurg. Psychiatry 2016, 87, 53–63. [Google Scholar] [CrossRef] [Green Version]
- Busemeyer, J.R.; Wang, Z.; Townsend, J.T.; Eidels, A. (Eds.) The Oxford Handbook of Computational and Mathematical Psychology; Oxford University Press: Oxford, UK, 2015. [Google Scholar]
- Sun, R. (Ed.) The Cambridge Handbook of Computational Psychology; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Augusto, L.M. Unconscious representations 2: Towards an integrated cognitive architecture. Axiomathes 2014, 24, 19–43. [Google Scholar] [CrossRef]
- Elvevåg, B.; Foltz, P.W.; Weinberger, D.R.; Goldberg, T.E. Quantifying incoherence in speech: An automated methodology and novel application to schizophrenia. Schizophr. Res. 2007, 93, 304–316. [Google Scholar] [CrossRef] [Green Version]
- Maher, B.A.; Manschreck, T.C.; Linnet, J.; Candela, S. Quantitative assessment of the frequency of normal associations in the utterances of schizophrenia patients and healthy controls. Schizophr. Res. 2005, 78, 219–224. [Google Scholar] [CrossRef]
- Bringsjord, S. Declarative/Logic-based cognitive modeling. In The Cambridge Handbook of Computational Psychology; Sun, R., Ed.; Cambridge University Press: Cambridge, UK, 2008; pp. 127–169. [Google Scholar]
- Braine, M.D.S. The “Natural Logic” approach to reasoning. In Reasoning, Necessity, and Logic: Developmental Perspectives; Overton, W.F., Ed.; Lawrence Erlbaum Associates: Hillsdale, NJ, USA, 1990; pp. 133–157. [Google Scholar]
- Braine, M.D.S.; O’Brien, D.P. (Eds.) Mental Logic; Lawrence Erlbaum Associates: Mahwah, NJ, USA, 1998. [Google Scholar]
- Evans, J.S. Logic and human reasoning: An assessment of the deduction paradigm. Psychol. Bull. 2002, 128, 978–996. [Google Scholar] [CrossRef]
- Inhelder, B.; Piaget, J. The Growth of Logical Thinking from Childhood to Adolescence; Basic Books: New York, NY, USA, 1958. [Google Scholar]
- Rips, L.J. The Psychology of Proof: Deductive Reasoning in Human Thinking; MIT Press: Cambridge, MA, USA, 1994. [Google Scholar]
- Stenning, K.; van Lambalgen, M. Human Reasoning and Cognitive Science; MIT Press: Cambridge, MA, USA, 2008. [Google Scholar]
- Wason, P. Reasoning about a rule. Q. J. Exp. Psychol. 1968, 20, 273–281. [Google Scholar] [CrossRef]
- Johnson-Laird, P.N.; Yang, Y. Mental logic, mental models, and simulations of human deductive reasoning. In The Cambridge Handbook of Computational Psychology; Sun, R., Ed.; Cambridge University Press: Cambridge, UK, 2008; pp. 339–358. [Google Scholar]
- Lewandowsky, S.; Farrell, S. Computational Modeling in Cognition: Principles and Practice; Sage Publications: Thousand Oaks, CA, USA, 2011. [Google Scholar]
- Polk, T.A.; Newell, A. Deduction as verbal reasoning. In Cognitive Modeling; Polk, T.A., Seifert, C.M., Eds.; MIT: Cambridge, MA, USA, 2002; pp. 1045–1082. [Google Scholar]
- Sowa, J.F. Categorization in cognitive computer science. In Handbook of Categorization in Cognitive Science; Cohen, H., Lefebvre, C., Eds.; Elsevier: Amsterdam, The Netherlands, 2005; pp. 141–163. [Google Scholar]
- Fodor, J.A. The Language of Thought; Harvester Press: Sussex, UK, 1975. [Google Scholar]
- Augusto, L.M. From symbols to knowledge systems: A. Newell and H. A. Simon’s contribution to symbolic AI. J. Knowl. Struct. Syst. 2021, 2, 29–62. [Google Scholar]
- Newell, A.; Simon, H.A. Computer science as empirical inquiry: Symbols and search. Commun. ACM 1976, 19, 113–126. [Google Scholar] [CrossRef] [Green Version]
- Augusto, L.M. Transitions versus dissociations: A paradigm shift in unconscious cognition. Axiomathes 2018, 28, 269–291. [Google Scholar] [CrossRef]
- Augusto, L.M. Unconscious knowledge: A survey. Adv. Cogn. Psychol. 2010, 6, 116–141. [Google Scholar] [CrossRef]
- Augusto, L.M. Unconscious representations 1: Belying the traditional model of human cognition. Axiomathes 2013, 23, 645–663. [Google Scholar] [CrossRef]
- Augusto, L.M. Lost in dissociation: The main paradigms in unconscious cognition. Conscious. Cogn. 2016, 43, 293–310. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Enderton, H.B. Elements of Set Theory; Academic Press: New York, NY, USA, 1977. [Google Scholar]
- Augusto, L.M. Computational Logic. Vol. 1: Classical Deductive Computing with Classical Logic, 2nd ed.; College Publications: London, UK, 2020. [Google Scholar]
- Ashby, F.G.; Maddox, W.T. Human category learning. Annu. Rev. Psychol. 2005, 56, 149–178. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Markmann, A.B.; Ross, B.H. Category use and category learning. Psychol. Bull. 2003, 129, 592–613. [Google Scholar] [CrossRef] [PubMed]
- Rehder, B.; Hastie, R. Category coherence and category-based property induction. Cognition 2004, 91, 113–153. [Google Scholar] [CrossRef] [Green Version]
- Augusto, L.M. Logical Consequences. Theory and Applications: An Introduction, 2nd ed.; College Publications: London, UK, 2020. [Google Scholar]
- Tversky, A. Features of similarity. Psychol. Rev. 1977, 84, 327–352. [Google Scholar] [CrossRef]
- Sjöberg, L. A cognitive theory of similarity. Goteb. Psychol. Rep. 1972, 2, 1–23. [Google Scholar]
- Augusto, L.M. Formal Logic: Classical Problems and Proofs; College Publications: London, UK, 2019. [Google Scholar]
- Goldberg, T.E.; Aloia, M.S.; Gourovitch, M.L.; Missar, D.; Pickar, D.; Weinberger, D.R. Cognitive substrates of thought disorder, I: The semantic system. Am. J. Psychiatry 1998, 155, 1671–1676. [Google Scholar] [CrossRef]
- Andreasen, N.C. Thought, language and communication disorders: I. Clinical assessment, definition of terms and evaluation of their reliability. Arch. Gen. Psychiatry 1979, 36, 1315–1321. [Google Scholar] [CrossRef] [PubMed]
- Andreasen, N.C. Scale for the assessment of Thought, Language, and Communication (TLC). Schizophr. Bull. 1986, 12, 473–482. [Google Scholar] [PubMed] [Green Version]
- Liddle, P.F.; Ngan, E.T.; Caissie, S.L.; Anderson, C.M.; Bates, A.T.; Quested, D.J.; White, R.; Weg, R. Thought and Language Index: An instrument for assessing thought and language in schizophrenia. Br. J. Psychiatry 2002, 181, 326–330. [Google Scholar] [CrossRef] [Green Version]
- Docherty, N.M.; DeRosa, M.; Andreasen, N.C. Communication disturbances in schizophrenia and mania. Arch. Gen. Psychiatry 1996, 53, 358–364. [Google Scholar] [CrossRef]
- American Psychiatric Association. Diagnostic and Statistical Manual of Mental Disorders, 5th ed.; American Psychiatric Press: Washington, DC, USA, 2013. [Google Scholar]
- Payne, R.W. An experimental study of schizophrenic thought disorder. J. Ment. Sci. 1959, 105, 627–652. [Google Scholar] [PubMed]
- Bleuler, E. Dementia Praecox, or the Group of the Schizophrenias; Zinkin, J., Translator; International Universities Press: New York, NY, USA, 1911; (English translation in 1950). [Google Scholar]
- Chaika, E.O. Understanding Psychotic Speech: Beyond Freud and Chomsky; Charles C. Thomas: Springfield, IL, USA, 1990. [Google Scholar]
- Chapman, J.P. The early symptoms of schizophrenia. Br. J. Psychiatry 1966, 112, 225–251. [Google Scholar]
- American Psychiatric Association. Diagnostic and Statistical Manual of Mental Disorder, 3rd ed.; American Psychiatric Press: Washington, DC, USA, 1980. [Google Scholar]
- Goldstone, R.L.; Son, J.Y. Similarity. In The Cambridge Handbook of Thinking and Reasoning; Holyoak, K.J., Morrison, R.G., Eds.; Cambridge University Press: Cambridge, UK, 2005; pp. 13–36. [Google Scholar]
- Chaika, E.O. A linguist looks at ‘schizophrenic’ language. Brain Lang. 1974, 1, 257–276. [Google Scholar] [CrossRef]
- Spitzer, M.; Braun, U.; Hermle, L.; Maier, S. Associative semantic network dysfunction in thought-disordered schizophrenic patients: Direct evidence from indirect semantic priming. Biol. Psychiatry 1993, 15, 864–877. [Google Scholar] [CrossRef]
- Schreber, D.P. Memoirs of My Nervous Illness; Macalpine, I.; Hunter, R.A., Translators; New York Review of Books: New York, NY, USA, 2000; (Work originally published in 1903). [Google Scholar]
- Laffal, J.; Lenkoski, L.D.; Ameen, L. “Opposite speech” in a schizophrenic patient. J. Abnorm. Soc. Psychol. 1956, 52, 409–413. [Google Scholar] [CrossRef]
- Chomsky, N. Aspects of the Theory of Syntax; MIT Press: Cambridge, MA, USA, 1965. [Google Scholar]
- Berwick, R.C.; Chomsky, N. Why Only us. Language and Evolution; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Badie, F.; Augusto, L.M. The Form in Formal Thought Disorder: A Model of Dyssyntax in Semantic Networking. AI 2022, 3, 353-370. https://doi.org/10.3390/ai3020022
Badie F, Augusto LM. The Form in Formal Thought Disorder: A Model of Dyssyntax in Semantic Networking. AI. 2022; 3(2):353-370. https://doi.org/10.3390/ai3020022
Chicago/Turabian StyleBadie, Farshad, and Luis M. Augusto. 2022. "The Form in Formal Thought Disorder: A Model of Dyssyntax in Semantic Networking" AI 3, no. 2: 353-370. https://doi.org/10.3390/ai3020022
APA StyleBadie, F., & Augusto, L. M. (2022). The Form in Formal Thought Disorder: A Model of Dyssyntax in Semantic Networking. AI, 3(2), 353-370. https://doi.org/10.3390/ai3020022





