Abstract
Formal thought disorder (FTD) is a clinical mental condition that is typically diagnosable by the speech productions of patients. However, this has been a vexing condition for the clinical community, as it is not at all easy to determine what “formal” means in the plethora of symptoms exhibited. We present a logic-based model for the syntax–semantics interface in semantic networking that can not only explain, but also diagnose, FTD. Our model is based on description logic (DL), which is well known for its adequacy to model terminological knowledge. More specifically, we show how faulty logical form as defined in DL-based Conception Language (CL) impacts the semantic content of linguistic productions that are characteristic of FTD. We accordingly call this the dyssyntax model.
1. Introduction
Semantic networks have been influential in applied linguistics since the late 1960s [1,2,3,4,5]. Although they have been criticized both for lacking a formal semantics and failing to provide an account of the mental representation of meaning (e.g., [6]) they have provided adequate models of human semantic memory and terminological knowledge. Here, we adopt them as such. Additionally, we eliminate the criticism above by equipping semantic networks with a formal semantics via description logic (DL), which is known to model adequately terminological knowledge (see [7,8,9,10,11,12]), and we consider them in the framework of semantic or terminological memory, thus providing an account of the mental representation of meaning. Semantic networks and frame-based systems (based on which knowledge may be divided into interrelated sub-structural frames, in order to be represented; see [13,14]) are at the very foundations of DL (see [15,16]). Every DL is a decidable fragment of predicate logic and description logics are a well-known family of knowledge representation formalisms that are among the most widely used knowledge representation formalisms in semantics-based systems. DL was developed out of the attempt to represent terminological knowledge and to provide an adequate formal semantics over terminological knowledge structures, in order to establish a common ground for cognition/knowledge for humans and artificial agents.
These properties make DL an adequate basis for the modeling of storage in, and activation of, semantic networks seen as terminological knowledge bases, with respect to both their normal functioning and some speech–thought pathologies. A speech–thought pathology that has been for long a cause of vexation for clinicians is formal thought disorder (FTD). One of the reasons for this vexation has been the difficulty toidentify the “formal” in the label, especially because the condition has been considered mostly as a pathology involving semantics—the dyssemantic hypothesis, as it is often found in the literature (e.g., [17]). We hypothesize that FTD is instead a dysfunction in the application of syntactic rules that impacts on the semantic contents of speech productions, and we call this the dyssyntactic hypothesis. More specifically, this is a dysfunction that roots in the categorization of concepts, a cognitive process that is also tightly linked to conceptual association and which is considered to be the basis of all human cognition (e.g., [18]). The model we propose, called the dyssyntax model, makes good use of the properties above of DL, namely via the DL-based Conception language (CL), to the point that it can actually be applied in (valid and reliable) diagnosis of FTD.
The present work is part of the current trend of applying AI methods and techniques to the study of human cognitive skills from the viewpoint of (mental) health (e.g., [19]). This ranges from medical software and electronic devices (e.g., [20,21,22]), which can be included in the larger field of (mental) telehealth (e.g., [23,24]), to the application of computational principles in psychology and psychiatry (e.g., [25,26,27]). The application of formal languages, namely of symbolic logic, is in our opinion an interesting means to bridge these two poles. Symbolic logic is believed to formalize adequately human reasoning and cognitive skills tightly connected to language; when associated to computational assumptions and/or techniques, we believe this to be a fruitful path to research into formal aspects of human language production [12,28].
Although a computational focus on FTD research is not new (e.g., [29,30]), our use of DL in this framework is wholly original, namely when coupled with CL. Despite this originality our work belongs to the paradigm called declarative/logic-based cognitive modeling [31], which is well established in the research into human reasoning and thinking (e.g., [32,33,34,35,36,37,38]). As is often the case in this cognitive modeling paradigm, we are more interested in creating a theoretical model than in testing its assumptions by means of experimentation with human subjects. We are well aware of the relevance of this to psychology and psychiatry, namely as far as reliability and validity of diagnostic methods are concerned, but our focus is, at least for the time being, theoretical. To be more precise, in this work we lay down the theoretical foundations of the dyssyntax model; in future work, we plan to apply the theory on computer simulations, a common practice in computational logic-based, or symbolic, cognitive modeling (e.g., [39,40,41]), and especially so in the context of conceptual categorization (e.g., [42]). In fact, we have already produced a logic-based algorithmic diagnostic procedure that is expected to be published shortly after the publication of the present article [7].
This article is structured as follows: In Section 2, we elaborate on semantic networking already with a view to the application of DL/CL and we do so from the viewpoint of both storage and retrieval of semantic material in what we see as necessarily a syntax-semantic interface. Section 3 is wholly dedicated to the discussion of FTD from both a historical and a contemporary perspective. In Section 4, we elaborate on our model in due detail, which in turn requires a comprehensive discussion of both DL and CL. In the Conclusions (Section 5), we reflect on the work done and we elaborate briefly on work to be done in our model.
2. Semantic Networking
2.1. Semantic Networks
We here consider a semantic network to be a collection of concepts/words linked to each other essentially by means of the (set-theoretic) relations of membership and inclusion. Formally, and taken generally, a semantic network can be defined as a (directed) graph in which the nodes correspond to concepts/words and the edges may be labeled with roles (see Figure 1). An individual semantic network will additionally have nodes for individuals, such as (my friend) John, (our cat) Kitty, (their city) Madrid, etc. In this definition, we consider individuals (or individual names), concepts (or concept names), and roles (or role names) as defined in description logic (DL; see below). From a cognitive and lexical viewpoint, these are all concepts and/or words. The context should disambiguate between concepts in this sense and concepts in DL, which, as will be seen, largely coincide. The relation between concepts and words is not yet well understood, but it is believed that it is not bi-univocal, i.e., not all concepts may have a word associated with them and vice-versa. This notwithstanding, we shall consider that words and concepts are largely associated with each other. Some concept names may stand for categories, too (e.g., vehicles).
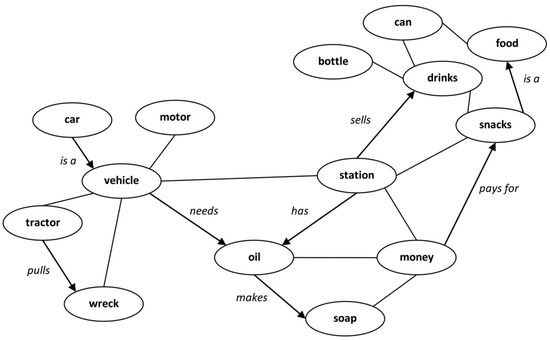
Figure 1.
A fragment of a semantic network for the core concept “filling station”. Undirected edges stand for unspecified relationships; directed edges are labeled with roles (e.g., “a car is a vehicle”).
A semantic network, or semantic memory system, as it can be called in the case of humans (e.g., [1,2]), provides what would otherwise be a mere collection of concepts/words with a structure. In particular, it clusters together concepts/words that are highly related to each other (see Figure 1), which can account for a fast retrieval of words when speaking. It has to be complex enough to contain a vast number of categories and concepts/words capable of mapping the perceived world, all interconnected with each other in many, possibly infinite ways. Although it is not a rigid representational structure, with concepts/words and categories being more or less frequently formed (introduced), transformed, or reformed, or even perhaps forgotten or deleted, and the relations among them being subject to constant revisions or adaptations, it has to be stable in the sense that the individual—thinker or speaker—can access it in only a few milliseconds; moreover, it must be compact enough to allow retrieval in useful time. This is commonly the case when we produce speech in our native language, and it is hypothesized that this is the case when we think, too (e.g., [43]). This can only be achieved if there is a set of rules of storage and retrieval that account for the dynamics and economics of this cognitive task that is basically one of symbolic (data) storage and search, which are the two fundamental processes of any computational implementation, as has been assumed for a long time in the field of cognitive science (e.g., [44,45]). We shall refer to this activity of storage and search as semantic networking.
If these rules are misapplied, or are in any other way disrespected, the semantic aspect of an information processing event is bound to be affected in the sense of a deviation, degradation, or even loss in meaning. Although the adjective formal characterizes both aspects of information processing, syntactic and semantic alike, the syntactic aspect has computational priority, being mostly carried out in an unconscious, often automatic mode that is not directly controllable by the cognitive agent; this is what is called System 1 of the dual-system model of the human cognitive architecture (see [46]; see also [28,47,48,49]). Thus, it can happen that the syntactic mode or aspect runs defectively, even when the individual is aware, wholly or in part, that things are going definitely wrong as far as what they are trying to think and want to communicate is concerned. In this case, it makes sense to speak of a “syntactic disorder”. This appears to be the case in FTD.
2.2. The Syntax–Semantics Interface, Set Theory, and Logic
The structure of a semantic network is believed to be formally accounted for by the operations and relations defined by set theory. Fleshing out the above introduction with respect to the rules of set theory (see, e.g., [50] for an introduction to set theory; ([51], Chapter 1) contains the basics of set theory required for computational implementations of classical logic), we must be capable of correctly applying the relations of membership (denoted by ∈, ∉) and inclusiveness (⊆, ⊇, ⊄, ⊋, etc.) (e.g., “robins are birds”; “penguins are not fish”; “trees are plants”; “vehicles are inanimate objects”; etc.), as well as the operations of union (⋃; e.g., “cats, tigers, lions, and pumas are either wild animals or pets”), intersection (⋂; e.g., “cats, dogs, hamsters, and goldfish are both vertebrates and pets”), and complementation and difference (∖ and –; e.g., “felines are not canids”; “lions are not spotted felines”; “numbers are not physical entities”). What dictates the application of these rules is, from a more logical point of view, property inference, which is prompted by perceived and/or abstracted proximity relations based on similarity or family resemblance, prototypicality, and/or representativeness or exemplarity: at every storage and retrieval step, we infer (i.e., deduce or induce) the properties of categories and subcategories, both vertically and horizontally (e.g., “cats are animate beings because animals are animate beings and cats are animals”; “cat1 is a feline and cat2 is a feline and cat3 is a feline … therefore this catn is a feline”) (see [52,53,54]).
This is to say that the main features of our semantic networks, to wit, semantic similarity, or conceptual relatedness, and semantic distance are, though stable and compact, not fixed, being inferentially activated/inhibited at the moment of storage and retrieval. This is particularly true of atypical concepts, which can fit into more than one category (e.g., tomatoes might be fruits or vegetables) and some of which often can be singly categorized only in a tentative way (for instance, rugs might be furniture): in different contexts, atypical concepts are categorized and associated differentially, and ad hoc inferences are required for this end. All this explains why we more or less frequently make categorization and association mistakes: were our semantic networks rigidly and fixedly structured, and no ad hoc inference operations required, normal categorization and association mistakes in speech would be difficult to account for.
Because, as said, these operations are related to inference, we need to consider them from the viewpoint of logic (depending on whether taken from a syntactic or semantic viewpoint, inference can be further specified as deduction or entailment, respectively; see [55] for a comprehensive treatment of these relations). From this perspective, it suffices to employ a logical language with a set of operators, or connectives, containing solely (symbols for) negation (¬; read “not”), conjunction (∧; read “and”), and disjunction (∨; read “or”). In effect, the cognitive operations of categorization and association of semantic material need not take place at the higher-level thought processing of reasoning, typically believed to employ the logical connectives of material implication (→; read “if …, then …”) and material equivalence (↔; read “if and only if”). Such operations can be described by mathematical(-like) computations (see below), for instance. Moreover, these latter connectives can be expressed by the connectives for negation, conjunction, and disjunction; for instance, the formula P → Q is equivalent to the formula ¬P ∨ Q.
The rules governing the storage and retrieval of concepts and categories can be described formally by applying the tools of set theory and logic at a more complex level; for instance, in [56] contrast model the computation of similarity between two objects or entities, a and b, characterized by the sets of features A and B, respectively, can be described by the computation formula:
S(a, b) = θ f(A ∩ B) − α f(A − B) − β f(B − A),
In which (A ∩ B) represents the common features in both A and B, (A – B) has the features that A has but B does not have, (B – A) has the features that B has but A does not have, and θ, α, and β are weights for the common and distinctive features. Another, non-linearly contrastive, approach is the application of a ratio function in which the important set-theoretic operation of union may also play an important role: for instance, within the ratio model approach, [57] defined similarity as f(A ∩ B)/f(A ∪ B). Prototypicality, or the property of an object to represent an entire class (e.g., an apple is an exceptional representative of fruit) can be computed by the function:
according to which an object a is attributed a degree of prototypicality P with relation to a class Λ with cardinality n (see [56]). It is obvious that these computations wholly fail if, to begin with, the cognitive agent is incapable of correctly carrying out the set-theoretic operations of intersection, union, and difference, which are expressible in terms of inference by the logical connectives of conjunction, disjunction, and negation, respectively.
P(a, Λ) = pn(λΣ f(A ∩ B) − Σ(f(A − B) + f(B − A))),
For this reason, we think that set theory and logic are adequate tools to model semantic networking. Importantly, logic can be considered from a normative viewpoint as regulating the relations and operations that define semantic networking. Thus, a concept is said to be well categorized if its negation is false (denoted by the symbol ⊥), and two concepts are said to be well associated if their conjunction or disjunction is evaluated to true (denoted by ⊤), which is classically the case when both concepts are true in conjunction or at least one of the concepts is true in disjunction (see [58] for the classical logical evaluations). Whenever categorization or association processes go against these evaluations, we can consider them as logically false, and as such faulty from the viewpoint of semantic networking. If we denote storage by σ and retrieval by ρ, then we would have, say, v(σ(¬Feline)) = ⊤ for the concept Dog but v(σ(¬Feline)) = ⊥ for Cat, where v denotes the evaluation function v: C → V mapping concepts to the set of truth values V = {⊥,⊤}; the association v(ρ(Walk ∨ Stop)) = ⊤ (for example, at a streetlight), but v(ρ(Walk ∧ Stop)) = ⊥, namely because it corresponds to a contradiction (namely by Stop = ¬Walk).
3. Formal Thought Disorder
Failures such as the ones mentioned above (contradictory representations; inadequate/faulty categorization of objects) can occur in normals when categorizing novel objects, for instance, but it appears to be predictable in patients with FTD; as would be expected, these are most manifest at the level of fluent speech (see, e.g., [59] for the specific case of schizophrenia), which imposes greater syntactic requirements on the individual. It is when asked to talk (or write) fluently that the plethora of formal deficits characteristic of FTD becomes most evident; the literature on this is extensive. Standard references, are, e.g., [60,61,62,63]. Ref. [17] provides a comprehensive discussion of FTD with meta-analyses. It should be remarked that the standard literature associates FTD with schizophrenia to the point that it can be used as an element for the diagnosis of this clinical condition (cf. [64], the current vade mecum of the psychiatric community, typically referred to as DSM-5). Because of this, we may use the words “schizophrenia” and “schizophrenic”, without intending any clinical connotation. Patients may produce incoherent and often completely incomprehensible statements and texts (a feature known in the literature as incoherence or word salad) in which ideas are only loosely or not at all connected (derailment); they may show moderate to severe distractibility, and their speech/text may be characterized by loss of goal (absence of a train of thought) and circumstantiality (delay in reaching a goal idea). When faced with a question, the answers are often only tangentially relevant (tangentiality). Moreover, speech is frequently hasty and literally unstoppable (pressure of speech), often filled with the persistent repetition of the same elements (perseveration), also displaying word approximations and even neologisms.
It can be hypothesized that all of the above deficits are due to the inability to carry out, with the required speed and/or accuracy, the formal operations describable by (standard) set theory and logic, leaving the patient with FTD with a disorganized, often chaotically activated semantic network at the stages of both categorization and association of concepts/lexical material. In clearer set-theoretic terms, the formation of sets and subsets is irregular, resulting in over- and/or underinclusiveness (data on this are conflicting (see, for instance, [60,65], but perhaps only apparently so, as no truly systematic study of the problem has been carried out so far), where either more or fewer members, respectively, than those generally agreed by a community are included in sets. That is, the relations of membership, inclusion, and identity are not respected. This makes it that the patient is incapable of isolating relevant sets from the universe or domain of speech, which results in, for instance, the inability to focus on basic-level categories and concepts when producing oral or written discourse. This, in turn, may cause the need to struggle for words and/or concepts, leaving no alternative to the patient but the production of approximations and even neologisms, or it may lead the patient into being more concerned with producing a somehow impressive speech (stilted speech). Clanging, or the supremacy of sound (e.g., rhymes) over meaning, may also be an effect of this failure in respecting the syntax of thought that might cause the diversion of attention to secondary associations.
Moreover, the patient is incapable of carrying out correct operations of union and intersection of sets: this causes the overall loosening of associations that impedes the production of a goal-oriented, precise, informative speech, and that early on was seen as a major, pathognomonic deficit in schizophrenia (cf. [66]). All this may cause the impression to the speaker that they are failing in the task of producing a more or less coherent message, which can prompt a haste that in turn can considerably worsen the speech produced; in fact, the patient commonly starts “losing control”—sometimes consciously so (see [67,68])—of their speech after a few coherent utterances, and the problems enumerated above gradually increase and/or become more manifest proportionally to speech length, until what is produced often resembles a “word salad”.
The following—which we shall refer to as Case 1—provides a good illustration of this “word salad”. Asked to express their opinion on current political issues like the energy crisis, a patient produced the following answer (cf. [61]):
“They’re destroying too many cattle and oil just to make soap. If we need soap when you can jump into a pool of water, and then when you go to buy your gasoline, my folks always thought they should, get pop but the best thing to get, is motor oil, and, money. May may as well go there and, trade in some, pop caps and, uh, tires, and tractors to grup, car garages, so they can pull cars away from wrecks, is what I believe in. So I didn’t go there to get no more pop when my folks said it. I just went there to get a ice-cream cone, and some pop, in cans, or we can go over there to get a cigarette.”
In effect, many of the features above are present in this sample: the whole reply appears tangential with respect to the question that was asked; concepts are only loosely associated (e.g., cattle and oil and soap does not appear to be a common association); “grup” appears to be a neologism; the word “pop” occurs repeatedly in what can be seen as perseveration, etc. All in all, [61] concludes that this sample constitutes a “word salad”, being thus an element in a positive diagnosis of FTD.
4. The Dyssyntax Model
We believe that the above features of FTD speech can be reduced to categorization and/or association faulty processes in semantic networking. By making this reduction, we are actually following the trend in psychiatry, as the DSM-5 also reduces the above to three symptoms to wit, derailment or loose associations, tangentiality, and incoherence or “word salad” (compare this with the full plethora of symptoms in [69], referred to as DSM-III). We abbreviate this trio as DTI. Because these processes are syntactic, we call this the dyssyntax hypothesis.
4.1. Logical Form
Although Tversky’s equations (see above) and his axiomatic theory of similarity (see the Appendix in [56]), as well as other mathematical—or mathematically inspired—theories of categorization based on similarity (see, e.g., [70]), might be useful for implementations of models of human thinking in artificial intelligence, it is unlikely that humans make semantic categorizations by applying such computations other than very loosely. On the contrary, the inferential rules of logic appear to be necessarily more or less strictly applicable if we are to give a good form to our thoughts, i.e., if our thoughts are to be well formed and therefore communicable. We shall refer to this good form as logical form, which is accountable for by the normative perspective on logic. From this perspective we can see that the classical logical tables for negation, conjunction, and disjunction, governing the activation or inhibition of associations, are not respected in FTD; in other words, they do not preserve logical form (in Figure 2, we indicate only schizophrenic retrieval, but one may assume that storage might be already faulty; this might be so particularly for negation, in which case “schizophrenic storage” would be denoted by σ*(¬C)). This might be so because the inference rules for the introduction (especially) of negation, conjunction, and disjunction (see Figure 3) are not respected to begin with.

Figure 2.
Truth tables for the classical logical rules for negation, conjunction, and disjunction adapted for concepts (C) and showing (in grey) “schizophrenic retrieval” (ρ*(·)).

Figure 3.
Rules of inference and their classical account in classical propositional logic. v denotes the evaluation function v: F → {⊥, ⊤}, for F a set of formulas and V = {⊥, ⊤} the set of classical truth values with ⊥ denoting falsity and ⊤ truth. The formal expression “⊨ P” reads “(formula) P holds (i.e., is valid) in classical propositional logic”; on the contrary, “⊭ P” denotes that P does not hold. “Iff” is read “if and only if”.
As a matter of fact, and interestingly, it appears that there is a tendency to disrespect these logical operations and inference rules in a predictable way (shown in Figure 2 as “schizophrenic retrieval”): patients with schizophrenia may tend to activate (i.e., equate or confuse) antonyms ([71,72]; see [73], for first-hand evidence) (a study [74] reported on the interesting case of a schizophrenic patient who systematically disregarded the antonymy of “yes” (and, in fact, based on their conceptions of the negation of the concept Yes) and “no” (based on their conceptions of the negation of the concept No), but did not extend this to other opposites (and, in fact, to other conceptions of the negations of other concepts)). Moreover, they activate (i.e., they do not inhibit the activation of) unrelated semantic material, making conjunctions of (i.e., associating) unrelated concepts and words, and failing to conjoin related semantic material. Disjunction also fails in that, faced with a choice in which both or one of the concepts or words should be selected, none is, whereas two inappropriate concepts or words may actually be selected. These errors are responsible for the overall illogical appearance of speech in FTD: the pillars of classical logic, to wit, the principle of non-contradiction, denoted by “¬(P ∧ ¬P)”, and the law of excluded middle (P ∨ ¬P), collapse; the patient does not distinguish between a concept and its negation or opposite, conjoining them and failing to disjoin them.
An example suffices here to show how these pillars of classical logic collapse. Asked how they liked it in the hospital, a patient answered the examiner’s question in the following way:
Well, er… not quite the same as, er… don’t know quite how to say it. It isn’t the same, being in hospital as, er… working. Er… the job isn’t quite the same, er… very much the same but, of course, it isn’t exactly the same.([17], p. 10)
While the use of negation is perfectly correct from the grammatical viewpoint, the patient clearly fails to either affirm or negate a predicate or property of an object: for them, the job is and at the same time is not—quite/very much/exactly—the same as being in the hospital.
4.2. Description Logic
As pointed out above, semantic networks can be seen formally as constituted by concepts, roles, and individuals. For this reason, description logic (DL) is more adequate than classical logic for formalizing semantic networking. Let us say that the assertions we produce, called propositions, are actually descriptions (e.g., “Soap is a basic toiletry”), denoted by D; these, in turn, are constituted by concepts (e.g., “soap”, “toiletry”), denoted by A, and roles (e.g., “is a”), denoted by r. DL is syntactically structured based on a finite set of logical constants Cons = {¬, ⊔, ⊓, →, ≡, ∀, ∃, ⊤, ⊥}, where the top concept “⊤” and the bottom concept “⊥”, respectively, represent the logical concepts of tautology and contradiction, “∀” and “∃” are quantifiers, “¬” is a unary logical connective, and “⊔”, “⊓”, and “→” are binary logical connectives (for simplicity, we make the top and bottom concepts coincide with the truth values true and false, respectively). For our aims, we shall actually only consider Cons0 = {¬, ⊔, ⊓, ≡, ⊤, ⊥}. DLs are further constructed over the following non-logical symbols that we shall collect in a set Γ: (1) Individual symbols, which are constant symbols and the instances of concepts; (2) Concepts, which correspond to a distinct, conceptual, entity and can be regarded to be equivalent to unary predicates in standard predicate logic; and (3) Roles, which are either relations or properties, and can be interpreted to be equivalent to binary predicates in standard predicate logic. In this research, the elements of Γ are constructed over the elements of the Roman alphabet together with the auxiliary elements of γ = {<, >}, known as conceptual identifiers (e.g., <Soap> identifies the word “soap” as being a concept).
As seen above, the syntax of DL is strongly dependent on concepts and their interrelationships. Actually, the logical structures of DL are fundamentally describable based on atomic symbols, of which there are three kinds: (i) individuals (e.g., brian, red), (ii) atomic concepts (e.g., <Toiletry>, <Soap>), and (iii) atomic roles (e.g., <isA>, <paysFor>). Atomic symbols are the elementary descriptions from which we inductively build complex concept (and role) descriptions based on concept (and role) constructors (which are the elements of Cons0). We call any specific collection Σ = {individual, atomic concept, atomic role} a signature. For example, considering (i) individual ::= b, (ii) atomic concept ::= <B>, and (iii) atomic role ::= <isB>, where the symbol “::=” means “can be written as”, the collection Σ = {b, <B>, <isB>} represents a signature.
In order to compute logically with terminological descriptions, we let A1 and A2 be two atomic concepts and r1 and r2 two atomic roles. We have four fundamental terminological descriptions in DL: (a) The concept equivalence A1 ≡ A2 expresses the fact that A1 and A2 are logically, and terminologically, equivalent. (b) The role equivalence r1 ≡ r2 expresses the property that r1 and r2 are logically, and terminologically, equivalent. (c) The concept subsumption A1 ⊑ A2 expresses the property that A1 is logically, and terminologically, subsumed under A2; in other words, A1 is the sub-concept of A2. (d) The role subsumption r1 ⊑ r2 expresses the fact that r1 is logically, and terminologically, subsumed under r2; in other words, r1 is the sub-role of r2.
If we postulate that the relations and operations of set theory are at the root of the operations of logical inference in the sense that they describe/express the cognitive processing of (categories of) words, as well as of concepts (see below for the relation between words and concepts), that constitute the descriptions we utter and that are analyzable by logic (i.e., let D designate a description and let this be conceived as a set of words (and concepts); then, we have it that the words w1, w2, … ∈ D), then, even when D is (terminologically and) grammatically well formed, it will inherit the defective or faulty processing over concepts resulting in (concept) descriptions marked as semantically inadequate/anomalous in the following way: (C1 ⊑ C2)⊥ and hasA⊥, or does⊥, denote that the retrieval of the concept descriptions <C1> and <C2> and the retrieval of the role descriptions <hasA> and <does> are wrong or anomalous as in Figure 2. Thus, semantic anomaly or wrongness equates with the convenient truth value false and with the logical concept <Falsity>), which can be extended to include non-denotation, i.e., absence of reference in the world (e.g., a four-legged bird)—besides non-veridicality. Figure 3 shows the classical account of some classical inferential rules, and one can easily see how the anomalous or wrong description construction that is characteristic of FTD goes against them (see [51] for a comprehensive account of the symbol ⊨, denoting (semantic) logical consequence. We leave it to the reader to adapt Figure 2 and Figure 3 to DL; this adaptation can be checked in [7]. It is now easy to see how an anomalous, or just plain wrong, implementation of the inference rules of DL, which inherit from the anomalous or wrong computations in set-theoretic terms, can formally describe/express the thought processes believed to be responsible for the speech productions characteristic of FTD as they are interpreted via logical falsity.
The above very briefly introduces the syntax of DL, which, as seen, considers exactly the elements of semantic networks. It is precisely this semantic function of the syntax of DL that makes it interesting to us in the sense that it models semantic networking; it does so, in fact, by providing semantic networks with a formal semantics in what is a particularly good account of the syntax–semantics interface. In effect, the syntactic rules of DL are interpreted via the set-theoretic relations and operations that we see as describing categorization and association processes in semantic networks.
In detail, an interpretation (denoted by I) is structured upon (i) a non-empty set ∆I that is the interpretation domain and consists of any individuals that may occur in our concept descriptions, and (ii) an interpretation function (in the form “.I “). Hence, we have the pair I = (ΔI, I). The function .I: Γ → ΔI assigns to every individual symbol a ∈ Γ an element aI ∈ ∆I, to every atomic concept symbol A ∈ Γ a set AI ∈ ∆I, and to every atomic role symbol r ∈ Γ a binary relation rI ⊆ ∆I × ∆I. The semantics of concept/role constructors in standard DL (ALC: Attributive Concept Language with Complements) is defined as follows:
- 1.
- The interpretation of some atomic concept A is equivalent to AI, so that we have (A)I = AI ∈ ∆I.
- 2.
- The interpretation of some atomic role r is equivalent to rI, so that we have (r)I = rI ⊆ ∆I × ∆I.
- 3.
- The interpretation of the top concept (⊤) is equivalent to ∆I. This means that the logical concept <Truth> expresses the validity of the interpretation of all members of the interpretation domain.
- 4.
- The interpretation of the bottom concept (⊥) is equivalent to Ø. This means that the logical concept <Falsity> expresses the fact that the interpretations of all members of the interpretation domain are invalid (i.e., meaningless).
- 5.
- The interpretation of the concept conjunction A1 ⊓ A2, or (A1 ⊓ A2)I, is equivalent to A1I ∩ A2I.
- 6.
- The interpretation of the concept disjunction A1 ⊔ A2, or (A1 ⊔ A2)I, is equivalent to A1I ∪ A2I.
- 7.
- The interpretation of the concept negation ¬A, or (¬A)I, is equivalent to ∆I\AI. More precisely, those elements of the interpretation domain (which do not exist within the concept description A) are interpreted as the constructors of the concept negation ¬A.
In addition, the semantics of terminological and assertional descriptions of concepts are defined as follows:
- 8.
- The interpretation of the concept subsumption A1 ⊑ A2 is equivalent to A1I ⊆ A2I.
- 9.
- The interpretation of the role subsumption r1 ⊑ r2 is equivalent to r1I ⊆ r2I.
- 10.
- The interpretation of the concept equivalence A1 ≡ A2 is equivalent to A1I = A2I.
- 11.
- The interpretation of the role equivalence r1 ≡ r2 is equivalent to r1I = r2I.
- 12.
- The existence of the concept assertion A(a) expresses the fact that individual a is interpreted to be an instance of concept A, i.e., aI∈ AI.
- 13.
- The existence of the role assertion r(a, b) expresses the property that the individuals a and b are interpreted to be related together by means of role r, i.e., (aI, bI) ∈ rI.
Importantly, every concept C, every role r, and every singular a, as well as their combination by means of the connectives of DL, can be subsumed under the concepts <Truth> and <Falsity>, so that we have, for instance:
which allows us to write simply <Dog>, or <Mammals>, indicating that both the conceptions of dog and mammals are correct, or:
and we write either <Zebra⊥>, or <ChessGame⊥> to indicate that the conceptions of zebra or chess game are incorrect or anomalous.
(<Dog> ⊑ <Mammals>) ⊑ <Truth>
(<Zebra> ⊑ <ChessGame>) ⊑ <Falsity>
4.3. Conception Language
Simply applying DL to account for normal and abnormal categorization and association processes in semantic memory would, however, result in a trivial model of FTD. Our main tool will be Conception Language (CL), a DL-based language conceived precisely for modeling terminological knowledge and cognitive agents’ associated conceptions of the world [8,9,10,11]. By assuming that concepts are distinct mental phenomena/entities that are construed by agents in a particular state of awareness, a possible interpretation is that concepts can be identified with the contents in, for example, linguistic expressions (which are basically in the form of words), formal expressions (which are basically in the form of symbols and special characters), and/or numerical expressions (which are in the form of numbers) by becoming manifested in the form of conceptions.
Let Ag stand for some agent. CL is syntactically defined based on (1) Ag’s conceptions (which are equivalent to Ag’s conceptions of [their mental] concepts) and on (2) Ag’s conceptions’ effects (which are equivalent to Ag’s conceptions of [their mental concepts’] roles), as well as based on (3) singulars (which are equivalent to Ag’s conceptions of various individuals). For example, Bob’s conceptions of the concepts <Book>, <Female>, and <BrownSquirrel> are symbolically represented by the conceptions <BobBook>, <BobFemale>, and <BobBrownSquirrel>, respectively. Additionally, Bob’s conceptions of the roles <does>, <isA>, and <produceA> are regarded as his conceptions’ effects and are respectively representable by <Bobdoes>, <BobisA>, and <BobproduceA>. In addition, Bob’s conceptions of the individuals monkey, white, and flower are, respectively, represented by the singulars Bobmonkey, Bobwhite, and Bobflower. Conceptions, effects, and singulars are respectively denoted by C, E, and s. In addition, CL (as a DL) is capable of applying the relations of “membership” (of a singular under Ag’s some conception) as well as of “subsumption” (of Ag’s some conception under Ag’s some other conception). CL can also support the conjunction (of two, or more, Ag’s conceptions), disjunction (of two, or more, Ag’s conceptions), and negation (of some conception of Ag).
Importantly, <Book> and <BobBook> stand, respectively, for the general concept of book and Bob’s specific conception of book, the same distinction being applicable for effects and singulars. The point to be made here is that they can be so different as to result in, say, <BobBook⊥> if Bob’s conception of a book is at odds with the usual concept as it is formalized by means of DL, i.e., <Book>. This makes it specific that <BobBook⊥> is a deviant or faulty conception of Bob’s alone, and as such may require particular attention—as is the case in FTD.
Based on the formalism described above, conception descriptions are analyzable in the following way: any conception description can fundamentally be understood to be in the forms of conception equality (formally representing: AgC1 ≡ AgC2), conception subsumption (or: AgC1 ⊑ AgC2), conception’s effect equality (or: AgE1 ≡ AgE2), conception’s effect subsumption (or: AgE1 ⊑ AgE2), conception assertion (or: AgC(s)), and conception’s effect assertion (or: AgE(s1, s1)).
From a deeper logical perspective, an agent’s semantic interpretation of (as well as their inferencing based on) their conception of interconceptual relationships can fundamentally be prompted by their atomic conception(s) of with interconceptual proximity relationships based on similarities, prototypicality, and/or representativeness or exemplarity. In effect, at every storage and retrieval step (which takes place in a particular state of awareness of Ag), Ag conceptualizes, interprets, and (deductively or inductively) infers the attributes of concepts (as well as of classes of various singulars), both vertically and horizontally. For example, Mary (conceptualizes and) describes that “Dogs are animate beings because dogs are animals and animals are animate beings”. Formally, her conception of the concept <Dog> is subsumed under her conception of the concept <Animal>, and her conception of the concept <Animal> is subsumed under her conception of the concept <AnimateBeing>. Using symbolic notation: ((MaryDog ⊑ MaryAnimal) ⊑ MaryAnimateBeing). Therefore, we have the interpretation: ((MaryDogI ⊆ MaryAnimalI) ⊆ MaryAnimateBeingI). Hence, <MaryDog> ⊑ <Truth>, and thus, simply <MaryDog> (note that <MaryTruth>, or <MaryFalsity>, for that matter, are not allowed). Another example: David conceptualizes and describes that “This cat is a feline, this cat is a feline, this cat is a feline, …, and this cat is a feline. Therefore, these cats are all felines”. In fact, David’s conception of the singulars cat1, cat2, cat3, …, and catn (formally: Davidcat1, Davidcat2, Davidcat3, …, and Davidcatn) are placed under his conception of the concept <Cat> (formally: DavidCat). Additionally, his conception < DavidCat> is subsumed under his conception of <BeingFeline> (formally: DavidBeingFeline), and his conception of <BeingFeline> is subsumed under his conception of <Feline> (formally: DavidFeline). Symbolically: ((DavidCat ⊑ DavidBeingFeline) ⊑ DavidFeline). Semantically, we have: (i) {Davidcat1I, Davidcat2I, Davidcat3I, …, DavidcatnI} ∈ DavidCatI, and (ii) ((DavidCatI ⊆ DavidBeingFelineI) ⊆ DavidFelineI). Hence, <DavidcatnI > ⊑ <Truth>, and thus, simply <DavidcatnI >. Mary and David’s conceptions in the given examples are both “inferentially activated/inhibited” at the moment of storage and retrieval (which take place in a particular state of awareness by Mary and David). For instance, Mary was not at all conscious of this process, because, say, her attention was focused elsewhere. More typically, though, these appear to be largely unconscious processes. For how thought processes involving concepts can be wholly (or partly) unconscious, see [28,46,48,49].
In order to compute with conceptual categorization and association logically, we shall draw on signatures. Just as in DL, we call any specific collection of an agent’s conception of singular, atomic conception, and atomic effect a signature. For instance, considering (i) singular :: = Ags, (ii) atomic conception :: = <AgS>, and (iii) atomic effect :: = <AgisS>, the collection Σ = {Ags, <AgS>, <AgisS>} is a signature in our CL-based formal system. Conceptual categorization and association in this system are called conception categorization and conception association, respectively, in order to emphasize the conceptualizing role of the agent over concepts.
Conception Categorization and Association in Thought Processes in CL
Ag’s conception association is supported by the assumption that concepts (as mental entities that are constructible and archivable—i.e. categorizable—in Ag’s mind) and their instances are logically correlatable to each other in Ag’s mind. Ag’s conception association can be interpreted to demonstrate how Ag’s conception effects may cognitively be designed based on and derived from Ag’s conceptions. Subsequently, Ag’s conception association can indicate that Ag’s conception effects are not necessarily the fundamental logical building blocks of a CL-based formalism. In fact, relying on CL-based analysis of conception categorizations and associations, conception effects are understood to be the productions of conceptions (and not the primary non-logical symbols, like those DL symbols in in the set Γ). Consequently, in order to use CL in our formal-logical analysis of conception association we need to use, and rely solely on, conceptions and singulars.
Let the description “We kill too many cows and bulls to produce leather.” be expressed by Mary. According to Mary’s conception description, the elements of the set {Cow, Bull, Leather} are Mary’s atomic conceptions. Accordingly, we have:
- Singular ::= Marycow and atomic conception ::= <MaryCow>. More specifically, Marycow expresses Mary’s conception of some individual “cow” in the world. Additionally, the atomic conception <MaryCow> expresses Mary’s conception of her constructed concept <Cow>. In Mary’s view, any cow is an instance of <Cow>.
- Singular ::= Marybull, atomic conception ::= <MaryBull>.
- Singular ::= Maryleather, atomic conception ::= <MaryLeather>.
It should be remarked that the conceptions <MaryCow>, <MaryBull>, and <MaryLeather> and the singulars Marycow, Marybull, and Maryleather have become all correlated, in order to support the most significant conception association in Mary’s conception description. In particular, the association of the elements of {Marycow, <MaryCow>} and of {Marybull, <MaryBull>} has become associated with the elements of the set {Maryleather, <MaryLeather>}. Consequently, the association of the conceptions <MaryCow ⊓ MaryBull> and <MaryLeather> is constructed by Mary. Symbolically, we have the conception association <((MaryCow ⊓ MaryBull) ⊓ MaryLeather)> (we name it “Association 1”). Moreover, Mary’s conception description “We kill too many cows and bulls to produce leather.” can be transformed into “We kill too many cows and we kill too many bulls to produce leather.” Mary’s main conception effects would be exhibited in the atomic descriptions “We kill cows.”, “We kill bulls.”, and “We produce leather.” Thus, the elements of {to-kill-cow, to-kill-bull, to-produce-leather} are Mary’s atomic conception effects. Then, we have:
- Singular ::= MarykilledCow and atomic conception ::= <MaryKilledCow>. More specifically, MarykilledCow is equivalent to Mary’s conception of some individual “killed-cow”. Additionally, the atomic conception <MaryKilledCow> expresses Mary’s conception of her constructed concept <KilledCow>. In Mary’s view, any individual killedCow is an instance of her constructed concept <KilledCow>.
- Singular ::= MarykilledBull and atomic conception ::= <MaryKilledBull>.
- Singular ::= MaryproducedLeather and atomic conception ::= <MaryProducedLeather>.
Here, the association of the conceptions <MaryKilledCow ⊓ MaryKilledBull> and <MaryProducedLeather> is constructed by Mary. Symbolically, we have the conception association <((MaryKilledCow ⊓ MaryKilledBull) ⊓ MaryProducedLeather)> (we name it “Association 2”). Note that Associations 1 and 2 are logically and semantically associated with each other.
Ag’s conception categorization is defined based on our assumption that concepts, and their interrelationships, are constructible and classifiable in Ag’s mind. It follows that Ag can reflect on different classes of conceptual entities and represent them in their mind. Correspondingly, the contents with which concepts are being identified, namely by becoming described and explained, can also be classified in Ag’s mind. Consequently, Ag can mentally classify various conceptual descriptions and, in fact, Ag can categorize their conceptions. Let the description “Bats are mammals.” be expressed by John. Formally analyzing this description, the sets {Johnbat, <JohnBat>, <JohnisBat>} and {Johnmammal, <JohnMammal>, <JohnisMammal>} are two signatures based on John’s conceptualization. According to John, the conceptions of “bat” (and of “being-bat”) are logically and semantically subsumed under his conceptions of “mammal” (and of “being-mammal”). More specifically, the conception categorization JohnBat ⊑ JohnMammal (which can also be translated into the [conception] effect classification JohnisBat ⊑ JohnisMammal) is constructible.
However, we believe that at retrieval, as is the case in speech production, an agent’s activity is largely at the level of association. Let us refocus on Mary’s conception description “We kill too many cows and bulls to produce leather.” Again, we transform it into “We kill too many cows and we kill too many bulls to produce leather.” Here, we have the conception effect classifications (1) MaryproduceLeather ⊑ MarykillCow and (2)MaryproduceLeather ⊑ MarykillBull. In fact, Mary’s conception of “leather-production” is logically and semantically subsumed under her conception of “cow-killing” as well as under her conception of “bull-killing”. When speaking (or writing), we have the productions (1*) <MaryproduceLeather> ⊑ <MarykillCow> and (2*) <MaryproduceLeather> ⊑ <MarykillBull>. This shows that the categorization and the association processes in a semantic network may be independent, so that a concept that was correctly categorized may be incorrectly retrieved in an association process.
Importantly, when we say that some conception effect categorization is construable, we actually mean that it is enforceable in the sense that for an agent who categorizes and associates concepts, normally, there is typically only a single effect (except in cases of ambiguity, as seen above; e.g., tomato can be a fruit or a vegetable). To put it differently, we are saying that conceptions of concepts, of their effects, and of various singulars are not individual constructs, but rather collective—to the point of universality if we accept Chomsky’s [75] notion of the universal grammar (UG) (see also [76], for an update). In effect, UG is construed on the principle that humans innately possess a set of structural rules that is independent of their sensory experience of the world: regardless of the environment in which children grow, they will eventually create syntactic categories of words such as nouns and verbs, etc. Our theory is that these syntactic structures are extendable to all the syntactic rules of categorization and association of conceptions in such a way that normal cognitive agents categorize and associate concepts, effects, and singulars in a very uniform way that is described by classical theory and, hence, DL (see above). CL actually makes this clearer by means of an idiosyncratic notion of agent, namely by showing formally how some agent’s conceptions can be deviant or wholly faulty with respect to the rest of their community. Therefore, by writing <MaryBook⊥>, <MarykillsCow⊥>, and <Marycow⊥> in CL, we are formalizing the fact that Mary has misconceptions with respect to <Book>, <killsCow>, or <cow>. This notation will be essential, in our view, for any machine interpretation in which the conceptions of an agent Ag must be made clear to the machine.
4.4. Diagnosing FTD with CL
We now apply CL to the symptomatic speech productions exhibited by FTD patients. Clearly, <MaryBook⊥>, <MarykillsCow⊥>, and <Marycow⊥> alone do not allow for a diagnosis of FTD with respect to Mary. In effect, Mary could have thought of a book that was made of chocolate leaves (not our regular conception of the concept <Book>, but a possible object nonetheless). Similar plausible situations can be thought of for the remaining deviant conceptions of Mary’s. In effect, it is here that the domain ΔI plays a crucial role; we shall refer to it as simply context. For this reason, when in doubt, we write <…?> (e.g., <MaryBook?>, <MaryhasBook?>, <Marybook?>). However, if, given a sample of moderately long speech production by Mary in her mother tongue and in a normal state of awareness (say, she has not taken psychiatric medication or drunk alcohol), the number of ⊥-identifiers—to give these a simple name—is conspicuous, then we can conclude that FTD can be positively diagnosed.
Recall Case 1 introduced above. Let us call this patient Emma. Ref. [61] considered this sample of speech production to be a clear case of word salad, one of the symptoms that contribute to a diagnosis of FTD (in fact, this is such a strong indicator that it alone can be used for this diagnosis). By applying CL, we prefer to see it as a loosening of conception association. Loosening of conception association expresses that some agent Ag, in a particular state of awareness (suddenly) loses the sequence of their conception descriptions. Loosening the associative interconnections between constructed concepts will be manifested in the form of “conception association loosening” within an agent’s conception expressions. In particular, it will be exhibited by an interruption in Ag’s description (and between two of Ag’s conception descriptions, which are fundamentally in the forms of conception equality, conception subsumption, conception’s effect equality, conception’s effect subsumption, conception assertion, and conception’s effect assertion). Subsequently, Ag will have difficulty in expressing their right conception description again. Hence, Ag expresses a sequence of conception descriptions that are not closely related to each other and are not semantically correlated with the previous conception descriptions. Moreover, within-description anomalies already occur in the form of neologisms, mis-associations, etc., among the many faulty features listed above.
In order to analyze Emma’s speech by applying CL we refer the reader to Figure 1, which can be considered a semantic network whose main context (Δ) is a filling station, which, in turn, is associated to sub-contexts (or sub-domains), such as vehicles (Δ0), supermarket (Δ1), etc. (Δk). For instance, we take into consideration Emma’s description “They’re destroying too many cattle and oil just to make soap”. (we identify this description by (*)). According to (*), the conception association <((EmmaCattle ⊓ EmmaOil) ⊓ EmmaSoap)> is produced. Note that Emma’s conception description <((EmmaCattle ⊓ EmmaOil) ⊓ EmmaSoap)> is a more or less preserved association of her (conceptions of) concepts. In fact, such a conception association is not common, though it is possible, as some kinds of soap can be made of cattle (so-called “tallow soap”) and oil. Maybe Emma knows a lot about soap. Hence, we write <((EmmaCattle ⊓ EmmaOil) ⊓ EmmaSoap)?>, instead of writing outright <((EmmaCattle ⊓ EmmaOil) ⊓ EmmaSoap)⊥>. After describing (*), Emma expresses that “If we need soap when you can jump into a pool of water, and then when you go to buy your gasoline, my folks always thought they should, get pop but the best thing to get, is motor oil, and, money” (**). At a first reading of (**), Emma might have begun to show some symptoms of FTD. Note that the two associations A1: (EmmaSoap ⊓ (EmmaWaterPool ⊓ EmmaJump)) and A2: (EmmaGasoline ⊓ EmmaPop ⊓ EmmaMotorOil ⊓ EmmaMoney) are, separately, in principle, not faulty. A1 can obviously be correct. Additionally, A2 can be associated with the concept <FillingStation>. However, the whole (**) gives us the impression of mis-association if analyzed at sub-association level. For instance, the sub-association A2′: ((EmmaMotorOil ⊓ EmmaMoney) ⊓ EmmaGetting) is faulty, because it is possible to get motor oil at a filling station but we cannot (normally) get money from it. On the other hand, A2 certainly is not a mis-association if one is a filling-station owner. Thus, again we cannot apply the ⊥-identifiers tout court.
If we focus now on (***) “go there and, trade in some, pop caps and, uh, tires, and tractors to grup, car garages, so they can pull cars away from wrecks”, we should notice that while the whole description appears somehow loose and it includes a neologism (grup), all the conceptions construed from singulars, to wit, <EmmaPopCap>, <EmmaTire>, <EmmaTractor>, <EmmaCarGarage>, <EmmaCar>, and <EmmaWreck>, are all indeed associated to a filling station, and moreover, the associated roles—with the exception of <grup>—are essentially not faulty. Indeed, we have <EmmaTradeIn(PopCap)>, as this might refer to kids trading in pop (e.g., Coke) caps (of the bottles), and <EmmapullFrom(Car, Wreck)>. Again, we cannot apply the ⊥-identifiers to the whole of (***), or parts thereof.
The same results can be applied to the remaining of the sample (“So I didn’t go there to get no more pop when my folks said it. I just went there to get a ice-cream cone, and some pop, in cans, or we can go over there to get a cigarette.”), as the reader will easily verify. Importantly, despite the apparent loosening of associations, Emma’s speech is through and through centered in the same domain conception (<FillingSation>), if incoherent overall. We conclude that there are not (enough) ⊥-identifiers, for which reason, and against the diagnosis by Andersen’s [61] TLC assessment test (and also of [6]), we are not willing to confirm a diagnosis of FTD in Emma’s case without further analysis.
It should be remarked that by doing this we are not concluding that Emma does not have FTD; we are simply concluding that she does not exhibit sufficient symptoms of FTD so as to be reliably diagnosed as having FTD. In turn, sufficiency may be related to the length and number of samples available: more, and longer, samples would be required for a possible uncontroversial diagnosis of FTD. In any case, CL provides us with a formal means to diagnose FTD that can be actually carried out algorithmically, as shown in [7].
We now introduce Case 2. Asked how life was at a hospital, an agent—John—replied (cf. [17]):
“Oh, it was superb, you know, the trains broke, and the pond fell in the front doorway.”
We have the conception <JohnBrokenTrain?>, as one can say of a defect train that it broke, but we have clearly the conceptions <JohnFallInPond⊥> as well as <(JohnFallInPond⊥ ⊓ JohnfallIn(doorway, pond)⊥)⊥>. Additionally, the association of the above with the concept <Hospital> is also obviously a mis-association, so that John’s speech sample could be “translated” into CL as:
<<JohnHospital⊥> ⊓ (<JohnBrokenTrain>⊥ ⊓ <JohnfallIn(Doorway, Pond)⊥)⊥)>.
Indeed, while it is possible that trains break, and thus, the cautious formalization <JohnBrokenTrain?>, trains do not break in hospitals, so that, in context, we actually, and necessarily, have the formalization <JohnBrokenTrain⊥>. In fact, we have identified a misconception of John’s. Therefore, in this Case 2, despite the shortness of the offered sample, we begin to suspect that a diagnosis of FTD might well be confirmed for John, as the number of ⊥-identifiers is conspicuous.
In our analysis of Cases 1 and 2, we focused only on what we call loosening of conception association, and which is clearly related to what in DTI is called “derailment or loose associations” and “incoherence or word salad”. In effect, from the viewpoint of lexical or conceptual association in either storage or retrieval in a semantic network, the “D” and the “I” amount to what we call loosening of conception association. As a matter of fact, so does the “T” for “tangentiality”, as we believe that what can be called “tangential speech productions” (i.e., irrelevant answers to questions or off-the-point observations) are only another way in which loosening of conception association can manifest itself. The same holds largely for other symptoms (see above), excepting perhaps to some extent neologisms and word approximations, which might be due to faulty categorization processes, which more typically result in over- or under-inclusiveness phenomena. In any case, our analysis result is the same. For instance, [61] reported the following descriptions, concluding that they fall under the diagnosis of FTD for containing neologisms:
- ($)
- I got so angry I picked up a dish and threw it at the geshinker.
- (&)
- So I sort of bawked the whole thing up.
According to our application of CL in the analysis of samples of speech, for whomever agent who uttered the samples above, we have:
<AgGeshinker> ⊑ Ø ≡ <AgGeshinker> ⊑ <Falsity> ≡ <AgGeshinker⊥>
<AgbawkUp(x)> ≡ ⊥ ≡ <AgbawkUp(TheWholeThing)⊥>
However, in ($), we have the “translation” for CL:
where we have <Agthrow(I,(Dish,⊥))⊥> because of the falsity of <AgGeshinker⊥>. However, perhaps the agent can produce a normal word/concept if required to, or explain what this neologism means for them. In any case, even if the agent cannot do so, as seen in the “translation” above, we do not have sufficient faultiness identifiers to output an uncontroversial diagnosis. A similar analysis could be carried out with respect to (&).
<<AggetAngry(Ag)> ⊓ (<AgpickUp(Ag,Dish)> ⊓ <Agthrow(Ag,(Dish,⊥)) ⊥>)>
5. Conclusions
Formal thought disorder (FTD) is a clinical mental condition that can be diagnosed by the speech productions of patients. This diagnosing, however, is often neither reliable nor valid, to a great extent due to the fact that the “formal” in FTD is not (clearly) identified in the usual diagnostic methods. In the present article, we focus on a logic-based analysis of FTD as it is manifested in the processes of association and categorization over a semantic network; in doing this, we clearly identify the “formal” in FTD. More specifically, utilizing description logic (DL), we offer a logical-terminological model for the interface syntax–semantics in semantic networking for FTD patients. We accordingly call this the dyssyntax model, because we believe that FTD is essentially a manifestation at the semantic level of faulty syntactic processes over an individual semantic network. It should be emphasized that our dyssyntax model does not only explain FTD, but can also diagnose it. In fact, the dyssyntax model is designed based on the logical clarification of how faulty (and defective) logical forms in our DL-based Conception Language (CL) can affect the semantic content of linguistic productions characteristic of FTD. This is a wholly novel approach to this condition that focuses directly on the root of the “formal deficits” that appear at the surface as semantic in nature: we turn this semantic appearance into a real formal semantics, as taken in the logical sense of the word, by coupling it to a formal syntax that can adequately formalize human thought processes recruited in language production.
We have designed CL for modeling terminological knowledge, as well as for representing cognitive agents’ associated conceptions of the world. By employing CL, we analyze conception categorization and conception association in thought processes that are recruited when agents verbalize their conceptualizations. We construe a formal analysis that is already essentially computational in the sense of computational logic-based cognitive modeling. We believe that the presented model of dyssyntax in semantic networking is computational in a more practical sense, too: it can be easily implemented computationally and executed in software systems (see [7]). In addition, it is expected that this computation will be assisted by Web Ontology Language (OWL) and/or other formal-language services in semantic technologies; this will prove useful to check individual conceptions with respect to their frequency or normalcy in large corpora that will (shortly) be available within the context of the Semantic Web.
Author Contributions
Conceptualization, F.B. and L.M.A.; methodology, F.B. and L.M.A.; software, n/a; validation, n/a; formal analysis, F.B. and L.M.A.; investigation, F.B. (DL/CL) and L.M.A. (FTD). All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Collins, A.M.; Loftus, E.F. A spreading activation theory of semantic processing. Psychol. Rev. 1975, 82, 407–428. [Google Scholar] [CrossRef]
- Collins, A.M.; Quillian, M.R. Retrieval time from semantic memory. J. Verbal Learn. Verbal Behav. 1969, 8, 240–248. [Google Scholar] [CrossRef]
- Quillian, M.R. Word concepts: A theory and simulation of some basic semantic capabilities. Behav. Sci. 1967, 12, 410–439. [Google Scholar] [CrossRef]
- Quillian, M.R. Semantic networks. In Semantic Information Processing; Minsky, M.L., Ed.; MIT Press: Cambridge, MA, USA, 1968; pp. 227–270. [Google Scholar]
- Quillian, M.R. The Teachable Language Comprehender: A simulation program and theory of language. Commun. ACM 1969, 12, 459–476. [Google Scholar] [CrossRef]
- Johnson-Laird, P.N.; Herrmann, D.J.; Chaffin, R. Only connections: A critique of semantic networks. Psychol. Bull. 1984, 96, 292–315. [Google Scholar] [CrossRef]
- Augusto, L.M.; Badie, F. Formal thought disorder and logical form: A symbolic computational model of terminological knowledge. J. Knowl. Struct. Syst. forthcoming.
- Badie, F. On logical characterisation of human concept learning based on terminological systems. Log. Log. Philos. 2018, 27, 545–566. [Google Scholar] [CrossRef] [Green Version]
- Badie, F. A description logic based knowledge representation model for concept understanding. In Agents and Artificial Intelligence; van den Herik, J., Rocha, A., Filipe, J., Eds.; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2018; Volume 10839. [Google Scholar]
- Badie, F. A formal ontology for conception representation in terminological systems. In Reasoning: Logic, Cognition, and Games; Urbanski, M., Skura, T., Lupkowski, P., Eds.; College Publications: London, UK, 2020; pp. 137–157. [Google Scholar]
- Badie, F. Logic and constructivism: A model of terminological knowledge. J. Knowl. Struct. Syst. 2020, 1, 23–39. [Google Scholar]
- Badie, F. Towards contingent world descriptions in description logics. Log. Log. Philos. 2020, 29, 115–141. [Google Scholar] [CrossRef]
- Minsky, M. A Framework for Representing Knowledge (AIM-306); MIT Artificial Intelligence Laboratory: Cambridge, MA, USA, 1974. [Google Scholar]
- Minsky, M. A framework for representing knowledge. In The Psychology of Computer Vision; Wiston, P., Ed.; McGraw Hill: New York, NY, USA, 1975; pp. 211–277. [Google Scholar]
- Baader, F.; McGuiness, D.L.; Nardi, D.; Patel-Schneider, P.F. (Eds.) The Description Logic Handbook: Theory, Implementation and Applications; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Baader, F.; Horrocks, I.; Lutz, C.; Sattler, U. An Introduction to Description Logic; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar]
- McKenna, P.; Oh, T. Schizophrenic Speech. Making Sense of Bathroots and Ponds That Fall in Doorways; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Harnad, S. To cognize is to categorize: Cognition is categorization. In Handbook of Categorization in Cognitive Science; Cohen, H., Lefebvre, C., Eds.; Elsevier: Amsterdam, The Netherlands, 2005; pp. 20–43. [Google Scholar]
- Briganti, G.; Le Moine, O. Artificial Intelligence in medicine: Today and tomorrow. Front. Med. 2020, 7, 27. [Google Scholar] [CrossRef]
- Aceto, G.; Persico, V.; Pescapé, A. Big data, and cloud computing for Healthcare 4.0. J. Ind. Inf. Integr. 2020, 18, 100129. [Google Scholar]
- Massaro, A.; Maritati, V.; Savino, N.; Galiano, A.M. Neural networks for automated smart health platforms oriented on heart predictive diagnostic big data systems. In Proceedings of the 2018 AEIT International Annual Conference, Bari, Italy, 3–5 October 2018; pp. 1–5. [Google Scholar]
- Massaro, A.; Ricci, G.; Selicato, S.; Raminelli, S.; Galiano, A.M. Decisional support system with Artificial Intelligence oriented on health prediction using a wearable device and big data. In Proceedings of the 2020 IEEE International Workshop on Metrology for Industry 4.0 & IoT, Roma, Italy, 3–5 June 2020; pp. 718–723. [Google Scholar]
- El-Sherif, D.M.; Abouzid, M.; Elzarif, M.T.; Ahmed, A.A.; Albakri, A.; Alshehri, M.M. Telehealth and Artificial Intelligence insights into healthcare during the COVID-19 pandemic. Healthcare 2022, 10, 385. [Google Scholar] [CrossRef] [PubMed]
- Zhou, X.; Edirippulige, S.; Bai, X.; Bambling, M. Are online mental health interventions for youth effective? A systematic review. J. Telemed. Telecare 2021, 27, 638–666. [Google Scholar] [CrossRef] [PubMed]
- Adams, R.A.; Huys, Q.J.M.; Roiser, J.P. Computational psychiatry: Towards a mathematically informed understanding of mental illness. J. Neurol. Neurosurg. Psychiatry 2016, 87, 53–63. [Google Scholar] [CrossRef] [Green Version]
- Busemeyer, J.R.; Wang, Z.; Townsend, J.T.; Eidels, A. (Eds.) The Oxford Handbook of Computational and Mathematical Psychology; Oxford University Press: Oxford, UK, 2015. [Google Scholar]
- Sun, R. (Ed.) The Cambridge Handbook of Computational Psychology; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Augusto, L.M. Unconscious representations 2: Towards an integrated cognitive architecture. Axiomathes 2014, 24, 19–43. [Google Scholar] [CrossRef]
- Elvevåg, B.; Foltz, P.W.; Weinberger, D.R.; Goldberg, T.E. Quantifying incoherence in speech: An automated methodology and novel application to schizophrenia. Schizophr. Res. 2007, 93, 304–316. [Google Scholar] [CrossRef] [Green Version]
- Maher, B.A.; Manschreck, T.C.; Linnet, J.; Candela, S. Quantitative assessment of the frequency of normal associations in the utterances of schizophrenia patients and healthy controls. Schizophr. Res. 2005, 78, 219–224. [Google Scholar] [CrossRef]
- Bringsjord, S. Declarative/Logic-based cognitive modeling. In The Cambridge Handbook of Computational Psychology; Sun, R., Ed.; Cambridge University Press: Cambridge, UK, 2008; pp. 127–169. [Google Scholar]
- Braine, M.D.S. The “Natural Logic” approach to reasoning. In Reasoning, Necessity, and Logic: Developmental Perspectives; Overton, W.F., Ed.; Lawrence Erlbaum Associates: Hillsdale, NJ, USA, 1990; pp. 133–157. [Google Scholar]
- Braine, M.D.S.; O’Brien, D.P. (Eds.) Mental Logic; Lawrence Erlbaum Associates: Mahwah, NJ, USA, 1998. [Google Scholar]
- Evans, J.S. Logic and human reasoning: An assessment of the deduction paradigm. Psychol. Bull. 2002, 128, 978–996. [Google Scholar] [CrossRef]
- Inhelder, B.; Piaget, J. The Growth of Logical Thinking from Childhood to Adolescence; Basic Books: New York, NY, USA, 1958. [Google Scholar]
- Rips, L.J. The Psychology of Proof: Deductive Reasoning in Human Thinking; MIT Press: Cambridge, MA, USA, 1994. [Google Scholar]
- Stenning, K.; van Lambalgen, M. Human Reasoning and Cognitive Science; MIT Press: Cambridge, MA, USA, 2008. [Google Scholar]
- Wason, P. Reasoning about a rule. Q. J. Exp. Psychol. 1968, 20, 273–281. [Google Scholar] [CrossRef]
- Johnson-Laird, P.N.; Yang, Y. Mental logic, mental models, and simulations of human deductive reasoning. In The Cambridge Handbook of Computational Psychology; Sun, R., Ed.; Cambridge University Press: Cambridge, UK, 2008; pp. 339–358. [Google Scholar]
- Lewandowsky, S.; Farrell, S. Computational Modeling in Cognition: Principles and Practice; Sage Publications: Thousand Oaks, CA, USA, 2011. [Google Scholar]
- Polk, T.A.; Newell, A. Deduction as verbal reasoning. In Cognitive Modeling; Polk, T.A., Seifert, C.M., Eds.; MIT: Cambridge, MA, USA, 2002; pp. 1045–1082. [Google Scholar]
- Sowa, J.F. Categorization in cognitive computer science. In Handbook of Categorization in Cognitive Science; Cohen, H., Lefebvre, C., Eds.; Elsevier: Amsterdam, The Netherlands, 2005; pp. 141–163. [Google Scholar]
- Fodor, J.A. The Language of Thought; Harvester Press: Sussex, UK, 1975. [Google Scholar]
- Augusto, L.M. From symbols to knowledge systems: A. Newell and H. A. Simon’s contribution to symbolic AI. J. Knowl. Struct. Syst. 2021, 2, 29–62. [Google Scholar]
- Newell, A.; Simon, H.A. Computer science as empirical inquiry: Symbols and search. Commun. ACM 1976, 19, 113–126. [Google Scholar] [CrossRef] [Green Version]
- Augusto, L.M. Transitions versus dissociations: A paradigm shift in unconscious cognition. Axiomathes 2018, 28, 269–291. [Google Scholar] [CrossRef]
- Augusto, L.M. Unconscious knowledge: A survey. Adv. Cogn. Psychol. 2010, 6, 116–141. [Google Scholar] [CrossRef]
- Augusto, L.M. Unconscious representations 1: Belying the traditional model of human cognition. Axiomathes 2013, 23, 645–663. [Google Scholar] [CrossRef]
- Augusto, L.M. Lost in dissociation: The main paradigms in unconscious cognition. Conscious. Cogn. 2016, 43, 293–310. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Enderton, H.B. Elements of Set Theory; Academic Press: New York, NY, USA, 1977. [Google Scholar]
- Augusto, L.M. Computational Logic. Vol. 1: Classical Deductive Computing with Classical Logic, 2nd ed.; College Publications: London, UK, 2020. [Google Scholar]
- Ashby, F.G.; Maddox, W.T. Human category learning. Annu. Rev. Psychol. 2005, 56, 149–178. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Markmann, A.B.; Ross, B.H. Category use and category learning. Psychol. Bull. 2003, 129, 592–613. [Google Scholar] [CrossRef] [PubMed]
- Rehder, B.; Hastie, R. Category coherence and category-based property induction. Cognition 2004, 91, 113–153. [Google Scholar] [CrossRef] [Green Version]
- Augusto, L.M. Logical Consequences. Theory and Applications: An Introduction, 2nd ed.; College Publications: London, UK, 2020. [Google Scholar]
- Tversky, A. Features of similarity. Psychol. Rev. 1977, 84, 327–352. [Google Scholar] [CrossRef]
- Sjöberg, L. A cognitive theory of similarity. Goteb. Psychol. Rep. 1972, 2, 1–23. [Google Scholar]
- Augusto, L.M. Formal Logic: Classical Problems and Proofs; College Publications: London, UK, 2019. [Google Scholar]
- Goldberg, T.E.; Aloia, M.S.; Gourovitch, M.L.; Missar, D.; Pickar, D.; Weinberger, D.R. Cognitive substrates of thought disorder, I: The semantic system. Am. J. Psychiatry 1998, 155, 1671–1676. [Google Scholar] [CrossRef]
- Andreasen, N.C. Thought, language and communication disorders: I. Clinical assessment, definition of terms and evaluation of their reliability. Arch. Gen. Psychiatry 1979, 36, 1315–1321. [Google Scholar] [CrossRef] [PubMed]
- Andreasen, N.C. Scale for the assessment of Thought, Language, and Communication (TLC). Schizophr. Bull. 1986, 12, 473–482. [Google Scholar] [PubMed] [Green Version]
- Liddle, P.F.; Ngan, E.T.; Caissie, S.L.; Anderson, C.M.; Bates, A.T.; Quested, D.J.; White, R.; Weg, R. Thought and Language Index: An instrument for assessing thought and language in schizophrenia. Br. J. Psychiatry 2002, 181, 326–330. [Google Scholar] [CrossRef] [Green Version]
- Docherty, N.M.; DeRosa, M.; Andreasen, N.C. Communication disturbances in schizophrenia and mania. Arch. Gen. Psychiatry 1996, 53, 358–364. [Google Scholar] [CrossRef]
- American Psychiatric Association. Diagnostic and Statistical Manual of Mental Disorders, 5th ed.; American Psychiatric Press: Washington, DC, USA, 2013. [Google Scholar]
- Payne, R.W. An experimental study of schizophrenic thought disorder. J. Ment. Sci. 1959, 105, 627–652. [Google Scholar] [PubMed]
- Bleuler, E. Dementia Praecox, or the Group of the Schizophrenias; Zinkin, J., Translator; International Universities Press: New York, NY, USA, 1911; (English translation in 1950). [Google Scholar]
- Chaika, E.O. Understanding Psychotic Speech: Beyond Freud and Chomsky; Charles C. Thomas: Springfield, IL, USA, 1990. [Google Scholar]
- Chapman, J.P. The early symptoms of schizophrenia. Br. J. Psychiatry 1966, 112, 225–251. [Google Scholar]
- American Psychiatric Association. Diagnostic and Statistical Manual of Mental Disorder, 3rd ed.; American Psychiatric Press: Washington, DC, USA, 1980. [Google Scholar]
- Goldstone, R.L.; Son, J.Y. Similarity. In The Cambridge Handbook of Thinking and Reasoning; Holyoak, K.J., Morrison, R.G., Eds.; Cambridge University Press: Cambridge, UK, 2005; pp. 13–36. [Google Scholar]
- Chaika, E.O. A linguist looks at ‘schizophrenic’ language. Brain Lang. 1974, 1, 257–276. [Google Scholar] [CrossRef]
- Spitzer, M.; Braun, U.; Hermle, L.; Maier, S. Associative semantic network dysfunction in thought-disordered schizophrenic patients: Direct evidence from indirect semantic priming. Biol. Psychiatry 1993, 15, 864–877. [Google Scholar] [CrossRef]
- Schreber, D.P. Memoirs of My Nervous Illness; Macalpine, I.; Hunter, R.A., Translators; New York Review of Books: New York, NY, USA, 2000; (Work originally published in 1903). [Google Scholar]
- Laffal, J.; Lenkoski, L.D.; Ameen, L. “Opposite speech” in a schizophrenic patient. J. Abnorm. Soc. Psychol. 1956, 52, 409–413. [Google Scholar] [CrossRef]
- Chomsky, N. Aspects of the Theory of Syntax; MIT Press: Cambridge, MA, USA, 1965. [Google Scholar]
- Berwick, R.C.; Chomsky, N. Why Only us. Language and Evolution; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).