Performance Evaluation of Deep Neural Network Model for Coherent X-ray Imaging
Abstract
:1. Introduction
2. Materials and Methods
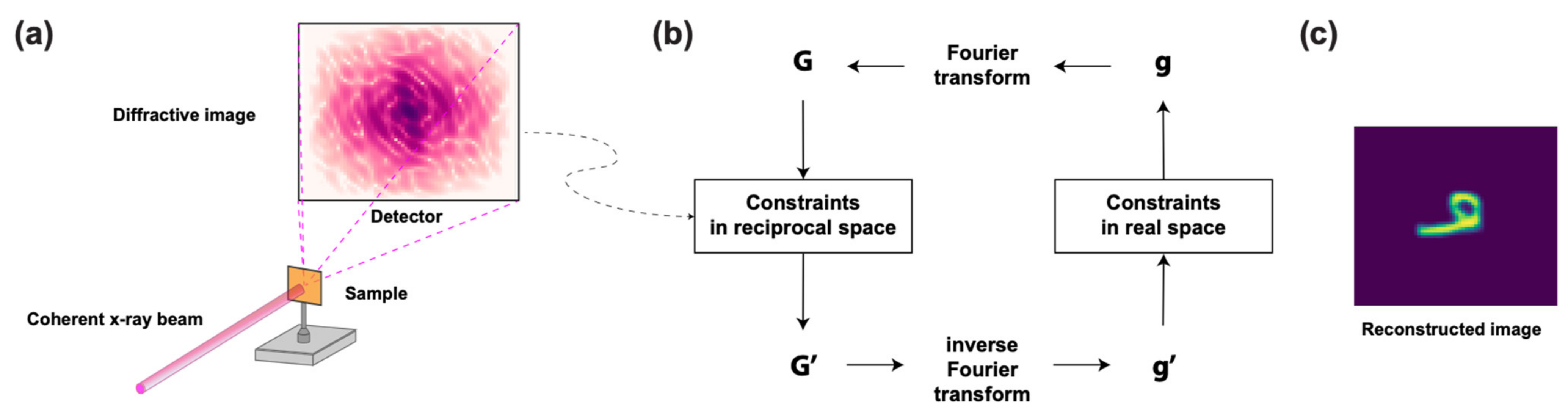
2.1. Coherent X-ray Imaging
2.2. Scope of Image Qualities
2.2.1. Degree of Coherence
2.2.2. Detection Dynamic Range
2.2.3. Noise Level
2.3. Architecture and Parameters of Convolutional Neural Network
3. Results
3.1. Degree of Coherence
3.2. Detection Dynamic Range
3.3. Noise Level
4. Discussion
4.1. Degree of Coherence
4.2. Detection Dynamic Range
4.3. Noise Level
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Paul, H. Phase retrieval in quantum mechanics. Phys. Rev. A 1994, 50, R921–R924. [Google Scholar]
- Zuo, J.M.; Vartanyants, I.; Gao, M.; Zhang, R.; Nagahara, L.A. Atomic Resolution Imaging of a Carbon Nanotube from diffraction intensities. Science 2003, 300, 1419–1422. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Miao, J.; Charalambous, R.; Kirz, J.; Sayre, D. Extending the methodology of x-ray crystallography to allow imaging of micrometre-sized non-crystalline specimens. Nature 1999, 400, 342–344. [Google Scholar] [CrossRef]
- Gerchberg, R.W.; Saxton, W.O. A practical algorithm for the determination of phase from image and diffraction plane pictures. Optik 1972, 35, 237–246. [Google Scholar]
- Dainty, J.C.; Fienup, J.R. Phase retrieval and image reconstruction for astronomy. In Image Recovery: Theory and Application; Stark, H., Ed.; Academic Press: New York, NY, USA, 1987; pp. 231–275. [Google Scholar]
- Robinson, I.K.; Vartanyants, I.A.; Williams, G.J.; Pfeifer, M.A.; Pitney, J.A. Reconstruction of the shapes of gold nanocrystals using coherent x-ray diffraction. Phys. Rev. Lett. 2001, 87, 195505. [Google Scholar] [CrossRef] [Green Version]
- Robinson, I.; Harder, R. Coherent X-ray diffraction imaging of strain at the nanoscale. Nat. Mater. 2009, 8, 291–298. [Google Scholar] [CrossRef]
- Miao, J.; Sayre, D.; Chapman, H.N. Phase retrieval from the magnitude of the Fourier transforms of nonperiodic objects. J. Opt. Soc. Am. A 1998, 15, 1662–1669. [Google Scholar] [CrossRef]
- Miao, J.; Sayre, D. On possible extensions of X-ray crystallography through diffraction-pattern oversampling. Acta Cryst. A 2000, 56, 596–605. [Google Scholar] [CrossRef] [Green Version]
- Kim, J.W.; Manna, S.; Dietze, S.H.; Ulvestad, A.; Harder, R.; Fohtung, E.; Fullerton, E.E.; Shpyrko, O.G. Curvature-induced and thermal strain in polyhedral gold nanocrystals. Appl. Phys. Lett. 2014, 105, p173108. [Google Scholar] [CrossRef]
- Pfeifer, M.A.; Williams, G.J.; Vartanyants, I.A.; Harder, R.; Robinson, I.K. Three-dimensional mapping of a deformation field inside a nanocrystal. Nature 2006, 442, 63–66. [Google Scholar] [CrossRef]
- Newton, M.C.; Leake, S.J.; Harder, R.; Robinson, I.K. Three-dimensional imaging of strain in a single ZnO nanorod. Nat. Mater. 2010, 9, 120. [Google Scholar] [CrossRef]
- Marchesini, S.; He, H.; Chapman, H.N.; Hau-Riege, S.P.; Noy, A.; Howells, M.R.; Weierstall, U.; Spence, J.C.H. X-ray image reconstruction from a diffraction pattern alone. Phys. Rev. B 2003, 68, 140101(R). [Google Scholar] [CrossRef] [Green Version]
- Elser, V. Solution of the crystallographic phase problem by iterated projections. Acta Crystallogr. A 2003, 59, 201–209. [Google Scholar] [CrossRef] [Green Version]
- Fienup, J.R. Reconstruction of a complex-valued object from the modulus of its Fourier transform using a support constraint. JOSA A 1987, 4, 118–123. [Google Scholar] [CrossRef]
- Fienup, J.R. Reconstruction of an object from the modulus of its Fourier transform. Opt. Lett. 1978, 3, 27–29. [Google Scholar] [CrossRef]
- Clark, J.N.; Beitra, L.; Xiong, G.; Higginbotham, A.; Fritz, D.M.; Lemke, H.T.; Zhu, D.; Chollet, M.; Williams, G.J.; Messerschmidt, M.; et al. Ultrafast three-dimensional imaging of lattice dynamics in gold nanocrystals. Science 2013, 341, 56–59. [Google Scholar] [CrossRef] [Green Version]
- Clark, J.N.; Ihli, J.; Schenk, A.S.; Kim, Y.; Kulak, A.N.; Campbell, J.M.; Nisbet, G.; Meldrum, F.C.; Robinson, I.K. Three-dimensional imaging of dislocation propagation during crystal growth and dissolution. Nat. Mater. 2015, 14, 780–784. [Google Scholar] [CrossRef]
- Ulvestad, A.; Singer, A.; Clark, J.N.; Cho, H.M.; Kim, J.W.; Harder, R.; Maser, J.; Meng, Y.S.; Shpyrko, O.G. Topological defect dynamics in operando battery nanoparticles. Science 2015, 348, 1344–1347. [Google Scholar] [CrossRef] [Green Version]
- Ulvestad, A.; Cherukara, M.J.; Harder, R.; Cha, W.; Robinson, I.K.; Soog, S.; Nelson, S.; Zhu, D.; Stephenson, G.B.; Heinonen, O.; et al. Bragg coherent diffractive imaging of zinc oxide acoustic phonons at picosecond timescales. Sci. Rep. 2017, 7, 9823. [Google Scholar] [CrossRef] [Green Version]
- Meneau, F.; Rochet, A.; Harder, R.; Cha, W.; Passos, A.R. Operando 3D imaging of defects dynamics of twinned-nanocrystal during catalysis. J. Phys. Condens. Matter 2021, 33, 274004. [Google Scholar] [CrossRef]
- Li, L.; Xie, Y.; Maxey, E.; Harder, R. Methods for operando coherent X-ray diffraction of battery materials at the Advanced Photon Source. J. Synchrotron Rad. 2019, 26, 220–229. [Google Scholar] [CrossRef]
- Cherukara, M.J.; Nashed, Y.S.G.; Harder, R. Real-time coherent diffraction inversion using deep generative networks. Sci. Rep. 2018, 8, 16520. [Google Scholar] [CrossRef]
- Cherukara, M.J.; Zhou, T.; Nashed, Y.; Enfedaque, P.; Hexemer, A.; Harder, R.J.; Holt, M.V. AI-enabled high-resolution scanning coherent diffraction imaging. Appl. Phys. Lett. 2019, 117, 044103. [Google Scholar] [CrossRef]
- Chan, H.; Nashed, Y.S.; Kandel, S.; Hruszkewycz, S.O.; Sankaranarayanan, S.K.; Harder, R.J.; Cherukara, M.J. Real-time 3D nanoscale coherent imaging via physics-aware deep learning. Appl. Phys. Rev. 2021, 8, 021407. [Google Scholar] [CrossRef]
- Wu, L.; Yoo, S.; Suzana, A.F.; Assefa, T.A.; Diao, J.; Harder, R.J.; Cha, W.; Robinson, I.K. Three-dimensional coherent x-ray diffraction imaging via deep convolutional neural networks. Npj Comput. Mater. 2021, 7, 1–8. [Google Scholar] [CrossRef]
- Kamilov, U.S.; Papadopoulos, I.N.; Shoreh, M.H.; Goy, A.; Vonesch, C.; Unser, M.; Psaltis, D. Learning approach to optical tomography. Optica 2015, 2, 517–522. [Google Scholar] [CrossRef] [Green Version]
- Nguyen, T.C.; Bui, V.; Nehmetallah, G. Computational optical tomography using 3-D deep convolutional neural networks. Opt. Eng. 2018, 57, 043111. [Google Scholar]
- Lyu, M.; Wang, W.; Wang, H.; Wang, H.; Li, G.; Chen, N.; Situ, G. Deep-learning-based ghost imaging. Sci. Rep. 2017, 7, 17865. [Google Scholar] [CrossRef]
- Hu, Y.; Wang, G.; Dong, G.; Zhu, S.; Chen, H.; Zhang, A.; Xu, Z. Ghost imaging based on deep learning. Sci. Rep. 2018, 8, 6469. [Google Scholar]
- Yu, J.; Zhang, W. Face mask wearing detection algorithm based on improved YOLO-v4. Sensors 2021, 21, 3263. [Google Scholar] [CrossRef]
- Roy, A.M.; Bhaduri, J. Real-time growth stage detection model for high degree of occultation using DenseNet-fused YOLOv4. Comput. Electron. Agric. 2022, 193, 106694. [Google Scholar] [CrossRef]
- Goy, A.; Arthur, K.; Li, S.; Barbastathis, G. Low photon count phase retrieval using deep learning. Phys. Rev. Lett. 2018, 121, 243902. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cha, E.; Lee, C.; Jang, M.; Ye, J.C. DeepPhaseCut: Deep Relaxation in Phase for Unsupervised Fourier Phase Retrieval. arXiv 2020, arXiv:2011.10475. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Noack, M.A.; Vagovic, P.; Fezzaa, K.; Garcia-Moreno, F.; Ritschel, T.; Villanueva-Perez, P. PhaseGAN: A deep-learning phase-retrieval approach for unpaired datasets. Opt. Express 2021, 29, 19593–19604. [Google Scholar] [CrossRef]
- Clark, J.N.; Huang, X.; Harder, R.; Robinson, I.K. High-resolution three-dimensional partially coherent diffraction imaging. Nat. Commun. 2012, 3, 993. [Google Scholar] [CrossRef]
- Hu, W.; Huang, X.; Yan, H. Dynamic diffraction artefacts in Bragg coherent diffractive imaging. J. Appl. Crystallogr. 2018, 51, 167–174. [Google Scholar] [CrossRef] [Green Version]
- Fienup, J.R. Phase retrieval algorithms: A comparison. App. Opt. 1982, 21, 2758–2769. [Google Scholar] [CrossRef] [Green Version]
- Williams, G.; Pfeifer, M.; Vartanyants, I.; Robinson, I. Effectiveness of iterative algorithms in recovering phase in the presence of noise. Acta Cryst. 2007, A63, 36–42. [Google Scholar] [CrossRef] [Green Version]
- Kim, C.; Kim, Y.; Song, C.; Kim, S.S.; Kim, S.; Kang, H.C.; Hwu, Y.; Tsuei, K.-D.; Liang, K.S.; Noh, D.Y. Resolution enhancement in coherent x-ray diffraction imaging by overcoming instrumental noise. Opt. Express 2014, 22, 29161–29169. [Google Scholar] [CrossRef]
- Rodriguez, J.A.; Xu, R.; Chen, C.-C.; Zou, Y.; Miao, J. Oversampling smoothness: An effective algorithm for phase retrieval of noisy diffraction intensities. J. Appl. Cryst. 2013, 46, 312–318. [Google Scholar] [CrossRef]
- Huang, X.; Miao, H.; Steinbrener, J.; Nelson, J.; Shapiro, D.; Stewart, A.; Turner, J.; Jacobsen, C. Signal-to-noise and radiation exposure considerations in conventional and diffraction x-ray microscopy. Opt. Express 2009, 17, 13541–13553. [Google Scholar] [CrossRef] [Green Version]
- Vartanyants, I.; Robinson, I. Partial coherence effects on the imaging of small crystals using coherent x-ray diffraction. J. Phys. Condens. Matter 2001, 13, 10593–10611. [Google Scholar] [CrossRef]
- Xiong, G.; Moutanabbir, O.; Reiche, M.; Harder, R.; Robinson, I. Coherent X-ray diffraction imaging and characterization of strain in silicon-on-insulator nanostructures. Adv. Mater. 2014, 26, 7747–7763. [Google Scholar] [CrossRef] [Green Version]
- Williams, G.J.; Quiney, H.M.; Peele, A.G.; Nugent, K.A. Coherent diffractive imaging and partial coherence. Phys. Rev. B 2007, 75, 104102. [Google Scholar] [CrossRef] [Green Version]
- Vartanyants, I.A.; Singer, A. Coherence properties of hard x-ray synchrotron sources and x-ray free electron lasers. New J. Phys. 2010, 12, 035004. [Google Scholar] [CrossRef]
- Burdet, N.; Shi, X.; Parks, D.; Clark, J.N.; Huang, X.; Kevan, S.D.; Robinson, I.K. Evaluation of partial coherence correction in X-ray ptychography. Opt. Express 2015, 23, 5452–5467. [Google Scholar] [CrossRef] [Green Version]
- Nugent, K.A. Coherent methods in the X-ray sciences. Adv. Phys. 2010, 59, 1–99. [Google Scholar] [CrossRef] [Green Version]
- Yang, W.; Huang, X.; Harder, R.; Clark, J.N.; Robinson, I.K.; Mao, H.K. Coherent diffraction imaging of nanoscale strain evolution in a single crystal under high pressure. Nat. Commun. 2013, 4, 1680. [Google Scholar] [CrossRef] [Green Version]
- Berenguer de la Cuesta, F.; Wenger, M.P.E.; Bean, R.J.; Bozec, L.; Horton, M.A.; Robinson, I.K. Coherent X-ray diffraction from collagenous soft tissues. Proc. Natl. Acad. Sci. USA 2009, 106, 15297–15301. [Google Scholar] [CrossRef] [Green Version]
- Hemonnot, C.Y.J.; Koster, S. Imaging of biological materials and cells by X-ray scattering and diffraction. ACS Nano 2017, 11, 8542–8599. [Google Scholar] [CrossRef] [Green Version]
- Ozturk, H.; Huang, X.; Yan, H.; Robinson, I.K.; Noyan, I.C.; Chu, Y.S. Performance evaluation of Bragg coherent diffraction imaging. New J. Phys. 2017, 19, 103001. [Google Scholar] [CrossRef]
- Martin, A.V.; Wang, F.; Loh, N.D.; Ekeberg, T.; Maia, F.R.N.C.; Hantke, M.; van der Schot, G.; Hampton, C.Y.; Sierra, R.G.; Aquila, A.; et al. Noise-robust coherent diffractive imaging with a single diffraction pattern. Opt. Express 2012, 20, 16650. [Google Scholar] [CrossRef]
- Shen, C.; Bao, X.; Tan, J.; Liu, S.; Liu, Z. Two noise-robust axial scanning multi-image phase retrieval algorithms based on Pauta criterion and smoothness constraint. Opt. Express 2017, 25, 16235–16249. [Google Scholar] [CrossRef]
- Lim, B.; Bellec, E.; Dupraz, M.; Leake, S.; Resta, A.; Coati, A.; Sprung, M.; Almog, E.; Rabkin, E.; Schulli, T.; et al. A convolutional neural network for defect classification in Bragg coherent X-ray diffraction. Npj Comput. Mater. 2021, 7, 1–8. [Google Scholar] [CrossRef]
- Kim, J.W.; Cherukara, M.J.; Tripathi, A.; Jiang, Z.; Wang, J. Inversion of coherent surface scattering images via deep learning network. Appl. Phys. Lett. 2021, 119, 191601. [Google Scholar] [CrossRef]
- Wu, L.; Juhas, P.; Yoo, S.; Robinson, I. Complex imaging of phase domains by deep neural networks. IUCrJ 2021, 8, 12–21. [Google Scholar] [CrossRef]
- King, M.A.; Ba, J. Adams: A Method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, G.S.; Davis, A.; Dean, J.; Devin, M.; et al. Tensorflow: Large-scale machine learning on heterogeneous distributed systems. arXiv 2016, arXiv:1603.04467. [Google Scholar]
- Prabhu, V.U. Kannada-MNIST: A new handwritten digits dataset for the Kannada language. arXiv 2019, arXiv:1908.01242. [Google Scholar]
- Calvo-Almazán, I.; Allain, M.; Maddali, S.; Chamard, V.; Hruszkewycz, S.O. Impact and mitigation of angular uncertainties in Bragg coherent x-ray diffraction imaging. Sci. Rep. 2019, 9, 6386. [Google Scholar] [CrossRef]
- Flenner, S.; Bruns, S.; Longo, E.; Parnell, A.J.; Stockhausen, K.E.; Müller, M.; Greving, I. Machine learning denoising of high-resolution X-ray nanotomography data. J. Synchrotron Radiat. 2022, 29, 230–238. [Google Scholar] [CrossRef] [PubMed]
- Luke, D.R. Relaxed averaged alternating reflections for diffraction imaging. Inverse Probl. 2004, 21, 37–50. [Google Scholar] [CrossRef] [Green Version]
- Shechtman, Y.; Eldar, Y.C.; Cohen, O.; Chapman, H.N.; Miao, J.; Segev, M. Phase retrieval with application to optical imaging. IEEE Signal Process. Mag. 2015, 32, 87–109. [Google Scholar] [CrossRef] [Green Version]






| Relative Size of MCF | 1.3 | 1.0 | 0.7 |
|---|---|---|---|
| 0.043 | 0.061 | 0.109 |
| Detection Dynamic Range | 91% | 84% | 78% |
|---|---|---|---|
| 0.071 | 0.075 | 0.099 |
| Signal-to-Noise Ratio | 106 | 105 | 104 |
|---|---|---|---|
| 0.054 | 0.054 | 0.150 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, J.W.; Messerschmidt, M.; Graves, W.S. Performance Evaluation of Deep Neural Network Model for Coherent X-ray Imaging. AI 2022, 3, 318-330. https://doi.org/10.3390/ai3020020
Kim JW, Messerschmidt M, Graves WS. Performance Evaluation of Deep Neural Network Model for Coherent X-ray Imaging. AI. 2022; 3(2):318-330. https://doi.org/10.3390/ai3020020
Chicago/Turabian StyleKim, Jong Woo, Marc Messerschmidt, and William S. Graves. 2022. "Performance Evaluation of Deep Neural Network Model for Coherent X-ray Imaging" AI 3, no. 2: 318-330. https://doi.org/10.3390/ai3020020
APA StyleKim, J. W., Messerschmidt, M., & Graves, W. S. (2022). Performance Evaluation of Deep Neural Network Model for Coherent X-ray Imaging. AI, 3(2), 318-330. https://doi.org/10.3390/ai3020020






