Abstract
We present a deep learning-based generative model for the enhancement of partially coherent diffractive images. In lensless coherent diffractive imaging, a highly coherent X-ray illumination is required to image an object at high resolution. Non-ideal experimental conditions result in a partially coherent X-ray illumination, lead to imperfections of coherent diffractive images recorded on a detector, and ultimately limit the capability of lensless coherent diffractive imaging. The previous approaches, relying on the coherence property of illumination, require preliminary experiments or expensive computations. In this article, we propose a generative adversarial network (GAN) model to enhance the visibility of fringes in partially coherent diffractive images. Unlike previous approaches, the model is trained to restore the latent sharp features from blurred input images without finding coherence properties of illumination. We demonstrate that the GAN model performs well with both coherent diffractive imaging and ptychography. It can be applied to a wide range of imaging techniques relying on phase retrieval of coherent diffraction patterns.
1. Introduction
Phase retrieval, which is a reconstruction of phase distribution from measured intensity alone, is essential to lensless coherent diffractive imaging techniques such as coherent diffractive imaging [1,2,3,4,5] and ptychography [6,7]. In coherent diffractive imaging, a diffraction pattern is recorded on a detector by illuminating coherent wavefields toward a sample of interest. The missing phase of the diffracted wave can be retrieved by the iterative phase retrieval algorithm [8,9]. It enables us to image an object in two or three dimensions at high resolution [10,11]. Ptychography is a scanning type of coherent diffractive imaging (CDI) technique [12]. It measures a series of far-field diffraction patterns from partly overlapping areas of an object. The neighboring diffraction patterns play the role of the constraints in an iterative phase retrieval algorithm to reconstruct both the object and the illumination function (i.e., probe) [13]. In both CDI and ptychography, the iterative phase retrieval algorithms have a tacit assumption that the incoming X-ray beam is fully coherent. It allows for a Fourier transformation relationship between an object and its diffracted intensity. If the illumination is partially coherent, the reconstructed object image results in a degradation such as a low resolution, incorrect shape, an inclusion of defects, etc. Under the experimental environments at third-generation synchrotron or free-electron laser sources, X-ray beam illumination is not fully coherent but is highly coherent [14,15,16,17]. Furthermore, various uncertainties can contribute to even less coherent illuminations.
In order to overcome the negative effects of partial coherence, there have been two different approaches. (1) A priori knowledge of the illumination’s coherence property is implemented in the phase retrieval algorithm [18]. (2) A coherence property of the illumination is recovered during the iterative algorithm [19,20]. Both methods ultimately find the coherence property, which varies with the X-ray source environments. The former requires preliminary experiments to reveal the coherence property, and it has a limited applicability [21]. The latter works when the illumination is sufficiently coherent because it needs to solve a deconvolution problem [19].
Unlike previous studies, our approach is to restore the latent fully coherent diffractive images from partially coherent diffractive input images based on the generative adversarial network. It requires neither additional experiments nor high degrees of coherence. The framework treats the improvement in the partial coherence as deblurring diffractive images via image-to-image translation. Generative Adversarial Networks (GANs) have revolutionized deep learning research and shown promise in the area of image enhancement such as image inpainting, denoising, style transformation, super high-resolution images, etc. [22,23,24,25]. A particular type of GAN has been proven to be suitable for deblurring images, which is an ill-posed image problem [26]. GANs train both the generator and discriminator in such a way that they compete with each other. In our proposed architectures, the generator produces coherence-enhanced diffractive images and the discriminator tries to distinguish them from fully coherent diffractive images. While it is being trained, the model increases its ability to restore the visibility and contrast of fringes in the diffractive images.
It has been shown that the diffractive images in the presence of partial coherence can be expressed as the following equation [18,19,27].
where and are partially coherent diffractive image and fully coherent diffractive image, respectively; represents a convolution operator; and is the Fourier transformation of the mutual coherence function (MCF), which is related to the properties of coherence. In a similar fashion, the formulation for a blurred image can be expressed as the convolution of a sharp image with a blur kernel.
where and are blurred and sharp images, respectively, and is a blur kernel. A partially coherent diffractive image and a blurred image can be interpreted as degraded images from a fully coherent diffractive image and a sharp image with the convolution of a kernel, respectively. In our study, the images for training and testing are synthesized. The sharp images, corresponding to the fully coherent diffractive images, are created by Fourier transformation of the image dataset. Subsequently, the blurred images are generated by the convolution of fully coherent diffractive images with a Gaussian blur kernel to mimic partially coherent diffractive images. After training, the model generates the coherence-enhanced diffractive images from partially coherent diffractive images.
2. Proposed Approach
2.1. Conditional GAN
GAN was first proposed by Goodfellow et al. [28] to train a generative network in an adversarial process. As described above, it consists of two neural networks. The generator generates a fake image from input noise z, while the discriminator estimates the probability that a fake image is from the training data rather than generated by the generator. These two networks are simultaneously trained until the discriminator cannot distinguish if the image is real or fake. This process can be summarized as a two-player min–max game with the following function:
where Pdata denotes a distribution over training data x and Pz is a distribution of input noise z. In the original GAN, there is no control over the data to be generated. However, the conditional GAN [29] can increase the flexibility in the output of generative models. The conditional GAN architecture has shown the general image-to-image translation [30]. In the network, a conditional variable c is added to the generator and discriminator to guide the data generation process. Therefore, conditional GANs provide an approach to synthesizing images with user-specified content. It is suitable for the image generation of diffraction patterns because, typically, there is a peak intensity in the center of the image and the intensity decays as it goes far from the center. The conditional GAN generates images from the domain of diffraction patterns. The new objective function becomes the following:
Kupyn et al. [26] utilized Wasserstein loss with gradient penalty [31,32] and perceptual loss [33] to train a conditional GAN for the deblurring image problem. We adopted both loss functions because the former helps to achieve effective and reliable adversarial training and the latter provides accurate results regarding style transfer.
2.2. Coherence-Enhanced GAN
In the network of our GAN, the generator uses partially coherent diffractive images as input to generate the coherence-enhanced diffractive images. Figure 1a shows the details of the convolutional neural network in the generator. There are three convolutional layers in the initial part of the generator to extract the features of partially coherent diffractive images, and the last part of the generator consists of two deconvolutional layers and a convolutional layer to reconstruct the restored image. In the middle, there are nine residual blocks (ResBlocks) [34], which consist of two convolution layers. The first convolution layer is followed by batch normalization and ReLU activation. The output is passed through a second convolution layer followed by batch normalization. The output obtained from this is then added to the original input. It makes the generator more efficient and faster in the extraction of image features. In addition, the global skip connection is employed [35,36], which adds the input of the network directly to the output so that the generator can learn the residual between the partially and fully coherent diffractive images. Since the partially and fully coherent diffractive images have many similar features, it is computationally efficient to allow the generator to learn only the residual during the training process. The architecture of the generator is similar to DeblurGAN [26]. In the network, the discriminator is responsible for discriminating coherence-enhanced images from fully coherent diffractive images. During the training, the discriminator also helps the generator’s learning by feeding the adversarial loss. The architecture of the discriminator network shown in Figure 1b is similar to PatchGAN [37,38], which is more suitable for learning deblurring than the ordinary discriminators [39].
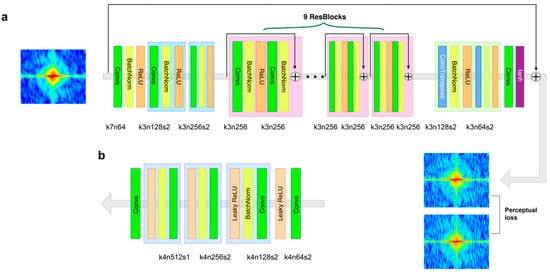
Figure 1.
The conceptual architecture of the (a) generator and (b) discriminator with the corresponding number of kernel size (k), feature maps (n), and stride (s) indicated for each convolutional layer.
2.3. Loss Functions
The loss function consists of two terms: (a) the adversarial loss , which drives the generator network to achieve the desired transformation, and (b) the content loss to preserve the image contents.
where is a balancing factor, 100. The adversarial loss ensures the network generates fully coherent diffractive images to fool the discriminator network.
The perceptual loss is more suitable for preserving image texture compared with the pixel-wise difference-based loss such as L1 (mean absolute error) or L2 (mean squared error).
Equation (7) is the L2 difference between the feature maps of the ground truth and the deblurred image of a specific layer in the VGG-19 [40] network, where represents the feature map acquired by the j-th convolution before the i-th max-pooling layer in the VGG-19 network, pretrained on ImageNet [41]. and are the ground truth and the predicted frame, respectively. and are the width and height dimensions of the feature maps, respectively. In our study, we use the VGG3,3 convolutional layer [39] and duplicate the gray-scaled diffractive images to make RGB channels because the input of the network is a color image.
3. Image Synthesis for Computational Experiments
3.1. Synthesis of Partially Coherent Diffractive Images
We consider the diffraction phenomenon in the kinetic regime, which can be analytically described using the classical formulation of the kinetic scattering of X-rays from crystalline materials [42]. Therefore, fully coherent diffractive images can be simulated using Fourier transformation of image dataset and partially coherent diffractive images are generated by the convolution of the Gaussian blur kernel [43]. The diffractive images are converted to logarithmic scale before being used in the model and converted back to linear scale for phase retrieval. We employ a publicly available image dataset, which is English alphabet letters [44]: 13,920 pairs of gray-scale images are selected for training, and the test set consists of 310 sample images uniformly distributed across the 26 letters. The 28 × 28 pixel sizes of the original images are interpolated to 64 × 64 pixel sizes using a bicubic method and enlarged to 256 × 256 pixel-size images by padding zero matrices. The ratio of the entire image to the portion occupied by the object determines the oversampling ratio as 4. It allows us to invert the diffraction pattern to the object image via phase retrieval because the oversampling ratio meets the lowest number of requirements, two, for the image reconstruction of CDI [1].
Equation (1) can be rewritten with 2D coordinates as follows:
We define the mutual coherence function (MCF) in reciprocal space as follows because it is well approximated with a Gaussian function [42]:
where the coefficient A is the amplitude, and and are the standard deviations along the and directions, respectively. The standard deviations determine the degree of blurriness. Figure 2a–c show a fully coherent diffractive image, the blur kernel with the standard deviation 2 along both the and directions, and the resultant image, respectively. Figure 2d shows the line-outs that pass through the center of the diffraction images along the qy direction. The blur kernel in Figure 2b was applied to all input images for training.
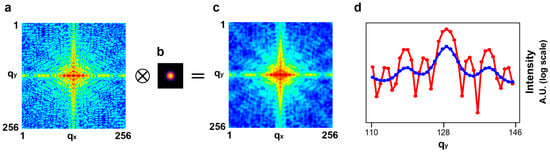
Figure 2.
The method used to generate partially coherent diffractive images. (a) A fully coherent diffractive image created by Fourier transformation of one alphabet. (b) A Gaussian blur kernel with the standard deviation 2 along both the qx and qy directions, which is applied to all input images for training the model. (c) A partially coherent diffractive image results from the convolution between the fully coherent diffractive image (a) and the Gaussian blur kernel in (b). (d) Line-outs through the center of the diffraction images in (a,c), denoted by red and blue lines, respectively.
3.2. Degree of Coherence
We can estimate the standard deviation σ of MCF in real space, which is associated with the degree of coherence. It turns out to be approximately 20 based on the formula σ = N/(2π), with N as the number of pixels in a given direction, which is 256, and being the standard deviation of the blur kernel, which is 2. The traditional methods based on the correction of coherence property work with a limited degree of coherence. It is required that the normalized MCF must be non-zero across a width twice the size of the object [19]. The normalized MCF with the standard deviation 20 has the value 0.007 at ±64, which is twice the size of the object. Since it barely meets the condition, the blurriness defined as the standard deviation 2 for the partially coherent diffractive images is challenging for traditional methods relying on the refinement of coherence property [19].
4. Model Validation and Discussion
4.1. Model Details and Parameters
Our model is implemented using the PyTorch framework, and the numerical experiments have been performed on the NVIDIA Tesla K80 GPU. The learning rate was set to 10−4 for both the generator and the discriminator. We evaluate the performance of our GAN model in reciprocal space, which is an original domain, and further in real space by reconstruction using CDI and ptychography. In reciprocal space, we employ the structural similarity index measure (SSIM) [45] and the peak signal-to-noise ratio (PSNR) to measure the quality of coherence-enhanced diffractive images with respect to the fully coherent diffractive images. The SSIM index ranges from 0 to 1, where 1 corresponds to identical images and 0 is interpreted as a loss of all similarity. The training was stopped at the epoch 80, where the SSIM and PSNR index were stabilized, as shown in Figure 3a.
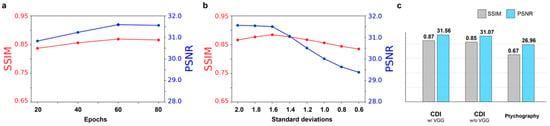
Figure 3.
The performance evaluation of the model with the SSIM and PSNR index. (a) Both indices are stabilized at epoch 80. (b) The GAN model trained with the images blurred by the Gaussian blur kernel of the standard deviation 2 is evaluated when it is applied to the different levels of blurriness. (c) The comparison of model performance when the perceptual loss is included and not considered. In addition, both indices decrease when the model is applied to the ptychographic imaging. The SSIM and PSNR index for CDIs and ptychography are averaged over 310 test images and 6 images, that are used in our study on ptychography, respectively.
4.2. Comparison of Performance
The model trained with partially coherent diffractive images blurred by the convolution of fully coherent diffractive images and a Gaussian blur kernel with the standard deviation 2 was applied to the different degree of coherent diffractive images. Figure 3b shows that our model can robustly handle the various degrees of coherence. Even though the degree of coherence deviates from the one for training, the PSNR and SSIM index still remain at high levels. We applied our GAN model created for CDI to ptychography, although there are two differences in the image texture. First, the oversampling ratio in ptychography is less than the one in CDI because, by definition, the entire object is not isolated by X-ray illumination in ptychography. Second, in our study, the diffraction images in ptychography are from multiple letters, whereas the diffraction images in the training dataset come from single letters. They can lead to a different input image style than the images used in training and, consequently, lower the SSIM and PSNR, as shown in Figure 3c. In addition, it turns out that the perceptual loss that aims to restore finer texture details via an external perception network [41] increases the capability of the model.
4.3. Performance of Coherent Diffractive Imaging
We performed phase retrieval with the three different diffraction patterns, which are fully coherent, partially coherent, and coherence-enhanced diffractive images, as shown in Figure 4a. The performance of reconstruction with the coherence-enhanced diffractive images is significantly improved. Figure 4b shows that the image reconstructed from the coherence-enhanced diffractive image is almost identical to the result from the fully coherent diffractive image, whereas the reconstruction of partially coherent diffractive image failed. It indicates that our GAN model can restore the original fringes from partially coherent diffractive images so accurately that the phase retrieval produces a true object image, which otherwise would be impossible. We used alternating projection-based methods, which are widely used for phase retrieval. The classical Gerchberg–Saxton error reduction (ER) [46] and Fienup’s hybrid input–output (HIO) [47] methods impose constraints on the amplitudes in real space.
where is the object density at n-th iterations, and and are the projectors in real space and reciprocal space, respectively. The support projector acts on the object when set to 0 at the density of the object outside a given region, which is called a support. The modulus projector acts on the Fourier transformation of the density in reciprocal space. The magnitude of Fourier transformation of the object is replaced with the square root of the intensity. During the phase retrieval process, a total of 500 iterations are performed with periodically updating object support using a ‘shrink-wrap’ algorithm [48].

Figure 4.
The performance of coherence-enhanced GAN in transmission coherent diffractive imaging. (a) Fully coherent, partially coherent, and coherence-enhanced diffractive images (from left to right). (b) The reconstructed images from fully coherent (left), partially coherent (middle), and coherence-enhanced diffractive images (right). The original image size is 256 × 256, but the images in (b) are 128 × 128 crops around the object. (c) Line-outs through the center of the diffraction patterns.
4.4. Performance of Ptychography
Ptychographic imaging is performed by the inversion of multiple diffraction images simultaneously. During the data acquisition process, a localized illumination probe scans the object while recording diffraction images in the far field. We specifically adopted the extended Ptychographic Iterative Engine (ePIE) algorithm [49]. The ePIE starts with initial guess of object and probe . The diffraction patterns are addressed in a sequence and a guess of the exit wave is formed by multiplication of the current object guess with a shifted probe guess.
where the i-th exit wave is termed and r is real space coordinate vectors. The probe and object wavefronts are denoted as and , respectively. The vector presents the relative shift between the object and probe. The modulus of the Fourier transform of this exit wave is then replaced with the square root of the -th intensity. It is similar to the modulus projector in Equation (10).
An updated exit wave is then calculated via an inverse Fourier transform,
and updated object and probe guesses are extracted from the above results using two update functions as follows.
where and are the adjustable step parameters for convergence, and is used in our study. During the above iterative process, the object and probe functions are repeatedly updated. Successful inversion of ptychographic imaging data requires fully coherent illuminations and a proper ratio of overlap between two adjacent illuminating areas. Figure 5a shows the schematic setup of ptychography. As the object shifts, six coherent diffractive images are obtained with the overlapping ratio 73%. The probe is defined as an ellipse with a major and minor axes of 140 and 100 pixels, respectively. The oversampling ratios estimated by the ratio of the probe size to the object size illuminated by the probe are 2.2 and 1 along the longitudinal and transverse directions, respectively. They are different from those of the images for CDI, which are four along both directions. Figure 5b–d show fully coherent, partially coherent, and coherence-enhanced diffractive images, respectively. The diffractive images in Figure 5c are generated by the convolution of fully coherent diffractive images in Figure 5b with the Gaussian blur kernel in Figure 2b. The images in Figure 5c are enhanced by the coherence-enhanced GAN model, as shown in Figure 5d. Figure 5e shows three enlarged images of the first images in Figure 5b–d. Figure 5f shows three image reconstructions from fully coherent, partially coherent, and coherence-enhanced diffractive images. Despite the fact that this GAN model is trained for CDI, it produces high-quality solutions in ptychography so that the final reconstruction image is reasonably accurate.
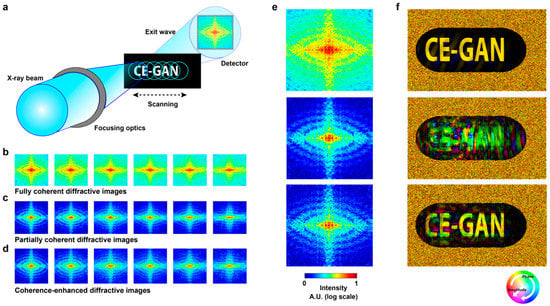
Figure 5.
The performance of coherence-enhanced GAN in ptychography. (a) Schematic setup for ptychography. A 2D object is scanned with a focused fully or partially coherent beam while collecting far-field diffraction images on a detector. The overlapping ratio between the adjacent illuminating areas is 73% (b–d) Six diffraction images from fully coherent, partially coherent, and coherence-enhanced illuminations, respectively. (e) The enlarged images of the left side images in (b,c), and (d) (from top to bottom). (f) The reconstructed images of three different series of diffraction images, fully coherent diffractive images, partially coherent diffractive images, and coherence-enhanced diffractive images (from top to bottom).
4.5. Discussion
We have shown that the coherence-enhanced GAN model improves the partially coherent diffractive images significantly based on the indices of SSIM and PSNR in diffraction patterns and the image reconstructions by CDI and ptychography in real space. The degree of partial coherence used throughout this study is challenging for the previous approaches. It is revealed that if the model is trained with a certain degree of coherence, it also performs well with a higher degree of partially coherent diffractive images. It implies that once the model is trained with a worst case of partially coherent diffractive images, the model would deal with any images of qualities. In addition, it turns out that our GAN model is insensitive to the oversampling ratio of diffractive images. Therefore, the coherence-enhanced GAN model can provide a clear input solution for the phase retrieval of both CDI and ptychography.
5. Conclusions
In summary, we presented a generative adversarial network model for the enhancement of partially coherent diffractive images. Lensless coherent diffractive imaging techniques relying on the phase retrieval require fully coherent diffractive images. In reality, however, there are uncertainties in experiments that can prevent the wavefronts of X-ray beams from being fully coherent. Since the partial coherence limits the accuracy of the imaging techniques, the efforts that mitigate the adverse effect of partial coherence have been made rigorously. Unlike the previous approaches, our generative adversarial network model is trained to restore the visibility and contrast of fringes in diffraction patterns directly. Because the coherence-enhanced GAN model robustly deals with various degrees of partially coherent diffractive images, it can be used for a wide range of lensless coherent diffractive imaging techniques.
Author Contributions
Conceptualization, J.W.K.; Funding acquisition, W.S.G.; Investigation, J.W.K., M.M.; Project administration, W.S.G.; Resources, M.M.; Software, J.W.K.; Supervision, M.M. and W.S.G.; Validation, J.W.K.; Writing—original draft, J.W.K.; Writing—review & editing, J.W.K., M.M. and W.S.G. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by NSF award 1935994.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Miao, J.; Charalambous, P.; Kirz, J.; Sayre, D. Extending the methodology of X-ray crystallography to allow imaging of micrometre-sized non-crystalline specimens. Nature 1999, 400, 342–344. [Google Scholar] [CrossRef]
- Robinson, I.; Harder, R. Coherent X-ray Diffraction Imaging of Strain at the Nanoscale. Nat. Mater. 2009, 8, 291–298. [Google Scholar] [CrossRef] [PubMed]
- Williams, G.J.; Pfeifer, M.A.; Vartanyants, I.A.; Robinson, I.K. Three-Dimensional Imaging of Microstructure in Au Nanocrystals. Phys. Rev. Lett. 2003, 90, 175501. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kim, J.W.; Manna, S.; Dietze, S.; Ulvestad, A.; Harder, R.; Fohtung, E.; Fullerton, E.; Shpyrko, O. Curvature-induced and thermal strain in polyhedral gold nanocrystals. Appl. Phys. Lett. 2014, 105, 173108. [Google Scholar] [CrossRef]
- Kim, J.W.; Ulvestad, A.; Manna, S.; Harder, R.; Fullerton, E.E.; Shpyrko, O.G. 3D Bragg coherent diffractive imaging of five-fold multiply twinned gold nanoparticle. Nanoscale 2017, 9, 13153–13158. [Google Scholar] [CrossRef]
- Seaberg, M.D.; Zhang, B.; Gardner, D.F.; Shanblatt, E.R.; Murnane, M.M.; Kapteyn, H.R.; Adams, D.E. Tabletop nanometer extreme ultraviolet imaging in an extended reflection mode using coherent Fresnel ptychography. Optica 2014, 1, 39–44. [Google Scholar] [CrossRef]
- Rodenburg, J.M. Ptychography and related diffractive imaging methods. Adv. Imaging Electron Phys. 2008, 150, 87. [Google Scholar]
- Fienup, J.R.; Marron, J.C.; Schulz, T.J.; Seldin, J.H. Hubble space telescope characterized by using phase-retrieval algorithms. Appl. Opt. 1993, 32, 1747. [Google Scholar] [CrossRef] [Green Version]
- Miao, J.; Kirz, J.; Sayre, D. The oversampling phasing method. Acta Crystallogr. D 2000, 56, 1312. [Google Scholar] [CrossRef] [Green Version]
- Chapman, H.N.; Nugent, K.A. Coherent lensless X-ray imaging. Nat. Photon. 2010, 4, 833–839. [Google Scholar] [CrossRef]
- Pfeifer, M.A.; Williams, G.J.; Vartanyants, I.A.; Harder, R.; Robinson, I.K. Three-dimensional mapping of a deformation field inside a nanocrystal. Nature 2006, 442, 63–66. [Google Scholar] [CrossRef] [PubMed]
- Rodenburg, J.M.; Faulkner, H.M.L. A phase retrieval algorithm for shifting illumination. Appl. Phys. Lett. 2004, 85, 4795–4797. [Google Scholar] [CrossRef] [Green Version]
- Thibault, P.; Dierolf, M.; Bunk, O.; Menzel, A.; Pfeiffer, F. Probe retrieval in ptychographic coherent diffractive imaging. Ultramicroscopy 2009, 109, 338–343. [Google Scholar] [CrossRef] [PubMed]
- Xiong, G.; Moutanabbir, O.; Reiche, M.; Harder, R.; Robinson, I. Coherent X-ray diffraction imaging and characterization of strain in silicon-on-insulator nanostructures. Adv Mater. 2014, 26, 7747–7763. [Google Scholar] [CrossRef] [Green Version]
- Williams, G.J.; Quiney, H.M.; Peele, A.G.; Nugent, K.A. Coherent diffractive imaging and partial coherence. Phys. Rev. B 2007, 75, 104102. [Google Scholar] [CrossRef] [Green Version]
- Vartanyants, I.A.; Singer, A. Coherence properties of hard X-ray synchrotron sources and free-electron lasers. New J. Phys. 2010, 12, 035004. [Google Scholar] [CrossRef]
- Graves, W.S.; Bessuille, J.; Brown, P.; Carbajo, S.; Dolgashev, V.; Hong, K.-H.; Ihloff, E.; Khaykovich, B.; Lin, H.; Murari, K.; et al. Compact X-ray source based on burst-mode inverse Compton scattering at 100 kHz. Phys. Rev. ST Accel. Beams 2014, 17, 120701. [Google Scholar] [CrossRef]
- Whitehead, L.W.; Williams, G.J.; Quiney, H.M.; Vine, D.J.; Dilanian, R.A.; Flewett, S.; Nugent, K.A.; Peele, A.G.; Balaur, E.; McNulty, I. Diffractive imaging using partially coherent X-rays. Phys. Rev. Lett. 2009, 103, 243902. [Google Scholar] [CrossRef] [Green Version]
- Clark, J.N.; Huang, X.; Harder, R.; Robinson, I.K. High-resolution three-dimensional partially coherent diffraction imaging. Nat. Commun. 2012, 3, 993. [Google Scholar] [CrossRef]
- Clark, J.N.; Peele, A.G. Simultaneous sample and spatial coherence characterization using diffractive imaging. Appl. Phys. Lett. 2011, 99, 154103. [Google Scholar] [CrossRef] [Green Version]
- Parks, D.H.; Shi, X.; Kevan, S.D. Partially coherent X-ray diffractive imaging of complex objects. Phys. Rev. A 2014, 89, 063824. [Google Scholar] [CrossRef]
- Jiang, Y.; Xu, J.; Yang, B.; Xu, J.; Zhu, J. Image inpainting based on generative adversarial networks. IEEE Access 2020, 8, 22884–22892. [Google Scholar] [CrossRef]
- Wolterink, J.M.; Leiner, T.; Viergever, M.A.; Isgum, I. Generative adversarial networks for noise reduction in low-dose CT. IEEE Trans Med Imaging 2017, 36, 2536–2545. [Google Scholar] [CrossRef] [PubMed]
- Karras, T.; Laine, S.; Aila, T. A style-based generator architecture for generative adversarial networks. In Proceedings of the IEEE CVPR, Long Beach, CA, USA, 15–20 June 2019; pp. 4401–4410. [Google Scholar]
- Ledig, C.; Theis, L.; Huszar, F.; Caballero, J.; Cunningham, A.; Acosta, A.; Aitken, A.; Tejani, A.; Totz, J.; Wang, Z.; et al. Photo-realistic single image super-resolution using a generative adversarial network. In Proceedings of the IEEE CVPR, Honolulu, HI, USA, 21–26 July 2017; pp. 4681–4690. [Google Scholar]
- Kupyn, O.; Budzan, V.; Mykhailych, M.; Mishkin, D.; Matas, J. DeblurGAN: Blind motion deblurring using conditional adversarial networks. In Proceedings of the IEEE CVPR, Salt Lake City, UT, USA, 18–22 June2018; pp. 8183–8192. [Google Scholar]
- Tran, C.Q.; Peele, A.G.; Roberts, A.; Nugent, K.A.; Paterson, D.; McNulty, I. Synchrotron beam coherence: A spatially resolved measurement. Opt. Lett. 2005, 30, 204. [Google Scholar] [CrossRef] [PubMed]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial nets. In Advances Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2014; p. 27. [Google Scholar]
- Mirza, M.; Osindero, S. Conditional generative adversarial nets. arXiv 2014, arXiv:1411.1784. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional networks for biomedical image segmentation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Munich, Germany, 5–9 October 2015; Springer: Cham, Switzerland, 2015; pp. 234–241. [Google Scholar]
- Arjovsky, M.; Chintala, S.; Bottou, L. Wasserstein GAN. arXiv 2017, arXiv:1701.07875. [Google Scholar]
- Gulrajani, I.; Ahmed, F.; Arjovsky, M.; Dumoulin, V.; Courville, A. Improved Training of Wasserstein GANs. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2017; p. 30. [Google Scholar]
- Johnson, J.; Alahi, A.; Fei-Fei, L. Perceptual losses for real-time style transfer and super-resolution. In Proceedings of the European Conference on Computer Vision, Munich, Germany, 8–14 September 2016. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. arXiv 2015, arXiv:1512.03385. [Google Scholar]
- Kim, J.; Lee, J.K.; Lee, K.M. Accurate image super-resolution using very deep convolutional networks. In Proceedings of the IEEE CVPR, Las Vegas, NV, USA, 27–30 June 2016; pp. 1646–1654. [Google Scholar]
- Ramakrishnan, S.; Pachori, S.; Gangopadhyay, S.; Raman, S. Deep generative filter for motion deblurring. In Proceedings of the IEEE CVPR, Honolulu, HI, USA, 21–26 July 2017; pp. 2993–3000. [Google Scholar]
- Isola, P.; Zhu, J.-Y.; Zhou, T.; Efros, A.A. Image-to-image translation with conditional adversarial network. arXiv 2016, arXiv:1611.07004. [Google Scholar]
- Li, C.; Wand, M. Precomputed real-time texture synthesis with Markovian generative adversarial networks. In Proceedings of the European Conference on Computer Vision, Munich, Germany, 8–14 September 2016; Springer: Cham, Switzerland, 2016; pp. 702–716. [Google Scholar]
- Feng, H.; Guo, J.; Xu, H.; Ge, S.S. SharpGAN: Dynamic scene deblurring method for smart ship based on receptive field block and generative adversarial networks. Sensors 2021, 21, 3641. [Google Scholar] [CrossRef]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Deng, J.; Dong, W.; Socher, R.; Li, L.-J.; Li, K.; Fei-Fei, L. ImageNet: A Large-Scale Hierarchical Image Database. In Proceedings of the CVPR09, Miami, FL, USA, 20–25 June 2009. [Google Scholar]
- Vartanyants, I.A.; Robinson, I.K. Partial coherence effects on the imaging of small crystals using coherent X-ray diffraction. J. Phys. Condens. Matter 2001, 13, 10593–10611. [Google Scholar] [CrossRef]
- Maddali, S.; Allain, M.; Cha, W.; Harder, R.; Park, J.-S.; Kenesei, R.; Almer, J.; Nashed, Y.; Hruszkewycz, S.O. Phase retrieval for Bragg coherent diffraction imaging at high X-ray energies. Phys. Rev. A 2019, 99, 053838. [Google Scholar] [CrossRef] [Green Version]
- Lin, T.; Asokan, R. Alphabet Characters Fonts Dataset. Available online: https://www.kaggle.com/thomasqazwsxedc/alphabet-characters-fonts-dataset (accessed on 10 November 2021).
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fienup, J.R. Reconstruction of an object from the modulus of its Fourier transform. Opt. Lett. 1978, 3, 27–29. [Google Scholar] [CrossRef] [PubMed]
- Fienup, J.R. Reconstruction of a complex-valued object from the modulus of its Fourier transform using a support constraint. J. Opt. Soc. Am. A 1987, 4, 118–123. [Google Scholar] [CrossRef]
- Marchesini, S.; He, H.; Chapman, H.N.; Hau-Riege, A.P.; Noy, A.; Howells, M.R.; Weierstall, U.; Spence, J.C.H. X-ray image reconstruction from a diffraction pattern alone. Phys. Rev. B 2003, 68, 140101. [Google Scholar] [CrossRef] [Green Version]
- Maiden, A.M.; Rodenburg, J.M. An improved ptychographical phase retrieval algorithm for diffractive imaging. Ultramicroscopy 2009, 109, 1256–1262. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).