An Artificial Neural Network-Based Approach for Predicting the COVID-19 Daily Effective Reproduction Number Rt in Italy
Abstract
:1. Introduction
Related Works
2. Materials and Methods
2.1. Data Sources and Preprocessing
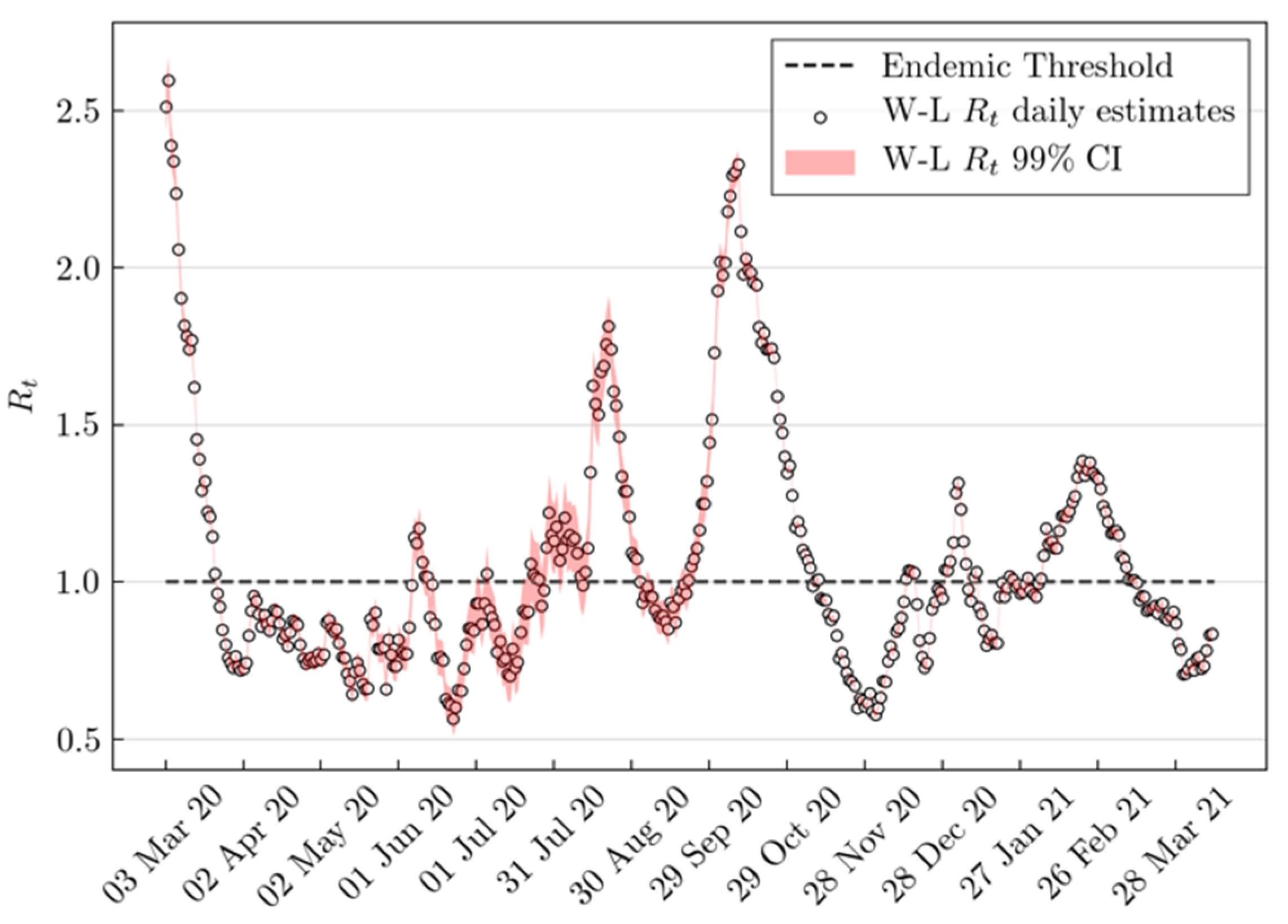
2.1.1. Daily Effective Reproduction Number Estimation
| Algorithm1 Daily growth rate estimation |
| Input:p (time series of new positive cases) |
| Output:rlist (growth rate for each day in the list) |
| Initializations: |
|
LOOP Process:
|
2.2. Artificial Neural Network (ANN) Architectures
- a Fully Connected Neural Network (FCNN), which represents a baseline NN;
- a Mono-dimensional Convolutional Neural Network (1D CNN), used for extracting the inherent information (i.e., the internal representation of features) of a one-dimensional sequence of observations, such as time series data;
- a Long Short-Term Neural Network (LSTM), typically used for selectively retaining the long- to short-term temporal relationships included in sequence data;
2.2.1. Fully Connected Neural Networks
2.2.2. 1-D Convolutional Neural Networks (1D CNNs)
2.2.3. Long Short-Term Memory (LSTM) Neural Networks
2.3. Experimental Setup
| Algorithm2 95% Prediction Interval (PI) estimation |
| Input:X (input data), K (number of iterations), s_train (training set size), s_val (validation set size), s_test (test set size), modeltype (architecture type) |
| Output: (average predictions), (lower bound of PI), (upper bound of PI) |
| Initializations: |
|
LOOP Process:
|
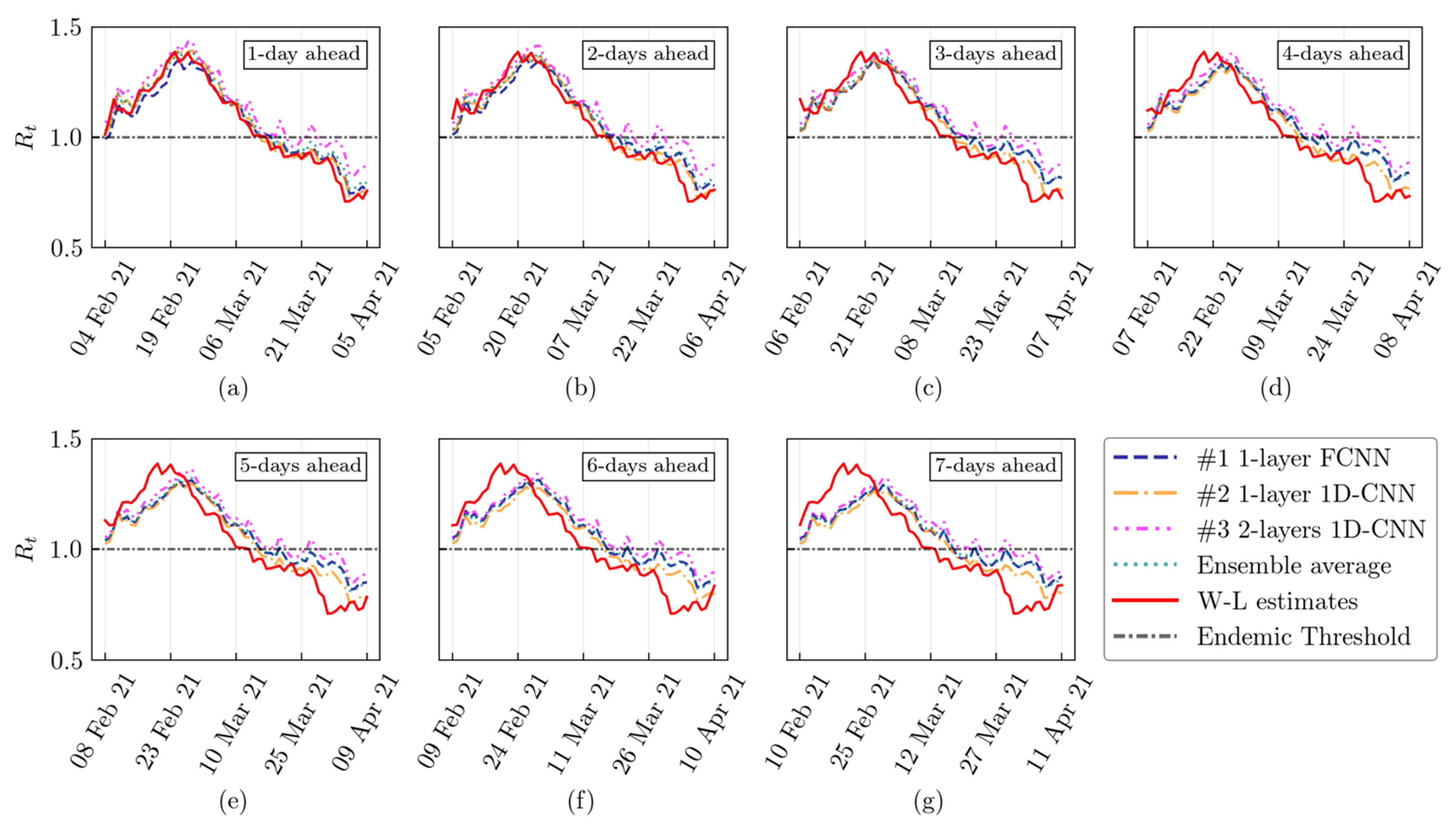
2.4. The Rolling Approach
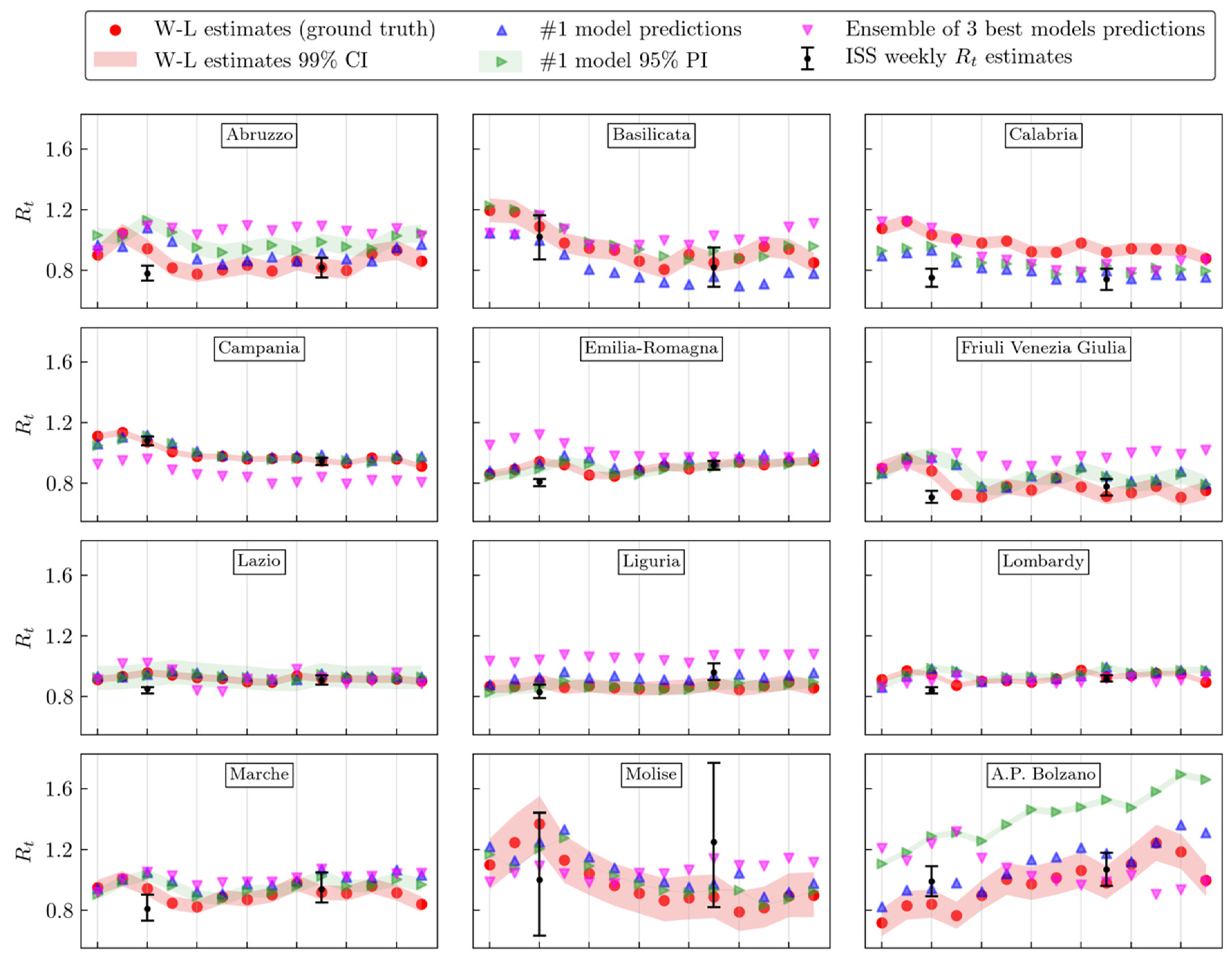
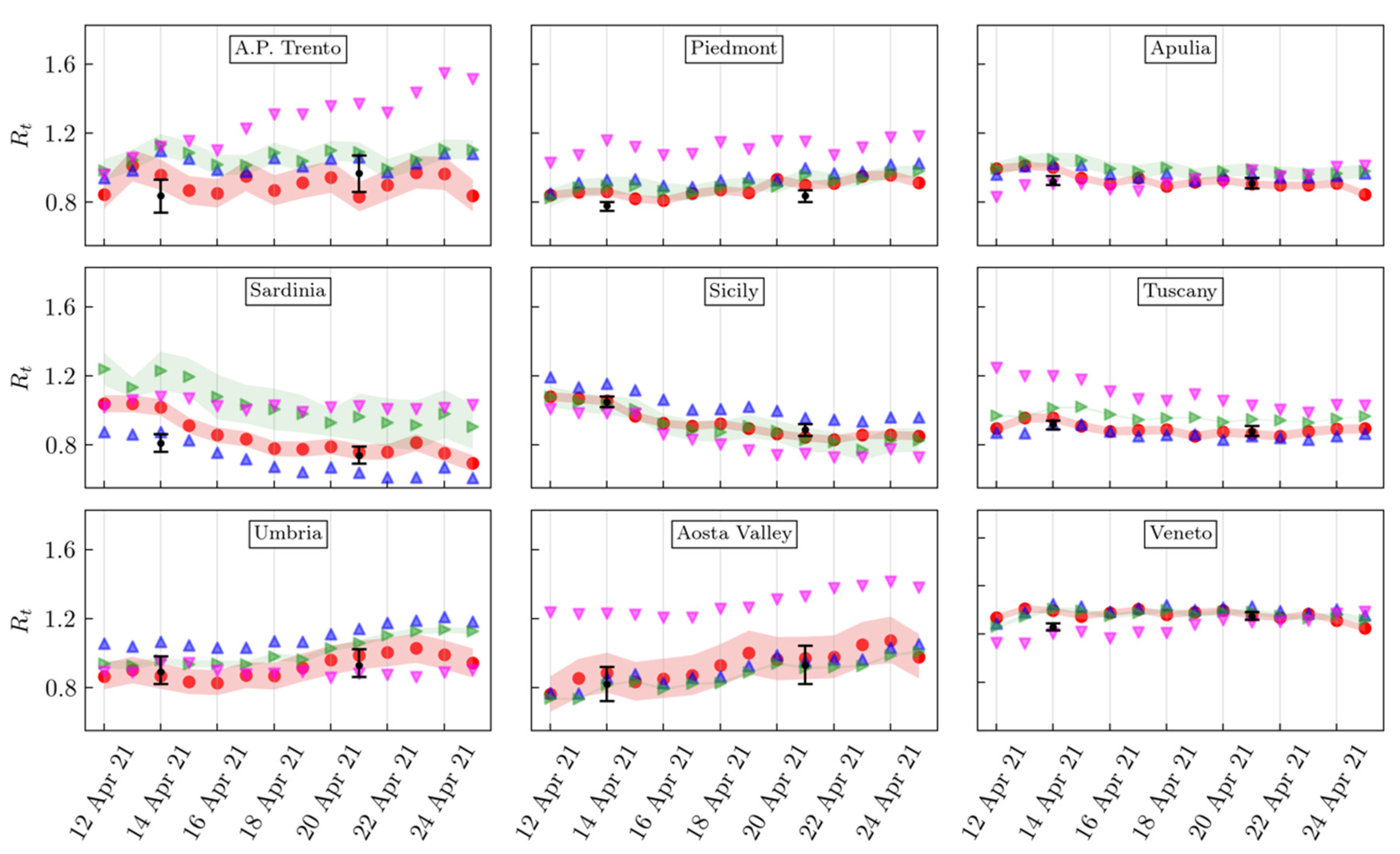
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhu, N.; Zhang, D.; Wang, W.; Li, X.; Yang, B.; Song, J.; Zhao, X.; Huang, B.; Shi, W.; Lu, R.; et al. A novel coronavirus from patients with pneumonia in China, 2019. N. Engl. J. Med. 2020, 382, 727–733. [Google Scholar] [CrossRef] [PubMed]
- WHO. Naming the Coronavirus Disease (COVID-19) and the Virus that Causes It. 2020. Available online: https://www.who.int/emergencies/diseases/novel-coronavirus-2019/technical-guidance/naming-the-coronavirus-disease-(COVID-2019)-and-the-virus-that-causes-it (accessed on 26 January 2022).
- Guan, W.-J.; Ni, Z.-Y.; Hu, Y.; Liang, W.-H.; Ou, C.-Q.; He, J.-X.; Liu, L.; Shan, H.; Lei, C.-L.; Hui, D.S.C.; et al. Clinical characteristics of coronavirus disease 2019 in China. N. Engl. J. Med. 2020, 382, 1708–1720. [Google Scholar] [CrossRef]
- Prime Minister Decree. Further Implementing Provisions of the Decree-Law 23 February 2020, No. 6, with Urgent Measures in Relation to Containment and Management of the Epidemiological Emergency from COVID-19, Applicable throughout the Country. (20A01605) G.U. General Series, no. 64 (In Italian). 11 March 2020. Available online: https://www.trovanorme.salute.gov.it/norme/dettaglioAtto?id=73643 (accessed on 26 January 2022).
- Gazzettaufficiale.it. Prime Minister Decree. 3 November 2020. Available online: https://www.gazzettaufficiale.it/eli/id/2020/11/04/20A06109/sg (accessed on 26 January 2022).
- Wallinga, J.; Lipsitch, M. How generation intervals shape the relationship between growth rates and reproductive numbers. Proc. R. Soc. B Boil. Sci. 2006, 274, 599–604. [Google Scholar] [CrossRef] [Green Version]
- Clement, J.C.; Ponnusamy, V.; Sriharipriya, K.C.; Nandakumar, R. A survey on mathematical, machine learning and deep learning models for COVID-19 transmission and diagnosis. IEEE Rev. Biomed. Eng. 2021, 15, 325–340. [Google Scholar]
- Shorten, C.; Khoshgoftaar, T.; Furht, B. Deep learning applications for COVID-19. J. Big Data 2021, 8, 1–54. [Google Scholar] [CrossRef]
- Zou, D.; Wang, L.; Xu, P.; Chen, J.; Zhang, W.; Gu, Q. Epidemic Model Guided Machine Learning for COVID-19 Forecasts in the United States. Medrxiv 2020. [Google Scholar] [CrossRef]
- Zhou, T.; Liu, Q.; Yang, Z.; Liao, J.; Yang, K.; Bai, W.; Lu, X.; Zhang, W. Preliminary prediction of the basic reproduction number of the Wuhan novel coronavirus 2019-nCoV. J. Evid.-Based Med. 2020, 13, 3–7. [Google Scholar] [CrossRef] [PubMed]
- Peirlinck, M.; Linka, K.; Costabal, F.S.; Bhattacharya, J.; Bendavid, E.; Ioannidis, J.P.; Kuhl, E. Visualizing the invisible: The effect of asymptomatic transmission on the outbreak dynamics of COVID-19. Comput. Methods Appl. Mech. Eng. 2020, 372, 113410. [Google Scholar] [CrossRef]
- Giuliani, D.; Dickson, M.; Espa, G.; Santi, F. Modelling and predicting the spatio-temporal spread of COVID-19 in Italy. BMC Infect. Dis. 2020, 20, 700. [Google Scholar] [CrossRef] [PubMed]
- Gatto, A.; Accarino, G.; Aloisi, V.; Immorlano, F.; Donato, F.; Aloisio, G. Limits of Compartmental Models and New Opportunities for Machine Learning: A Case Study to Forecast the Second Wave of COVID-19 Hospitalizations in Lombardy, Italy. Informatics 2021, 8, 57. [Google Scholar] [CrossRef]
- Zheng, N.; Du, S.; Wang, J.; Zhang, H.; Cui, W.; Kang, Z.; Yang, T.; Lou, B.; Chi, Y.; Long, H.; et al. Predicting COVID-19 in China Using Hybrid AI Model. IEEE Trans. Cybern. 2020, 50, 2891–2904. [Google Scholar] [CrossRef]
- Deng, Q. Dynamics and development of the COVID-19 epidemic in the United States: A compartmental model enhanced with deep learning techniques. J. Med. Internet Res. 2020, 22, e21173. [Google Scholar] [CrossRef]
- Abbasimehr, H.; Paki, R. Prediction of COVID-19 confirmed cases combining deep learning methods and bayesian optimization. Chaos Solitons Fractals 2021, 142, 110511. [Google Scholar] [CrossRef]
- Solanki, A.; Singh, T. COVID-19 Epidemic Analysis and Prediction Using Machine Learning Algorithms. In Studies in Systems, Decision and Control; Springer: Berlin/Heidelberg, Germany, 2021; pp. 57–78. [Google Scholar]
- Punn, N.; Sonbhadra, S.; Agarwal, S. COVID-19 epidemic analysis using machine learning and deep learning algorithms. medRxiv 2020. [Google Scholar] [CrossRef] [Green Version]
- Zeroual, A.; Harrou, F.; Dairi, A.; Sun, Y. Deep learning methods for forecasting COVID-19 time-series data: A comparative study. Chaos, Solitons Fractals 2020, 140, 110121. [Google Scholar] [CrossRef] [PubMed]
- Davahli, M.; Fiok, K.; Karwowski, W.; Aljuaid, A.; Taiar, R. Predicting the dynamics of the COVID-19 Pandemic in the United States using graph theory-based neural networks. Int. J. Environ. Res. Public Health 2021, 18, 3834. [Google Scholar] [CrossRef]
- Italian Civil Protection Department (ICPD). GitHub Data Repository. 2020. Available online: https://github.com/pcm-dpc/COVID-19 (accessed on 6 May 2021).
- Iss.it. Monitoraggio Settimanale—ISS. 2021. Available online: https://www.iss.it/monitoraggio-settimanale (accessed on 9 June 2021).
- Cori, A.; Ferguson, N.; Fraser, C.; Cauchemez, S. A new framework and software to estimate time-varying reproduction numbers during epidemics. Am. J. Epidemiol. 2013, 178, 1505–1512. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Iss.it. FAQ sul Calcolo del Rt—ISS. 2021. Available online: https://www.iss.it/coronavirus/-/asset_publisher/1SRKHcCJJQ7E/content/faq-sul-calcolo-del-rt (accessed on 9 June 2021).
- Cereda, D.; Manica, M.; Tirani, M.; Rovida, F.; Demicheli, V.; Ajelli, M.; Poletti, P.; Trentini, F.; Guzzetta, G.; Marziano, V.; et al. The early phase of the COVID-19 epidemic in Lombardy, Italy. Epidemics 2021, 37, 100528. [Google Scholar] [CrossRef]
- Wallinga, J.; Teunis, P. Different epidemic curves for severe acute respiratory syndrome reveal similar impacts of control measures. Am. J. Epidemiol. 2004, 160, 509–516. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fine, T. Feedforward Neural Network Methodology; Springer: New York, NY, USA, 2005. [Google Scholar]
- Kiranyaz, S.; Avci, O.; Abdeljaber, O.; Ince, T.; Gabbouj, M.; Inman, D. 1D convolutional neural networks and applications: A survey. Mech. Syst. Signal Process. 2021, 151, 107398. [Google Scholar] [CrossRef]
- Kiranyaz, S.; Ince, T.; Abdeljaber, O.; Avci, O.; Gabbouj, M. 1-D convolutional neural networks for signal processing applications. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brighton, UK, 12–17 May 2019. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Pascanu, R.; Mikolov, T.; Bengio, Y. On the difficulty of training recurrent neural networks. arXiv 2012, arXiv:1211.5063v2. [Google Scholar]
- Bengio, Y.; Simard, P.; Frasconi, P. Learning long-term dependencies with gradient descent is difficult. IEEE Trans. Neural Netw. 1994, 5, 157–166. [Google Scholar] [CrossRef]
- Keras. Keras: The Python Deep Learning API. Available online: https://keras.io/ (accessed on 26 January 2022).
- Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, G.S.; Davis, A.; Dean, J.; Devin, M.; et al. Tensorflow: Large-scale machine learning on heterogeneous distributed systems. arXiv 2016, arXiv:1603.04467. [Google Scholar]

| Model | 1-Layer FCNN | 2-Layers FCNN | 1-Layer 1D-CNN | 2-Layers 1D-CNN | 1-Layer LSTM | 2-Layers LSTM |
|---|---|---|---|---|---|---|
| #Units (per layer) | 42 | 21; 21 | - | - | 42 | 21; 21 |
| #Filters (per layer) | - | - | 21 | 10; 10 | - | - |
| Kernel size (per layer) | - | - | 1 | 1; 1 | - | - |
| Stride (per layer) | - | - | 1 | 1; 1 | - | - |
| Activation function (per layer) | ReLU | ReLU; ReLU | Sigmoid | ReLU; ReLU | Tanh | Tanh; Tanh |
| Weights Regularizer (per layer) | L1 (0.001) | L1 (0.01); L1 (0.01) | L1 (0.001) | L1 (0.001); L1 (0.001) | L1(0.001)/L2(0.01) | L1 (0.001)/L2(0.01); L1 (0.001)/L2(0.01) |
| Bias Regularizer (per layer) | L1 (0.001) | L1 (0.01); L1 (0.01) | L1 (0.001) | L1 (0.001); L1 (0.001) | L1(0.001)/L2(0.01) | L1(0.001)/L2(0.01); L1 (0.001)/L2(0.01) |
| Weights Initializer (per layer) | Uniform | Uniform; Uniform | Uniform | Uniform; Uniform | Glorot | Uniform; Uniform |
| Bias Initializer (per layer) | Uniform | Uniform; Uniform | Uniform | Uniform; Uniform | Glorot | Uniform; Uniform |
| Model | 1-Layer FCNN | 2-Layers FCNN | 1-Layer 1D-CNN | 2-Layers 1D-CNN | 1-Layer LSTM | 2-Layers LSTM |
|---|---|---|---|---|---|---|
| Batch Size | 4 | 4 | 2 | 2 | 4 | 4 |
| Learning Rate | 0.0001 | 0.0001 | 0.0001 | 0.0001 | 0.001 | 0.001 |
| Decay Rate | 0.9 | 0.9 | 0.9 | 0.9 | 0.9 | 0.9 |
| Loss Early Stopping (patience) | 50 | 50 | 50 | 50 | 50 | 50 |
| Validation Loss Early Stopping (patience) | 50 | 50 | 50 | 50 | 50 | 50 |
| Epochs | 4000 | 4000 | 4000 | 4000 | 4000 | 4000 |
| Shuffle | True | True | True | True | False | False |
| Region | Architecture | f(t + 1) RMSE | f(t + 2) RMSE | f(t + 3) RMSE | f(t + 4) RMSE | f(t + 5) RMSE | f(t + 6) RMSE | f(t + 7) RMSE |
|---|---|---|---|---|---|---|---|---|
| Abruzzo | 1-L FCNN | 0.071 | 0.113 | 0.144 | 0.172 | 0.221 | 0.249 | 0.252 |
| 1-L 1D CNN | 0.08 | 0.104 | 0.083 | 0.109 | 0.095 | 0.11 | 0.106 | |
| 2-Ls 1D CNN | 0.107 | 0.113 | 0.119 | 0.114 | 0.12 | 0.121 | 0.117 | |
| Ensemble | 0.085 | 0.109 | 0.113 | 0.131 | 0.142 | 0.157 | 0.156 | |
| Aosta Valley | 1-L FCNN | 0.101 | 0.113 | 0.137 | 0.155 | 0.163 | 0.158 | 0.149 |
| 1-L 1D CNN | 0.137 | 0.128 | 0.151 | 0.161 | 0.167 | 0.163 | 0.162 | |
| 2-Ls 1D CNN | 0.137 | 0.13 | 0.144 | 0.163 | 0.175 | 0.172 | 0.177 | |
| Ensemble | 0.119 | 0.121 | 0.142 | 0.159 | 0.168 | 0.164 | 0.162 | |
| Apulia | 1-L FCNN | 0.043 | 0.059 | 0.065 | 0.075 | 0.083 | 0.086 | 0.09 |
| 2-Ls 1D CNN | 0.098 | 0.094 | 0.098 | 0.098 | 0.107 | 0.105 | 0.111 | |
| 1-L 1D CNN | 0.094 | 0.101 | 0.081 | 0.101 | 0.11 | 0.115 | 0.115 | |
| Ensemble | 0.075 | 0.081 | 0.079 | 0.089 | 0.098 | 0.1 | 0.104 | |
| Basilicata | 1-L LSTM | 0.136 | 0.134 | 0.132 | 0.137 | 0.144 | 0.166 | 0.179 |
| 1-L FCNN | 0.066 | 0.095 | 0.115 | 0.143 | 0.172 | 0.206 | 0.217 | |
| 1-L 1D CNN | 0.066 | 0.091 | 0.105 | 0.124 | 0.138 | 0.165 | 0.178 | |
| Ensemble | 0.078 | 0.101 | 0.115 | 0.134 | 0.149 | 0.176 | 0.187 | |
| Calabria | 1-L LSTM | 0.134 | 0.159 | 0.177 | 0.192 | 0.209 | 0.222 | 0.225 |
| 1-L FCNN | 0.064 | 0.096 | 0.119 | 0.139 | 0.163 | 0.187 | 0.187 | |
| 2-Ls 1D CNN | 0.12 | 0.12 | 0.11 | 0.107 | 0.107 | 0.113 | 0.105 | |
| Ensemble | 0.105 | 0.124 | 0.134 | 0.144 | 0.158 | 0.171 | 0.169 | |
| Campania | 1-L FCNN | 0.032 | 0.052 | 0.065 | 0.072 | 0.081 | 0.088 | 0.094 |
| 2-Ls 1D CNN | 0.032 | 0.055 | 0.067 | 0.072 | 0.08 | 0.091 | 0.093 | |
| 1-L 1D CNN | 0.032 | 0.054 | 0.065 | 0.073 | 0.083 | 0.093 | 0.098 | |
| Ensemble | 0.031 | 0.053 | 0.066 | 0.072 | 0.081 | 0.091 | 0.095 | |
| Emilia-Romagna | 1-L FCNN | 0.027 | 0.038 | 0.043 | 0.049 | 0.06 | 0.069 | 0.077 |
| 2-Ls 1D CNN | 0.066 | 0.09 | 0.112 | 0.134 | 0.16 | 0.18 | 0.198 | |
| 1-L 1D CNN | 0.025 | 0.039 | 0.043 | 0.057 | 0.073 | 0.084 | 0.093 | |
| Ensemble | 0.031 | 0.042 | 0.053 | 0.065 | 0.081 | 0.095 | 0.107 | |
| Friuli Venezia Giulia | 1-L FCNN | 0.072 | 0.108 | 0.149 | 0.178 | 0.209 | 0.229 | 0.237 |
| 1-L 1D CNN | 0.074 | 0.108 | 0.136 | 0.18 | 0.207 | 0.214 | 0.238 | |
| 2-Ls 1D CNN | 0.15 | 0.179 | 0.2 | 0.246 | 0.285 | 0.286 | 0.309 | |
| Ensemble | 0.096 | 0.13 | 0.161 | 0.2 | 0.233 | 0.243 | 0.261 | |
| Lazio | 1-L FCNN | 0.026 | 0.04 | 0.052 | 0.062 | 0.074 | 0.085 | 0.092 |
| 2-Ls 1D CNN | 0.167 | 0.168 | 0.173 | 0.173 | 0.165 | 0.163 | 0.167 | |
| 1-L 1D CNN | 0.115 | 0.139 | 0.127 | 0.108 | 0.123 | 0.112 | 0.124 | |
| Ensemble | 0.098 | 0.105 | 0.103 | 0.098 | 0.1 | 0.096 | 0.103 | |
| Liguria | 1-L FCNN | 0.061 | 0.083 | 0.104 | 0.118 | 0.131 | 0.148 | 0.162 |
| 1-L 1D CNN | 0.035 | 0.048 | 0.065 | 0.079 | 0.092 | 0.102 | 0.11 | |
| 2-Ls 1D CNN | 0.039 | 0.067 | 0.077 | 0.089 | 0.101 | 0.115 | 0.126 | |
| Ensemble | 0.04 | 0.061 | 0.078 | 0.092 | 0.106 | 0.119 | 0.13 | |
| Lombardy | 1-L FCNN | 0.041 | 0.059 | 0.077 | 0.088 | 0.099 | 0.108 | 0.117 |
| 1-L 1D CNN | 0.035 | 0.048 | 0.061 | 0.069 | 0.083 | 0.096 | 0.106 | |
| 2-Ls 1D CNN | 0.084 | 0.093 | 0.101 | 0.109 | 0.118 | 0.129 | 0.138 | |
| Ensemble | 0.046 | 0.062 | 0.077 | 0.085 | 0.097 | 0.108 | 0.118 | |
| Marche | 1-L FCNN | 0.067 | 0.101 | 0.137 | 0.156 | 0.181 | 0.207 | 0.22 |
| 2-Ls 1D CNN | 0.185 | 0.177 | 0.151 | 0.144 | 0.155 | 0.145 | 0.149 | |
| 2-Ls FCNN | 0.045 | 0.064 | 0.078 | 0.1 | 0.117 | 0.128 | 0.137 | |
| Ensemble | 0.091 | 0.107 | 0.118 | 0.131 | 0.148 | 0.156 | 0.164 | |
| Molise | 1-L LSTM | 0.097 | 0.112 | 0.128 | 0.133 | 0.142 | 0.144 | 0.15 |
| 1-L FCNN | 0.091 | 0.098 | 0.121 | 0.12 | 0.123 | 0.118 | 0.136 | |
| 1-L 1D CNN | 0.092 | 0.119 | 0.136 | 0.146 | 0.155 | 0.167 | 0.18 | |
| Ensemble | 0.093 | 0.108 | 0.127 | 0.131 | 0.139 | 0.141 | 0.154 | |
| Piedmont | 1-L FCNN | 0.061 | 0.083 | 0.092 | 0.118 | 0.12 | 0.136 | 0.151 |
| 1-L 1D CNN | 0.037 | 0.051 | 0.065 | 0.071 | 0.079 | 0.086 | 0.092 | |
| 2-Ls 1D CNN | 0.069 | 0.087 | 0.101 | 0.115 | 0.131 | 0.14 | 0.144 | |
| Ensemble | 0.045 | 0.063 | 0.074 | 0.088 | 0.099 | 0.109 | 0.116 | |
| Sardinia | 1-L FCNN | 0.158 | 0.213 | 0.233 | 0.252 | 0.286 | 0.315 | 0.346 |
| 1-L 1D CNN | 0.07 | 0.093 | 0.122 | 0.147 | 0.175 | 0.199 | 0.217 | |
| 2-Ls 1D CNN | 0.091 | 0.119 | 0.154 | 0.182 | 0.205 | 0.234 | 0.261 | |
| Ensemble | 0.08 | 0.123 | 0.156 | 0.182 | 0.212 | 0.24 | 0.266 | |
| Sicily | 1-L FCNN | 0.054 | 0.076 | 0.092 | 0.112 | 0.118 | 0.129 | 0.128 |
| 2-Ls 1D CNN | 0.188 | 0.227 | 0.231 | 0.232 | 0.226 | 0.219 | 0.224 | |
| 1-L 1D CNN | 0.068 | 0.052 | 0.055 | 0.057 | 0.06 | 0.065 | 0.079 | |
| Ensemble | 0.098 | 0.108 | 0.115 | 0.119 | 0.117 | 0.116 | 0.108 | |
| A.P. Bolzano | 1-L FCNN | 0.08 | 0.137 | 0.173 | 0.184 | 0.207 | 0.215 | 0.232 |
| 2-Ls 1D CNN | 0.141 | 0.229 | 0.298 | 0.367 | 0.406 | 0.455 | 0.462 | |
| 2-Ls FCNN | 0.172 | 0.182 | 0.191 | 0.197 | 0.205 | 0.211 | 0.217 | |
| Ensemble | 0.127 | 0.18 | 0.218 | 0.245 | 0.268 | 0.288 | 0.298 | |
| A.P. Trento | 1-L FCNN | 0.077 | 0.097 | 0.113 | 0.13 | 0.141 | 0.154 | 0.158 |
| 2-Ls 1D CNN | 0.21 | 0.238 | 0.264 | 0.294 | 0.309 | 0.332 | 0.353 | |
| 1-L 1D CNN | 0.081 | 0.103 | 0.127 | 0.145 | 0.171 | 0.184 | 0.196 | |
| Ensemble | 0.111 | 0.136 | 0.159 | 0.181 | 0.199 | 0.218 | 0.23 | |
| Tuscany | 1-L FCNN | 0.048 | 0.053 | 0.057 | 0.063 | 0.072 | 0.076 | 0.08 |
| 2-Ls 1D CNN | 0.05 | 0.056 | 0.073 | 0.082 | 0.105 | 0.085 | 0.088 | |
| 1-L 1D CNN | 0.048 | 0.051 | 0.055 | 0.072 | 0.067 | 0.076 | 0.08 | |
| Ensemble | 0.03 | 0.041 | 0.047 | 0.056 | 0.067 | 0.067 | 0.069 | |
| Umbria | 1-L FCNN | 0.078 | 0.128 | 0.16 | 0.178 | 0.224 | 0.234 | 0.249 |
| 2-Ls 1D CNN | 0.119 | 0.122 | 0.119 | 0.121 | 0.121 | 0.119 | 0.116 | |
| 1-L LSTM | 0.365 | 0.391 | 0.411 | 0.415 | 0.435 | 0.433 | 0.434 | |
| Ensemble | 0.168 | 0.199 | 0.217 | 0.227 | 0.246 | 0.248 | 0.254 | |
| Veneto | 1-L FCNN | 0.066 | 0.085 | 0.106 | 0.134 | 0.155 | 0.175 | 0.185 |
| 2-Ls 1D CNN | 0.143 | 0.145 | 0.156 | 0.161 | 0.17 | 0.181 | 0.19 | |
| 1-L 1D CNN | 0.087 | 0.094 | 0.1 | 0.108 | 0.125 | 0.135 | 0.141 | |
| Ensemble | 0.095 | 0.105 | 0.119 | 0.132 | 0.149 | 0.161 | 0.168 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gatto, A.; Aloisi, V.; Accarino, G.; Immorlano, F.; Chiarelli, M.; Aloisio, G. An Artificial Neural Network-Based Approach for Predicting the COVID-19 Daily Effective Reproduction Number Rt in Italy. AI 2022, 3, 146-163. https://doi.org/10.3390/ai3010009
Gatto A, Aloisi V, Accarino G, Immorlano F, Chiarelli M, Aloisio G. An Artificial Neural Network-Based Approach for Predicting the COVID-19 Daily Effective Reproduction Number Rt in Italy. AI. 2022; 3(1):146-163. https://doi.org/10.3390/ai3010009
Chicago/Turabian StyleGatto, Andrea, Valeria Aloisi, Gabriele Accarino, Francesco Immorlano, Marco Chiarelli, and Giovanni Aloisio. 2022. "An Artificial Neural Network-Based Approach for Predicting the COVID-19 Daily Effective Reproduction Number Rt in Italy" AI 3, no. 1: 146-163. https://doi.org/10.3390/ai3010009
APA StyleGatto, A., Aloisi, V., Accarino, G., Immorlano, F., Chiarelli, M., & Aloisio, G. (2022). An Artificial Neural Network-Based Approach for Predicting the COVID-19 Daily Effective Reproduction Number Rt in Italy. AI, 3(1), 146-163. https://doi.org/10.3390/ai3010009






