Hybrid Machine Learning Models for Forecasting Surgical Case Volumes at a Hospital
Abstract
:1. Introduction
2. Materials and Methods
2.1. Model Building
2.1.1. SARIMA Model
2.1.2. SVR Model
2.1.3. MLP Model
2.1.4. LSTM Model
2.1.5. Hybrid Model
- SARIMA–SVR;
- SVR–SARIMA;
- SARIMA–MLP;
- MLP–SARIMA;
- SARIMA–LSTM;
- LSTM–SARIMA;
- SVR–MLP;
- MLP–SVR;
- SVR–LSTM;
- LSTM–SVR;
- MLP–LSTM;
- LSTM–MLP.
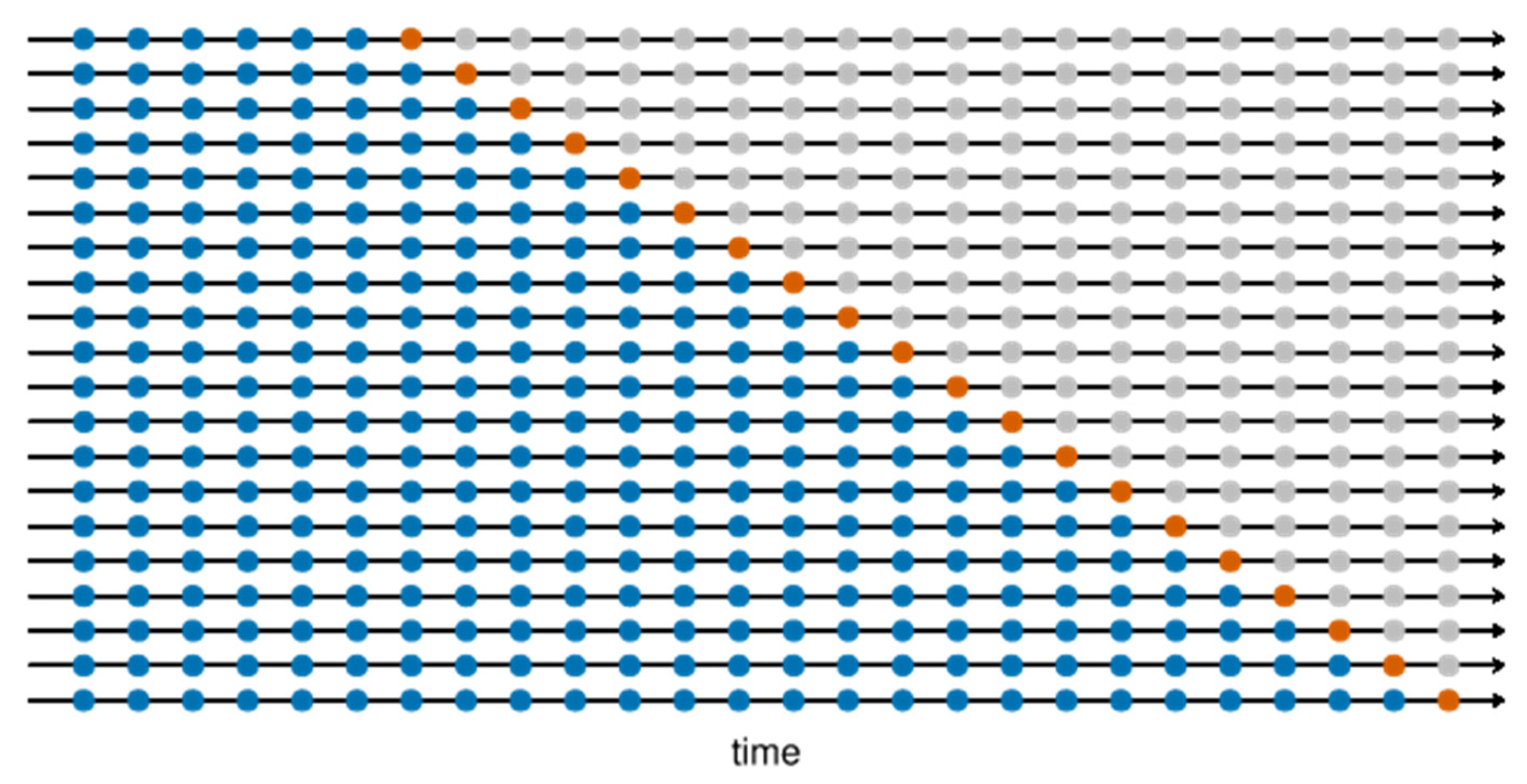
2.2. Model Evaluation
3. Results
3.1. Model Results
3.2. Accuracy Comparison
4. Discussion
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Taylor, R.A.; Pare, J.R.; Venkatesh, A.K.; Mowafi, H.; Melnick, E.R.; Fleischman, W.; Hall, M.K. Prediction of In-hospital Mortality in Emergency Department Patients With Sepsis: A Local Big Data-Driven, Machine Learning Approach. Acad. Emerg. Med. 2016, 23, 269–278. [Google Scholar] [CrossRef] [Green Version]
- Perng, J.W.; Kao, I.H.; Kung, C.T.; Hung, S.C.; Lai, Y.H.; Su, C.M. Mortality Prediction of Septic Patients in the Emergency Department Based on Machine Learning. J. Clin. Med. 2019, 8, 1906. [Google Scholar] [CrossRef] [Green Version]
- Raita, Y.; Goto, T.; Faridi, M.K.; Brown, D.F.M.; Camargo, C.A., Jr.; Hasegawa, K. Emergency department triage prediction of clinical outcomes using machine learning models. Crit. Care 2019, 23, 64. [Google Scholar] [CrossRef] [Green Version]
- Lucini, F.R.; Reis, M.A.d.; Silveira, G.J.C.d.; Fogliatto, F.S.; Anzanello, M.J.; Andrioli, G.G.; Nicolaidis, R.; Beltrame, R.C.F.; Neyeloff, J.L.; Schaan, B.D.A. Man vs. machine: Predicting hospital bed demand from an emergency department. PLoS ONE 2020, 15, e0237937. [Google Scholar] [CrossRef]
- Lin, A.X.; Ho, A.F.W.; Cheong, K.H.; Li, Z.; Cai, W.; Chee, M.L.; Ng, Y.Y.; Xiao, X.; Ong, M.E.H. Leveraging Machine Learning Techniques and Engineering of Multi-Nature Features for National Daily Regional Ambulance Demand Prediction. Int. J. Environ. Res. Public Health 2020, 17, 4179. [Google Scholar] [CrossRef] [PubMed]
- Chen, A.Y.; Lu, T.-Y. A GIS-Based Demand Forecast Using Machine Learning for Emergency Medical Services. In Computing in Civil and Building Engineering (2014); American Society of Civil Engineers: Orlando, FL, USA, 2014; pp. 1634–1641. [Google Scholar]
- Chan, E.W.; Taylor, S.E.; Marriott, J.; Barger, B. An intervention to encourage ambulance paramedics to bring patients’ own medications to the ED: Impact on medications brought in and prescribing errors. Emerg. Med. Australas 2010, 22, 151–158. [Google Scholar] [CrossRef] [PubMed]
- Ekström, A.; Kurland, L.; Farrokhnia, N.; Castrén, M.; Nordberg, M. Forecasting emergency department visits using internet data. Ann. Emerg. Med. 2015, 65, 436–442.e431. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Farmer, R.D.; Emami, J. Models for forecasting hospital bed requirements in the acute sector. J. Epidemiol. Community Health 1990, 44, 307–312. [Google Scholar] [CrossRef] [Green Version]
- Jones, S.A.; Joy, M.P.; Pearson, J. Forecasting demand of emergency care. Health Care Manag. Sci. 2002, 5, 297–305. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schweigler, L.M.; Desmond, J.S.; McCarthy, M.L.; Bukowski, K.J.; Ionides, E.L.; Younger, J.G. Forecasting models of emergency department crowding. Acad. Emerg. Med. 2009, 16, 301–308. [Google Scholar] [CrossRef] [PubMed]
- Zhou, L.; Zhao, P.; Wu, D.; Cheng, C.; Huang, H. Time series model for forecasting the number of new admission inpatients. BMC Med. Inform. Decis. Mak. 2018, 18, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Zinouri, N.; Taaffe, K.M.; Neyens, D.M. Modelling and forecasting daily surgical case volume using time series analysis. Health Syst. 2018, 7, 111–119. [Google Scholar] [CrossRef] [PubMed]
- Purwanto; Eswaran, C.; Logeswaran, R. An enhanced hybrid method for time series prediction using linear and neural network models. Appl. Intell. 2012, 37, 511–519. [Google Scholar] [CrossRef]
- Yolcu, U.; Egrioglu, E.; Aladag, C.H. A new linear & nonlinear artificial neural network model for time series forecasting. Decis. Support Syst. 2013, 54, 1340–1347. [Google Scholar] [CrossRef]
- Gupta, D.; Pratama, M.; Ma, Z.; Li, J.; Prasad, M. Financial time series forecasting using twin support vector regression. PLoS ONE 2019, 14, e0211402. [Google Scholar] [CrossRef] [PubMed]
- Tsai, M.-C.; Cheng, C.-H.; Tsai, M.-I.; Shiu, H.-Y. Forecasting leading industry stock prices based on a hybrid time-series forecast model. PLoS ONE 2019, 13, e0209922. [Google Scholar] [CrossRef] [Green Version]
- Zhang, G.P. Time series forecasting using a hybrid ARIMA and neural network model. Neurocomputing 2003, 50, 159–175. [Google Scholar] [CrossRef]
- Golmohammadi, D. Predicting hospital admissions to reduce emergency department boarding. Int. J. Prod. Econ. 2016, 182, 535–544. [Google Scholar] [CrossRef]
- Guo, Y.; Feng, Y.; Qu, F.; Zhang, L.; Yan, B.; Lv, J. Prediction of hepatitis E using machine learning models. PLoS ONE 2020, 15, e0237750. [Google Scholar] [CrossRef]
- Volkova, S.; Ayton, E.; Porterfield, K.; Corley, C.D. Forecasting influenza-like illness dynamics for military populations using neural networks and social media. PLoS ONE 2017, 12, e0188941. [Google Scholar] [CrossRef] [Green Version]
- Zou, J.-J.; Jiang, G.-F.; Xie, X.-X.; Huang, J.; Yang, X.-B. Application of a combined model with seasonal autoregressive integrated moving average and support vector regression in forecasting hand-foot-mouth disease incidence in Wuhan, China. Medicine 2019, 98, e14195. [Google Scholar] [CrossRef]
- Wang, H.; Tian, C.W.; Wang, W.M.; Luo, X.M. Time-series analysis of tuberculosis from 2005 to 2017 in China. Epidemiol. Infect. 2018, 146, 935–939. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.-w.; Shen, Z.-z.; Jiang, Y. Comparison of autoregressive integrated moving average model and generalised regression neural network model for prediction of haemorrhagic fever with renal syndrome in China: A time-series study. BMJ Open 2019, 9, e025773. [Google Scholar] [CrossRef] [Green Version]
- Taskaya-Temizel, T.; Casey, M.C. A comparative study of autoregressive neural network hybrids. Neural Netw. 2005, 18, 781–789. [Google Scholar] [CrossRef] [Green Version]
- Boyle, J.; Jessup, M.; Crilly, J.; Green, D.; Lind, J.; Wallis, M.; Miller, P.; Fitzgerald, G. Predicting emergency department admissions. Emerg. Med. J. 2012, 29, 358. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Litvak, E.; Long, M.C. Cost and quality under managed care: Irreconcilable differences. Am. J. Manag. Care 2000, 6, 305–312. [Google Scholar] [PubMed]
- Tiwari, V.; Furman, W.R.; Sandberg, W.S. Predicting Case Volume from the Accumulating Elective Operating Room Schedule Facilitates Staffing Improvements. Anesthesiology 2014, 121, 171–183. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Syntetos, A.A.; Boylan, J.E.; Croston, J.D. On the categorization of demand patterns. J. Oper. Res. Soc. 2005, 56, 495–503. [Google Scholar] [CrossRef]
- Hyndman, R.J.; Athanasopoulos, G. Forecasting: Principles and Practice, 3rd ed.; OTexts: Melbourne, VIC, Australia, 2021. [Google Scholar]
- Hyndman, R.J.; Khandakar, Y. Automatic Time Series Forecasting: The forecast Package for R. J. Stat. Softw. 2008, 27, 22. [Google Scholar] [CrossRef] [Green Version]
- Chollet, F.; Allaire, J.J. Deep Learning with R; Manning Publications: Shelter Island, NY, USA, 2018; p. 360. [Google Scholar]
- Yu, G.; Feng, H.; Feng, S.; Zhao, J.; Xu, J. Structure of the SARIMA–NNAR combined model. PLoS ONE 2021. [Google Scholar] [CrossRef]
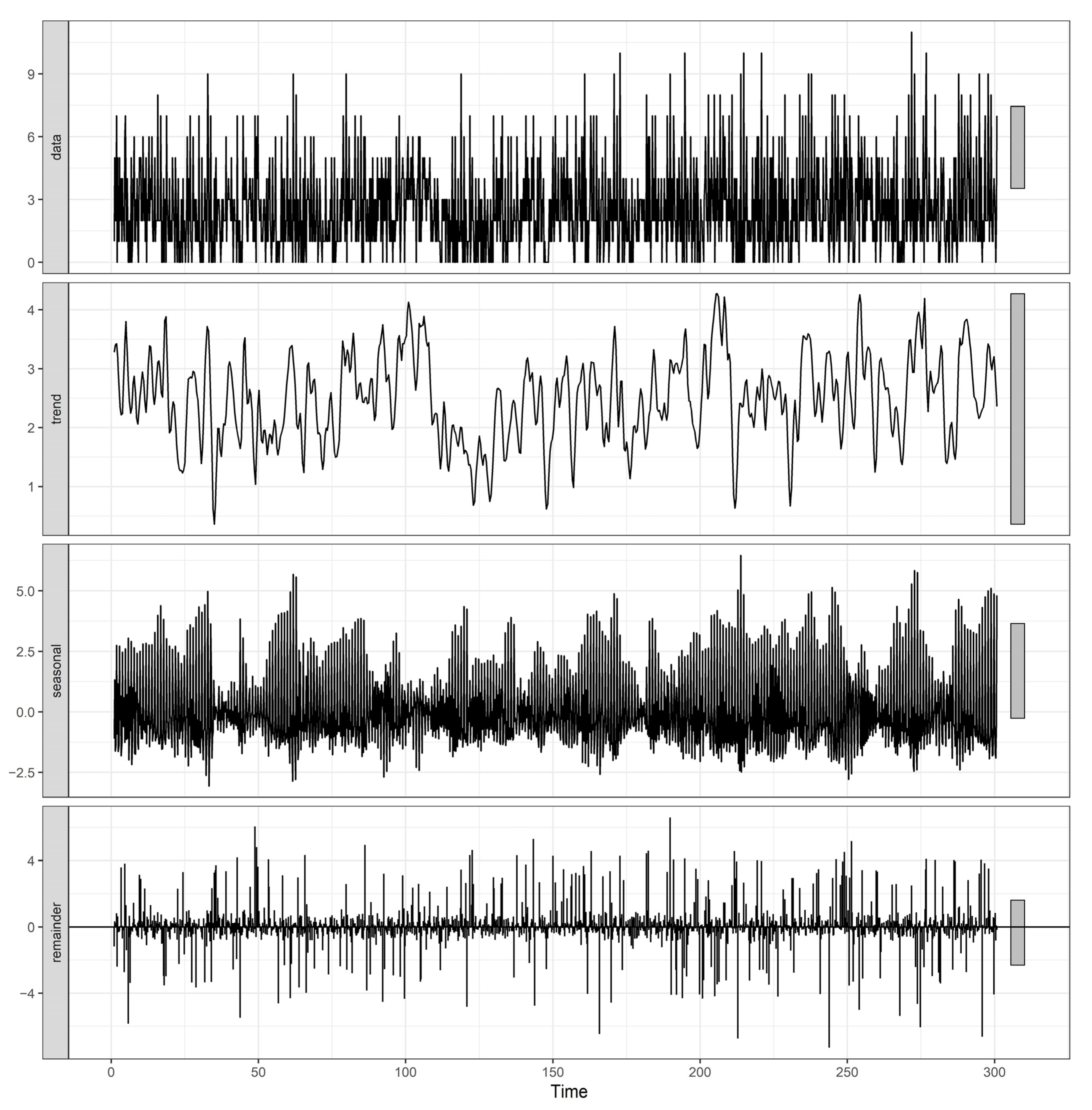
- Cleveland, R.B.; Cleveland, W.S.; McRae, J.E.; Terpenning, I. STL: A seasonal-trend decomposition. J. Off. Stat. 1990, 6, 3–73. [Google Scholar]




| Surgical Units | Percentage Share of Surgeries (%) | |||||
|---|---|---|---|---|---|---|
| Monday | Tuesday | Wednesday | Thursday | Friday | Overall | |
| EN | 0.77% | 3.49% | 1.02% | 2.87% | 1.60% | 9.75% |
| GA | 3.52% | 4.24% | 3.96% | 3.84% | 12.10% | 27.65% |
| KA | 0.51% | 1.66% | 0.73% | 0.74% | 0.52% | 4.16% |
| UR | 9.77% | 3.53% | 13.81% | 4.22% | 4.99% | 36.31% |
| BA | 3.64% | 3.53% | 2.69% | 6.77% | 5.49% | 22.13% |
| Total | 18.21% | 16.45% | 22.21% | 18.44% | 24.70% | 100.00% |
| Surgical Units | Elective Patients | Emergency Patients | Total Patients | % of Emergency Patients |
|---|---|---|---|---|
| EN | 1705 | 65 | 1770 | 3.67% |
| GA | 3793 | 1225 | 5018 | 24.41% |
| KA | 510 | 245 | 755 | 32.45% |
| UR | 6232 | 358 | 6590 | 5.43% |
| BA | 3639 | 377 | 4016 | 9.39% |
| Total | 15,879 | 2270 | 18,149 | 12.51% |
| Models | EN | GA | KA | UR | BA | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| MAE | RMSE | MAE | RMSE | MAE | RMSE | MAE | RMSE | MAE | RMSE | |
| Baseline | 0.677 | 0.971 | 1.760 | 2.394 | 0.543 | 0.866 | 1.173 | 1.585 | 1.197 | 1.607 |
| SARIMA | 0.587 | 0.894 | 1.393 | 1.787 | 0.323 | 0.661 | 0.997 | 1.290 | 0.880 | 1.208 |
| SVR | 1.340 | 2.759 | 2.580 | 3.772 | 0.880 | 1.939 | 2.140 | 3.632 | 1.417 | 2.410 |
| MLP | 0.613 | 0.852 | 1.620 | 2.254 | 0.327 | 0.663 | 1.090 | 1.411 | 0.913 | 1.238 |
| LSTM | 0.670 | 0.998 | 1.347 | 1.806 | 0.303 | 0.646 | 1.030 | 1.360 | 0.890 | 1.218 |
| SARIMA–SVR | 0.730 | 1.193 | 3.063 | 5.749 | 0.613 | 1.317 | 2.927 | 7.046 | 1.640 | 2.725 |
| SVR–SARIMA | 0.980 | 1.701 | 2.703 | 4.657 | 0.863 | 2.003 | 2.657 | 4.978 | 1.860 | 3.733 |
| SARIMA–MLP | 0.517 | 0.810 | 1.413 | 1.800 | 0.343 | 0.661 | 1.007 | 1.332 | 0.873 | 1.197 |
| MLP–SARIMA | 0.597 | 0.889 | 1.673 | 2.205 | 0.323 | 0.646 | 1.040 | 1.347 | 0.880 | 1.200 |
| SARIMA–LSTM | 0.663 | 0.995 | 1.380 | 1.780 | 0.300 | 0.643 | 0.963 | 1.295 | 0.883 | 1.221 |
| LSTM–SARIMA | 0.583 | 0.896 | 1.360 | 1.791 | 0.310 | 0.651 | 0.980 | 1.288 | 0.827 | 1.134 |
| SVR–MLP | 0.883 | 1.432 | 3.037 | 6.211 | 0.707 | 1.554 | 2.013 | 2.920 | 2.077 | 3.894 |
| MLP–SVR | 1.180 | 2.371 | 2.703 | 4.234 | 0.837 | 1.825 | 2.410 | 4.267 | 1.863 | 3.349 |
| SVR–LSTM | 1.083 | 1.857 | 2.353 | 3.804 | 1.110 | 2.937 | 2.153 | 3.503 | 1.867 | 3.271 |
| LSTM–SVR | 1.107 | 3.474 | 2.670 | 4.684 | 0.737 | 1.731 | 1.957 | 2.854 | 1.723 | 3.015 |
| MLP–LSTM | 0.637 | 0.964 | 1.587 | 2.117 | 0.303 | 0.646 | 1.000 | 1.306 | 0.973 | 1.349 |
| LSTM–MLP | 0.633 | 0.876 | 1.477 | 1.972 | 0.333 | 0.663 | 1.010 | 1.310 | 0.887 | 1.200 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aravazhi, A. Hybrid Machine Learning Models for Forecasting Surgical Case Volumes at a Hospital. AI 2021, 2, 512-526. https://doi.org/10.3390/ai2040032
Aravazhi A. Hybrid Machine Learning Models for Forecasting Surgical Case Volumes at a Hospital. AI. 2021; 2(4):512-526. https://doi.org/10.3390/ai2040032
Chicago/Turabian StyleAravazhi, Agaraoli. 2021. "Hybrid Machine Learning Models for Forecasting Surgical Case Volumes at a Hospital" AI 2, no. 4: 512-526. https://doi.org/10.3390/ai2040032
APA StyleAravazhi, A. (2021). Hybrid Machine Learning Models for Forecasting Surgical Case Volumes at a Hospital. AI, 2(4), 512-526. https://doi.org/10.3390/ai2040032






