Shape Optimization of a Wooden Baseball Bat Using Parametric Modeling and Genetic Algorithms
Abstract
:1. Introduction
2. Materials and Methods
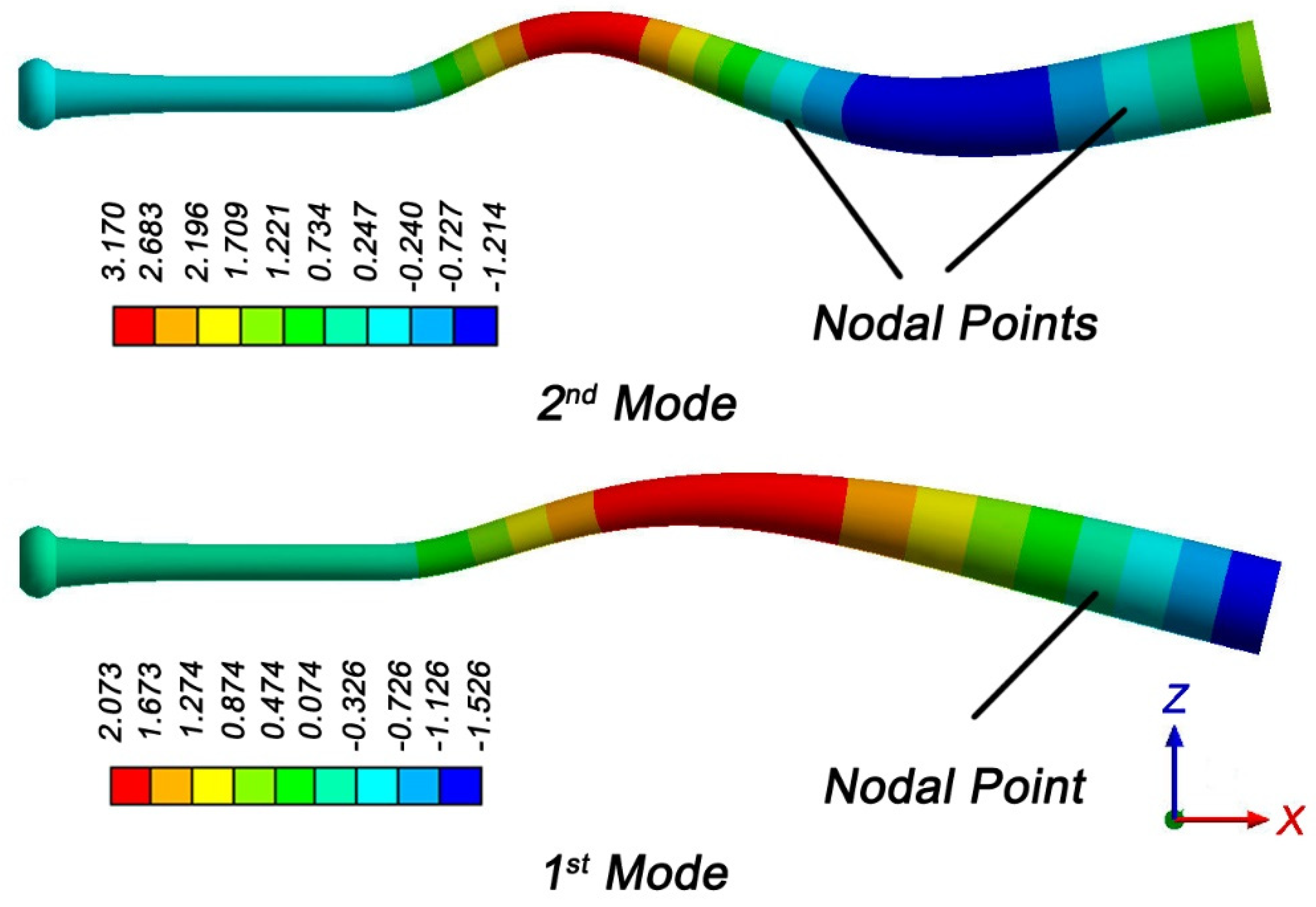
2.1. Nodal Points
2.2. Center of Percussion
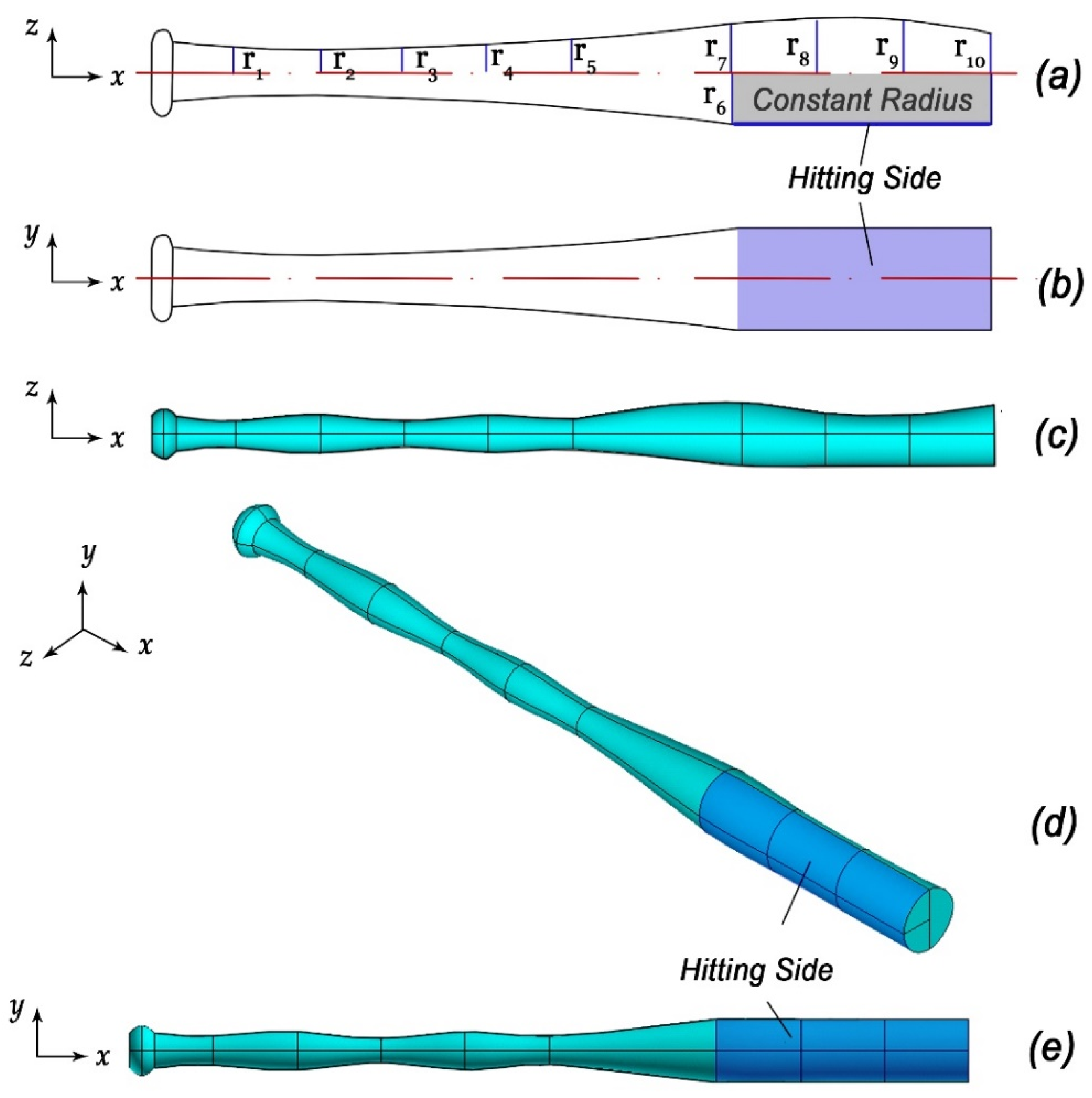
2.3. Parametric Design
2.4. Finite Element Modeling
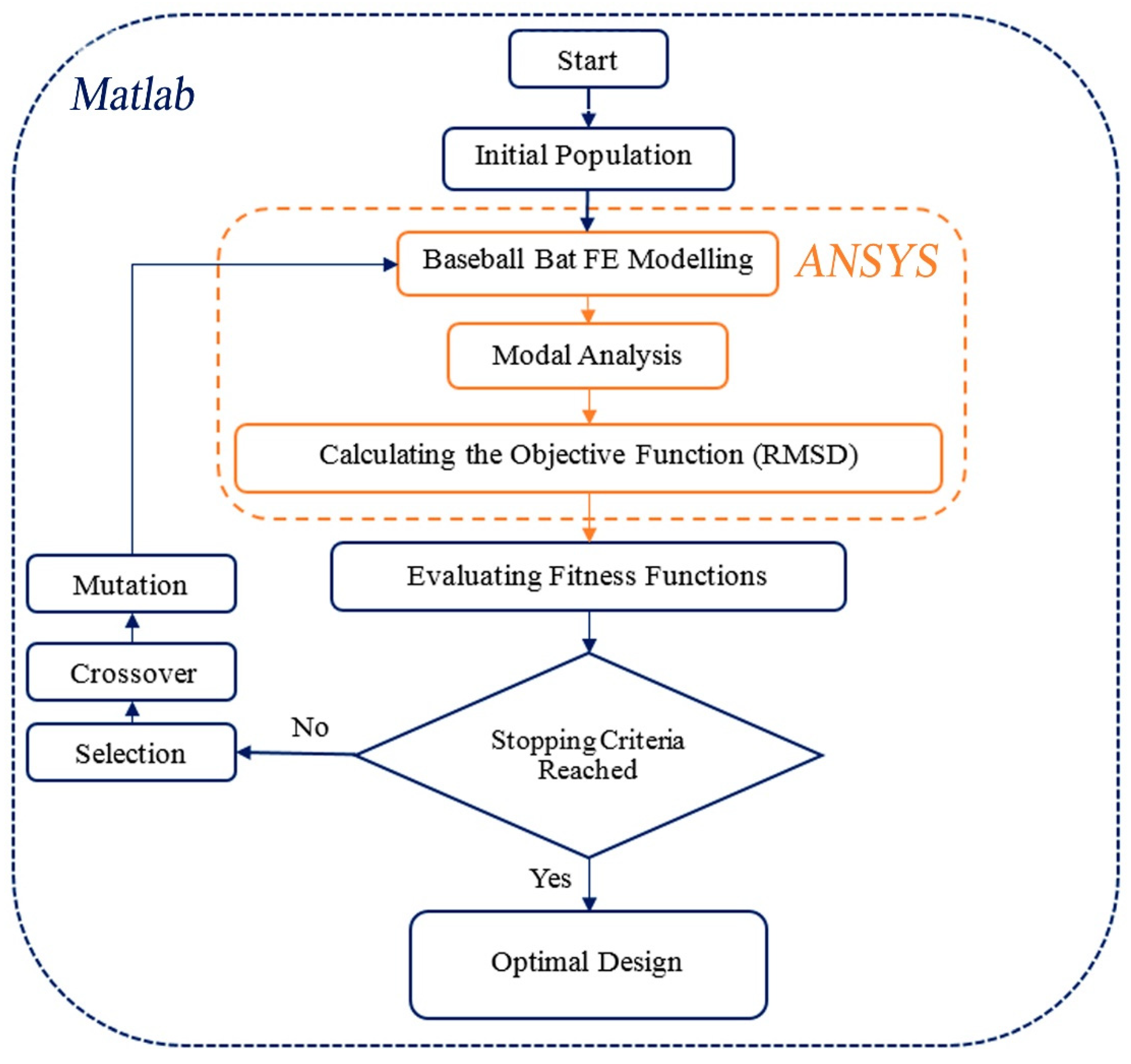
3. Optimization of the Performance of the Baseball Bat
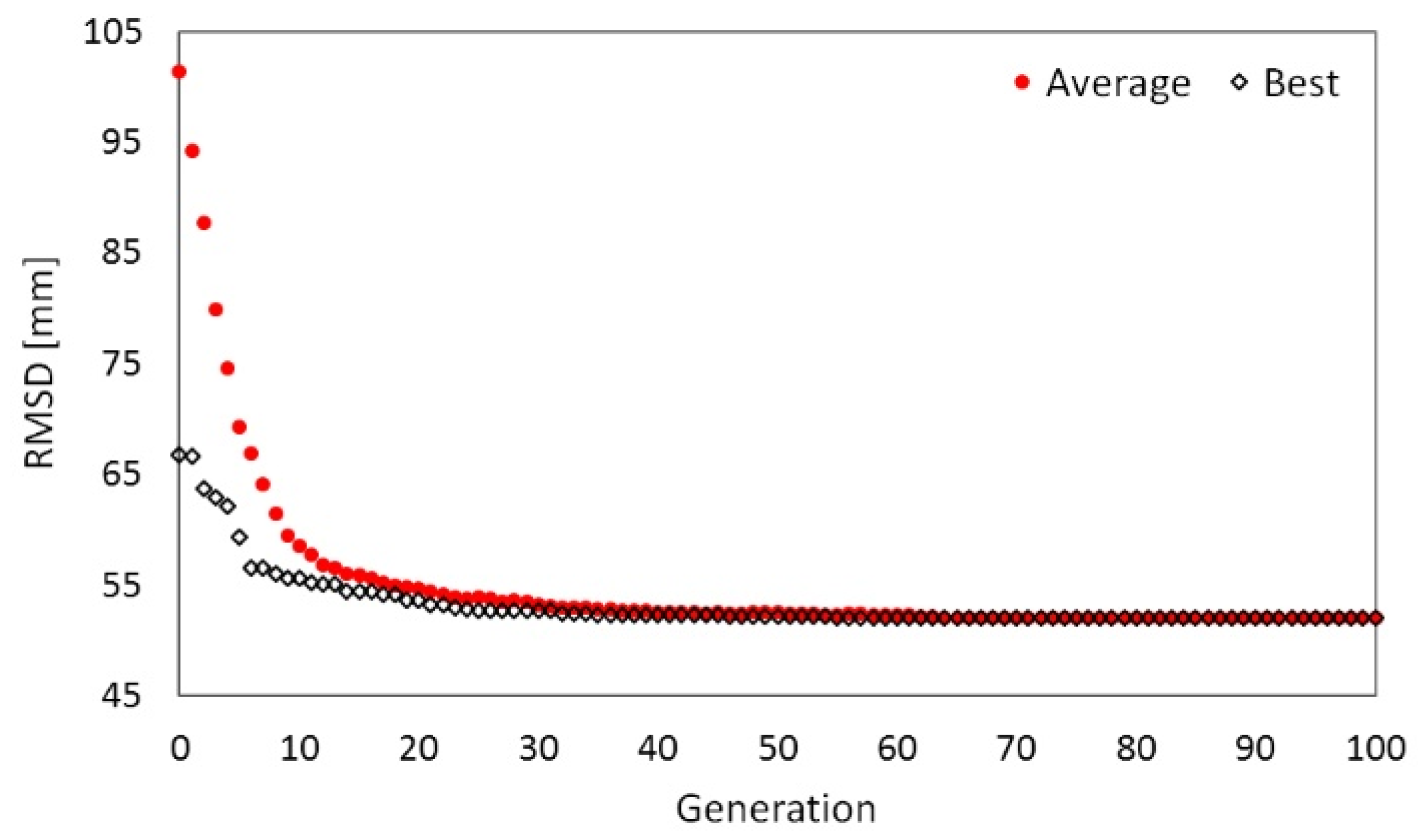
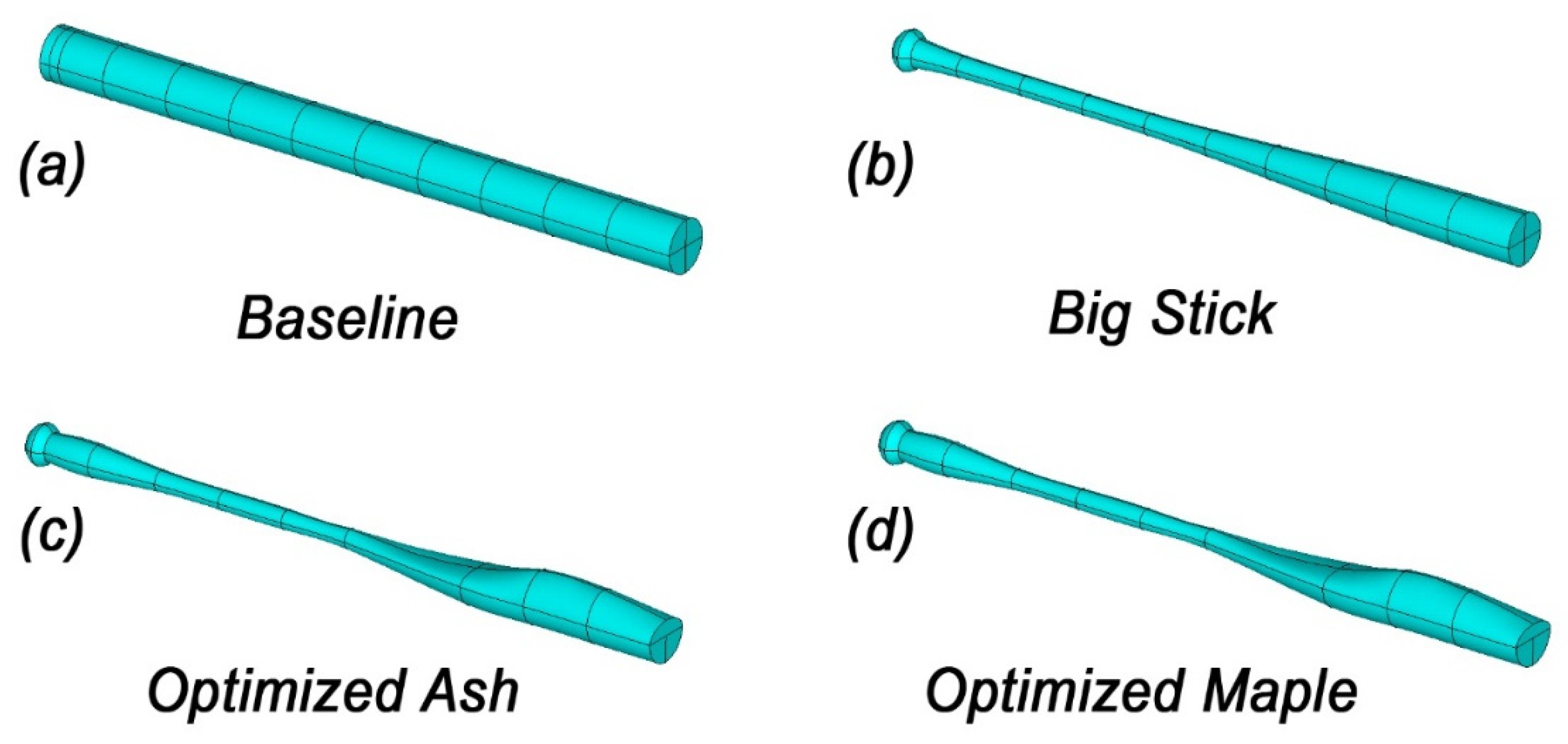
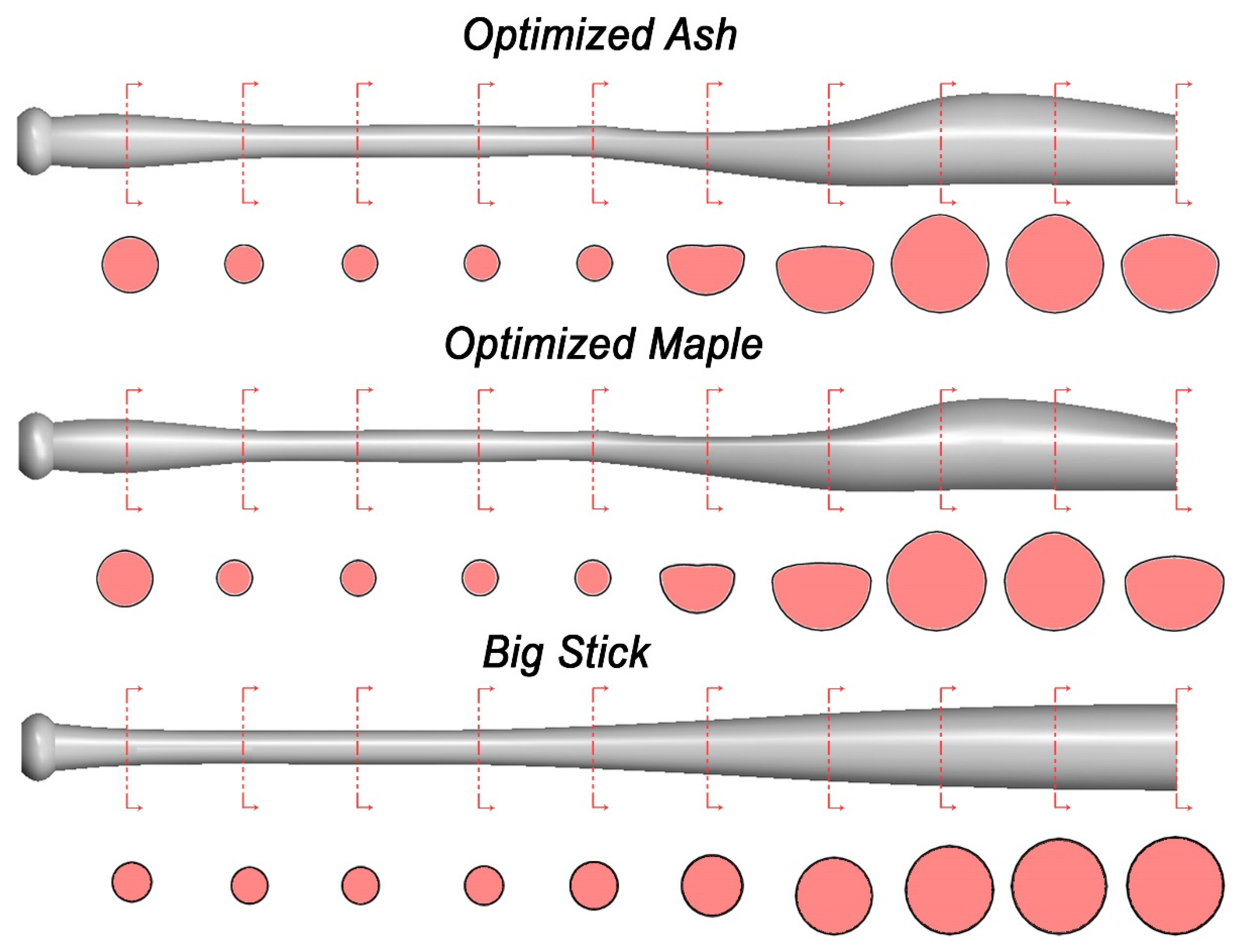
4. Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kelly, W. Japan: Professional Baseball Enters the Twenty-First Century. In Baseball Beyond Our Borders; Gmelch, G., Nathan, D.A., Eds.; University of Nebraska Press: Lincoln, Nebraska, 2017; pp. 183–202. [Google Scholar]
- Zirin, D. Mike Trout’s Mega Deal and Baseball’s Economic Rot. Available online: https://www.thenation.com/article/archive/mike-trout-mlb-players-union-dave-zirin/ (accessed on 18 February 2019).
- Central Intelligence Agency. The World Factbook. Available online: https://www.cia.gov/library/publications/the-world-factbook/fields/208rank.html (accessed on 18 February 2019).
- Fallon, L.P.; Sherwood, J.A. A study of the barrel constructions of baseball bats. In Proceedings of the 4th International Conference on the Engineering of Sport, Kyoto, Japan, 3–6 September 2002. [Google Scholar]
- Noble, L. Inertial and vibrational characteristics of softball and baseball bats: Research and design implications. In Proceedings of the Conference on International Society of Biomechanics in Sports, Konstanz, Germany, 21–25 July 1998; pp. 86–97. [Google Scholar]
- Adair, R.K. The physics of baseball. Phys. Today 1995, 48, 26–31. [Google Scholar] [CrossRef]
- Drane, P.J.; Sherwood, J.A.; Jones, J.W.; Connelly, T.P. The effect of baseball construction on the game of baseball. In Proceedings of the 7th ISEA Conference, Biarritz, France, 3–6 June 2008; p. 275. [Google Scholar]
- Lepperd, T. (Ed.) Official Baseball Rules, 2018 ed.; The Office of the Commissioner of Baseball: New York, NY, USA, 2018. [Google Scholar]
- Ruggiero, E.; Sherwood, J.; Drane, P.; Kretschmann, D. An investigation of bat durability by wood species. Procedia Eng. 2012, 34, 427–432. [Google Scholar] [CrossRef] [Green Version]
- Bahill, A.T. The Science of Baseball, Modeling Bat-Ball Collisions and the Flight of the Ball; Springer: Berlin, Germany, 2019. [Google Scholar]
- Cross, R. Physics of Baseball & Softball; Springer: New York, NY, USA, 2011. [Google Scholar]
- Sherwood, J.A.; Ph, D.; Mustone, T.J.; Fallon, L.P. Characterizing the performance of baseball bats using experimental and finite element methods. Sport Eng. 2000, 15, 377–388. [Google Scholar]
- Watts, R.G.; Bahill, A.T. Keep Your Eye on the Ball: The Science and Folklore of Baseball; W. H. Freeman and Co.: New York, NY, USA, 1990. [Google Scholar]
- Noble, L.; Eck, J. Effects of selected softball bat loading strategies on impact reaction impulse. Med. Sci. Sport. Exerc. 1986, 18, 50–59. [Google Scholar] [CrossRef]
- Penrose, J.M.T.; Hose, D.R. An impact analysis of a flexible bat using an iterative solver. J. Sports Sci. 1999, 17, 677–682. [Google Scholar] [CrossRef]
- Weyrich, A.S.; Messier, S.P.; Ruhmann, B.S.; Berry, M.J. Effects of bat composition, grip firmness, and impact location on postimpact ball velocity. Med. Sci. Sports Exerc. 1989, 21, 199–205. [Google Scholar] [CrossRef]
- Russel, D.A. Acoustics and vibration of baseball and soft ball bats. Acoust. Today 2017, 13, 35–42. [Google Scholar]
- Cross, R. The sweet spot of a baseball bat. Am. J. Phys. 1998, 66, 772–779. [Google Scholar] [CrossRef]
- Knowles, S.; Brooks, F.; Mather, J.S.B. Novel design of sports equipment through impact vibration analysis. In Proceedings of the 14th Modal Analysis Conference, Dearborn, MI, USA, 12–15 February 1996; pp. 390–396. [Google Scholar]
- Noble, L.; Walker, H. Baseball bat inertial and vibrational characteristics and discomfort following ball–bat impacts. J. Appl. Biomech. 1994, 10, 132–144. [Google Scholar] [CrossRef]
- Van Zandt, L.L. The dynamical theory of the baseball bat. Am. J. Phys. 1992, 60, 172–181. [Google Scholar] [CrossRef]
- Mazloomi, M.S.; Saadatfar, M.; Evans, P.D. Designing cricket bats using parametric modeling and genetic algorithms. Wood Sci. Technol. 2020, 54, 755–768. [Google Scholar] [CrossRef]
- Nathan, A.M. Dynamics of the baseball—Bat collision. Am. J. Phys. 2000, 68, 979–990. [Google Scholar] [CrossRef]
- Nathan, A.M. Characterizing the performance of baseball bats. Am. J. Phys. 2003, 71, 134–143. [Google Scholar] [CrossRef] [Green Version]
- Brooks, R.; Mather, J.S.B.; Knowles, S. The influence of impact vibration modes and frequencies on cricket bat performance. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2006, 220, 237–248. [Google Scholar] [CrossRef]
- Eftaxiopoulou, T.; Narayanan, A.; Dear, J.P.; Bull, A.M.J. A performance comparison between cricket bat designs. Proc. Inst. Mech. Eng. Part P J. Sport. Eng. Technol. 2012, 226, 16–23. [Google Scholar] [CrossRef]
- Smith, L.V. Evaluating baseball bat performance. Sport. Eng. 2001, 4, 205–214. [Google Scholar] [CrossRef]
- Cross, R.; Nathan, A.M. Performance versus moment of inertia of sporting implements. Sport. Technol. 2009, 2, 7–15. [Google Scholar] [CrossRef]
- Vedula, G.; Sherwood, J.A. An experimental and finite element study of the relationship amongst the sweet spot, cop and vibration nodes in baseball bats. In Proceedings of the 5th Conference of Engineering of Sport, Davis, CA, USA, 13–16 September 2004; Volume 2, pp. 626–632. [Google Scholar]
- Leinert, B.R. Baseball Bat; WO 2009/064798 Al; World Intellectual Property Organization: Geneva, Switzerland, 2009. [Google Scholar]
- Ruggiero, E.; Sherwood, J.; Drane, P.; Duffy, M.; Kretschmann, D. Finite element modeling of wood bat profiles for durability. Procedia Eng. 2014, 72, 527–532. [Google Scholar] [CrossRef] [Green Version]
- Fortin-smith, J.; Sherwood, J.; Drane, P.; Kretschmann, D. Characterization of maple and ash material properties as a function of wood density for bat/ball impact modeling in LS-DYNA. Procedia Eng. 2016, 147, 413–418. [Google Scholar] [CrossRef] [Green Version]
- Fortin-smith, J.; Sherwood, J.; Drane, P.; Kretschmann, D. Characterization of maple and ash material properties for the finite element modeling of wood baseball bats. Appl. Sci. 2018, 8, 2256. [Google Scholar] [CrossRef] [Green Version]
- Swanson Analysis System Inc. ANSYS. Academia Research, Release 14; Swanson Analysis System Inc.: Canonsburg, PA, USA, 2014. [Google Scholar]
- Fu, Z.-F.; He, J. Modal Analysis, 1st ed.; Butterworth-Heinemann: Oxford, UK, 2001. [Google Scholar]
- Ross, R.J. (Ed.) Wood Handbook: Wood as an Engineering Material; U.S. Department of Agriculture, Forest Service, Forest Products Laboratory: Madison, WI, USA, 2010. [Google Scholar]
- McKay, M.; Beckman, R.; Conover, W. A Comparison of three methods for selecting values of input variables in the analysis of output from a computer code. Technometrics 1979, 21, 239–245. [Google Scholar]
- Mazloomi, M.S.; Ranjbar, M.; Boldrin, L.; Scarpa, F.; Ozada, N. Structural-acoustic optimization of 2-D Gradient Auxetic Sandwich Panels. In Proceedings of the Medyna 2017: 2nd Euro-Mediterranean Conference on Structural Dynamics and Vibroacoustics, Sevilla, Spain, 25–27 April 2017; 2017; pp. 194–199. [Google Scholar]
- Mazloomi, M.S.; Ranjbar, M.; Boldrin, L.; Scarpa, F.; Patsias, S.; Ozada, N. Vibroacoustics of 2D gradient auxetic hexagonal honeycomb sandwich panels. Compos. Struct. 2018, 187, 593–603. [Google Scholar] [CrossRef]
- McHutchon, M.; Manson, G.; Carre’, M. A Fresh Approach to Sports Equipment Design: Evolving Hockey Sticks Using Genetic Algorithms. In The Engineering of Sport 6; Moritz, E.F., Haake, S., Eds.; Springer: New York, NY, USA, 2006. [Google Scholar]
- Turrin, M.; Von Buelow, P.; Stouffs, R. Design explorations of Performance driven geometry in architectural design using parametric modeling and genetic algorithms. Adv. Eng. Inform. 2011, 25, 656–675. [Google Scholar] [CrossRef]




| Wood | Density (kg/m3) | Young’s Modulus (MPa) | Shear Modulus (MPa) | Poisson’s Ratio | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Ex | Ey | Ez | Gxy | Gxz | Gyz | uyx | uzx | uzy | ||
| Maple | 706 | 12,600 | 820 | 1660 | 760 | 1400 | 12 | 0.037 | 0.07 | 0.35 |
| Ash | 672 | 12,000 | 960 | 1500 | 920 | 1310 | 12 | 0.051 | 0.06 | 0.36 |
| Design | Wood Species | Design Variables (mm) | RMSD (mm) | Mass (kg) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| r1 | r2 | r3 | r4 | r5 | r6 | r7 | r8 | r9 | r10 | ||||
| Baseline | Maple | 33.2 | 33.2 | 33.2 | 33.2 | 33.2 | 33.2 | 33.2 | 33.2 | 33.2 | 33.2 | 166.00 | 2.034 |
| Big Stick | Maple | 13.4 | 12.5 | 12.7 | 13.2 | 16.2 | 20.5 | 25.5 | 29.2 | 31.5 | 32.2 | 72.29 | 0.878 |
| GA Optimized | Maple | 19.9 | 12.1 | 12.0 | 12.2 | 12.1 | 33.1 | 12.2 | 33.0 | 32.5 | 17.0 | 52.13 | 0.931 |
| Baseline | Ash | 33.2 | 33.2 | 33.2 | 33.2 | 33.2 | 33.2 | 33.2 | 33.2 | 33.2 | 33.2 | 165.90 | 1.936 |
| Big Stick | Ash | 13.4 | 12.5 | 12.7 | 13.2 | 16.2 | 20.5 | 25.5 | 29.2 | 31.5 | 32.2 | 72.53 | 0.836 |
| GA Optimized | Ash | 20.0 | 13.0 | 12.0 | 12.0 | 12.0 | 32.4 | 12.1 | 33.1 | 33.1 | 19.7 | 52.05 | 0.873 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mazloomi, M.S.; Evans, P.D. Shape Optimization of a Wooden Baseball Bat Using Parametric Modeling and Genetic Algorithms. AI 2021, 2, 381-393. https://doi.org/10.3390/ai2030024
Mazloomi MS, Evans PD. Shape Optimization of a Wooden Baseball Bat Using Parametric Modeling and Genetic Algorithms. AI. 2021; 2(3):381-393. https://doi.org/10.3390/ai2030024
Chicago/Turabian StyleMazloomi, Mohammad Sadegh, and Philip D. Evans. 2021. "Shape Optimization of a Wooden Baseball Bat Using Parametric Modeling and Genetic Algorithms" AI 2, no. 3: 381-393. https://doi.org/10.3390/ai2030024
APA StyleMazloomi, M. S., & Evans, P. D. (2021). Shape Optimization of a Wooden Baseball Bat Using Parametric Modeling and Genetic Algorithms. AI, 2(3), 381-393. https://doi.org/10.3390/ai2030024






