A Neurally Inspired Model of Figure Ground Organization with Local and Global Cues
Abstract
1. Introduction
2. Related Work
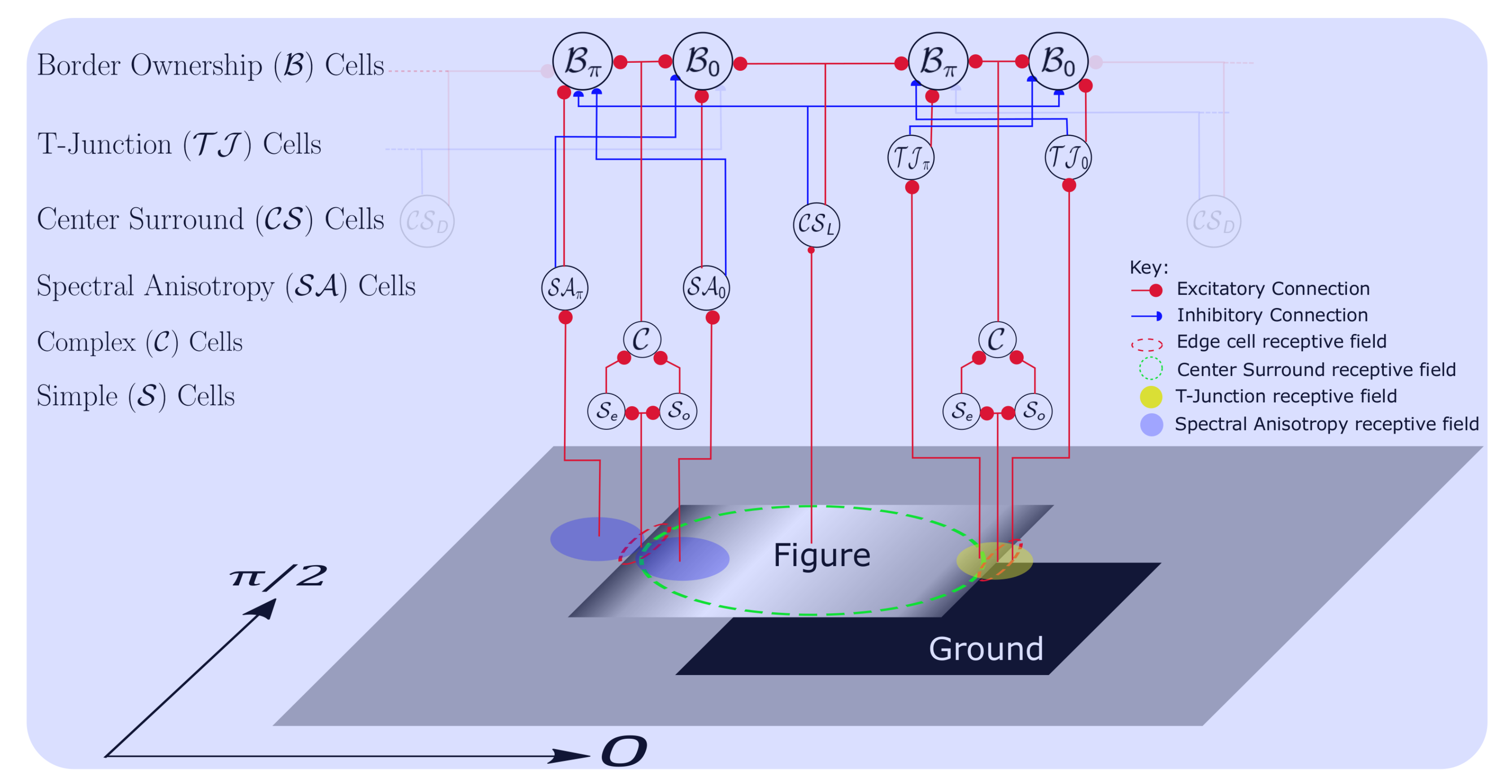
3. Model Description
3.1. Computation of Feature Channels
3.1.1. Intensity Channel
3.1.2. Color Opponency Channels
3.1.3. Orientation Channel
3.2. Multiscale Pyramid Decomposition
3.3. Border Ownership Pyramid Computation
4. Adding Local Cues
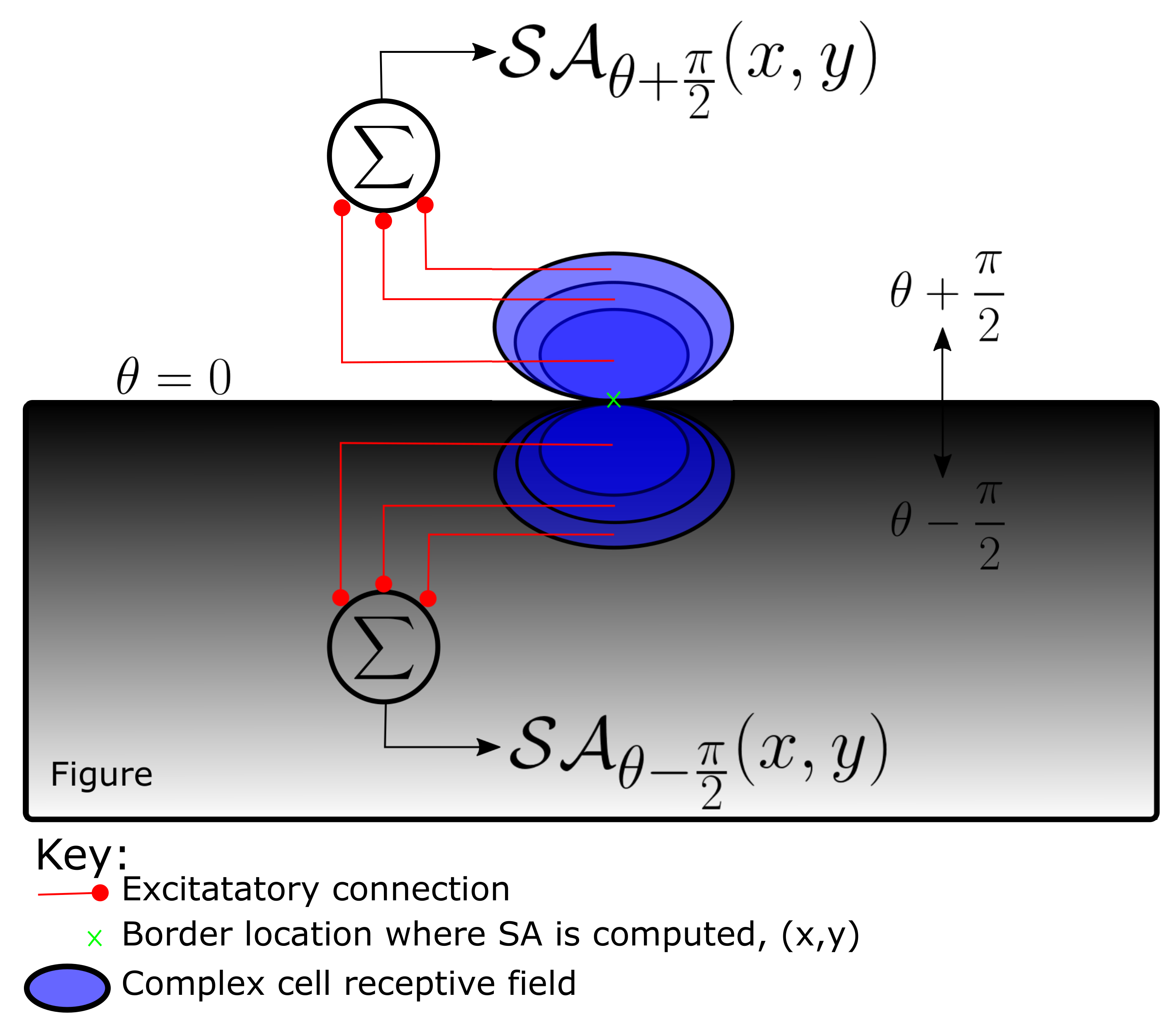
4.1. Computation of Spectral Anisotropy
4.2. Detecting of T-Junctions
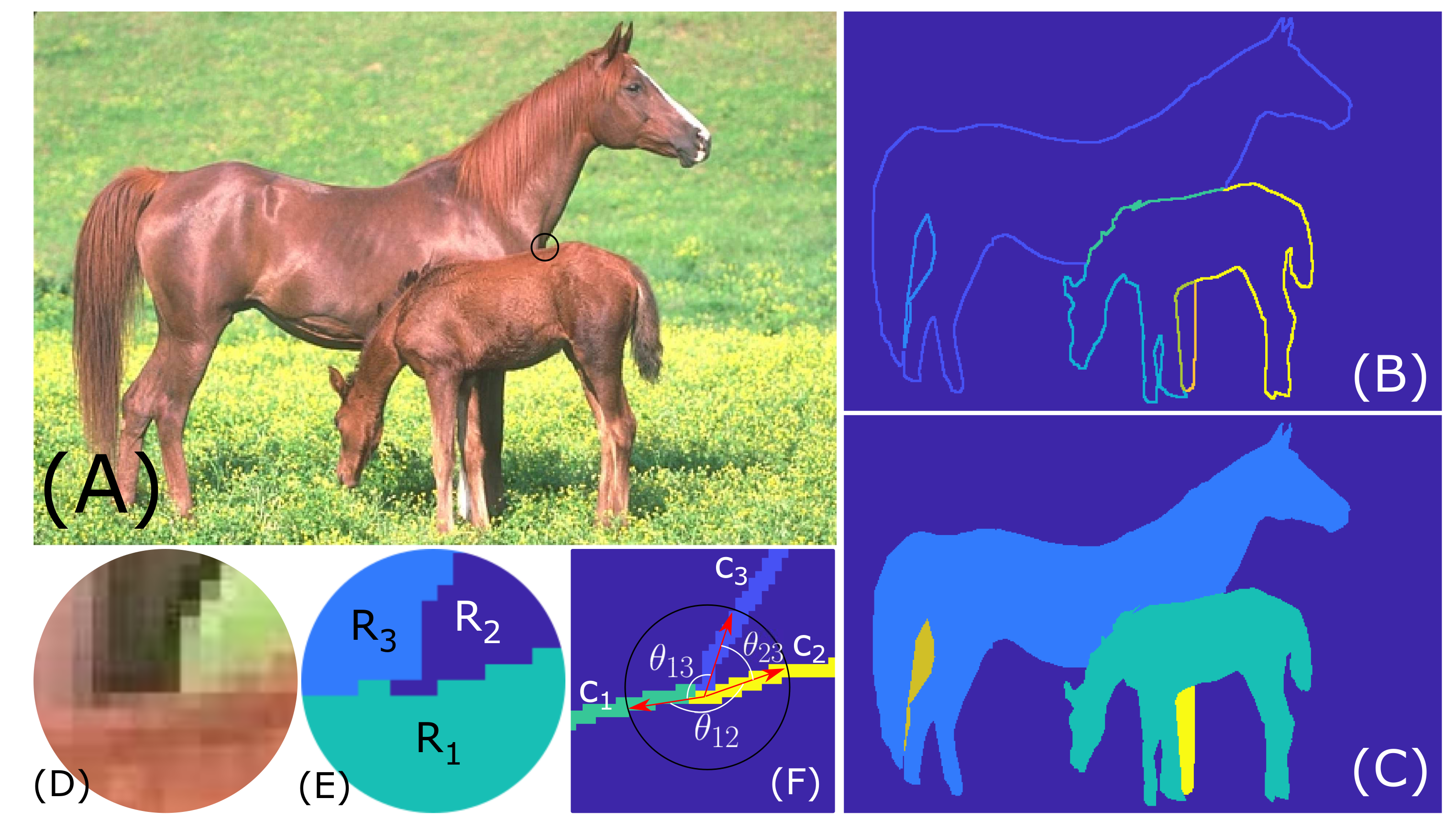
4.2.1. Area Based T-Junction Determination
4.2.2. Angle Based T-Junction Determination
5. Data and Methods
6. Results
6.1. Effect of Adding Spectral Anisotropy
6.2. Effect of Adding T-Junctions
6.3. Effect of Adding Both Spectral Anisotropy and T-Junctions
7. Discussion
8. Conclusions
9. Future Work
Funding
Conflicts of Interest
Appendix A. Computational Complexity and Cost of Adding Local Cues
- Reference model computation-no local cues: 133,787,537,703 FLOPs
- Reference model + SA (current implementation): 170,001,489,671. As stated in Section 9, the computational cost of SA can be reduced by using a fixed size filter, reducing the number of orientations and using only Simple cell responses. Without these optimizations, the overhead is 27.068%. Having these optimization, in an ideal implementation, would dramatically reduce the computational overhead.
- Reference model + SA (ideal implementation): 143,393,171,688 FLOPs (computational overhead: 7.17%). In the ideal case, filter size would be kept constant and SA would be computed based on image pyramid. Moreover, by reducing the number of orientations to 4, instead of 8, the cost can be reduced by half to ≈3.5%. Additionally, only Simple cells can be used to reduce the computational cost even more (See Section 9).
- Reference model + T-Junctions (without edge segmentation step): 141,749,861,545 FLOPs (computational overhead: 5.95%)
Appendix B. Local Cues Influencing Only Top 2 Layers
| Model | K = 2 | K = 10 |
|---|---|---|
| Ref Model | - | 58.44% |
| Ref + SA | 62.42% | 62.69% |
| Ref + T-Junctions (gPb edges) | 59.12% | 59.48% |
References
- Wagemans, J.; Elder, J.H.; Kubovy, M.; Palmer, S.E.; Peterson, M.A.; Singh, M.; von der Heydt, R. A century of Gestalt psychology in visual perception: I. Perceptual grouping and figure–ground organization. Psychol. Bull. 2012, 138, 1172. [Google Scholar] [CrossRef] [PubMed]
- Wagemans, J.; Feldman, J.; Gepshtein, S.; Kimchi, R.; Pomerantz, J.R.; van der Helm, P.A.; van Leeuwen, C. A century of Gestalt psychology in visual perception: II. Conceptual and theoretical foundations. Psychol. Bull. 2012, 138, 1218. [Google Scholar] [CrossRef] [PubMed]
- Koffka, K. Principles of Gestalt Psychology; Harcourt-Brace: New York, NY, USA, 1935. [Google Scholar]
- Bahnsen, P. Eine Untersuchung uber Symmetrie und Asymmetrie bei visuellen Wahrnehmungen. Z. Fur Psychol. 1928, 108, 129–154. [Google Scholar]
- Palmer, S.E. Vision Science-Photons to Phenomenology; MIT Press: Cambridge, MA, USA, 1999. [Google Scholar]
- Fowlkes, C.; Martin, D.; Malik, J. Local figure-ground cues are valid for natural images. J. Vis. 2007, 7, 2. [Google Scholar] [CrossRef] [PubMed]
- Heitger, F.; Rosenthaler, L.; von ver Heydt, R.; Peterhans, E.; Kübler, O. Simulation of neural contour mechanisms: From simple to end-stopped cells. Vis. Res. 1992, 32, 963–981. [Google Scholar] [CrossRef]
- Huggins, P.; Chen, H.; Belhumeur, P.; Zucker, S. Finding folds: On the appearance and identification of occlusion. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Kauai, HI, USA, 8–14 December 2001; Volume 2, pp. 2–718. [Google Scholar]
- Palmer, S.; Ghose, T. Extremal edges: A powerful cue to depth perception and figure-ground organization. Psychol. Sci. 2008, 19, 77–84. [Google Scholar] [CrossRef]
- Ramenahalli, S.; Mihalas, S.; Niebur, E. Extremal edges: Evidence in natural images. In Proceedings of the 45th Annual Conference on Information Sciences and Systems (CISS), Baltimore, MD, USA, 23–25 March 2011; pp. 1–5. [Google Scholar]
- Zhou, H.; Friedman, H.S.; von der Heydt, R. Coding of border ownership in monkey visual cortex. J. Neurosci. 2000, 20, 6594–6611. [Google Scholar] [CrossRef]
- Williford, J.R.; von der Heydt, R. Figure-ground organization in visual cortex for natural scenes. eNeuro 2016, 3. [Google Scholar] [CrossRef]
- Craft, E.; Schutze, H.; Niebur, E.; von der Heydt, R. A neural model of figure-ground organization. J. Neurophysiol. 2007, 97, 4310–4326. [Google Scholar] [CrossRef]
- Roelfsema, P.R.; Lamme, V.A.; Spekreijse, H.; Bosch, H. Figure ground segregation in a recurrent network architecture. J. Cogn. Neurosci. 2002, 14, 525–537. [Google Scholar] [CrossRef]
- Zhaoping, L. Border ownership from intracortical interactions in visual area V2. Neuron 2005, 47, 143–153. [Google Scholar] [CrossRef] [PubMed]
- Mihalas, S.; Dong, Y.; von der Heydt, R.; Niebur, E. Mechanisms of perceptual organization provide auto-zoom and auto-localization for attention to objects. Proc. Natl. Acad. Sci. USA 2011, 108, 7583–7588. [Google Scholar] [CrossRef] [PubMed]
- Hu, B.; von der Heydt, R.; Niebur, E. Figure-Ground Organization in Natural Scenes: Performance of a Recurrent Neural Model Compared with Neurons of Area V2. eNeuro 2019, 6. [Google Scholar] [CrossRef] [PubMed]
- Ramenahalli, S.; Mihalas, S.; Niebur, E. Local spectral anisotropy is a valid cue for figure–ground organization in natural scenes. Vis. Res. 2014, 103, 116–126. [Google Scholar] [CrossRef][Green Version]
- Ramenahalli, S.; Mihalas, S.; Niebur, E. Figure-ground classification based on spectral anisotropy of local image patches. In Proceedings of the 46th Annual IEEE Conference on Information Sciences and Systems (IEEE-CISS), Princeton, NJ, USA, 21–23 March 2012; pp. 1–5. [Google Scholar]
- Ramenahalli, S.; Mihalas, S.; Niebur, E. Spectral inhomogeneity provides information for figure-ground organization in natural images. In Proceedings of the Society for Neuroscience Annual Meeting, Washington, DC, USA, 12–16 November 2011. [Google Scholar]
- Ghose, T.; Palmer, S. Extremal edges versus other principles of figure-ground organization. J. Vis. 2010, 10, 3. [Google Scholar] [CrossRef]
- Palmer, S.; Ghose, T. Extremal edges dominate other cues to figure-ground organization. J. Vis. 2006, 6, 96. [Google Scholar] [CrossRef]
- Rubin, E. Visuell wahrgenommene Figuren. In Visual Perception: Essential Readings; Yantis, S., Ed.; Psychology Press: London, UK, 2001. [Google Scholar]
- Schirillo, J.A. The anatomical locus of T-junction processing. Vis. Res. 2009, 49, 2011–2025. [Google Scholar] [CrossRef][Green Version]
- Heitger, F.; von der Heydt, R. A computational model of neural contour processing: Figure-ground segregation and illusory contours. In Proceedings of the 4th International Conference on Computer Vision, Berlin, Germany, 11–14 May 1993; IEEE Computer Society Press: Los Alamitos, CA, USA, 1993; pp. 32–40. [Google Scholar]
- Hansen, T.; Neumann, H. A Biologically Motivated Scheme for Robust Junction Detection. In Proceedings of the Second International Workshop on Biologically Motivated Computer Vision, Tübingen, Germany, 22–24 November 2002; pp. 16–26. [Google Scholar] [CrossRef]
- Rubin, E. Visuell Wahrgenommene Figuren; Glydenalske Boghandel: Kobenhaven, Denmark, 1921. [Google Scholar]
- Wertheimer, M. Untersuchungen zur Lehre von der Gestalt II. Psychol. Forsch. 1923, 4, 301–350. [Google Scholar] [CrossRef]
- Lamme, V.A. The neurophysiology of figure-ground segregation in primary visual cortex. J. Neurosci. 1995, 15, 1605–1615. [Google Scholar] [CrossRef]
- Super, H.; Lamme, V.A. Altered figure-ground perception in monkeys with an extra-striate lesion. Neuropsychologia 2007, 45, 3329–3334. [Google Scholar] [CrossRef]
- Williford, J.R.; von der Heydt, R. Early Visual Cortex Assigns Border Ownership in Natural Scenes According to Image Context. J. Vis. 2014, 14, 588. [Google Scholar] [CrossRef]
- Ren, X.; Fowlkes, C.C.; Malik, J. Figure/ground assignment in natural images. In European Conference on Computer Vision; Springer: Berlin/Heidelberg, Germany, 2006; pp. 614–627. [Google Scholar]
- Hoiem, D.; Efros, A.A.; Hebert, M. Recovering occlusion boundaries from an image. Int. J. Comput. Vis. 2011, 91, 328–346. [Google Scholar] [CrossRef]
- Teo, C.L.; Fermüller, C.; Aloimonos, Y. Fast 2D Border Ownership Assignment. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 5117–5125. [Google Scholar]
- Hoiem, D.; Stein, A.N.; Efros, A.A.; Hebert, M. Recovering occlusion boundaries from a single image. In Proceedings of the IEEE 11th International Conference on Computer Vision, ICCV, Rio de Janeiro, Brazil, 14–21 October 2007; pp. 1–8. [Google Scholar]
- Amer, M.R.; Raich, R.; Todorovic, S. Monocular Extraction of 2.1D Sketch. In Proceedings of the International Conference on Image Processing, ICIP 2010, Hong Kong, China, 26–29 September 2010; pp. 3437–3440. [Google Scholar]
- Amer, M.R.; Yousefi, S.; Raich, R.; Todorovic, S. Monocular Extraction of 2.1D Sketch Using Constrained Convex Optimization. Int. J. Comput. Vis. 2015, 112, 23–42. [Google Scholar] [CrossRef]
- Leichter, I.; Lindenbaum, M. Boundary ownership by lifting to 2.1D. In Proceedings of the IEEE 12th International Conference on Computer Vision, Kyoto, Japan, 29 September–2 October 2009; pp. 9–16. [Google Scholar]
- Palou, G.; Salembier, P. Monocular depth ordering using T-junctions and convexity occlusion cues. IEEE Trans. Image Process. 2013, 22, 1926–1939. [Google Scholar] [CrossRef] [PubMed]
- Palou, G.; Salembier, P. From local occlusion cues to global monocular depth estimation. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Kyoto, Japan, 25–30 March 2012; pp. 793–796. [Google Scholar]
- Palou, G.; Salembier, P. Occlusion-based depth ordering on monocular images with binary partition tree. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Prague, Czech Republic, 22–27 May 2011; pp. 1093–1096. [Google Scholar]
- Salembier, P.; Garrido, L. Binary partition tree as an efficient representation for image processing, segmentation, and information retrieval. IEEE Trans. Image Process. 2000, 9, 561–576. [Google Scholar] [CrossRef]
- Nishigaki, M.; Fermüller, C.; DeMenthon, D. The image torque operator: A new tool for mid-level vision. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012; pp. 502–509. [Google Scholar]
- Yu, S.X.; Lee, T.S.; Kanade, T. A Hierarchical Markov Random Field Model for Figure-Ground Segregation. In Proceedings of the Third International Workshop on Energy Minimization Methods in Computer Vision and Pattern Recognition, Sophia Antipolis, France, 3–5 September 2001; pp. 118–133. [Google Scholar]
- Baek, K.; Sajda, P. Inferring figure-ground using a recurrent integrate-and-fire neural circuit. IEEE Trans. Neural Syst. Rehabil. Eng. 2005, 13, 125–130. [Google Scholar] [CrossRef][Green Version]
- Maire, M. Simultaneous segmentation and figure/ground organization using angular embedding. In European Conference on Computer Vision–ECCV; Springer: Berlin/Heidelberg, Germany, 2010; pp. 450–464. [Google Scholar]
- Yu, S. Angular embedding: From jarring intensity differences to perceived luminance. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 2302–2309. [Google Scholar]
- Ion, A.; Carreira, J.; Sminchisescu, C. Image segmentation by figure-ground composition into maximal cliques. In Proceedings of the IEEE International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011; pp. 2110–2117. [Google Scholar]
- Ion, A.; Carreira, J.; Sminchisescu, C. Probabilistic joint image segmentation and labeling by figure-ground composition. Int. J. Comput. Vis. 2014, 107, 40–57. [Google Scholar] [CrossRef]
- Kogo, N.; Strecha, C.; van Gool, L.; Wagemans, J. Surface construction by a 2-D differentiation–integration process: A neurocomputational model for perceived border ownership, depth, and lightness in Kanizsa figures. Psychol. Rev. 2010, 117, 406. [Google Scholar] [CrossRef]
- Froyen, V.; Feldman, J.; Singh, M. A Bayesian Framework for Figure-Ground Interpretation. In Advances in Neural Information Processing Systems 23; Lafferty, J., Williams, C., Shawe-Taylor, J., Zemel, R., Culotta, A., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2010; pp. 631–639. [Google Scholar]
- Kienker, P.K.; Sejnowski, T.J.; Hinton, G.E.; Schumacher, L.E. Separating figure from ground with a parallel network. Perception 1986, 15, 197–216. [Google Scholar] [CrossRef]
- Grossberg, S.; Mingolla, E. Neural dynamics of form perception: Boundary completion, illusory figures, and neon color spreading. Psychol. Rev. 1985, 92, 173. [Google Scholar] [CrossRef]
- Grossberg, S. 3-D vision and figure-ground separation by visual cortex. Percept. Psychophys. 1994, 55, 48–121. [Google Scholar] [CrossRef] [PubMed]
- Sajda, P.; Finkel, L. Intermediate-Level Visual Representations and the Construction of Surface Perception. J. Cogn. Neurosci. 1995, 7, 267–291. [Google Scholar] [CrossRef] [PubMed]
- Jehee, J.F.; Lamme, V.A.; Roelfsema, P.R. Boundary assignment in a recurrent network architecture. Vis. Res. 2007, 47, 1153–1165. [Google Scholar] [CrossRef] [PubMed]
- Li, Z. V1 mechanisms and some figure–ground and border effects. J. Physiol. Paris 2003, 97, 503–515. [Google Scholar] [PubMed]
- Li, Z. Can V1 Mechanisms Account for Figure-Ground and Medial Axis Effects? In Advances in Neural Information Processing Systems 12; Solla, S.A., Leen, T.K., Müller, K., Eds.; MIT Press: Cambridge, MA, USA, 2000; pp. 136–142. [Google Scholar]
- Kapadia, M.K.; Ito, M.; Gilbert, C.D.; Westheimer, G. Improvement in visual sensitivity by changes in local context: Parallel studies in human observers and in V1 of alert monkeys. Neuron 1995, 15, 843–856. [Google Scholar] [CrossRef]
- Slllito, A.M.; Grieve, K.L.; Jones, H.E.; Cudeiro, J.; Davls, J. Visual cortical mechanisms detecting focal orientation discontinuities. Nature 1995, 378, 492–496. [Google Scholar] [CrossRef]
- Knierim, J.J.; van Essen, D.C. Neuronal responses to static texture patterns in area V1 of the alert macaque monkey. J. Neurophysiol. 1992, 67, 961–980. [Google Scholar] [CrossRef]
- Kikuchi, M.; Akashi, Y. A model of border-ownership coding in early vision. In International Conference on Artificial Neural Networks–ICANN; Springer: Berlin/Heidelberg, Germany, 2001; pp. 1069–1074. [Google Scholar]
- Russell, A.F.; Mihalas, S.; von der Heydt, R.; Niebur, E.; Etienne-Cummings, R. A model of proto-object based saliency. Vis. Res. 2014, 94, 1–15. [Google Scholar] [CrossRef]
- Molin, J.L.; Russell, A.F.; Mihalas, S.; Niebur, E.; Etienne-Cummings, R. Proto-object based visual saliency model with a motion-sensitive channel. In Proceedings of the Biomedical Circuits and Systems Conference (BioCAS), Rotterdam, The Netherlands, 31 October–2 November 2013; pp. 25–28. [Google Scholar]
- Hu, B.; Niebur, E. A recurrent neural model for proto-object based contour integration and figure-ground segregation. J. Comput. Neurosci. 2017. [Google Scholar] [CrossRef]
- Layton, O.W.; Mingolla, E.; Yazdanbakhsh, A. Dynamic coding of border-ownership in visual cortex. J. Vis. 2012, 12, 8. [Google Scholar] [CrossRef]
- Domijan, D.; Šetić, M. A feedback model of figure-ground assignment. J. Vis. 2008, 8, 10. [Google Scholar] [CrossRef] [PubMed]
- Sakai, K.; Nishimura, H.; Shimizu, R.; Kondo, K. Consistent and robust determination of border ownership based on asymmetric surrounding contrast. Neural Netw. 2012, 33, 257–274. [Google Scholar] [CrossRef] [PubMed]
- Nishimura, H.; Sakai, K. Determination of border ownership based on the surround context of contrast. Neurocomputing 2004, 58, 843–848. [Google Scholar] [CrossRef]
- Nishimura, H.; Sakai, K. The computational model for border-ownership determination consisting of surrounding suppression and facilitation in early vision. Neurocomputing 2005, 65, 77–83. [Google Scholar] [CrossRef]
- Rensink, R.A. The dynamic representation of scenes. Vis. Cogn. 2000, 7, 17–42. [Google Scholar] [CrossRef]
- Adelson, E.; Bergen, J. Spatiotemporal energy models for the perception of motion. J. Opt. Soc. Am. A 1985, 2, 284–299. [Google Scholar] [CrossRef]
- MATLAB. 2-D Cross-Correlation. Available online: https://www.mathworks.com/help/signal/ref/xcorr2.html (accessed on 30 September 2013).
- Itti, L.; Koch, C.; Niebur, E. A model of saliency-based visual attention for rapid scene analysis. IEEE Trans. Pattern Anal. Mach. Intell. 1998, 20, 1254–1259. [Google Scholar] [CrossRef]
- Weisstein, E.W. Von Mises Distribution. Available online: http://mathworld.wolfram.com/vonMisesDistribution.html (accessed on 30 September 2014).
- Arbelaez, P.; Maire, M.; Fowlkes, C.; Malik, J. Contour Detection and Hierarchical Image Segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2011, 33, 898–916. [Google Scholar] [CrossRef]
- Martin, D.; Fowlkes, C.; Tal, D.; Malik, J. A database of human segmented natural images and its application to evaluating segmentation algorithms and measuring ecological statistics. In Proceedings of the Eighth IEEE International Conference on Computer Vision, ICCV 2001, Vancouver, BC, Canada, 7–14 July 2001; Volume 2, pp. 416–423. [Google Scholar]
- Tse, P.U.; Albert, M.K. Amodal completion in the absence of image tangent discontinuities. Perception 1998, 27, 455–464. [Google Scholar] [CrossRef]
- McDermott, J. Psychophysics with junctions in real images. Perception 2004, 33, 1101–1127. [Google Scholar] [CrossRef]
- van der Helm, P.A. Bayesian confusions surrounding simplicity and likelihood in perceptual organization. Acta Psychol. 2011, 138, 337–346. [Google Scholar] [CrossRef] [PubMed]
- Troscianko, T.; Montagnon, R.; Clerc, J.L.; Malbert, E.; Chanteau, P.L. The role of colour as a monocular depth cue. Vis. Res. 1991, 31, 1923–1929. [Google Scholar] [CrossRef]
- Zaidi, Q.; Li, A. Three-dimensional shape perception from chromatic orientation flows. Vis. Neurosci. 2006, 23, 323–330. [Google Scholar] [CrossRef] [PubMed]
- Ardila, D.; Mihalas, S.; Niebur, E. How perceptual grouping affects the salience of symmetry. In Proceedings of the Society for Neuroscience Annual Meeting, Washington DC, USA, 12–16 November 2011. [Google Scholar]
- Ardila, D.; Mihalas, S.; von der Heydt, R.; Niebur, E. Medial axis generation in a model of perceptual organization. In Proceedings of the 46th IEEE Annual Conference on Information Sciences and Systems, Princeton, NJ, USA, 21–23 March 2012; pp. 1–4. [Google Scholar]
- Leordeanu, M.; Sukthankar, R.; Sminchisescu, C. Generalized boundaries from multiple image interpretations. IEEE Trans. Pattern Anal. Mach. Intell. 2014, 36, 1312–1324. [Google Scholar] [CrossRef]
- Huss, J.E.; Pennline, J.A. A comparison of five benchmarks. In NASA Technical Memorandum 88956; NASA: Greenbelt, MD, USA, 1987. [Google Scholar]


| Parameter | Value |
|---|---|
| 0.5 | |
| 2.24 | |
| 1.57 | |
| 0.90 | |
| 2.70 | |
| 2.0 | |
| 1.0 | |
| 3.2 | |
| 0.8 | |
| 0.7854 | |
| 10 |
| Parameter | Value |
|---|---|
| Min Filter Size | 9 |
| Max Filter Size | 25 |
| Filter Size Increment Step | 2 |
| Aspect Ratio () | 0.8 |
| (Simple Even cells, ) | 4 |
| (Simple Odd cells, ) | 5 |
| Std dev (Gaussian) () |
| FGCA (std. dev) | %Age Increase | Stat Sig? | p-Value | |
|---|---|---|---|---|
| Reference Model | 58.44% (0.1146) | - | - | - |
| With SA | 62.69% (0.1204) | 7.3% | Yes | |
| With T-Junctions (gPb [76] based boundaries) | 59.48% (0.1127) | 1.78% | Yes | |
| With SA and T-Junctions (gPb [76] based boundaries) | 63.57% (0.1179) | 8.78% | Yes | 0 |
| Algorithm | FGCA |
|---|---|
| M. Maire etal, ECCV, 2010 [46] | 62% |
| Proposed Model | 63.6% |
| X. Ren etal, ECCV, 2006 [32] | 68.9% |
| P. Salembier etal, IEEE TIP, 2013 [39] | 71.3% |
| CL. Teo, etal, CVPR 2015 [34] | 74.7% |
| D. Hoiem etal, ICCV 2007 [33] | 79% |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ramenahalli, S. A Neurally Inspired Model of Figure Ground Organization with Local and Global Cues. AI 2020, 1, 436-464. https://doi.org/10.3390/ai1040028
Ramenahalli S. A Neurally Inspired Model of Figure Ground Organization with Local and Global Cues. AI. 2020; 1(4):436-464. https://doi.org/10.3390/ai1040028
Chicago/Turabian StyleRamenahalli, Sudarshan. 2020. "A Neurally Inspired Model of Figure Ground Organization with Local and Global Cues" AI 1, no. 4: 436-464. https://doi.org/10.3390/ai1040028
APA StyleRamenahalli, S. (2020). A Neurally Inspired Model of Figure Ground Organization with Local and Global Cues. AI, 1(4), 436-464. https://doi.org/10.3390/ai1040028





