Facing the Forecaster’s Dilemma: Reflexivity in Ocean System Forecasting
Abstract
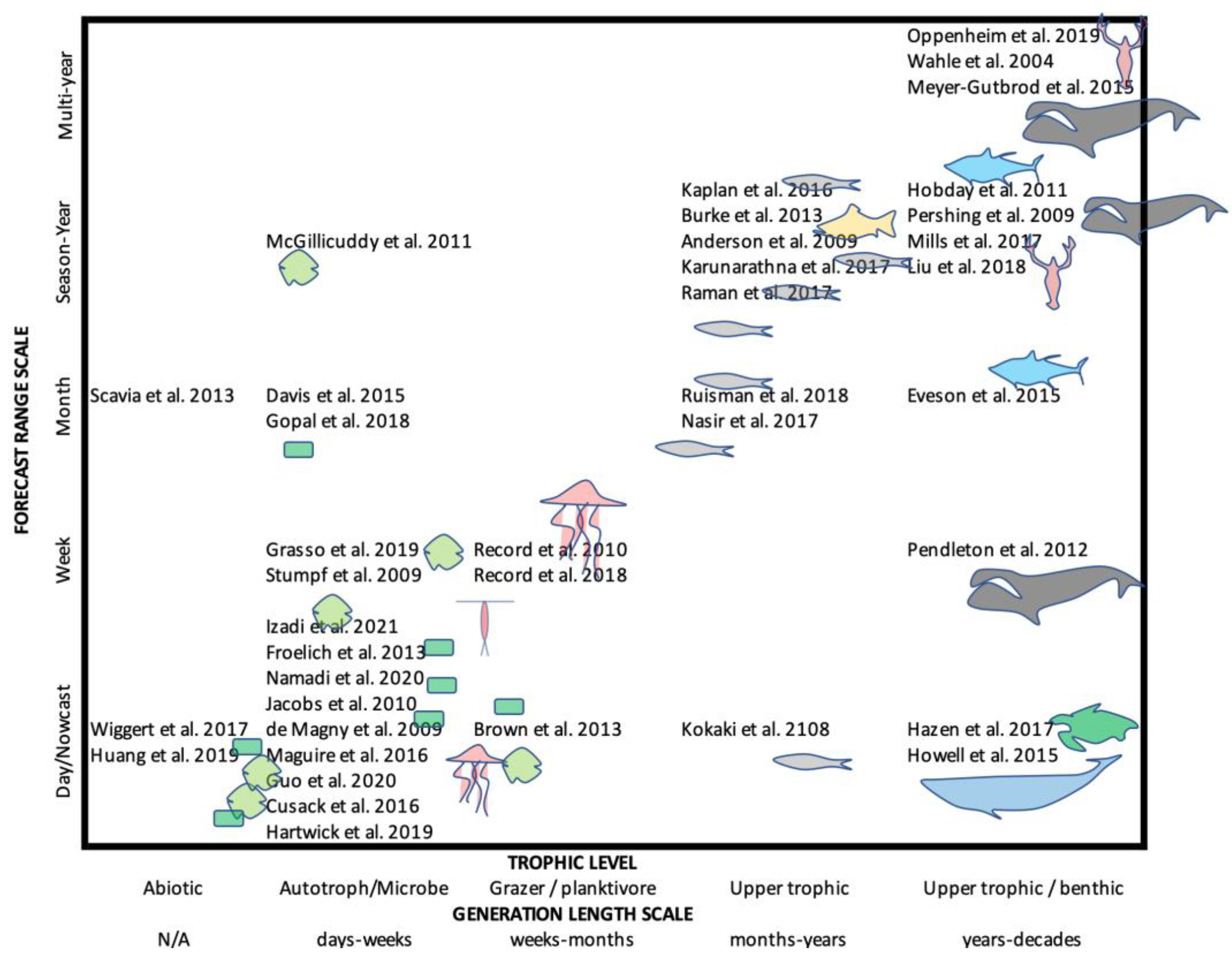
1. Introduction
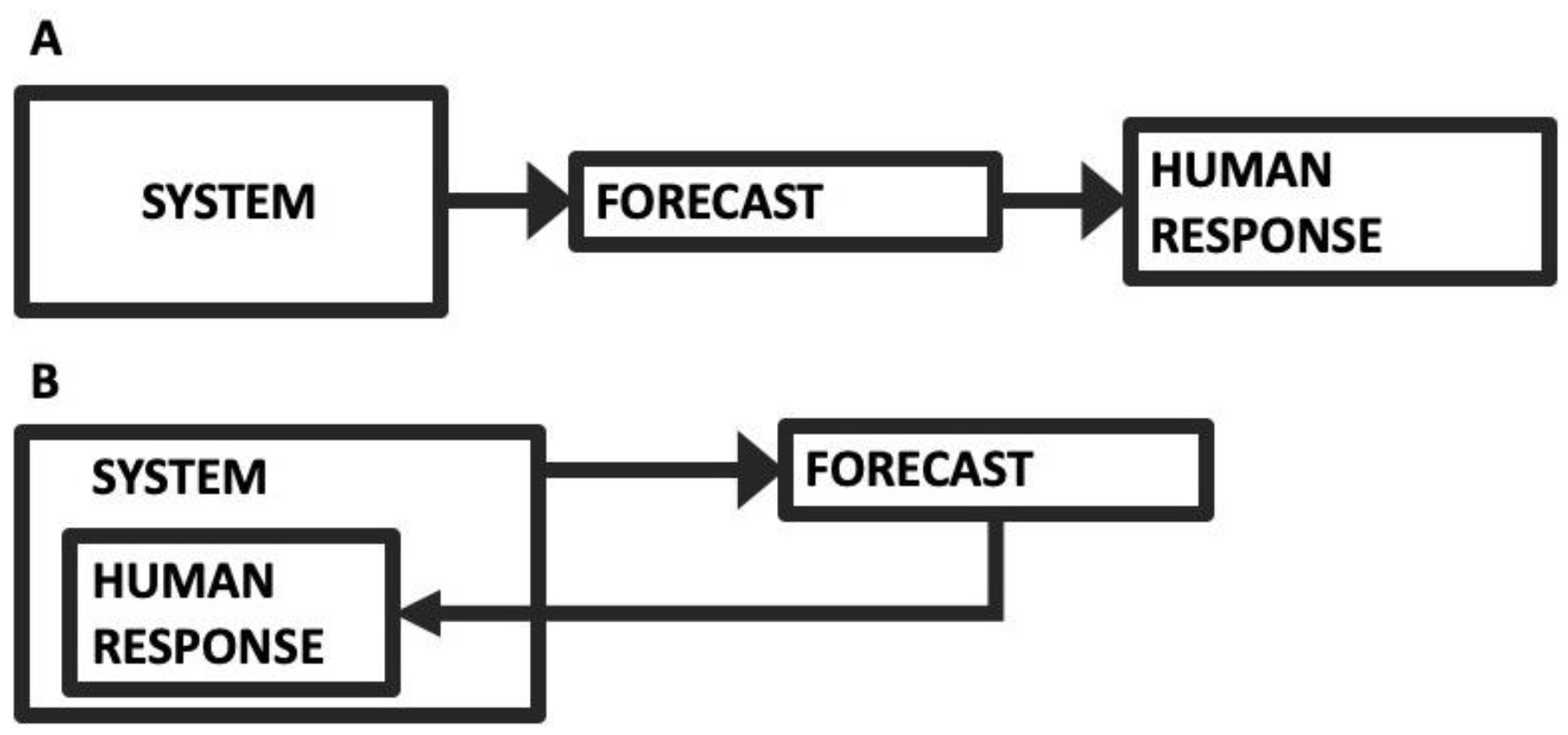
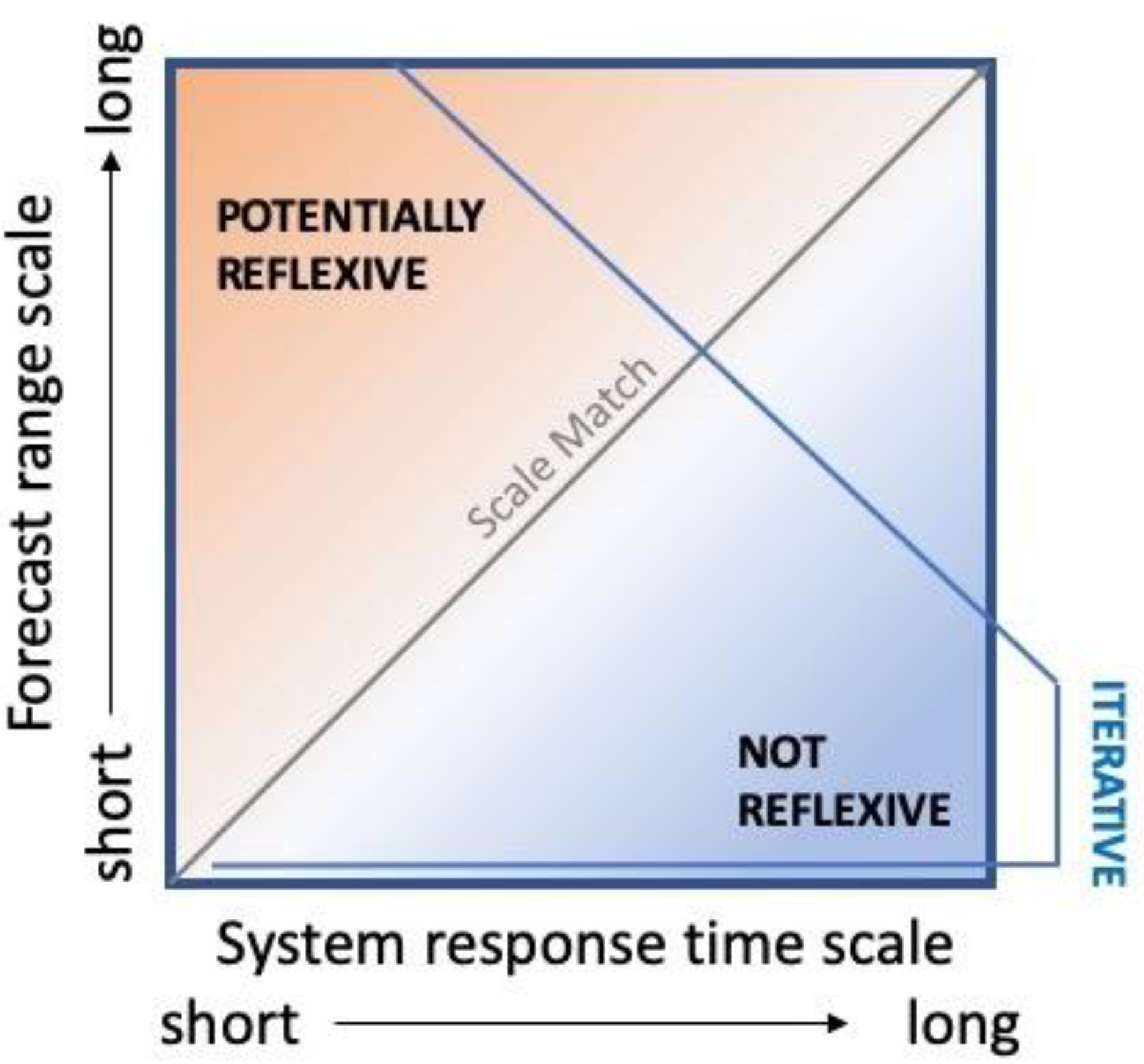
2. Theory
3. The Forecaster’s Dilemma
4. Solving the Forecaster’s Dilemma
4.1. Step 1: Identify How Reflexivity Could Occur in the System
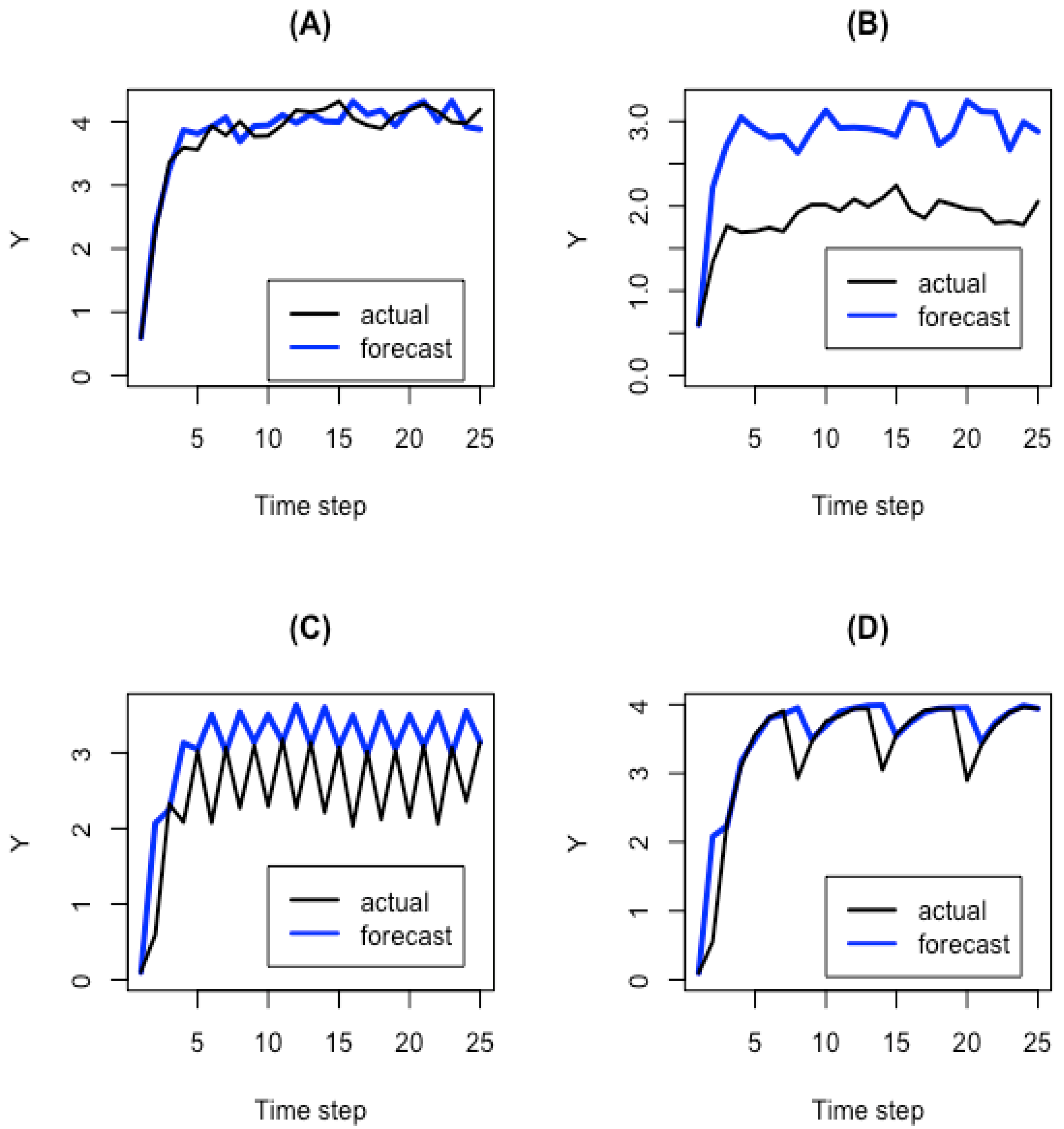
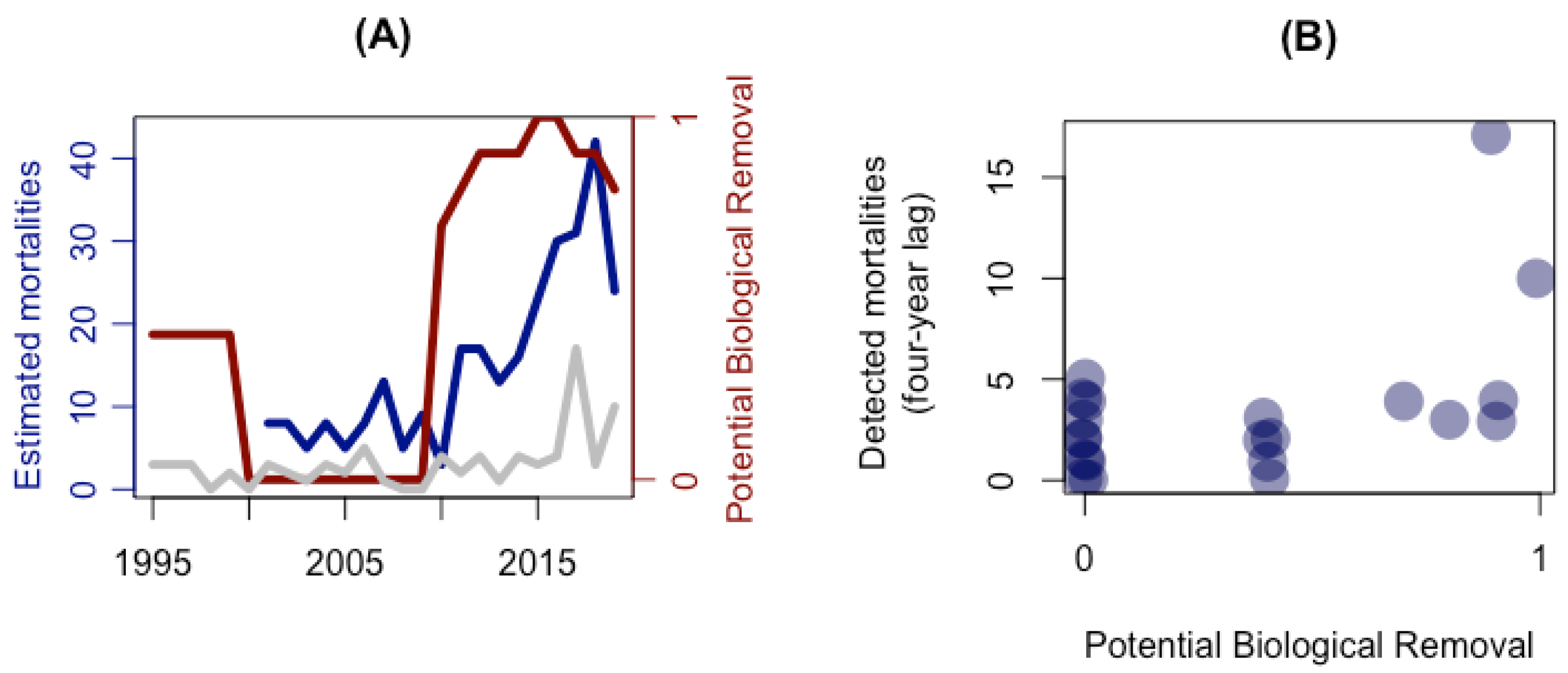
4.2. Step 2: Determine Whether Reflexivity Is Self-Defeating, Self-Fulfilling, or a Combination of Both
4.3. Step 3: Incorporate Human Response into a Forecast Model
5. Conclusions: Reflexivity in the Changing Ocean
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Alberti, M.; Asbjornsen, H.; Baker, L.A.; Brozović, N.; Drinkwater, L.E.; Drzyzga, S.A.; Jantz, C.A.; Fragoso, J.; Holland, D.S.; Kohler, T.A.; et al. Research on Coupled Human and Natural Systems (Chans): Approach, Challenges, and Strategies. Bull. Ecol. Soc. Am. 2011. [Google Scholar] [CrossRef]
- Kopec, M. A More Fulfilling (and Frustrating) Take on Reflexive Predictions. Philos. Sci. 2011, 78, 1249–1259. [Google Scholar] [CrossRef][Green Version]
- Henshel, R.L. The Boundary of the Self-Fulfilling Prophecy and the Dilemma of Social Prediction. Br. J. Sociol. 1982, 33, 511–528. [Google Scholar] [CrossRef]
- Simon, H. Bandwagon and Underdog Effects of Election Predictions,(1954,[1957]). Models Man 1954, 18, 245–253. [Google Scholar]
- Grunberg, E.; Modigliani, F. The Predictability of Social Events. J. Political Econ. 1954, 62, 465–478. [Google Scholar] [CrossRef]
- Stack, G.J. Reflexivity, Prediction and Paradox. Dialogos 1978, 13, 91–101. [Google Scholar]
- Soros, G. Fallibility, Reflexivity, and the Human Uncertainty Principle. J. Econ. Methodol. 2013, 20, 309–329. [Google Scholar] [CrossRef]
- Record, N.R.; Pershing, A.J. A Note on the Effects of Epidemic Forecasts on Epidemic Dynamics. PeerJ 2020, 8, e9649. [Google Scholar] [CrossRef]
- European Union. EU Regulation (Eu) No 1380/2013 of the European Parliament and of the Council of 11 December 2013 on the Common Fisheries Policy, Amending Council Regulations (Ec) No 1954/2003 and (Ec) No 1224/2009 and Repealing Council Regulations (Ec) No 2371/2002 and (Ec) No 639/2004 and Council Decision 2004/585/Ec. J. Eur. Union Bruss. 2013, 354, 22–61. [Google Scholar]
- McDonald, D.G.; Glynn, C.J.; Kim, S.-H.; Ostman, R.E. The Spiral of Silence in the 1948 Presidential Election. Commun. Res. 2001, 28, 139–155. [Google Scholar] [CrossRef]
- Smith, G.C. The Law of Forecast Feedback. Am. Stat. 1964, 18, 11–14. [Google Scholar]
- Dietze, M.C. Prediction in Ecology: A First-Principles Framework. Ecol. Appl. 2017, 27, 2048–2060. [Google Scholar] [CrossRef] [PubMed]
- Beinhocker, E.D. Reflexivity, Complexity, and the Nature of Social Science. J. Econ. Methodol. 2013, 20, 330–342. [Google Scholar] [CrossRef]
- Payne, M.R.; Hobday, A.J.; MacKenzie, B.R.; Tommasi, D.; Dempsey, D.P.; Fässler, S.M.; Haynie, A.C.; Ji, R.; Liu, G.; Lynch, P.D.; et al. Lessons from the First Generation of Marine Ecological Forecast Products. Front. Mar. Sci. 2017, 4, 289. [Google Scholar] [CrossRef]
- Andersen, K.H.; Berge, T.; Gonçalves, R.J.; Hartvig, M.; Heuschele, J.; Hylander, S.; Jacobsen, N.S.; Lindemann, C.; Martens, E.A.; Neuheimer, A.B.; et al. Characteristic Sizes of Life in the Oceans, from Bacteria to Whales. Annu. Rev. Mar. Sci. 2016, 8, 217–241. [Google Scholar] [CrossRef]
- Meyer-Gutbrod, E.L.; Greene, C.H.; Sullivan, P.J.; Pershing, A.J. Climate-Associated Changes in Prey Availability Drive Reproductive Dynamics of the North Atlantic Right Whale Population. Mar. Ecol. Prog. Ser. 2015, 535, 243–258. [Google Scholar] [CrossRef]
- Oppenheim, N.G.; Wahle, R.A.; Brady, D.C.; Goode, A.G.; Pershing, A.J. The Cresting Wave: Larval Settlement and Ocean Temperatures Predict Change in the American Lobster Harvest. Ecol. Appl. 2019, 29, e02006. [Google Scholar] [CrossRef]
- Froelich, B.; Bowen, J.; Gonzalez, R.; Snedeker, A.; Noble, R. Mechanistic and Statistical Models of Total Vibrio Abundance in the Neuse River Estuary. Water Res. 2013, 47, 5783–5793. [Google Scholar] [CrossRef]
- McGillicuddy, D.J. Models of harmful algal blooms: Conceptual, empirical, and numerical approaches. J. Mar. Syst. J. Eur. Assoc. Mar. Sci. Tech. 2010, 83, 105. [Google Scholar] [CrossRef]
- Gopal, K.; Shitan, M. Development of a Web Portal to Forecast the Monthly Mean Chlorophyll Concentration of the Waters off Peninsular Malaysia’s West Coast. Malays. J. Math. Sci. 2018, 12, 99–119. [Google Scholar]
- Wahle, R.A.; Incze, L.S.; Fogarty, M.J. First Projections of American Lobster Fishery Recruitment Using a Settlement Index and Variable Growth. Bull. Mar. Sci. 2004, 74, 101–114. [Google Scholar]
- Anderson, J.J.; Beer, W.N. Oceanic, Riverine, and Genetic Influences on Spring Chinook Salmon Migration Timing. Ecol. Appl. 2009, 19, 1989–2003. [Google Scholar] [CrossRef]
- De Magny, G.C.; Long, W.; Brown, C.W.; Hood, R.R.; Huq, A.; Murtugudde, R.; Colwell, R.R. Predicting the Distribution of Vibrio Spp. in the Chesapeake Bay: A Vibrio Cholerae Case Study. EcoHealth 2009, 6, 378–389. [Google Scholar] [CrossRef]
- Pershing, A.J.; Record, N.R.; Monger, B.C.; Mayo, C.A.; Brown, M.W.; Cole, T.V.; Kenney, R.D.; Pendleton, D.E.; Woodard, L.A. Model-Based Estimates of Right Whale Habitat Use in the Gulf of Maine. Mar. Ecol. Prog. Ser. 2009, 378, 245–257. [Google Scholar] [CrossRef]
- Stumpf, R.P.; Tomlinson, M.C.; Calkins, J.A.; Kirkpatrick, B.; Fisher, K.; Nierenberg, K.; Currier, R.; Wynne, T.T. Skill Assessment for an Operational Algal Bloom Forecast System. J. Mar. Syst. 2009, 76, 151–161. [Google Scholar] [CrossRef] [PubMed]
- Jacobs, J.M.; Rhodes, M.M.R.; Brown, C.W.; Hood, R.R.; Leight, A.; Long, W.; Wood, R. Predicting the Distribution of Vibrio Vulnificus in Chesapeake Bay; NOAA Technical Memorandum NOS NCCOS 112; NOAA National Centers for Coastal Ocean Science, Center for Coastal Environmental Health and Biomolecular Research, Cooperative Oxford Laboratory: Oxford, MD, USA, 2010. [Google Scholar]
- Record, N.; Pershing, A.; Runge, J.; Mayo, C.; Monger, B.; Chen, C. Improving Ecological Forecasts of Copepod Community Dynamics Using Genetic Algorithms. J. Mar. Syst. 2010, 82, 96–110. [Google Scholar] [CrossRef]
- Hobday, A.J.; Hartog, J.R.; Spillman, C.M.; Alves, O. Seasonal Forecasting of Tuna Habitat for Dynamic Spatial Management. Can. J. Fish. Aquat. Sci. 2011, 68, 898–911. [Google Scholar] [CrossRef]
- McGillicuddy, D.J.; Townsend, D.; He, R.; Keafer, B.; Kleindinst, J.; Li, Y.; Manning, J.; Mountain, D.; Thomas, M.; Anderson, D.M. Suppression of the 2010 Alexandrium Fundyense Bloom by Changes in Physical, Biological, and Chemical Properties of the Gulf of Maine. Limnol. Oceanogr. 2011, 56, 2411–2426. [Google Scholar] [CrossRef]
- Pendleton, D.E.; Sullivan, P.J.; Brown, M.W.; Cole, T.V.; Good, C.P.; Mayo, C.A.; Monger, B.C.; Phillips, S.; Record, N.R.; Pershing, A.J. Weekly Predictions of North Atlantic Right Whale Eubalaena Glacialis Habitat Reveal Influence of Prey Abundance and Seasonality of Habitat Preferences. Endanger. Species Res. 2012, 18, 147–161. [Google Scholar] [CrossRef][Green Version]
- Brown, C.W.; Hood, R.R.; Long, W.; Jacobs, J.; Ramers, D.; Wazniak, C.; Wiggert, J.; Wood, R.; Xu, J. Ecological Forecasting in Chesapeake Bay: Using a Mechanistic–empirical Modeling Approach. J. Mar. Syst. 2013, 125, 113–125. [Google Scholar] [CrossRef]
- Burke, B.J.; Peterson, W.T.; Beckman, B.R.; Morgan, C.; Daly, E.A.; Litz, M. Multivariate Models of Adult Pacific Salmon Returns. PLoS ONE 2013, 8, e54134. [Google Scholar] [CrossRef]
- Scavia, D.; Evans, M.A.; Obenour, D.R. A Scenario and Forecast Model for Gulf of Mexico Hypoxic Area and Volume. Environ. Sci. Technol. 2013, 47, 10423–10428. [Google Scholar] [CrossRef]
- Eveson, J.P.; Hobday, A.J.; Hartog, J.R.; Spillman, C.M.; Rough, K.M. Seasonal Forecasting of Tuna Habitat in the Great Australian Bight. Fish. Res. 2015, 170, 39–49. [Google Scholar] [CrossRef]
- Howell, E.A.; Hoover, A.; Benson, S.R.; Bailey, H.; Polovina, J.J.; Seminoff, J.A.; Dutton, P.H. Enhancing the Turtlewatch Product for Leatherback Sea Turtles, a Dynamic Habitat Model for Ecosystem-Based Management. Fish. Oceanogr. 2015, 24, 57–68. [Google Scholar] [CrossRef]
- Dabrowski, T.; Lyons, K.; Nolan, G.; Berry, A.; Cusack, C.; Silke, J. Harmful Algal Bloom Forecast System for Sw Ireland. Part I: Description and Validation of an Operational Forecasting Model. Harmful Algae 2016, 53, 64–76. [Google Scholar] [CrossRef] [PubMed]
- Kaplan, I.C.; Williams, G.D.; Bond, N.A.; Hermann, A.J.; Siedlecki, S.A. Cloudy with a Chance of Sardines: Forecasting Sardine Distributions Using Regional Climate Models. Fish. Oceanogr. 2016, 25, 15–27. [Google Scholar] [CrossRef]
- Maguire, J.; Cusack, C.; Ruiz-Villarreal, M.; Silke, J.; McElligott, D.; Davidson, K. Applied Simulations and Integrated Modelling for the Understanding of Toxic and Harmful Algal Blooms (Asimuth): Integrated Hab Forecast Systems for Europe’s Atlantic Arc. Harmful Algae 2016, 53, 160–166. [Google Scholar] [CrossRef]
- Mills, K.E.; Pershing, A.J.; Hernández, C.M. Forecasting the Seasonal Timing of Maine’s Lobster Fishery. Front. Mar. Sci. 2017, 4, 337. [Google Scholar] [CrossRef]
- Hazen, E.L.; Palacios, D.M.; Forney, K.A.; Howell, E.A.; Becker, E.; Hoover, A.L.; Irvine, L.; DeAngelis, M.; Bograd, S.J.; Mate, B.R.; et al. WhaleWatch: A Dynamic Management Tool for Predicting Blue Whale Density in the California Current. J. Appl. Ecol. 2017, 54, 1415–1428. [Google Scholar] [CrossRef]
- Nasir, N.; Samsudin, R.; Shabri, A. Forecasting of Monthly Marine Fish Landings Using Artificial Neural Network. Int. J. Adv. Soft Compu. Appl. 2017, 9, 75–89. [Google Scholar]
- Raman, R.K.; Sathianandan, T.; Sharma, A.; Mohanty, B. Modelling and Forecasting Marine Fish Production in Odisha Using Seasonal Arima Model. Natl. Acad. Sci. Lett. 2017, 40, 393–397. [Google Scholar] [CrossRef]
- Wiggert, J.D.; Hood, R.R.; Brown, C.W. Modeling hypoxia and its ecological consequences in chesapeake bay. In Modeling Coastal Hypoxia; Springer: New York, NY, USA, 2017; pp. 119–147. [Google Scholar]
- Kokaki, Y.; Tawara, N.; Kobayashi, T.; Hashimoto, K.; Ogawa, T. Sequential Fish Catch Forecasting Using Bayesian State Space Models. In Proceedings of the 2018 24th International Conference on Pattern Recognition (ICPR), Beijing, China, 20–24 August 2018; pp. 776–781. [Google Scholar]
- Liu, G.; Eakin, C.M.; Chen, M.; Kumar, A.; De La Cour, J.L.; Heron, S.F.; Geiger, E.F.; Skirving, W.J.; Tirak, K.V.; Strong, A.E. Predicting Heat Stress to Inform Reef Management: NOAA Coral Reef Watch’s 4-Month Coral Bleaching Outlook. Front. Mar. Sci. 2018, 5, 57. [Google Scholar] [CrossRef]
- Record, N.R.; Tupper, B.; Pershing, A.J. The Jelly Report: Forecasting Jellyfish Using Email and Social Media. Anthr. Coasts 2018, 1, 34–43. [Google Scholar]
- Rusiman, M.S.; Sufahani, S.; Robi, N.A.I.M.; Abdullah, A.W.; Azmi, N.A. Predictive Modelling of Marine Fish Landings in Malaysia. Adv. Appl. Stat. 2018, 53, 123–135. [Google Scholar] [CrossRef]
- Davis, B.J.; Jacobs, J.M.; Zaitchik, B.; DePaola, A.; Curriero, F.C. Vibrio Parahaemolyticus in the Chesapeake Bay: Operational in Situ Prediction and Forecast Models Can Benefit from Inclusion of Lagged Water Quality Measurements. Appl. Environ. Microbiol. 2019, 85, e01007-19. [Google Scholar] [CrossRef] [PubMed]
- Grasso, I.; Archer, S.D.; Burnell, C.; Tupper, B.; Rauschenberg, C.; Kanwit, K.; Record, N.R. The Hunt for Red Tides: Deep Learning Algorithm Forecasts Shellfish Toxicity at Site Scales in Coastal Maine. Ecosphere 2019, 10, e02960. [Google Scholar] [CrossRef]
- Hartwick, M.A.; Urquhart, E.A.; Whistler, C.A.; Cooper, V.S.; Naumova, E.N.; Jones, S.H. Forecasting Seasonal Vibrio Parahaemolyticus Concentrations in New England Shellfish. Int. J. Environ. Res. Public Health 2019, 16, 4341. [Google Scholar] [CrossRef] [PubMed]
- Huang, P.; Trayler, K.; Wang, B.; Saeed, A.; Oldham, C.E.; Busch, B.; Hipsey, M.R. An Integrated Modelling System for Water Quality Forecasting in an Urban Eutrophic Estuary: The Swan-Canning Estuary Virtual Observatory. J. Mar. Syst. 2019, 199, 103218. [Google Scholar] [CrossRef]
- Guo, J.; Dong, Y.; Lee, J.H. A Real Time Data Driven Algal Bloom Risk Forecast System for Mariculture Management. Mar. Pollut. Bull. 2020, 161, 111731. [Google Scholar] [CrossRef]
- Namadi, P.; Deng, Z. Modeling and Forecasting Vibrio Parahaemolyticus Concentrations in Oysters. Water Res. 2021, 189, 116638. [Google Scholar] [CrossRef]
- Taylor, B.L.; Wade, P.R.; De Master, D.P.; Barlow, J. Incorporating Uncertainty into Management Models for Marine Mammals. Conserv. Biol. 2000, 14, 1243–1252. [Google Scholar] [CrossRef]
- Lonergan, M. Potential Biological Removal and Other Currently Used Management Rules for Marine Mammal Populations: A Comparison. Mar. Policy 2011, 35, 584–589. [Google Scholar] [CrossRef]
- Barlow, J.; Swartz, S.L.; Eagle, T.C.; Wade, P.R. US Marine Mammal Stock Assessments: Guidelines for Preparation, Background, and a Summary of the 1995 Assessments. NOAA Tech. Memo. NMFS-OPR 1995, 6, 73. [Google Scholar]
- Barraquand, F.; Picoche, C.; Detto, M.; Hartig, F. Inferring Species Interactions Using Granger Causality and Convergent Cross Mapping. Theor. Ecol. 2021, 14, 87–105. [Google Scholar] [CrossRef]
- San Liang, X. Information Flow and Causality as Rigorous Notions Ab Initio. Phys. Rev. E 2016, 94, 052201. [Google Scholar] [CrossRef] [PubMed]
- Ye, H.; Beamish, R.J.; Glaser, S.M.; Grant, S.C.; Hsieh, C.-h.; Richards, L.J.; Schnute, J.T.; Sugihara, G. Equation-Free Mechanistic Ecosystem Forecasting Using Empirical Dynamic Modeling. Proc. Natl. Acad. Sci. USA 2015, 112, E1569–E1576. [Google Scholar] [CrossRef] [PubMed]
- Pettis, H.; Pace, R.; Hamilton, P. North Atlantic Right Whale Consortium 2020 Annual Report Card. In Report to the North Atlantic Right Whale Consortium; NOAA: Washington, DC, USA, 2021. [Google Scholar]
- Davies, K.T.; Brillant, S.W. Mass Human-Caused Mortality Spurs Federal Action to Protect Endangered North Atlantic Right Whales in Canada. Mar. Policy 2019, 104, 157–162. [Google Scholar] [CrossRef]
- Record, N.R.; Runge, J.A.; Pendleton, D.E.; Balch, W.M.; Davies, K.T.; Pershing, A.J.; Johnson, C.L.; Stamieszkin, K.; Ji, R.; Feng, Z.; et al. Rapid Climate-Driven Circulation Changes Threaten Conservation of Endangered North Atlantic Right Whales. Oceanography 2019, 32, 162–169. [Google Scholar] [CrossRef]
- Rätz, H.-J.; Charef, A.; Abella, A.; Colloca, F.; Ligas, A.; Mannini, A.; Lloret, J. A Medium-Term, Stochastic Forecast Model to Support Sustainable, Mixed Fisheries Management in the Mediterranean Sea. J. Fish Biol. 2013, 83, 921–938. [Google Scholar] [CrossRef]
- Bowden, R.J. Feedback Forecasting Games: An Overview. J. Forecast. 1989, 8, 117–127. [Google Scholar] [CrossRef]
- Verweij, M.; Van Densen, W.; Mol, A. The Tower of Babel: Different Perceptions and Controversies on Change and Status of North Sea Fish Stocks in Multi-Stakeholder Settings. Mar. Policy 2010, 34, 522–533. [Google Scholar] [CrossRef]
- Rothe, D. Jellyfish Encounters: Science, Technology and Security in the Anthropocene Ocean. Crit. Stud. Secur. 2020, 8, 145–159. [Google Scholar] [CrossRef]
- Chandler, D.; Pugh, J. Islands and the Rise of Correlational Epistemology in the Anthropocene: Rethinking the Trope of the “Canary in the Coalmine”. Isl. Stud. J. 2020. [Google Scholar] [CrossRef]
- Chen, L.; Ma, R.; Hannák, A.; Wilson, C. Investigating the Impact of Gender on Rank in Resume Search Engines. In Proceedings of the Proceedings of the 2018 CHI Conference on Human Factors in Computing Systems, Montreal, QC, Canada, 21–26 April 2018; pp. 1–14. [Google Scholar]
- Pershing, A.J.; Mills, K.E.; Dayton, A.M.; Franklin, B.S.; Kennedy, B.T. Evidence for Adaptation from the 2016 Marine Heatwave in the Northwest Atlantic Ocean. Oceanography 2018, 31, 152–161. [Google Scholar] [CrossRef]
- Hobday, A.J.; Hartog, J.R.; Manderson, J.P.; Mills, K.E.; Oliver, M.J.; Pershing, A.J.; Siedlecki, S. Ethical Considerations and Unanticipated Consequences Associated with Ecological Forecasting for Marine Resources. ICES J. Mar. Sci. 2019, 76, 1244–1256. [Google Scholar] [CrossRef]
- Crawford, K.; Schultz, J. Big Data and Due Process: Toward a Framework to Redress Predictive Privacy Harms?(2014). Boston Coll. Law Rev. 2014, 55, 93. [Google Scholar]
- Shah, H. Algorithmic Accountability. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2018, 376, 20170362. [Google Scholar] [CrossRef]
- Grasso, I.; Russell, D.; Matthews, A.; Matthews, J.; Record, N.R. Applying Algorithmic Accountability Frameworks with Domain-Specific Codes of Ethics: A Case Study in Ecosystem Forecasting for Shellfish Toxicity in the Gulf of Maine. In Proceedings of the 2020 ACM-IMS on Foundations of Data Science Conference, New York, NY, USA, 19–20 October 2020; pp. 83–91. [Google Scholar]
- Cramer, E.Y.; Ray, E.L.; Lopez, V.K.; Bracher, J.; Brennen, A.; Rivadeneira, A.J.C.; Gerding, A.; Gneiting, T.; House, K.H.; Huang, Y.; et al. Evaluation of Individual and Ensemble Probabilistic Forecasts of COVID-19 Mortality in the US. medRxiv 2021. [Google Scholar] [CrossRef]
- Ioannidis, J.P.; Cripps, S.; Tanner, M.A. Forecasting for COVID-19 Has Failed. Int. J. Forecast. 2020. In Press. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Record, N.R.; Pershing, A.J. Facing the Forecaster’s Dilemma: Reflexivity in Ocean System Forecasting. Oceans 2021, 2, 738-751. https://doi.org/10.3390/oceans2040042
Record NR, Pershing AJ. Facing the Forecaster’s Dilemma: Reflexivity in Ocean System Forecasting. Oceans. 2021; 2(4):738-751. https://doi.org/10.3390/oceans2040042
Chicago/Turabian StyleRecord, Nicholas R., and Andrew J. Pershing. 2021. "Facing the Forecaster’s Dilemma: Reflexivity in Ocean System Forecasting" Oceans 2, no. 4: 738-751. https://doi.org/10.3390/oceans2040042
APA StyleRecord, N. R., & Pershing, A. J. (2021). Facing the Forecaster’s Dilemma: Reflexivity in Ocean System Forecasting. Oceans, 2(4), 738-751. https://doi.org/10.3390/oceans2040042





