Previous Article in Journal
Combined Effect of Zinc Oxide and Titanium Dioxide Nanoparticles on Color Stability and Antifungal Activity of Maxillofacial Silicone Elastomers: An In Vitro Study
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Prosthesis
Volume 7
Issue 5
10.3390/prosthesis7050123
prosthesis-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Regenerated Bone Quality as a Determinant of Bone Turnover and Prognosis in Short Plateau Implants: A Finite Element Study

by
Vladislav Demenko
1,
Igor Linetskiy
2,
Oleg Yefremov
3,
Larysa Linetska
4,
Natalia Smetankina
5,* and
Andrii Kondratiev
6,7,*
1
Department of Aircraft Strength, National Aerospace University “Kharkiv Aviation Institute”, Vadym Manko Str. 17, 61070 Kharkiv, Ukraine
2
Department of Oral and Maxillofacial Surgery, General University Hospital in Prague, U Nemocnice 499/2, 128 08 Prague 2, Czech Republic
3
Department of Postgraduate Education, National Aerospace University “Kharkiv Aviation Institute”, Vadym Manko Str. 17, 61070 Kharkiv, Ukraine
4
Department of Rehabilitation Medicine, National Technical University “Kharkiv Polytechnic Institute”, Kyrpychova Str. 2, 61002 Kharkiv, Ukraine
5
Department of Vibration and Thermostability Studies, A. Pidgornyi Institute of Mechanical Engineering Problems of the National Academy of Sciences of Ukraine, Pozharskogo Str. 2/10, 61046 Kharkiv, Ukraine
6
Institute of Lightweight Engineering and Polymer Technology, TUD Dresden University of Technology, 01069 Dresden, Germany
7
Department of Engineering, University of Cambridge, Trumpington Str., Cambridge CB2 1PZ, UK
*
Authors to whom correspondence should be addressed.
Prosthesis 2025, 7(5), 123; https://doi.org/10.3390/prosthesis7050123
Submission received: 12 August 2025 / Revised: 12 September 2025 / Accepted: 22 September 2025 / Published: 25 September 2025
(This article belongs to the Special Issue Finite Element Analysis in Prosthesis and Orthosis Research)
Browse Figures
Versions Notes

Abstract

Background/Objectives: Finite element analysis (FEA) can predict biomechanical performance of dental implants in compromised bone. In the posterior maxilla, low bone density, thin cortex, and variable regenerated bone stiffness may lead to pathological peri-implant strains. This study examined the effects of implant diameter, cortical thickness, cancellous bone type, and regenerated bone elasticity on strain distribution in short plateau (Bicon SHORT®) implants. Methods: Three-dimensional FEA models of type III and IV maxillae with cortical layers of 1.0, 0.75, and 0.5 mm were developed. Implants of 4.5, 5.0, and 6.0 mm diameter were tested, with regenerated bone elasticity set to 25–100% of cortical values. An oblique load of 120.9 N at 75° was applied under full osseointegration, and first principal strains were compared with Frost’s 3000 με threshold. Results: Cortical strains remained at physiological levels, but cancellous bone in type IV often exceeded 3000 με, especially with smaller diameters and low regenerated stiffness. Enlarging implant diameter to 6.0 mm lowered cancellous maximal first principal strain by up to 56% in type III and 36% in type IV bone. Reduced regenerated bone elasticity markedly increased risk, particularly with cortical thickness < 0.75 mm. Conclusions: Biomechanical risk depends on implant diameter and regenerated bone quality. Wide short implants (6.0 mm) most effectively limited pathological strain under low cortical support and poor regenerated stiffness. Patient-specific FEA may guide implant choice and improve outcomes in atrophic maxilla rehabilitation.

1. Introduction

The long-term stability of dental implants [1,2], which depends on secure fixation within the surrounding bone, is primarily determined by maintaining physiological strain levels and avoiding excessive stresses in peri-implant tissues. This stability is influenced by multiple aspects, such as bone volume at the site, implant geometry and dimensions, as well as the mechanical features of both the bone and implant materials [3,4]. Continuous and balanced bone remodeling plays a central role in preserving osseointegration throughout the functional lifetime of the implant [5,6].
Despite the generally high survival rates of dental implants, biomechanical challenges still limit predictable long-term outcomes [7,8]. Failures occur most frequently in the posterior maxilla, where bone density is low, alveolar height is reduced, and masticatory loading is high [9]. In such compromised sites, the use of short implants has been proposed as an alternative to sinus augmentation and subsequent conventional implant placement [10,11]. Clinical data demonstrate that short implants can achieve survival rates comparable to longer implants [12]. Nonetheless, their reduced length decreases the bone–implant contact area, increasing stress and strain concentration in the crestal bone compared with standard implants. To mitigate this drawback, wide short implants have been introduced for molar regions with limited bone height and higher occlusal loads. By enlarging the functional surface area, these implants improve load distribution and reduce strain levels, particularly around the implant neck—a key zone of the bone–implant interface [13].
Plateau implants, first introduced in 1985, constitute a specific design class characterized by a root form with circular fins or plateaus instead of conventional threads. The Bicon® screwless system, based on this plateau body design, is one of the most widely adopted [14]. Compared with threaded implants of equal dimensions, plateau implants provide nearly 30% greater surface area. Their short length (<8 mm) minimizes the necessity for invasive procedures such as sinus lifting or grafting, making them particularly suitable for patients with limited bone height. The increased contact area promotes more uniform stress transfer and lowers peri-implant strain, an especially important feature in atrophic maxillae. Furthermore, plateau implants are known to reduce marginal bone loss. An additional advantage is the presence of “healing chambers”—spaces generated between implant fins and bone due to drill design. These voids initially fill with blood clots, which are gradually replaced by woven bone through intramembranous-like healing [15].
Extensive research has investigated the survival and biomechanical behavior of short implants, analyzing how length, diameter, macrogeometry, and bone healing responses affect outcomes. Continuous modifications of plateau root-form implants have raised their cumulative survival rates above 90%, while also enhancing the biological processes during the early stages of bone integration.
Sufficient bone volume is one of the main prerequisites for predictable implant osseointegration. Autologous bone harvested from the patient remains the gold-standard grafting material [16]. It offers superior biological compatibility, absence of immune reaction, low risk of disease transmission, and a high capacity for osseointegration, thereby supporting long-term implant stability. Moreover, autogenous grafts can be used together with adjunctive materials such as growth factors, bone morphogenetic proteins, or synthetic scaffolds to accelerate regeneration and enhance bone quality.
For plateau implants, placing autogenous bone within the gap between the implant neck and the osteotomy wall is often recommended, particularly in subcrestal placement where the cervical space is larger. This approach promotes better marginal bone integration, strengthening anchorage and improving load-bearing performance. However, the mechanical performance of regenerated bone remains uncertain; its elasticity and strength strongly influence implant success but are difficult to predict. Since physiological bone turnover is the main mechanism protecting against bone loss, understanding the behavior of regenerated bone becomes critical [17].
Bone strain is widely acknowledged as a key mechanical signal regulating bone turnover and maintaining its mechanical integrity, mediated through mechanosensitive structures such as primary cilia in osteogenic cells [18]. Throughout life, bone architecture adapts to functional loading via this mechanobiological feedback [19,20]. Frost’s mechanostat framework connects bone mass to applied strain, describing how modeling and remodeling maintain structural competence. According to Frost [21], when the minimum effective strain pathological threshold (MESp, ~3000 με) is exceeded, microdamage accumulation may cause bone failure. Conversely, maintaining strain levels above the modeling threshold (MESm, 1000–1500 με) is essential to stimulate bone formation and maintain bone mass [22].
Therefore, predicting implant prognosis and supporting favorable bone turnover requires selecting implant designs that maintain strain within safe limits while also fitting available bone volume. Preoperative evaluation typically includes morphometric analysis of the maxilla, with attention to the dimensions and location of the planned site. Nonetheless, bone mechanical properties are often underestimated, despite their critical importance in preventing resorption. In thin atrophic ridges, cancellous bone provides poor mechanical support, and the stiffness of regenerated bone in the cervical region becomes decisive. Reinforcement with autologous bone may strengthen this area and improve resistance to occlusal forces. Thus, implant selection remains particularly challenging in poor-quality bone with limited cortical support and high variability of mechanical properties [23,24].
The complex interaction between implant geometry, bone properties, and strain distribution can be studied effectively in silico by finite element analysis (FEA), a powerful computational approach for simulating implant biomechanics under masticatory loading [9,12,25,26]. FEA provides insights into how implant diameter, length, and shape interact with bone density and volume, as well as how regenerated bone influences strain concentration [9,12,27].
Although numerous FEA studies have assessed peri-implant strains across different implant geometries and bone types [9,12,25,26,28,29], their results are highly variable, and few directly relate strain ranges to pathological thresholds in the critical crestal region. As a result, guidance on implant size selection for extremely resorbed maxillae remains limited [30].
The objective of this investigation was therefore to evaluate the impact of short finned implants, crestal bone thickness, and regenerated bone stiffness on peri-implant strain magnitudes through FEA modeling. By doing so, this study sought to clarify bone turnover dynamics in the posterior maxilla and to provide recommendations for selecting Bicon Integra-CP™ short plateau implants that ensure sufficient load-bearing capacity while preventing cortical and cancellous bone loss.

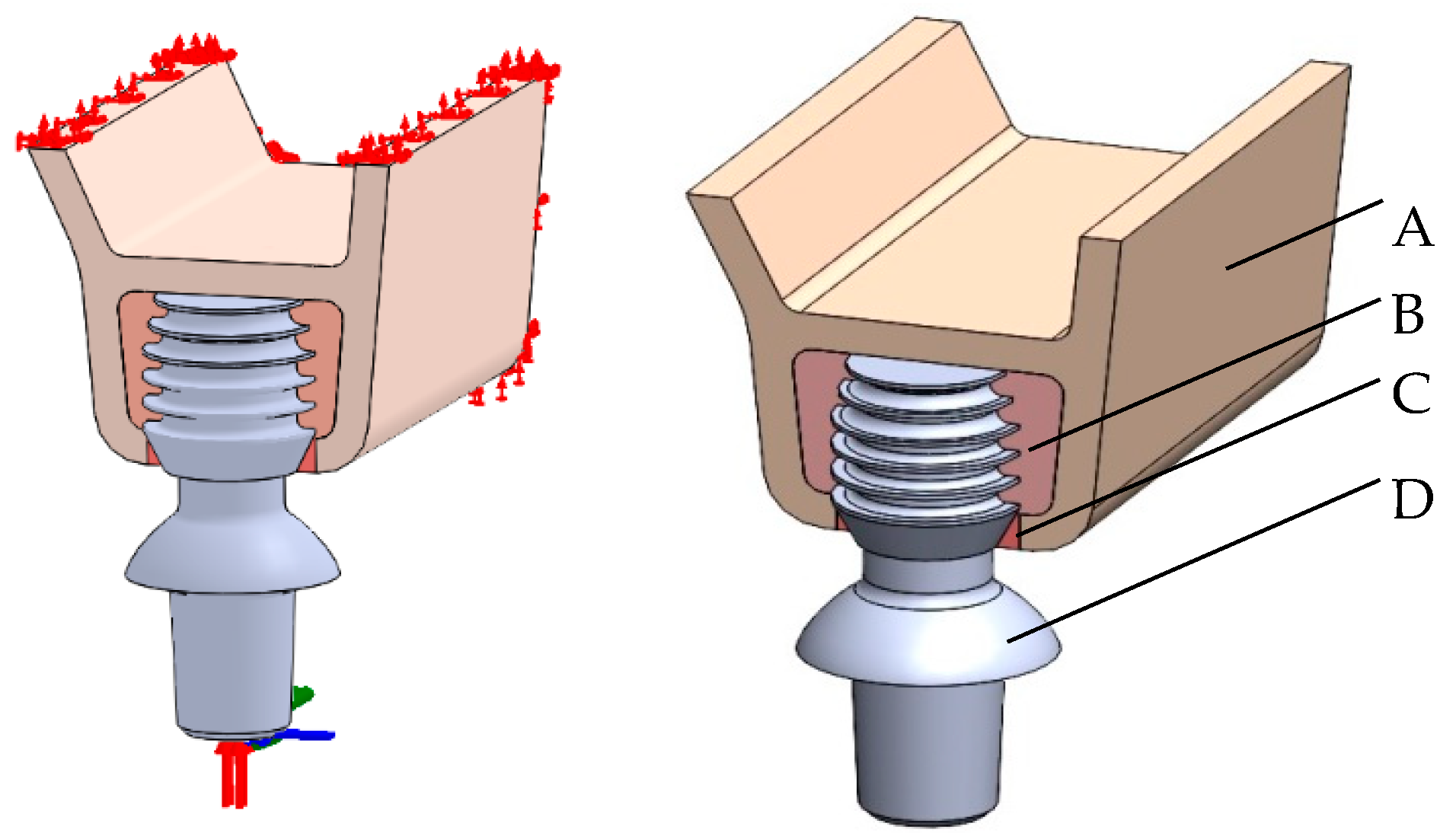
2. Materials and Methods

Three configurations of Bicon SHORT® implants were considered in this study: 4.5 × 5.0 mm (N), 5.0 × 5.0 mm (M), and 6.0 × 5.0 mm (W), each having the same height of 5.0 mm. The external and abutment geometries were reconstructed based on measurements performed with digital calipers, complemented by high-resolution imaging and light optical microscopy.
A solid model of a posterior maxilla alveolar bone segment was reconstructed from computed tomographic (CT) images (DICOM format) of anonymous patients from the authors’ database, allowing clear identification of cortical and cancellous bone contours. Simplified 3D geometries, 30 mm in length, were generated in SolidWorks 2022 (Dassault Systèmes SolidWorks Corporation, Waltham, MA, USA) based on these data (Figure 1).
The implants were positioned at the crestal level within nine maxillary posterior segment models, which simulated type III and IV bone according to the Lekholm and Zarb classification. Variations in cancellous bone quality were represented by assigning distinct elastic modulus values.
All materials were assumed to be homogeneous, linearly elastic, and isotropic. The implant–abutment assembly was modeled as a single titanium alloy unit (elastic modulus 114 GPa, Poisson’s ratio 0.34) [10,31]. The Poisson’s ratio for both cortical and cancellous bone was set to 0.30 [7,19,32]. Cortical bone was assigned an elastic modulus of 13.7 GPa [10,19,33]; cancellous bone was set to 1.37 GPa for type III and 0.69 GPa for type IV.
Regenerated bone in the cervical gap was modeled as an isotropic elastic solid with four elasticity levels, expressed as a percentage of the adjacent cortical bone modulus (13.7 GPa): E1: 100% (13.7 GPa); E2: 75% (10.3 GPa); E3: 50% (6.85 GPa); E4: 25% (3.43 GPa).
In all models, regenerated bone was represented as a cervical ring-shaped layer surrounding the implant neck, extending circumferentially around the implant body. The vertical height of this region was set equal to the thickness of the crestal cortical bone in each scenario (0.5, 0.75, or 1.0 mm), while its radial thickness corresponded to the gap between the implant neck and the osteotomy wall. This configuration reflects the clinical scenario of graft material placement in the subcrestal gap during plateau implant installation. The elastic modulus of this regenerated region was varied according to the four predefined levels (E1–E4) to simulate different stages of healing and maturation.
The range for the elastic modulus of regenerated bone (25–100% of cortical stiffness) was chosen to reflect the variability reported in experimental studies. In work [34], regenerated intraosseous bone measured after 6 weeks exhibited only about 5% of cortical stiffness, while at 12 weeks values increased up to ~50%. Similarly, in study [35], early-stage regenerated bone showed elastic moduli of ~3–6 GPa, which approached 9–10 GPa in more mature tissue, close to cortical bone values.
Disto-mesial surfaces of the bone segment, as well as the upper cortical shell planes, were fully constrained (Figure 2).
Functional loading was applied to the center of a 7 Series Low 0° abutment as a 3D oblique force of 120.9 N [36,37] at approximately 75° to the abutment top surface. This load was decomposed into axial (116.3 N), lingual (17.4 N), and disto-mesial (23.8 N) components, the latter two combining into a horizontal component of 29.5 N in the plane of the bone–implant interface. All implants were assumed to be fully osseointegrated.
Numerical simulations were carried out in SolidWorks Simulation. To establish the appropriate discretization, a mesh refinement study was performed by progressively reducing the element size from 1.8 mm to 0.010 mm. Convergence was reached once changes in the maximum first principal strain at the bone–implant interface were below 2%. The final mesh incorporated a minimum element size of 0.020 mm in the cervical region, which provided stable maximal first principal strains values within the convergence threshold. Verification of the finite element setup was performed by assessing force balance at the implant–bone assembly. The total reaction forces at the boundary constraints were compared with the applied oblique load of 120.9 N, and the discrepancy was consistently below 1%, confirming numerical stability of the model. For validation, the simulated cortical strain values under oblique loading (approximately 500–1300 με) were compared with ranges reported in experimental and numerical studies of implant-supported restorations. Moreover, the observed increase in cancellous strain with decreasing cortical thickness and reduced bone quality followed trends described in previous finite element analyses. These comparisons support both the credibility and the robustness of the present computational model.
Each model contained between 1,659,134 and 2,000,652 finite elements and 2,238,052 to 2,695,410 nodes. The distribution per component was as follows: cortical bone (94,903–199,426 elements), cancellous bone (727,326–909,618), implant (287,247–288,284), and regenerated bone (74,987–200,452). The corresponding node counts were 157,747–302,449; 1,036,339–1,291,758; 402,509–419,792; and 109,007–287,296, respectively (Figure 3).
First principal strains (FPS) were selected as the mechanical indicator of bone turnover. Their spatial distributions in peri-implant bone were analyzed for all bone–implant configurations. The maximal FPS (MFPS) values along the critical bone–implant contact line were compared against Frost’s pathological threshold (MESp = 3000 με) [19,21,22] to evaluate the likelihood of pathological remodeling and to inform implant size recommendations for the studied conditions.

3. Results

Figure 4 presents the spatial distribution of first principal strains (FPS) along the bone–implant interface.

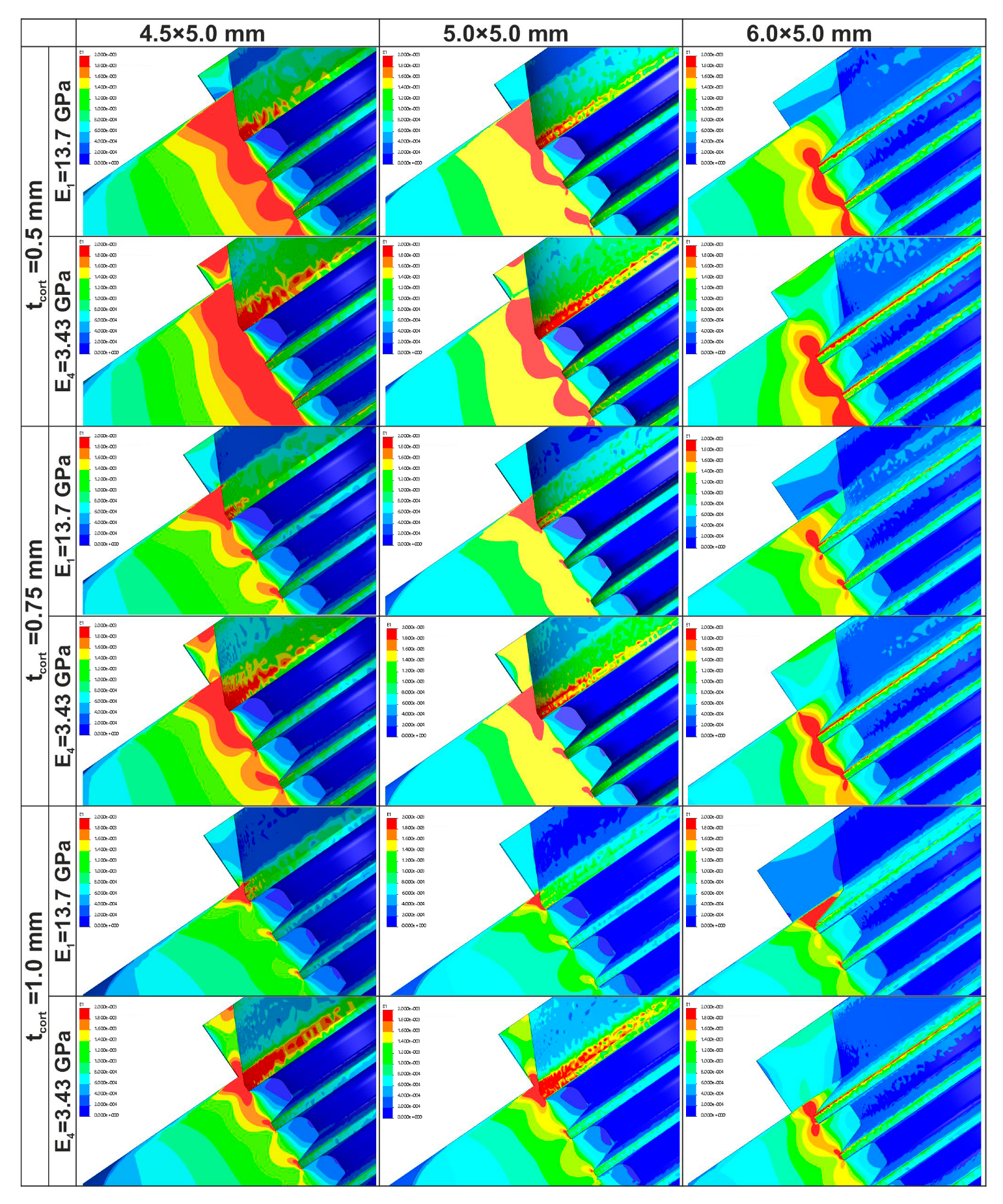
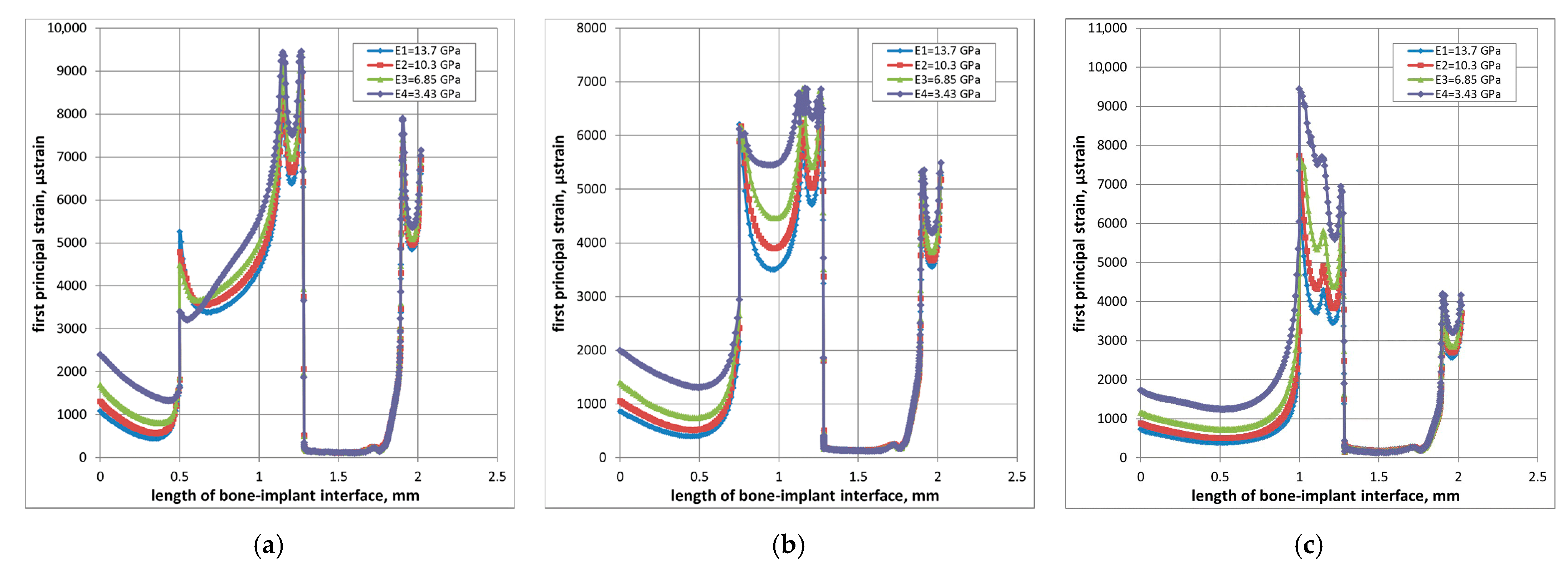
3.1. Strain Localization

In cortical bone, the maximal first principal strains (MFPS) were consistently located on the crestal surface (Figure 4 and Figure 5). Across all implant diameters, bone qualities, regenerated bone elasticities, and cortical thicknesses, no overstrains (MFPS > 3000 με) were observed in the implant neck region. The MFPS in the crestal cortical bone remained within the safe physiological range (520–1320 με), with the 6.0 × 5.0 mm (W) implant producing the lowest values (520–660 με) and the 4.5 × 5.0 mm (N) implant the highest (780–1320 με). In cancellous bone, MFPS were located at the tip of the first fin.
These values were influenced by implant diameter, bone quality, regenerated bone elasticity, and cortical bone thickness (Figure 6).

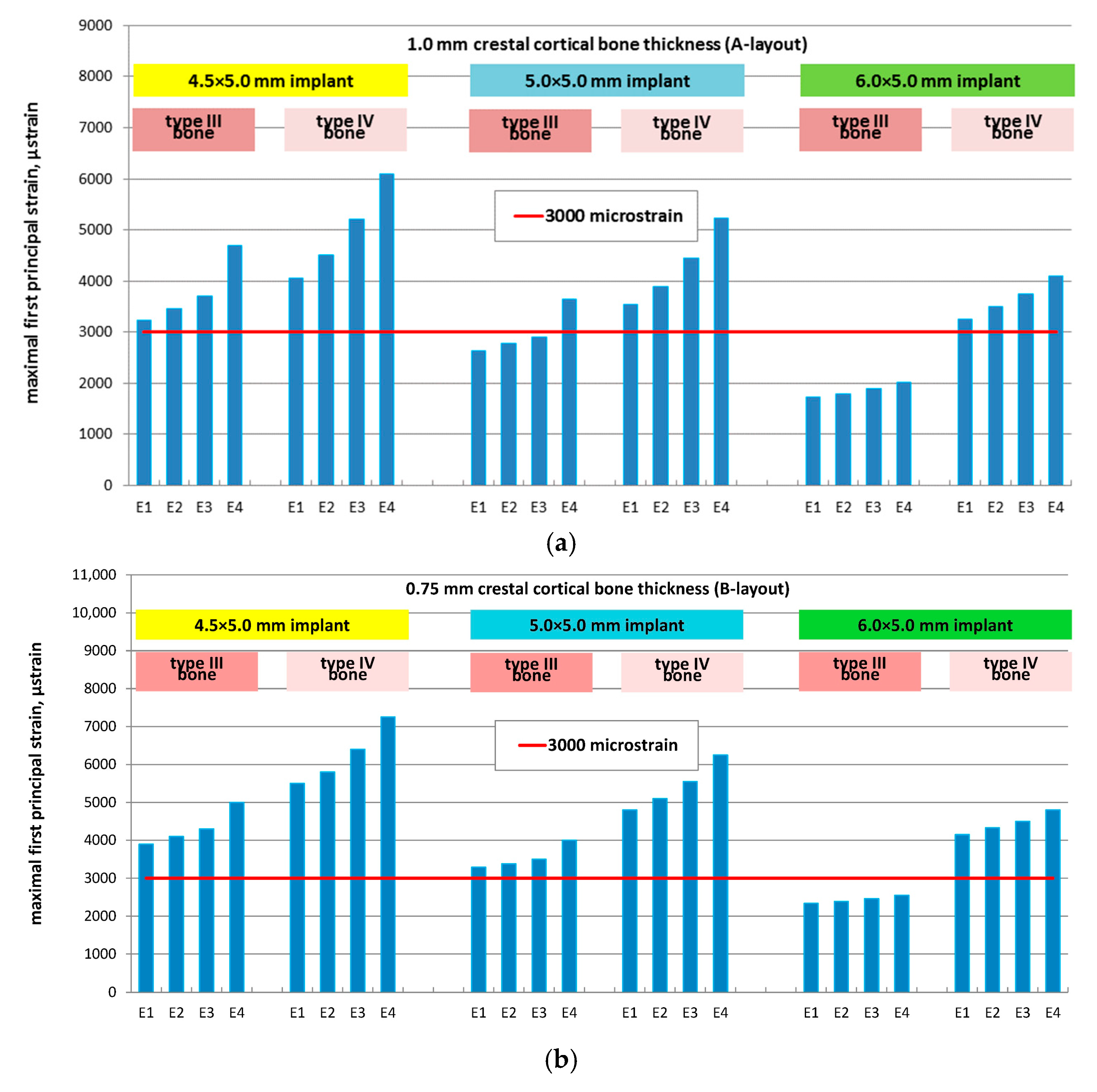
3.2. Effect of Implant Diameter

For regenerated bone elasticity levels E1–E4 and type III bone, increasing the implant diameter from 4.5 mm to 6.0 mm reduced MFPS as follows:
  • A-layout (1.0 mm cortical): 47%, 48%, 50%, and 56%
  • B-layout (0.75 mm cortical): 40%, 42%, 44%, and 49%
  • C-layout (0.5 mm cortical): 38%, 39%, 40%, and 43%
For type IV bone, the corresponding reductions were:
  • A-layout: 20%, 23%, 26%, and 32%
  • B-layout: 24%, 26%, 29%, and 34%
  • C-layout: 30%, 31%, 33%, and 36%
These trends are summarized in Figure 7.

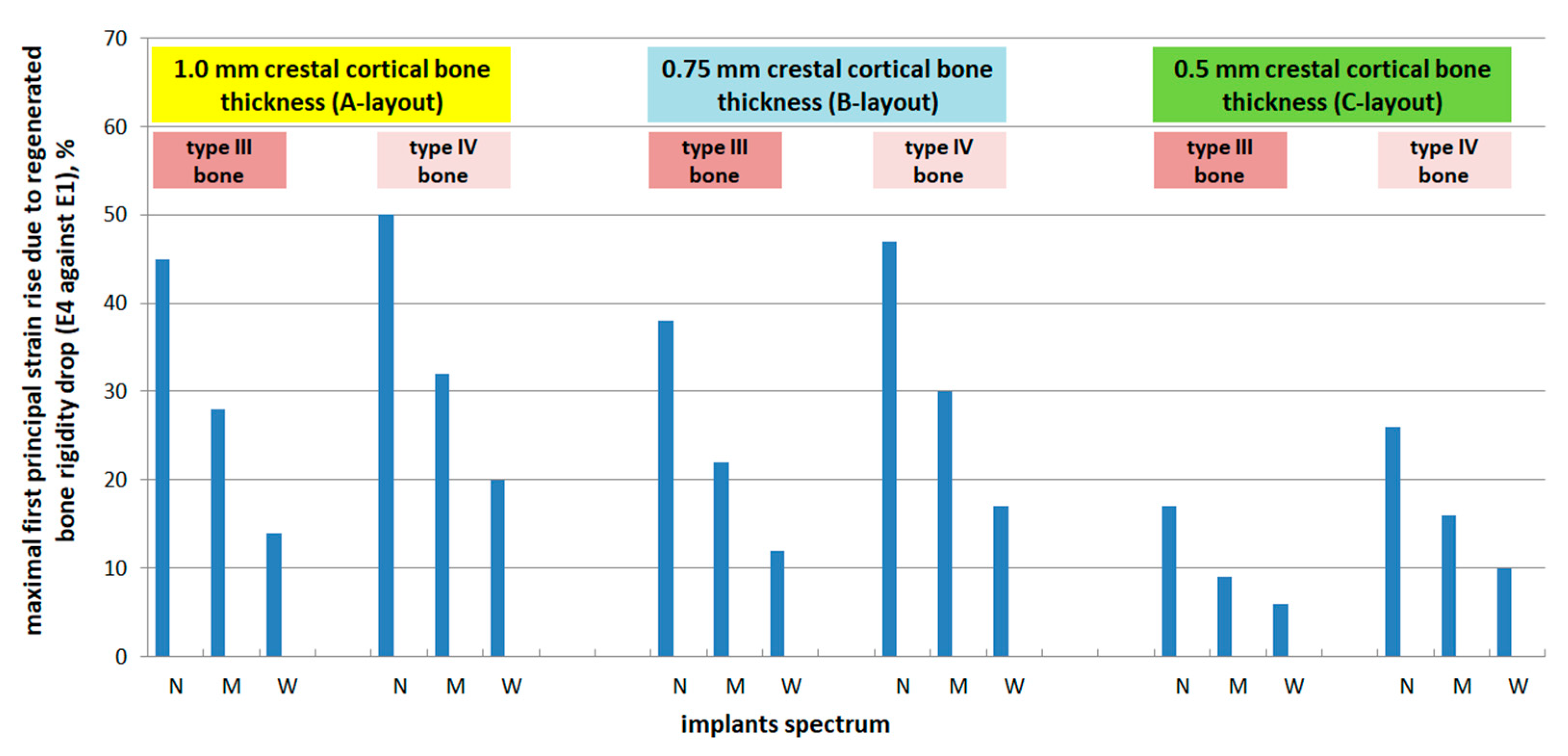
3.3. Effect of Cancellous Bone Quality

Reducing the elastic modulus of cancellous bone by 50% (0.69 vs. 1.37 GPa) led to substantial MFPS increases in cortical bone for all implant diameters at E1 regenerated bone elasticity:
  • A-layout: +25% (N), +34% (M), +88% (W)
  • B-layout: +41% (N), +46% (M), +78% (W)
  • C-layout: +53% (N), +57% (M), +73% (W)
For regenerated bone elasticities E2–E4, similar patterns were observed, with the magnitude of MFPS rise increasing as regenerated bone became more compliant (Figure 8).

3.4. Effect of Regenerated Bone Elasticity

A marked MFPS increase in cancellous bone was associated with reduced regenerated bone elasticity (E4 vs. E1). For type III bone:
  • A-layout: +45% (N), +28% (M), +14% (W)
  • B-layout: +38% (N), +22% (M), +12% (W)
  • C-layout: +17% (N), +9% (M), +6% (W)
For type IV bone:
  • A-layout: +50% (N), +32% (M), +20% (W)
  • B-layout: +47% (N), +30% (M), +17% (W)
  • C-layout: +26% (N), +16% (M), +10% (W)
The greatest relative increases were observed in 4.5 × 5.0 mm implants within type IV bone and thicker cortices (Figure 9).

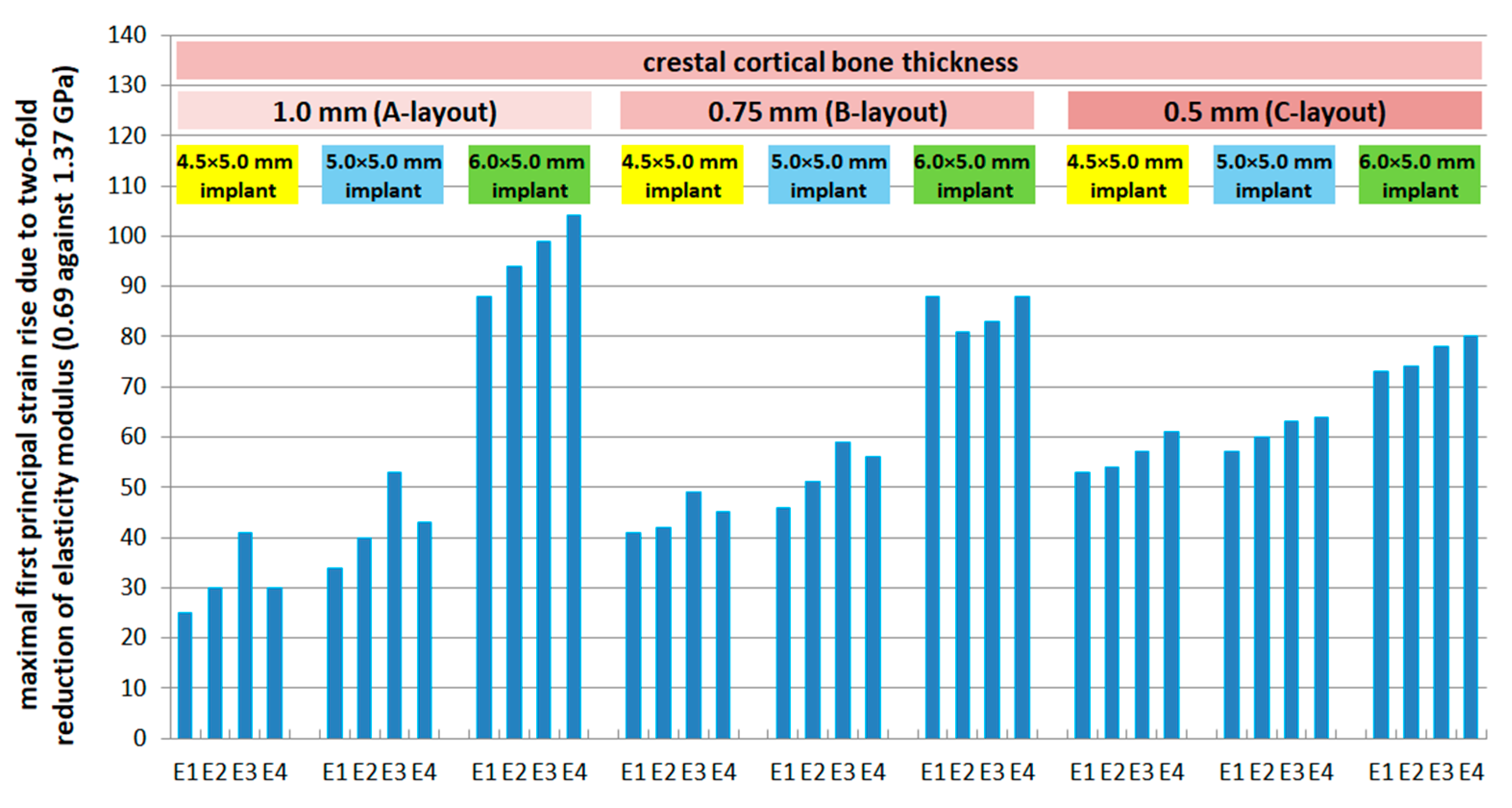
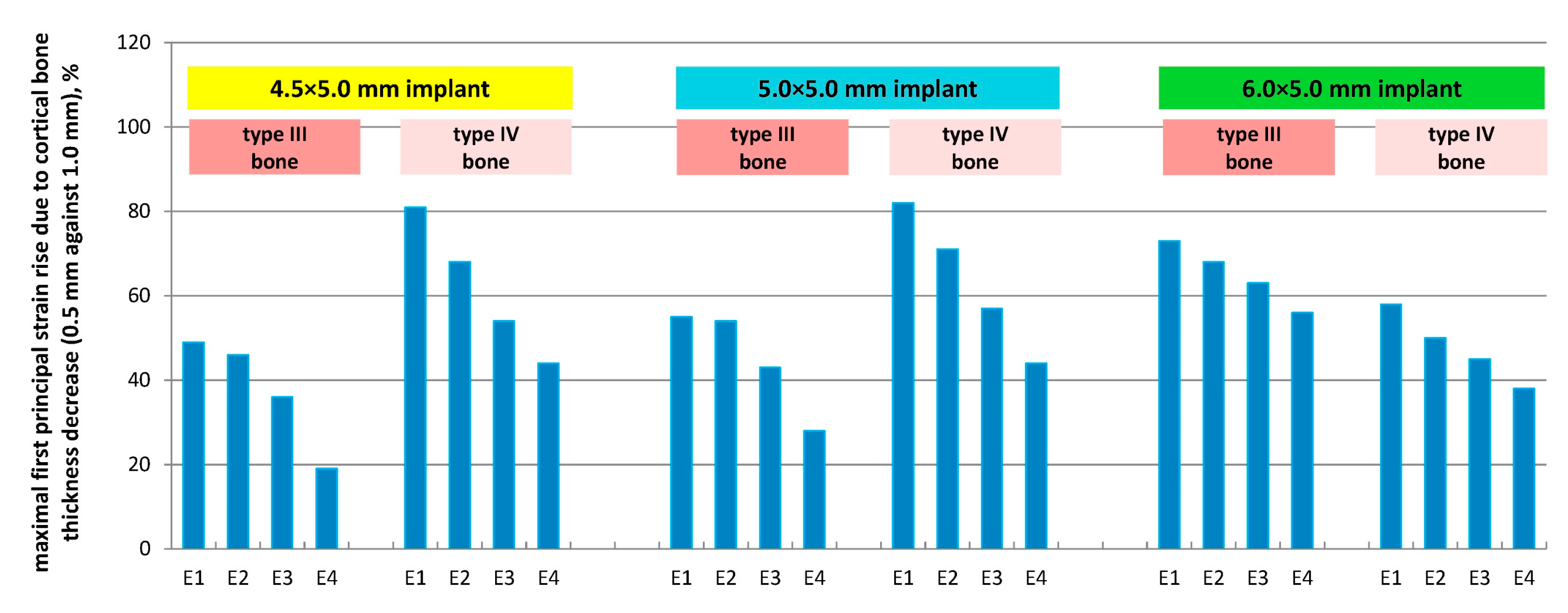
3.5. Effect of Cortical Bone Thickness

Reducing cortical thickness from 1.0 mm to 0.5 mm caused substantial MFPS increases:
For type III bone:
  • E1: +49% (N), +55% (M), +73% (W)
  • E2: +46% (N), +54% (M), +68% (W)
  • E3: +36% (N), +43% (M), +63% (W)
  • E4: +19% (N), +28% (M), +56% (W)
For type IV bone:
  • E1: +81% (N), +82% (M), +58% (W)
  • E2: +68% (N), +71% (M), +50% (W)
  • E3: +54% (N), +57% (M), +45% (W)
  • E4: +44% (N), +44% (M), +38% (W)
These results are illustrated in Figure 10.

4. Discussion

The placement of autogenous bone into the gap between the plateau implant neck and the osteotomy bed is an important factor for improving osseointegration and reinforcing implant anchorage. In compromised posterior maxillae—characterized by insufficient bone volume and poor quality (types III and IV) [38]—understanding how regenerated bone elasticity affects strain distribution in the cervical region is crucial for maintaining physiological bone turnover and preventing early marginal bone loss.
Clinically, the objective of grafting is to achieve regenerated bone with high mechanical rigidity and interconnected porosity, allowing predictable load transfer and stable osseointegration. However, despite extensive research, the resulting density and elastic properties of grafted bone remain unpredictable, and current clinical recommendations for selecting specific graft materials are often non-specific. Although novel bone substitutes are widely available, evidence-based data on their mechanical performance and long-term stability are still limited [39].
The unpredictability of regenerated bone’s biomechanical response under functional loading cannot be fully addressed by clinical or experimental studies alone. While modern CT imaging allows estimation of bone density via Hounsfield units, and empirical correlations between density and elastic modulus exist [40], these methods cannot establish comprehensive quantitative relationships among mechanical stresses/strains, anatomical geometry, and material properties in patient-specific cases. This gap underscores the importance of in silico approaches such as finite element analysis (FEA), which enables systematic evaluation of bone–implant biomechanics across a controlled spectrum of parameters [25,26,29,41,42].
The present study integrates FEA with Frost’s mechanostat theory to create a threshold-based method for implant selection. Unlike conventional clinical workflows that primarily assess bone morphology and dimensions, this approach incorporates the mechanical properties of both native and regenerated bone, allowing for predictive identification of conditions that avoid pathological strain (>3000 με). Such predictive capability is clinically relevant for reducing the risk of peri-implant bone loss, particularly in atrophic maxillae.
Previous FEA studies on dental implants have produced valuable insights [28,29], yet their clinical translation has been limited by inconsistent strain thresholds, insufficient anatomical standardization, or lack of direct correlation to pathological strain limits at the most critical bone–implant interface zones. In this study, model design was standardized to control for anatomical variability while retaining sufficient anatomical fidelity for biomechanical relevance [43,44]. Complete osseointegration was assumed, as is common in comparative modeling [25,41,44,45], to ensure consistency with other studies and eliminate uncertainties associated with partial integration.
In addition to the internal convergence and plausibility checks, the reliability of our finite element framework should also be considered in the broader context of methodological validation. In computational biomechanics, credibility is commonly supported through mesh convergence, sensitivity testing, and comparisons with established experimental or numerical data [46]. Recent reviews in dental bioengineering emphasize that combining geometric fidelity of the modeled structures with such methodological verification represents a robust strategy for validating in silico studies [47]. Our approach, which included systematic mesh refinement, evaluation of cortical and cancellous strain ranges against reported physiological values, and analysis of strain trends with varying bone quality and cortical thickness, is consistent with these recommended practices. This alignment reinforces the validity of our results and their applicability for predicting peri-implant bone behavior.
While isotropic, homogeneous, and linearly elastic material assumptions are widely adopted in dental biomechanics [41,45], they inevitably simplify the reality that cortical bone is transversely isotropic and inhomogeneous [48]. Including anisotropy and heterogeneity could yield more localized variations in strain fields [49], but reliable patient-specific elastic data for regenerated bone are not yet available. Given the comparative nature of this study and the wide variability in clinical bone quality, the isotropic assumption remains reasonable and consistent with prior validated models [28,41,45,50]. Future research should incorporate anisotropic, heterogeneous models when the necessary input data become available.
From a clinical perspective, the simulated elasticity ranges E1 = 13.7 GPa (100%)–E4 = 3.43 GPa (25%) may be associated with different grafting approaches. Autogenous bone blocks and cortical bone particles typically provide greater initial stiffness and faster integration, and therefore are more likely to approximate higher elastic moduli E1 = 13.7 GPa (100%)–E2 = 10.3 GPa (75%). Conversely, slower-resorbing xenogeneic grafts such as deproteinized bovine bone mineral tend to maintain lower stiffness for longer periods, resembling the intermediate to lower ranges E3 = 6.85 GPa (50%)–E4 = 3.43 GPa (25%). Thus, when limited bone height and type IV bone quality coincide, the use of grafting materials favoring higher elastic response may help reduce biomechanical risk in the crestal cancellous bone around short plateau implants.
A key factor in FEA accuracy is the assignment of elastic modulus values to bone structures. While advanced methods can map heterogeneous moduli from DICOM data [33,51], such mapping is not yet possible for regenerated bone due to unpredictable density distributions. Here, a phenomenological approach—using averaged experimental moduli obtained from ultrasonic or nanoindentation testing [23]—was adopted to enable comparison with other studies and to generalize trends across a clinically relevant elasticity range.
Loading was modeled as a 120.9 N oblique force [36,37] at ~75° to the abutment surface to simulate realistic occlusal conditions. This loading direction produces maximum effective stresses approximately twice those of an equivalent vertical load [52], ensuring a conservative (worst-case) evaluation of strain magnitudes. Although dental implants are subject to cyclic loading in vivo [53], static loading was chosen in line with most comparative FEA studies [25,28,45,54,55], as the inertial effects of occlusal forces occur over fractions of a second and are negligible in static analyses. Incorporating fatigue effects remains a future extension of this work.
The simulation results confirm that MFPS in cancellous bone are highly sensitive to regenerated bone elasticity, cortical thickness, and implant diameter. Clinically, this means that in cases with thin cortices (<0.75 mm) and low-quality regenerated bone (E3–E4), smaller-diameter implants are more likely to produce pathological strains, particularly in type IV bone. Conversely, wider implants (6.0 mm) can maintain physiological strains even with reduced regenerated bone elasticity, provided cortical thickness is sufficient. This finding supports the preferential selection of wider short implants when bone quality is uncertain and cortical thickness is not severely compromised.
Limitations of this study include:
  • The isotropic material assumption, which does not capture anisotropy-related local strain variations.
  • The assumption of complete osseointegration, which may overestimate load transfer efficiency in poor-quality bone.
  • The use of static rather than cyclic loading, which may underestimate long-term fatigue-related effects.
Despite these limitations, the combination of high mesh resolution, a systematic parametric approach, and a threshold-based evaluation framework provides clinically relevant guidance for implant selection in compromised maxillae. The methodology can be extended to patient-specific simulations once reliable regenerated bone property data become available, thereby bridging the gap between biomechanical modeling and individualized treatment planning.

5. Conclusions

Based on finite element analysis of short finned Bicon SHORT® implants placed in posterior maxilla models with varying cortical thickness, cancellous bone quality (types III–IV), and regenerated bone elasticity, the following conclusions were drawn:
  • Strains in the cortical layer remained within physiological limits in all scenarios, whereas cancellous bone in type IV maxillae frequently exceeded Frost’s pathological threshold (MESp = 3000 με), particularly with smaller implant diameters and reduced regenerated bone stiffness.
  • Implant diameter had a major effect on strain distribution: increasing the diameter from 4.5 mm to 6.0 mm lowered MFPS by up to 56% in type III bone and up to 36% in type IV bone. The protective effect of wider implants was most evident in cases with thicker cortical bone and lower regenerated bone elasticity.
  • The mechanical quality of regenerated bone proved critical: when elasticity was reduced (E3–E4), cancellous strains rose substantially, especially with cortical thicknesses < 0.75 mm. Under these conditions, only 6.0 mm implants maintained strains within safe ranges in most cases.
  • From a clinical standpoint, biomechanical risk is jointly determined by implant diameter and regenerated bone quality. Wide-diameter short implants (6.0 mm) are particularly advantageous when bone quality is uncertain and cortical thickness is limited, whereas narrower implants may only be advisable if regenerated bone elasticity approaches cortical levels.

Author Contributions

Conceptualization, V.D. and A.K.; methodology, A.K., V.D. and N.S.; validation, I.L. and L.L.; formal analysis, I.L., N.S. and V.D.; investigation, O.Y., A.K., N.S. and I.L.; resources, V.D., I.L., O.Y. and N.S.; data curation V.D., I.L., L.L. and N.S.; writing—original draft preparation, O.Y., L.L. and V.D.; writing—review and editing N.S., I.L. and A.K.; visualization, O.Y., A.K. and N.S.; supervision, A.K. and V.D.; project administration, A.K. and V.D. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Data are contained within the article.

Acknowledgments

The authors would like to express gratitude to the University of Cambridge for its support and to Michael Sutcliffe for his valuable collaboration and assistance.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Overmann, A.L.; Aparicio, C.; Richards, J.T.; Mutreja, I.; Fischer, N.G.; Wade, S.M.; Potter, B.K.; Davis, T.A.; Bechtold, J.E.; Forsberg, J.A.; et al. Orthopaedic osseointegration: Implantology and future directions. J. Orthop. Res. 2020, 38, 1445–1454. [Google Scholar] [CrossRef]
  2. Fernandes, G.; Costa, B.; Trindade, H.F.; Castilho, R.M.; Fernandes, J. Comparative analysis between extra-short implants (≤6 mm) and 6 mm-longer implants: A meta-analysis of randomized controlled trial. Aust. Dent. J. 2022, 67, 194–211. [Google Scholar] [CrossRef]
  3. Fuda, S.; Martins, B.G.D.S.; Castro, F.C.; Heboyan, A.; Gehrke, S.A.; Fernandes, J.C.H.; Mello-Moura, A.C.V.; Fernandes, G.V.O. Marginal Bone Level and Clinical Parameter Analysis Comparing External Hexagon and Morse Taper Implants: A Systematic Review and Meta-Analysis. Diagnostics 2023, 13, 1587. [Google Scholar] [CrossRef] [PubMed]
  4. Alqahtani, A.R.; Desai, S.R.; Patel, J.R.; Alqhtani, N.R.; Alqahtani, A.S.; Heboyan, A.; Fernandes, G.V.O.; Mustafa, M.; Karobari, M.I. Investigating the impact of diameters and thread designs on the biomechanics of short implants placed in D4 bone: A 3D finite element analysis. BMC Oral Health 2023, 23, 686. [Google Scholar] [CrossRef] [PubMed]
  5. Meslier, Q.; Shefelbine, S.J. Using Finite Element Modeling in Bone Mechanoadaptation. Curr. Osteoporos. Rep. 2023, 21, 105–116. [Google Scholar] [CrossRef]
  6. Kondratiev, A.; Demenko, V.; Linetskiy, I.; Weisskircher, H.-W.; Linetska, L. Evaluation of bone turnover around short finned implants in atrophic posterior maxilla: A finite element study. Prosthesis 2024, 6, 1170–1188. [Google Scholar] [CrossRef]
  7. Li, J.; Jansen, J.A.; Walboomers, X.F.; van den Beucken, J.J. Mechanical aspects of dental implants and osseointegration: A narrative review. J. Mech. Behav. Biomed. Mater. 2020, 103, 103574. [Google Scholar] [CrossRef]
  8. Martins, S.C.; Marques, M.D.C.; Vidal, M.G.; Tolentino, P.H.M.P.; Dinelli, R.G.; Fernandes, G.V.d.O.; Shibli, J.A. Is the facial bone wall critical to achieving esthetic outcomes in immediate implant placement with immediate restoration? A systematic review. Adv. Clin. Exp. Med. 2024, 33, 979–997. [Google Scholar] [CrossRef]
  9. Hingsammer, L.; Pommer, B.; Hunger, S.; Stehrer, R.; Watzek, G.; Insua, A. Influence of implant length and associated parameters upon biomechanical forces in finite element analyses: A systematic review. Implant. Dent. 2019, 28, 296–305. [Google Scholar] [CrossRef]
  10. Cenkoglu, B.G.; Balcioglu, N.B.; Ozdemir, T.; Mijiritsky, E. The Effect of the Length and Distribution of Implants for Fixed Prosthetic Reconstructions in the Atrophic Posterior Maxilla: A Finite Element Analysis. Materials 2019, 12, 2556. [Google Scholar] [CrossRef]
  11. Esposito, M.; Buti, J.; Barausse, C.; Gasparro, R.; Sammartino, G.; Felice, P. Short implants versus longer implants in vertically augmented atrophic mandibles: A systematic review of randomised controlled trials with a 5-year post-loading follow-up. Int. J. Oral Implantol. 2019, 12, 267–280. [Google Scholar]
  12. Qiu, P.; Cao, R.; Li, Z.; Fan, Z. A comprehensive biomechanical evaluation of length and diameter of dental implants using finite element analyses: A systematic review. Heliyon 2024, 10, e26876. [Google Scholar] [CrossRef]
  13. Anitua, E.; Larrazabal Saez de Ibarra, N.; Morales Martín, I.; Saracho Rotaeche, L. Influence of Dental Implant Diameter and Bone Quality on the Biomechanics of Single-Crown Restoration. Dent. J. 2021, 9, 103. [Google Scholar] [CrossRef]
  14. Calì, M.; Zanetti, E.M.; Oliveri, S.M. Influence of thread shape and inclination on the biomechanical behaviour of plateau implant systems. Dent. Mater. 2018, 34, 460–469. [Google Scholar] [CrossRef]
  15. Coelho, P.G.; Suzuki, M.; Marin, C.; Granato, R.; Gil, L.F.; Tovar, N.; Jimbo, R.; Neiva, R.; Bonfante, E.A. Osseointegration of Plateau Root Form Implants: Unique Healing Pathway Leading to Haversian-Like Long-Term Morphology. Adv. Exp. Med. Biol. 2015, 881, 111–128. [Google Scholar] [CrossRef] [PubMed]
  16. McKenna, G.J.; Gjengedal, H.; Harkin, J.; Holland, N.; Moore, C.; Srinivasan, M. Effect of autogenous bone graft site on dental implant survival and donor site complications: A systematic review and meta-analysis. J. Evid. Based Dent. Pract. 2022, 22, 101731. [Google Scholar] [CrossRef]
  17. Linetska, L.; Kipenskyi, A.; Demenko, V.; Linetskiy, I.; Kondratiev, A.; Yefremov, O. Finite element study of biomechanical behavior of short dental implants with bone loss effects—Evaluation of bone turnover. In Proceedings of the 2023 IEEE 4th KhPI Week on Advanced Technology (KhPIWeek), Kharkiv, Ukraine, 2–6 October 2023; pp. 1–6. [Google Scholar] [CrossRef]
  18. Zhang, C.; Zeng, C.; Wang, Z.; Zeng, T.; Wang, Y. Optimization of stress distribution of bone-implant interface (BII). Biomater. Adv. 2023, 147, 213342. [Google Scholar] [CrossRef] [PubMed]
  19. Misch, C.E. (Ed.) Chapter 32—Progressive bone loading: Increasing the density of bone with a prosthetic protocol. In Dental Implant Prosthetics; Elsevier: Amsterdam, The Netherlands, 2015; pp. 913–937. [Google Scholar] [CrossRef]
  20. Kreve, S.; Ferreira, I.; da Costa Valente, M.L.; Dos Reis, A.C. Relationship between dental implant macro-design and osseointegration: A systematic review. Oral Maxillofac. Surg. 2024, 28, 1–14. [Google Scholar] [CrossRef]
  21. Frost, H.M. A 2003 update of bone physiology and Wolff’s Law for clinicians. Angle Orthod. 2004, 74, 3–15. [Google Scholar] [CrossRef] [PubMed]
  22. Frost, H.M. Bone mass and the mechanostat: A proposal. Anat. Rec. 1987, 219, 1–9. [Google Scholar] [CrossRef]
  23. Verma, A.; Singh, S.V.; Arya, D.; Shivakumar, S.; Chand, P. Mechanical failures of dental implants and supported prostheses: A systematic review. J. Oral Biol. Craniofac. Res. 2023, 13, 306–314. [Google Scholar] [CrossRef] [PubMed]
  24. Saab, X.E.; Griggs, J.A.; Powers, J.M.; Engelmeier, R.L. Effect of abutment angulation on the strain on the bone around an implant in the anterior maxilla: A finite element study. J. Prosthet. Dent. 2007, 97, 85–92. [Google Scholar] [CrossRef]
  25. Falcinelli, C.; Valente, F.; Vasta, M.; Traini, T. Finite element analysis in implant dentistry: State of the art and future directions. Dent. Mater. 2023, 39, 539–556. [Google Scholar] [CrossRef]
  26. Lisiak-Myszke, M.; Marciniak, D.; Bieliński, M.; Sobczak, H.; Garbacewicz, Ł.; Drogoszewska, B. Application of Finite Element Analysis in Oral and Maxillofacial Surgery-A Literature Review. Materials 2020, 13, 3063. [Google Scholar] [CrossRef] [PubMed]
  27. Linetskiy, I.; Sutcliffe, M.; Kondratiev, A.; Demenko, V.; Linetska, L.; Yefremov, O. A novel method of load bearing ability analysis of short plateau implants placed in compromised bone. In Proceedings of the 2023 IEEE 4th KhPI Week on Advanced Technology (KhPIWeek), Kharkiv, Ukraine, 2–6 October 2023; pp. 1–6. [Google Scholar] [CrossRef]
  28. Chou, H.Y.; Müftü, S.; Bozkaya, D. Combined effects of implant insertion depth and alveolar bone quality on periimplant bone strain induced by a wide-diameter, short implant and a narrow-diameter, long implant. J. Prosthet. Dent. 2010, 104, 293–300. [Google Scholar] [CrossRef]
  29. Sugiura, T.; Yamamoto, K.; Horita, S.; Murakami, K.; Tsutsumi, S.; Kirita, T. The effects of bone density and crestal cortical bone thickness on micromotion and peri-implant bone strain distribution in an immediately loaded implant: A nonlinear finite element analysis. J. Periodontal. Implant. Sci. 2016, 46, 152–165. [Google Scholar] [CrossRef]
  30. Demenko, V.; Linetskiy, I.; Linetska, L.; Sutcliffe, M.; Kondratiev, A. Prognosis of crestally placed short plateau implants in posterior maxilla. Int. J. Numer. Methods Biomed. Engng. 2025, 41, e70025. [Google Scholar] [CrossRef]
  31. Bozkaya, D.; Muftu, S.; Muftu, A. Evaluation of load transfer characteristics of five different implants in compact bone at different load levels by finite elements analysis. J. Prosthet. Dent. 2004, 92, 523–530. [Google Scholar] [CrossRef] [PubMed]
  32. Lemos, C.A.A.; Verri, F.R.; Noritomi, P.Y.; Kemmoku, D.T.; Souza Batista, V.E.; Cruz, R.S.; de Luna Gomes, J.M.; Pellizzer, E.P. Effect of bone quality and bone loss level around internal and external connection implants: A finite element analysis study. J. Prosthet. Dent. 2021, 125, 137.e1–137.e10. [Google Scholar] [CrossRef]
  33. Soodmand, I.; Becker, A.K.; Sass, J.O.; Jabs, C.; Kebbach, M.; Wanke, G.; Dau, M.; Bader, R. Heterogeneous material models for finite element analysis of the human mandible bone—A systematic review. Heliyon 2024, 10, e40668. [Google Scholar] [CrossRef]
  34. Lodoso-Torrecilla, I.; Konka, J.; Kreuzer, M.; Jimenez-Pique, E.; Espanol, M.; Ginebra, M.-P. Quality assessment of regenerated bone in intraosseous and intramuscular scaffolds by spectroscopy and nanoindentation. Biomater. Adv. 2024, 164, 213982. [Google Scholar] [CrossRef]
  35. Blázquez-Carmona, P.; Mora-Macías, J.; Pajares, A.; Mármol, Á.; Reina-Romo, E. On the influence of structural and chemical properties on the elastic modulus of woven bone under healing. Front. Bioeng. Biotechnol. 2024, 12, 1476473. [Google Scholar] [CrossRef]
  36. Mericske-Stern, R.; Zarb, G.A. In vivo measurements of some functional aspects with mandibular fixed prostheses supported by implants. Clin. Oral Implant. Res. 1996, 7, 153–161. [Google Scholar] [CrossRef]
  37. Sahin, S.; Cehreli, M.C.; Yalçin, E. The influence of functional forces on the biomechanics of implant-supported prostheses—A review. J. Dent. 2002, 30, 271–282. [Google Scholar] [CrossRef]
  38. Tolstunov, L. Implant zones of the jaws: Implant location and related success rate. J. Oral Implantol. 2007, 33, 211–220. [Google Scholar] [CrossRef] [PubMed]
  39. Bhatt, R.A.; Rozental, T.D. Bone graft substitutes. Hand Clin. 2012, 28, 457–468. [Google Scholar] [CrossRef]
  40. Hiasa, K.; Abe, Y.; Okazaki, Y.; Nogami, K.; Mizumachi, W.; Akagawa, Y. Preoperative computed tomography-derived bone densities in hounsfield units at implant sites acquired primary stability. ISRN Dent. 2011, 2011, 678729. [Google Scholar] [CrossRef]
  41. Oliveira, H.; Brizuela Velasco, A.; Ríos-Santos, J.V.; Sánchez Lasheras, F.; Lemos, B.F.; Gil, F.J.; Carvalho, A.; Herrero-Climent, M. Effect of Different Implant Designs on Strain and Stress Distribution under Non-Axial Loading: A Three-Dimensional Finite Element Analysis. Int. J. Environ. Res. Public Health 2020, 17, 4738. [Google Scholar] [CrossRef] [PubMed]
  42. Chen, J.; Guo, J.; Yang, L.; Wang, L.; Zhang, X. Effect of different implant angulations on the biomechanical performance of prosthetic screws in two implant-supported, screw-retained prostheses: A numerical and experimental study. J. Prosthet. Dent. 2023, 130, 240.e1–240.e10. [Google Scholar] [CrossRef] [PubMed]
  43. Yan, X.; Zhang, X.; Chi, W.; Ai, H.; Wu, L. Comparing the influence of crestal cortical bone and sinus floor cortical bone in posterior maxilla bi-cortical dental implantation: A three-dimensional finite element analysis. Acta Odontol. Scand. 2015, 73, 312–320. [Google Scholar] [CrossRef] [PubMed]
  44. Okumura, N.; Stegaroiu, R.; Kitamura, E.; Kurokawa, K.; Nomura, S. Influence of maxillary cortical bone thickness, implant design and implant diameter on stress around implants: A three-dimensional finite element analysis. J. Prosthodont. Res. 2010, 54, 133–142. [Google Scholar] [CrossRef]
  45. Barbosa, F.T.; Zanatta, L.C.S.; de Souza Rendohl, E.; Gehrke, S.A. Comparative analysis of stress distribution in one-piece and two-piece implants with narrow and extra-narrow diameters: A finite element study. PLoS ONE 2021, 16, e0245800. [Google Scholar] [CrossRef]
  46. Anderson, A.E.; Ellis, B.J.; Weiss, J.A. Verification, validation and sensitivity studies in computational biomechanics. Comput. Methods Biomech. Biomed. Eng. 2007, 10, 171–184. [Google Scholar] [CrossRef] [PubMed]
  47. de Matos, J.D.M.; Queiroz, D.A.; Nakano, L.J.N.; Andrade, V.C.; Ribeiro, N.D.R.; Borges, A.L.S.; Bottino, M.A.; Lopes, G.D.S. Bioengineering tools applied to dentistry: Validation methods for In Vitro and In Silico analysis. Dent. J. 2022, 10, 145. [Google Scholar] [CrossRef] [PubMed]
  48. Tretto, P.H.W.; Dos Santos, M.B.F.; Spazzin, A.O.; Pereira, G.K.R.; Bacchi, A. Assessment of stress/strain in dental implants and abutments of alternative materials compared to conventional titanium alloy. Comput. Methods Biomech. Biomed. Eng. 2020, 23, 372–383. [Google Scholar] [CrossRef]
  49. Kondratiev, A.; Gaidachuk, V.; Nabokina, T.; Tsaritsynskyi, A. New Possibilities of Creating the Efficient Dimensionally Stable Composite Honeycomb Structures for Space Applications. In Integrated Computer Technologies in Mechanical Engineering. Advances in Intelligent Systems and Computing; Springer: Cham, Switzerland, 2020; Volume 1113. [Google Scholar] [CrossRef]
  50. Zhang, N.; Karl, M.; Wendler, F. Finite Element Analysis on Stress Development in Alveolar Bone During Insertion of a Novel Dental Implant Design. Appl. Sci. 2025, 15, 8366. [Google Scholar] [CrossRef]
  51. Celik, H.K.; Koc, S.; Kustarci, A.; Rennie, A.E. A literature review on the linear elastic material properties assigned in finite element analyses in dental research. Mater. Today Commun. 2022, 30, 103087. [Google Scholar] [CrossRef]
  52. Chun, H.J.; Cheong, S.Y.; Han, J.H.; Heo, S.J.; Chung, J.P.; Rhyu, I.C.; Choi, Y.C.; Baik, H.K.; Ku, Y.; Kim, M.H. Evaluation of design parameters of osseointegrated dental implants using finite element analysis. J. Oral Rehabil. 2002, 29, 565–574. [Google Scholar] [CrossRef]
  53. Khosravani, M.R. Mechanical behavior of restorative dental composites under various loading conditions. J. Mech. Behav. Biomed. Mater. 2019, 93, 151–157. [Google Scholar] [CrossRef]
  54. Bordin, D.; Castro, M.B.; Carvalho, M.A.; Araujo, A.M.; Cury, A.A.D.B.; Lazari-Carvalho, P.C. Different treatment modalities using dental implants in the posterior maxilla: A finite element analysis. Braz. Dent. J. 2021, 32, 34–41. [Google Scholar] [CrossRef]
  55. Byun, S.H.; Seo, J.H.; Cho, R.Y.; Yi, S.M.; Kim, L.K.; Han, H.S.; On, S.W.; Kim, W.H.; An, H.W.; Yang, B.E. Finite Element Analysis of a New Non-Engaging Abutment System for Three-Unit Implant-Supported Fixed Dental Prostheses. Bioengineering 2022, 9, 483. [Google Scholar] [CrossRef] [PubMed]
Prosthesis 07 00123 g001
Figure 1. Plane views of maxillary bone segments with 1.0, 0.75, and 0.5 mm crestal and sinus cortical bone thickness (A, B-, C- layouts) with inserted 4.5 × 5.0, 5.0 × 5.0 and 6.0 × 5.0 mm implants.
Figure 1. Plane views of maxillary bone segments with 1.0, 0.75, and 0.5 mm crestal and sinus cortical bone thickness (A, B-, C- layouts) with inserted 4.5 × 5.0, 5.0 × 5.0 and 6.0 × 5.0 mm implants.
Prosthesis 07 00123 g001
Prosthesis 07 00123 g002
Figure 2. Three-dimensional view of maxillary bone segment of 1.0 mm crestal and sinus cortical bone thickness with inserted 5.0 × 5.0 mm implant: A—cortical bone, B—cancellous bone, C—newly formed bone, D—implant/abutment assembly.
Figure 2. Three-dimensional view of maxillary bone segment of 1.0 mm crestal and sinus cortical bone thickness with inserted 5.0 × 5.0 mm implant: A—cortical bone, B—cancellous bone, C—newly formed bone, D—implant/abutment assembly.
Prosthesis 07 00123 g002
Prosthesis 07 00123 g003
Figure 3. Example of FE discretization of a maxillary bone section incorporating 1.0 mm cortical thickness at both the crestal and sinus sides and a 5.0 × 5.0 mm implant. The neck region of the bone–implant interface was refined with mapped meshing; the smallest element dimension was 0.020 mm.
Figure 3. Example of FE discretization of a maxillary bone section incorporating 1.0 mm cortical thickness at both the crestal and sinus sides and a 5.0 × 5.0 mm implant. The neck region of the bone–implant interface was refined with mapped meshing; the smallest element dimension was 0.020 mm.
Prosthesis 07 00123 g003
Prosthesis 07 00123 g004
Figure 4. Localization of first principal strains in the critical bone–implant interface plane for Bicon SHORT® implants, modeled in type IV bone, with regenerated bone elasticity represented by moduli E1 and E4.
Figure 4. Localization of first principal strains in the critical bone–implant interface plane for Bicon SHORT® implants, modeled in type IV bone, with regenerated bone elasticity represented by moduli E1 and E4.
Prosthesis 07 00123 g004
Prosthesis 07 00123 g005
Figure 5. Illustration of first principal strain distribution along the critical line of bone-implant interface for 5.0 × 5.0 mm implant placed in 0.5 mm (a), 0.75 mm (b), 1.0 mm (c) cortical bone and type IV bone at E1…E4 levels of regenerated bone elasticity.
Figure 5. Illustration of first principal strain distribution along the critical line of bone-implant interface for 5.0 × 5.0 mm implant placed in 0.5 mm (a), 0.75 mm (b), 1.0 mm (c) cortical bone and type IV bone at E1…E4 levels of regenerated bone elasticity.
Prosthesis 07 00123 g005
Prosthesis 07 00123 g006aProsthesis 07 00123 g006b
Figure 6. Dependence of MFPS in cancellous bone on implant diameter, bone quality, regenerated bone modulus of elasticity and cortical bone thickness for the spectrum of implants placed in types III and IV bone segments with 1.0 (a), 0.75 (b), 0.5 mm (c) cortical bone (A-, B-, C-layouts). The red line indicates the pathological threshold of Frost’s mechanostat, set at 3000 microstrain.
Figure 6. Dependence of MFPS in cancellous bone on implant diameter, bone quality, regenerated bone modulus of elasticity and cortical bone thickness for the spectrum of implants placed in types III and IV bone segments with 1.0 (a), 0.75 (b), 0.5 mm (c) cortical bone (A-, B-, C-layouts). The red line indicates the pathological threshold of Frost’s mechanostat, set at 3000 microstrain.
Prosthesis 07 00123 g006aProsthesis 07 00123 g006b
Prosthesis 07 00123 g007
Figure 7. Reduction in MFPS associated with an implant diameter increase from 4.5 mm to 6.0 mm in bone segments with cortical thicknesses of 0.5, 0.75, and 1.0 mm for both type III and type IV bone.
Figure 7. Reduction in MFPS associated with an implant diameter increase from 4.5 mm to 6.0 mm in bone segments with cortical thicknesses of 0.5, 0.75, and 1.0 mm for both type III and type IV bone.
Prosthesis 07 00123 g007
Prosthesis 07 00123 g008
Figure 8. Effect of bone quality on MFPS values, modeled by halving the elastic modulus (0.69 vs. 1.37 GPa), for implants inserted in bone segments with cortical thicknesses of 0.5, 0.75, and 1.0 mm.
Figure 8. Effect of bone quality on MFPS values, modeled by halving the elastic modulus (0.69 vs. 1.37 GPa), for implants inserted in bone segments with cortical thicknesses of 0.5, 0.75, and 1.0 mm.
Prosthesis 07 00123 g008
Prosthesis 07 00123 g009
Figure 9. Increase in MFPS associated with reduced regenerated bone elasticity (E4 compared to E1) for implants placed in bone segments with cortical thicknesses of 0.5, 0.75, and 1.0 mm.
Figure 9. Increase in MFPS associated with reduced regenerated bone elasticity (E4 compared to E1) for implants placed in bone segments with cortical thicknesses of 0.5, 0.75, and 1.0 mm.
Prosthesis 07 00123 g009
Prosthesis 07 00123 g010
Figure 10. Increase in MFPS resulting from a reduction in cortical bone thickness from 1.0 mm to 0.5 mm, for implants inserted into type III and IV bone models.
Figure 10. Increase in MFPS resulting from a reduction in cortical bone thickness from 1.0 mm to 0.5 mm, for implants inserted into type III and IV bone models.
Prosthesis 07 00123 g010
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Demenko, V.; Linetskiy, I.; Yefremov, O.; Linetska, L.; Smetankina, N.; Kondratiev, A. Regenerated Bone Quality as a Determinant of Bone Turnover and Prognosis in Short Plateau Implants: A Finite Element Study. Prosthesis 2025, 7, 123. https://doi.org/10.3390/prosthesis7050123

AMA Style

Demenko V, Linetskiy I, Yefremov O, Linetska L, Smetankina N, Kondratiev A. Regenerated Bone Quality as a Determinant of Bone Turnover and Prognosis in Short Plateau Implants: A Finite Element Study. Prosthesis. 2025; 7(5):123. https://doi.org/10.3390/prosthesis7050123

Chicago/Turabian Style

Demenko, Vladislav, Igor Linetskiy, Oleg Yefremov, Larysa Linetska, Natalia Smetankina, and Andrii Kondratiev. 2025. "Regenerated Bone Quality as a Determinant of Bone Turnover and Prognosis in Short Plateau Implants: A Finite Element Study" Prosthesis 7, no. 5: 123. https://doi.org/10.3390/prosthesis7050123

APA Style

Demenko, V., Linetskiy, I., Yefremov, O., Linetska, L., Smetankina, N., & Kondratiev, A. (2025). Regenerated Bone Quality as a Determinant of Bone Turnover and Prognosis in Short Plateau Implants: A Finite Element Study. Prosthesis, 7(5), 123. https://doi.org/10.3390/prosthesis7050123

Article Metrics

Back to TopTop