The Roles of Leaflet Geometry in the Structural Deterioration of Bioprosthetic Aortic Valves ^†

Abstract

Objectives: Our goal was to assess the role of leaflet geometry on the structural deterioration of bioprosthetic aortic valves (BAVs) in a closed configuration. Methods: With a Fung-type orthotropic model, finite element modeling was used to create ten cases with parabolic, circular and spline leaflet curvatures and six leaflet angles. Results: A circular circumferential curvature led to lower von Mises and compressive stresses in both the coaptation and load-bearing areas, reduced tensile stresses in the coaptation regions, and increased tensile stresses in the load-bearing areas. A parabolic radial curvature reduced von Mises stresses in the coaptation, as well as the load-bearing regions, reduced compressive stresses in the coaptation, and reduced tensile stresses in the load-bearing regions, leading to a slight increase in the minimized tensile stress in the coaptation regions (1.794 vs. 1.765 MPa) and the minimized compressive stress in the load-bearing regions (0.772 vs. 0.768 MPa). Within a range of downward inclination of the leaflets, all stresses in the coaptation regions decreased. A parabolic circumferential curvature, a linear radial curvature, and, for most cases, upward leaflet inclinations were associated with larger contact pressures between the leaflets. Conclusions: A parabolic radial curvature and downward leaflet inclination likely lead to the longer durability of BAVs.

1. Introduction

There is a high demand for prosthetic aortic valves. Annually 280,000 heart valve replacement (HVR) surgeries are performed worldwide [1], and this number is estimated to increase three-fold in the next 35 years [2]. There are two types of prosthetic heart valves: bioprosthetic and mechanical. Mechanical heart valves require lifelong anticoagulation with an associated risk of hemorrhagic complications [3,4]. There are rare reports of thrombosis in bioprosthetic aortic valves (BAVs) (0.1–5.7% per patient-year [5]). As such, BAVs are preferred in comparison to mechanical heart valves. Moreover, BAVs are expected to acquire a larger portion of the market as their design is shifting toward transcatheter implantation, which significantly reduces the risks of heart valve replacement surgery.

The primary limitation of BAVs is their lifetime [6]. Currently, they last for only 10–15 years [7]. As such, not only are young patients not usually qualified for using BAVs, but the recommended age for a prescription of BAVs is also older than 60 years, as recommended by American and European standards [8,9]. Structural Valve Deterioration (SVD) involves non-calcification (purely mechanical) and calcification-related deteriorations that initiate the failure of the leaflets [10]. In non-calcification mechanisms, high mechanical stresses invade the integrity of the leaflets’ structure, and in calcification-related deterioration, stresses within the leaflets initiate the calcification process [11,12,13]. Therefore, understanding the stress distribution in leaflets is crucial for understanding the SVD mechanisms in BAVs.

There are more than 50 heart valve designs on the market [14]. These designs have distinct differences in terms of the materials of the leaflets and frames, leaflet angles (the inclination of the leaflets toward the sinus), curvatures of the leaflets, the height of the valve, attachments of the leaflets to the supporting housing, etc. The importance of assessing the effects of these parameters in SVD is realized when one considers the catastrophic outcomes with faulty designs in the past. For instance, the Ionescu–Shiley valve was clinically withdrawn because of the short durability of this valve, caused by high mechanical stresses due to a rigid stent and a stitch-related hole near the commissure region [15,16,17,18]. Similarly, the Hancock pericardial xenograft was a faulty design where stitches near the commissures caused too high stresses, which led to early valve failures [19,20,21]. In another example, the profile of a conventional mitral porcine xenograft was designed to be short to resolve complications with the excessive protrusions of the posts into the ventricle. Consequently, the durability of the leaflets was adversely affected due to excessive mechanical stresses caused by the too-short profile [17,22,23].

There are studies on the effects of geometry on the mechanics of closed BHVs, which contribute to a better understanding of SVD in BHVs. Hamid et al. studied the effects of valve height on stresses in the leaflets [22]. Lim et al. examined the effects of leaflet shape on stresses within the leaflets [24]. Xiong et al. compared stentless, molded, and conventional designs of prosthetic aortic valves [25]. Fan et al. reported a design process for the optimization of a pulmonary heart valve [26]. Loerakker et al. studied the effects of geometry on the mechanics of tissue-engineered heart valves [27]. The effects of leaflet curvatures and angles on the mechanics and SVD of BAVs are not clear.

The goal of this study was to understand the roles of geometrical factors in the SVD of BAVs, considering the closed configuration of BAVs. In particular, the effects of leaflet curvatures and angles were studied using finite element modeling. Ten computational cases with different curvatures and angles were analyzed. A Fung-type orthotropic model, based on biaxial test data, was used to account for the anisotropy of the leaflets. According to our knowledge, this is the first study that systematically studies the role of leaflet curvature and angle in the mechanics of BAVs in a closed configuration.

2. Methods

We assumed the valve diameter, the leaflet height, and the commissure height were approximately 19, 11, and 3.5 mm, respectively. To model different geometrical parameters, ten cases were considered. Three parameters were included as follows: the circumferential and radial curvatures and leaflet angles. These parameters are shown in Figure 1 and summarized in

Table 1. Ten cases were considered with the geometrical parameters specified below. The radial and circumferential curvatures were for the load-bearing part of the leaflets. The coaptation height was the same for all cases. The cases were used to study the effects of circumferential curvature (1–3), radial curvature (3–5), and leaflet angle (3, 6–10).

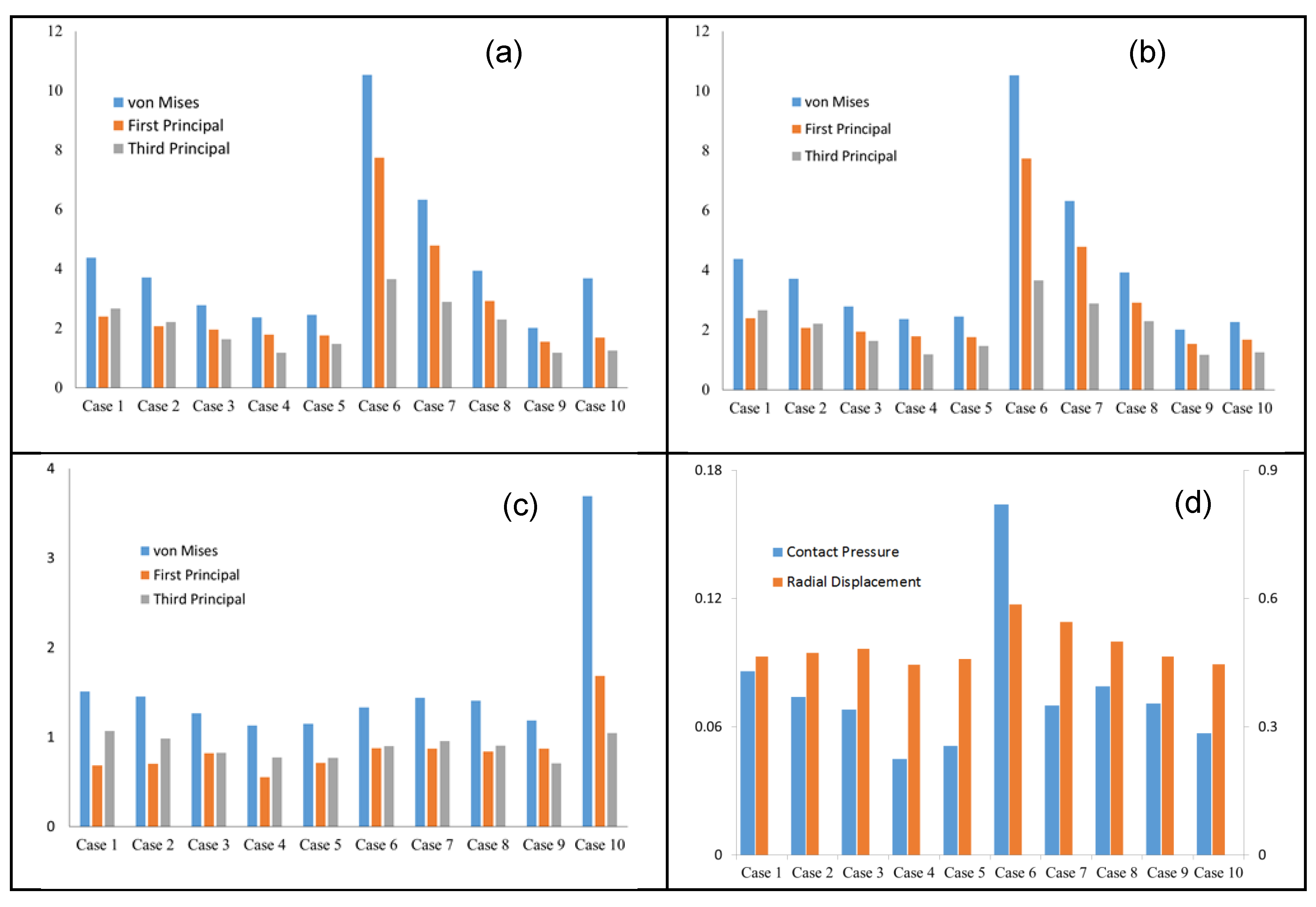
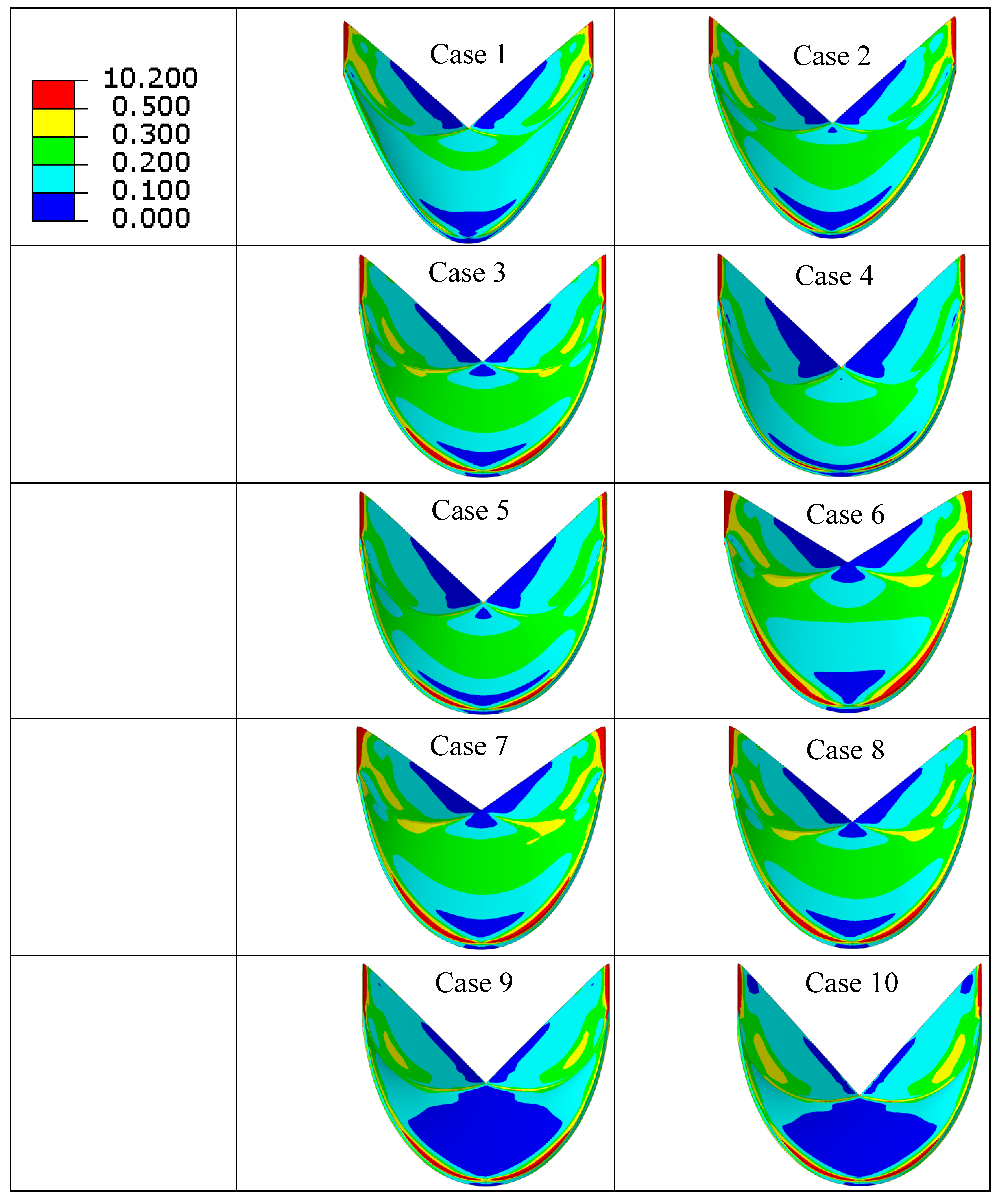
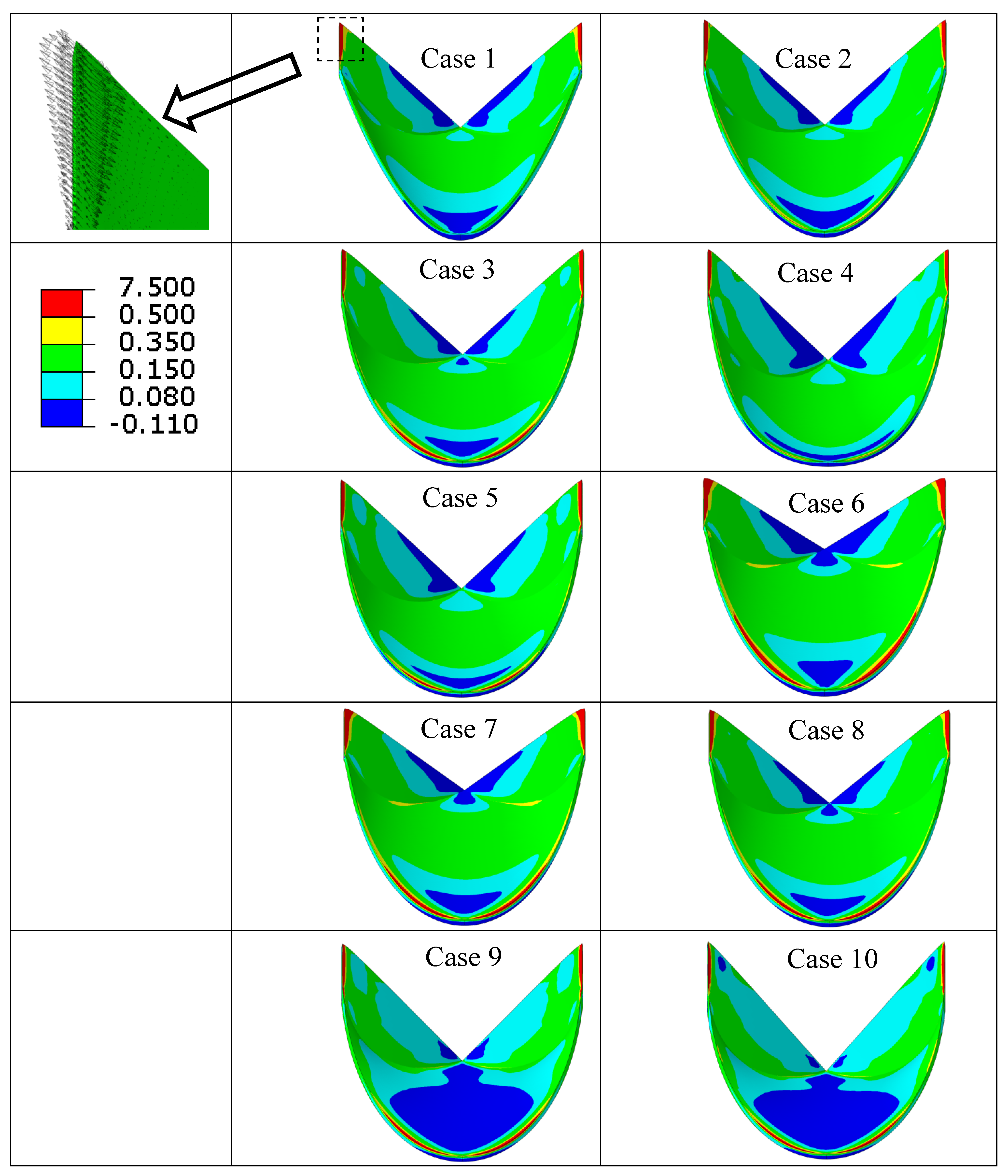
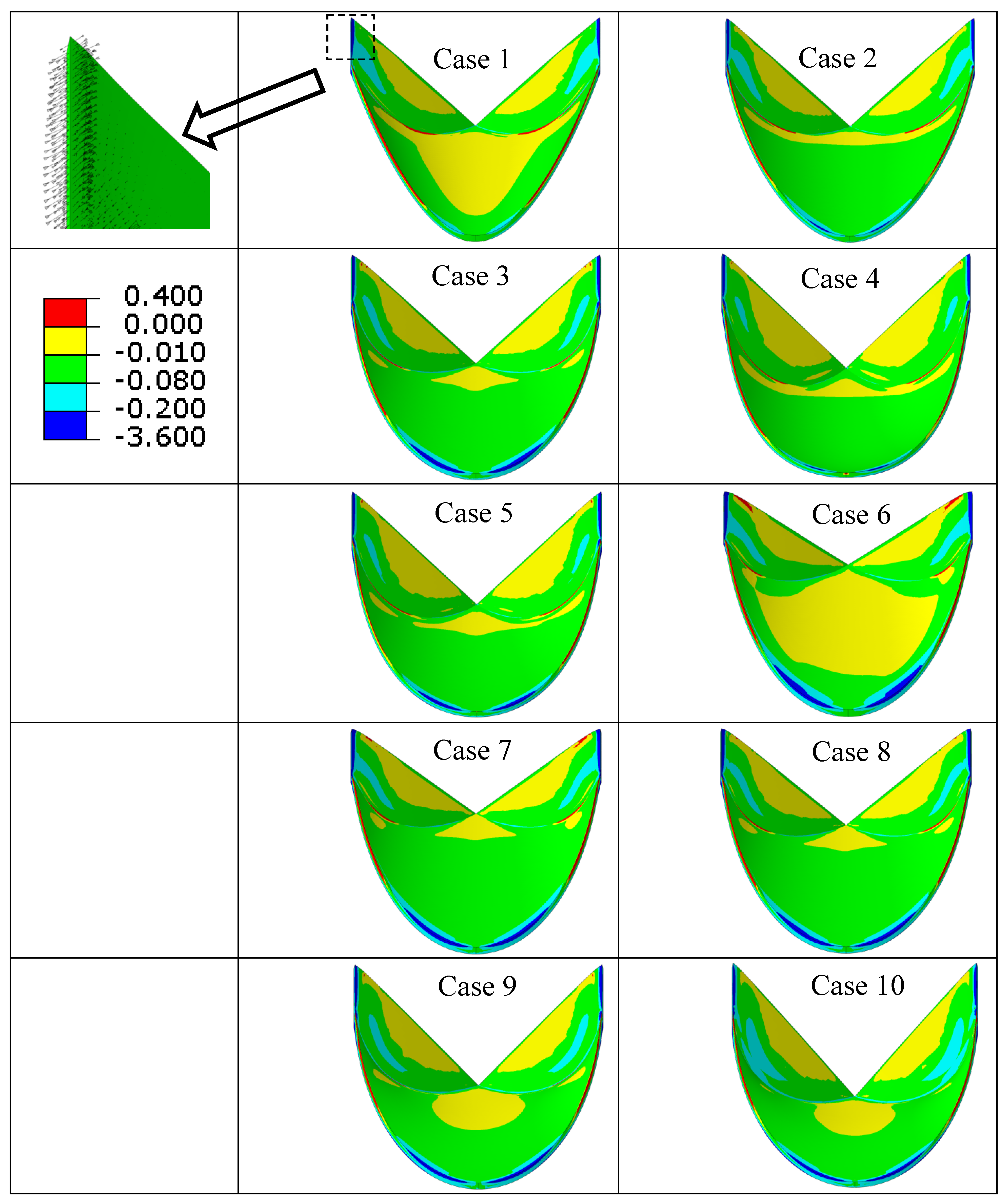
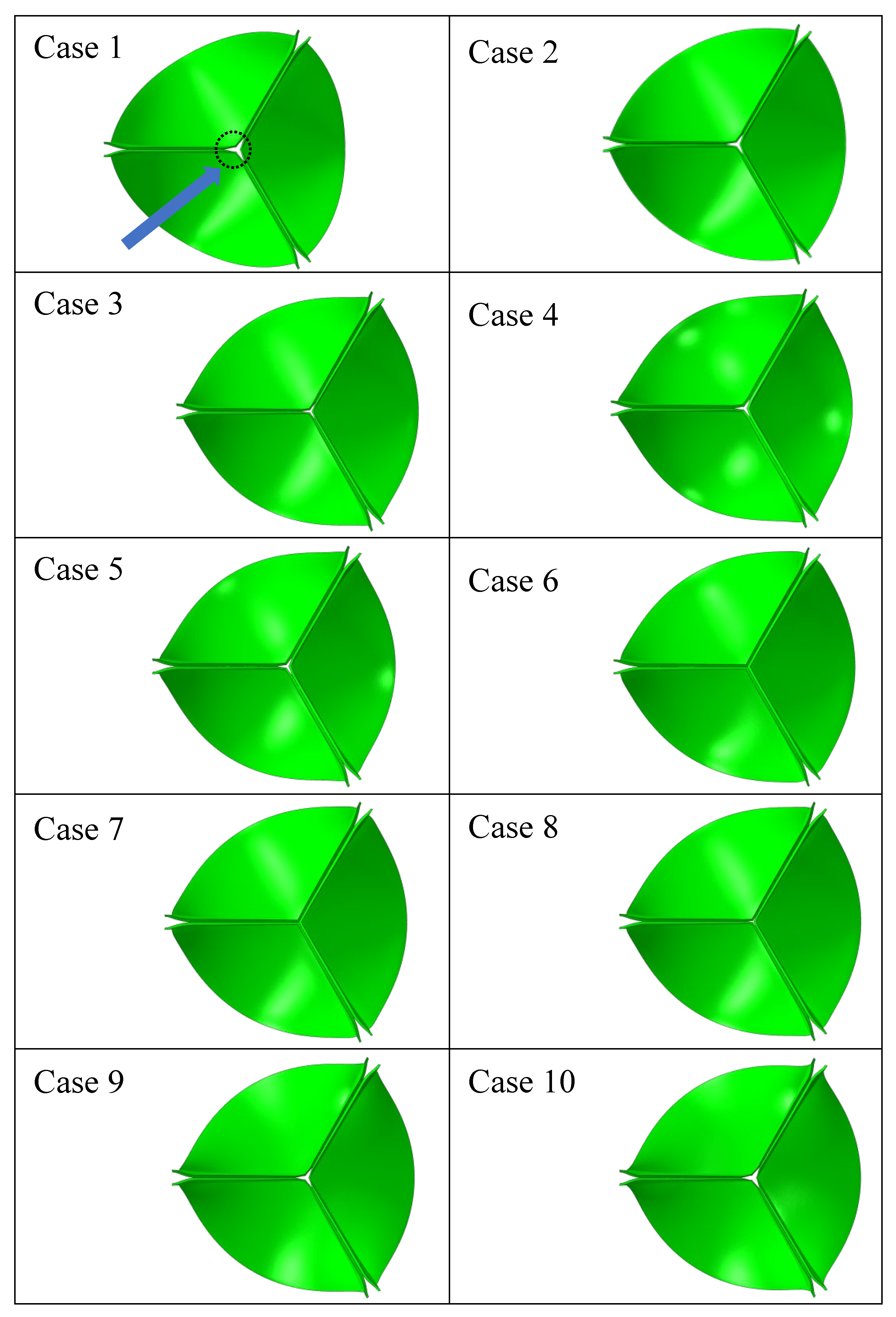
Case Number	Leaflet Angle (Degree)	Radial Curvature	Circumferential Curvature
1	54.4	linear	Parabola
2	54.4	Linear	Spline
3	54.4	Linear	Circular
4	-	Parabola	Circular
5	-	Circular	Circular
6	45.0	Linear	Circular
7	47.85	Linear	Circular
8	50.97	Linear	Circular
9	58.14	Linear	Circular
10	62.22	Linear	Circular

. Additionally, these parameters have been described in our previous report [28]. The commissure height was similar for all cases. SolidWorks (SolidWorks Corp, Waltham, MA, USA, version 2014) was used to create the geometries, which were exported to Pointwise (Pointwise Inc., Fort Worth, TX, USA, version 17.2) for meshing [28]. Using structured meshes, each leaflet was discretized into 13,962 elements, with two layers of elements for the thickness direction. The number of elements was based on several computations with different mesh sizes, which assured the study was not dependent on the mesh size. The meshes were exported to ABAQUS (Simulia, Providence, RI, USA), where finite element calculations were performed using C3D8 (continuum three-dimensional eight-node) elements.

The ABAQUS standard was used for the finite element calculations. Three leaflets were considered in each case. “Surface to surface general contact” was used between leaflets. The friction coefficient was 0.3 [29]. The load was a uniform pressure equal to 8 kPa. All displacements were set to zero at the fixed edges, where leaflets were attached to the stent.

Based on a pseudoelastic assumption for the pericardium [30], the orthotropic Fung model in ABAQUS was used to characterize the leaflets (the ABAQUS manual):

$$\mathrm{w}={\displaystyle \frac{\mathrm{c}}{2}}\left(\exp \left(\mathrm{Q}\right)-1\right)+{\displaystyle \frac{1}{\mathrm{D}}}\left({\displaystyle \frac{{\left(J^{el}\right)}^2-1}{2}}-\mathrm{l}\mathrm{n}{\left(J^{el}\right)}^2\right)$$

(1)

$$\mathrm{Q}={\overline{\mathsf{ϵ}}}_{\mathrm{i}\mathrm{j}}^{\mathrm{G}}{b}_{ijkl}{\overline{\mathsf{ϵ}}}_{\mathrm{k}\mathrm{l}}^{\mathrm{G}}\mathrm{i},\mathrm{j},\mathrm{k},\mathrm{l}=\mathrm{1,2},3$$

with

$${\overline{\mathsf{ϵ}}}^{\mathrm{G}}={\displaystyle \frac{1}{2}}\left(\overline{\mathbf{C}}-\mathbf{I}\right)={\displaystyle \frac{1}{2}}\left({\mathrm{J}}^{-{\displaystyle \frac{2}{3}}}\mathbf{C}-\mathbf{I}\right)={\displaystyle \frac{1}{2}}\left[{\left(\mathrm{d}\mathrm{e}\mathrm{t}\left(\mathbf{F}\right)\right)}^{-{\displaystyle \frac{2}{3}}}\mathbf{F}.{\mathbf{F}}^{\mathrm{T}}-\mathbf{I}\right]$$

where $\mathrm{c}$ and $b_{ijkl}$ are material constants, $J^{el}$ is the elastic volume ratio, and $\mathbf{F}$ is the deformation gradient matrix. Biaxial tensile tests were performed on a sample of the pericardium to determine the material constants. The methodology of calculating material constants using biaxial tests is provided in our other report [31] and is extensively described in the literature [29,32,33,34]. Briefly, beef pericardium was used in the tests, the specimen’s size was 20 by 20 mm, and the tests were displacement-controlled, with a maximum 0.16 strain and 0.008 1/s rate using a Bose machine. The fibers were assumed to be mainly oriented in the circumferential and radial directions, as shown in Figure 1. The material constants are summarized in

Table 2. Material constants used in the Fung model [31].

$\mathit{c}$ (kPa).	${\mathit{b}}_{1111}$	${\mathit{b}}_{1122}$	${\mathit{b}}_{2222}$	${\mathit{b}}_{1133}$	${\mathit{b}}_{2233}$	${\mathit{b}}_{3333}$	${\mathit{b}}_{1212}$	${\mathit{b}}_{1313}$	${\mathit{b}}_{2323}$
8.297	151.375	0	56.994	0	0	50	200	60	60

[31]. The constant $\mathrm{D}$ was set to 1.0 × 10⁻⁷ Pa⁻¹ for all cases to account for tissue incompressibility.

3. Results

Considering the whole valve structure, a circular circumferential curvature led to the lowest values of von Mises, tensile, and compressive stresses in comparison to a parabolic or spline curvature (Figure 2a: Case 3 vs. Cases 1 and 2). The coaptation areas experienced a similar reduction in stresses when a circular circumferential curvature was used (Figure 2b: Case 3 vs. Cases 1 and 2). For the load-bearing area, a circular circumferential curvature led to the lowest von Mises and compressive stresses, but the lowest tensile stresses were obtained by a parabolic circumferential curvature (Figure 2c: Cases 3–5).

For the whole valve structure, a parabolic radial curvature led to the lowest von Mises and compressive stresses compared to a linear or circular radial curvature (Figure 2a: Case 4 vs. Cases 3 and 5). However, a circular radial curvature provided the lowest tensile stresses (Figure 2a: Case 4 vs. Cases 3 and 5). Similarly, when the coaptation areas are considered, the parabolic curvature led to the lowest von Mises and compressive stresses, whereas a circular curvature led to the lowest tensile stress (Figure 2b: Cases 4–5). For both the whole valve structure and the coaptation regions, the tensile stresses caused by the parabolic and circular curvatures were noticeably close (1.794 vs. 1.765 MPa). Considering the load-bearing areas, similar to the whole valve and coaptation regions, a parabolic curvature led to the lowest von Mises stresses. The von Mises stress computed for the circular radial curvature was noticeably close to the parabolic curvature (1.147 vs. 1.13 MPa). Unlike the whole valve and the coaptation areas, the lowest tensile and compressive stresses were computed for a parabolic and a circular radial curvature, respectively. Furthermore, the compressive stresses computed for the parabolic and circular radial curvatures were noticeably close (0.772 vs. 0.768 MPa).

Considering the whole valve structure, as the leaflets inclined downward (away from the sinus), the von Mises, tensile, and compressive stresses decreased (Figure 2a: Cases 3, 6–9), but when the leaflets inclined downward too far, the stresses increased (Figure 2a: Case 10). The coaptation regions showed a trend similar to the whole valve structure (Figure 2b: Cases 3, 6–10). Considering the load-bearing area, a trend was not observed in terms of a reduction or increase in the stresses with leaflet angle (Figure 2c: Cases 3, 6–10); however, for the valve with the highest downward inclination of the leaflet, the stresses were the highest (Figure 2c: Case 10). The peak von Mises and tensile stresses in the whole valve structure were the same peak stresses as in the coaptation regions until the leaflets inclined downward the most, at which point the peak stresses in the whole valve structure became the peak stresses in the load-bearing areas (Figure 2a,c: Case 10).

A parabolic circumferential curvature caused a higher maximum contact pressure compared to a circular or spline curvature (Figure 2d: Case 1 vs. Cases 2 and 3). A linear radial curvature caused a higher maximum pressure compared to a parabolic or circular radial curvature (Figure 2d: Case 3 vs. Cases 4 and 5). When the leaflets inclined upward (toward the sinus), the maximum contact pressure trended to increase (Figure 2d: Cases 6, 8–10); however, not all cases followed this trend (Figure 2d: Cases 3 and 7).

The commissures and lower parts of the fixed-edge region experienced the largest stresses (Figure 3, Figure 4 and Figure 5). The commissures always experienced the largest stresses regardless of the design specifications. Despite the commissure area experiencing high values of tensile and compressive stresses, the directions of these stresses were different (Figure 4 and Figure 5). The contours of contact pressure were also similar for all cases (Figure 6). In all cases, the adjacent leaflets were in contact. (Noticeable contact discontinuity was not seen.)

A circular circumferential curvature provided a higher displacement tip in comparison to a parabolic or spline curvature (Figure 2d: Case 3 vs. Cases 1 and 2). Regarding the radial curvature, a linear curvature provided the highest radial displacement compared to a parabolic or circular curvature (Figure 2d: Case 3 vs. Cases 4 and 5). Regarding the effects of the leaflet angle on the leaflet tip displacements, as the leaflets inclined downward, the radial displacements tended to decrease (Figure 2d: Cases 3, 6–10). The central gap became smaller when the radial displacement increased (Figure 2d and Figure 7).

4. Discussion

The primary limitation of BAVs is their short durability, which is directly related to SVD caused by high mechanical stresses. Mechanical stresses are profoundly affected by the geometrical specifications of the valve. We assessed the effects of the geometrical parameters on the SVD of BAVs, using computational modeling. Different valve design scenarios with different circumferential and linear curvatures and leaflet angles were studied.

The effects of the circumferential curvature were not similar for the coaptation regions and the load-bearing regions (Figure 2b,c: Cases 1–3). Considering the coaptation regions, a circular circumferential curvature would provide superior valve durability as a circumferential curvature provided the lowest von Mises, first, and third principal stresses (Figure 2b: Case 3 vs. Cases 1 and 2). The load-bearing region, however, would experience higher tensile stresses if a circular circumferential curvature was used in comparison to a parabolic or spline curvature (Figure 2c: Case 3 vs. Cases 1 and 2).

The effects of the radial curvature were not similar for the coaptation areas and the load-bearing regions (Figure 2b,c: Cases 3–5). Nonetheless, a parabolic radial curvature would be preferred as it caused lower von Mises stresses compared to a radial and circular curvature (Figure 2b,c: Case 4 vs. Cases 3 and 5). Although a parabolic radial curvature would cause slightly higher tensile (Figure 2b: 1.794 vs. 1.765 MPa) and compressive stresses (Figure 2c: 0.772 vs. 0.768), this effect might be practically unimportant.

The leaflet angle does not have similar effects on the coaptation and load-bearing regions (Figure 2b,c). Regarding the coaptation regions, the more the leaflets are inclined downward, the lower the von Mises, first principal, and third principal stresses would be (Figure 2b: Cases 3, 6–9). However, if the leaflets are highly inclined downward, the stresses might increase (Figure 2b: Case 10). The stresses in the load-bearing regions did not show a straightforward reaction to the changes in leaflet angle (Figure 2c: Cases 3, 6–10). If the leaflets are highly deviated from the sinus, the load-bearing areas might experience large stresses (Figure 2c: Case 10).

The load-bearing areas, as well as the coaptation areas, do not react to changes in leaflet curvatures and leaflet angles in the same way (Figure 2b,c). A valve design might lead to improved (lower) stresses in the commissure regions and, at the same time, cause higher stresses in the load-bearing area. The importance of this finding becomes clearer when one notes that, despite experiencing the largest stresses, the commissure region might not be the most critical area, as the thickness and mechanical properties might not be uniform within the leaflets [35,36,37,38]. The belly might deteriorate before the commissure due to a weaker tissue in the region. Therefore, it is crucial to examine the effects of the design parameters on all parts of the leaflet rather than merely the areas of highest stresses within the whole valve.

The changes in the stresses in the whole valve structure were represented by the stresses in the coaptation areas, as well as the load-bearing areas (Figure 2a–c). One might make an invalid conclusion regarding the importance of the geometrical parameters if one only considers the results for the whole valve structure. For instance, the importance of radial curvature on tensile stresses would not be noticeable unless the load-bearing areas are separately considered (Figure 2a,c: Cases 3–5).

The stress contours were not noticeably affected by the leaflet angle or curvature. The commissure regions and the lower parts of the fixed-edge region experienced large von Mises, first principal, and third principal stresses (Figure 3, Figure 4 and Figure 5). These locations correspond to the regions of frequent calcifications and tearing of BAVs [11,12,39]. In addition, the exposure of the commissure area to high stress values (Figure 3 and Figure 4) confirms previous numerical studies that calculated high stresses in this area [40]. It should be noted that the first principal and third principal stresses were in different directions (Figure 4 and Figure 5), which can have key roles in the fatigue life of the valve.

The sealing and coaptation between leaflets are crucial factors for optimal valve performance [36,41,42,43]. As in all cases where leaflets have full coaptation (Figure 6), the higher contact pressure means the leaflets provide better sealing between them when the valve is closed. Regarding the effects of circumferential curvature, a parabolic curvature provided better sealing between adjacent leaflets compared to a circular or spline curvature (Figure 2d: Case 1 vs. Cases 2 and 3). Regarding the radial curvature, a linear radial curvature provided better sealing between adjacent leaflets compared to a parabolic or circular curvature (Figure 2d: Case 3 vs. Cases 4 and 5). Most likely, there is a trend regarding the effects of leaflet inclination on the sealing between adjacent leaflets: the more the leaflets are inclined upward, the better the sealing between adjacent leaflets (Figure 2d: Cases 6, 8–10); however, this trend might not be valid (Cases 3 and 7).

A circular circumferential curvature provides lower chances of regurgitation at the central gap when the leaflet is closed (Figure 2d and Figure 7: Case 3 vs. Cases 1 and 2, Figure 7: Case 3). A radial curvature provides stronger central gap closure compared to a parabolic or circular curvature (Figure 2d and Figure 7: Case 3 vs. Cases 4 and 5). The more the leaflets are inclined upward, the lower the chances of regurgitation at the central gap become (Figure 2d and Figure 7: Case 3, 6–10). It should be noted that leaflets might wrinkle and pinwheel if contact, which is too strong, occurs between leaflets in the central area [44].

Mercer et al. measured the dimensions of the load-bearing part of the human aortic valve and concluded that they display a parabolic curvature in circumferential and radial directions [45]. Our results confirm the results obtained by Mercer et al.: a parabola is the optimized radial curvature for leaflets (Figure 2c: Case 3 vs. Cases 4 and 5). However, according to our results, although the maximum tensile stresses would be lower with a parabolic circumferential curvature, the von Mises and compressive stresses would be higher for a parabolic curvature compared to a spline or circular curvature (Figure 2c: Case 1 vs. Cases 2 and 3). Considering the results in our study and those by Mercer et al., it might be concluded that the circumferential curvature of the load-bearing part of the native aortic valve is optimized to have minimum tensile stresses (and not von Mises and compressive stresses). However, it should be noted that in the native valve, the leaflets function as one of the components of the aortic root assembly during the whole cardiac cycle. The mechanics of the native valve are in harmony with the aortic root, which could affect the optimum valve geometry [46,47,48]. The optimum curvature of the native valve is not merely determined by the leaflets' geometry but also by their dynamic motion in synchrony with the aortic root.

We studied the effects of the geometrical parameters on the mechanics of BAVs when a uniform pressure load was applied to the leaflets. In reality, the load on the leaflets is not a simple uniform pressure load but a result of the complex interaction between blood flow and leaflets. However, this limitation is not thought to revoke the findings of our study as far as the comparative importance of geometrical factors is considered. Furthermore, we studied the closed valve where the leaflet displacements are not as large as when the valve opens and closes. The blood pressure would more noticeably be affected by the leaflets’ motion when they open and close. Since our goal was to compare different valve designs, the lower end of diastolic pressure (8 kPa) was used, which is computationally more efficient.

We used a nonlinear Fung-type constitutive equation for the leaflets. The constants of the Fung model were based on biaxial test data for only one sample. The constants would likely change if more samples were used in the biaxial tests. However, the objective of the study was not affected by this limitation, as the same constants were used in all the case studies.

Fiber orientation directly affects the material properties of leaflets. Based on experimental data for porcine aortic valve leaflets [36,49,50], we assumed the fibers are oriented in two main directions (Figure 1). In reality, the mapping of fibers within the leaflets of BAVs might be basically different from our assumption. This limitation is not thought to notably affect the results of this study, as fiber orientation was similar in all cases. If a study aims to particularly examine the contours and values of stresses for a specific valve design, the orientation of the fibers throughout the leaflet needs to be based on more precise measurements.

In these simulations, we did not use the dimensions of any specific prosthetic valve currently available on the market. However, the leaflet shapes were generally similar to those of the native valve and certain commercially available prosthetic valves. Rather than focusing on a particular geometry, we aimed to study the effects of geometrical variations on valve mechanics.

The results of this study should be interpreted with caution. This investigation presented the importance of geometrical parameters when the valve is closed (a static condition). When the valve opens and closes (a dynamic behavior), the effects of geometrical parameters might not be similar to a closed valve configuration. We recently showed that during systole, the von Mises stress reduces when the leaflets incline upward, which is not similar to the effects of leaflet inclination for a closed valve [28]. It is, therefore, crucial to consider both the systole and diastole (the whole cardiac cycle) when studying the mechanics of BAVs.

We studied the effects of geometrical parameters on the mechanics of BAVs when the valve is closed. Different leaflet circumferential and radial curvatures, as well as the angle of the leaflets, were examined in ten case studies. The results show that the load-bearing area and the coaptation regions might not react similarly when the leaflets’ geometrical parameters are altered. Considering the mechanics of closed BAVs, the chances of SVD could be less if leaflets have a circular circumferential curvature, a parabolic radial curvature, and are inclined more downward within a range. These results could contribute to a better understanding of the mechanisms of SVD in BAVs and lead to better BAV durability.