Finite Element Analysis of Dental Diamond Burs: Stress Distribution in Dental Structures During Cavity Preparation

Abstract

Background/Objectives: Dental cavity preparation is a critical procedure in restorative dentistry that involves the removal of decayed tissue while preserving a healthy tooth structure. Excessive stress during tooth preparation leads to enamel cracking, dentin damage, and long term compressive pulp health. This study employed finite element analysis (FEA) to investigate the stress distribution in dental structures during cavity preparation using round diamond burs of varying diameters and depths of cut (DOC). Methods: A three-dimensional human maxillary first molar was generated from computed tomography (CT) scan data using 3D Slicer, Fusion 360, and ANSYS Space Claim 2024 R-2. Finite element analysis (FEA) was conducted using ANSYS Workbench 2024. Round diamond burs with diameters of 1, 2, and 3 mm were modeled. Cutting simulations were performed for DOC of 1 mm and 2 mm. The burs were treated as rigid bodies, whereas the dental structures were modeled as deformable bodies using the Cowper–Symonds model. Results: The simulations revealed that larger bur diameters and deeper cuts led to higher stress magnitudes, particularly in the enamel and dentin. The maximum von Mises stress was reached at 136.98 MPa, and dentin 140.33 MPa. Smaller burs (≤2 mm) and lower depths of cut (≤1 mm) produced lower stress values and were optimal for minimizing dental structural damage. Pulpal stress remained low but showed an increasing trend with increased DOC and bur size. Conclusions: This study provides clinically relevant guidance for reducing mechanical damage during cavity preparation by recommending the use of smaller burs and controlled cutting depths. The originality of this study lies in its integration of CT-based anatomy with dynamic FEA modeling, enabling a realistic simulation of tool–tissue interaction in dentistry. These insights can inform bur selection, cutting protocols, and future experimental validations.

1. Introduction

Dental cavity or root canal preparation is a common procedure in dental surgeries. In this procedure, the dentist prepares the teeth for better access to fillings, crowns, and veneers. The cavity shape supports long-term restoration retention, esthetic optimization, and preservation of the structural integrity of the tooth. The dental enamel is the hardest structure of the outer tooth and has unique biomechanical properties. Enamel consist mainly of hydroxyapatite crystals, forming a highly mineralized structure with exceptional hardness and brittleness [1]. Despite its mechanical robustness, enamel is susceptible to microfractures and chipping during tooth preparation, which can compromise tooth longevity and the success of restorative treatments [2,3]. Dental instruments such as diamond burs are commonly used for tooth preservation because of their cutting efficiency [4]. These instruments are bonded with abrasive particles on a metal substrate, allowing effective slicing of the enamel while minimizing heat generation and vibration during rotation. The choice of diamond bur is crucial for the clinical success of the procedure. These small rotating instruments are typically made of high-speed steel or tungsten carbide, and they come in a variety of shapes and sizes to accommodate different dental procedures. For instance, round burs are commonly employed for cavity preparation, whereas tapered fissure burs are ideal for creating precise angles in tooth structures. Factors such as grit size, rotational speed, and clinician technique significantly influence the precision and safety of enamel removal [5]. The size of the bur is equally important. Round burs are categorized by their diameter, ranging from 0.5 mm to 4 mm. Smaller burs are typically used for intricate work, such as accessing narrow canals in endodontics, whereas larger burs are suited for large material removals. Understanding the appropriate size and type of bur can significantly affect the efficiency of the procedure and overall comfort of the patient. ISO- 806 314 001 is the most used round bur in dentistry [6]. This is due to the versatility and efficiency of dental procedures. Modern burs often have spherical heads coated with diamond grit, which offers enhanced control and cutting performance. Despite their widespread use, the interaction between diamond burs and enamel under various loading conditions is not fully understood, and further investigation of the biomechanical response of enamel during tooth preparation is required.

Enamel machinability refers to the ease and quality with which the enamel can be cut or shaped using dental instruments. It is a critical factor influencing clinical outcomes, including the precision of cavity margins, preservation of sound tooth structure, and reduction of iatrogenic damage such as microcracks or thermal injury [7,8]. Optimal dental machinability ensures the minimal removal of healthy tissues during dental procedures. However, the highly mineralized and anisotropic structure of enamel presents challenges in achieving constant machinability across different zones of the tooth [9]. Understanding enamel machinability is essential for developing optimized bur designs and clinical protocols that enhance procedural efficiency and patient safety [10,11]. Song et al. [12] introduced the quantitative effect of diamond grit size on subsurface damage during dental adjustment of porcelain surfaces. Their findings revealed that coarse burs induced significantly deeper subsurface damage than fine burs, highlighting the importance of grit size in controlling the damage depth. Watson et al. [13] compared the cutting dynamics of high-speed, high-torque handpieces and high-speed, low-torque air-turbine handpieces, focusing on enamel cracking and tooth temperature changes during cavity preparation. Their research highlighted the importance of handpiece controlling the torque to minimize potential damage to the tooth structure during dental procedures. Al-Omari et al. [14] examined the roughness of the enamel’s surface along with its wettability, as well as the dentine surfaces that were prepared using various dental burs. The authors highlighted that smoother surfaces were more favorable for bonding procedures, emphasizing the need for appropriate bur selection to achieve optimal surface characteristics for restorative treatments. Zhao et al. [15] investigated the cutting mechanisms and performances of different dental burs in enamel machining. Fissure, diamond, and round burs were compared during the drilling and milling experiments on various tooth surfaces. Their findings highlight the need to select burs based on their cutting performance and structural characteristics. Li et al. [16] examined the machinability of enamel during grinding using diamond dental burs. The results indicated that occlusal surface grinding generated higher normal forces and rougher surfaces than axial surface grinding did. Fine diamond burs, lower grinding speeds, and reduced depths were found to improve surface quality by minimizing brittle failure and enhancing enamel surface smoothness.

Finite element analysis (FEA) is a computational modeling technique that is widely used in biomechanical engineering to analyze stress distribution and material deformation in complex structures. In the context of dental research, FEA is a powerful tool for simulating the mechanical interactions between the dental burs and enamel during cavity preparation. By discretizing the enamel structure into smaller elements, FEA enables a detailed study of stress patterns, strain distribution, and potential fracture initiation within the tissue [17,18]. Song et al. [19] utilized FEA to investigate the stress fields and subsurface damage in ceramic prostheses during simulated intraoral dental resurfacing. This study focused on the effects of operational parameters, such as the depth of cut and chip thickness, on subsurface damage. The results revealed that tensile, shear, and compressive stress were concentrated under the diamond bur contact zone, and the subsurface damage increased with the depth of cut. Guan et al. [20] conducted a finite element study to simulate stress distribution within the mandible during dental implant insertion. The results indicated that the stress levels in the cancellous and cortical bones were significantly lower in the thread-forming scenario. The study highlighted that greater stress occurs in the cancellous bone than in the cortical bone during insertion. The application of FEA in dental research has provided valuable contributions to understanding tooth biomechanics, such as stress distribution in restorative materials, fracture risk in endodontically treated teeth, and the load-bearing capacity of dental implants [21,22,23]. However, the use of FEA to evaluate enamel machinability during tooth preparation using diamond burs remains limited. Existing studies have primarily focused on gross stress patterns without sufficient attention to the localized mechanical behavior of enamel and the influence of bur design parameters on stress propagation [16,20,23]. The present study utilized ANSYS Workbench to model and analyze the explicit dynamics of diamond burs of varying diameters during cavity preparation to investigate stress distribution in dental structures. The null hypothesis (H₀) for this study was that variations in bur diameter and cutting depth do not significantly influence stress distribution in enamel, dentin, or pulp during cavity preparation. The alternative hypothesis (H₁) is that both the bur diameter and depth of cut significantly affect stress magnitudes and propagation patterns within dental tissues.

2. Materials and Methods

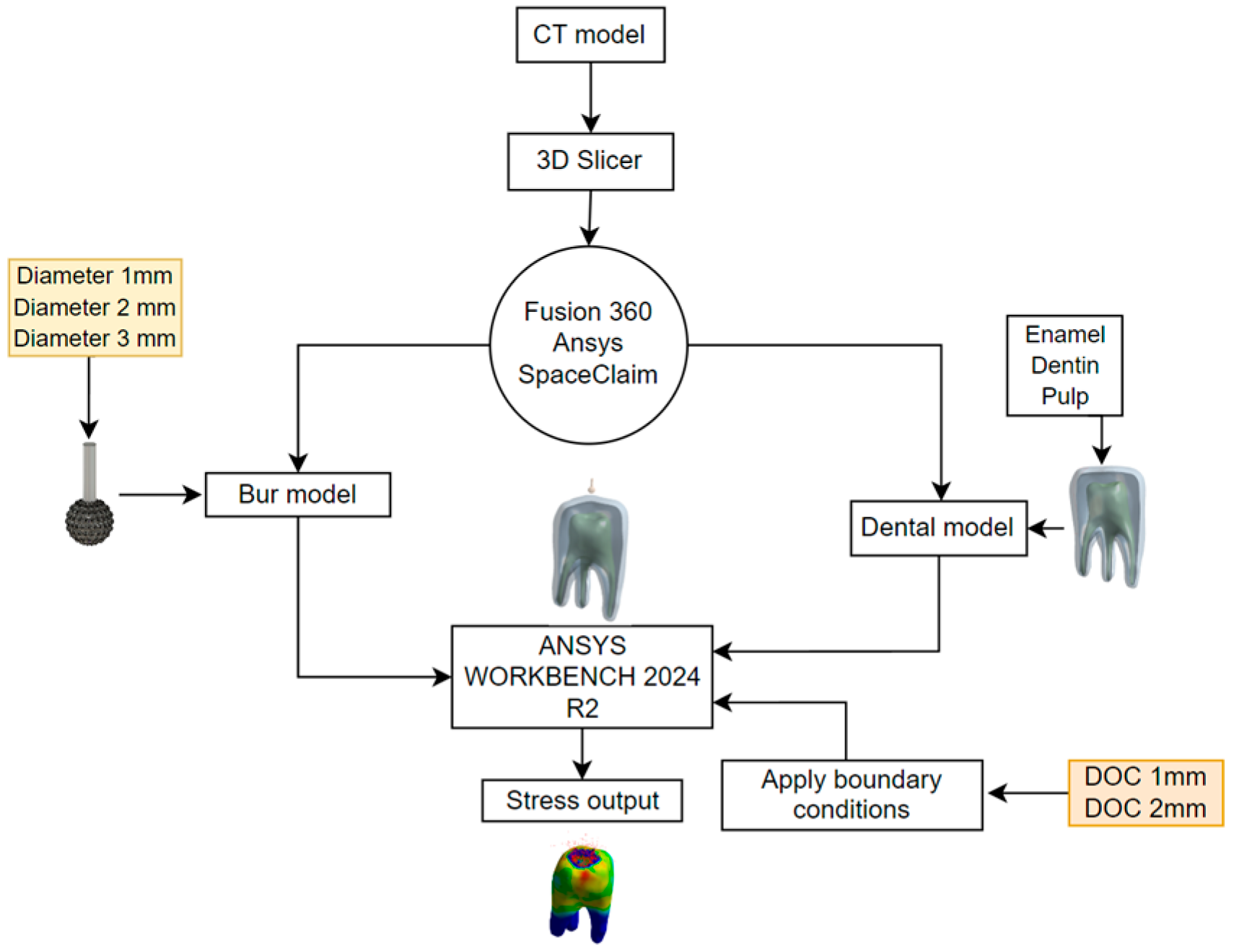
A three-dimensional human maxillary first molar model was generated from computed tomography (CT) scan data using a 3D Slicer software. DICOM CT images were processed to create a solid model that retained accurate anatomical features. This model was then refined using Fusion 360 and ANSYS Space Claim 2024 to smoothen surface irregularities and ensure mesh compatibility.

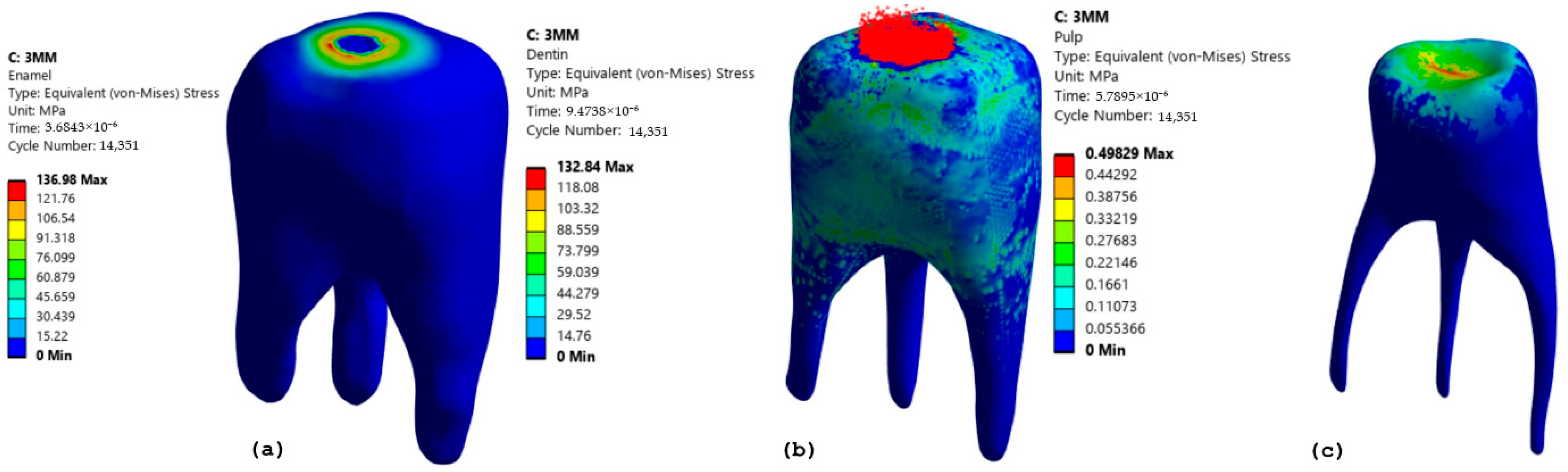
The dental structural components (enamel, dentin, and pulp) were segmented and modeled up to 1 mm from the occlusal surface. Diamond-coated round burs of three diameters (1 mm, 2 mm, and 3 mm) were modeled using Fusion 360 and assembled with the tooth model in ANSYS Workbench 2024 R2. These burs were considered rigid bodies in the simulation, whereas dental tissues were modeled as deformable using the Cowper–Symonds material model.

2.1. Modeling

As shown in Figure 1, a dental model was generated using CT data acquired using a I-CAT 17-19 scanner (imaging Science international LLC, Hatfield, PA, USA). The DICOM-format images were processed using 3D Slicer software, version 5.2.2 (Brigham and Women’s Hospital, Harvard Medical School, Boston, MA, USA), an open-source medical imaging platform. The DICOM and Communications in Medicine format of the CT images was used to model the actual tooth structure. As this was a computational study based on a single anatomical model derived from CT data, randomization was not applicable. Similar simulation-based approaches have been reported without randomization [23]. The images were processed using the 3D Slicer open-source software. The software was used for image analysis and scientific visualization. The DICOM CT images were opened in a 3D slicer, and the model was generated. The original CT-derived model included an anatomically accurate crown morphology with grooves, pits, cusps, and ridges. However, during the geometry cleaning and preparation phase, these surface details were intentionally smoothed using Fusion 360 and ANSYS SpaceClaim 2024 to facilitate the mesh quality, convergence, and solver stability in an explicit dynamic simulation environment. Highly detailed surfaces tend to produce complex, irregular element shapes that lead to excessive simulation time, non-physical stress concentrations, or convergence failure. The dental structural model, enamel, dentin, and pulp were considered at a distance of 1 mm from the top surface. The dental structure and its components are shown in Figure 2a. 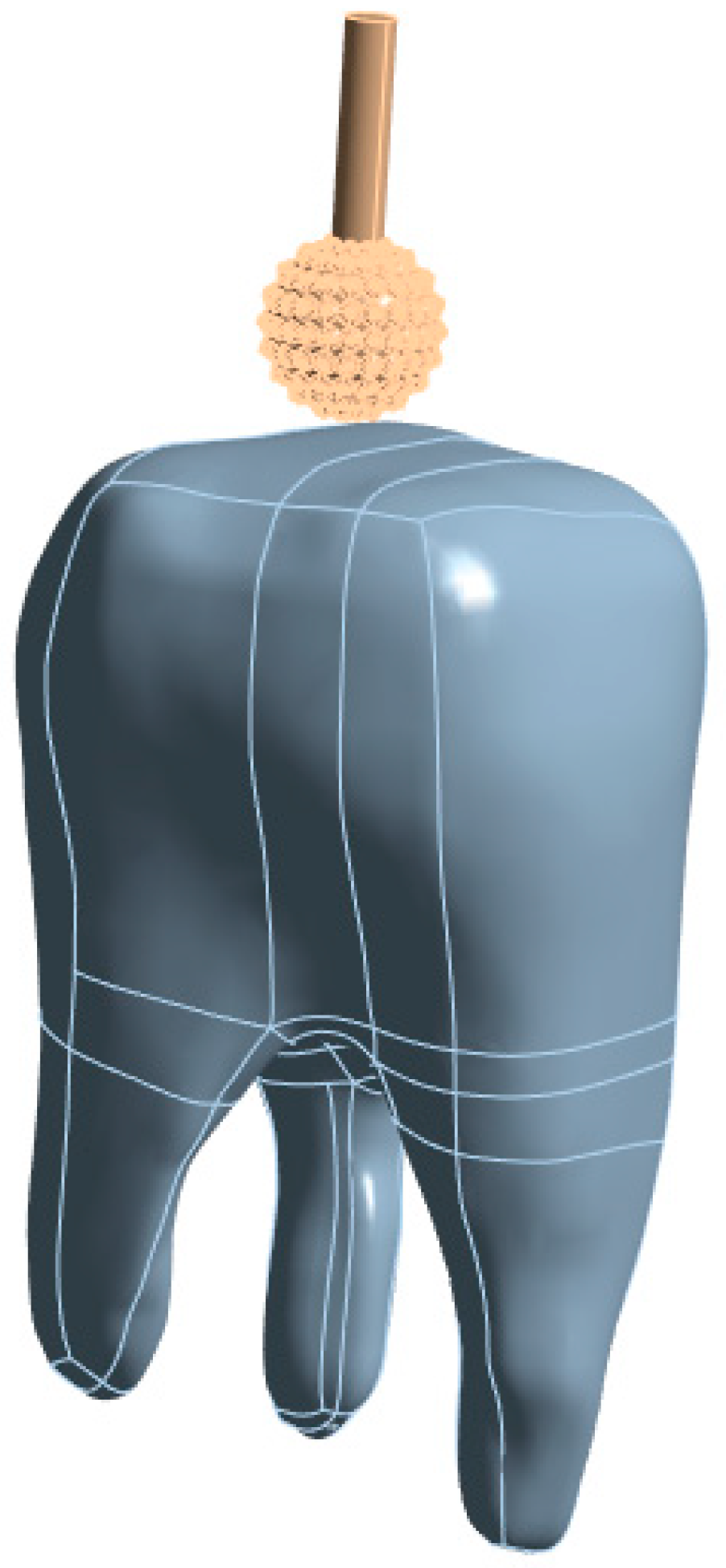As the tooth selected is the upper first molar, the tooth structures are shown as in Figure 2b with the crown directed downwards. A diamond-coated round bur tool was modeled to analyze the cavity preparation in the tooth structure. The grit arrangement is assumed to be compatible with the simulation results. The assumed bur was modeled using Fusion 360. In the current analysis, we considered three models with diameters of 1 mm, 2 mm, and 3 mm. The modeled burs cover a wide range and are commonly used in cavity preparation and tooth cutting. Smaller burs were used for fine and precise cavity access, whereas larger burs were used for material removal and tooth shaping. In addition, these ranges allowed us to investigate stress distribution during the procedure for cutting efficiency and structural impact on dental structures. Figure 2b shows the assumed diamond round-bur model with a defined diameter. The assembly of the bur and dental structure models is shown in Figure 3. These models were used for simulation in ANSYS Workbench 2024 R2. The minimum distance between the burs and the teeth was maintained to avoid a longer simulation time.

2.2. Meshing and Boundary Conditions

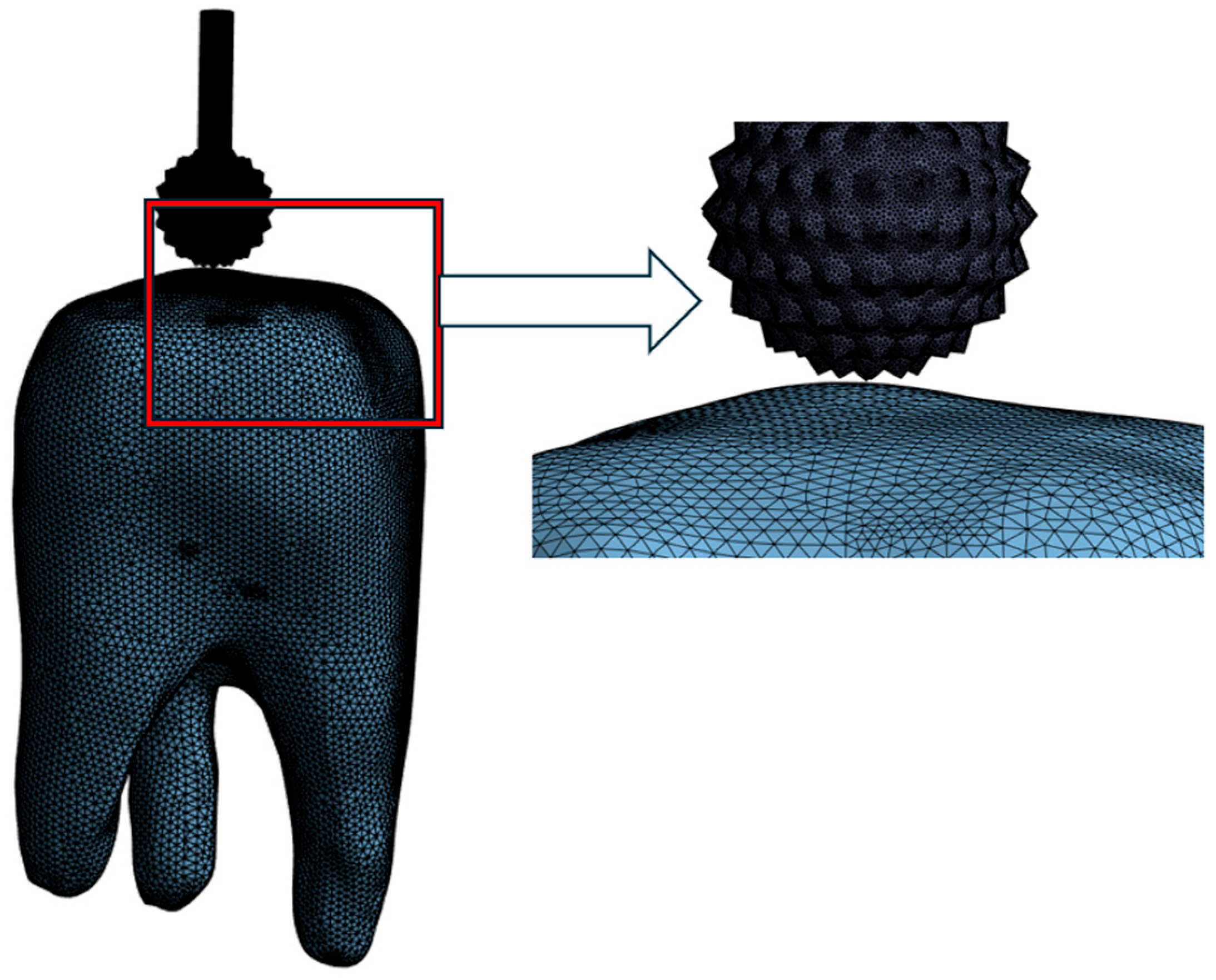
Figure 4 shows the meshed model. Four nodded tetrahedral elements were adopted for meshing.

Table 1. Specifications of the models, including the associated nodes and elements for each model.

Component	Stiffness Behavior	Nodes	Elements
Enamel	Flexible	10,555	20,134
Dentin	Flexible	63,548	124,376
Pulp	Flexible	23,251	45,151
Bur	Rigid	12,461	22,522

presents the quantities of nodes and elements. The behavior of the bur is characterized as rigid, whereas the dental structure is regarded as deformable or flexible.

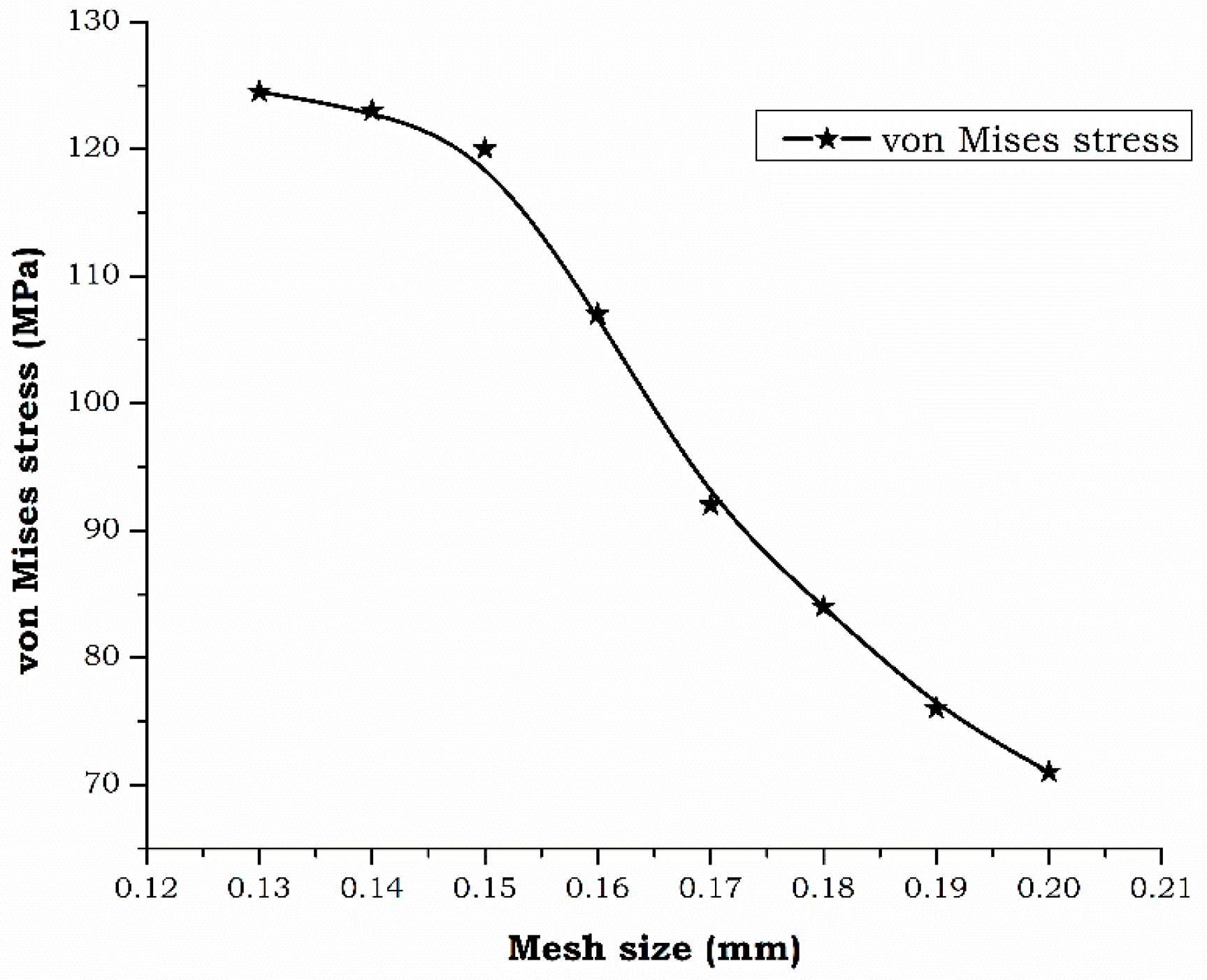
Figure 5 presents the grid independence study conducted during the simulation of the dental bur cavity access preparation. The research focused on altering the elemental mesh size to assess its impact on simulation outcomes, aiming to identify the least computational resources needed to produce precise and dependable outcomes. During the explicit simulation, the mesh size was varied between 0.1 mm and 0.2 mm. The selected range was chosen to evaluate the impact of varying levels of discretization on the computed stress values. The maximum von Mises stress on the enamel served as the standard for determining grid independence. Through multiple reiterations, it was observed that 0.15 mm mesh size consistently produced reliable outcomes. This mesh results offers ideal stability among computational speed and the detail required for precise simulation. This mesh size enables the formation of nodes and elements for the simulation [17,19]. Figure 4 presents the mesh, illustrating the discretization of the bur and dental structure. Table 1 provides the specification of the models, including the number of elements and nodes.

The Cowper–Symonds model was employed for dynamic analysis. In this model, the bur is considered rigid, whereas dental structures such as enamel, dentin, and pulp are treated as deformable bodies [Table 1]. The Cowper–Symonds model was chosen because of its capability to simulate high-strain-rate deformation behavior in hard biological tissues, such as enamel and dentin, without requiring temperature-dependent inputs. The material constants were sourced and adapted from prior literature on dental FEA and bone cutting studies [24,25,26]. The Cowper–Symonds model is characterized by its independence from temperature variables, relying exclusively on the strain rate constant. This model is a kinematic hardening model and is considered more appropriate than existing models such as the Johnson–Cook, power law creep, and viscoelasticity models.

According to the ANSYS help manual, the Cowper–Symonds model is detailed in Equation (1).

$${\sigma }_y=\left[1+{\left({\displaystyle \frac{\dot{\epsilon }}{C}}\right)}^{1/p}\right]\left({\sigma }_0+\beta E_p{\epsilon }_p^{eff}\right)$$

(1)

$$E_p={\displaystyle \frac{E_{tan}E}{E-E_{tan}}}$$

(2)

In this Equation (1), σ₀ denotes the initial yield stress measured in MPa, ε signifies the strain rate in s⁻¹, and β is the hardening parameter, with a value of 0 indicating kinematic hardening and 1 indicating isotropic hardening. The parameters C and p are associated with the Cowper–Symonds model, which also involves the effective plastic strain, denoted as ${\epsilon }_p^{eff}$. The plastic hardening modulus, Eₚ, is influenced by both Young’s modulus (E) and the tangent modulus (Eₜₐₙ), as detailed in Equation (2).

Table 2. Characteristics of materials and Cowper–Symonds parameters.

Properties	Enamel	Dentin	Pulp	Pilot Drill
Density (kg/m3)	2958	2140	1950	7856
Young’s modulus (MPa)	>84,000	>18,000	>2	>220
Poisson’s ratio	0.31	0.30	0.45	0.3
Initial yield stress (MPa)	23
Tangent modulus (MPa)	0.91
Hardening parameter	0.1
C	2.5
P	7
Failure strain	0.05

provides a complete list of the material properties alongside the corresponding Cowper–Symonds model parameters.

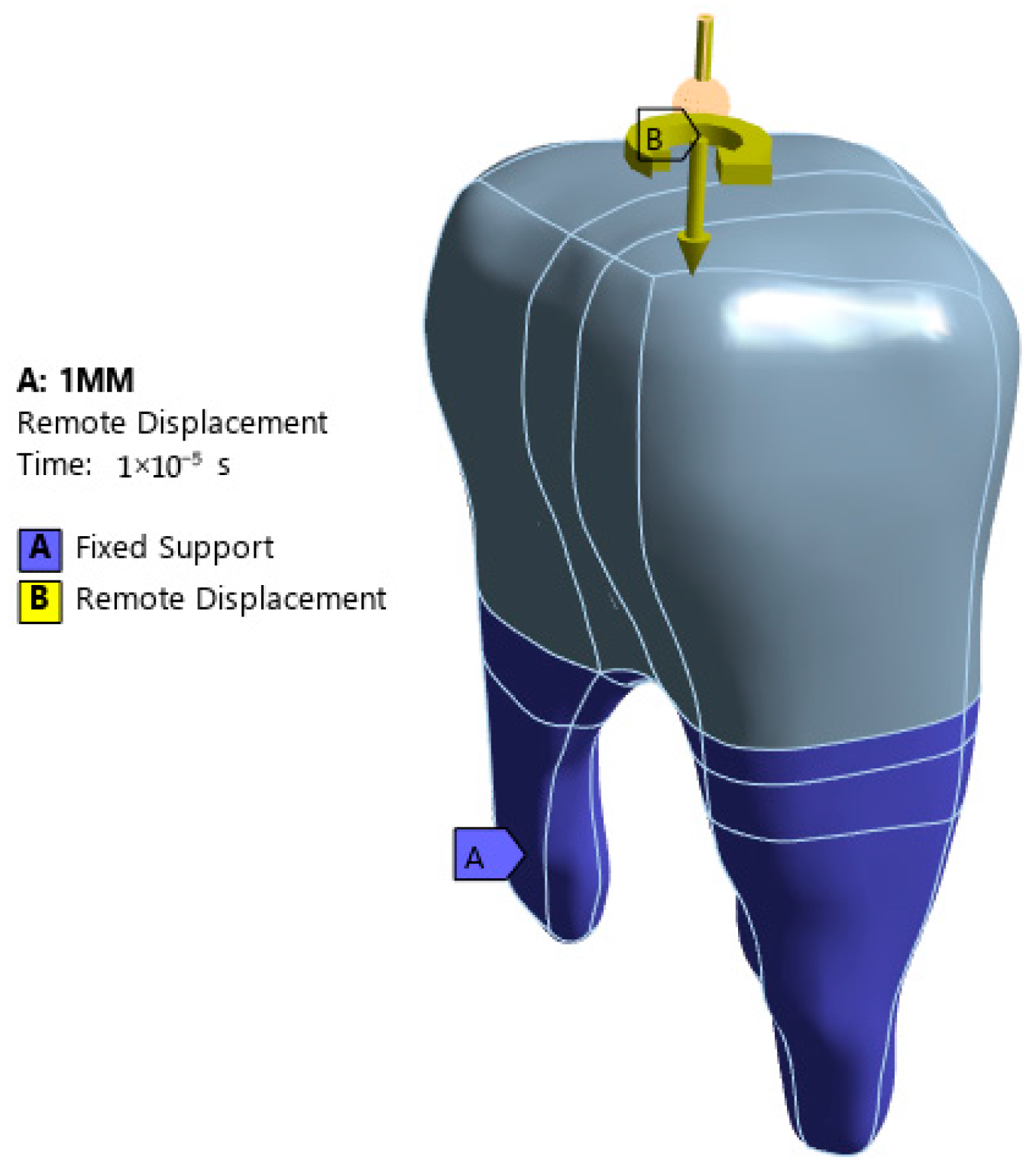
In the current study, the bur was rotated by providing an angle of rotation, and the lower surfaces of the teeth were fixed in all directions [Figure 6]. An ANSYS workbench was used to conduct explicit dynamic analysis. The erosion properties were enabled for short-term simulations. As shown in Figure 6, the tooth surface was fixed with all degrees of freedom. The 360-degree angular rotation and depth of cut (DOC) in the displacement format were added to the remote displacement loading condition. The analysis was performed at two different cutting depths. A 1 mm DOC is often used for initial access and precise cutting, while a 2 mm DOC is used for deeper material removal or cavity shaping. By comparing the two DOC, we analyzed the stress distribution and its effects on the dental structure.

3. Results

3.1. Stress Distribution Patterns

The FEA simulations revealed distinct stress distribution patterns associated with each bur diameter. A larger diameter (3 mm) induced broader stress zones, whereas a smaller diameter (1 mm) concentrated the stress more narrowly near the cavity edge. The stress patterns were analyzed for different bur diameters. In addition, DOC plays a vital role in material removal. Dental structure consists of three components: enamel, dentin, and pulp. The first contact region for the bur is the enamel. An enormous amount of stress is generated during the first contact.

3.2. Stress Pattern for Different Bur Diameters with DOC 1 mm and DOC 2 mm

As shown in Figure 7, for a diameter of 1 mm and DOC of 1 mm, the maximum stress generated was 121.72 MPa at the point of contact between the bur and enamel [15] [Figure 7a]. This stress was then transferred to the dentin. Dentin absorbs the stress transferred from the enamel, with a maximum recorded stress of 111.1 MPa [Figure 7b]. Being softer than enamel, it helps to distribute the load further into the tooth structure. The pulp experiences the least amount of stress (0.163 MPa as shown in Figure 7c) because most of the stress is absorbed by the enamel and dentin.

Figure 8 provides insight into increasing the DOC from 1 mm to 2 mm for a 1 mm diameter bur. The maximum stress increased to 127.83 MPa from 121.72 MPa as compared with 1 mm DOC [Figure 8a]. This indicates that an increase in DOC results in higher localized stress on the enamel. In addition, there was a large increase in stress in the dentinal region. The stress recorded in the dentin was 122.67 MPa [Figure 8b]. When compared to the 1 mm DOC, this suggests that a larger DOC transfers more stress to the deeper layer of the tooth. Although the pulp experiences low overall stress, an increase in stress from 0.163 to 0.305 MPa indicates that deeper cuts could potentially influence pulpal health over repeated procedures [Figure 8c]. From Figure 7 and Figure 8, it can be concluded that stress increased from 1 mm DOC to 2 mm DOC. Dentin experiences higher stress absorption, which may lead to the risk of structural damage. Even if the pulp stress remains low, repeated exposure may affect pulpal health.

A similar analysis was carried out for bur diameters of 2 mm and 3 mm and 1 mm and 2 mm, as shown in Figure 9, Figure 10, Figure 11 and Figure 12.

Figure 9 and Figure 10 with the stress patterns show similar trends as the 1 mm bur diameter output, but with slightly higher magnitudes of stress owing to the larger contact area. In Figure 9a, the enamel recorded a high stress value of 126.33 MPa, which is a direct reflection of its role as the primary force-bearing tissue. The stress value in the dentin (Figure 9b, 123.77 MPa) is very close to that of the enamel. This indicates that the occlusal forces are effectively transmitted through the enamel and into the dentin, which acts as a foundational support layer. The enamel and dentin efficiently absorb and dissipate the high masticatory forces, effectively shielding the delicate inner pulp from mechanical stress. The pulp shows a significantly lower stress value of 0.202 MPa (Figure 9c). In a separate analysis, when the diameter of the bur is 2 mm, the maximum stress obtained in the enamel and dentin increased to 133.14 MPa and 126.77 MPa, respectively (Figure 10a and Figure 10b). Similarly, the pulp, while still shielded by the enamel and dentin, recorded a higher stress value of 1.0347 MPa under these specific conditions (Figure 10c).

Figure 11 and Figure 12 illustrate the stress patterns for the 3 mm diameter bur under different conditions. For a depth of cut (DOC) of 1 mm, Figure 11 shows the maximum enamel stress obtained was 136.14 MPa [Figure 11a]. Correspondingly, Figure 11b indicates a stress value in the dentin of 132.84 MPa, and Figure 11c shows a pulp stress value of 0.49829 MPa. Similarly, in Figure 12, the enamel records 129.85 MPa [Figure 12a]. For the dentin, the maximum recorded was 140.43 MPa [Figure 12b], which stands out as the highest among all cases presented. This finding supports the conclusion that deeper and larger burs significantly increase stress transfer to the dentin [27]. Additionally, the pulp shows an increased stress magnitude of 1.0345 MPa in this scenario [Figure 12c].

3.3. Stress Plot Analysis for DOC 1 mm and DOC 2 mm

Figure 13 shows the stress distribution in the enamel for different bur diameters for a DOC of 1 mm [Figure 13a] and a DOC of 2 mm [Figure 13b]. As shown in Figure 13a, at the point of bur contact with the surface of the enamel, the highest stress concentration occurs. Initially, the stress was zero until the bur made contact with the enamel surface. An increase in stress concentration begins with the cutting points in contact with the surface. The 3 mm bur diameter experiences the highest stress of 136.98 MPa, followed by 2 mm and 1 mm bur stresses, recorded as 126.33 MPa and 121.72 MPa, respectively. This is because a larger diameter creates a border contact area and increases resistance to cutting forces. The minimum stress was recorded in the 1 mm bur diameter because it removes a smaller volume of the enamel, producing less force distribution. From Figure 13b, it is observed that the stress value for the bur diameter of 3 mm exhibits a slight drop in stress from 136.98 MPa at 1 mm DOC to 129.85 MPa at 2 mm DOC. This is because at a DOC of 2 mm, the bur interacts with a large volume, and the interaction between the cutting edge and enamel may change, leading to a decrease in the stress magnitude.

Figure 14 shows the stress distribution for dentin with 1 mm DOC and 2 mm DOC. At a DOC of 1 mm, as shown in Figure 14a, the stress distribution followed an increasing trend, with a large bur diameter producing the peak stresses. As shown in Figure 14b, all bur diameters show an increase in stress, and the 3 mm bur diameter exhibits the highest stress of 140.33 MPa. This trend is more linear and predictable than that of enamel, indicating a more uniform stress distribution in the dentin. One of the reasons for the highest stress is the material properties of dentin, which are more elastic than those of enamel. It is also observed from Figure 14 that the 3 mm bur diameter records a high magnitude of stress at both levels of DOCs owing to large cutting surfaces, increased resistance, and higher energy absorption. When compared with enamel stress plots [Figure 15], dentin did not show a stress drop at a deeper DOC for the 3 mm bur diameter. This is because dentin distributes stress more evenly and does not exhibit brittle fractures in the same manner as enamel. This leads to stress build-up to a peak value of 140.43 MPa at 2 mm DOC.

Figure 14 shows the stress distribution in the pulp for different DOC and bur diameters. It was observed that for a bur diameter of 1 mm, the stress increased moderately, that is, from 0.1603 to 0.3052 MPa. For the 2 mm and 3 mm bur diameters, the stress increases drastically, that is, from 0.2029 MPa to 1.0347 MPa for the 2 mm bur and from 0.4984 MPa to 1.0360 MPa for the 3 mm bur. However, when compared with enamel and dentin [Figure 13 and Figure 14], the pulp stress was much lower. Pulp stress is indirectly influenced by accumulation of dentin stress.

From Figure 13, Figure 14 and Figure 15, it is clear that smaller-diameter burs (≤2 mm) and lower DOCs (≤1 mm) are recommended to minimize the stress developed in dental structures. Deep cavities can be prepared with controlled force, intermittent cutting, and sufficient cooling to avoid excessive stress build-up in enamel, dentin, and pulp.

Figure 16 presents the von Mises stress distributions in enamel, dentin, and pulp for different bur diameters (1, 2, and 3 mm) at two depths of cut [DOC 1 mm in Figure 16a and DOC 2 mm in Figure 16b]. The stress values for the enamel, dentin, and pulp were visually compared for each bur size. Figure 16a shows that the stress values in the enamel and dentin are nearly equal for all bur diameters. The stress in the pulp was lower than that in the enamel and dentin. However, a distinct pattern of increasing stress was evident with both increasing bur diameter and depth of cut. For the 1 mm bur at 1 mm DOC, the pulpal stress was recorded at approximately 0.160 MPa, while at 2 mm DOC it increased to 0.305 MPa. The 2 mm and 3 mm burs produced higher pulpal stress values, reaching 1.034 MPa and 1.036 MPa, respectively, at 2 mm DOC. Similarly, Figure 16b shows that the stress levels were high for all the bur sizes. The dentin stress is higher than the enamel bur diameters, which contrasts with the trends shown in Figure 16a, because dentin acts as the primary load-bearing tissue for deeper cuts or DOC. The stresses in the pulp remain negligible compared to those in the enamel and dentin; however, the trend shows that as the DOC increases, the pulp stress becomes more significant during cavity preparation. Although these stress magnitudes are relatively low and unlikely to cause immediate damage, the trend indicates that larger burs and deeper cuts can transmit stress to the pulp through dentin, especially in deep cavity preparations. This suggests that repeated procedures or insufficiently cooled environments can influence pulpal health over time. From Figure 13, it can be concluded that minimizing DOC and using appropriate bur sizes helps to reduce stress accumulation and avoids excessive enamel and dentin damage.

4. Discussion

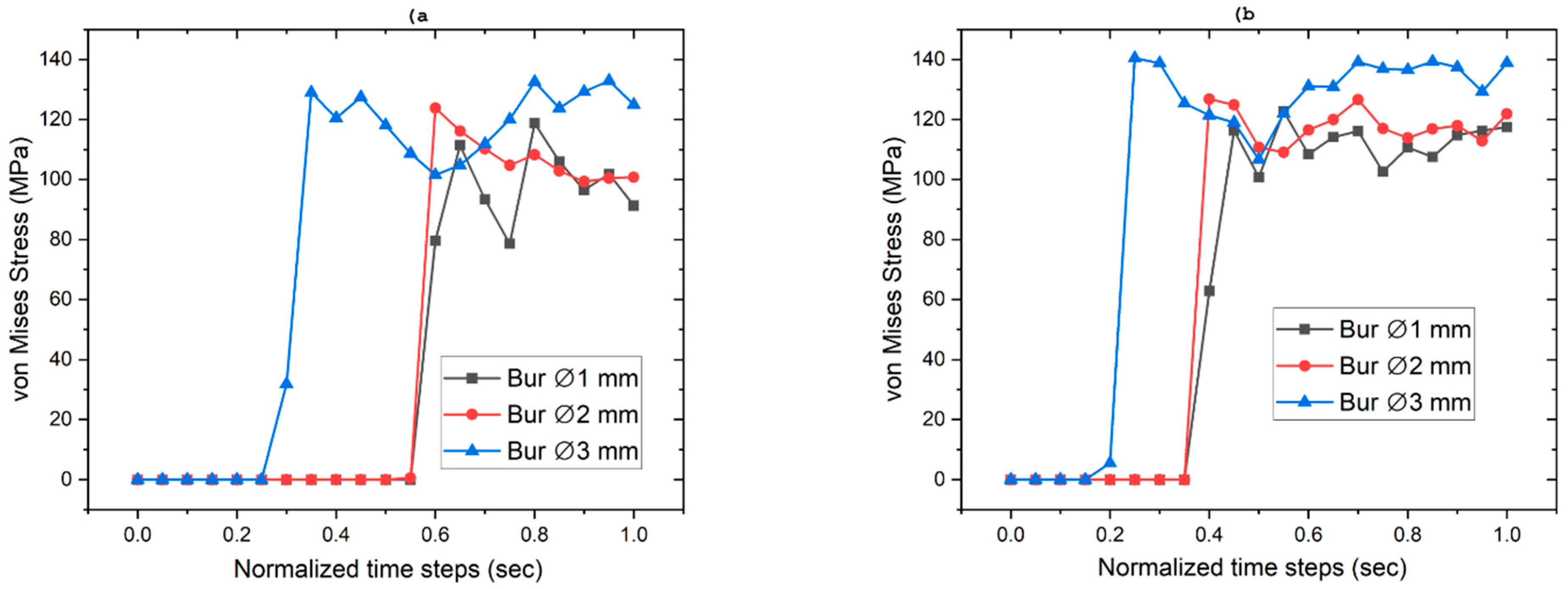
The finite element analysis (FEA) conducted in this study offers significant insights into the stress distribution patterns observed in dental structures during cavity preparation using diamond burs of varying diameters. The results indicated that larger bur diameters (3 mm) induced broader stress zones, whereas smaller diameters (1 mm) concentrated stresses more narrowly at the cavity edges. This finding suggests that while larger burs may be more efficient for material removal, they also impose greater mechanical loads on enamel and dentin, potentially increasing the risk of structural damage. Alam et al. [28] showed a similar type of stress distribution in cortical bone drilling, and feed rate affects stress formation in and around the bone.

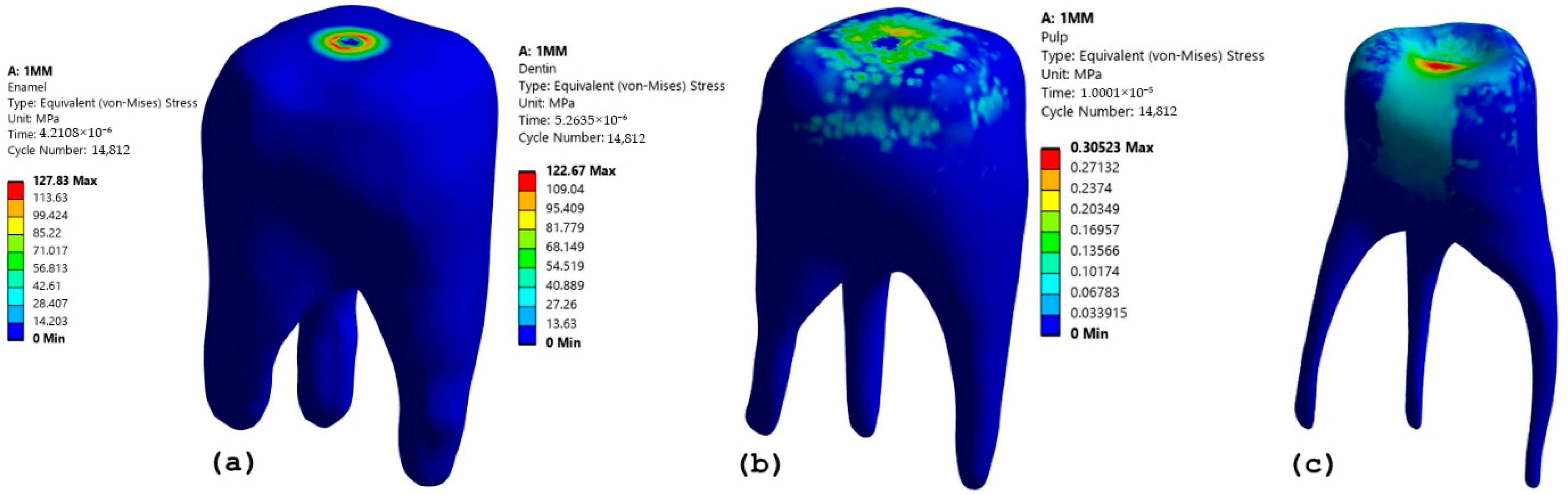
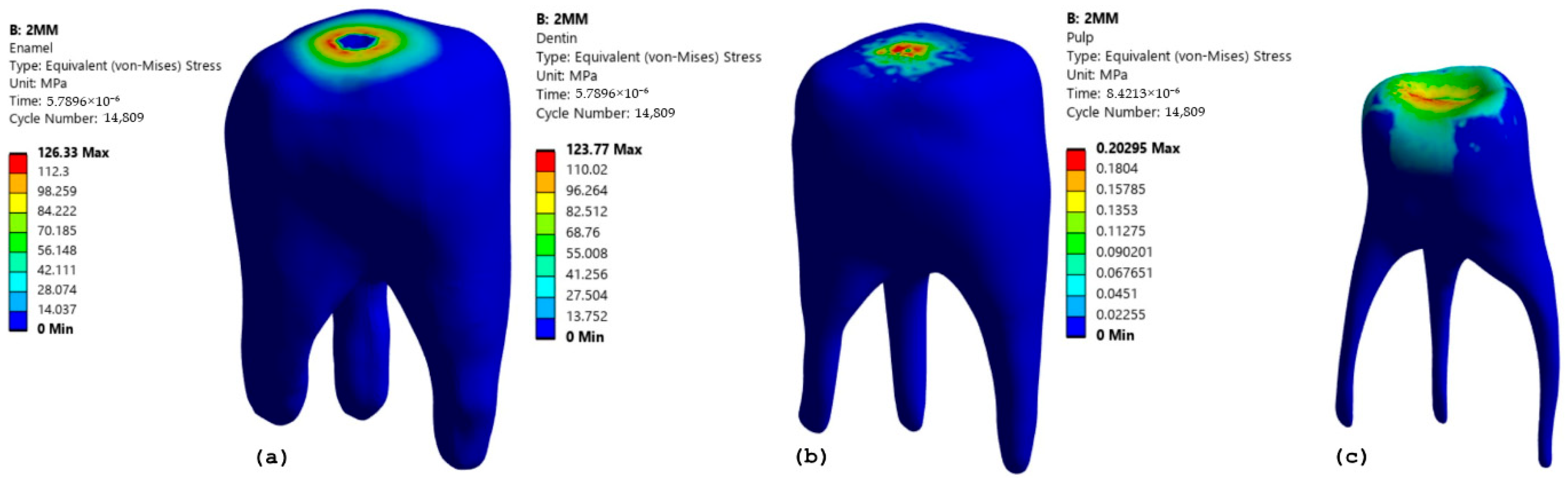
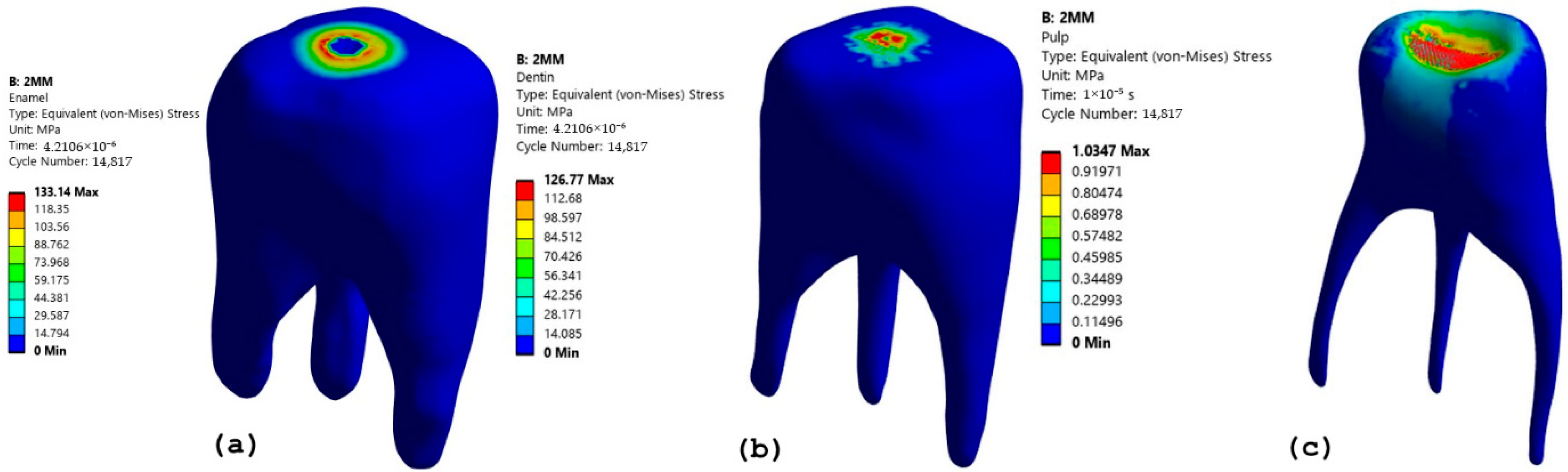
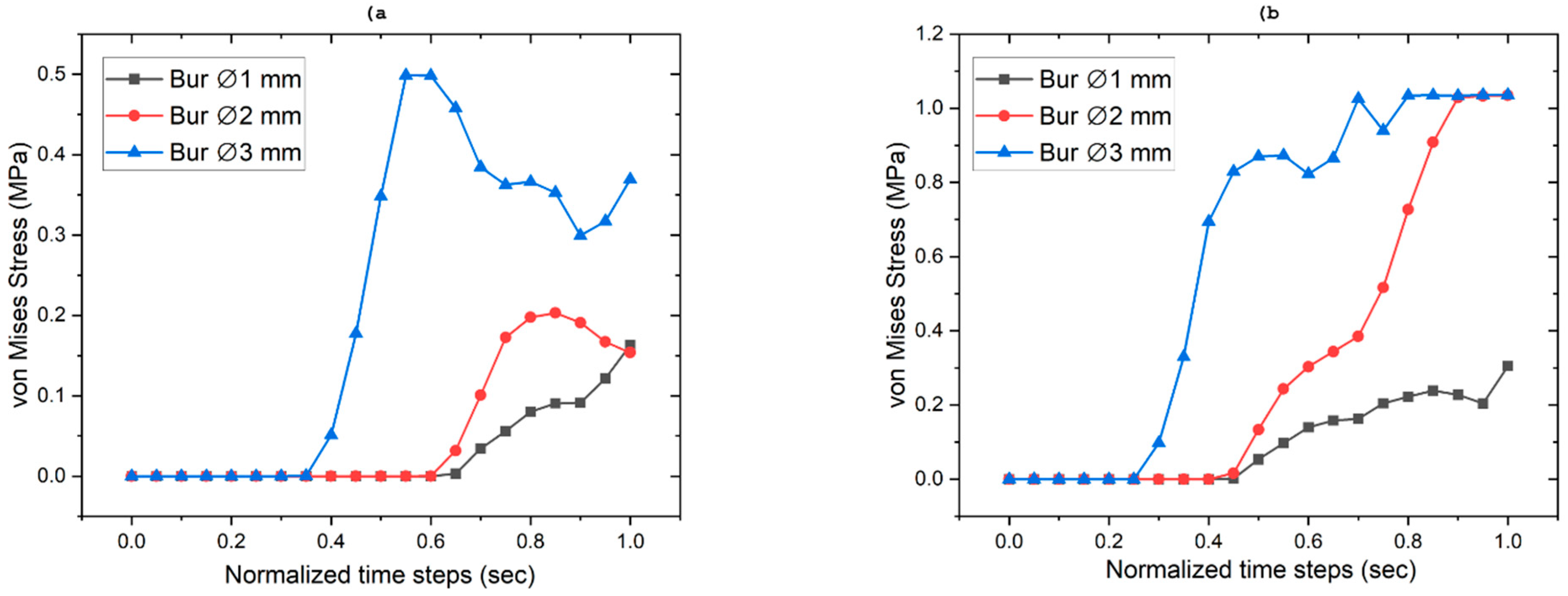
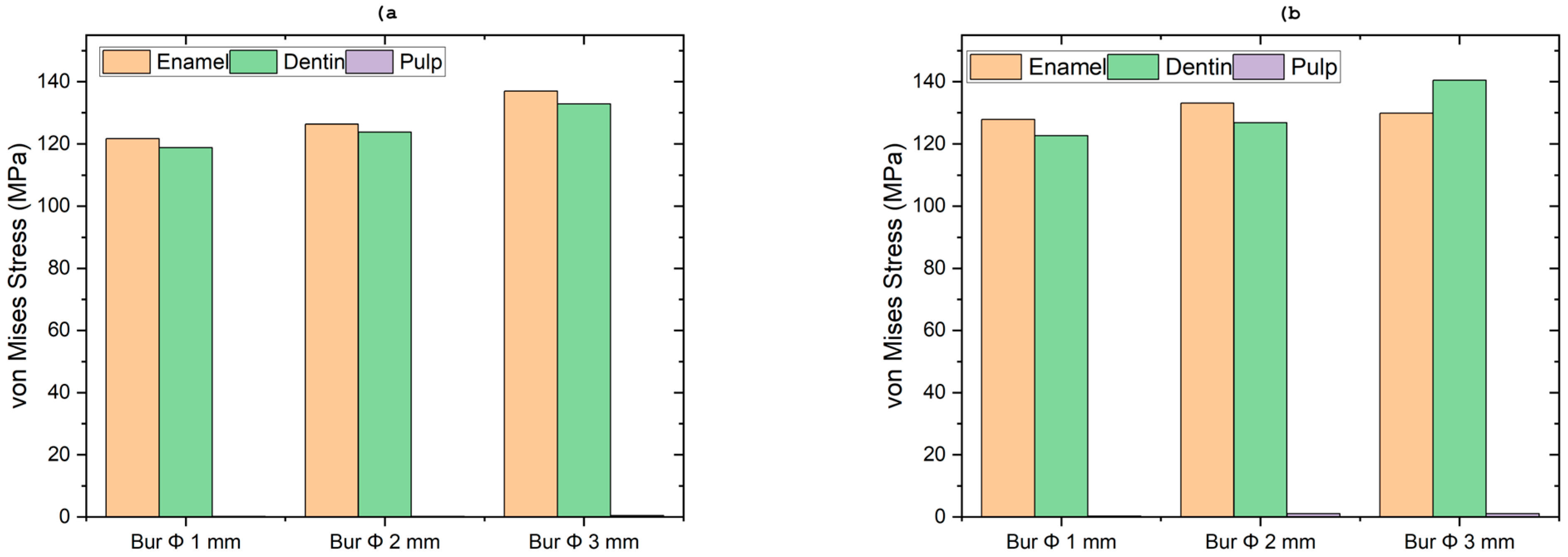
One significant outcome of this research is the impact of depth of cut (DOC) on stress distribution. When the DOC was increased from 1 to 2 mm, there was a notable increase in stress, especially in dentin and enamel. The stress in enamel rose from 121.72 MPa to 127.83 MPa with a 1 mm bur, indicating a heightened risk of enamel fracture if deeper cuts are made without sufficient cooling or controlled force. Similarly, dentin experiences greater stress with increased DOC, underscoring its function as a primary load-bearing tissue in deeper cavity preparations. Although stress accumulation in the pulp was relatively low, this suggests that repeated exposure to high stress could eventually cause pulpal damage, highlighting the need for controlled cavity preparation methods.

In a comparative analysis of various bur diameters, it was determined that the 3 mm bur induced the highest stress levels in dentin, reaching up to 140.33 MPa. This phenomenon is primarily attributed to the larger contact area, which increases resistance to cutting forces. Similar observations were reported by Zhao et al. [15], who examined the cutting forces generated by various dental burs and concluded that as the bur contacts the enamel, high stress is generated. The agreement between our simulation outcomes and empirical studies supports the validity of our modeling approach and highlights its relevance in optimizing clinical procedures. Notably, while enamel stress slightly decreased at a greater depth of cut (DOC) with a 3 mm bur, the stress in dentin continued to rise. This suggests that dentin has greater stress distribution than the enamel because of its relatively higher elasticity. Importantly, the elastic properties of dentin allow it to act as a shock absorber, distributing stress more uniformly than the enamel. This behavior was observed in our stress distribution plots, particularly at greater cutting depths, where dentin exhibited higher but evenly distributed von Mises stress. This mechanical behavior supports the notion that dentin plays a crucial role in maintaining structural resilience during aggressive tooth preparation, a concept also reflected in the work by Li et al. [16] and Bechtle et al. [8]. These results imply that clinicians should carefully choose the bur diameter and DOC to optimize cutting efficiency while minimizing structural damage to dental tissues.

These findings highlight the significance of utilizing smaller burs (≤2 mm) and maintaining a lower depth of cut (≤1 mm) to minimize excessive stress buildup in dental structures. Because high stress levels in enamel and dentin can lead to microcracks, fractures, and potential long-term issues, it is advisable to apply a controlled force, use intermittent cutting, and implement effective cooling methods during cavity preparation. Siegel et al. [5] and Ben-Hanan et al. [29] provided proof of the effect of load on cutting efficiency. In our study, similar observations were noted, and as the size increased, the stress in the dental structure also increased. The study also endorses the use of computational simulations, such as finite element analysis (FEA), to enhance dental tools and clinical practices, providing valuable insights into stress distribution patterns that can guide future advancements in bur design and procedural standards.

Limitations of the Current Work

This study provides valuable insights into the dental stress distribution during dental cavity preparation using FEA. Despite these valuable insights, this study had several limitations. The simulation was based on a single maxillary first molar reconstructed from CT data. Anatomical variations across different teeth and individual patients were not considered. No clinical experiments have been conducted to validate the simulation results. The model used realistic boundary conditions and material properties. The diamond bur was modeled as rigid. This excluded the potential effect of tool deformation that may occur during clinical use. To facilitate meshing and reduce the computational load, the anatomical crown features were smoothed. This leads to an underestimation of localized stress concentrations that occur in actual tooth surfaces. The influence of heat generated by friction during cutting was not considered. Developed temperature during the procedure can affect both material properties and dental structures and should be included in the future studies. However, the statistical analysis was not performed in the current research work and in the future work the statistical analysis such as ANOVA and optimization techniques can be implemented. The simulation was limited to single pass cutting scenarios. Repeated motion of the tool over the teeth leads to fatigue and cumulative damages to the tooth.

5. Conclusions

This study employed finite element analysis to assess the distribution of stress in dental structures during cavity preparation with diamond burs of different sizes and different cutting depths. The results reveal that using larger bur diameters and deeper cuts leads to increased stress levels, especially in the enamel and dentin, which may jeopardize the integrity of the tooth. This study suggests that opting for smaller bur diameters (≤2 mm) and shallower depths of cut (≤1 mm) is advisable to reduce excessive stress accumulation and maintain the dental structure. The research also underscores the importance of dentin as a vital load-bearing tissue that efficiently absorbs the stress transferred from the enamel during deeper incisions. Nonetheless, the accumulation of stress in the pulp, although smaller than that in the enamel and dentin, raises concerns about its long-term effects on pulpal health, particularly in situations involving repeated dental procedures. The results of this study highlight the importance of developing optimized clinical protocols that include the selection of suitable burs, precise cutting methods, and effective cooling techniques to avoid structural harm. Future research should aim to improve bur design and investigate alternative cutting methods to further enhance the accuracy and safety of dental procedures. This study underscores the significance of computational simulations in deepening our understanding of biomechanical interactions in dentistry, leading to improved clinical outcomes and increased patient safety.