Scaling Mechanical Knee Joints for Pediatric Transfemoral Prostheses: Does a Linear Geometric Factor Work?

Abstract

Introduction: Pediatric prosthetic knee joints must be appropriately scaled from adult designs to ensure proper gait biomechanics. However, direct dimensional scaling without considering the biomechanical implications may lead to functional discrepancies. This study aimed to evaluate whether using a linear scaling factor can effectively adapt a knee for pediatric use. The study assessed whether such an approach yields a viable pediatric prosthetic knee joint by applying a fixed scaling factor and analyzing the resultant knee geometry. Methods: The linear scaling factor was determined based on the pylon tube diameter, a key constraint in compact pediatric knee design. Given a pediatric pylon diameter of 22 mm, the length of the tibial link was set to 22 mm, yielding a scaling factor of 0.6875 when compared to the adult-sized knee. This scaling factor was used to determine the dimensions of the pediatric four-bar (scaled) knee joint. Static geometric analysis was conducted using GeoGebra^® to model the lower-body segment lengths. The knee joint’s performance was evaluated based on stance and swing phase parameters. These metrics were compared between the scaled knee and a commercial pediatric knee. Results: The geometric analysis revealed that while using the linear scaling factor maintained proportional relationships, certain biomechanical parameters deviated from the expected pediatric norms. The scaled knee achieved a toe clearance of 13.5 mm compared to 19.7 mm in the commercial design and demonstrated a swing-phase heel clearance of 11.6 mm versus 13.3 mm, maintaining negative x/y ratios at heel contact and showing significant stability in push-off moments, while the stance flexion angle remained within an acceptable range. The heel contact and push-off ratios (x/y) were found to be comparable, with the scaled model achieving values of −1.21 and −0.59, respectively. The stance flexion angle measured 10.6°, closely aligning with the commercial reference. Conclusions: Using a linear scaling factor provides a straightforward method for adapting adult prosthetic knee designs to pediatric use. However, deviations in key biomechanical parameters indicate that further experimental study may be required to validate the applicability of the scaled knee joint for pediatric users. Future work should explore dynamic simulations and experimental validations to refine the design further and ensure optimal gait performance.

1. Introduction

The development of pediatric prosthetic knee joints presents unique challenges due to children’s distinct biomechanical and anthropometric characteristics. In contrast to adult prosthetic knees, which have been extensively studied and optimized for function and durability, pediatric knee joints must accommodate lower loads, smaller anatomical dimensions, and different gait dynamics. Ensuring pediatric prostheses provide adequate stability during stance and sufficient clearance during the swing phase is critical for successful ambulation and long-term comfort [1,2].

Scaling techniques have been used in numerous engineering applications, including biomechanics and prosthetic design, to adapt existing designs for different population groups. In particular, linear dimensional scaling has been explored as a method to proportionally adjust the size of mechanical components while maintaining functional performance [3,4,5]. However, its applicability to pediatric prosthetic knee joints remains uncertain.

The International Organization for Standardization (ISO) standard 10328 outlines structural testing requirements for lower-limb prosthetic components, specifying loading conditions to evaluate the strength and durability of prosthetic knees under simulated use [6]. Although these standards provide guidelines for adult prostheses, adapting them for pediatric applications necessitates the appropriate scaling of both the geometric and loading parameters. An effective scaling method should preserve key biomechanical performance indicators, such as the stance-phase stability and swing-phase clearance, to ensure the safe and functional use of the prosthetic knee in young users.

Although scaling principles are commonly applied in prosthetic design, the validity of using a linear dimensional scaling factor for pediatric knee joints remains unclear. Existing adult prosthetic knees, such as the IITM Knee [7], have been designed to meet the demands of adult users, and their direct downscaling may not necessarily yield a functionally equivalent pediatric prosthetic knee. The primary concern is whether a uniform scaling approach adequately accounts for biomechanical constraints, such as joint stability and clearance, when transitioning from an adult-sized knee to a pediatric one.

This study aimed to assess if using a linear scaling factor can effectively translate the design of an existing adult knee joint into a pediatric version that meets the biomechanical requirements of children aged 3–5 years. Specifically, the research (i) developed a scaling methodology to adjust the dimensions and loading conditions of the adult knee based on a predetermined scaling factor, (ii) validated the scaled design through biomechanical analysis, focusing on the stance-phase stability and swing-phase clearance, and (iii) compared the performance of the scaled knee joint against a commercial pediatric knee to assess its feasibility and effectiveness.

By addressing these objectives, this research sought to contribute to developing more effective and biomechanically sound pediatric knee prostheses, ultimately improving the mobility and quality of life for young transfemoral amputees.

Allometric and optimization-based scaling methods can offer greater accuracy but typically require clinical gait data, detailed anthropometric databases, and advanced computational tools, resources that are often limited in low-resource settings. In comparison, a linear geometric approach serves as a practical and accessible starting point for design adaptation and prototyping. This study focused on static geometric performance metrics critical for evaluating pediatric prosthesis design, in contrast to dynamic studies that investigate gait optimization and energy expenditure [8].

2. Methods

The overall method had five stages: (i) calculating the scaling factor and scaling the knee, (ii) the identification of the performance parameters, (iii) the determination of the segment length, (iv) geometrical reconstruction, and (v) analysis and comparison.

2.1. Calculating the Scaling Factor and Scaling the Knee

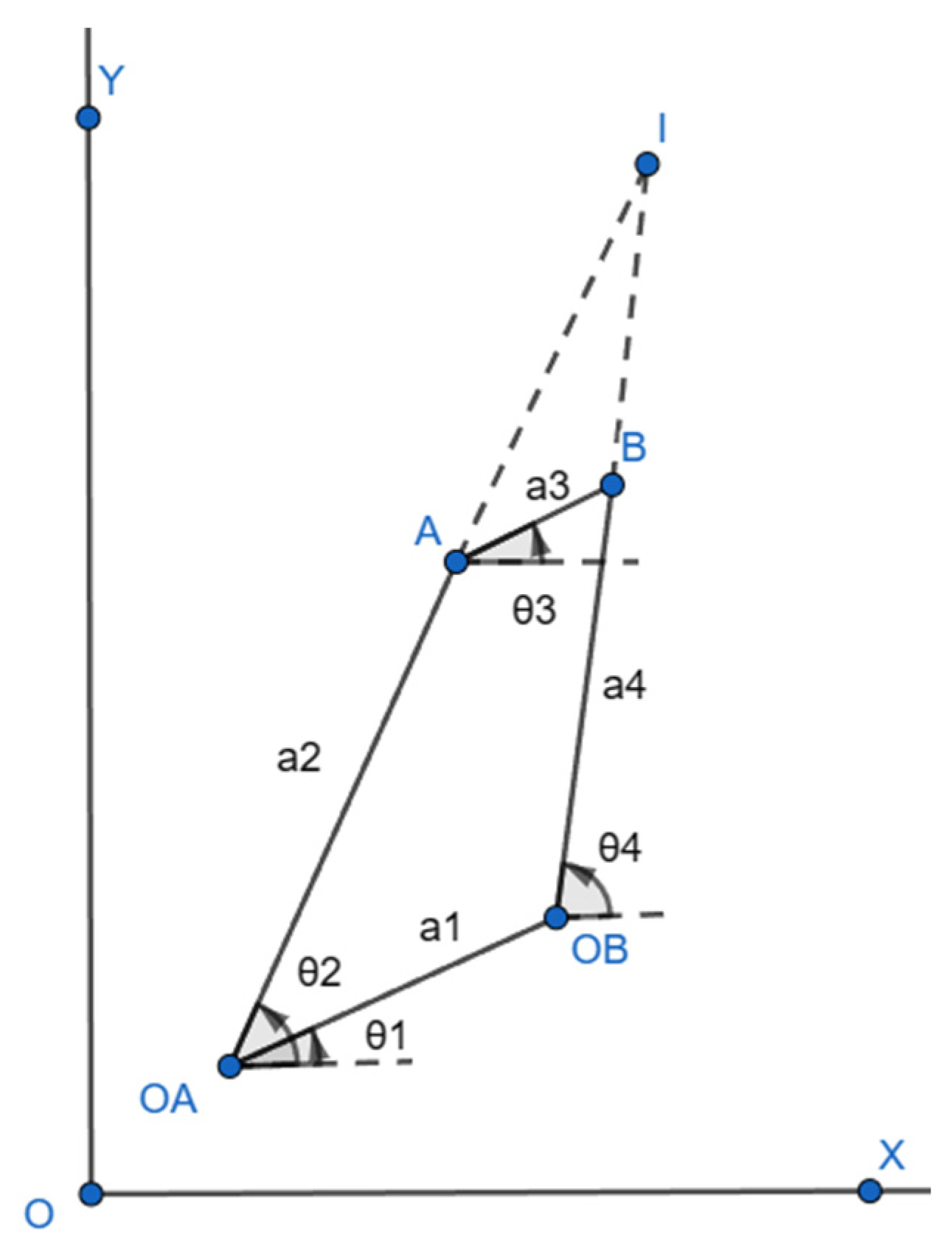
A typical four-bar mechanism with hinges A, B, OA, and OB and links a1, a2, a3, and a4 is shown in Figure 1. The angles made by the links in relation to OX are represented by θ1, θ2, θ3, and θ4. Point I is the instantaneous center of rotation (ICR) for the four-bar mechanism, formed by extending links a2 and a4 [9].

A four-bar knee joint was scaled down for toddlers based on the design of IITM Knee, a prosthetic knee joint indigenously designed by IIT Madras, India [7]. A scaled knee works on the principle of a four-bar mechanism permitting a specific range of motion. The design parameters for the scaled knee were derived based on the functional requirements of a prosthetic user. As the IITM Knee met most design parameters, like better stance-phase stability and swing-phase control, it was selected as a reference knee. It has been designed, optimized, and tested for adults, or the P5 category in ISO10328 [10].

The pylon diameter was one of the limiting factors in making the scaled knee as compact as possible. Considering the pylon tube diameter, which is generally 22 mm for pediatric cases, the length of the link that was just above the pylon was set to 22 mm. Thus, the factor to scale the link dimensions from the reference knee to the scaled knee was calculated by dividing the length of the tibial link of the scaled knee by that of the reference knee joint.

$$\mathrm{S}\mathrm{c}\mathrm{a}\mathrm{l}\mathrm{i}\mathrm{n}\mathrm{g} \mathrm{F}\mathrm{a}\mathrm{c}\mathrm{t}\mathrm{o}\mathrm{r}={\displaystyle \frac{\mathrm{l}\mathrm{e}\mathrm{n}\mathrm{g}\mathrm{t}\mathrm{h} \mathrm{o}\mathrm{f} \mathrm{t}\mathrm{h}\mathrm{e} \mathrm{b}\mathrm{o}\mathrm{t}\mathrm{t}\mathrm{o}\mathrm{m} \mathrm{l}\mathrm{i}\mathrm{n}\mathrm{k} \mathrm{o}\mathrm{f} \mathrm{t}\mathrm{h}\mathrm{e} \mathrm{p}\mathrm{r}\mathrm{o}\mathrm{p}\mathrm{o}\mathrm{s}\mathrm{e}\mathrm{d} \mathrm{p}\mathrm{e}\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{t}\mathrm{r}\mathrm{i}\mathrm{c} \mathrm{k}\mathrm{n}\mathrm{e}\mathrm{e}}{\mathrm{l}\mathrm{e}\mathrm{n}\mathrm{g}\mathrm{t}\mathrm{h} \mathrm{o}\mathrm{f} \mathrm{t}\mathrm{h}\mathrm{e} \mathrm{b}\mathrm{o}\mathrm{t}\mathrm{t}\mathrm{o}\mathrm{m} \mathrm{l}\mathrm{i}\mathrm{n}\mathrm{k} \mathrm{o}\mathrm{f} \mathrm{t}\mathrm{h}\mathrm{e} \mathrm{r}\mathrm{e}\mathrm{f}\mathrm{e}\mathrm{r}\mathrm{e}\mathrm{n}\mathrm{c}\mathrm{e} \mathrm{k}\mathrm{n}\mathrm{e}\mathrm{e}}}=0.6875$$

(1)

The remaining three links were scaled down from their respective lengths in the reference knee using the calculated scaling factor of 0.6875.

The scaling factor was based on the pylon diameter due to its practical design constraints and clinical relevance. In pediatric prosthetics, a standardized 22 mm pylon influences both the design compactness and component compatibility. Using this fixed reference provided a consistent and manufacturable baseline for scaling. Although alternative methods like anthropometric or weight-based scaling are valid, the pylon-based approach offers a simple and repeatable solution, especially suitable for use in early-stage design and resource-limited settings.

2.2. Identification of Performance Parameters

Performance parameters indicate satisfaction with the design. For the scaled knee, the performance parameters were used to check the overall stability and swing-phase clearance. A prosthetic knee needs to be designed to ensure it will guarantee stable movement, avoiding non-intentional buckling. A total of nine performance parameters (six for the stance-phase stability and three for the swing-phase clearance) were identified with the help of the literature. The performance criteria/requirements for the identified parameters were also set based on the literature.

Table 1. Knee performance parameters and their interpretation and requirements.

SN	Performance Parameters	Interpretation	Ref.	Requirement
Stance Phase
1	Heel contact (x/y) ratio [${\left(\mathrm{x}/\mathrm{y}\right)}_{\mathrm{h}\mathrm{e}\mathrm{e}\mathrm{l}-\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{t}\mathrm{a}\mathrm{c}\mathrm{t}}]$	A negative value of the x/y ratio means stable heel contact (the distance posterior to the load line is negative)	[7,11]	Negative, <0
2	Push-off (x/y) ratio ${\left(\mathrm{x}/\mathrm{y}\right)}_{\mathrm{p}\mathrm{u}\mathrm{s}\mathrm{h}-\mathrm{o}\mathrm{f}\mathrm{f}}]$	A near-to-zero value of x/y means a smaller stabilizing moment, i.e., an easy-to-flex knee (the distance posterior to the load line is negative)	[7,11]	Near to zero
3	Stance flexion angle [θsf]	A larger stable knee flexion range means the knee will be stable even with the knee slightly flexed (until the value of the heel contact x/y ratio is negative)	[7]	≥0°
4	Stabilizing hip moment [SDstabilizing]	A smaller standard deviation of the positive heel strike x/y ratio would mean a smaller and more consistent stabilizing hip moment, a requirement for up to 15° of knee flexion	[7]	Standard deviation (SD) is small and consistent
5	α-stability [α]	Distance of ICR from TA line should be positive (posterior to TA line)	[9]	>0
6	β-stability [β]	Distance of ICR from anatomical knee center should be positive (ICR superior to anatomical knee center)	[9]	>0
Swing Phase
7	Toe clearance [Ct]	Toe clearance for normal walking at 23° hip flexion and 49° knee flexion	[7,12]	>0
8	Toe clearance [L]	Limb length (Ll) = distance from trochanter to ankle C1 = Ll @ full extension C2 = Ll @ 65° knee flexion during mid-swing	[9]	>0
9	Heel clearance [Ch]	During terminal swing, heel clearance is more significant than toe clearance	[10]	>0

depicts the performance parameters that were identified and the requirements for the identified performance parameters.

Here, x is the offset of the ICR from the load line, and y is the distance from the center of pressure in the foot to the ICR along the load line. According to [9] the ICR can be estimated by extending the two links of the four-bar and intersecting them at a point. Similarly, the α-value is the distance between the ICR and the load line. Then, a third straight line (the alpha line) is drawn to the load line. This alpha line indicates the stability of the system. The α-value is positive if the ICR moves further to the posterior side of the load line and negative if the ICR moves to the anterior side. Here, if the α-value is positive at full extension, the knee is considered stable.

The selection of these nine performance parameters was guided by their direct relevance to the stance-phase stability and swing-phase clearance, which are critical indicators of functional safety and usability in pediatric prosthetic knees. These parameters were identified through a literature review and were chosen to evaluate the geometric and mechanical behavior of the knee joint in static conditions. Metrics such as energy efficiency or comfort, though important, were excluded from this phase as they require dynamic analysis or user trials, which are planned for future investigations.

2.3. Determination of Segment Length

In [3], C. Colombo et al. devised a method to rescale the loading conditions based on predictions of the geometric dimensions through a comparison to Hybrid III dummies with dimensions adhering to the ISO10328 standard. The author used geometrical dimensions from Hybrid III dummies for 3-, 6-, and 10-year-old children as a reference to extrapolate the knee height (${\mathrm{u}}_{\mathrm{K}}$) for a 12-year-old boy. The projected knee height (${\mathrm{u}}_{\mathrm{K}}$) based on the dimensions from the Hybrid III dummies is represented by Equation (2).

$${\mathrm{u}}_{\mathrm{K}}=-1.12{\left(\mathrm{a}\mathrm{g}\mathrm{e}\right)}^2+34.41\left(\mathrm{a}\mathrm{g}\mathrm{e}\right)+148.86$$

(2)

Using Equation (2), the knee height for the required conditions can be approximated. As this equation was generated based on the geometrical dimensions from Hybrid III dummies representing 3-, 6-, and 10-year-olds, it cannot be used to estimate the knee height of an adult. The average knee height for a 5-year-old would be 292.92 mm.

Based on the method devised by [3], the ratio of ${\mathrm{u}}_{\mathrm{K}}$ for an adult and a child can be assumed to be a linear coefficient, k, to calculate other dimensions. The knee height for the P3 category in ISO10328 is 500 mm, which can be used in Equation (3) to get the value of the coefficient.

Thus, the ratio will be

$$\mathrm{k}={\displaystyle \frac{{\mathrm{u}}_{\mathrm{K}-5}}{{\mathrm{u}}_{\mathrm{K}-\mathrm{P}3}}}={\displaystyle \frac{292.92}{500}}=0.586\approx 0.59$$

(3)

where

• ${\mathrm{u}}_{\mathrm{K}-5}$: The knee height for a 5-year-old.
• ${\mathrm{u}}_{\mathrm{K}-\mathrm{P}3}$: The knee height for the P3 category in ISO 10328.

Another method to approximate the knee height is to use the growth chart published by the WHO and the knee height ratio proposed by [5], utilized by [4]. The WHO has published a table with approximated age vs. total height data for 0- to 5-year-old children, where the knee height equals 0.284 times the total height, as per [4,5]. The value of k was found to be 0.63 using Equation (3) when calculated based on the WHO growth chart [13] and Drillis and Contini [5]. The calculated knee heights and the values of the coefficient for 3- to 5-year-old children are shown in

Table 2. Knee height estimation and proportionality coefficient obtained using various methods.

Age [Years]	Knee Height ${\mathbf{u}}_{\mathbf{K}}$ [mm]		Proportionality Coefficient, k
	Using [3]	Using [5,13]	Using [3]	Using [5,13]
3	242.01	272.26	0.48	0.54
4	268.58	293.58	0.54	0.59
5	292.91	312.56	0.59	0.63

.

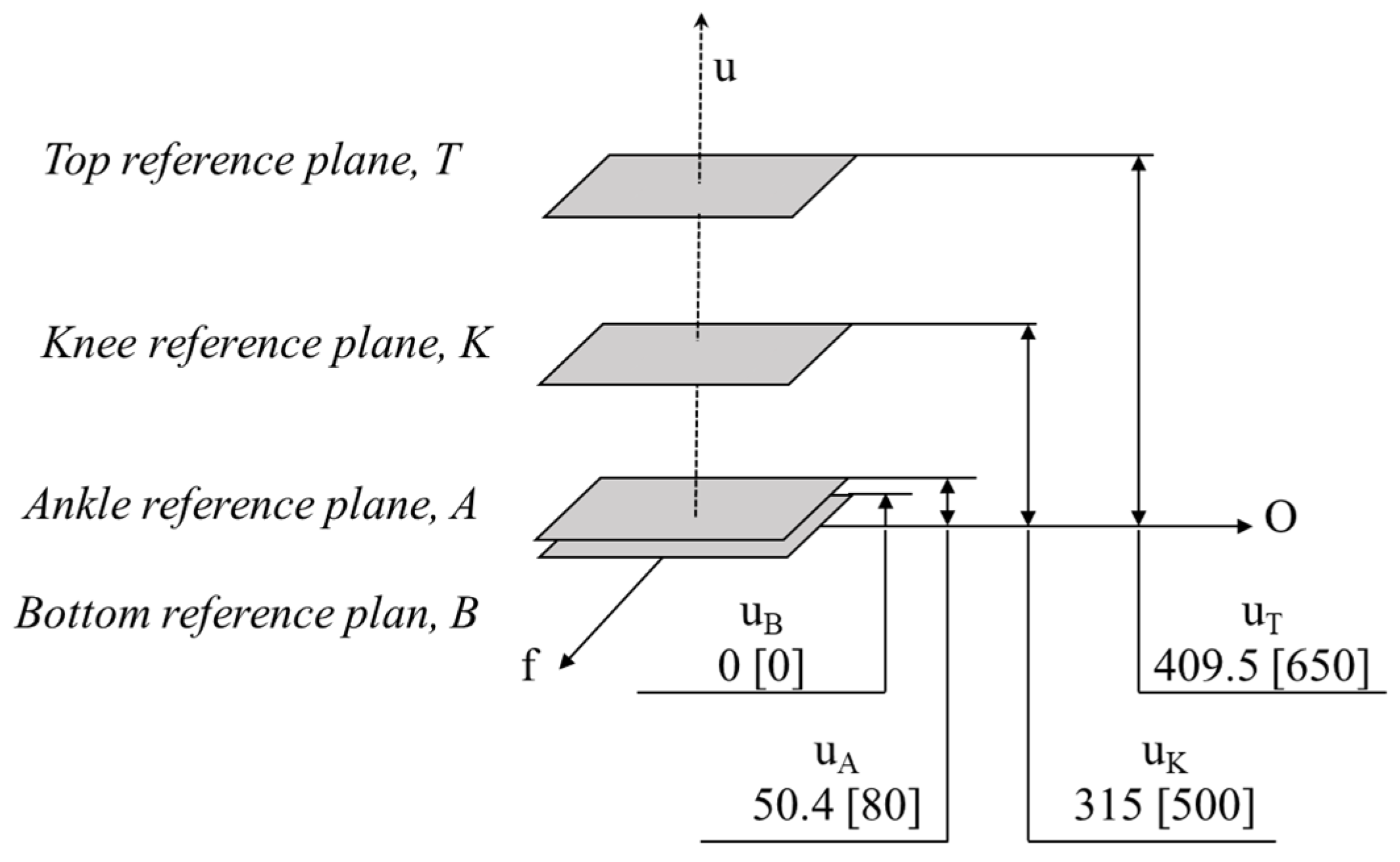
The largest of the calculated coefficients (k = 0.63) was taken as the proportionality coefficient. With the help of this coefficient, the distances required to specify the reference planes, offset distances, and loading conditions in compliance with ISO 10328 were identified. The values of the scaled reference planes and offset distances are shown in Figure 2, and the scaled values of the load for loading conditions 1 and 2 are shown in

Table 3. Structural test forces (principal tests).

Test Procedure and Test Load (in N)			Load (P3)		Load (P3*)
			I	II	I	II
Static and cyclic test procedures	Stabilizing test force	Fstab	50		50
	Settling test force	Fset	736	638	464	402
Static test procedure	Proof test force	Fsp	1610	1395	1014	879
	Ultimate static test force	Fsu,lower level	2415	2092	1521	1318
		Fsu,upper level	3220	2790	2029	1758
Cyclic test procedure	Minimum test force	Fcmin	50		50
	Cyclic range	Fcr	920	797	580	502
	Maximum test force	Fcmax = Fcmin + Fcr	970	847	630	552
	Mean test force	Fcmean = 0.5 (Fcmin + Fcmax)	510	449	340	301
	Cyclic amplitude	Fca = 0.5Fcr	460	399	290	251
	Final static force	Ffin = Fsp	1610	1395	1014	879
	Prescribed number of cycles		3 × 106		1.8 × 106

P3*: Scaled version of P3 category of ISO 10328 for a 5-year old.

.

As per ISO 10328, the axes of a coordinate system in relation to a prosthetic user who is standing in an upright position can be expressed in terms of u, f, and o, where u is upwards, f is forward, and o is outside. The top, knee, ankle, and bottom reference planes are located along the u-axis at a distance of ${\mathrm{u}}_{\mathrm{T}}$, ${\mathrm{u}}_{\mathrm{K}}$, ${\mathrm{u}}_{\mathrm{A}}$, and ${\mathrm{u}}_{\mathrm{B}}$ from the origin, respectively.

The plane distances and the load for a 5-year-old child were determined as shown in Figure 2 and Table 3, considering u_B = 0. The calculated distance of the plane from the origin was compared with the distance obtained by Theron [14] in his study, which was similar.

2.4. Geometrical Reconstruction

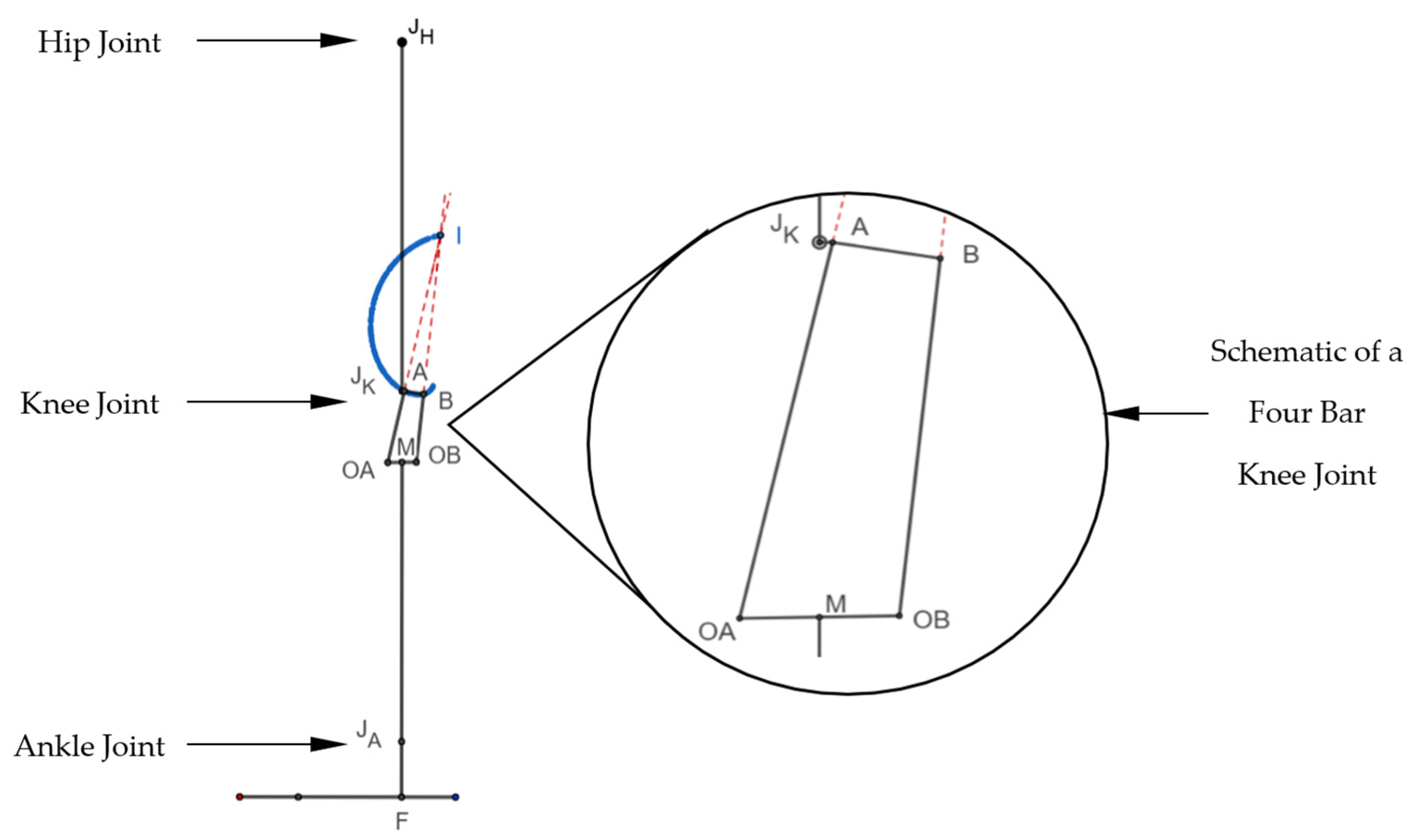
The obtained dimensions of the 5-year-old’s limbs were plotted along with the scaled knee mechanism, as shown in Figure 3. It shows the length of a lower limb from the hip joint (J_H) to the foot (F), including the knee joint (J_K) with the centrode of the ICR. This complete set of lower limbs for a 5-year-old was constructed in open-source software named GeoGebra^®, with lines representing various segments of the foot and the pediatric knee. Here, the points J_H, J_K, J_A, and F represent the anatomical hip joint, knee joint, ankle joint, and foot, respectively. Similarly, A-B, B-OB, OB-OA, and OA-A represent the four links of the knee. The instantaneous center of rotation (I) and the path traced by I are shown in Figure 3. Hinge A of the scaled knee joint lies posterior to the anatomical knee (J_K) at the same height from the base. Similarly, the link lengths of a commercial pediatric knee joint were measured, and its geometrical reconstruction was prepared. Both reconstructions (scaled knee and commercial knee) were evaluated side-by-side for each performance parameter, and we checked if they fulfilled the requirements.

The commercial pediatric knee used for comparison in this study was a passive polycentric mechanical knee, commonly prescribed for children aged 3–6 years. While proprietary restrictions limit our ability to provide access to detailed internal specifications, the design was based on standard ISO 10328 P3 category constraints. The key geometric features were measured directly and used for comparative analysis against the scaled model.

2.5. Analysis and Comparison

The geometric reconstruction of the lower limb in GeoGebra^® was simulated to evaluate the performance of the scaled knee and commercial knee in terms of their stance stability and swing-phase clearance. The performance of both knees in the simulation was compared with the reference values for the identified performance parameters.

3. Results

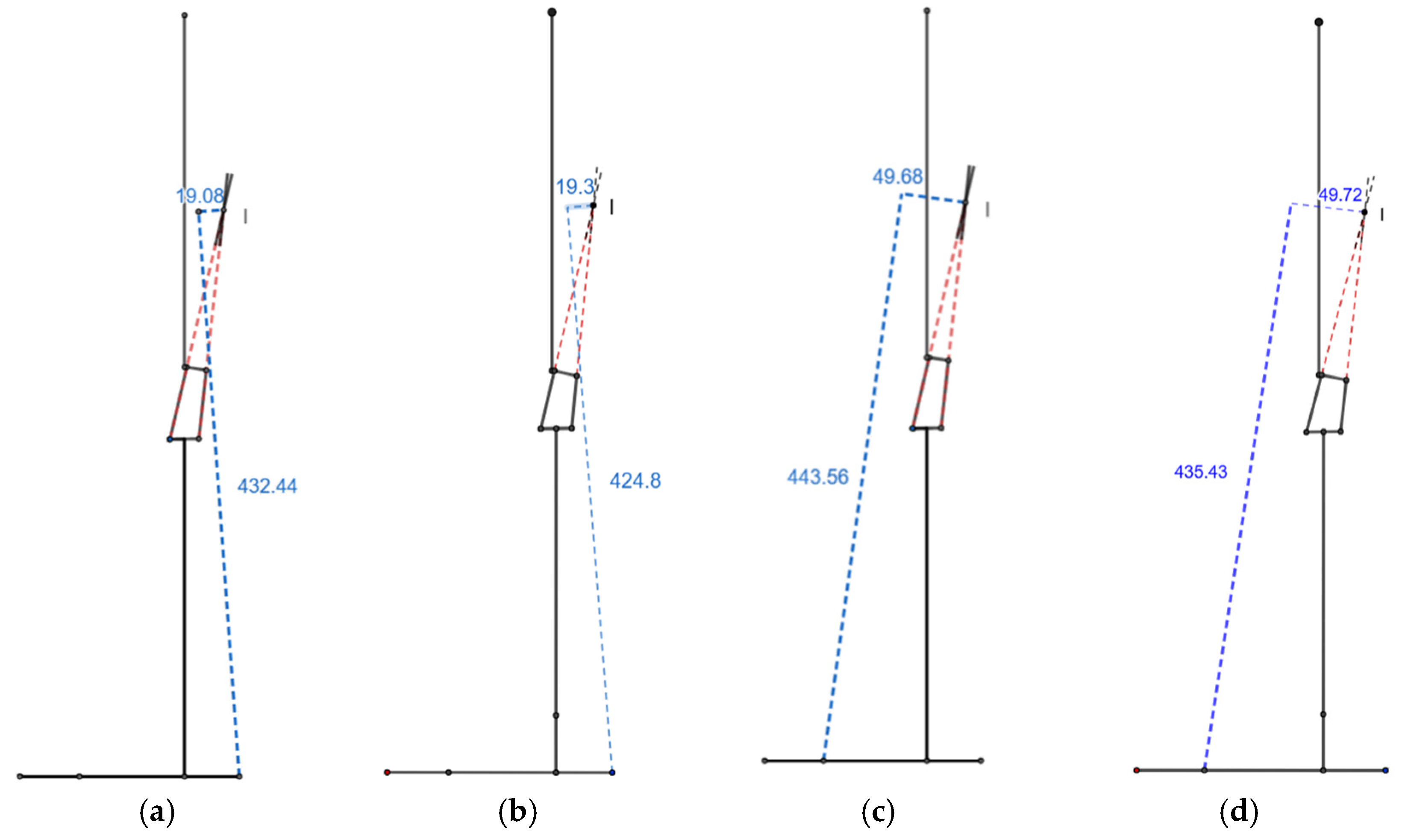
3.1. (X/Y) Ratio

The x and y values for the scaled knee during heel contact were −19.08 mm and 432.44 mm, respectively. They changed to −49.68 mm and 443.56 mm during push-off. The values were close to the x and y values of the commercial knee, which were −19.3 mm and 424.8 mm, respectively, for heel contact and −49.72 mm and 435.43 mm for push-off. This resulted in an (x/y) ratio of −0.044 and −0.045 for heel contact and −0.112 and −0.114 for push-off for the scaled and commercial knee joints, respectively (Figure 4).

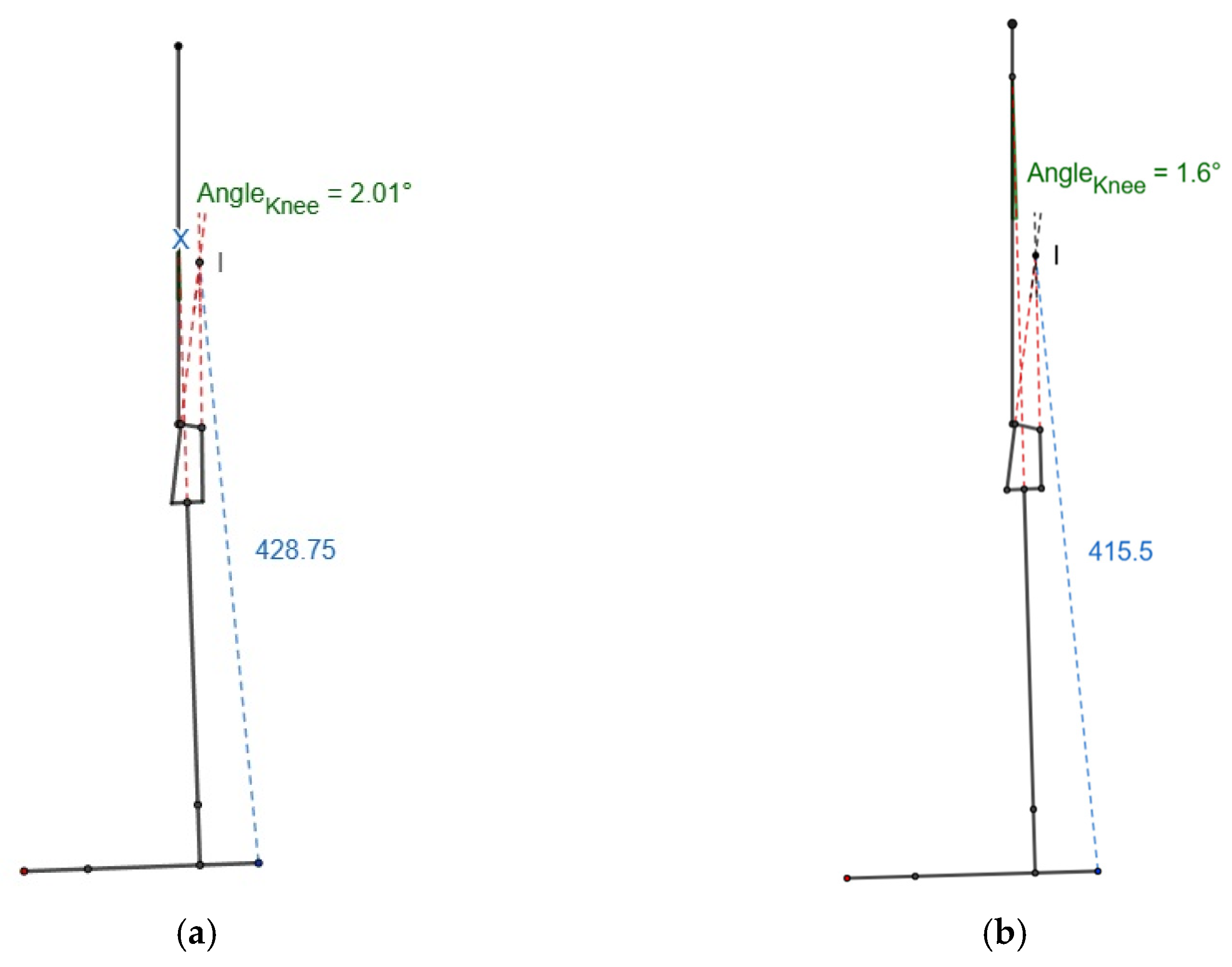
3.2. Stable Knee Flexion Angle

As the knee flexed, the ICR approached the load line, and the scaled knee joint could flex approximately 2.01°, whereas flexion was limited to 1.6° in the commercial knee before the (x/y) heel strike ratio became positive, as shown in Figure 5. The value of x was almost zero at this knee flexion angle for both knees.

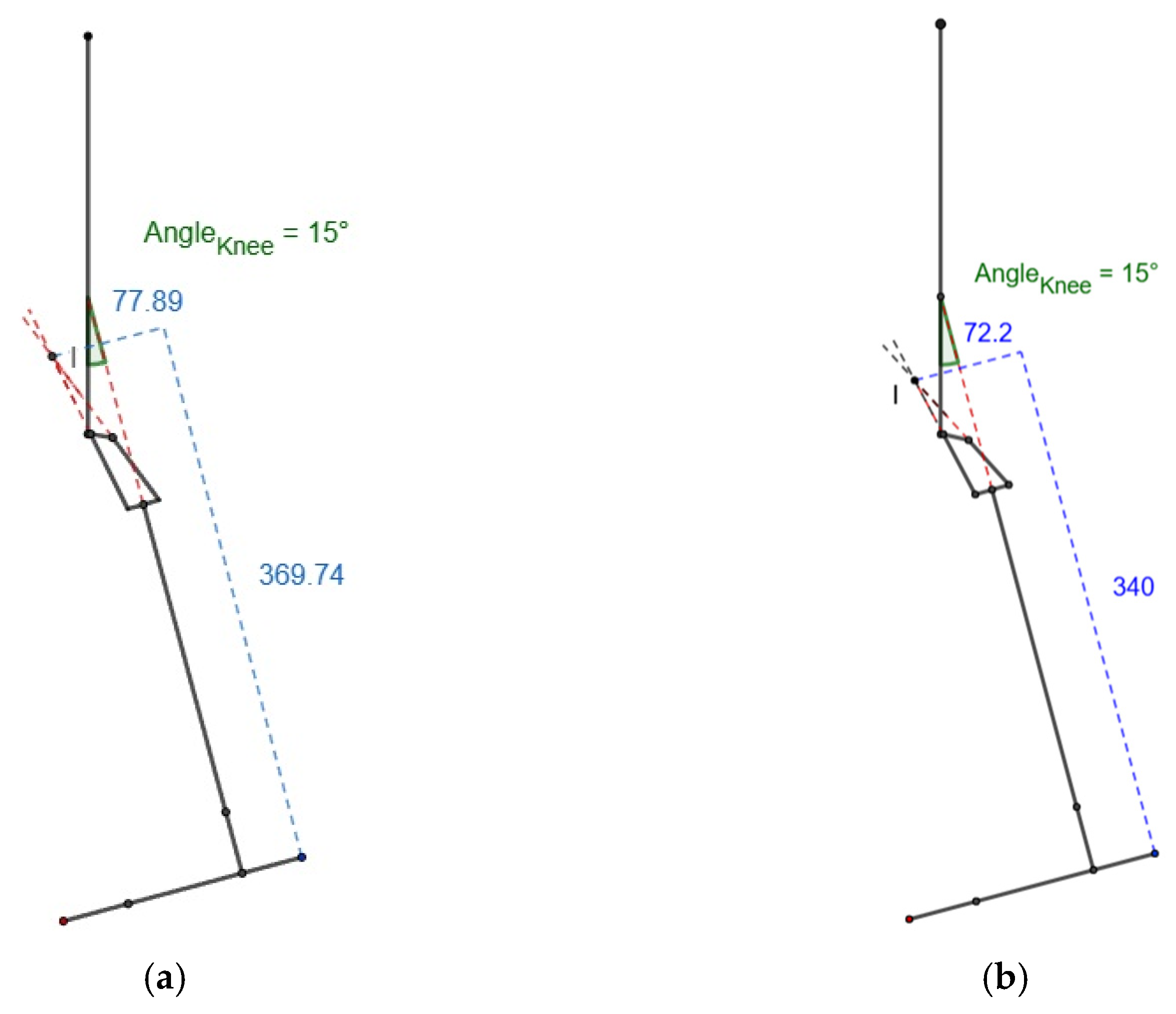
3.3. Stabilizing Hip Moment

At 15° knee flexion, the values of x and y were 77.89 mm (72.2 mm) and 369.74 mm (340 mm), respectively, as shown in Figure 6 for the scaled knee and commercial knee, resulting in a 0.21 (x/y) ratio for heel contact in both knees, which was near to zero. The standard deviation of the positive heel contact (x/y) ratio of the scaled knee was around 0.068, almost equal to 0.065, which was the result for the commercial knee. Both had a low standard deviation value, resulting in the requirement for a smaller stabilizing moment.

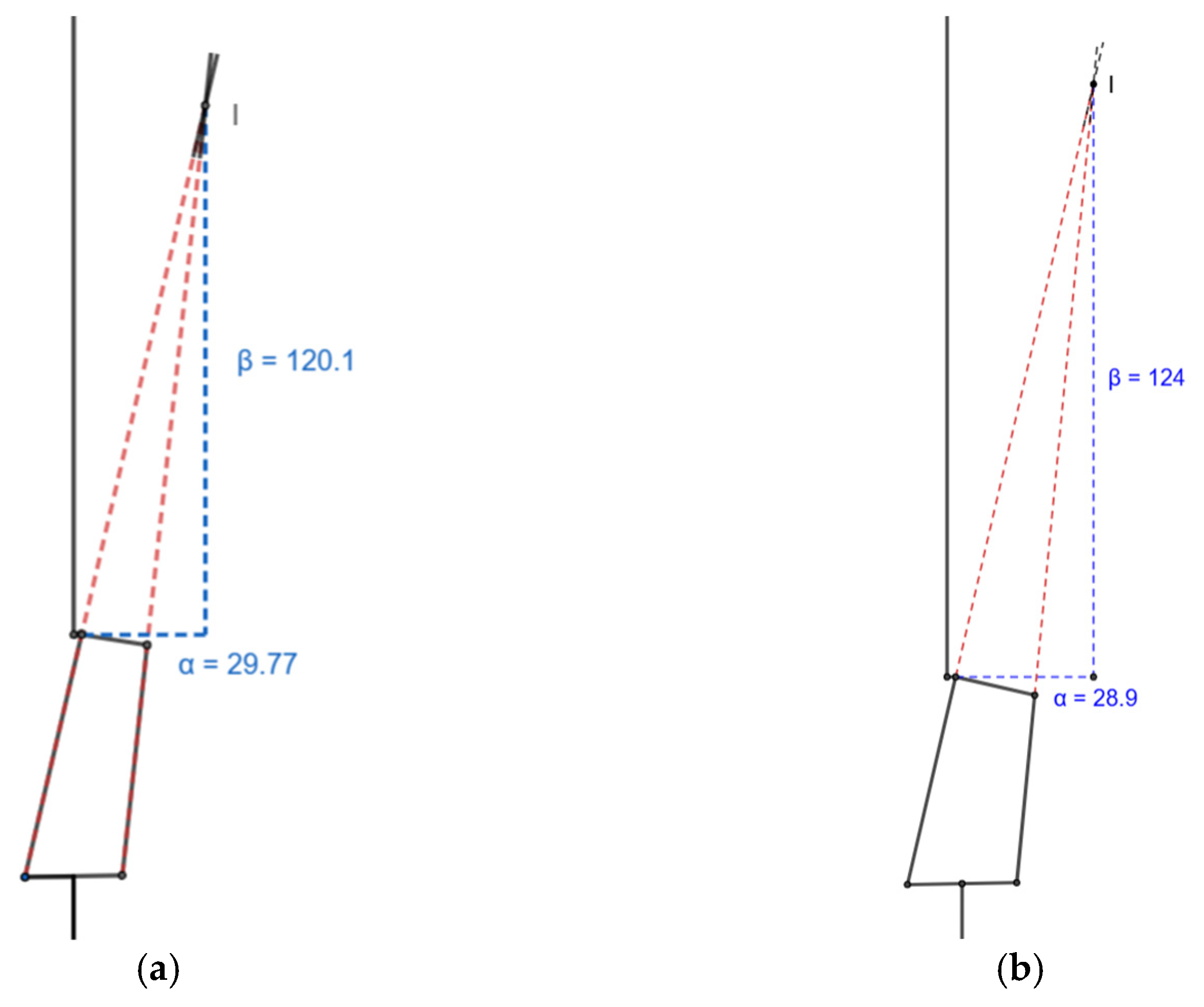
3.4. α- and β-Stability

The values of α and β were the distance of the ICR from the knee joint in the X and Y directions and were 29.77 mm and 120.1 mm for the scaled knee and 28.9 mm and 124 mm for the commercial knee, respectively. Both the values were positive, as required (Figure 7).

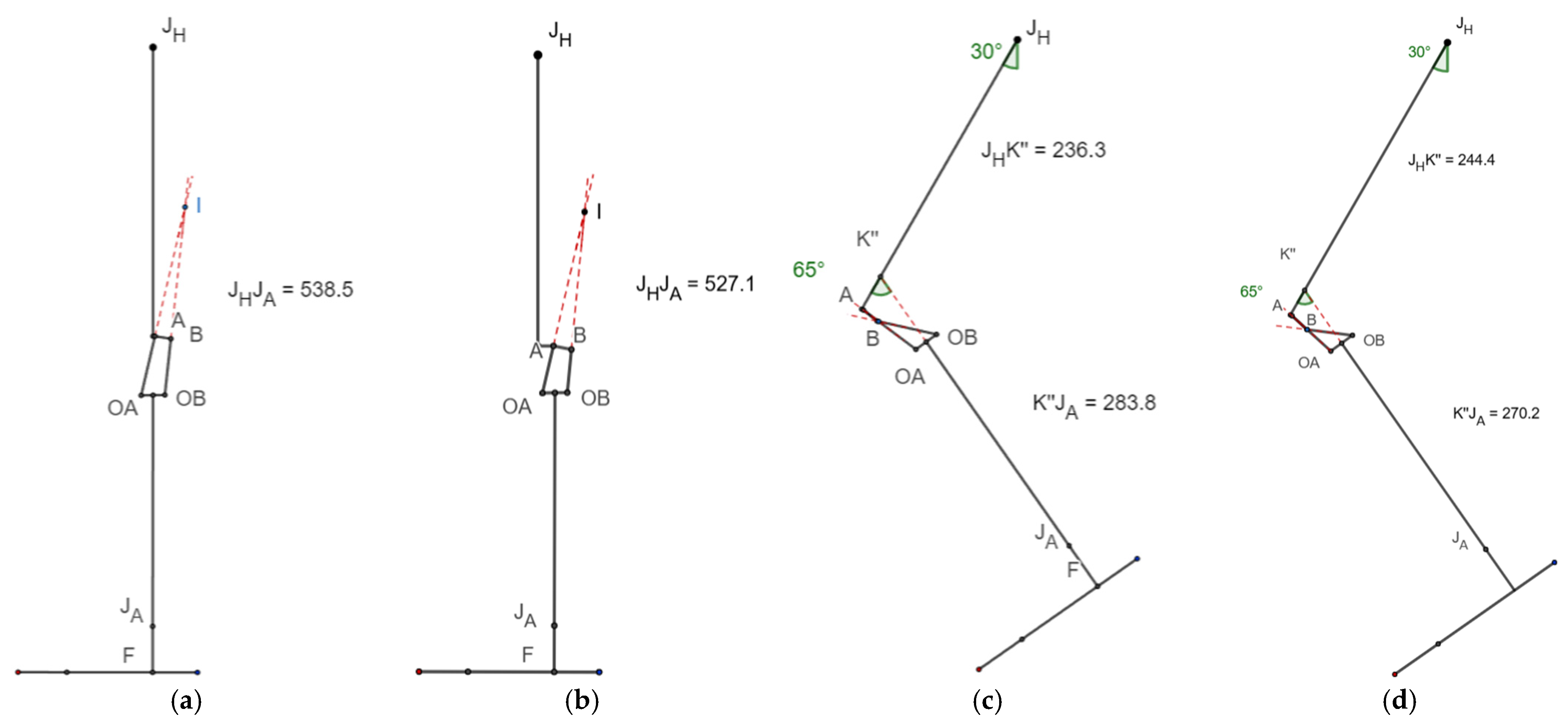
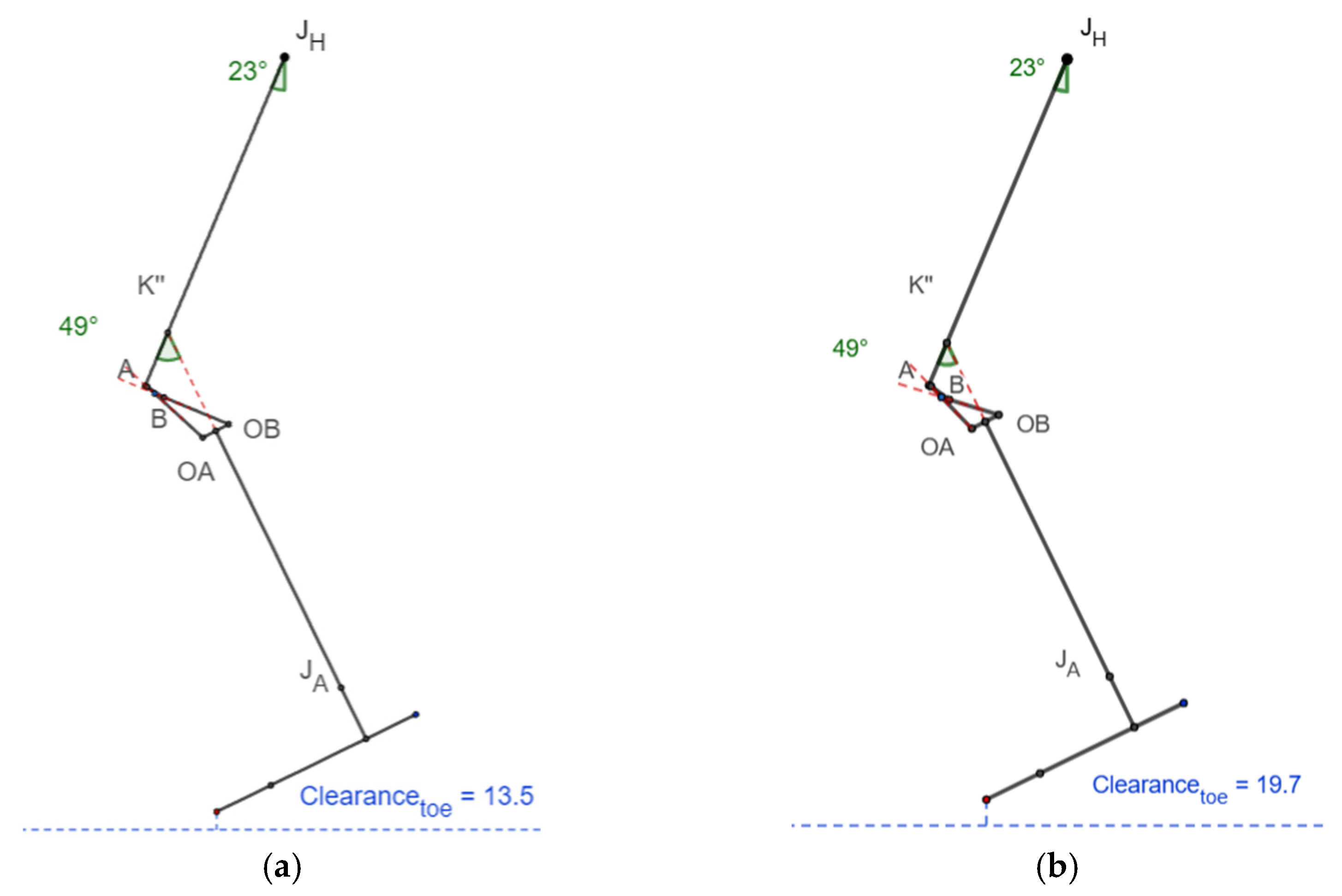
3.5. Toe Clearance

In Figure 8, K” is the intersection between the extended tibial line (J_A-M, as shown in Figure 3) and femoral line (J_H-J_K, as shown in Figure 3). C₁ is the overall length of the lower limb from the ankle to the hip joint (H), whereas C₂ is the length from the ankle to K” and from K” to the hip joint. L is the difference between C₁ and C₂, which provides the value by which the limb is shortened while the knee is flexed during the swing phase.

Thus, the leg was shortened by 18.2 mm in the scaled knee, which was higher than that of the commercial knee, which had 12.5 mm of shortening while swinging the leg due to the shortening effect of the polycentric four-bar knee, as shown in

Table 4. Shortening of length.

Knee	C1 [mm]	C2 [mm]	L = C1 − C2 [mm]
Scaled knee	538.3	236.3 + 283.8 = 520.1	18.2
Commercial knee	527.1	244.4 + 270.2 = 514.6	12.5

.

The minimum toe clearance while walking occurred at 23° hip flexion and 49° knee flexion [12], and its value was approximately 13.5 mm and 19.7 mm for the scaled and commercial knees, respectively, as shown in Figure 9.

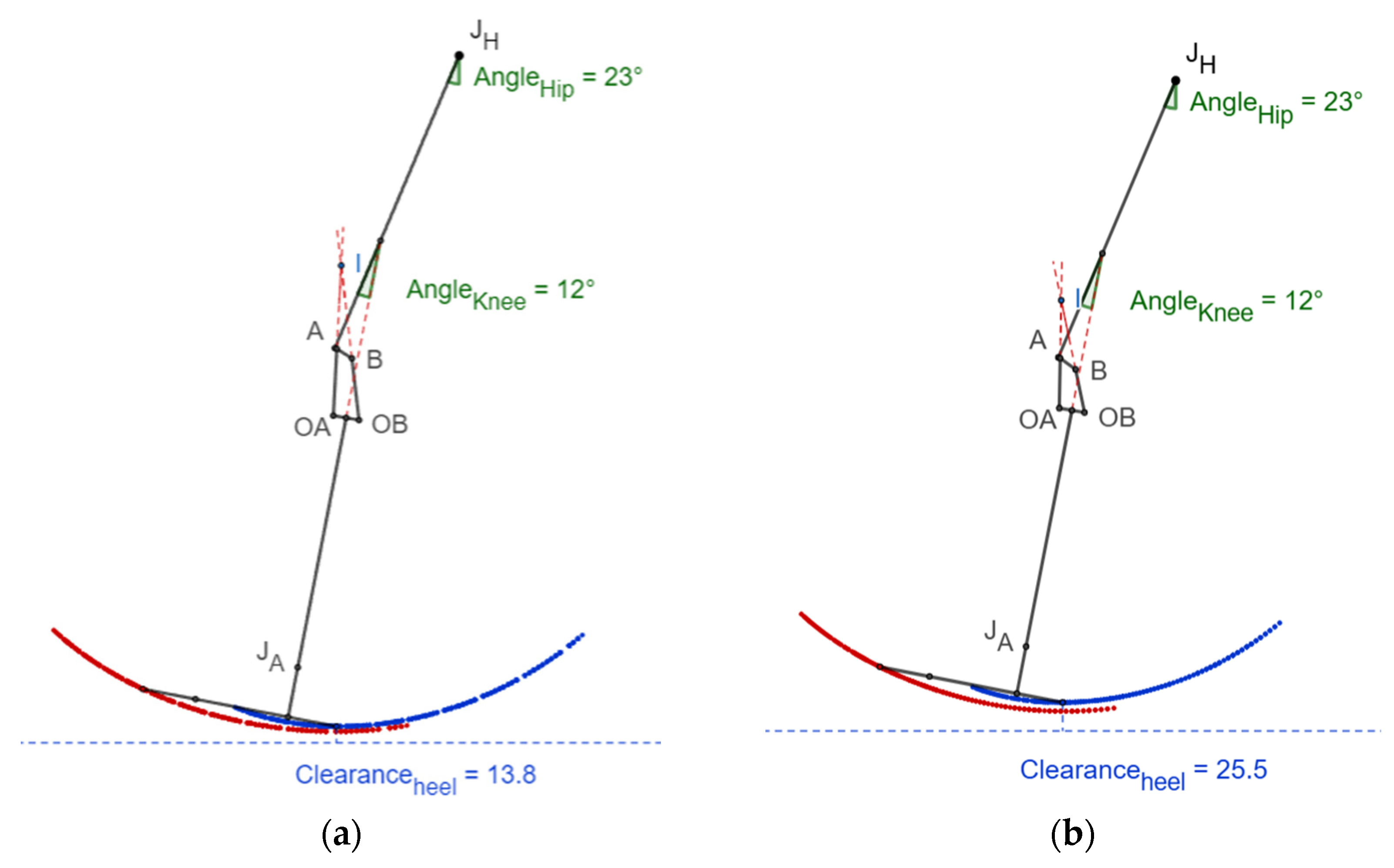
3.6. Heel Clearance

Figure 10 shows that the heel clearance remained positive while advancing from the mid-swing phase to the terminal swing phase. The minimum heel clearance of 13.8 mm from the ground for the scaled knee and 25.5 mm for the commercial knee was attained at 12° knee flexion.

4. Discussion

The GRF at the heel strike was almost 120% of the body weight, which demanded a greater hip moment for stability [11]. The stability could be parameterized using the (x/y) ratio during heel contact and push-off. For the scaled knee, the heel contact (x/y) ratio was found to be −0.044, almost equal to the value of −0.045 obtained for the commercial knee. The negative heel contact ratio implies that the knee was stable at heel contact without requiring a stabilizing hip moment to ensure stability. The scaled knee seemed as stable as the commercial knee.

As shown in

Table 5. Performance evaluation of scaled knee vs. commercial knee.

SN	Symbol	Suggested Values	Scaled Knee Values	Comparison	Commercial Knee Values	Remarks
Stance Phase
1	${\left(\mathrm{x}/\mathrm{y}\right)}_{\mathrm{h}\mathrm{e}\mathrm{e}\mathrm{l}-\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{t}\mathrm{a}\mathrm{c}\mathrm{t}}$	Negative, <0	−0.044	$\approx$	−0.045	Negative value, stable
2	${\left(\mathrm{x}/\mathrm{y}\right)}_{\mathrm{p}\mathrm{u}\mathrm{s}\mathrm{h}-\mathrm{o}\mathrm{f}\mathrm{f}}$	Near to zero	−0.112	$\approx$	−0.114	Negative and nearing zero, stable
3	θsf	≥0°	≈2.01°	>	≈1.6°	Positive value, greater than zero
4	SDstabilizing	Small	SD = 0.068	<	SD = 0.065	Small value, small hip moment required
5	α	>0	29.77 mm	>	28.9 mm	Positive value, posterior to load line, stable
6	β	>0	120.1 mm	<	124 mm	Superior to the knee center, a lower amount of hip moment required
Swing Phase
7	Ct	>0	13.5 mm	<	19.7 mm	Sufficient toe clearance
8	Lt	>0	18.2 mm	>	12.4 mm
9	Ch	>0	13.8 mm	<	25.5 mm	Sufficient heel clearance

, the push-off (x/y) ratio (−0.112) approached zero, which means the knee was stable and comparable to the commercial knee (−0.114). The knee could flex up to 2.01° during heel contact without buckling. Here, the scaled knee was even superior to the commercial knee, which could only flex up to 1.6° without buckling. As the value of the standard deviation of the positive heel contact (x/y) ratio was small and consistent up to 15°, the knee could maintain stability with the minimum hip moment and prevent buckling in the range of 2 to 15 degrees.

During full extension, if the α-value was positive, the knee was considered stable. Compared to the commercial knee joint, with an α-value of 28.9 mm, the scaled knee joint had a value of 29.77 mm, which lay on the posterior side of the load line and was considered stable at full extension.

Here, the β-value represents the distance of the ICR from the mechanical knee center and is preferred to be greater than zero. For the scaled knee, the β-value was observed to be 120.1 mm, which is superior to the mechanical knee center, reducing the moment required to buckle the knee and increasing the stability. However, the moment required was slightly higher than that in the commercial knee, having a β-value of 124 mm.

The minimum toe clearance of 13.5 mm was observed in the scaled knee joint at 23° hip flexion and 49° knee flexion, which was slightly less than the 19.7 mm clearance in the commercial knee. Similarly, the minimum heel clearance at 23° hip flexion and 12° knee flexion was 11.7 mm less than that of the commercial knee. Though the toe and heel clearances were higher than zero and would avoid stumbling while walking, they were lower than the commercial knee’s clearances.

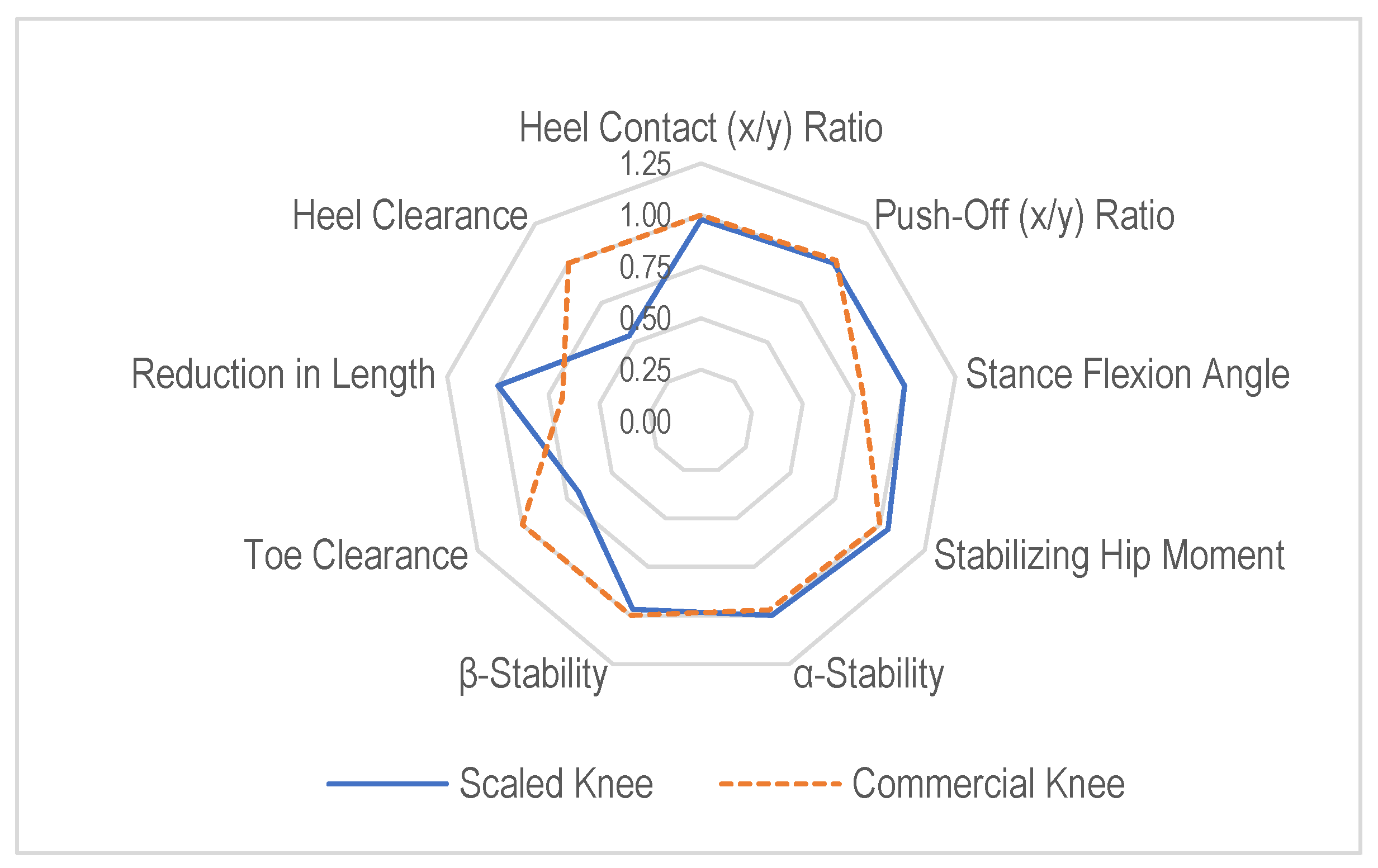
The spider chart (radar chart) shown in Figure 11 compares the scaled knee (solid line) and the commercial knee (dashed line) across the multiple biomechanical performance parameters identified earlier. Each axis represents a key performance metric, and the normalized values range outward from 0 (center) to 1.25 (outer ring), with higher values indicating better or stronger performance in that metric. Both the scaled knee and commercial knee had similar values in these metrics, suggesting that the scaled knee retained comparable stability during the initial heel contact and push-off. The scaled knee followed a similar pattern to the commercial knee, indicating that its stance-phase biomechanics were comparable. The commercial knee performed slightly better in terms of the heel contact (x/y) ratio, β-stability, toe clearance, and heel clearance, particularly regarding the toe clearance and heel clearance, which are crucial for the swing-phase clearance. The scaled knee showed a significant reduction in length, confirming that the scaling method successfully minimized the overall prosthesis size while still maintaining essential biomechanical functions.

The scaled knee maintained stability and stance-phase performance close to that of the commercial knee, making it a promising alternative for pediatric prostheses. The swing-phase metrics required further refinement, as the scaled knee had a lower toe clearance and β-stability, which could increase the risk of tripping. The linear scaling approach effectively reduced the prosthetic size, but adjustments in certain link lengths may be necessary to optimize the performance. However, the scaled knee showed reasonable values, meaning that its design still supports an effective walking gait.

This study employed static geometric analysis to evaluate the stance stability and swing-phase clearance. However, dynamic factors such as muscle activation, joint loading, and user adaptation were not considered. While this approach allows for rapid and reproducible assessments, it does not capture the full complexity of real-world gait. Future work will include dynamic simulations and physical testing to validate the functional performance under typical loading conditions.

This initial evaluation did not include a statistical or sensitivity analysis, as the modeling was based on fixed-input parameters from the literature and geometry. Future work will explore parameter sensitivity—particularly joint positioning and link length tolerances—to better understand how small variations influence the performance.

5. Conclusions

The thorough examination provided in this study highlights that the scaled knee joint satisfies the crucial requirements for stability and clearance necessary for a normal gait, as painstakingly detailed in Table 5. The encouraging results firmly support the practicality of using a scaled knee joint in pediatric situations.

• This study successfully demonstrated that a linear geometric scaling factor can be used to translate the dimensions of an adult prosthetic knee joint into pediatric transfemoral prostheses. The scaled knee maintained proportional geometric relationships while meeting key stance stability and swing-phase clearance criteria.
• The scaled knee exhibited heel contact and push-off (x/y) ratios comparable to those of a commercial pediatric knee, ensuring stability during stance and gait. The stance flexion angle and stabilizing hip moment values indicate that the scaled knees provided reliable support during loading.
• The scaled knee achieved positive toe and heel clearance values, minimizing the risk of stumbling. While slightly lower than the commercial knee, these clearances remained functional, indicating a strong basis for further refinement.
• Linear scaling offers a straightforward and reproducible method for designing pediatric knee joints, reducing the complexity in design and manufacturing. This approach allows for the adaptation of existing adult prosthetic designs to meet pediatric needs, enhancing accessibility.
• This study establishes a strong foundation for scaling adult knee prosthetic designs to pediatric applications. With further refinements, this method can significantly improve the mobility and quality of life for young transfemoral amputees.

This study suggests a promising first step in scaling adult prosthetic knees for pediatric use through a linear geometric approach. Although based on static analysis, the results are encouraging and set the stage for future validation through dynamic simulations and gait testing. Given the rapid growth and evolving biomechanics in children, future designs will consider modular or adjustable components to accommodate changes in the limb length and gait, thereby extending the prosthesis’s usability and supporting long-term mobility during development.

Furthermore, the method’s effective implementation in scaling a prosthetic knee joint validates its dependability and establishes a basis for its wider applicability. The results provide an important perspective on prosthetic improvements by validating the scaling method and furthering the understanding of the effectiveness of scaled knee joints in pediatric instances. Physical prototyping and gait analysis can be conducted to validate theoretical predictions, ensuring that the proposed scaling method translates effectively into real-world applications.