Evaluation of Bone Turnover around Short Finned Implants in Atrophic Posterior Maxilla: A Finite Element Study
Abstract
1. Introduction
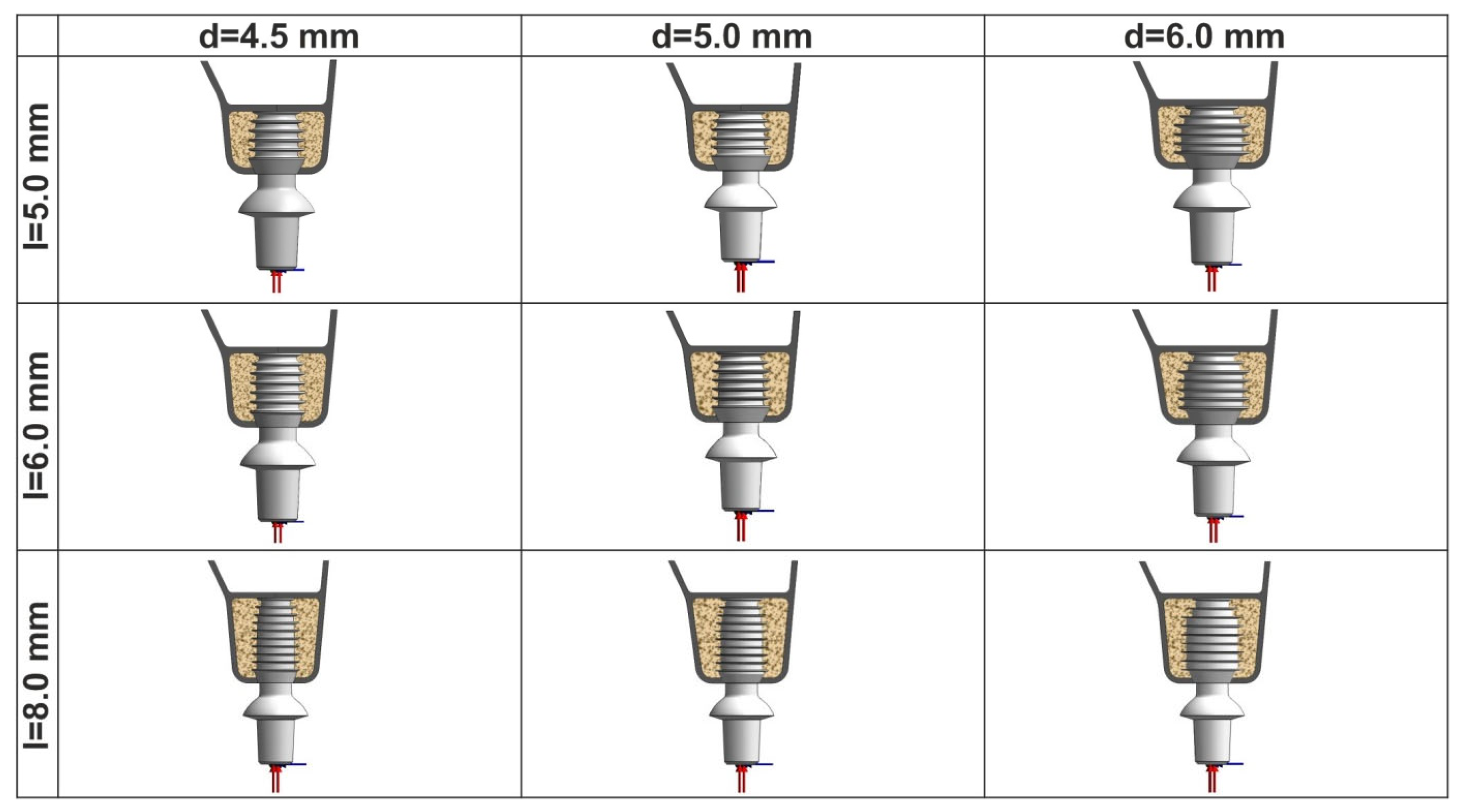
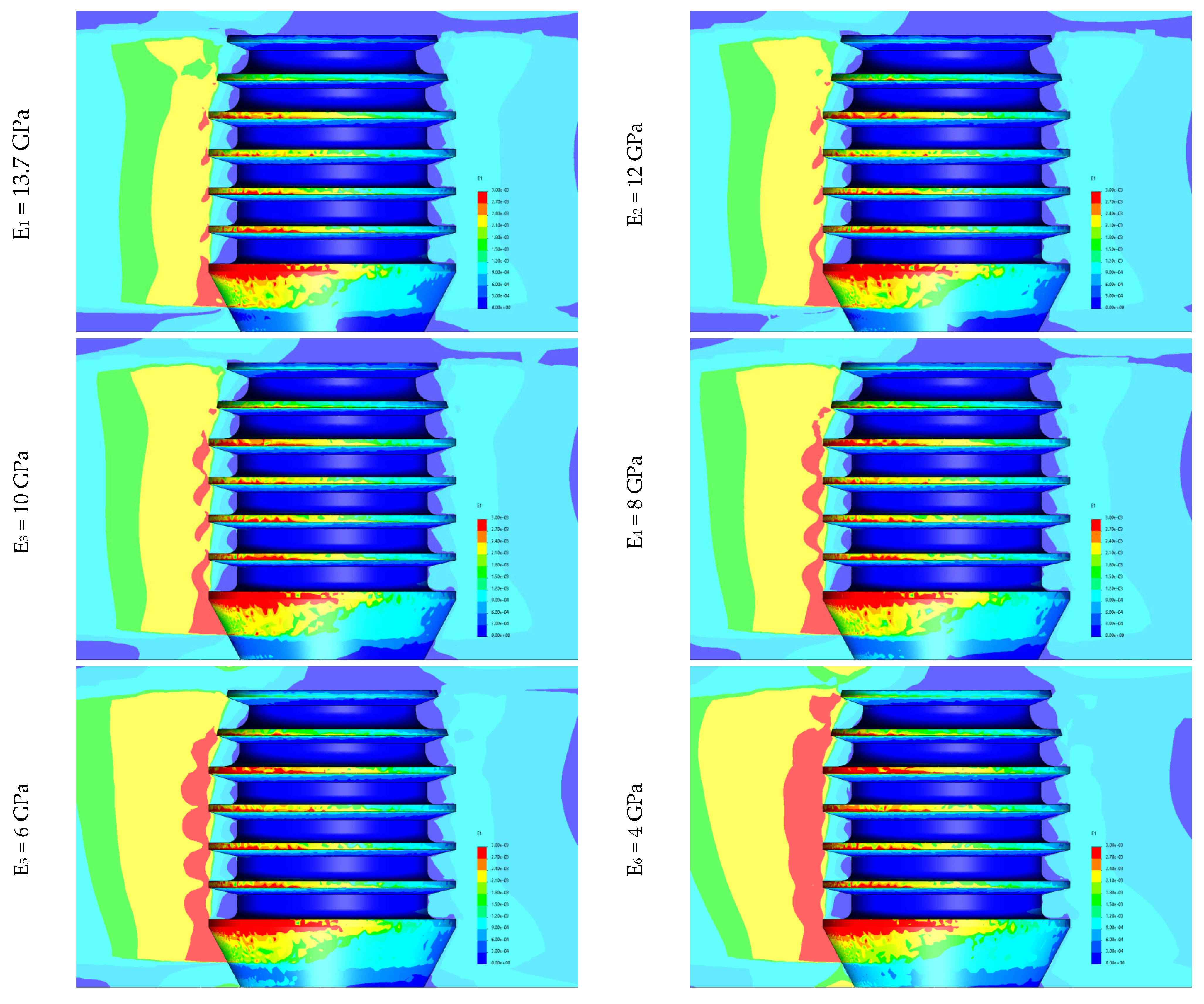
2. Materials and Methods
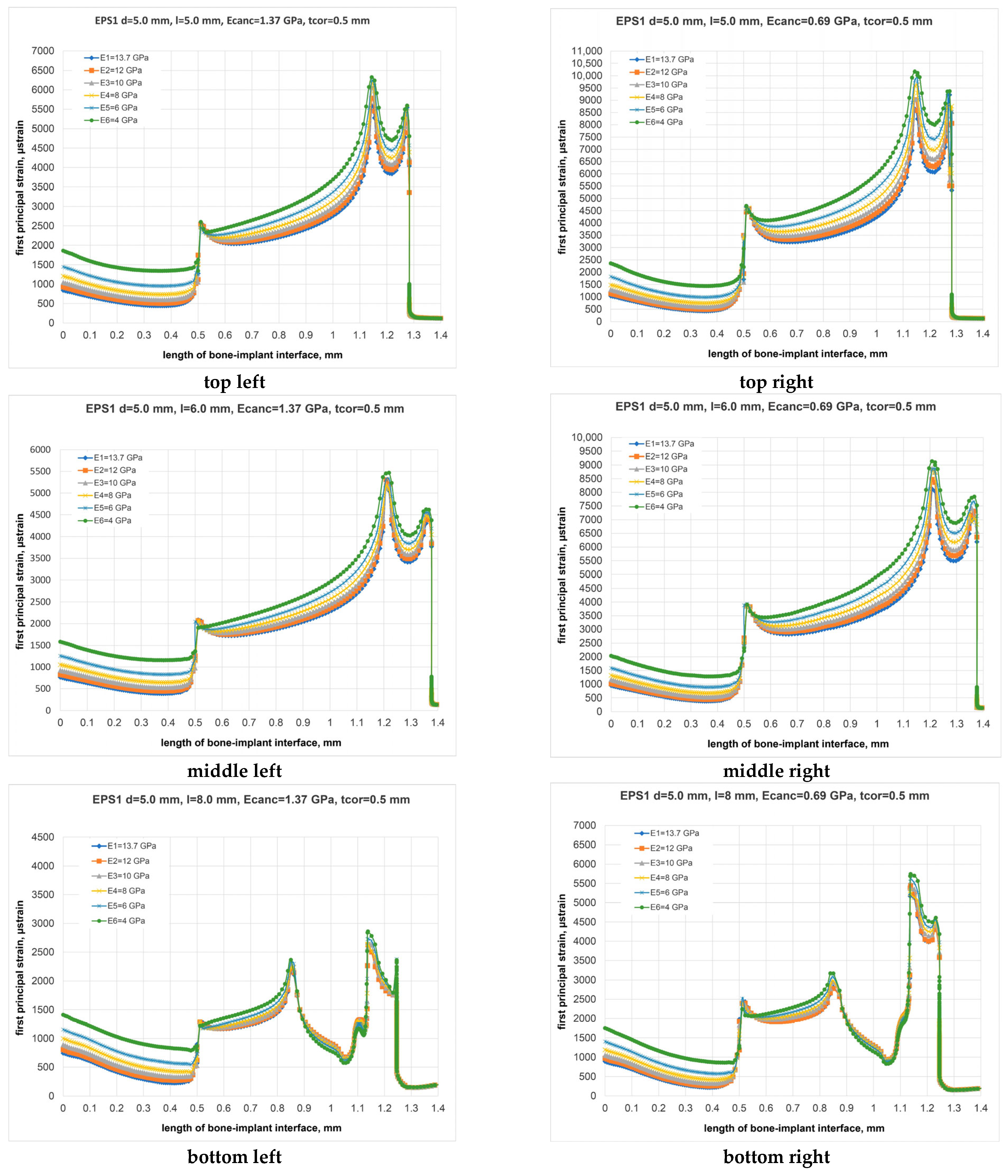
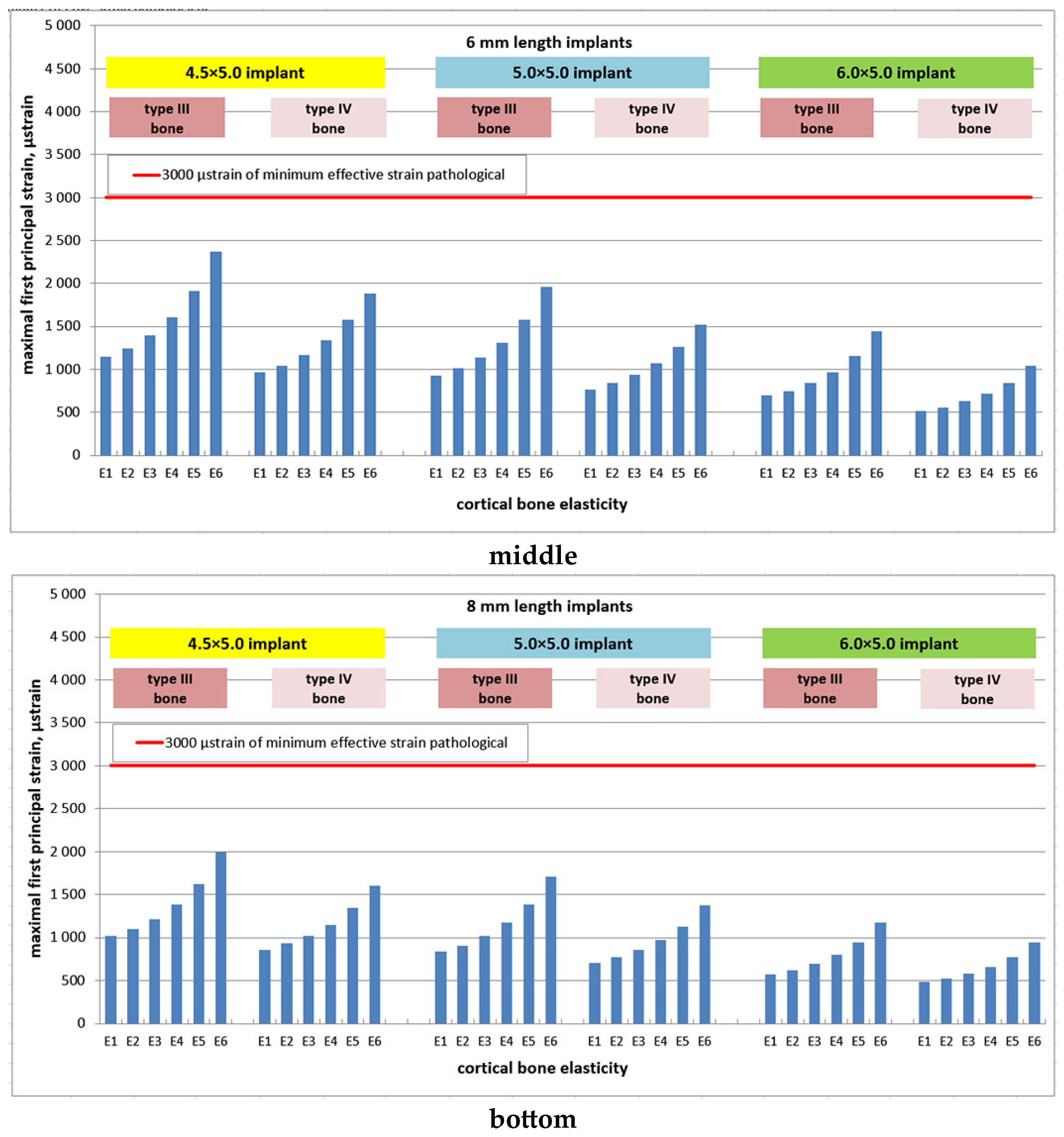
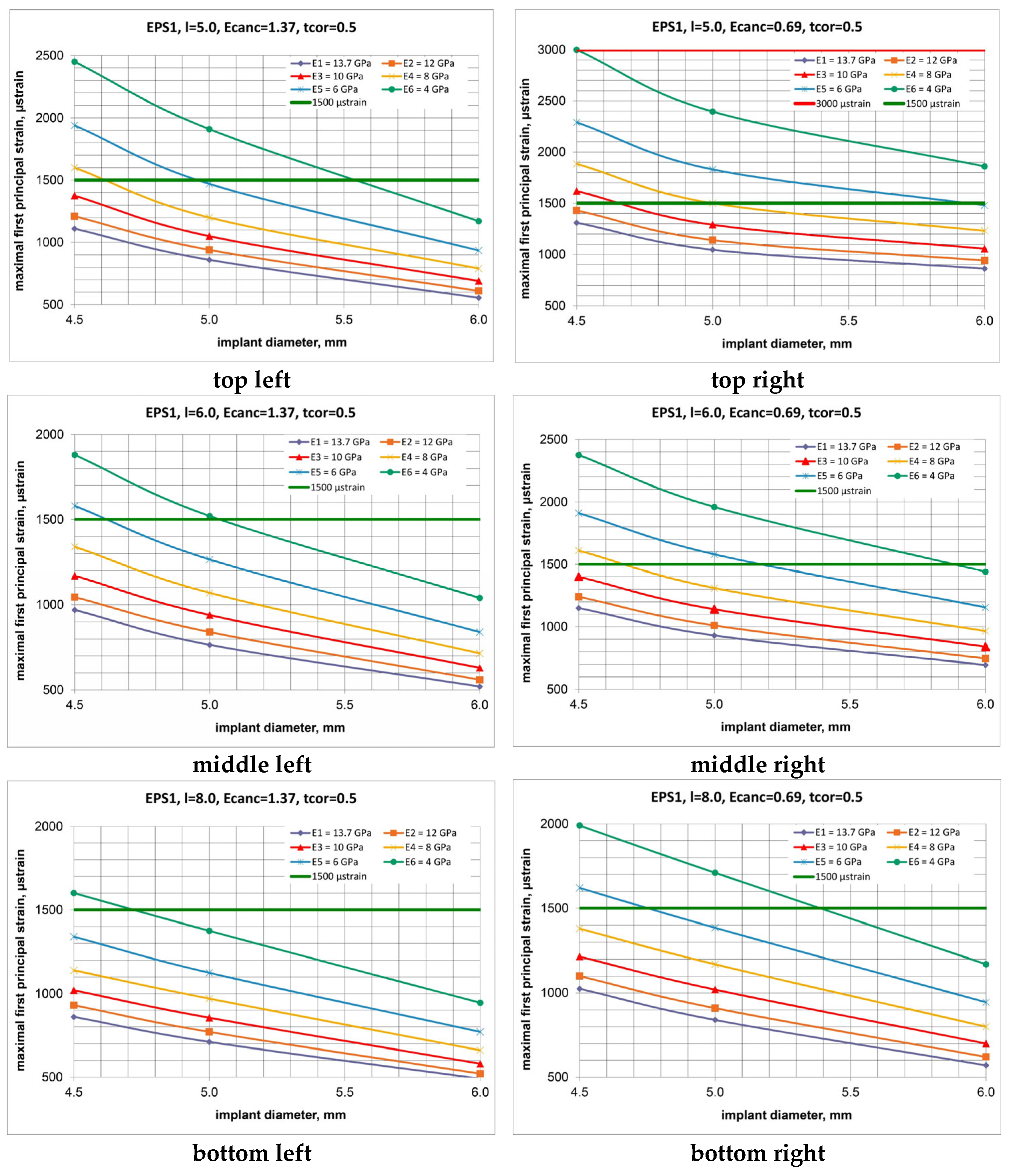
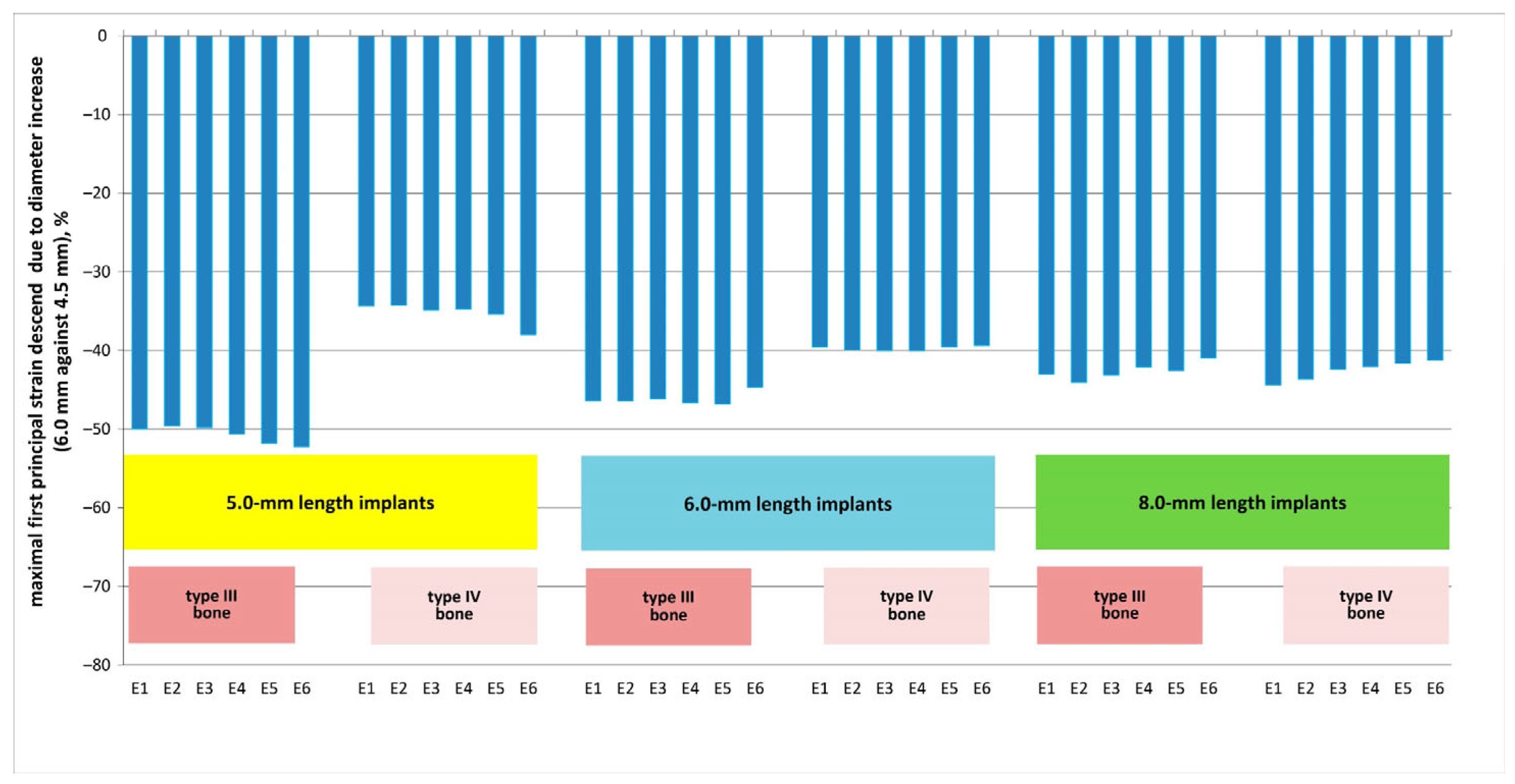
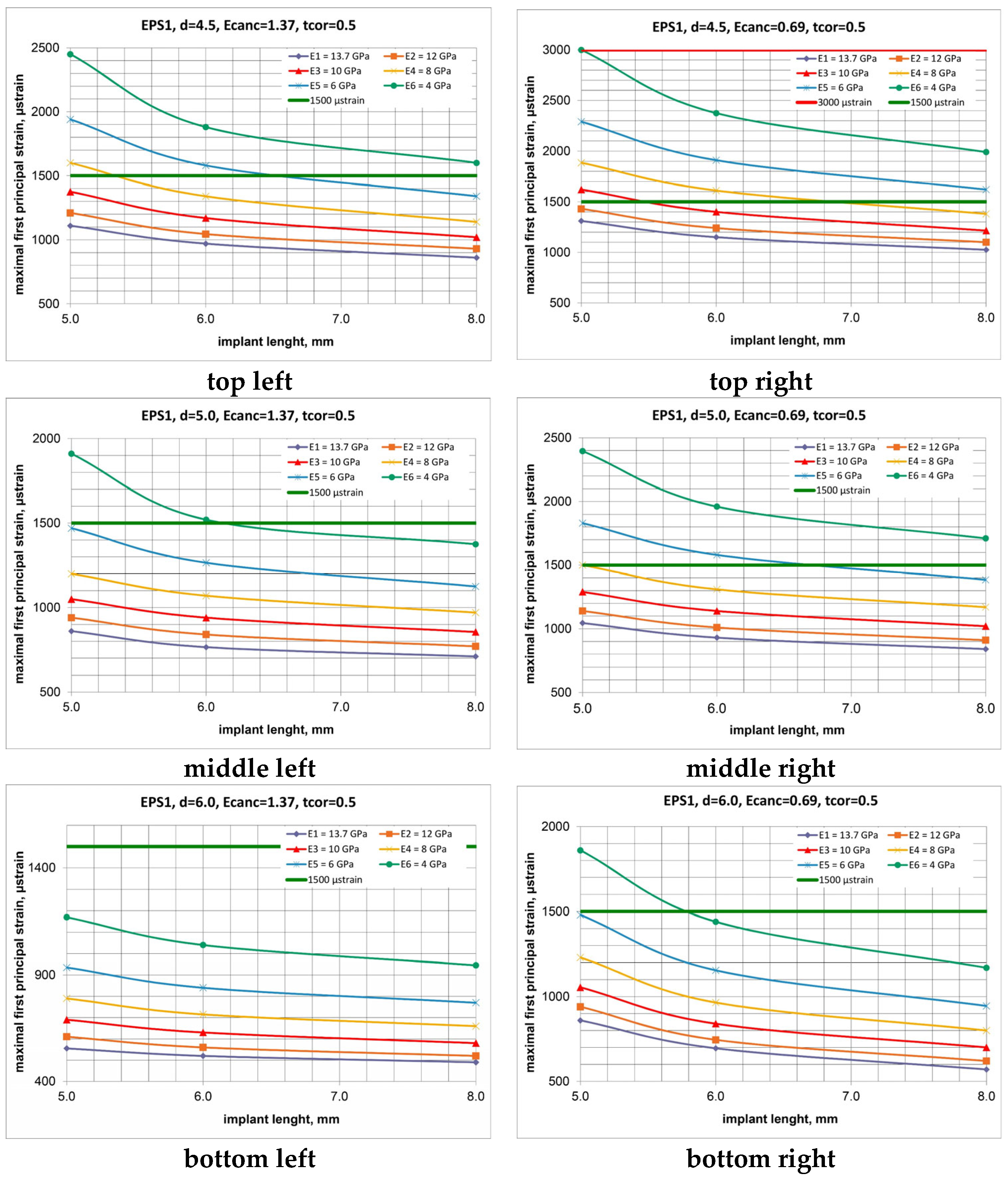
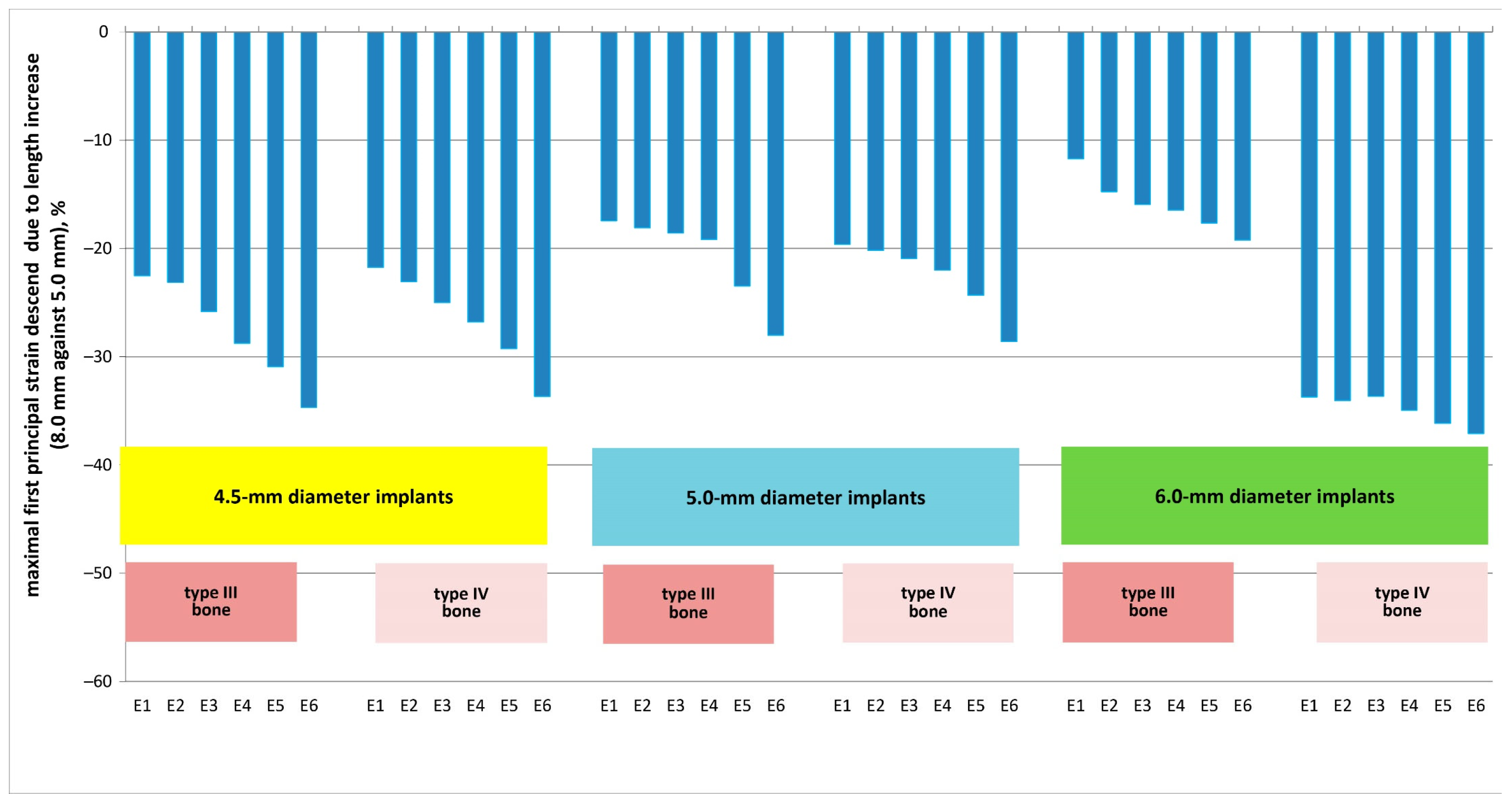
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Overmann, A.L.; Aparicio, C.; Richards, J.T.; Mutreja, I.; Fischer, N.G.; Wade, S.M.; Potter, B.K.; Davis, T.A.; Bechtold, J.E.; Forsberg, J.A.; et al. Orthopaedic osseointegration: Implantology and future directions. J. Orthopaed. Res. 2020, 38, 1445–1454. [Google Scholar] [CrossRef] [PubMed]
- Verma, A.; Singh, S.V.; Arya, D.; Shivakumar, S.; Chand, P. Mechanical failures of dental implants and supported prostheses: A systematic review. J. Oral Biol. Craniofac. Res. 2023, 13, 306–314. [Google Scholar] [CrossRef] [PubMed]
- Segal, P.; Makhoul, A.; Eger, M.; Lucchina, A.G.; Winocur, E.; Mijiritsky, E. Preliminary Study to Evaluate Marginal Bone Loss in Cases of 2- and 3-Implant-Supported Fixed Partial Prostheses of the Posterior Mandible. J. Craniofac. Surg. 2019, 30, 1068–1072. [Google Scholar] [CrossRef] [PubMed]
- Hingsammer, L.; Pommer, B.; Hunger, S.; Stehrer, R.; Watzek, G.; Insua, A. Influence of Implant Length and Associated Parameters Upon Biomechanical Forces in Finite Element Analyses: A Systematic Review. Implant Dent. 2019, 28, 296–305. [Google Scholar] [CrossRef] [PubMed]
- Fernandes, G.V.O.; Ferreira, N.D.R.N.; Heboyan, A.; Nassani, L.M.; Pereira, R.M.A.; Fernandes, J.C.H. Clinical assessment of short (>6 mm and ≤8.5 mm) implants in posterior sites with an average follow-up of 74 Months: A Retrospective Study. Int. J. Oral Maxillofac. Implant 2023, 38, 915–926. [Google Scholar] [CrossRef]
- Cenkoglu, B.G.; Balcioglu, N.B.; Ozdemir, T.; Mijiritsky, E. The Effect of the Length and Distribution of Implants for Fixed Prosthetic Reconstructions in the Atrophic Posterior Maxilla: A Finite Element Analysis. Materials 2019, 12, 2556. [Google Scholar] [CrossRef]
- Fernandes, G.; Costa, B.; Trindade, H.F.; Castilho, R.M.; Fernandes, J. Comparative analysis between extra-short implants (≤6 mm) and 6 mm-longer implants: A meta-analysis of randomized controlled trial. Aust. Dent. J. 2022, 67, 194–211. [Google Scholar] [CrossRef]
- Markose, J.; Eshwar, S.; Srinivas, S.; Jain, V. Clinical outcomes of ultrashort sloping shoulder implant design: A survival analysis. Clin. Implant Dent. Relat. Res. 2018, 20, 646–652. [Google Scholar] [CrossRef]
- Taschieri, S.; Lolato, A.; Testori, T.; Francetti, L.; Del Fabbro, M. Short dental implants as compared to maxillary sinus augmentation procedure for the rehabilitation of edentulous posterior maxilla: Three-year results of a randomized clinical study. Clin. Implant Dent. Relat. Res. 2018, 20, 9–20. [Google Scholar] [CrossRef]
- Cruz, R.S.; Lemos, C.A.A.; Batista, V.E.S.; Oliveira, H.F.F.E.; Gomes, J.M.L.; Pellizzer, E.P.; Verri, F.R. Short implants versus longer implants with maxillary sinus lift. A systematic review and meta-analysis. Braz. Oral Res. 2018, 32, e86. [Google Scholar] [CrossRef]
- Linetskiy, I.; Demenko, V.; Yefremov, O.; Linetska, L.; Kondratiev, A. Crestal versus subcrestal short plateau implant placement. In Integrated Computer Technologies in Mechanical Engineering; ICTM 2023 Lecture Notes in Networks and Systems; Springer International Publishing: Cham, Switzerland, 2024; Volume 1008, pp. 258–267. [Google Scholar] [CrossRef]
- Alqahtani, A.R.; Desai, S.R.; Patel, J.R.; Alqhtani, N.R.; Alqahtani, A.S.; Heboyan, A.; Fernandes, G.V.O.; Mustafa, M.; Karobari, M.I. Investigating the impact of diameters and thread designs on the Biomechanics of short implants placed in D4 bone: A 3D finite element analysis. BMC. Oral Health 2023, 23, 686. [Google Scholar] [CrossRef] [PubMed]
- Linetska, L.; Kipenskyi, A.; Demenko, V.; Linetskiy, I.; Kondratiev, A.; Yefremov, O. Finite element study of biomechanical behavior of short dental implants with bone loss effects–evaluation of bone turnover. In Proceedings of the 2023 IEEE 4th KhPI Week on Advanced Technology (KhPIWeek), Kharkiv, Ukraine, 2–6 October 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Calì, M.; Zanetti, E.M.; Oliveri, S.M.; Asero, R.; Ciaramella, S.; Martorelli, M.; Bignardi, C. Influence of thread shape and inclination on the biomechanical behaviour of plateau implant systems. Dent. Mater. 2018, 34, 460–469. [Google Scholar] [CrossRef] [PubMed]
- McKenna, G.J.; Gjengedal, H.; Harkin, J.; Holland, N.; Moore, C.; Srinivasan, M. Effect of autogenous bone graft site on dental implant survival and donor site complications: A systematic review and meta-analysis. J. Evid. Based Dent. Pract. 2022, 22, 101731. [Google Scholar] [CrossRef] [PubMed]
- Qiu, P.; Cao, R.; Li, Z.; Fan, Z. A comprehensive biomechanical evaluation of length and diameter of dental implants using finite element analyses: A systematic review. Heliyon 2024, 10, e26876. [Google Scholar] [CrossRef] [PubMed]
- Leucht, P.; Monica, S.D.; Temiyasathit, S.; Lenton, K.; Manu, A.; Longaker, M.T.; Jacobs, C.R.; Spilker, R.L.; Guo, H.; Brunski, J.B.; et al. Primary cilia act as mechanosensors during bone healing around an implant. Med. Eng. Phys. 2013, 35, 392–402. [Google Scholar] [CrossRef]
- Frost, H.M. A 2003 update of bone physiology and Wolff’s Law for clinicians. Angle Orthod. 2004, 74, 3–15. [Google Scholar] [CrossRef]
- Frost, H.M. Bone “mass” and the “mechanostat”: A proposal. Anat. Rec. 1987, 219, 1–9. [Google Scholar] [CrossRef]
- Misch, C.E. (Ed.) Chapter 32—Progressive Bone Loading: Increasing the Density of Bone with a Prosthetic Protocol. In Dental Implant Prosthetics; Mosby: Maryland Heights, MO, USA, 2015; pp. 913–937. [Google Scholar] [CrossRef]
- Saab, X.E.; Griggs, J.A.; Powers, J.M.; Engelmeier, R.L. Effect of abutment angulation on the strain on the bone around an implant in the anterior maxilla: A finite element study. J. Prosthet. Dent. 2007, 97, 85–92. [Google Scholar] [CrossRef]
- Falcinelli, C.; Valente, F.; Vasta, M.; Traini, T. Finite element analysis in implant dentistry: State of the art and future directions. Dent. Mater. 2023, 39, 539–556. [Google Scholar] [CrossRef]
- Lisiak-Myszke, M.; Marciniak, D.; Bieliński, M.; Sobczak, H.; Garbacewicz, Ł.; Drogoszewska, B. Application of Finite Element Analysis in Oral and Maxillofacial Surgery-A Literature Review. Materials 2020, 13, 3063. [Google Scholar] [CrossRef]
- Linetskiy, I.; Sutcliffe, M.; Kondratiev, A.; Demenko, V.; Linetska, L.; Yefremov, O. A novel method of load bearing ability analysis of short plateau implants placed in compromised bone. In Proceedings of the 2023 IEEE 4th KhPI Week on Advanced Technology (KhPIWeek), Kharkiv, Ukraine, 2–6 October 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Sugiura, T.; Yamamoto, K.; Horita, S.; Murakami, K.; Tsutsumi, S.; Kirita, T. The effects of bone density and crestal cortical bone thickness on micromotion and peri-implant bone strain distribution in an immediately loaded implant: A nonlinear finite element analysis. J. Periodontal Implant Sci. 2016, 46, 152–165. [Google Scholar] [CrossRef] [PubMed]
- Bozkaya, D.; Muftu, S.; Muftu, A. Evaluation of load transfer characteristics of five different implants in compact bone at different load levels by finite elements analysis. J. Prosthet. Dent. 2004, 92, 523–530. [Google Scholar] [CrossRef] [PubMed]
- Lemos, C.A.A.; Verri, F.R.; Noritomi, P.Y.; Kemmoku, D.T.; Souza Batista, V.E.; Cruz, R.S.; de Luna Gomes, J.M.; Pellizzer, E.P. Effect of bone quality and bone loss level around internal and external connection implants: A finite element analysis study. J. Prosthet. Dent. 2021, 125, 137.e1–137.e10. [Google Scholar] [CrossRef]
- Mericske-Stern, R.; Zarb, G.A. In vivo measurements of some functional aspects with mandibular fixed prostheses supported by implants. Clin. Oral Implants Res. 1996, 7, 153–161. [Google Scholar] [CrossRef] [PubMed]
- Sahin, S.; Cehreli, M.C.; Yalçin, E. The influence of functional forces on the biomechanics of implant-supported prostheses—A review. J. Dent. 2002, 30, 271–282. [Google Scholar] [CrossRef]
- Li, J.; Jansen, J.A.; Walboomers, X.F.; van den Beucken, J.J. Mechanical aspects of dental implants and osseointegration: A narrative review. J. Mech. Behav. Biomed. Mater. 2020, 103, 103574. [Google Scholar] [CrossRef]
- Gere, J.M.; Timoshenko, S.P. Mechanics of Materials; Chapman & Hall: London, UK, 1991. [Google Scholar]
- Kondratiev, A.; Potapov, O.; Tsaritsynskyi, A.; Nabokina, T. Optimal design of composite shelled sandwich structures with a honeycomb filler. In Advances in Design, Simulation and Manufacturing IV. DSMIE 2021; Lecture Notes in Mechanical Engineering; Springer: Berlin/Heidelberg, Germany, 2021; pp. 546–555. [Google Scholar] [CrossRef]
- Jafarian, M.; Mirhashemi, F.S.; Emadi, N. Finite element analysis of stress distribution around a dental implant with different amounts of bone loss: An in vitro study. Dent. Med. Probl. 2019, 56, 27–32. [Google Scholar] [CrossRef]
- Yalçın, M.; Kaya, B.; Laçin, N.; Arı, E. Three-Dimensional Finite Element Analysis of the Effect of Endosteal Implants with Different Macro Designs on Stress Distribution in Different Bone Qualities. Int. J. Oral Maxillofac. Implant 2019, 34, e43–e50. [Google Scholar] [CrossRef]
- Oliveira, H.; Brizuela Velasco, A.; Ríos-Santos, J.V.; Sánchez, L.F.; Lemos, B.F.; Gil, F.J.; Carvalho, A.; Herrero-Climent, M. Effect of Different Implant Designs on Strain and Stress Distribution under Non-Axial Loading: A Three-Dimensional Finite Element Analysis. Int. J. Environ. Res. Public Health 2020, 17, 4738. [Google Scholar] [CrossRef]
- Chen, J.; Guo, J.; Yang, L.; Wang, L.; Zhang, X. Effect of different implant angulations on the biomechanical performance of prosthetic screws in two implant-supported, screw-retained prostheses: A numerical and experimental study. J. Prosthet. Dent. 2023, 130, 240.e1–240.e10. [Google Scholar] [CrossRef]
- Demenko, V.; Linetskiy, I.; Nesvit, K.; Hubalkova, H.; Nesvit, V.; Shevchenko, A. Importance of diameter-to-length ratio in selecting dental implants: A methodological finite element study. Comput. Methods Biomech. Biomed. Eng. 2014, 17, 443–449. [Google Scholar] [CrossRef] [PubMed]
- Yoda, N.; Zheng, K.; Chen, J.; Li, W.; Swain, M.; Sasaki, K.; Li, Q. Bone morphological effects on post-implantation remodeling of maxillary anterior buccal bone: A clinical and biomechanical study. J. Prosthodont. Res. 2017, 61, 393–402. [Google Scholar] [CrossRef] [PubMed]
- De Matos, J.D.M.; Queiroz, D.A.; Nakano, L.J.N.; Andrade, V.C.; Ribeiro, N.D.R.; Borges, A.L.S.; Bottino, M.A.; Lopes, G.D.S. Bioengineering tools applied to dentistry: Validation methods for in vitro and in silico analysis. Dent. J. 2022, 10, 145. [Google Scholar] [CrossRef] [PubMed]
- Hannam, A.G. Current computational modelling trends in craniomandibular biomechanics and their clinical implications. J. Oral Rehabil. 2011, 38, 217–234. [Google Scholar] [CrossRef]
- Anderson, A.E.; Ellis, B.J.; Weiss, J.A. Verification, validation and sensitivity studies in computational biomechanics. Comput. Methods Biomech. Biomed. Eng. 2007, 10, 171–184. [Google Scholar] [CrossRef]
- Yan, X.; Zhang, X.; Chi, W.; Ai, H.; Wu, L. Comparing the influence of crestal cortical bone and sinus floor cortical bone in posterior maxilla bi-cortical dental implantation: A three-dimensional finite element analysis. Acta Odontol. Scand. 2015, 73, 312–320. [Google Scholar] [CrossRef]
- Okumura, N.; Stegaroiu, R.; Kitamura, E.; Kurokawa, K.; Nomura, S. Influence of maxillary cortical bone thickness, implant design and implant diameter on stress around implants: A three-dimensional finite element analysis. J. Prosthodont. Res. 2010, 54, 133–142. [Google Scholar] [CrossRef]
- Barbosa, F.T.; Zanatta, L.C.S.; de Souza Rendohl, E.; Gehrke, S.A. Comparative analysis of stress distribution in one-piece and two-piece implants with narrow and extra-narrow diameters: A finite element study. PLoS ONE 2021, 16, e0245800. [Google Scholar] [CrossRef]
- Chou, I.-C.; Lee, S.-Y.; Ming-Chang, W.; Sun, C.W.; Jiang, C.P. Finite element modelling of implant designs and cortical bone thickness on stress distribution in maxillary type IV bone. Comput. Methods Biomech. Biomed. Eng. 2014, 17, 516–526. [Google Scholar] [CrossRef]
- Alper, B.; Gultekin, P.; Yalci, S. Application of Finite Element Analysis in Implant Dentistry. In Finite Element Analysis-New Trends and Developments; InTech: Rijeka, Croatia, 2012. [Google Scholar] [CrossRef]
- Tretto, P.H.W.; Dos Santos, M.B.F.; Spazzin, A.O.; Pereira, G.K.R.; Bacchi, A. Assessment of stress/strain in dental implants and abutments of alternative materials compared to conventional titanium alloy-3D non-linear finite element analysis. Comput. Methods Biomech. Biomed. Eng. 2020, 23, 372–383. [Google Scholar] [CrossRef]
- Limbert, G.; van Lierde, C.; Muraru, O.L.; Walboomers, X.F.; Frank, M.; Hansson, S.; Middleton, J.; Jaecques, S. Trabecular bone strains around a dental implant and associated micromotions--a micro-CT-based three-dimensional finite element study. J. Biomech. 2010, 43, 1251–1261. [Google Scholar] [CrossRef] [PubMed]
- Frost, H.M. The mechanostat: A proposed pathogenic mechanism of osteoporoses and the bone mass effects of mechanical and nonmechanical agents. Bone. Miner. 1987, 2, 73–85. [Google Scholar] [PubMed]
- Grauer, D.; Cevidanes, L.S.; Proffit, W.R. Working with DICOM craniofacial images. Am. J. Orthod. Dentofac. Orthop. 2009, 136, 460–470. [Google Scholar] [CrossRef] [PubMed]
- Bordin, D.; Castro, M.B.; Carvalho, M.A.; Araujo, A.M.; Cury, A.A.D.B.; Lazari-Carvalho, P.C. Different Treatment Modalities Using Dental Implants in the Posterior Maxilla: A Finite Element Analysis. Braz. Dent. J. 2021, 32, 34–41. [Google Scholar] [CrossRef] [PubMed]
- Khosravani, M.R. Mechanical behavior of restorative dental composites under various loading conditions. J. Mech. Behav. Biomed. Mater. 2019, 93, 151–157. [Google Scholar] [CrossRef]
- Kurniawan, D.; Nor, F.M.; Lee, H.Y.; Lim, J.Y. Finite element analysis of bone-implant biomechanics: Refinement through featuring various osseointegration conditions. Int. J. Oral Maxillofac. Surg. 2012, 41, 1090–1096. [Google Scholar] [CrossRef]






Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kondratiev, A.; Demenko, V.; Linetskiy, I.; Weisskircher, H.-W.; Linetska, L. Evaluation of Bone Turnover around Short Finned Implants in Atrophic Posterior Maxilla: A Finite Element Study. Prosthesis 2024, 6, 1170-1188. https://doi.org/10.3390/prosthesis6050084
Kondratiev A, Demenko V, Linetskiy I, Weisskircher H-W, Linetska L. Evaluation of Bone Turnover around Short Finned Implants in Atrophic Posterior Maxilla: A Finite Element Study. Prosthesis. 2024; 6(5):1170-1188. https://doi.org/10.3390/prosthesis6050084
Chicago/Turabian StyleKondratiev, Andrii, Vladislav Demenko, Igor Linetskiy, Hans-Werner Weisskircher, and Larysa Linetska. 2024. "Evaluation of Bone Turnover around Short Finned Implants in Atrophic Posterior Maxilla: A Finite Element Study" Prosthesis 6, no. 5: 1170-1188. https://doi.org/10.3390/prosthesis6050084
APA StyleKondratiev, A., Demenko, V., Linetskiy, I., Weisskircher, H.-W., & Linetska, L. (2024). Evaluation of Bone Turnover around Short Finned Implants in Atrophic Posterior Maxilla: A Finite Element Study. Prosthesis, 6(5), 1170-1188. https://doi.org/10.3390/prosthesis6050084






