Abstract
The purpose of this study is to numerically analyze a 3D model of an implant under fatigue loads. A bone and a V shape implant were modeled using SolidWorks2008 software. In order to obtain an exact model, the bone was assumed as a linear orthotropic material. Mechanical loads were applied in terms of fastening torque to the abutment and mastication force applied at the top of the crown. The abutment was tightened into the implant by applying a 35 N.cm torque causing tensile stress within the abutment screw as a preload that is harmful not only for the fatigue life of the abutment, but also for the stability of the implant-abutment interface. A 700 N force at an angle of 30 degrees to the vertical direction was applied to the crown. The mechanical analysis results showed that the abutment is the critical component of the implant system in terms of fatigue failure. This is due to the fact that the tensile preloads originated from the fastening torque. The results were presented in terms of fatigue life in the abutment. Fatigue life of the abutment and implant were calculated based on the Goodman, Soderberg, Smith–Watson–Topper (SWT), and Marrow theories. According to the results of the fatigue life prediction, abutment screws may fail after about 3 × 105 cycles. The predicted results by the Goodman theory are at a very good accordance with the clinical data.
1. Introduction
For many years, dental implants have been studied as a replacement for missing teeth. The performance of implants is extremely related to their stability, resistance against applied loads, and minimization of the stress they impose to the jaw bone. Implants are produced in different shapes and sizes, so as to decrease the distribution of the stress in BII (bone implant interface) and implant components. As the implant is continuously under mechanical loads and stresses, it is essential to perform fatigue analysis to evaluate the fatigue life.
Titanium implants were first applied by Branemark in 1965 [1]. Since then, many modifications have been made to the initial design in order to improve the performance of the implants. However, due to limitations confining experimental studies, numerical analyses were used widely. FEM (finite element method) analysis helps to have a better understanding of the effects of different variables in the implant structure on its performance. Akpinar et al. presented a 2D model to study the stress distribution and stress concentration within the implants [2]. In 2002, Holmgren et al. used a 2D model to survey the effect of osseointegration level on implant stress [3]. When a horizontal load is applied to a simulated mandible, the location and direction of maximum stress around the dental implants appeared to be influenced much more by the structural characters of the mandibles when compared with vertical loads [4]. The results of some of 2D models are often far from the actual situation and the stresses predicted by a 2D model are less accurate than that of 3D counterpart [5]. Thus, in-vitro models have been widely implemented by researchers so as to validate FEM analysis to enhance the reliability of numerical analysis [6,7]. Geometrical parameters such as length and diameter of implants and abutments coupled with implant-abutment connection types play influential role in stress distribution in bone implant interface and other components, and also directly affect screw loosening and screw fracture [7,8,9]. A study showed that an increase in the implant diameter, rather than an increase in its length had more contribution to a reduction in the maximum Von Mises equivalent stress around the implant neck [10]. Also, the shape of implant neck and its threat pattern can change the stress distribution in cortical and cancellous bones [11]. Moreover, alongside dimensional parameters, materials utilized for construction of prosthetics have significant effects on stress distribution and stress concentration in bones [12,13]. Compared to static loads, dynamic loads are associated with more critical effects, causing higher stress within the implant structures [14]. Regarding the possible effect of thread pitch of the implant on the stress distribution over the bones, Kong et al. exhibited that the cancellous bone, rather than cortical bone, is more sensitive to thread pitch which played an important role in protecting dental implants against axial loads [15]. The thread height, however, plays a more significant role in affecting bone stress and implant-abutment complex stability than the thread width [16]. Furthermore, the thickness of cortical bone and the density of cancellous bone affect the distribution of stress and strain produced by implants [17]. That is, the stress distribution over a compact bone is better than that over the bones of other qualities [18]. In this study, a 3D model of an ITI (international team for implantology) standard implant is created to investigate the effects of the abutment fastening torque and mastication force applied to the crown on the stress distribution and the fatigue life of the implants.
2. Material and Methods
2.1. Preliminary Modeling
A cancellous bone with a surrounding 2 mm thickness cortical bone were simulated [14,18] based on the CT scan images [19] in Mimics software (Mimics®, Materialise Corp., Leuven, Belgium), based on which a 3D model was generated in SolidWorks 2008 (Dassault Systems SOLIDWORKS Corp., Waltham, MA, USA) [15]. Based on the ITI standard, a dental implant model was generated with a diameter of 4.1 mm and length of 10 mm. A solid abutment of 5.5 mm height, a framework of 7 mm and a crown of 10 mm height were selected for this study. Figure 1 shows the final assembled 3D model.
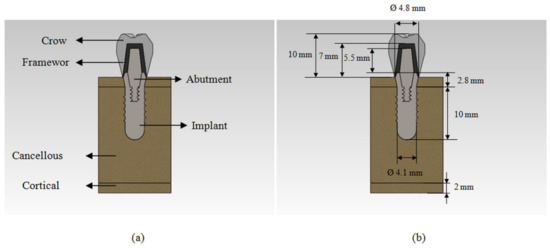
Figure 1.
(a) Cut view ofthe 3D model of implant, abutment, framework, crown, and bones; (b) the dimensions of components.
2.2. Material Properties
Table 1 shows the material properties of implant, abutment, framework, and crown [14]. These materials were assumed to follow the linear isotropic material behavior models [14]. Cortical and cancellous bones were modeled with different material properties. The bones were represented with a transversely isotropic material model which is shown in Table 2 [20].

Table 1.
Mechanical properties and materials of the implant [14].

Table 2.
Mechanical properties of the bones [20].
2.3. Finite Element Modeling
After modeling the piecework in SolidWorks2008 software, the 3D model was imported into FE code (Abaqus 6.10, ABAQUS Inc., Dassault Systemes Simulia Corp., Providence, RI, USA). The implant was completely reinforced into the jaw bone being tied along their entire interface [15]. The same type of contact was assumed for abutment-framework and framework-crown interfaces [21]. Surface to surface contact with a frictional coefficient of 0.3 was taken for implant-abutment interface [20]. The mesial-distal surfaces of mandibular bone were constrained to zero displacement in x, y and z directions as the boundary conditions which is shown in Figure 2a [15,16]. The loads were applied to the model in two steps. In the first step, a 35 N.cm fastening torque was applied to the upper surface of abutment like how applied in real situation to create sufficient tensile preload in the abutment screw, while in the second step, a 700 N mastication load was applied to the top of the crown surface at an angle of 30° from the vertical direction according to ISO14801 (Figure 2b) [22,23].

Figure 2.
(a) Assumed loading and boundary conditions for the model, (b) the directions of the loads.
At the end of the modeling process and after the adequate convergence was achieved in the meshing size, the complete model had a total of about 114,000 tetrahedral linear and quadrature elements, including 30,000 and 4000 quadrature elements for the implant and the abutment, respectively, and 1200, 21,000, 8000 and 50,000 linear element for the framework, the crown, the cortical bone and the cancellous bone, respectively. Convergence in the mesh size for the crown and the framework was investigated as shown in Figure 3. Figure 4 shows the final model prepared with tetrahedral mesh for the analysis.

Figure 3.
Von Mises stress in normalized distance (for unifying the figures the selected path for investigating Von Mises stress was inverted to scale of 0 to 1) for different sizes of the elements (a) in the crown and (b) in the framework.

Figure 4.
Final model with a complete tetrahedral mesh.
3. Result
The results are presented as the stress distribution within the components as well as the fatigue life of the implant and the abutment.
3.1. Stress Analysis
The distribution of the Von Mises stress in the bone and the other components were investigated with the results being obtained from the FEM model performed at the end of analysis.
The maximum Von Mises stresses on the crown were located on the top and the bottom regions of the crown, as shown in Figure 5. In the framework, the maximum Von Mises stresses were concentrated at the framework-implant contact area (Figure 6). The stress distribution over the abutment is shown in Figure 7 and Figure 8. Due to the fastening torque, the first thread was the critical area hosting the maximum Von Mises stress, so as it was prone to fatigue failure. Figure 9 represents the Von Mises stress distribution in the implant with its maximum at the top of the implant where the framework stands. For the bones, the maximum stresses were concentrated on the region around the implant edge. The maximum stress in the cortical bone was higher than that in the cancellous bone, since the modules of elasticity in cancellous bone was lower than that in the cortical bone (Figure 10 and Figure 11). The maximum Von Mises stress within each component is presented in Table 3.
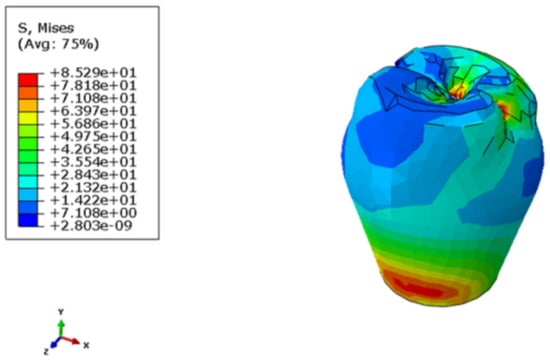
Figure 5.
Stress distribution in the crown.

Figure 6.
Stress distribution in the framework.

Figure 7.
Stress distribution in the abutment.

Figure 8.
Susceptible area for fatigue failure in the abutment.

Figure 9.
Stress distribution in the implant.

Figure 10.
Stress distribution in the cortical bone.
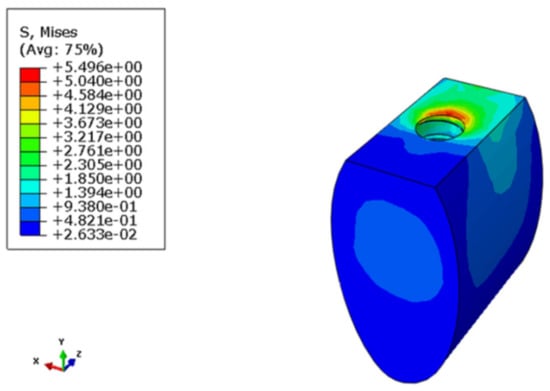
Figure 11.
Stress distribution in the cancellous bone.

Table 3.
Maximum Von Mises stress.
3.2. Fatigue Life Estimation
In this study, the fatigue failure was estimated using stress-based approaches. By this approach, the expected life in the abutment and the implant can be estimated using the following Basquin equation predicting an S-N curve [22]:
where:
σar = Equivalent completely reversible stress amplitude,
σ’f = Fatigue strength coefficient,
b = Fatigue strength exponent or Basquin exponent,
Nt = Fatigue life.
The fatigue properties of the titanium alloy used in Basquin equation are shown in Table 4 [24].

Table 4.
Fatigue properties of Ti-6Al-4V [24].
For calculation of the mean stress and stress amplitude, two stress approaches were used; one used the Von Mises stress given by Equations (2) and (3), while the other one used the effective stress amplitude and effective mean stress given in Equations (4) and (5).
Based on the Von Mises stress, the mean stress and stress amplitude are given by [14]:
However, based on the effective stress amplitude and effective mean stress, the mean stress and the stress amplitude are given by [22]:
These quantities can be combined into an equivalent completely reversible stress. Goodman, Soderberg, Marrow, and Smith-Watson-Topper (SWT) developed this quantity as follows [22]:
Using the results of the stress distribution over the implant and the abutment, their fatigue lives under mechanical loads were calculated implementing the theories presented in Equations (6)–(9) and the fatigue characteristics given in Table 4. Fatigue life could be computed based on the critical points and the elements shown in Figure 8 and Figure 9.
Figure 12 shows the theories by taking a constant life of Nf = 106. Figure 12 indicates that, for all theories, the implant enjoyed a longer life than that was specified in the corresponding standard. In Figure 13, the Von Mises stress approach was followed to calculate the equivalent completely reversible stress, while Figure 14 was built on the basis of the principal stresses method. Considering the mentioned explanations and positive contributions of the compression stresses, it is obvious that the fatigue life improved in the latter case.

Figure 12.
Average stress and stress range in the implant compared to the theories computed by taking a constant life of Nf = 106.

Figure 13.
Plot of σar (Von Mises)-Log (Nf) for different models describing the implant.

Figure 14.
Plot of σar (principal stress)-Log (Nf) for different models describing the implant.
Considering Figure 13 and employing the Basquin relationship, the implant life was predicted within the range of 108 to 3 × 109 cycles. This was in accordance with ISO14801, where a 106-cycle life is recommended for implants.
The fatigue life for the abutment was calculated based on the critical elements within the first thread, as shown in Figure 8. Abutment was fixed on the implant by applying a fastening torque within the course of assembly. Such a torque resulted in a pre-stress to be developed in the abutment’s thread. Once the other components were assembled on the top of the abutment, it was subjected to the varying loads of mastication. In order to obtain the mean stress and stress amplitude, the Von Mises approach and the principal stress method were utilized, just as explained in Section 2. The initial value of stress at the implant edges was zero, while it was resulted from the fastening torque in the abutment. These stresses could develop throughout the part in the form of a tensile pre-loading. Secondary stresses were those developed in the abutment as a result of mastication.
Figure 15 shows the mean stress and the stress amplitude at the critical points within the abutment, by taking a constant life of Nf = 106. Considering the curves for the said theories, the abutment life was fall within the confidence interval with its life being found on the infinite life region, when the life was calculated via the Von Mises stress approach. Nevertheless, the Von Mises stress approach failed to properly predict the effects of the mean stress. However, the principal stresses method resulted in a mean stress and stress amplitude for which a less than infinite life was predicted according to the Goodman theory. Figure 16 and Figure 17 illustrate the predicted life by different theories using the Von Mises stress and the principal stress methodologies, respectively.

Figure 15.
Average stress and stress range in the abutment compared to the theories computed by taking a constant life of Nf = 106.

Figure 16.
Plot of σar (Von Mises)-Log (Nf) for different models describing the abutment.
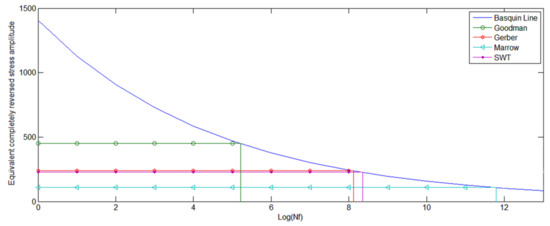
Figure 17.
Plot of σar (principal stress)-Log (Nf) for different theories describing the abutment.
According to Figure 16, the theories tended to predict an infinite life for the abutment, when the Von Mises approach was implicated. In some theories, the life of the abutment was observed to be even longer than that of the implant, which may not be an acceptable or realistic result. It can be explained by the fact that the amplitude of the applied stress to the abutment was almost half of that to the implant. Since, the Von Mises approach may not predict the effect of the mean stress, the calculated life based on this approach were relatively high. However, an abutment screw is generally subjected to a tension resulted from the fastening torque, so that the principal stresses and hence the mean stresses may generally have positive values. This leaves a detrimental effect on the fatigue properties which was not evident in the Von Mises stress approach. In Figure 17, the life prediction is illustrated via different theories using the principal stresses method.
According to Figure 17, it is evident that there was a big discrepancy between the calculated life via the Von Mises approach and those of the principal stress methods. This can be explained by highly detrimental effects of the tensile mean stress on this component. Since, the stress amplitude was limited while the mean value of stress was high, theoretical discrepancy tended to increase. As it is evident from Figure 15, the corresponding curves for the different theories tended to diverge on lower stress amplitude and higher mean values of stress so that for very low stress amplitude, SWT may not predict a fatigue life for any mean value of stress. However, the curves tended to converge for higher stress amplitude and lower values of mean stress with the predicted life being so close to each other. Finally, the acceptable values of the fatigue life would be the ones within the amplitude calculated by the Goodman theory as well as the Gerber and SWT theories, wherein the abutment’s life was predicted to be on full cycle life region.
4. Discussion
According to what is mentioned so far, one may suggest that the abutment is a critical part in terms of the fatigue failure. The fastening torque applied to the abutment would produce some tensile pre-stresses within the abutment. Although such pre-stresses may contribute to the stability of the parts as well as the assembly, they may also lead to a decrease in their fatigue life. The abutment is experienced as a fatigue failure if these pre-stresses remain in its screw. However, if they tend to reduce through the time, an abutment screw loosening would be expectable. Both cases are undesired situations where the patient has no choice, but to refer to the dentist [25,26]. However, in the implant itself, one may observe a concentration of the compression stresses on the edges [14]. Although, these compression stresses may contribute to improve the fatigue characteristics, they may also cause pitting in the neck of the implant.
Clinical and radiological results presented in Nergiz et al. have indicated that the failure which occurred in the osseointegration state at the abutment screw would lead the abutment screw to stick inside the implant [25]. The results reported that the failure occurred nine months after the complete osseointegration. Knowing that a human applies in average, 450 mastication cycles per 24 h [22], the results of Nergiz et al. have reported an average of 1.2 × 105 cycles before an abutment fails [25]. The radiographic image clearly shows that the ossification is well developed around the implant and no separation is seen at the interface between the implant and the bone; one may see that the abutment is failed at the first thread, so that the abutment screw has stuck inside the implant [25]. The numerical results had also predicted the failure to be occurred at the first thread, as shown in Figure 8. According to this analysis, the abutment fails at the first thread with the abutment screw being stuck inside the implant. The fatigue life is obtained based on the stresses applied at these points. Abutment failure is as common as some specific tools have been developed to extract the abutment from the implant interior [25].
The results obtained from this clinical report are in good agreement with those obtained from the Goodman theory which had predicted the implant life to be about 3 × 105 cycles. In 2008, Theoharidou et al. collected different information from literature and clinical reports to estimate an average interval of from 3 to 10 years between successive referral of the patients with ITI implant to the dentists, given these referrals are due to the problems with the abutments [26]. In Table 5, the life values obtained from the present numerical analysis as well as the fatigue life based on Goodman theory are compared with the clinical data.

Table 5.
A comparison between the results obtained from theories with the clinical data.
The predicted results by the Goodman theory (Figure 17) are in a very good accordance with the clinical data. Thus, it can be concluded that the Goodman theory is in the most agreement with the clinical data in terms of abutment screw’s life prediction, while the other theories (Figure 16 and Figure 17) predicted somehow longer life for the abutment. The results by the Goodman theory exhibits more sensitivity to the variations of the mean stress; since high mean stress is thought to be the main cause of failure in an abutment, one may suggest that the life predictions by the Goodman theory are more accurate and closer to the clinical observations.
5. Conclusions
Fracture of the abutment can be a serious problem as the fragment remaining inside the implant may prevent the implant from functioning efficiently. In this study, using a 3D model and FE code, the stress distribution in implant components and bones as well as the fatigue life of the abutment and the implant are investigated. The results indicate that:
- Among the entire assembly, the abutment is a critical component which is prone to the fatigue failure due to the tensile stresses resulted from the fastening torque.
- For the bones, the maximum stress is concentrated on the region around the top of implant neck. The maximum stress in the cortical bone is higher than that in the cancellous bone.
- Generally speaking, mechanical stresses developed within an implant are compression, which although contribute to a better fatigue life, they also increase the probability of detachment of upper parts of the implant when mastication forces and corresponding compression stresses are present.
- According to the results of the fatigue life prediction, the abutment screw may fail after about 3 × 105 cycles. Such a failure is likely to occur at the first thread. These results are obtained from the Goodman theory and are at a very good agreement with the clinical data.
Author Contributions
The authors have participated in the preparation of the manuscript, and have given their permission to submit this manuscript with its present format. Conceptualization, B.Z. and S.M.R.K.; data curation, B.Z.; formal analysis, B.Z.; investigation, B.Z. and S.M.R.K.; methodology, B.Z. and S.M.R.K.; software, B.Z.; supervision, S.M.R.K.; validation, B.Z.; writing—original draft, B.Z.; writing—review and editing, S.M.R.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
There is no conflicts of interest regarding the publication of this paper.
References
- Branemark, P.I.; Hansson, B.O.; Adell, R.; Breine, U.; Lindström, J.; Hallén, O.; Ohman, A. Osseointegrated implants in the treatment of the edentulous jaw. Experience from a 10-year period. Scand. J. Plastreconstr. Surg. Suppl. 1997, 16, 1–132. [Google Scholar]
- Akpinar, I.; Demirel, F.; Parnas, L.; Sahin, S. A comparison of stress and strain distribution characteristics of two different rigid implant designs for distal-extension fixed prostheses. Quintessence Int. 1996, 27, 11–17. [Google Scholar] [PubMed]
- Holmgren, E.P.; Seckinger, R.J.; Kilgren, L.M.; Mante, F. Evaluating parameters of osseointegrated dental implants using finite element analysis—A two dimensional comparative study examining the effects of implant diameter, implant shape, and load direction. J. Oral Implantol. 1998, 24, 80–88. [Google Scholar] [CrossRef]
- Nagasao, T.; Kobayashi, M.; Tsuchiya, Y.; Kaneko, T.; Nakajima, T. Finite element analysis of the stresses around fixtures in various reconstructed mandibular models. J. Craniomaxillofac. Surg. 2003, 31, 168–175. [Google Scholar] [CrossRef]
- Van Staden, R.C.; Guan, H.; Loo, Y.-C. Application of the finite element method in dental implant research. Comput. Methods Biomech. Biomed. Eng. 2006, 9, 257–270. [Google Scholar] [CrossRef] [Green Version]
- Edwards Rezende, C.E.; Chase-Diaz, M.; Costa, M.D.; Albarracin, M.L.; Paschoeto, G.; Capello Sousa, E.A.; Rubo, J.H.; Sanches Borges, A.F. Stress distribution in single dental implant system: Three-Dimensional finite element analysis based on an in vitro experimental model. J. Craniofac. Surg. 2015, 26, 2196–2200. [Google Scholar] [CrossRef] [PubMed]
- Kanneganti, K.C.; Vinnakota, D.N.; Pottem, S.R.; Pulagam, M. Comparative effect of implant abutment connections, abutment angulations, and screw lengths on preloaded abutment screw using three dimensional finite element analysis: An in vitro stud. J. Indian Prosthodont. Soc. 2018, 18, 161–167. [Google Scholar] [PubMed]
- Oh, J.-H.; Kim, Y.-S.; Lim, J.Y.; Choi, B.-H. Stress Distribution on the Prosthetic Screws in the All-on-4 Concept: A Three-Dimensional Finite Element Analysis. J. Oral Implant. 2020, 46, 3–12. [Google Scholar] [CrossRef]
- Chikr, Y.C.; Merdji, A.; Gouasmi, S. Effects of the geometric parameters on the interfacial stresses bone/implant. Nat. Technol. 2020, 22, 20–29. [Google Scholar]
- Himmlová, L.; Dostálová, T.; Kácovský, A.; Konvicčková, S. Influence of implant length and diameter on stress distribution: A finite element analysis. J. Prosthet. Dent. 2004, 91, 20–25. [Google Scholar] [CrossRef]
- Paracchini, L.; Barbieri, C.; Redaelli, M.; Di Croce, D.; Vincenzi, C.; Guarnieri, R. Finite Element Analysis of a New Dental Implant Design Optimized for the Desirable Stress Distribution in the Surrounding Bone Region. Prosthesis 2020, 2, 19. [Google Scholar] [CrossRef]
- Burgoa-la-Forcada, S.M.; Edwards Rezende, C.; Castiglia Gonzaga, C.; Cesar Zielak, J.; Yoshio Furuse, A. Photoelastic analysis of dynamic stress distribution around short implants restored with different materials. J. Osseointegr. 2018, 10, 44–49. [Google Scholar]
- Arinc, H. Effects of Prosthetic Material and Framework Design on Stress Distribution. Med. Sci. Monit. 2018, 24, 4279–4287. [Google Scholar] [CrossRef]
- Kayabaşı, O.; Yuzbasioglu, E.; Erzincanlı, F. Static, dynamic and fatigue behaviors of dental implant using finite element method. Adv. Eng. Softw. 2006, 37, 649–658. [Google Scholar] [CrossRef]
- Kong, L.; Zhao, Y.; Hu, K.; Li, D.; Zhou, H.; Wu, Z.; Liu, B. Selection of the implant thread pitch for optimal biomechanical properties: A three-dimensional finite element analysis. Adv. Eng. Softw. 2009, 40, 474–478. [Google Scholar] [CrossRef]
- Ao, J.; Li, T.; Liu, Y.; Ding, Y.; Wu, G.; Hu, K.; Kong, L. Optimal design of thread height and width on an immediately loaded cylinder implant: A finite element analysis. Comput. Biol. Med. 2009, 40, 681–686. [Google Scholar] [CrossRef]
- Oliveira, H.; Brizuela Velasco, A.; Ríos-Santos, J.V.; Sánchez Lasheras, F.; Lemos, B.F.; Gil, F.J.; Carvalho, A.; Herre-ro-Climent, M. Effect of Different Implant Designs on Strain and Stress Distribution under Non-Axial Loading: A Three-Dimensional Finite Element Analysis. Int. J. Environ. Res. Public Health 2020, 17, 4738. [Google Scholar] [CrossRef] [PubMed]
- Sevimay, M.; Turhan, F.; Kılıçarslan, M.A.; Eskitascioglu, G. Three-dimensional finite element analysis of the effect of different bone quality on stress distribution in an implant-supported crown. J. Prosthet. Dent. 2005, 93, 227–234. [Google Scholar] [CrossRef]
- Nesappan, T.; Ariga, P. Comparison of Stresses around Dental Implants Placed in Normal and Fibula Reconstructed Mandibular Models using Finite Element Analysis. J. Clin. Diagn. Res. 2014, 8, ZC45–ZC50. [Google Scholar] [CrossRef]
- Huang, H.L.; Hsu, J.T.; Fuh, L.J.; Lin, D.J.; Chen, M.Y.C. Biomechanical simulation of various surface rough-nesses and geometric designs on an immediately loaded dental implant. Comput. Biol. Med. 2010, 40, 525–532. [Google Scholar] [CrossRef]
- Merdji, A.; BachirBouiadjra, B.; Achour, T.; Serier, B.; OuldChikh, B.; Feng, Z.O. Stress analysis in dental prosthesis. Comput. Mater. Sci. 2010, 49, 126–133. [Google Scholar] [CrossRef]
- Ilieş, H.T.; Flanagan, D.; McCullough, P.T.; McQuoid, S. Determining the Fatigue Life of Dental Implants. J. Med. Devices 2008, 2, 011003. [Google Scholar] [CrossRef] [Green Version]
- Gibbs, C.H.; Anusavice, K.J.; Young, H.M.; Jones, J.S.; Esquivel Upshaw, J.F. Maximum Clenching Force of Patients with Moderate Loss of Posterior Tooth Support: A Pilot Study. J. Prosthet Dent. 2002, 88, 498–502. [Google Scholar] [CrossRef]
- Wierszycki, M.; Kakail, W.; Lodygowski, T. Fatigue algorithm for dental implant. Found. Civ. Environ. Eng. 2006, 7, 363–380. [Google Scholar]
- Nergiz, I.; Schmage, P.; Shahin, R. Removal of a fractured implant abutment screw: A clinical report. J. Prosthet. Dent. 2004, 91, 513–517. [Google Scholar] [CrossRef]
- Theoharidou, A.; Petridis, H.P.; Tzannas, K.; Garefis, P. Abutment screw loosening in single-implant restorations: A systematic review. Int. J. Oral Maxillofac. Implant. 2008, 23, 681–690. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).