Fluid-Structure Interaction Analysis of Subject-Specific Mitral Valve Regurgitation Treatment with an Intra-Valvular Spacer
Abstract
:1. Introduction
2. Materials and Methods
2.1. Model Development
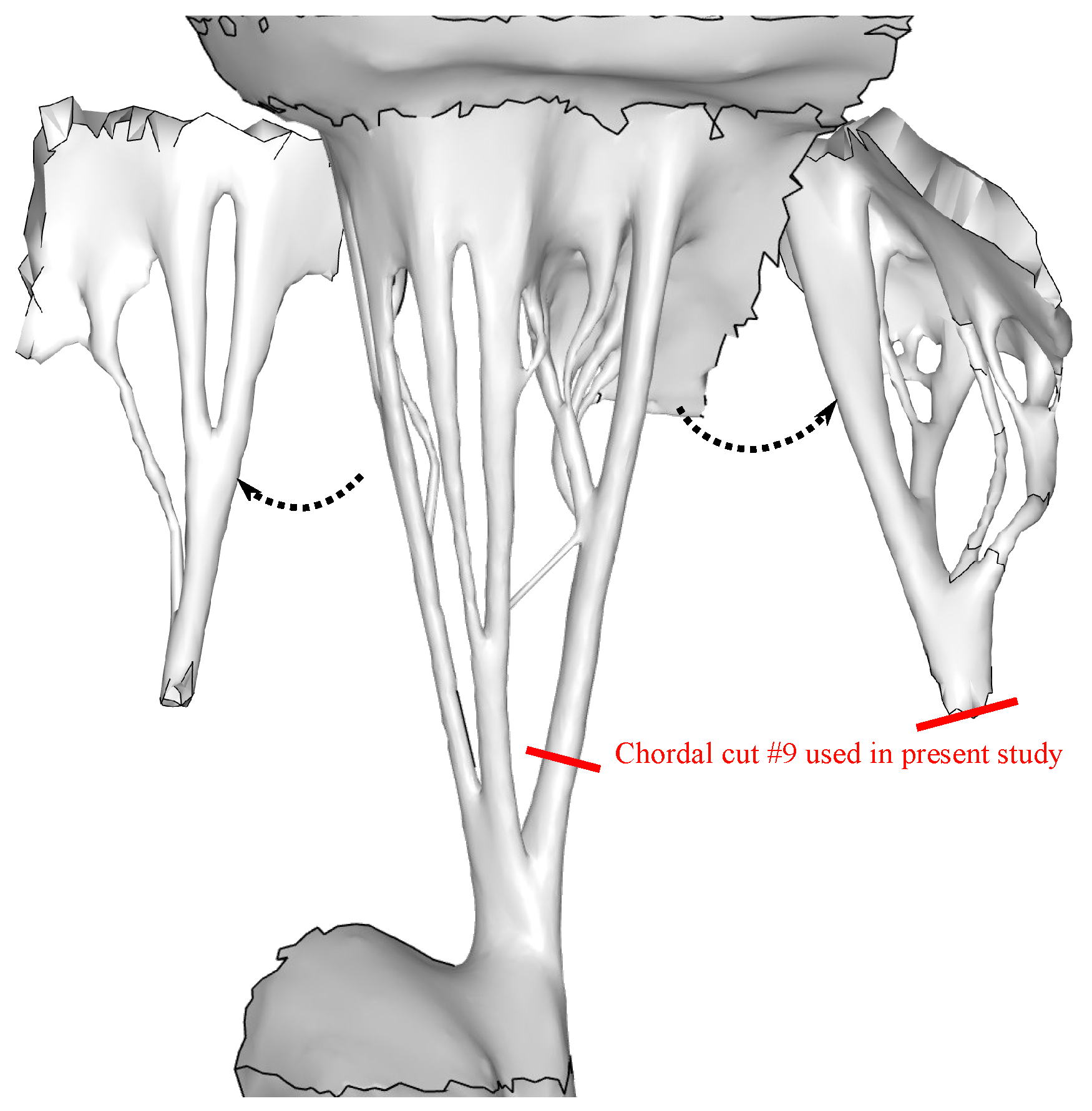
2.2. Fiber Orientation
2.3. Constitutive Model
2.4. Numerical Methods
2.5. Application to Assessment of Spacer Efficacy
3. Results
4. Discussion
5. Limitations and Future Work
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| MR | Mitral Regurgitation |
| DMR | Degenerative Mitral Regurgitation |
| FMR | Functional Mitral Regurgitation |
| FDA | Food and Drug Administration |
| MV | Mitral Valve |
| FSI | Fluid-Structure Interaction |
| ROA | Regurgitant Orifice Area |
| CT | Micro-Computed Tomography |
| SPH | Smoothed Particle Hydrodynamics |
| GPU | Graphics Processing Unit |
| 3D | Three-Dimensional |
| 1D | One-Dimensional |
References
- Statistical Abstract of the U.S., 125th Edition, Section 3: Health and Nutrition, Table 158; U.S. Census Bureau: Washington, DC, USA, 2006.
- Mirabel, M.; Iung, B.; Baron, G.; Messika-Zeitoun, D.; Detaint, D.; Vanoverschelde, J.L.; Butchart, E.G.; Ravaud, P.; Vahanian, A. What are the characteristics of patients with severe, symptomatic, mitral regurgitation who are denied surgery? Eur. Heart J. 2007, 28, 1358–1365. [Google Scholar] [CrossRef] [Green Version]
- Svensson, L.G.; Ye, J.; Piemonte, T.C.; Kirker-Head, C.; Leon, M.B.; Webb, J.G. Mitral valve regurgitation and left ventricular dysfunction treatment with an intravalvular spacer. J. Card. Surg. 2015, 30, 53–54. [Google Scholar] [CrossRef]
- Kunzelman, K.S.; Cochran, R.P.; Chuong, C.J.; Ring, W.S.; Verier, E.D.; Eberhart, R.C. Finite element analysis of the mitral valve. J. Heart Valve Dis. 1993, 2, 326–340. [Google Scholar]
- Kunzelman, K.S.; Cochran, R.P.; Verrier, E.D.; Chuong, C.J.; Ring, W.S.; Eberhart, R.C. Finite element analysis of mitral valve pathology. J. Long Term Eff. Med. Implants 1993, 3, 161–179. [Google Scholar]
- Kunzelman, K.S.; Reimink, M.S.; Cochran, R.P. Annular dilatation increases stress in the mitral valve and delays coaptation: A finite element computer model. Cardiovasc. Surg. 1997, 5, 427–434. [Google Scholar] [CrossRef]
- Kunzelman, K.S.; Reimink, M.S.; Cochran, R.P. Flexible versus rigid ring annuloplasty for mitral valve annular dilation: A finite element model. J. Heart Valve Dis. 1998, 7, 108–116. [Google Scholar]
- Cochran, R.P.; Kunzelman, K.S. Effect of papillary muscle position on mitral valve function: Relationship to mitral homografts. Ann. Thorac. Surg. 1998, 66, S155–S161. [Google Scholar] [CrossRef]
- Reimink, M.S.; Kunzelman, K.S.; Verrier, E.D.; Cochran, R.P. The effect of anterior chordal replacement on mitral valve function and stresses. ASAIO Trans. 1995, 41, M754–M762. [Google Scholar] [CrossRef]
- Kunzelman, K.; Reimink, M.S.; Verrier, E.D.; Cochran, R.P. Replacement of mitral valve posterior chordae tendineae with expanded polytetrafluoroethylene suture: A finite element study. J. Card. Surg. 1996, 11, 136–145. [Google Scholar] [CrossRef] [PubMed]
- Reimink, M.S.; Kunzelman, K.S.; Cochran, R.P. The effect of chordal replacement suture length on function and stresses in repaired mitral valves: A finite element study. J. Heart Valve Dis. 1996, 5, 365–375. [Google Scholar]
- Einstein, D.R.; Reinhall, P.G.; Kunzelman, K.S.; Cochran, R.P. Nonlinear finite element analysis of the mitral valve. J. Heart Valve Dis. 2005, 3, 376–385. [Google Scholar]
- Einstein, D.R.; Kunzelman, K.S.; Reinhall, P.G.; Nicosia, M.A.; Cochran, R.P. The relationship of normal and abnormal microstructural proliferation to the mitral valve closure sound. Trans. ASME 2005, 127, 134–147. [Google Scholar] [CrossRef] [PubMed]
- Kunzelman, K.S.; Einstein, D.R.; Cochran, R.P. Fluid–structure interaction models of the mitral valve: Function in normal and pathological states. Philos. Trans. R. Soc. B 2007, 362, 1393–1406. [Google Scholar] [CrossRef] [Green Version]
- Einstein, D.R.; Del Pin, F.; Jiao, X.; Kuprat, A.P.; Carson, J.P.; Kunzelman, K.S.; Cochran, R.P.; Guccione, J.M.; Ratcliffe, M.B. Fluid-structure interactions of the mitral valve and left heart: Comprehensive strategies, past, present, and future. Int. J. Numer. Methods Biomed. Eng. 2010, 26, 348–380. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Toma, M.; Jensen, M.A.; Einstein, D.R.; Yoganathan, A.P.; Cochran, R.P.; Kunzelman, K.S. Fluid-structure interaction analysis of papillary muscle forces using a comprehensive mitral valve model with 3D chordal structure. Ann. Biomed. Eng. 2016, 44, 942–953. [Google Scholar] [CrossRef] [Green Version]
- Chandran, K.B.; Kim, H. Computational mitral valve evaluation and potential clinical applications. Ann. Biomed. Eng. 2015, 43, 1348–1362. [Google Scholar] [CrossRef] [Green Version]
- Rim, Y.; Laing, S.T.; McPherson, D.D.; Kim, H. Mitral valve repair using ePTFE sutures for ruptured mitral chordae tendineae: A computational simulation study. Ann. Biomed. Eng. 2014, 42, 139–148. [Google Scholar] [CrossRef]
- Mansi, T.; Voigt, I.; Georgescu, B.; Zheng, X.; Mengue, E.A.; Hackl, M.; Ionasec, R.I.; Noack, T.; Seeburger, J.; Comaniciu, D. An integrated framework for finite-element modeling of mitral valve biomechanics from medical images: Application to mitralclip intervention planning. Med. Image Anal. 2012, 16, 1330–1346. [Google Scholar] [CrossRef]
- Schievano, S.; Kunzelman, K.; Nicosia, M.A.; Cochran, R.P.; Einstein, D.R.; Khambadkone, S.; Bonhoeffer, P. Percutaneous mitral valve dilatation: Single balloon versus double balloon. A finite element study. J. Heart Valve Dis. 2009, 18, 28–34. [Google Scholar]
- Wenk, J.F.; Zhang, Z.; Cheng, G.; Malhotra, D.; Acevedo-Bolton, G.; Burger, M.; Suzuki, T.; Saloner, D.A.; Wallace, A.W.; Guccione, J.M.; et al. First finite element model of the left ventricle with mitral valve: Insights into ischemic mitral regurgitation. Ann. Thorac. Surg. 2010, 89, 1546–1553. [Google Scholar] [CrossRef] [Green Version]
- Maisano, F.; Redaelli, A.; Soncini, M.; Votta, E.; Arcobasso, L.; Alfieri, O. An annular prosthesis for the treatment of functional mitral regurgitation: Finite element model analysis of a dog bone–shaped ring prosthesis. Ann. Thorac. Surg. 2005, 79, 1268–1275. [Google Scholar] [CrossRef] [PubMed]
- Stevanella, M.; Maffessanti, F.; Conti, C.A.; Votta, E.; Arnoldi, A.; Lombardi, M.; Parodi, O.; Caiani, E.G.; Redaelli, A. Mitral valve patient-specific finite element modeling from cardiac MRI: Application to an annuloplasty procedure. Cardiovas. Eng. Technol. 2011, 2, 66–76. [Google Scholar] [CrossRef] [Green Version]
- Lau, K.D.; Diaz, V.; Scambler, P.; Burriesci, G. Mitral valve dynamics in structural and fluid–structure interaction models. Med. Eng. Phys. 2010, 32, 1057–1064. [Google Scholar] [CrossRef] [PubMed]
- Bloodworth, C.H.; Pierce, E.L.; Easley, T.F.; Drach, A.; Khalighi, A.H.; Toma, M.; Jensen, M.O.; Sacks, M.S.; Yoganathan, A.P. Ex Vivo methods for informinig computational models of the mitral valve. Ann. Biomed. Eng. 2017, 45, 496–507. [Google Scholar] [CrossRef] [Green Version]
- Toma, M.; Bloodworth, C.H.; Einstein, D.R.; Pierce, E.L.; Cochran, R.P.; Yoganathan, A.P.; Kunzelman, K.S. High-resolution subject-specific mitral valve imaging and modeling: Experimental and computational methods. Biomech. Model. Mechanobiol. 2016, 15, 1619–1630. [Google Scholar] [CrossRef]
- Toma, M.; Einstein, D.R.; Bloodworth, C.H., IV; Cochran, R.P.; Yoganathan, A.P.; Kunzelman, K.S. Fluid–structure interaction and structural analyses using a comprehensive mitral valve model with 3d chordal structure. Int. J. Numer. Methods Biomed. Eng. 2017, 33, e2815. [Google Scholar] [CrossRef] [Green Version]
- Rabbah, J.P.; Saikrishnan, N.; Yoganathan, A.P. A novel lef heart simulator for the multi-modality characterization of native mitral valve geometry and fluid mechanics. Ann. Biomed. Eng. 2013, 41, 305–315. [Google Scholar] [CrossRef] [PubMed]
- Carson, J.P.; Kuprat, A.P.; Jiao, X.; Dyedov, V.; Del Pin, F.; Guccione, J.M.; Ratcliffe, M.B.; Einstein, D.R. Adaptive generation of multimaterial grids from imaging data for biomedical Lagrangian fluid-structure simulations. Biomech. Model. Mechanobiol. 2010, 9, 187–201. [Google Scholar] [CrossRef] [Green Version]
- Toma, M.; Bloodworth, C.H.; Pierce, E.L.; Einstein, D.R.; Cochran, R.P.; Yoganathan, A.P.; Kunzelman, K.S. Fluid-structure interaction analysis of ruptured mitral chordae tendineae. Ann. Biomed. Eng. 2017, 45, 619–631. [Google Scholar] [CrossRef] [PubMed]
- Freed, A.; Einstein, D.; Vesely, I. Invariant formulation for dispersed transverse isotropy in aortic heart valves: An efficient means for modeling fiber splay. Biomech. Model. Mechanobiol. 2005, 4, 100–117. [Google Scholar] [CrossRef]
- Toma, M.; Oshima, M.; Takagi, S. Decomposition and parallelization of strongly coupled fluid-structure interaction linear subsystems based on the Q1/P0 discretization. Comput. Struct. 2016, 173, 84–94. [Google Scholar] [CrossRef]
- Toma, M.; Nguyen, P.D. Coup-contrecoup brain injury: Fluid-structure interaction simulations. Int. J. Crashworthiness 2020, 25, 175–182. [Google Scholar] [CrossRef]
- Grinberg, A.R.; Finkielman, J.D.; Piñeiro, D.; Festa, H.; Cazenave, C. Rupture of mitral chorda tendinae following blunt chest trauma. Clin. Cardiol. 1998, 21, 300–301. [Google Scholar] [CrossRef]
- Portugese, S.; Amital, H.; Tenenbaum, A.; Bar-Dayan, Y.; Levy, Y.; Afek, A.; Shemesh, J.; Shoenfeld, Y. Clinical characteristics of ruptured chordae tendineae in hospitalized patients: Primary tear versus infective endocarditis. Clin. Cardiol. 1998, 21, 813–816. [Google Scholar] [CrossRef] [PubMed]
- Anderson, Y.; Wilson, N.; Nicholson, R.; Finucane, K. Fulminant mitral regurgitation due to ruptured chordae tendinae in acute rheumatic fever. J. Paediatr. Child Health 2008, 44, 134–137. [Google Scholar] [CrossRef]
- Kaymaz, C.; Özdemir, N.; Özkan, M. Differentiating clinical and echocardiographic characteristics of chordal rupture detected in patients with rheumatic mitral valve disease and floppy mitral valve: Impact of the infective endocarditis on chordal rupture. Eur. J. Echocardiogr. 2005, 6, 117–126. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gabbay, U.; Yosefy, C. The underlying causes of chordae tendinae rupture: A systematic review. Int. J. Cardiol. 2010, 143, 113–118. [Google Scholar] [CrossRef] [PubMed]
- Amberg, B.; Romdhani, S.; Vetter, T. Optimal step nonrigid icp algorithms for surface registration. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition CVPR’07, Minneapolis, MN, USA, 17–22 June 2007; pp. 1–8. [Google Scholar]






© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Toma, M.; Einstein, D.R.; Bloodworth, C.H., IV; Kohli, K.; Cochran, R.P.; Kunzelman, K.S.; Yoganathan, A.P. Fluid-Structure Interaction Analysis of Subject-Specific Mitral Valve Regurgitation Treatment with an Intra-Valvular Spacer. Prosthesis 2020, 2, 65-75. https://doi.org/10.3390/prosthesis2020007
Toma M, Einstein DR, Bloodworth CH IV, Kohli K, Cochran RP, Kunzelman KS, Yoganathan AP. Fluid-Structure Interaction Analysis of Subject-Specific Mitral Valve Regurgitation Treatment with an Intra-Valvular Spacer. Prosthesis. 2020; 2(2):65-75. https://doi.org/10.3390/prosthesis2020007
Chicago/Turabian StyleToma, Milan, Daniel R. Einstein, Charles H. Bloodworth, IV, Keshav Kohli, Richard P. Cochran, Karyn S. Kunzelman, and Ajit P. Yoganathan. 2020. "Fluid-Structure Interaction Analysis of Subject-Specific Mitral Valve Regurgitation Treatment with an Intra-Valvular Spacer" Prosthesis 2, no. 2: 65-75. https://doi.org/10.3390/prosthesis2020007
APA StyleToma, M., Einstein, D. R., Bloodworth, C. H., IV, Kohli, K., Cochran, R. P., Kunzelman, K. S., & Yoganathan, A. P. (2020). Fluid-Structure Interaction Analysis of Subject-Specific Mitral Valve Regurgitation Treatment with an Intra-Valvular Spacer. Prosthesis, 2(2), 65-75. https://doi.org/10.3390/prosthesis2020007





