Abstract
Due to the important role of quantum information technology in the future development of science and technology, researchers have extensively studied the preparation, characterization, and application of quantum systems. It is of great significance to further study the universality and generalization of multi-qubit entangled states. Especially in quantum communication, the actual quantum system is always affected by various noises from the environment. Noise has a significant impact on the properties of the actual quantum system, so we study the effects of noise on a prepared two-photon four-qubit state by two methods. We experimentally simulated the most common bit-flip noise in quantum systems. The law of evolution of the fidelity of two-dimensional four-qubit states and violation of the Mermin inequality and the Ardehali inequality for LR under different levels of bit-flip noise are investigated. The experimental results show that entanglement fidelity and nonlocality can be used to judge the degree of noise interference in the quantum channel and, thus, judge the security of the quantum communication channel. This judgment is of great significance for the realization of practical long-distance multi-node quantum communication.
1. Introduction
Entanglement, a unique quantum mechanical phenomenon, has become a valuable resource without any classical equivalent. Deepening the study of many-body quantum systems is important for a better understanding of the relationship between classical and quantum physics [1,2,3]. Meanwhile, multipartite entangled states are also important resources for applications in quantum information processing. Some examples include quantum computing [4,5,6], quantum metrology [7,8], quantum teleportation [9,10,11,12], entanglement swapping [13,14], quantum key distribution (QKD) protocols [15,16], quantum secret sharing (QSS) [17,18], and quantum secure communication (QSC) [19,20]. In the past decade, people have conducted a lot of theoretical and experimental research on the preparation and manipulation of more qubits. At the same time, researchers have found that multi-qubit entanglement systems based on polarization entanglement photons have good controllability and application value [21]. Spontaneous parametric down conversion (SPDC) can be generated by a short-wave laser pulse incident into a nonlinear crystal, which can produce entangled photon pairs [22,23]. In this process, these photon pairs are correlated in the required degree of freedom such as polarization, orbital angular momentum (OAM), energy, and time. Among these degrees of freedom, we can determine the degree of correlation between photons by measuring the photon’s polarization state. However, there are many challenges involved in the preparation and characterization of multipartite entangled states. In order to meet more research needs, scientists are still trying to explore more particle numbers of entanglement schemes. In particular, the Greenberger–Horne–Zeilinger (GHZ) state is the most extensively studied system for the investigation of the interaction between parts of a complex many-body system [24]. For example, the realization of the GHZ state negates the view of Einstein–Podolsky–Rosen (EPR) quantum mechanical correlation local realism [25].
Quantum nonlocality is one of the most striking aspects of quantum mechanics without a classical analog in reality. It can be characterized as correlated outcomes when we measure multipartite entangled quantum states. The EPR paradox is the contradiction between the nonlocality of quantum correlation and the local realism in the understanding of the completeness of quantum mechanics [26]. Based on the two-particle system, Bell proposed an inequality to determine the locality and nonlocality of the system [27]. Later, Clauser, Horne, Shimony, and Holt (CHSH) further optimized Bell’s inequality and proposed the CHSH inequality that can be experimentally measured [28]. Bell’s inequality and the CHSH inequality can judge whether there is nonlocality in a many-body system and give a measurable physical quantity that describes nonlocality. The Mermin inequality is the measurable form of Bell’s inequality generalized to more particles [29]. Theoretical and experimental studies show that these inequalities are confirmed in the pure GHZ entangled state [30]. Experimental verification of the Mermin inequality for a system of n-particles requires measurements on n-particles, which is difficult to implement. Ardehali simplified Bell’s inequality and derived the Bell-type inequality for the n-particle GHZ state more conveniently for experimental verification [31]. The values of the Pauli operators measured in different projection directions can verify the Mermin inequality and the Ardehali inequality [32,33,34]. Theoretical and experimental investigations have proven that the inequalities of the violation of LR are sufficient conditions to determine whether there is entanglement in a many-body system. Moreover, the greater the degree of violation of LR, the stronger the entanglement between particles. These results are of great importance not only in quantum theoretical research but also in quantum information applications, such as improving dense coding and determining the security of teleportation [9,10].
In a realistic environment, different types of noise will couple into the entangled system, and the pure entangled state will evolve into a mixed state, which will lead to a decrease or failure in quantum information processing [35]. However, due to the complexity of the noise in the entangled system, there are few experimental studies on the influence of noise on the robustness of a multipartite system or multipartite systems. Fortunately, the Bell-type inequality, which can be experimentally measured, provides an experimental method to measure the influence of entanglement on the noise robustness. Therefore, it is of great theoretical significance and application value to further experimentally study the influence of noise on the robustness of Bell-type inequalities in multi-particle entangled systems [36].
In this work, motivated by further understanding the dissipation of multi-qubit entangled states in practical applications, the influence of bit-flip noise on violation of the Mermin inequality and Ardehali inequality against the LR in two-photon four-qubit hyper-entangled states was studied. As a basis for further research, we prepared a two-photon entangled pair with a high fidelity of 0.99 by SPDC technology, designed an interferometer that can couple the polarization and spatial path of a photon, and prepared two-photon four-qubit GHZ hyper-entangled states for the polarization and spatial path of photons. By using the heralded detection and post-selection technique, a two-photon four-qubit GHZ hyper-entangled state for photon polarization and spatial path was prepared. Furthermore, a common bit-flip noise in the simulation of quantum information processes was constructed by using linear optical devices such as a half-wave plate (HWP) and a quarter-wave plate (QWP). Finally, we experimentally investigated the evolution law of the fidelity of the two-photon four-qubit hyper-entangled state and the violation of the Mermin and the Ardehali inequality to LR under different bit-flip noise levels.
2. The Mermin Inequality and Ardehali Inequality of a Four-Qubit Entangled State
For two particles A and B, which are completely spatially separated, Alice chooses operator and to measure one particle while Bob chooses operator and to measure the other. The choices are random. () and () are the eigenvalues of the operators () and (), respectively. The joint probability can be obtained when Alice and Bob measure two photons of the entangled system synchronously.
When two photons in an entangled state are measured simultaneously by Alice and Bob, the joint measurement probability can be calculated as
For two-particle entangled states , we can measure the probability of the joint operation , , , independently. According to LR theory, the Bell-type inequality is written in the following form:
But according to the theory of quantum mechanics, the particles measured jointly by Alice and Bob have nonlocal correlations [37]. The maximum expectation value of the CHSH operator in the quantum system of maximum correlation is . This bound is known as Tsirelson’s bound [38]. The measurement results between 2– are the violation of quantum nonlocality against local realism. It is known that all two qubit pure states violate the bipartite Bell-type inequality (BTI), namely, the CHSH inequality [39]. In addition, as the degree of entanglement between particles increases, so does the violation of the inequality [40]. The violation against LR for multipartite entangled systems can be detected by using the Mermin inequality [29]. We can generalize the Bell inequality from a two-particle system to more particles. The multiparticle Mermin inequality can be recursively defined by a general rule [41,42].
Here, the operators can be obtained from upon changing → and →. and are mutually exclusive measurements performed on any particle of entangled particles (with = 1, …, n). Ideally, the results of these measurements are ±1. The operators may be represented by , where () are the Pauli matrices. According to the quantum ideal theory, the Mermin inequality has the maximum value, which is given by the following inequality:
For the four-qubit entangled system studied in this paper, the Mermin inequality can be written as:
with a classical bound of and a quantum bound of .
Ardehali [31] promoted the Bell-type inequality for the GHZ state of n-particles that can be directly measured in the experiment. Consider an -particle GHZ state , where and are the horizontal and vertical polarization of the particle. According to the assumption of quantum mechanical principles, the nonlocal nature of a quantum system can be described by an operator .
and
where and are defined as and , respectively. and are the Pauli operators, which are experimentally measured in +/− and R/L bases, respectively, with , , , and . Using the generalized CHSH lemma [28], one can obtain the upper bound on the operator from LR theory [31].
In comparison, the expected value of according to the standard rules of QM is calculated as
When n is odd and even, the values predicted by quantum theory exceed the limits given by LR theory are and , respectively. The results of quantum mechanics theory and the local realistic theory predict the Ardehali inequality, respectively.
The bit flip noise often appears in quantum systems, with probability flipping the state of a quantum bit from to or from to . It is obvious that the intensity of the bit-flip noise introduced into the quantum system can be expressed by .
The flipped noise operator is usually expanded into the form of the Kraus operator using the Pauli operator [43].
where is the identity matrix in the Hilbert space of the qubits. The action of the bit-flip noise described by the density matrix on any quantum bit is
For four-qubit GHZ states with bit-flip noise, the density matrix is given by
By using a linear optical device consisting of a half-wave plate and two quarter-wave plates, a bit-flip noise generation device [44] (see Figure 1) is composed to emulate the quantum channel with bit-flip noise. When the HWP switches angle , the angles of HWP and QWP are both relative to the direction of their respective crystal optical axes. We can then simulate a quantum channel with a bit flip noise of strength in the experiment.
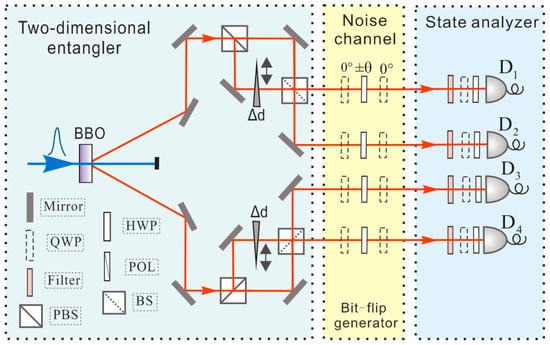
Figure 1.
Schematic diagram of the experimental system. The average power of the ultraviolet laser filtered by the filter after mixing the infrared laser is 100 mW. Interference rings composed of PBS, BS, mirrors, and quartz plates produce a hyper-entangled state. A bit-flit noise simulator is composed of a half-wave plate and a quarter-wave plate.
The fidelity of the GHZ state can be calculated by using the target state tomography method [45]. Each particle of this GHZ state is subjected by the flip operation with probability on each qubit .
3. Preparation and Characterization of Two-Photon Four-Qubit Hyper-Entangled States
In the experiment, we used the SPDC technique of type-II nonlinear process in a β-barium borate (BBO) crystal and ring interferometer. This interferometer can couple the polarization mode and the spatial path mode of the photons. Thus, a two-photon four-qubit GHZ hyper-entangled state was prepared [46]. Using the target state density matrix to describe the fine structure of the prepared quantum state, the addition of noise, the GHZ state was measured, and data was taken for each prepared state under the three sets of orthogonal measurement bases, and the density matrix of the four-qubit GHZ hyper-entangled state in the absence of noise was reconstructed, as shown in Figure 2. The fidelity can be calculated as = 0.83 ± 0.01. This confirms with high statistical significance that the GHZ state prepared in our experiment is a strongly entangled four-qubit state. This is because the photon number statistics of a femtosecond laser and the detector counting obey the Poisson distribution. The error of entangled photon measurement and counting in the experiment is obtained from the standard deviation of the Poisson counting statistics of the original measurement counting. For each state, we collected experimental data for 1296 combinations of measured underlying , , and R/L, where and . The main factors affecting the fidelity of the GHZ state in the experiment include the detector efficiency and the double-pair effect in SPDC.
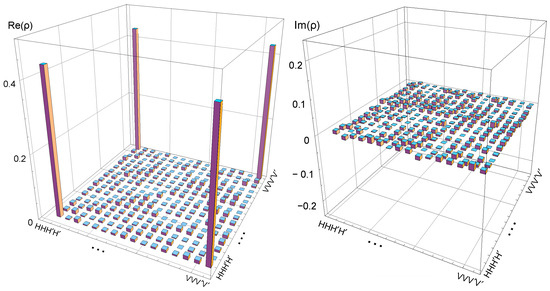
Figure 2.
The density matrix of the two-photon four-qubit GHZ hyper-entangled state was reconstructed using the measured data in the basis. To increase the statistical significance of the data, each group of joint measurements on the , , and bases was 60 s.
4. Impact of Bit-Flip Noise on the Fidelity and Robustness of Entanglement Channels
Firstly, we investigated the influence of channel noise on the quality of entanglement. Different noise intensities in the channel can be simulated by changing the angle of the HWP. From the data in Figure 3, we can clearly see that the channel noise has a direct impact on the entanglement fidelity. With the increase in noise intensity, the entanglement fidelity decreases monotonically. Researchers typically consider a fidelity of less than 0.5 as a threshold for the system not being entangled [47]. When p > 0.12, the fidelity of F < 0.5. We can assert that the entanglement of the entangled channel has disappeared due to the noise. Furthermore, we studied the evolution law of channel robustness with the noise intensity when bit-flip noise is introduced. In the experiment, the noise is changed by changing the angle of the HWP, and the expected values of the Mermin operator and the Ardehali operator vary with different intensities of noise. Figure 4 shows the experimental robustness results of the Mermin inequality and the Ardehali inequality in the presence of different intensities of bit-flip noise. It is clear from the results that the expected values of both the Mermin and the Ardehali operators are greater than the classical bound of 4 when the noise intensity is less than 0.12. The results are consistent with the relationship between the entanglement fidelity and the noise intensity. We can thus assert that entanglement fidelity and nonlocality can be used to judge the degree to which noise in a quantum channel affects the system. That is, the security of a given channel can be judged by the above quantum fidelity and robustness. When the expectation value of the Mermin operator and the Ardehali operator is used as the criterion, a noise intensity of 0.12 can be used as the noise threshold to judge whether the quantum communication channel is safe.
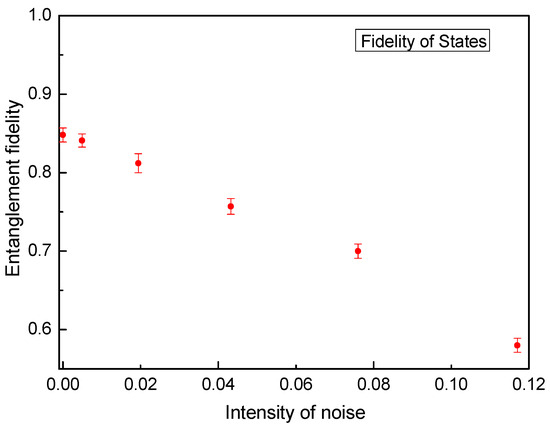
Figure 3.
Experimental results of the entanglement fidelity with different noise intensities. The photon accumulation time for each point is 60 s, repeated three times.
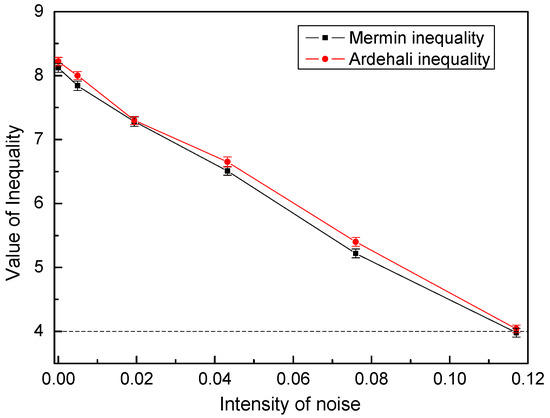
Figure 4.
Experimental values of the Mermin operator and the Ardehali operator varies with different noise. The photon accumulation time for each point is 60 s, repeated three times.
5. Conclusions
In summary, a two-photon four-qubit hyper entangled state was prepared, or an entangled state was prepared by using SPDC technology. The quantum state was measured by quantum tomography under the H/V basis, the +/− basis, and the R/L basis. The density matrix of the prepared hyper-entangled state was reconstructed by quantum state tomography. The fidelity of the quantum state was calculated, and the result was 0.83. Since noise plays an important role in the properties of the actual quantum system, we investigated the effects of noise on the prepared two-photon four-qubit hyper entangled states through two methods. That is, the influences of different intensities of noise on the quantum fidelity and nonlocality were investigated. The experimental results show that the effect of noise on the quantum fidelity and nonlocality, measured by the expectation value of the Mermin operator and the Ardehali operator, is consistent. When the noise intensity is greater than 0.12, the fidelity of the state is less than 0.5. We can assert that the entanglement of the entangled channel disappears due to the noise effect. Meanwhile, the expected value of the Mermin operator and the Ardehali operator is less 4. The conclusion of the study of the effect of different noise intensities on quantum systems by the two methods is consistent. We can assert that entanglement fidelity and nonlocality can be used to judge the degree of influence of noise in quantum channels on the system and, thus, judge the security of quantum communication channels. This judgment is an important step for future practical long-distance multi-node quantum communication. Information security is a prerequisite for the promotion and use of quantum information technology [48].
Author Contributions
Conceptualization and methodology, J.Z., M.W., L.C., Y.Y., X.L. and H.L.; investigation, M.W. and J.Z.; resources, J.Z.; writing—original draft preparation, M.W. and J.Z.; writing—review and editing, H.Q., M.W., Q.Z., K.A.D. and J.Z.; funding acquisition, J.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the Natural Science Foundation of China (grant nos. 62005199, 12204355) and by the Natural Science Foundation of Shandong Province (grant nos. ZR2021LLZ011, ZR2020QA072, ZR2020LLZ001).
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Palazuelos, C. Super-activation of quantum non-locality. Phys. Rev. Lett. 2012, 109, 190401. [Google Scholar] [CrossRef] [PubMed]
- Erhard, M.; Krenn, M.; Zeilinger, A. Advances in high-dimensional quantum entanglement. Nat. Rev. Phys. 2020, 2, 365–381. [Google Scholar] [CrossRef]
- Giustina, M.; Versteegh, M.A.; Wengerowsky, S.; Handsteiner, J.; Hochrainer, A.; Phelan, K.; Steinlechner, F.; Kofler, J.; Larsson, J.; Abellán, C.; et al. Significant-loophole-free test of Bell’s theorem with entangled photons. Phys. Rev. Lett. 2015, 115, 250401. [Google Scholar] [CrossRef]
- Dawson, C.M.; Haselgrove, H.L.; Nielsen, M.A. Noise thresholds for optical quantum computers. Phys. Rev. Lett. 2006, 96, 020501. [Google Scholar] [CrossRef]
- Amico, M.; Dittel, C. Simulation of wave-particle duality in multi-path interferometers on a quantum computer. Phys. Rev. A 2020, 102, 032605. [Google Scholar] [CrossRef]
- Harrow, A.W.; Montanaro, A. Quantum computational supremacy. Nature 2017, 549, 203–209. [Google Scholar] [CrossRef] [PubMed]
- Baak, J.G.; Uwe, R. Fischer Classical and quantum metrology of the Lieb-Liniger model. Phys. Rev. A 2022, 106, 062442. [Google Scholar] [CrossRef]
- Ying, Z.J.; Felicetti, S.; Liu, G. Daniel braak critical quantum metrology in the non-linear quantum rabi model. Entropy 2022, 24, 1015. [Google Scholar] [CrossRef]
- Tittel, W.; Brendel, J.; Zbinden, H.; Gisin, N. Violation of Bell inequalities by photons more than 10 km apart. Phys. Rev. Lett. 1998, 81, 3563–3566. [Google Scholar] [CrossRef]
- Kiktenko, E.O.; Popov, A.A.; Fedorov, A.K. Bidirectional imperfect quantum teleportation with a single Bell state. Phys. Rev. A 2016, 93, 062305. [Google Scholar] [CrossRef]
- Patro, S.; Chakrabarty, I.; Ganguly, N. Non-negativity of conditional von Neumann entropy and global unitary operations. Phys. Rev. A 2017, 96, 062102. [Google Scholar] [CrossRef]
- Lee, S.M.; Lee, S.W.H.; Jeong, H.; Park, H.S. Quantum teleportation of shared quantum secret. Phys. Rev. Lett. 2020, 124, 060501. [Google Scholar] [CrossRef]
- Pan, J.W.; Bouwmeester, D.; Weinfurter, H.; Zeilinger, A. Experimental entanglement swapping: Entangling photons that never interacted. Phys. Rev. Lett. 1998, 80, 3891. [Google Scholar] [CrossRef]
- Agustí, A.; Sabín, C. Non-gaussian entanglement swapping between three-mode spontaneous parametric down conversion and three qubits. Phys. Rev. A 2022, 105, 022401. [Google Scholar]
- Long, G.L.; Liu, X.S. Theoretically efficient high capacity quantum-key-distribution scheme. Phys. Rev. A 2002, 65, 032302. [Google Scholar] [CrossRef]
- Kwek, L.C.; Cao, L.; Luo, W.; Wang, Y.; Sun, S.; Wang, X.; Liu, A.Q. Chip-based quantum key distribution. AAPPS Bull. 2021, 31, 1. [Google Scholar] [CrossRef]
- Hillery, M.; Buzek, V.; Berthiaume, A. Quantum secret sharing. Phys. Rev. A 1999, 59, 1829. [Google Scholar] [CrossRef]
- Ju, X.X.; Zhong, W.; Sheng, Y.B.; Zhou, L. Measurement-device-independent quantum secret sharing with hyper-encoding. Chin. Phys. B 2022, 31, 100302. [Google Scholar] [CrossRef]
- Roy, P.; Bera, S.; Gupta, S.; Majumdar, A.S. Device-independent quantum secure direct communication under non-markovian quantum channels. Quantum Inf Process. 2024, 23, 170–183. [Google Scholar] [CrossRef]
- Zhang, W.; Ding, D.S.; Sheng, Y.B.; Zhou, L.; Shi, B.S.; Guo, G.C. Quantum secure direct communication with quantum memory. Phys. Rev. Lett. 2017, 118, 220501. [Google Scholar] [CrossRef]
- Gühne, O.; Cabello, A. Generalized Ardehali-Bell inequalities for graph states. Phys. Rev. A 2008, 77, 032108. [Google Scholar] [CrossRef]
- Yao, X.C.; Wang, T.X.; Xu, P.; Lu, H.; Pan, G.S.; Bao, X.H.; Peng, C.Z.; Lu, C.Y.; Chen, Y.A.; Pan, J.W. Observation of eight-photon entanglement. Nat. Photon. 2012, 6, 225–228. [Google Scholar] [CrossRef]
- Karan, S.; Aarav, S.; Bharadhwaj, H.; Taneja, L.; De, A.; Kulkarni, G.; Meher, N.; Jha, A.K. Phase matching in β-barium borate crystals for spontaneous parametric down-conversion. J. Opt. 2020, 22, 083501. [Google Scholar] [CrossRef]
- Einstein, A.; Podolsky, B.; Rosen, N. Can quantum-mechanical description of physical reality be considered complete? Phys. Rev. 1935, 47, 777–780. [Google Scholar] [CrossRef]
- Greenberger, D.M.; Horne, M.; Shimony, A.; Zeilinger, A. Bell’s theorem without inequalities. Am. J. Phys. 1990, 58, 1131–1143. [Google Scholar] [CrossRef]
- Kumar, C.; Saxena, G.; Arvind. Multiphoton Bell-type inequality: A tool to unearth nonlocality of continuous variable quantum optical systems. Phys. Rev. A 2021, 103, 042224. [Google Scholar] [CrossRef]
- Bell, J.S. On the Einstein Podolsky Rosen paradox. Physics 1964, 1, 195–200. [Google Scholar] [CrossRef]
- Clauser, J.F.; Horne, M.A.; Shimony, A.; Holt, R.A. Proposed experiment to test local hidden-variable theories. Phys. Rev. Lett. 1969, 23, 880–884. [Google Scholar] [CrossRef]
- Mermin, N.D. Extreme quantum entanglement in a superposition of macroscopically distinct states. Phys. Rev. Lett. 1990, 65, 1838. [Google Scholar] [CrossRef] [PubMed]
- Werner, R.F.; Wolf, M.M. Schmidt measure as a tool for quantifying multiparticle entanglement. Phys. Rev. A 2001, 64, 032112. [Google Scholar] [CrossRef]
- Ardehali, M. Bell inequalities with a magnitude of violation that grows exponentially with the number of particles. Phys. Rev. A 1992, 46, 5375. [Google Scholar] [CrossRef] [PubMed]
- Acin, A.; Bruss, D.; Lewenstein, M.; Sanpera, A. Classification of Mixed Three-Qubit States. Phys. Rev. Lett. 2001, 87, 040401. [Google Scholar] [CrossRef]
- Bourennane, M.; Eibl, M.; Kurtsiefer, C.; Gaertner, S.; Weinfurter, H. Experimental Detection of Multipartite Entanglement using Witness Operators. Phys. Rev. Lett. 2004, 92, 087902. [Google Scholar] [CrossRef]
- Li, T.; Liu, T.J.; Wang, S.; Jebarathinam, C.; Wang, Q. Experimental violation of Mermin steering inequality by three-photon entangled states with nontrivial GHZ-fidelity. Opt. Express 2019, 27, 13559–13567. [Google Scholar] [CrossRef]
- Almeida, M.L.; Barrett, S.J.; Toth, G.; Acin, A. Noise robustness of the nonlocality of entangled quantum states. Phys. Rev. Lett. 2007, 99, 040403. [Google Scholar] [CrossRef]
- Bovino, F.A.; Castagnoli, G.; Cabello, A.; Linares, A.L. Experimental noise resistant Bell-inequality violations for polarization-entangled photons. Phys. Rev. A 2006, 73, 062110. [Google Scholar] [CrossRef]
- Yuan, X.; Cao, Z.; Ma, X.F. Randomness requirement on CHSH Bell test in the multiple run scenario. Phys. Rev. A 2015, 91, 032111. [Google Scholar] [CrossRef]
- Tsirelson, B.S. Quantum analogues of the Bell inequalities the case of two spatially separated domains. J. Sov. Math. 1987, 36, 557–570. [Google Scholar] [CrossRef]
- Gisin, N. Bell inequality holds for all non-product states. Phys. Lett. A 1991, 154, 201–205. [Google Scholar] [CrossRef]
- Popescu, S.; Rohrlich, D. Generic quantum nonlocality. Phys. Lett. A 1992, 166, 293–297. [Google Scholar] [CrossRef]
- Collins, D. Bell-type inequalities to detect True n-body nonseparability. Phys. Rev. Lett. 2002, 88, 170405. [Google Scholar] [CrossRef]
- Alsina, D. Operational approach to Bell inequalities: Application to qutrits. Phys. Rev. A 2016, 94, 032102. [Google Scholar] [CrossRef]
- Raphael, F.; Gustavo, R. Fighting noise with noise in realistic quantum teleportation. Phys. Rev. A 2015, 92, 012338. [Google Scholar] [CrossRef]
- Lavoie, J.; Kaltenbaek, R.; Resch, K.J. Experimental violation of Svetlichny’s inequality. New J. Phys. 2009, 11, 073051. [Google Scholar] [CrossRef]
- Jungnitsch, B.; Niekamp, S.; Kleinmann, M.; Guhne, O.; Lu, H.; Gao, W.B.; Chen, Y.A.; Chen, Z.B.; Pan, J.W. Increasing the Statistical Significance of Entanglement Detection in Experiments. Phys. Rev. Lett. 2010, 104, 210401. [Google Scholar] [CrossRef] [PubMed]
- Zhao, J.; Wang, M.; Sun, B.; Cao, L.; Yang, Y.; Liu, X.; Zhang, Q.W.; Lu, H.X.; Driscoll, K.A. Preparation and Analysis of Two-Dimensional Four-Qubit Entangled States with Photon Polarization and Spatial Path. Entropy 2022, 24, 1388. [Google Scholar] [PubMed]
- Fung, C.H.F.; Chau, H.F. Physical time-energy cost of a quantum process determines its information fidelity. Phys. Rev. A 2014, 90, 022333. [Google Scholar] [CrossRef]
- Ayan, P.; Rivu, G.; Tamoghna, D.; Aditi, S.D. Dimensional advantage in secure information trading via the noisy dense coding protocol. Phys. Rev. A 2024, 110, 032419. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).