Thermodynamic and Magnetic Properties of Weakly Interacting Electron Gas Localized in a CdSe Cylindrical Core–Shell Quantum Dot
Abstract
1. Introduction
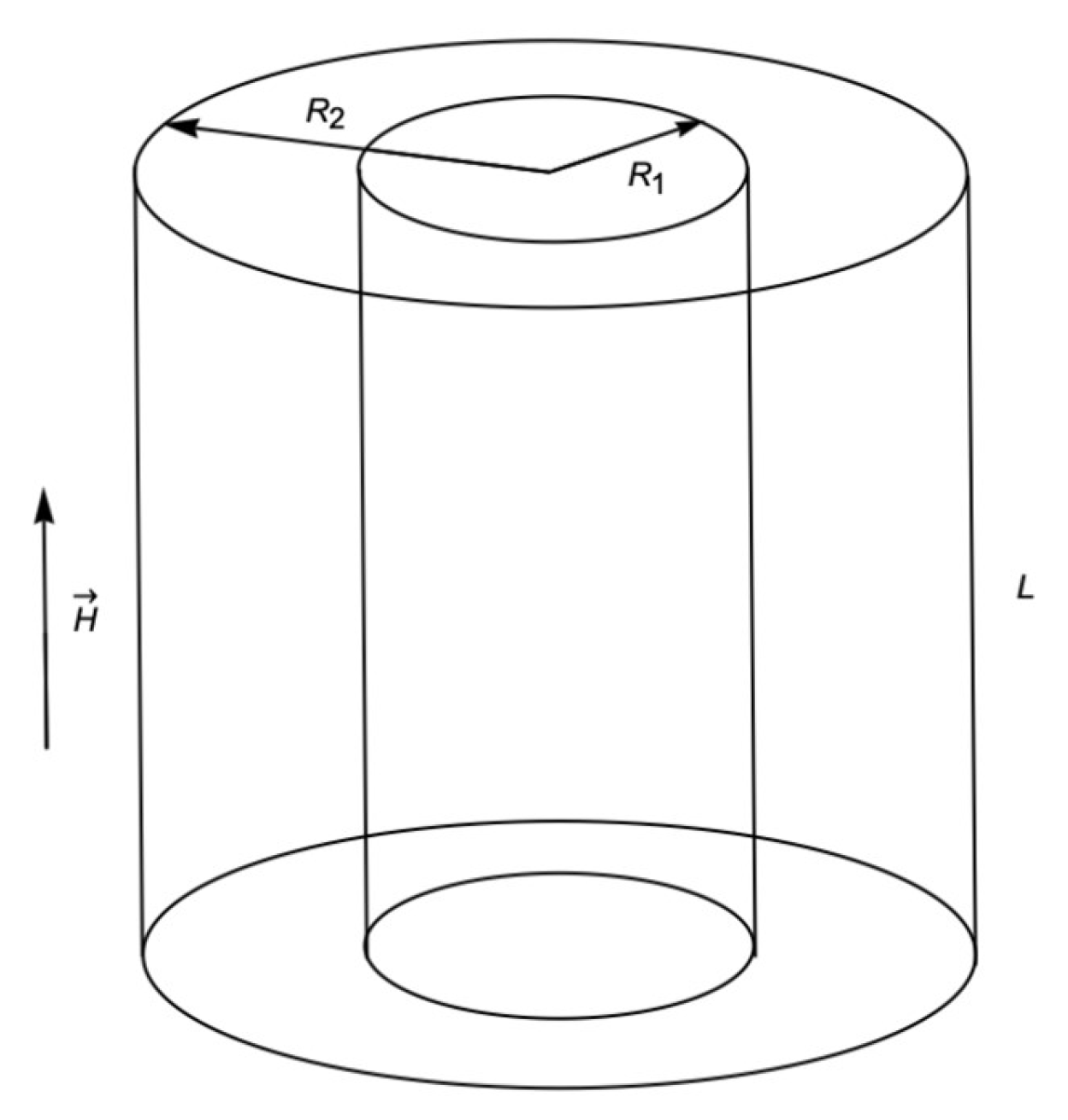
2. Theory
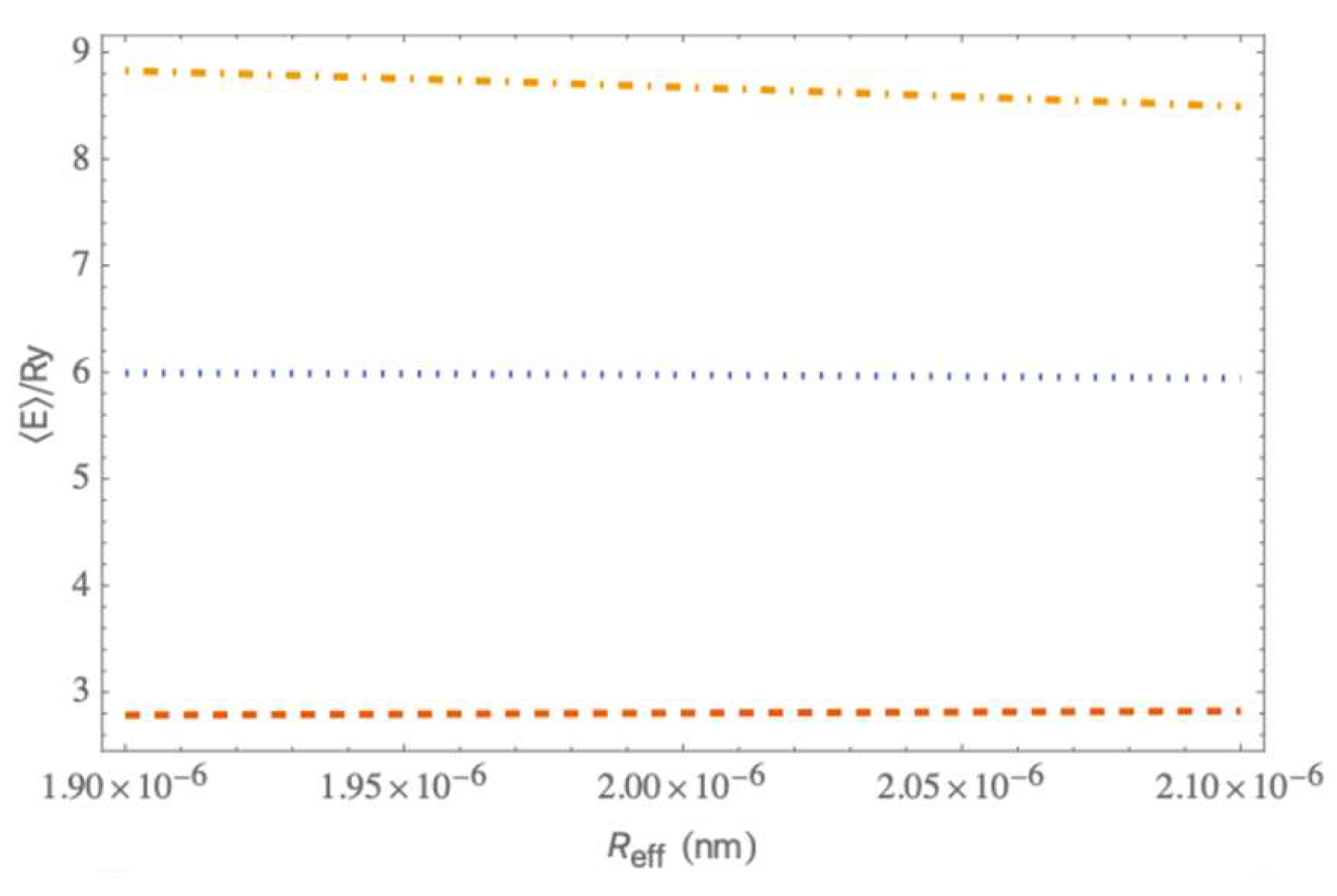
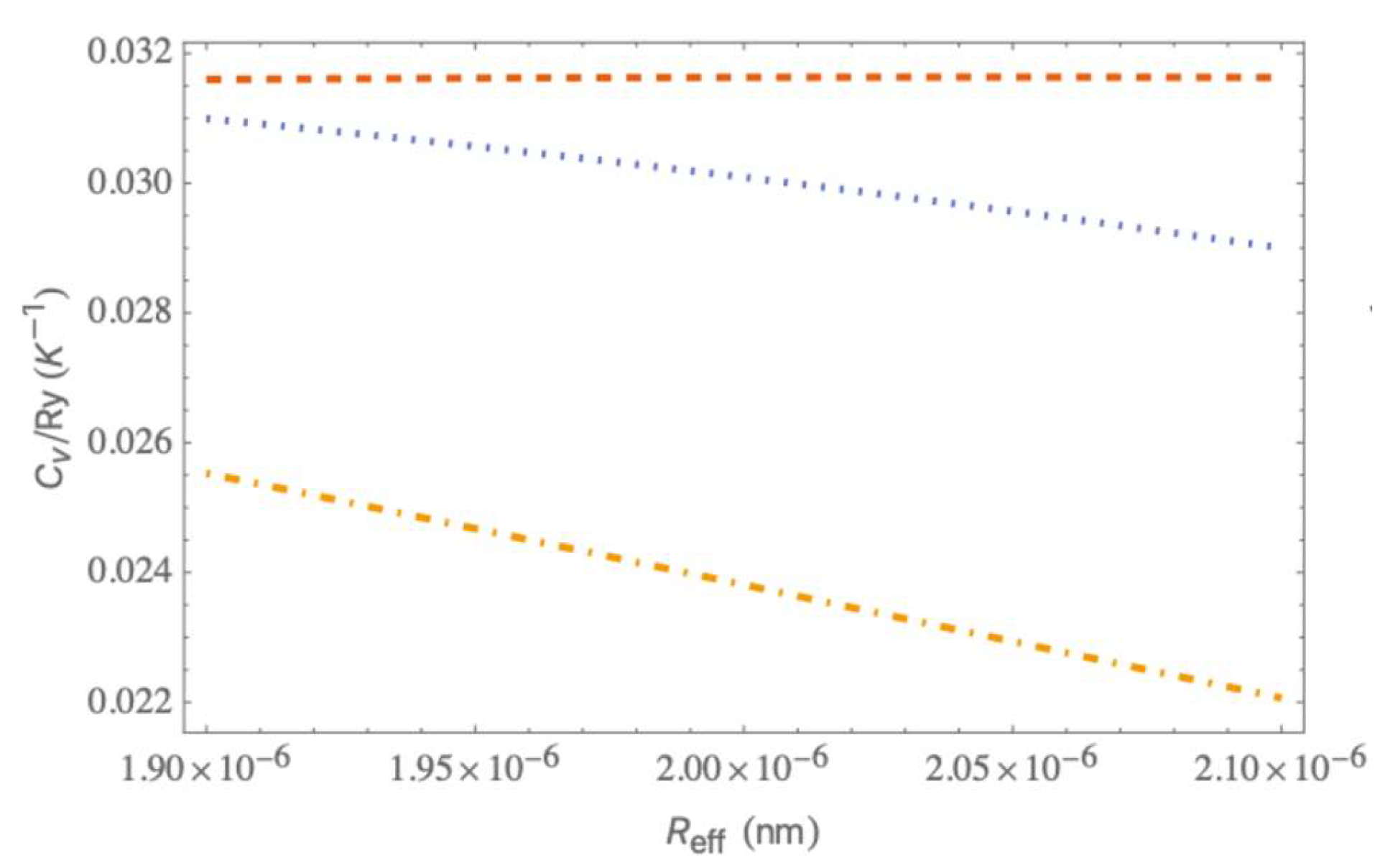
3. Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wu, J.; Wang, Z.M.; Dorogan, V.G.; Li, S.; Zhou, Z.; Li, H.; Lee, J.; Kim, E.S.; Mazur, Y.I.; Salamo, G.J. Strain-Free Ring-Shaped Nanostructures by Droplet Epitaxy for Photovoltaic Application. Appl. Phys. Lett. 2012, 101, 043904. [Google Scholar] [CrossRef]
- Lee, J.H.; Wang, Z.M.; Ware, M.E.; Wijesundara, K.C.; Garrido, M.; Stinaff, E.A.; Salamo, G.J. Super Low Density InGaAs Semiconductor Ring-Shaped Nanostructures. Cryst. Growth Des. 2008, 8, 1945–1951. [Google Scholar] [CrossRef]
- Rafiee, E.; Negahdari, R. Cancer Cell Detection Biosensor Based on Graphene-Plasmonic Split Square-Ring-Shaped Nanostructure. Plasmonics 2023, 18, 431–440. [Google Scholar] [CrossRef]
- Cui, W.; Li, L.; He, Z.; He, H.; He, X.; Xia, B.; Zhong, Z.; Song, C.; Li, L.; Xue, W.; et al. Enhanced Plasmonic Field and Focusing for Ring-Shaped Nanostructures via Radial Vector Beam. Results Phys. 2021, 26, 104412. [Google Scholar] [CrossRef]
- Movilla, J.L.; Climente, J.I.; Planelles, J. Dielectric Polarization in Axially-Symmetric Nanostructures: A Computational Approach. Comput. Phys. Commun. 2010, 181, 92–98. [Google Scholar] [CrossRef]
- Karn, N.K.; Sharma, M.M.; Awana, V.P.S. Non-Trivial Band Topology in the Superconductor AuSn4: A First Principle Study. Supercond. Sci. Technol. 2022, 35, 114002. [Google Scholar] [CrossRef]
- Lorke, A.; Luyken, R.J.; Govorov, A.O.; Kotthaus, J.P.; Garcia, J.M.; Petroff, P.M. Spectroscopy of Nanoscopic Semiconductor Rings. Phys. Rev. Lett. 2000, 84, 2223–2226. [Google Scholar] [CrossRef]
- Harutyunyan, V.A.; Hayrapetyan, D.B.; Kazaryan, E.M. Interband Absorption and Photoluminescence in the Cylindrical Layered CdS/HgS/CdS Heterostructure. J. Contemp. Phys. 2018, 53, 48–57. [Google Scholar] [CrossRef]
- Zeiri, N.; Baser, P.; Jahromi, H.D.; Yahyaoui, N.; Ed-Dahmouny, A.; Sfina, N.; Duque, C.A.; Said, M. Effects of the Size and Applied Electric Field on the Photoionization Cross-Section of Elliptical Cylindrical CdS/ZnS Core-Shell Quantum Dots Immersed in Various Dielectric Matrices. Opt. Laser Technol. 2025, 182, 111822. [Google Scholar] [CrossRef]
- El-Yadri, M.; El Hamdaoui, J.; Aghoutane, N.; Pérez, L.M.; Baskoutas, S.; Laroze, D.; Díaz, P.; Feddi, E.M. Optoelectronic Properties of a Cylindrical Core/Shell Nanowire: Effect of Quantum Confinement and Magnetic Field. Nanomaterials 2023, 13, 1334. [Google Scholar] [CrossRef]
- Harutyunyan, V.A. Electro-Optical Transitions in a Semiconductor Cylindrical Nanolayer. Phys. Solid State 2012, 54, 1096–1103. [Google Scholar] [CrossRef]
- Harutyunyan, V.A.; Kazaryan, E.M.; Kostanyan, A.A.; Sarkisyan, H.A. Interband Transitions in Cylindrical Layer Quantum Dot: Influence of Magnetic and Electric Fields. Phys. E Low-Dimens. Syst. Nanostructures 2007, 36, 114–118. [Google Scholar] [CrossRef]
- Aghekyan, N.G.; Kazaryan, E.M.; Petrosyan, L.S.; Sarkisyan, H.A. Two Electronic States in a Quantum Ring: Mathieu Equation Approach. J. Phys. Conf. Ser. 2010, 248, 012048. [Google Scholar] [CrossRef]
- Harutyunyan, V.A.; Aramyan, K.S.; Petrosyan, H.S.; Demirjian, G.H. Optical Transitions in Spherical Quantized Layer under the Presence of Radial Electrical Field. Phys. E Low-Dimens. Syst. Nanostructures 2004, 24, 173–177. [Google Scholar] [CrossRef]
- Wang, Y.; Dou, W. Interband and Intraband Transitions, as Well as Charge Mobility in Driven Two-Band Model with Electron–Phonon Coupling. J. Chem. Phys. 2024, 161, 204104. [Google Scholar] [CrossRef]
- Harutyunyan, V.A. Semiconductor Nanocylindrical Layer in a Strong Electric Field: Spectrum of Carriers and Intraband Transitions. Phys. Solid State 2010, 52, 1744–1749. [Google Scholar] [CrossRef]
- Ed-Dahmouny, A.; Zeiri, N.; Arraoui, R.; Es-Sbai, N.; Jaouane, M.; Fakkahi, A.; Sali, A.; El-Bakkari, K.; Duque, C.A. The Third-Order Nonlinear Optical Susceptibility in an Ellipsoidal Core-Shell Quantum Dot Embedded in Various Dielectric Surrounding Matrices. Phys. E Low-Dimens. Syst. Nanostructures 2023, 153, 115784. [Google Scholar] [CrossRef]
- Agarwal, K.; Rai, H.; Mondal, S. Quantum Dots: An Overview of Synthesis, Properties, and Applications. Mater. Res. Express 2023, 10, 062001. [Google Scholar] [CrossRef]
- Valizadeh, A.; Mikaeili, H.; Samiei, M.; Farkhani, S.M.; Zarghami, N.; Kouhi, M.; Akbarzadeh, A.; Davaran, S. Quantum Dots: Synthesis, Bioapplications, and Toxicity. Nanoscale Res. Lett. 2012, 7, 480. [Google Scholar] [CrossRef]
- Maksym, P.A.; Chakraborty, T. Effect of Electron-Electron Interactions on the Magnetization of Quantum Dots. Phys. Rev. B 1992, 45, 1947–1950. [Google Scholar] [CrossRef]
- Pietiläinen, P.; Halonen, V.; Chakraborty, T. Electron Correlations in Quantum Ring and Dot Systems. Phys. B Condens. Matter 1995, 212, 256–260. [Google Scholar] [CrossRef]
- Lafaurie, L.G.; Suaza, Y.A.; Laroze, D.; Gutiérrez, W.; Marín, J.H. Thermodynamic Properties of an Artificial Molecule Quantum Rings: Geometric and External Field Effects. Phys. B Condens. Matter 2024, 679, 415786. [Google Scholar] [CrossRef]
- Manninen, M.; Koskinen, M.; Reimann, S.M.; Mottelson, B. Magnetic Properties of Quantum Dots and Rings. Eur. Phys. J. D 2001, 16, 381–385. [Google Scholar] [CrossRef]
- Chouef, S.; Hbibi, M.; Boussetta, R.; El Moussaouy, A.; Mommadi, O.; Falyouni, F.; Duque, C.A. Influence of Magnetic Field and Temperature on Thermodynamic Properties of Curved Two-Low-Dimensional Nanostructures: Presence of Shallow Donor Impurity. J. Magn. Magn. Mater. 2025, 614, 172729. [Google Scholar] [CrossRef]
- Chakraborty, T.; Pietiläinen, P. Electron-Electron Interaction and the Persistent Current in a Quantum Ring. Phys. Rev. B 1994, 50, 8460–8468. [Google Scholar] [CrossRef]
- Tan, W.-C.; Inkson, J.C. Electron States in a Two-Dimensional Ring—An Exactly Soluble Model. Semicond. Sci. Technol. 1996, 11, 1635–1641. [Google Scholar] [CrossRef]
- Bandos, T.V.; Cantarero, A.; García-Cristóbal, A. Finite Size Effects on the Optical Transitions in Quantum Rings under a Magnetic Field. Eur. Phys. J. B 2006, 53, 99–108. [Google Scholar] [CrossRef]
- Flügge, S. Practical Quantum Mechanics; Springer: Berlin/Heidelberg, Germany, 1971; ISBN 978-3-540-65035-5. [Google Scholar]
- Pöschl, G.; Teller, E. Bemerkungen zur Quantenmechanik des anharmonischen Oszillators. Z. Phys. 1933, 83, 143–151. [Google Scholar] [CrossRef]
- Failla, M.; García Flórez, F.; Salzmann, B.B.V.; Vanmaekelbergh, D.; Stoof, H.T.C.; Siebbeles, L.D.A. Observation of the Quantized Motion of Excitons in CdSe Nanoplatelets. Phys. Rev. B 2020, 102, 195405. [Google Scholar] [CrossRef]
- Dabbousi, B.O.; Rodriguez-Viejo, J.; Mikulec, F.V.; Heine, J.R.; Mattoussi, H.; Ober, R.; Jensen, K.F.; Bawendi, M.G. (CdSe)ZnS Core–Shell Quantum Dots: Synthesis and Characterization of a Size Series of Highly Luminescent Nanocrystallites. J. Phys. Chem. B 1997, 101, 9463–9475. [Google Scholar] [CrossRef]
- Hbibi, M.; Mommadi, O.; Chouef, S.; Boussetta, R.; Belamkadem, L.; Moussaouy, A.E.; Falyouni, F.; Duque, C.M.; Vinasco, J.A.; Duque, C.A. Finite Confinement Potentials, Core and Shell Size Effects on Excitonic and Electron-Atom Properties in Cylindrical Core/Shell/Shell Quantum Dots. Sci. Rep. 2022, 12, 14854. [Google Scholar] [CrossRef] [PubMed]
- Pulgar-Velásquez, L.; Sierra-Ortega, J.; Vinasco, J.A.; Laroze, D.; Radu, A.; Kasapoglu, E.; Restrepo, R.L.; Gil-Corrales, J.A.; Morales, A.L.; Duque, C.A. Shallow Donor Impurity States with Excitonic Contribution in GaAs/AlGaAs and CdTe/CdSe Truncated Conical Quantum Dots under Applied Magnetic Field. Nanomaterials 2021, 11, 2832. [Google Scholar] [CrossRef] [PubMed]
- Baghdasaryan, D.A.; Harutyunyan, V.A.; Hayrapetyan, D.B.; Kazaryan, E.M.; Baskoutas, S.; Sarkisyan, H.A. Exciton States and.Optical Absorption in CdSe and PbS Nanoplatelets. Nanomaterials 2022, 12, 3690. [Google Scholar] [CrossRef]
- Ustimenko, R.V.; Vinnichenko, M.Y.; Karaulov, D.A.; Sarkisyan, H.A.; Hayrapetyan, D.B.; Firsov, D.A. Effect of Doping and Interband Pumping on the Optical Properties of GeSi/Si Quantum Dot Nanostructures for Infrared Detectors. ACS Appl. Nano Mater. 2024, 7, 27245–27253. [Google Scholar] [CrossRef]
- Brey, L.; Johnson, N.F.; Halperin, B.I. Optical and Magneto-Optical Absorption in Parabolic Quantum Wells. Phys. Rev. B 1989, 40, 10647–10649. [Google Scholar] [CrossRef]
- Karn, N.K.; Sharma, M.M.; Felner, I.; Awana, V.P.S. Anisotropy in Electronic and Magneto-Transport of 2D Superconductor NbSe2. J. Supercond. Nov. Magn. 2024, 37, 1381–1391. [Google Scholar] [CrossRef]
- Kumar, K.; Awana, V.P.S. Exploration of Magneto-Transport Properties of MnxSb2-xTe3(x = 0.0,0.1) Topological Insulator. Mater. Today Proc. 2023. [Google Scholar] [CrossRef]
- Takeuchi, Y.; Sepehri-Amin, H.; Sugimoto, S.; Hiroto, T.; Kasai, S. Magnetic and Magneto-Transport Properties of Non-Collinear Antiferromagnetic Mn3Ge Epitaxial Films. APL Mater. 2024, 12, 071110. [Google Scholar] [CrossRef]
- Paravicini-Bagliani, G.L.; Appugliese, F.; Richter, E.; Valmorra, F.; Keller, J.; Beck, M.; Bartolo, N.; Rössler, C.; Ihn, T.; Ensslin, K.; et al. Magneto-Transport Controlled by Landau Polariton States. Nat. Phys. 2019, 15, 186–190. [Google Scholar] [CrossRef]
- Sapienza, L.; Al-Khuzheyri, R.; Dada, A.; Griffiths, A.; Clarke, E.; Gerardot, B.D. Magneto-Optical Spectroscopy of Single Charge-Tunable InAs/GaAs Quantum Dots Emitting at Telecom Wavelengths. Phys. Rev. B 2016, 93, 155301. [Google Scholar] [CrossRef]
- Calvin, J.J.; Brewer, A.S.; Crook, M.F.; Kaufman, T.M.; Alivisatos, A.P. Observation of Negative Surface and Interface Energies of Quantum Dots. Proc. Natl. Acad. Sci. USA 2024, 121, e2307633121. [Google Scholar] [CrossRef]



| Parameter | CdSe |
|---|---|
| , nm | 0.3 |
| 0.144 (4.5 ML) | |
| 0.138 (5.5 ML) | |
| 0.13 (7.5 ML) | |
| 0.92 (4.5 ML) | |
| 0.9 (5.5 ML) | |
| 0.88 (7.5 ML) | |
| 0.09 (4.5 ML) | |
| 0.081 (5.5 ML) | |
| 0.076 (7.5 ML) | |
| 2.15 (4.5 ML) | |
| 2.0 (5.5 ML) | |
| 1.76 (7.5 ML) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tadevosyan, L.; Ghaltaghchyan, H.; Mamasakhlisov, Y.; Sarkisyan, H. Thermodynamic and Magnetic Properties of Weakly Interacting Electron Gas Localized in a CdSe Cylindrical Core–Shell Quantum Dot. Quantum Rep. 2025, 7, 13. https://doi.org/10.3390/quantum7010013
Tadevosyan L, Ghaltaghchyan H, Mamasakhlisov Y, Sarkisyan H. Thermodynamic and Magnetic Properties of Weakly Interacting Electron Gas Localized in a CdSe Cylindrical Core–Shell Quantum Dot. Quantum Reports. 2025; 7(1):13. https://doi.org/10.3390/quantum7010013
Chicago/Turabian StyleTadevosyan, Levon, Hayk Ghaltaghchyan, Yevgeni Mamasakhlisov, and Hayk Sarkisyan. 2025. "Thermodynamic and Magnetic Properties of Weakly Interacting Electron Gas Localized in a CdSe Cylindrical Core–Shell Quantum Dot" Quantum Reports 7, no. 1: 13. https://doi.org/10.3390/quantum7010013
APA StyleTadevosyan, L., Ghaltaghchyan, H., Mamasakhlisov, Y., & Sarkisyan, H. (2025). Thermodynamic and Magnetic Properties of Weakly Interacting Electron Gas Localized in a CdSe Cylindrical Core–Shell Quantum Dot. Quantum Reports, 7(1), 13. https://doi.org/10.3390/quantum7010013







