The Computational Universe: Quantum Quirks and Everyday Reality, Actual Time, Free Will, the Classical Limit Problem in Quantum Loop Gravity and Causal Dynamical Triangulation

Abstract

The simulation analogy presented in this work enhances the accessibility of abstract quantum theories, specifically the stochastic hydrodynamic model (SQHM), by relating them to our daily experiences. The SQHM incorporates the influence of fluctuating gravitational background, a form of dark energy, into quantum equations. This model successfully addresses key aspects of objective-collapse theories, including resolving the ‘tails’ problem through the definition of quantum potential length of interaction in addition to the De Broglie length, beyond which coherent Schrödinger quantum behavior and wavefunction tails cannot be maintained. The SQHM emphasizes that an external environment is unnecessary, asserting that the quantum stochastic behavior leading to wavefunction collapse can be an inherent property of physics in a spacetime with fluctuating metrics. Embedded in relativistic quantum mechanics, the theory establishes a coherent link between the uncertainty principle and the constancy of light speed, aligning seamlessly with finite information transmission speed. Within quantum mechanics submitted to fluctuations, the SQHM derives the indeterminacy relation between energy and time, offering insights into measurement processes impossible within a finite time interval in a truly quantum global system. Experimental validation is found in confirming the Lindemann constant for solid lattice melting points and the ⁴He transition from fluid to superfluid states. The SQHM’s self-consistency lies in its ability to describe the dynamics of wavefunction decay (collapse) and the measure process. Additionally, the theory resolves the pre-existing reality problem by showing that large-scale systems naturally decay into decoherent states stable in time. Continuing, the paper demonstrates that the physical dynamics of SQHM can be analogized to a computer simulation employing optimization procedures for realization. This perspective elucidates the concept of time in contemporary reality and enriches our comprehension of free will. The overall framework introduces an irreversible process impacting the manifestation of macroscopic reality at the present time, asserting that the multiverse exists solely in future states, with the past comprising the formed universe after the current moment. Locally uncorrelated projective decays of wavefunction, at the present time, function as a reduction of the multiverse to a single universe. Macroscopic reality, characterized by a foam-like consistency where microscopic domains with quantum properties coexist, offers insights into how our consciousness perceives dynamic reality. It also sheds light on the spontaneous emergence of gravity in discrete quantum spacetime evolution, and the achievement of the classical general relativity limit in quantum loop gravity and causal dynamical triangulation. The simulation analogy highlights a strategy focused on minimizing information processing, facilitating the universal simulation in solving its predetermined problem. From within, reality becomes the manifestation of specific physical laws emerging from the inherent structure of the simulation devised to address its particular issue. In this context, the reality simulation appears to employ an optimization strategy, minimizing information loss and data management in line with the simulation’s intended purpose.

1. Introduction

One of the most intriguing aspects of modern physics is its approach to infinitesimals and infinities as mathematical abstractions rather than real entities. This perspective has already yielded significant results, such as quantum loop gravity [1,2] and non-commutative string theories [3,4].

This study endeavors to showcase how adopting a discrete perspective can offer novel insights into age-old conundrums in physics.

Building on the sound hypothesis that spacetime is not continuous but discrete, we demonstrate the plausibility of drawing an analogy between our universe and a computerized N-body simulation.

Our goal is to present a sturdy framework of reasoning, which will be subsequently utilized to attain a more profound comprehension of our reality. This framework is founded on the premise that anyone endeavoring to create a computer simulation resembling our universe will inevitably confront the same challenges as the entity responsible for constructing the universe itself.

The fundamental aim is that, by tackling these challenges, we may unearth insights into the reasons behind the functioning of the universe. This is based on the notion that constructing something as extensive and intricate at higher levels of efficiency might have only one viable approach. The essence of the current undertaking is eloquently aligned with the dictum of Feynman: ‘What I cannot create, I do not understand’. Conversely, here, this principle is embraced in the affirmative: ‘What I can create, I can comprehend.’

One of the primary challenges in achieving this objective is the need for a physical theory that comprehensively describes reality, capable of portraying N-body evolution across the entire physical scale, spanning the microscopic quantum level to the macroscopic classical realm.

Regarding this matter, established physics falls short in providing a comprehensive and internally consistent theoretical foundation [5,6,7,8,9,10]. Numerous problematic aspects persist to this day, including the challenge posed by the probabilistic interpretation assigned to the wavefunction in quantum mechanics. Others persistent issues are the impossibility of assuming a well-defined concept of pre-existing reality before measurement and ensuring local relativistic causality.

Quantum theory, despite its well-defined mathematical apparatus, remains incomplete with respect to its foundational postulates. Specifically, the measurement process is not explicated within the framework of quantum mechanics. This requires acceptance of its probabilistic foundations regardless of the validity of the principle of causality.

This conflict is famously articulated through the objection posed by the EPR paradox. The EPR paradox, as detailed in a renowned paper [5], is rooted in the incompleteness of quantum mechanics concerning the indeterminacy of the wavefunction collapse and measurement outcomes. These fundamental aspects do not find a clear placement within a comprehensive theoretical framework.

The endeavor to formulate a theory encompassing the probabilistic nature of quantum mechanics within a unified theoretical framework can be traced back to the research of Nelson [6] and has persisted over time. However, Nelson’s hypotheses ultimately fell short due to the imposition of a specific stochastic derivative with time inversion symmetry, limiting its generality. Furthermore, the outcomes of Nelson’s theory do not fully align with those of quantum mechanics concerning the incompatibility of contemporary measurements of conjugated variables, as illustrated by Von Neumann’s proof [7] of the impossibility of reproducing quantum mechanics with theories based on underlying classical stochastic process.

Moreover, the overarching goal of incorporating the probabilistic nature of quantum mechanics while ensuring its reversibility through ‘hidden variables’ in local classical theories was conclusively proven to be impossible by Bell [8]. Nevertheless, Bohm’s non-local hidden variable theory [11] has arisen with some success. He endeavors to restore the determinism of quantum mechanics by introducing the concept of a pilot wave. The fundamental concept posits that, in addition to the particles themselves, there exists a ‘guidance’ or influence from the pilot wavefunction that dictates the behavior of the particles. Although this pilot wavefunction is not directly observable, it does impact the measurement probabilities of the particles.

Feynman’s integral path representation [12] of quantum mechanics constitutes the conclusive and accurate model, reducible to a stochastic framework. Here, as shown by Kleinert [13], it is established that quantum mechanics can be conceptualized as an imaginary-time stochastic process. These imaginary time quantum fluctuations differ from the more commonly known real-time fluctuations of the classical stochastic dynamics. They result in the ‘reversible’ evolution of probability waves (wavefunctions) that shows the pseudo-diffusion behavior of mass density evolution.

The distinguishing characteristic of quantum pseudo-diffusion is the inability to define a positive–definite diffusion coefficient. This directly stems from the reversible nature of quantum evolution, which, within a spatially distributed system, may demonstrate local entropy reduction over specific spatial domains. However, this occurs within the framework of an overall reversible deterministic evolution with a net entropy variation of zero [14].

This aspect is clarified by the Madelung quantum hydrodynamic model [15,16,17], which is perfectly equivalent to the Schrödinger description while being a specific subset of the Bohm theory [18]. In this model, quantum entanglement is introduced through the action of the so-called quantum potential.

Recently, with the emergence of evidence pointing to dark energy manifested as a gravitational background noise (GBN), whether originating from relics or the dynamics of bodies in general relativity, the author demonstrated that quantum hydrodynamic representation provides a means to describe self-fluctuating dynamics within a system without necessitating the introduction of an external environment [19]. The noise produced by ripples in spacetime curvature can be incorporated into Madelung’s quantum hydrodynamic framework by applying fundamental principles of relativity. This allows us to establish a mechanism through which the energy associated with spacetime curvature ripples generates fluctuations in mass density.

The resulting stochastic quantum hydrodynamic model (SQHM) avoids introducing divergent results that contradict established theories such as decoherence [9] and the Copenhagen foundation of quantum mechanics; instead, it enriches and complements our understanding of these theories. It indicates that in the presence of noise, quantum entanglement and coherence can be maintained on a microscopic scale much smaller than the De Broglie length and the range of action of the quantum potential. On a scale with a characteristic length much larger than the distance over which quantum potential operates, classical physics naturally emerges [19].

While the Bohm theory attributes the indeterminacy of the measurement process to the indeterminable pilot wave, the SQHM attributes its unpredictable probabilistic nature to the fluctuating gravitational background. Furthermore, it is possible to demonstrate a direct correspondence between the Bohm non-local hidden variable approach developed by Santilli in IsoRedShift Mechanics [20] and the SQHM. This correspondence reveals that the origin of the hidden variable is nothing but the perturbative effect of the fluctuating gravitational background on quantum mechanics [21].

The stochastic quantum hydrodynamic model (SQHM), adept at describing physics across various length scales, from the microscopic quantum to the classical macroscopic [19], offers the potential to formulate a comprehensive simulation analogy to N-body evolution within the discrete spacetime of the universe.

The work is organized as follows:

• Introduction to the stochastic quantum hydrodynamic model (SQHM)
• Quantum-to-classical transition and the emerging classical mechanics in large-sized systems
• The measurement process in quantum stochastic theory: the role of the finite range of non-local quantum potential interactions
• Maximum precision in measurements of mechanical variables in spacetime with fluctuating background and finite speed of light
• Minimum discrete length interval in 4D spacetime
• Dynamics of wavefunction collapse
• Evolution of the mass density distribution of quantum superposition of states in spacetime with GBN
• EPR paradox and pre-existing reality from the standpoint of the SQHM
• The computer simulation analogy for the N-body problem
• How the universe computes the next state: the unraveling of the meaning of time
• Free will
• The universal ‘pasta maker’ and actual time in 4D spacetime
• Discussion and future developments
• Extending free will
• Best future states problem-solving emergent from the Darwinian principle of evolution
• How the conscience captures the reality dynamics
• The spontaneous appearance of gravity in a discrete spacetime simulation
• The classical general relativity limit problem in quantum loop gravity and causal dynamical triangulation

2. The Quantum Stochastic Hydrodynamic Model

The Madelung quantum hydrodynamic representation transforms the Schrodinger equation [15,16,17] (italic indexes run from 1 to 3)

$$-i\hslash {\partial }_t\psi =\left(\frac{{\hslash }^2}{2m}{\partial }_i{\partial }_i-V_{(q)}\right)\psi$$

(1)

for the complex wavefunction $\psi =|\psi |{\mathrm{e}}^{-\frac{iS}{\hslash }}$ into two equations of real variables: the conservation equation for mass density $|\psi {|}^2$

$${\partial }_t|\psi {|}^2+{\partial }_i(|\psi {|}^2{\dot{q}}_i)=0$$

(2)

and the motion equation for momentum $m{\dot{q}}_i=p_i={\partial }_i{S}_{(q,t)}$,

$${\ddot{q}}_{j_{(t)}}=-\frac{1}{m}{\partial }_j\left(V_{(q)}+V_{q{u}_{(n)}}\right)$$

(3)

where $S_{(q,t)}=-\frac{\hslash }{2}\mathit{ln}\frac{\psi }{\psi *}$ and where

$$V_{qu}=-\frac{{\hslash }^2}{2m}\frac{1}{|\psi |}{\partial }_i{\partial }_i|\psi |.$$

(4)

The fluctuating energy content of gravitational background noise (GBN) leads to local variations in mass density. As demonstrated below, this results in the quantum potential producing a stochastic force, which extends the Madelung hydrodynamic analogy into a quantum–stochastic problem. The fluctuations in mass density can be understood by observing that gravitons are metric fluctuations that cause space itself to vibrate. This vibration contracts and elongates distances, similar to what is detected in the observation of gravitational waves at the LIGO and VIRGO laboratories. Consequently, when a mass element experiences elongation or shortening of distance, its density decreases or increases accordingly. As shown in [19], the SQHM is defined by the following assumptions:

• The additional mass density generated by GBN is described by the wavefunction ${\psi }_{gbn}$ with density $|{\psi }_{gbn}{|}^2$;
• The associated energy density $E$ of GBN is proportional to $|{\psi }_{gbn}{|}^2$;
• The additional mass $m_{gbn}$ is defined by the identity $E=m_{gbn}{c}^2|{\psi }_{gbn}{|}^2$
• The additional mass is assumed to not interact with the mass of the physical system (since the gravitational interaction is sufficiently weak to be disregarded).

Under this assumption, the wavefunction of the overall system ${\psi }_{tot}$ reads as

$${\psi }_{tot}\cong \psi {\psi }_{gbn}$$

(5)

Additionally, given that the energy density of gravitational background noise (GBN) $E$ is quite small, mass density $m_{gbn}|{\psi }_{gbn}{|}^2$ is presumed to be significantly smaller than the body mass density typically encountered in physical problems. Hence, considering the mass $m_{gbn}$ to be much smaller than the mass of the system and assuming in Equations (3) and (4) $m_{tot}=m_{gbn}+m\cong m$, the overall quantum potential can be expressed as follows

$$\begin{array}{l}{V}_{q{u}_{(n_{tot})}}=-\frac{{\hslash }^2}{2m_{tot}}|\psi {|}^{-1}|{\psi }_{gbn}{|}^{-1}{\partial }_i{\partial }_i|\psi ||{\psi }_{gbn}|=\\ =-\frac{{\hslash }^2}{2m}\left(|\psi {|}^{-1}{\partial }_i{\partial }_i|\psi |+|{\psi }_{gbn}{|}^{-1}{\partial }_i{\partial }_i|{\psi }_{gbn}|+2|\psi {|}^{-1}|{\psi }_{gbn}{|}^{-1}{\partial }_i|{\psi }_{gbn}|{\partial }_i|\psi |\right)\end{array}.$$

(6)

Through an analysis of the variation in quantum potential energy generated by each Fourier component of mass fluctuation and utilizing the Maxwell–Boltzmann law, we can derive the spectrum of this noise and subsequently determine its correlation function $G(\lambda )$.

To accomplish this, let us examine a fluctuating mass density with a wavelength $\lambda$

$${{|{\psi }_{gbn}|}^2}_{(\lambda )}\propto {cos}^2\frac{2\pi }{\lambda }q$$

(7)

related to the wavefunction of the mass fluctuation

$${\psi }_{gbn(\lambda )}\propto \pm cos\frac{2\pi }{\lambda }q.$$

(8)

With this, we find that the energy fluctuations resulting from the quantum potential

$$\delta {\overline{E}}_{qu}={\displaystyle \underset{V}{\int } n_{tot(q,t)}\delta V_{qu(q,t)}dV},$$

(9)

following the procedure described in reference [8] are expressed as:

$$\delta {\overline{E}}_{qu(\lambda )}\cong \frac{{\hslash }^2}{2m}{\left(\frac{2\pi }{\lambda }\right)}^2$$

(10)

that, in 3D space, read as

$$\delta {\overline{E}}_{qu(\lambda )}\cong \frac{{\hslash }^2}{2m}{\displaystyle \sum _i{\left(k_i\right)}^2}=\frac{{\hslash }^2}{2m}|k{|}^2$$

(11)

The outcome illustrated by Equation (11) indicates that the energy stemming from fluctuations in the mass density increases inversely with the square of its wavelength $\lambda$. Moreover, since fluctuations in quantum potential with extremely short wavelengths for $\lambda \to 0$ diverge, they can lead to a finite contribution even when the noise amplitudes approach zero (i.e., $T\to 0$). This situation raises concerns regarding the achievement of the deterministic zero noise limit (2)–(4) that represents quantum mechanics.

This occurs because the output of the quantum potential, due to its second derivative structure, is dependent on the correlation distance of the noise. Consequently, if we must nullify the fluctuations in the quantum potential in order to achieve convergence to the deterministic limit (2–4) of quantum mechanics for $T\to 0$, it follows that a condition of the correlation function of the quantum potential noise for $\lambda \to 0$ arises [9]. The derivation of the shape of the correlation of $G(\lambda )$ involves tedious stochastic calculations [9], which can be obtained by considering the probability of uncorrelated fluctuations occurring at increasingly shorter distances.

A simpler and more straightforward approach to calculating $G(\lambda )$ is through the spectrum $S(k)$ of the noise that reads as [8]

$$S_{(k)}\propto probabilit{y}_{(k=\frac{2\pi }{\lambda })}=exp\left[-\frac{\delta {\overline{E}}_{qu(\lambda )}}{kT}\right]=exp\left[-{\left(\frac{k{\lambda }_c}{2}\right)}^2\right]$$

(12)

In Equation (12), $k$ represents the Boltzmann constant and $T$ signifies the temperature (mean amplitude parameter) of mass density fluctuations. It is worth noting that Equation (12) exhibits a non-white characteristic, with probability of wavelengths $\lambda$ smaller than ${\lambda }_c$ rapidly approaching zero.

From (12), $G(\lambda )$ reads as [19,22]

$$\begin{array}{ll}{G}_{(\lambda )}& \propto {\displaystyle \underset{-\infty }{\overset{+\infty }{\int }}exp[ik\lambda ]S_{(k)}dk}\propto {\displaystyle \underset{-\infty }{\overset{+\infty }{\int }}exp[ik\lambda ]exp\left[-{\left(k\frac{{\lambda }_c}{2}\right)}^2\right]dk}\\ & \propto \frac{{\pi }^{1/2}}{{\lambda }_c}exp\left[-{\left(\frac{\lambda }{{\lambda }_c}\right)}^2\right]\end{array}.$$

(13)

where

$${\lambda }_c=\sqrt{2}\frac{\hslash }{{(mkT)}^{1/2}}.$$

(14)

At least for $\sqrt{2}$, ${\lambda }_c$ represents the De Broglie length ${\lambda }_{DB}=\frac{\hslash }{<p>}$, where $<p>={(mkT)}^{1/2}$ is the mean momentum of mass density fluctuations, observed as an ideal gas of particles. It is noteworthy that the De Broglie length corresponds to the wavelength associated with the momentum of mass density fluctuations behaving as waves (in accordance with the Lorentz transformation). Expression (12) reveals that uncorrelated mass density fluctuations are not capable of manifesting at increasingly shorter distances than ${\lambda }_c$. Consequently, we uncover a new role of the quantum potential in an open system: gradually suppressing fluctuations (due to their sharply increasing energy) on a microscopic scale. This elucidates the empirical observation that the micro-scale is governed by quantum mechanics.

This probability-mediated suppression enables the proposition of conventional quantum mechanics as the zero-noise ‘deterministic’ limit of the stochastic quantum hydrodynamics model (SQHM). Furthermore, since this phenomenon applies to systems with a physical length significantly smaller than the De Broglie length ${\lambda }_c$, the direct transposition of quantum mechanical behavior to macroscopic large-scale scenarios is not feasible at $T>0$. This is because the De Broglie length ${\lambda }_c$, within the framework of SQHM, disrupts scale invariance.

In the presence of GBN, which generates mass density fluctuations, the mass density distribution (MDD) $|\psi {|}^2$ becomes a stochastic function denoted as $\tilde{n}$, where ${\mathit{lim}}_{T\to 0}\tilde{n}\to |\psi {|}^2$. Based on this assumption, we can conceptually separate $\tilde{n}$ into two parts: $\tilde{n}=\overline{n}+\delta n$, where $\delta n$ is the fluctuating part and $\overline{n}$ is the regular part.

All these variables are connected by the limiting condition ${\mathit{lim}}_{T\to 0}\tilde{n}={\mathit{lim}}_{T\to 0}\overline{n}=|\psi {|}^2$.

Moreover, the features of the Madelung quantum potential, which fluctuate in the presence of stochastic noise, can be determined by positing it as comprising a regular component $\overline{V_{qu(\tilde{n})}}$ (to be defined) along with a fluctuating component $V_{st}$, such as

$$V_{q{u}_{(\tilde{n})}}=-\frac{{\hslash }^2}{2m}{\tilde{n}}^{-1/2}{\partial }_i{\partial }_i{\tilde{n}}^{1/2}=\overline{V_{qu(\tilde{n})}}+V_{st}$$

(15)

where the stochastic part of the quantum potential $V_{st}$ results in force noise

$$-{\partial }_i{V}_{st}=m{\varpi }_{(q,t,T)}$$

(16)

leading to the stochastic motion equation

$${\ddot{q}}_{j_{(t)}}=-\frac{1}{m}{\partial }_j\left(V_{(q)}+\overline{V_{qu(\tilde{n})}}\right)+{\varpi }_{(q,t,T)}.$$

(17)

Moreover, the regular part $\overline{V_{qu(\tilde{n})}}$ for microscopic systems ($\frac{L}{{\lambda }_c}\ll 1$), without loss of generality, can be reorganized as

$$\overline{V_{qu( \mathrm{n} ˜)}}=-\frac{{\hslash }^2}{2m}\overline{\left({\tilde{n}}^{-1/2}{\partial }_i{\partial }_i{\tilde{n}}^{1/2}\right)}=-\frac{{\hslash }^2}{2m}\frac{1}{{\rho }^{1/2}}{\partial }_i{\partial }_i{\rho }^{1/2}+\overline{\Delta V}=V_{q{u}_{(\rho )}}+\overline{\Delta V}$$

(18)

leading to the motion equation

$${\ddot{q}}_{j_{(t)}}=-\frac{1}{m}{\partial }_j\left(V_{(q)}+V_{qu(\rho )}+\overline{\Delta V}\right)+{\varpi }_{(q,t,T)}$$

(19)

where ${\rho }_{(q,t)}$ represents the probability mass density function (PMD) associated with the stochastic process (17) [23], which, in the deterministic limit, adheres to the condition ${\mathit{lim}}_{T\to 0}{\rho }_{(q,t)}={\mathit{lim}}_{T\to 0}\tilde{n}={\mathit{lim}}_{T\to 0}\overline{n}=|\psi {|}^2$.

For the sufficiently general case to be practically relevant, it can be assumed that the correlation function of ${\varpi }_{(q,t,T)}$ possesses zero correlation time, is isotropic in space and is independent among different coordinates, taking the form

$$\underset{T\to 0}{\mathit{lim}}<{\varpi }_{(q_{\alpha },t)},{\varpi }_{(q_{\beta }+\lambda ,t+\tau )}>\cong <{\varpi }_{(q_{\alpha })},{\varpi }_{(q_{\beta })}{>}_{(T)} \mathrm{G}(\lambda )\delta (\tau ){\delta }_{\alpha \beta }$$

(20)

with

$$\underset{T\to 0}{\mathit{lim}}<{\varpi }_{(q_{\alpha })},{\varpi }_{(q_{\beta })}{>}_{(T)}=0.$$

(21)

Furthermore, given that for microscopic systems ($\frac{L}{{\lambda }_c}\ll 1$)

$${\mathit{lim}}_{T\to 0}{G}_{(\lambda )}\propto \frac{1}{{\lambda }_c}exp\left[-{\left(\frac{\lambda }{{\lambda }_c}\right)}^2\right]\cong \frac{1}{{\lambda }_c}=\frac{1}{\hslash }\sqrt{\frac{mkT}{2}}$$

(22)

it follows that

$$\underset{T\to 0}{\mathit{lim}}<{\varpi }_{(q_{\alpha },t)},{\varpi }_{(q_{\beta }+\lambda ,t+\tau )}>\approx <{\varpi }_{(q_{\alpha })},{\varpi }_{(q_{\beta })}{>}_{(T)}\frac{1}{\hslash }\sqrt{\frac{mkT}{2}}\delta (\tau ){\delta }_{\alpha \beta }$$

(23)

and the motion described by Equation (17) takes the stochastic form of the Markov process [19]

$${\ddot{q}}_{j_{(t)}}=-\kappa {\dot{q}}_{j_{(t)}}-\frac{1}{m}\frac{\partial \left(V_{(q)}+V_{q{u}_{(\rho )}}\right)}{\partial q_j}+\kappa D^{1/2}{\xi }_{(t)}.$$

(24)

where

$$D^{1/2}=\left(\frac{L}{{\lambda }_c}\right){\left({\gamma }_D\frac{\hslash }{2m}\right)}^{1/2}=\sqrt{{\gamma }_D}\frac{L}{2}\sqrt{\frac{kT}{2\hslash }}$$

(25)

where ${\gamma }_D$ is a non-zero pure number.

In this case, ${\rho }_{(q,t)}$ is the probability mass density determined by the probability transition function (PTF) $P(q,z|t,0)$ of the Markov process (24) [23] through the relation $\rho (q,t)={\displaystyle \int P(q,z|t,0){\rho }_{(z,0)}}{d}^{6N}z$ where $P(q,z|t,0)$ obeys the Smoluchowski conservation equation [23]

$$P_{(q,q_0|t+\tau ,t_0)}={\displaystyle \underset{-\infty }{\overset{\infty }{\int }}{P}_{(q,z|\tau ,t)} P_{(z,q_0|t-t_0,t_0)}} d^{6N}z.$$

(26)

So, in summary, for the complex field

$$\mathsf{\psi }={\rho }^{1/2}{\mathrm{e}}^{-\frac{i\mathit{S}}{\hslash }}$$

(27)

the quantum–stochastic hydrodynamic system equation reads as

$$\rho (q,t)={\displaystyle \int P(q,z|t,0){\rho }_{(z,0)}}{d}^{r}z$$

(28)

$$m{\dot{q}}_i=p_i={\partial }_i{\mathit{S}}_{(q,t)},$$

(29)

$${\ddot{q}}_{j_{(t)}}=-\kappa {\dot{q}}_{j_{(t)}}-\frac{1}{m}\frac{\partial \left(V_{(q)}+V_{q{u}_{(\rho )}}\right)}{\partial q_j}+\kappa D^{1/2}{\xi }_{(t)}$$

(30)

$$V_{qu}=-\frac{{\hslash }^2}{2m}\frac{1}{{\rho }^{1/2}}{\partial }_i{\partial }_i{\rho }^{1/2}.$$

(31)

where

$${\mathit{S}}_{(q,t)}=-\frac{\hslash }{2}\mathit{ln}\frac{\mathsf{\psi }}{\mathsf{\psi }\ast }.$$

(32)

In the context of (28)–(31), $\mathsf{\psi }$, defined by (27) and determined by solving Equations (28)–(31), does not denote the quantum wavefunction; rather, it represents the probability wave defined by the stochastic generalization of quantum mechanics. With the exception of some specific cases (see (37)), this probability wave adheres to the limit

$$li{m}_{T\to 0}\mathsf{\psi }=\psi$$

(33)

It is worth noting that the SQHA Equations (28)–(31) show that gravitational dark energy leads to a self-fluctuating system in which noise is an intrinsic property of spacetime dynamical geometry that does not require the presence of an environment.

The agreement between the SQHM and the well-established quantum theory outputs can be additionally validated by applying it to mesoscale systems ($L<\sim {\lambda }_c$). In this scenario, the SQHM reveals that by posing $\mathsf{\psi }\cong \psi$ adheres to the Langevin-Schrodinger-like equation, which, for time-independent systems, is expressed as follows

$$-i\hslash {\partial }_t|\psi |=\frac{{\hslash }^2}{2m}{\partial }_i{\partial }_i\psi -\left(V_{(q)}+Const+\kappa S-qm\kappa D^{1/2}{\xi }_{(t)}+i\frac{Q_{(q,t)}}{2|\psi {|}^2}\right)\psi$$

(34)

that by using (32) can be readjusted as:

$$-i\hslash {\partial }_t|\psi |=\left(\frac{{\hslash }^2}{2m}{\partial }_i{\partial }_i-V_{(q)}-\kappa \left(\frac{\hslash }{2}\mathit{ln}\frac{\psi }{\psi *}+qm{D}^{1/2}{\xi }_{(t)}\right)-i\frac{Q_{(q,t)}}{2|\psi {|}^2}\right)\psi$$

(35)

The term $Q_{(q,t)}$ account for contributions from higher-order cumulants in the mass conservation equation derived from the Smoluchowski equation using Pontryagin’s method ([19] and references therein), which holds the property ${\mathit{lim}}_{D\to 0}{Q}_{(q,t)}=0$.

Moreover, the realization of quantum mechanics is ensured by introducing the semi-empirical parameter $\alpha$ close to zero noise, defined by the relation [19]

$${\mathit{lim}}_{T\to 0}\kappa \cong {\mathit{lim}}_{T\to 0}\alpha \frac{2kT}{mD}=\alpha \frac{8\hslash }{m{\gamma }_D{L}^2},$$

(36)

characterizing the system’s dissipation ability, satisfying the condition ${\mathit{lim}}_{T\to 0}\alpha =0$.

Although in the framework of quantum hydrodynamic formalism, quantum mechanics embodies the deterministic limit of the theory without dissipation, it is interesting to examine a scenario where, nearing the zero-noise threshold, the drag term $-\kappa {\dot{q}}_{j_{(t)}}$ in Equation (24) remains significant and non-zero. This occurs particularly when the parameter $\alpha$ remains relatively high, approaching the quantum limit $L⊲<{\lambda }_c$, such as

$${\mathit{lim}}_{\frac{L}{{\lambda }_c}orT\to 0}\alpha ={\alpha }_0.$$

(37)

In this case, as shown in the appendix, Equation (24) leads to the quantum Brownian motion equation.

The emergence of the Schrödinger–Langevin equation through the stochastic extension of the quantum hydrodynamic model is noteworthy, showcasing a precise alignment with traditional outcomes in literature.

2.1. Emerging Classical Mechanics on Large Size Systems

When manually nullifying the quantum potential in the equations of motion for quantum hydrodynamics (2–4), the classical equation of motion emerges [17]. However, despite the apparent validity of this claim, such an operation is not mathematically sound, as it alters the essential characteristics of the quantum hydrodynamic equations. Specifically, this action leads to the elimination of stationary configurations, i.e., eigenstates, as the balancing force of the quantum potential against the Hamiltonian force [24]—which establishes their stationary mass density distribution condition—is nullified. Consequently, even a small quantum potential cannot be disregarded in conventional quantum mechanics as described by the zero-noise ‘deterministic’ quantum hydrodynamic model (2)–(4).

Conversely, in the stochastic generalization, it is possible to correctly neglect the quantum potential in (3) and (24) when its force is much smaller than the force noise $\varpi$ such as $|\frac{1}{m}{\partial }_i{V}_{qu(\rho )}|\ll |{\varpi }_{(q,t,T)}|$ that by (25) leads to condition

$$|\frac{1}{m}{\partial }_i{V}_{qu(\rho )}|\ll \kappa \left(\frac{L}{{\lambda }_c}\right){\left({\gamma }_D\frac{\hslash }{2m}\right)}^{1/2}=\kappa \left(\frac{L\sqrt{mkT}}{2\hslash }\right){\left({\gamma }_D\frac{\hslash }{2m}\right)}^{1/2},$$

(38)

and hence, in a coarse-grained description with elemental cell side $\Delta q$, to

$${\mathit{lim}}_{q\to \Delta q}\left.\left|{\partial }_i{V}_{qu(\rho )}\right.\right|\ll m\kappa \left(\frac{L}{{\lambda }_c}\right){\left({\gamma }_D\frac{\hslash }{2m}\right)}^{1/2}=m\kappa \sqrt{{\gamma }_D}\frac{L}{2}\sqrt{\frac{kT}{2\hslash }},$$

(39)

where $L$ is the physical length of the system.

It is worth noting that, despite the noise ${\varpi }_{(q,t,T)}$ having a zero mean, the mean of the fluctuations in the quantum potential, denoted as ${\overline{V}}_{st(\mathrm{n},\mathrm{S})}\cong \kappa S$, is not null. This non-null mean generates to the dissipative force $-\kappa {\dot{q}}_{(t)}$ in Equation (24). Consequently, the stochastic sequence of noise inputs disrupts the coherent evolution of the quantum superposition of states, causing them to decay to a stationary mass density distribution with ${\dot{q}}_{(t)}=0$. Moreover, by observing that the stochastic noise

$$\kappa \left(\frac{L}{{\lambda }_c}\right){\left({\gamma }_D\frac{\hslash }{2m}\right)}^{1/2}{\xi }_{(t)}$$

(40)

grows with the size of the system, for macroscopic systems (i.e., $\frac{L}{{\lambda }_c}\to \infty$), condition (38) is satisfied if

$${\mathit{lim}}_{\frac{q}{{\lambda }_c}\to \infty \left(\frac{L}{{\lambda }_c}=\infty \right)}\left|\left.\frac{1}{m}{\partial }_i{V}_{qu({\mathrm{n}}_{(q)})}\right|\right.<\infty .$$

(41)

To attain a comprehensive portrayal devoid of quantum correlations for any large-scale system of physical length $L$, a stricter criterion must be enforced, such as

$${\mathit{lim}}_{\frac{q}{{\lambda }_c}\to \infty }\left|\left.\frac{1}{m}{\partial }_i{V}_{qu({\rho }_{(q)})}\right|\right.={\mathit{lim}}_{\frac{q}{{\lambda }_c}\to \infty }\frac{1}{m}\sqrt{{\partial }_i{V}_{qu({\rho }_{(q)})}{\partial }_i{V}_{qu({\rho }_{(q)})}}=0.$$

(42)

Therefore, acknowledging that

$${\mathit{lim}}_{q\to \infty }{V}_{qu(q)}\propto q^2,$$

(43)

holds for linear systems, from the standpoint of SQHM, it promptly follows that they are incapable of engendering the macroscopic classical phase.

In general, as the Hamiltonian potential strengthens, the wavefunction localization increases, and the quantum potential behavior at infinity becomes more prominent.

This is demonstrable by considering the MDD

$$|\psi {|}^2\propto exp\left[-{P^k}_{(q)}\right],$$

(44)

where ${P^k}_{(q)}$ is a polynomial of order k, and it becomes evident that a finite range of quantum potential interaction is achieved for $k<\frac{3}{2}$.

Hence, linear systems, characterized by $k=2$, exhibit an infinite range of quantum potential action, as well as the ballistic Gaussian coherent states.

Conversely, for gas phases where particles interact via the Lennard–Jones potential, whose long-distance wavefunction reads as [25]

$${lim}_{r\to \infty }|\psi |\propto a^{-1/2}\frac{1}{r},$$

(45)

the quantum potential reads as

$${\mathit{lim}}_{r\to \infty }{V}_{qu(\rho )}\cong {\mathit{lim}}_{q\to \infty }\frac{{\hslash }^2}{2m}\frac{1}{|\psi |}{\partial }_r{\partial }_r|\psi |=\frac{1}{r^2}=\frac{{\hslash }^2}{m}a|\psi {|}^2$$

(46)

leading to the quantum force

$${\mathit{lim}}_{r\to \infty }-{\partial }_r{V}_{qu(\rho )}={\mathit{lim}}_{q\to \infty }\frac{{\hslash }^2}{2m}{\partial }_r\frac{1}{|\psi |}{\partial }_r{\partial }_r|\psi |=\frac{{\hslash }^2}{2m}{\partial }_{r}r{\partial }_r{\partial }_r\frac{1}{r}=-2\frac{{\hslash }^2}{m}\frac{1}{r^3}=0,$$

(47)

Such that satisfying conditions (38) and (42) can lead to large-scale classical behavior [19] in a sufficiently rarefied phase.

It is noteworthy that in Equation (46), the quantum potential output aligns with the hard sphere potential within the ‘pseudo-potential Hamiltonian model’ of the Gross–Pitaevskij equation [26,27], where $\frac{a}{4\pi }$ represents the boson–boson s-wave scattering length.

By observing that, to meet condition (42), it is sufficient to require that

$${\displaystyle \underset{0}{\overset{\infty }{\int }}{r}^{-1}|\frac{1}{m}{\partial }_i{V}_{qu({\rho }_{(q)})}{|}_{(r,\theta ,\phi )}dr} < \infty \forall \theta ,\phi ,$$

(48)

it is possible to define the range of interaction of the quantum potential ${\lambda }_{qu}$ as [19]

$${\lambda }_{qu}={\lambda }_c\frac{{\displaystyle \underset{0}{\overset{\infty }{\int }}{r}^{-1}|{\partial }_i{V}_{qu({\rho }_{(q)})}{|}_{(r,\theta ,\phi )}dr}}{|{\partial }_i{V}_{qu({\rho }_{(q)})}{|}_{(r={\lambda }_c,\theta ,\phi )}}={\lambda }_c{I}_{qu}. I_{qu}>1$$

(49)

Relation (49) provides a measure of the physical length associated with quantum non-local interactions.

It is worth mentioning that quantum non-local interactions extend themselves up to the distance of order of the largest length between ${\lambda }_{qu}$ and ${\lambda }_c$. Below ${\lambda }_c$, due to noise damping, even a feeble quantum potential emerges. Above ${\lambda }_c$ but below ${\lambda }_{qu}$ the quantum potential is strong enough to overcome the fluctuations.

The quantum non-local effects can be extended by increasing ${\lambda }_c$, which can be accomplished by lowering the temperature or mass of the bodies (see (14)), or ${\lambda }_{qu}$, which increases with a stronger Hamiltonian potential. In the latter case, for instance, larger values of ${\lambda }_{qu}$ can be obtained by extending the linear range of Hamiltonian interaction between particles (see (43) and (44)).

2.2. The Lindemann Constant for Quantum Lattice-to-Classical Fluid Transition

For a system of Lennard–Jones interacting particles, the quantum potential range of interaction ${\lambda }_{qu}$ reads as

$${\lambda }_{qu}\cong {\displaystyle \underset{0}{\overset{d}{\int }}dq}+{{\lambda }_c}^4{\displaystyle \underset{d}{\overset{\infty }{\int }}\frac{1}{q^4}dq}=d\left(1+\frac{1}{3}{\left(\frac{{\lambda }_c}{d}\right)}^4\right)$$

(50)

where $d=r_0+\Delta =r_0\left(1+\epsilon \right)$ (with $\epsilon =\frac{\Delta }{r_0}$) represents the distance up to which the inter-atomic force is approximately linear, and $r_0$ denotes the atomic equilibrium distance.

Experimental validation of the physical significance of the quantum potential length of interaction is evident during the quantum-to-classical transition in a crystalline solid at its melting point. This transition occurs as the system shifts from a quantum lattice to a fluid amorphous classical phase.

If we assume that, within the quantum lattice, the atomic wavefunction extends over a distance smaller than the range of interaction of the quantum potential, and if, according to the SQHM perspective, the classical phase of an amorphous fluid is distinguished by molecular wavefunctions extending beyond the influence of the quantum potential (thus preventing the tails from reconstructing quantum coherence), we can infer that the melting point occurs when the variance of the wavefunction equals ${\lambda }_{qu}-r_0$.

Drawing from these assumptions, the Lindemann constant $L_C$, as defined by [28]

$$L_C=\frac{\left\{\begin{array}{l}\mathit{wave} \mathit{function} \mathit{variance}\\ \mathit{at} \mathit{transition}\end{array}\right\}}{r_0},$$

(51)

can be expressed as $L_C=\frac{{\lambda }_{qu}-r_0}{r_0}$. Moreover, it can be theoretically computed as

$${\lambda }_{qu}\approx r_0\left(\left(1+\epsilon \right)+\frac{1}{3}{\left(\frac{{\lambda }_c}{r_0}\right)}^3\right)$$

(52)

which, being typically $\epsilon \approx 0.05÷0.1$ and $\frac{{\lambda }_c}{r_0}\approx 0.8$, leads to

$$L_C\approx 0.217÷0.267.$$

(53)

A more accurate evaluation, employing the potential well approximation for molecular interaction [29,30], yields ${\lambda }_{qu}\cong 1.2357{ r}_0$, and provides a Lindemann constant value of $L_C=0.2357$. This value aligns with measured values, falling within the range of 0.2 to 0.25 [28].

2.3. The Fluid–Superfluid ${}^4\mathbf{H}\mathbf{e}$ $\lambda -$Transition

Given that the De Broglie distance ${\lambda }_c$ is temperature-dependent, its impact on the fluid–superfluid transition in monomolecular liquids at extremely low temperatures, as observed in ${}^4\mathrm{H}\mathrm{e}$, can be identified. The approach to this scenario is elaborated in reference [30], where, for the ${}^4\mathrm{H}\mathrm{e}$-${}^4\mathrm{H}\mathrm{e}$ interaction, the potential well is assumed to be

$$V_{\left(r\right)}=\infty 0<r<\sigma$$

(54)

$$V_{\left(r\right)}=-0.82 U \sigma <r<\sigma +2\Delta$$

(55)

$$V_{\left(r\right)}=0 r>\sigma +2\Delta$$

(56)

In this context, $U=10.9 {\mathrm{k}}_{\mathrm{B}}=1.5\times {10}^{-22} \mathrm{J}$ represents the Lennard–Jones potential depth, and $\sigma +\Delta =3.7\times {10}^{-10} \mathrm{m}$ denotes the mean ${}^4\mathrm{H}\mathrm{e}$-${}^4\mathrm{H}\mathrm{e}$ inter-atomic distance, where $\Delta =1.54\times {10}^{-10} \mathrm{m}$.

Ideally, at the superfluid transition, the De Broglie length attains approximately the mean ${}^4\mathrm{H}\mathrm{e}$-${}^4\mathrm{H}\mathrm{e}$ atomic distance. However, the induction of the superfluid ${}^4\mathrm{H}\mathrm{e}$-${}^4\mathrm{H}\mathrm{e}$ state occurs as soon as the De Broglie length overlaps with the ${}^4\mathrm{H}\mathrm{e}$-${}^4\mathrm{H}\mathrm{e}$ wavefunctions within the potential depth. Therefore, we observe the gradual increase of ${}^4\mathrm{H}\mathrm{e}$ superfluid concentration within the interval

$$\sigma <{\lambda }_c<\sigma +2\Delta .$$

(57)

For ${\lambda }_c<\sigma$, it follows that no superfluidity occurs, as all inter-atomic well potentials lie beyond the damped noise distance of the De Broglie length.

Conversely, for ${\lambda }_c>\approx \sigma +2\Delta$, 100% of molecular interactions are within the zone of quantum coherence, resulting in all molecules of ${}^4\mathrm{H}\mathrm{e}$ being in the superfluid state. Therefore, given that

$${\lambda }_c=\sqrt{2}\frac{\hslash }{{(mkT)}^{1/2}},$$

(58)

for a ${}^4\mathrm{H}\mathrm{e}$ mass of $m_{{}^4\mathrm{H}\mathrm{e}}=6.6\times {10}^{-27} \mathrm{kg}$, the superfluid ratio of 100% is reached at the temperature

$$T_{100\%}\approx \frac{2{\hslash }^2}{mk}{\left(\frac{1}{\sigma +2\Delta }\right)}^2=0.92 °K$$

(59)

consistent with the experimental data from reference [30], which gives $T_{100\%}=1.0 °K$.

Moreover, when the superfluid/normal ${}^4\mathrm{H}\mathrm{e}$ density ratio is 50%, it follows that the temperature $T_{50\%}$ is given by

$$T_{50\%}=\frac{2{\hslash }^2}{mk}{\left(\frac{1}{\sigma +\Delta }\right)}^2=1.92 °K.$$

(60)

This observation is further supported by experimental data, as reported in reference [31], confirming $T_{50\%}=1.95 °K$.

Moreover, by employing the definition that at the $\lambda$-point of ${}^4\mathrm{H}\mathrm{e}$, the superfluid ratio is 38%, such as that ${\lambda }_c=\sigma +38\%\left(2\Delta \right)$, the transition temperature $T_{\lambda }$ is determined as follows.

Furthermore, utilizing the definition that at the critical $\lambda$-point of ${}^4\mathrm{H}\mathrm{e}$, the superfluid ratio is 38%, and considering ${\lambda }_c=\sigma +38\%\left(2\Delta \right)$, the transition temperature $T_{\lambda }$ is determined as follows:

$$T_{\lambda }\approx \frac{2{\hslash }^2}{mk}{\left(\frac{1}{\sigma +0.76\Delta }\right)}^2=2.20 °K$$

(61)

in good agreement with the measured superfluid transition temperature of $2.17 °K$.

As a final remark, it is worth noting that there are two ways to establish quantum macroscopic behavior. One approach involves lowering the temperature, effectively increasing the De Broglie length. The second approach aims to increase the strength of the Hamiltonian interaction among the particles within the system, thereby extending the effective range of the quantum potential.

Regarding the latter, it is important to highlight that the limited strength of the Hamiltonian interaction over long distances is the key factor allowing classical behavior to manifest. When analyzing systems governed by a quadratic or stronger Hamiltonian potential, the range of interaction associated with the quantum potential becomes infinite, or at least remains so as long as the linear Hamiltonian interaction is maintained, as can be inferred from (43). Consequently, achieving a classical phase becomes unattainable when the system’s physical length is smaller than the typical distance up to which the interaction is linear.

In this particular scenario, we exclusively observe the complete manifestation of classical behavior on a macroscopic scale within systems featuring interactions that are sufficiently weak, weaker even than linear interactions. This condition is crucial, as emphasized in Section 2.6.2 and Section 2.6.3, where the chaotic nature of classical motion trajectories is essential for obtaining the Born rule, ensuring the possibility of reaching any eigenstate forming the superposition of states.

Hence, in this scenario, where the quantum potential is incapable of exerting its not-local influence over extensive distances, classical mechanics arises as a decoherent manifestation of quantum mechanics on macroscopic scale, in the presence of a fluctuating spacetime background.

2.4. Measurement Process and the Finite Range of Not-Local Quantum Potential Interactions

Throughout the course of measurement, there exists the possibility of a conventional quantum interaction between the sensing component within the experimental setup and the system under examination. This interaction concludes when the measuring apparatus is relocated to a considerable distance from the system. Within the SQHM framework, this relocation is imperative and must surpass specified distances ${\lambda }_c$ and ${\lambda }_{qu}$.

Following this relocation, the measuring apparatus takes charge of interpreting and managing the ‘interaction output.’ This typically involves a classical, irreversible process characterized by a distinct temporal progression, culminating in the determination of the macroscopic measurement result.

Consequently, the phenomenon of decoherence assumes a pivotal role in the measurement process. Decoherence facilitates the establishment of a large-scale classical framework, ensuring authentic quantum isolation between the measuring apparatus and the system, both pre- and post-measurement event.

This quantum-isolated state, both at the initial and final stages, holds paramount significance in determining the temporal duration of the measurement and in amassing statistical data through a series of independent repeated measurements.

It is crucial to underscore that, within the confines of the SQHM, merely relocating the measured system to an infinite distance before and after the measurement, as commonly practiced, falls short in guaranteeing the independence of the system and the measuring apparatus if either ${\lambda }_c=\infty$ or ${\lambda }_q=\infty$ is met. Therefore, the existence of a macroscopic classical reality remains indispensable for the execution of measurement process.

2.5. Maximum Measurement Precision in Fluctuating Spacetime

Any quantum theory aiming to elucidate the evolution of a physical system across various scales, at any order of magnitude, must inherently address the transition from quantum mechanical properties to the emergent classical behavior observed at larger magnitudes. The fundamental disparities between the two descriptions are encapsulated by the minimum uncertainty principle in quantum mechanics, signifying the inherent incompatibility of concurrently measuring conjugated variables, and the finite speed of propagation of interactions and information in local classical relativistic mechanics violating quantum mechanics’ principle of non-locality, which implies that interactions occur instantaneously over distances (in the Schrodinger formulation).

If a system strictly adheres to the deterministic principles of quantum mechanics within a distance smaller than ${\lambda }_c$, where its subparts lack individual identities, it then follows that an independent observer seeking information about the system must maintain a separation distance greater than a certain distance ${\mathcal{L}}_q\propto {\lambda }_c$, both before and after the process.

Therefore, due to the finite speed of propagation of interactions and information, in the framework of SQHM, the process cannot be executed in a timeframe shorter than

$$\Delta {\tau }_{\mathit{min}}>\frac{{\mathcal{L}}_q}{c}\propto \frac{{\lambda }_c}{c}\propto \frac{2\hslash }{{(2m{c}^{2}kT)}^{1/2}}.$$

(62)

Furthermore, considering the Gaussian noise in (24), with the diffusion coefficient proportional to $kT$, the mean value of energy fluctuation is $\delta E_{(T)}=\frac{kT}{2}$ for the degree of freedom. Moreover, if we assume the relativistic point of view, where the energy of the particle (both kinetic and potential) is encapsulated into its mass, being $m{c}^2>>kT$, it follows that a scalar structureless particle, with mass m, exhibits an energy variance $\Delta E$ of

$$\begin{array}{ll}\Delta E\approx & {(<{(m{c}^2+\delta E_{(T)})}^2-{(m{c}^2)}^2>)}^{1/2}\cong {(<{(m{c}^2)}^2+2m{c}^2\delta E-{(m{c}^2)}^2>)}^{1/2}\\ & \cong {(2m{c}^2<\delta E>)}^{1/2}\cong {(m{c}^{2}kT)}^{1/2}\end{array}$$

(63)

Equation (63) can be better understood by employing the mean energy $\overline{E}$ of the Schrodinger–Langevin equation (see (A4) in the Appendix A) in the final stationary state $\overline{E}={\overline{E}}_{pot}+\overline{V_{qu}}\equiv m{c}^2$ (where the superscript bars represent mean values), along with the stochastic contribution $<\psi |{\left(qm\kappa D^{1/2}{\xi }_{(t)}\right)}^2|\psi >=\frac{kT}{2}$, resulting in $\overline{E}={\overline{E}}_{pot}+\overline{V_{qu}}+\frac{kT}{2}\equiv m{c}^2+\frac{kT}{2}$.

Furthermore, from (63), it follows that

$$\Delta E\Delta t>\Delta E\Delta {\tau }_{\mathit{min}}\propto \frac{{(m{c}^{2}kT)}^{1/2}{\lambda }_c}{c})\propto \sqrt{2}\hslash ,$$

(64)

It is noteworthy that the product $\Delta E\Delta \tau$ remains constant, as the increase in energy variance with the square root of $T$ precisely offsets the corresponding decrease in the minimum acquisition time $\tau$. This outcome also holds true when establishing the maximum possible precision in measuring the position and momentum of a particle with mass m in the SQHM regime.

If we acquire information about the spatial position of a particle with precision $\Delta L$, we effectively exclude the space beyond this distance from the quantum non-local interaction of the particle, and consequently

$${\mathcal{L}}_q<\Delta L.$$

(65)

The variance $\Delta p$ of its relativistic momentum ${(p^{\mu }{p}_{\mu })}^{1/2}=mc$ due to the fluctuations reads as

$$\begin{array}{ll}\Delta p\approx & {(<{(mc+\frac{\delta E_{(T)}}{c})}^2-{(mc)}^2>)}^{1/2}\cong {(<{(mc)}^2+2m\delta E-{(mc)}^2>)}^{1/2}\\ & \cong {(2m<\delta E>)}^{1/2}\cong {(mkT)}^{1/2}\end{array}$$

(66)

and the maximum attainable precision reads as

$$\Delta L\Delta p>{\mathcal{L}}_q{(mkT)}^{1/2}\propto {\lambda }_c{(mkT)}^{1/2})\propto \sqrt{2}\hslash$$

(67)

Equating (64) and (67) to the quantum uncertainty value $\frac{\hslash }{2}$, such as

$$\Delta L\Delta p>{\mathcal{L}}_q{(2mkT)}^{1/2}=\frac{\hslash }{2}$$

(68)

and

$$\Delta E\Delta t>\Delta E\Delta {\tau }_{\mathit{min}}=\frac{{(2m{c}^{2}kT)}^{1/2}{\mathcal{L}}_q}{c}=\frac{\hslash }{2},$$

(69)

it follows that ${\mathcal{L}}_q=\frac{{\lambda }_c}{2\sqrt{2}}$ represents the physical length below which quantum entanglement is fully effective, and it signifies the physical length-scale below which the deterministic limit of the SQHM, specifically the realization of quantum mechanics, fully takes place.

By performing the limit of (68) and (69) for $T=0$(${\lambda }_c\to \infty$), within the non-relativistic limit ($c\to \infty$), it follows that

$$\Delta {\tau }_{\mathit{min}}=\frac{{\lambda }_c}{2c\sqrt{2}}\to \infty$$

(70)

$$\Delta E\cong {(m{c}^{2}kT)}^{1/2}=\sqrt{2}\frac{\hslash c}{{\lambda }_c}\to 0,$$

(71)

$${\mathcal{L}}_q=\frac{{\lambda }_c}{2\sqrt{2}}\to \infty$$

(72)

$$\Delta p\cong {(mkT)}^{1/2}\cong \frac{\sqrt{2}\hslash }{{\lambda }_c}\to 0$$

(73)

and therefore, for the deterministic limit of conventional quantum mechanics, it results in

$$\Delta E\Delta t>\Delta E\Delta {\tau }_{\mathit{min}}=\frac{\hslash }{2}$$

(74)

$$\Delta L\Delta p>{\mathcal{L}}_q{(mkT)}^{1/2}=\frac{\hslash }{2}$$

(75)

By associating the maximum precision of measurements with the variance of corresponding observables in quantum mechanics, (75) aligns with the concept of minimum uncertainty in quantum mechanics, which arises from the deterministic limit of the SQHM.

It is worth noting that, by (74), the SQHM extends uncertainty relations to all conjugate variables of 4D spacetime. This extension is notable since, in conventional quantum mechanics, the energy–time uncertainty is deemed impossible due to the lack of a defined time operator.

Moreover, it is intriguing to observe that in the realm of quantum mechanics, the minimum acquisition time for information is $\Delta {\tau }_{\mathit{min}}=\frac{{\mathcal{L}}_q}{c}$. This minimum time, in the context of the low-velocity limit of classical quantum mechanics, results in $\Delta {\tau }_{\mathit{min}}=\frac{{\mathcal{L}}_q}{c}\to \infty$. This result indicates that performing a measurement within a fully deterministic quantum mechanical global system is not feasible, as its duration would be infinite. Moreover, it must be noted that the Heisenberg minimum uncertainty relations refer to the quantum variance even though the measurement is not possible and the corresponding precision cannot be defined in a perfectly quantum universe. Since the deterministic limit of SQHM is reached through successive steps within the open SQHM regime, the limiting measurement precision is associated with the quantum variance of the corresponding observable.

Given that non-locality is restricted to domains with physical lengths on the order of $\frac{{\lambda }_c}{2\sqrt{2}}$, and information about a quantum system cannot be transmitted faster than the speed of light (otherwise it would violate the uncertainty principle), local realism is established within the coarse-grained macroscopic physics where domains of order of ${{\lambda }_c}^3$ reduce to a point.

The paradox of ‘spooky action at a distance’ is confined to microscopic distances (smaller than $\frac{{\lambda }_c}{2\sqrt{2}}$), where quantum mechanics are described within the low-velocity limit, assuming $c\to \infty$ and ${\lambda }_c\to \infty$. This leads to the apparently instantaneous transmission of interaction over a distance.

It is also noteworthy that in the presence of noise, the measured precision undergoes a relativistic correction, as expressed by $\Delta E\approx {(<{(m{c}^2+\frac{kT}{2})}^2-{(m{c}^2)}^2>)}^{1/2}={(m{c}^{2}kT)}^{1/2}\left(1+\frac{kT}{4m{c}^2}\right)$, resulting in the maximum precision in a quantum system subject to gravitational background noise ($T>0$)

$$\Delta E\Delta t>\frac{\hslash }{2}{\left(1+\frac{kT}{4m{c}^2}\right)}^{1/2}$$

(76)

and

$$\Delta L\Delta p>\frac{\hslash }{2}{\left(1+\frac{kT}{4m{c}^2}\right)}^{1/2}$$

(77)

This can become significant for light particles (with $m\to 0$), but in quantum mechanics, at $T=0$, the uncertainty relations remain unchanged.

2.6. Minimum Discrete Interval of Spacetime

Within the framework of the SQHM, incorporating the maximum precision of measure in a fluctuating quantum system and the maximum attainable velocity of the speed of light

$$\stackrel{·}{x}\le c,$$

(78)

by (68), in a fluctuating vacuum with $T>0$ possibly with classical large-scale behavior (enabling the presence of the measuring apparatus), it follows that

$$\Delta \stackrel{·}{x}=\frac{\Delta p}{m}=\frac{\hslash }{2m\Delta x}\le \stackrel{·}{x},$$

(79)

leading to $\frac{\hslash }{2m\Delta x}\le c$ and, consequently, to

$$\Delta x>\frac{\hslash }{2mc}=\frac{R_c}{2}.$$

(80)

where $R_c$ is the Compton length.

Identity (80) states that the highest possible concentration of a body’s mass is within an elemental volume with a side length equal to half of its Compton wavelength.

This result holds significant implications for black hole (BH) formation. To form a BH, all the mass must be contained within the gravitational radius $R_g$, giving rise to the relationship

$$R_g=\frac{2Gm}{c^2}>\frac{\Delta x}{2}=r_{\min }=\frac{R_c}{4},$$

(81)

which further leads to the condition

$$\frac{R_c}{4R_g}=\frac{\hslash }{8mc{R}_g}=\frac{\hslash c}{8m^{2}G}=\pi \frac{{m_p}^2}{m^2}<1$$

(82)

indicating that a BH’s mass, due to quantum effects, cannot be smaller than $\sqrt{\pi }{m}_p=\sqrt{\frac{\hslash c}{8m^{2}G}}$ to ensure all its mass is confined within its gravitational radius.

The validity of the result (82) is substantiated by the gravitational effects produced by the quantum mass distribution within spacetime. This demonstration elucidates that when mass density is condensed into a sphere with a diameter smaller than half the Compton wavelength, it engenders an outgoing quantum potential force that overcomes the compressive gravitational force within a black hole [32,33].

Considering a Planck mass black hole as the lightest configuration, with its mass compressed within a sphere of half the Compton wavelength, it logically follows that black holes with masses greater than $m_p$ [19] exhibit their mass as compressed into a sphere of smaller diameter. Consequently, given the significance of elemental volume as the volume inside which content is uniformly distributed, the consideration of the Planck length as the smallest discrete elemental volume of spacetime is not sustainable. This would make it impossible to compress the mass of large black holes within a sphere of a smaller diameter, consequently preventing the achievement of gravitational equilibrium [32].

This assumption conflicts with the fact that any existing black holes compress their mass into a nucleus smaller than the Planck length [33].

This compression is feasible if spacetime discretization allows for elemental cells of smaller volume, thereby distinguishing between the minimum measurable distance and the minimum discrete element of distance in the spacetime lattice. In the simulation analogy, the maximum grid density is equivalent to the elemental cell of the spacetime.

Finally, it is worth noting that the current theory leads to the assumption that the elemental discrete spacetime distance corresponds to the Compton length of the maximum possible mass, which is the energy/mass of the universe. Consequently, we have a criterion to rationalize the mass of the universe—why it is not higher than its value—being intricately linked to the minimum length of the discrete spacetime element. If the pre-Big Bang black hole (PBBH) was generated by a fluctuation anomaly in an elemental cell of spacetime, it could not have a mass/energy content smaller than that which the universe possesses.

2.6.1. Dynamics of Wavefunction Collapse

The Markov process (24) can be described by the Smoluchowski equation for the Markov probability transition function (PTF) [23]

$$P_{(q,q_0|t+\tau ,t_0)}={\displaystyle \underset{-\infty }{\overset{\infty }{\int }}{P}_{(q,z|\tau ,t)} P_{(z,q_0|t-t_0,t_0)}} d^{r}z$$

(83)

where the PTF $P_{(q,z|\tau ,t)}$ is the probability that in time interval τ is transferred to point q.

The conservation of the PMD shows that the PTF displaces the PMD according to the rule [23]

$$\rho (q,t)={\displaystyle \int P(q,z|t,0){\rho }_{(z,0)}}{d}^{r}z$$

(84)

Generally, in the quantum case, Equation (83) cannot be reduced to a Fokker–Planck equation (FPE). The functional dependence of $V_{{qu}_{(\rho )}}$ by ${\rho }_{(q,t)}$, and the PTF $P(q,z|t,0)$, produces non-Gaussian terms [19].

Nonetheless, if, at the initial time, ${\rho }_{(q,t_0)}$ is stationary (e.g., in a quantum eigenstate) and close to the long-time final stationary distribution ${\rho }_{eq}$, it is possible to assume that the quantum potential is constant in time as a Hamilton potential following the approximation

$$V_{qu}\cong -(\frac{{\hslash }^2}{4m})\left({\partial }_q{\partial }_q\left(\mathit{ln}{\rho }_{eq(q)}\right)+\frac{1}{2}{\left({\partial }_q\left(\mathit{ln}{\rho }_{eq(q)}\right)\right)}^2\right)$$

(85)

Being the quantum potential independent by the mass density time evolution, the stationary long-time solutions ${\rho }_{eq(q)}$ can be approximately described by the Fokker–Planck equation

$${\partial }_{t}P(q,z|t,0)+{\partial }_{i}P(q,z|t,0)\cdot {\upsilon }_i=0$$

(86)

where

$${\upsilon }_i=\frac{1}{m\kappa }{\partial }_i\left(\frac{{\hslash }^2}{4m}\left({\partial }_j{\partial }_j\mathit{ln}{\rho }_{eq}-\frac{1}{2}{\left({\partial }_j\mathit{ln}{\rho }_{eq}\right)}^2\right)+V_{(q)}\right)-\frac{D}{2}{\partial }_i\mathit{ln}{\rho }_{eq}$$

(87)

leading to the final equilibrium of the stationary quantum configuration

$$\frac{1}{m\kappa }{\partial }_i\left(V_{(q)}-\frac{{\hslash }^2}{4m}\left({\partial }_j{\partial }_j\left(\mathit{ln}{\rho }_{eq(q)}\right)+\frac{1}{2}{\left({\partial }_j\left(\mathit{ln}{\rho }_{eq(q)}\right)\right)}^2\right)\right)+\frac{D}{2}{\partial }_i\left(\mathit{ln}{\rho }_{eq}\right)=0$$

(88)

In ref. [19], the stationary states of a harmonic oscillator obeying (88) are shown. The results show that the quantum eigenstates are stable and maintain their shape (with a small change in their variance) when subject to fluctuations.

It is worth mentioning that in (88), $\rho$ does not represent the fluctuating quantum mass density $|\psi {|}^2$ but is the probability mass density (PMD) of it.

2.6.2. Evolution of the PMD of Superposition of States Submitted to Stochastic Noise

The quantum evolution of not-stationary state superpositions (not considering fast kinetics and jumps) involves the integration of Equation (24) that reads as

$$\dot{q}=-\frac{1}{\kappa m}{\partial }_q\left(V_{(q)}-\frac{{\hslash }^2}{4m}\left({\partial }_q\left({\partial }_q\mathit{ln}\rho \right)+\frac{1}{2}{\left({\partial }_q\mathit{ln}\rho \right)}^2\right)\right)+D^{1/2}{\xi }_{(t)}$$

(89)

By utilizing the associated conservation Equation (84) for the PMD $\rho$, it is possible to integrate (89) by using its second-order discrete expansion

$$q_{k+1}\cong q_k-\frac{1}{m\kappa }{\partial }_k\left(V_{(q_k)}+V_{qu({\rho }_{q_k,}{t}_k)}\right)\Delta t_k-\frac{1}{m\kappa }\frac{d}{dt}{\partial }_k\left(V_{(q_k)}+V_{qu({\rho }_{q_k,}{t}_k)}\right)\frac{\Delta {t_k}^2}{2}+D^{1/2}\Delta W_k$$

(90)

where

$$q_k=q_{(t_k)}$$

(91)

$$\Delta t_k=t_{k+1}-t_k$$

(92)

$$\Delta W_k=W_{(t_{k+1})}-W_{(t_k)}$$

(93)

where $\Delta W_k$ has a Gaussian zero mean and unitary variance whose probability function $P(\Delta W_k,\Delta t)$, for $\Delta t_k=\Delta t \forall k$, reads as

$$\begin{array}{ll}{\mathit{lim}}_{\Delta t\to 0}{P}_{(\Delta W_k,\Delta t)}& ={\mathit{lim}}_{\Delta t\to 0}\frac{D^{-1/2}}{{\left(4\pi \Delta t\right)}^{1/2}}exp-\frac{\Delta {W_k}^2}{4\Delta t}\\ & ={\mathit{lim}}_{\Delta t\to 0}\frac{D^{-1/2}}{{\left(4\pi \Delta t\right)}^{1/2}}exp-\frac{1}{4\Delta t}\frac{{\left(q_{k+1}-<q_{k+1}>\right)}^2}{D}\\ & ={\left(4\pi D\Delta t\right)}^{-1/2}exp-\frac{1}{4\Delta t}\frac{{\left(q_{k+1}-q_k-<{\dot{\overline{q}}}_k>\Delta t-\frac{<{\ddot{\overline{q}}}_k>}{2}\Delta t^2\right)}^2}{D}\end{array}$$

(94)

where the midpoint approximation has been introduced

$${\overline{q}}_k=\frac{q_{k+1}+q_k}{2}$$

(95)

and where

$$<{\dot{\overline{q}}}_k>=-\frac{1}{m\kappa }\frac{\partial \left(V_{({\overline{q}}_k)}+V_{qu({\rho }_{{\overline{q}}_k}{t}_k)}\right)}{\partial {\overline{q}}_k}$$

(96)

and

$$<{\ddot{\overline{q}}}_k>=-\frac{1}{2m\kappa }\frac{d}{dt}\frac{\partial \left(V_{({\overline{q}}_k)}+V_{qu({\rho }_{({\overline{q}}_k)},t_k)}\right)}{\partial {\overline{q}}_k}$$

(97)

are the solutions of the deterministic problem

$$<q_{k+1}>\cong <q_k>-\frac{1}{m\kappa }{\partial }_k\left(V_{(q_k)}+V_{qu({\rho }_{q_k,}{t}_k)}\right)\Delta t_k-\frac{1}{m\kappa }\frac{d}{dt}{\partial }_k\left(V_{(q_k)}+V_{qu({\rho }_{q_k,}{t}_k)}\right)\frac{\Delta {t_k}^2}{2}$$

(98)

As shown in ref. [19], the PTF $P_{(q_k,q_{k-1}|\Delta t,(k-1)\Delta t)}$ can be achieved after successive steps of approximation and reads as

$$\begin{array}{l}{P}_{(q_k,q_{k-1}|\Delta t,(k-1)\Delta t)}={\mathit{lim}}_{u\to \infty }{P^{(u)}}_{(q_k,q_{k-1}|\Delta t,(k-1)\Delta t)}\\ \cong {\left(4\pi D\Delta t\right)}^{-1/2}{\mathrm{e}}^{\frac{\Delta t}{4D}\left[-{\left({\dot{q}}_{k-1}-\frac{<{\dot{q}}_k{>}^{(\infty )}+<{\dot{q}}_{k-1}>}{2}\right)}^2+D\left({\partial }_{q_k}<{\dot{q}}_k{>}^{(\infty )}+{\partial }_{q_{k-1}}<{\dot{q}}_{k-1}>\right)\right]}\end{array}$$

(99)

and the PMD at the $k$-th instant reads as

$${{\rho }^{(\infty )}}_{(q_k,k\Delta t)}={\displaystyle \underset{-\infty }{\overset{\infty }{\int }}{P^{(\infty )}}_{(q_k,q_{k-1}|\Delta t,(k-1)\Delta t)} {\rho }_{(q_{k-1},\left(k-1\right)\Delta t)}}d{q}_{k-1}$$

(100)

leading to the velocity field

$$<{\dot{q}}_k{>}^{(\infty )}=-\frac{1}{m\kappa }{\partial }_{q_k}\left(V_{(q_k)}-\frac{{\hslash }^2}{4m}\left({\partial }_q{\partial }_q\left(\mathit{ln}{\rho }^{(\infty )}\right)+\frac{1}{2}{\left({\partial }_q\left(\mathit{ln}{\rho }^{(\infty )}\right)\right)}^2\right)\right)$$

(101)

Moreover, the continuous limit of the PTF gives

$$\begin{array}{l}{P}_{(q,q_0|t-t_0,0)}={\mathit{lim}}_{\Delta t\to 0}{P^{(\infty )}}_{(q_n,q_0|n\Delta t,0)}\\ ={\mathit{lim}}_{\Delta t\to 0}{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}{\prod }_{k=1}^{n}d{q}_{k-1}{P^{(\infty )}}_{(q_k,q_{k-1}|\Delta t,(k-1)\Delta t)}}\\ ={\displaystyle \underset{q_0}{\overset{q}{\int }}Dq}{\mathrm{e}}^{\left[-\frac{1}{2D}{\displaystyle \sum _{k=1}^n<{\dot{\overline{q}}}_{k-1}{>}^{(\infty )}\Delta q_k}\right]}{\mathrm{e}}^{-\frac{\Delta t}{4D}\left[{\displaystyle \sum _{k=1}^n\begin{array}{l}{\left(\frac{q_k-q_{k-1}}{\Delta t}\right)}^2\\ \end{array}}-2D\frac{\partial <{\dot{\overline{q}}}_{k-1}{>}^{(\infty )}}{\partial {\overline{q}}_{k-1}}+{<{\dot{\overline{q}}}_{k-1}>}^{{(\infty )}^2}\right]}\\ =\left({\mathrm{e}}^{{\displaystyle \underset{q_0}{\overset{q}{\int }}\frac{1}{2D}<\dot{q}>dq}}\right){\displaystyle \underset{q_0}{\overset{q}{\int }}Dq}{\mathrm{e}}^{-\frac{1}{4D}{\displaystyle \underset{t_0}{\overset{t}{\int }}dt\left({\dot{q}}^2+{<\dot{q}>}^2+2D{\partial }_q<\dot{q}>\right)}}\end{array}$$

(102)

where $<{\dot{\overline{q}}}_{k-1}{>}^{(\infty )}=\frac{1}{2}\left(<{\dot{q}}_k{>}^{(\infty )}+<{\dot{q}}_{k-1}{>}^{(\infty )}\right)$.

The resolution of the recursive Expression (102) offers the advantage of being applicable to nonlinear systems that are challenging to handle using conventional approaches [34,35,36,37].

2.6.3. General Features of Relaxation of the Quantum Superposition of States

The classical Brownian process admits the stationary long-time solution

$$P_{(q,q_{-\infty }|t-t_{-\infty },t_{-\infty })}={\mathit{lim}}_{t_0\to -\infty }N{\mathrm{e}}^{\frac{1}{D}{\displaystyle \underset{q_{-\infty }}{\overset{q}{\int }}{<\dot{q}>}_{({q^{\prime }}_{\left(t,t_0\right)})}d{q}^{\prime }}}=N{\mathrm{e}}^{\frac{1}{D}{\displaystyle \underset{q_{-\infty }}{\overset{q}{\int }}K(q^{\prime })d{q}^{\prime }}}$$

(103)

where $K(q)=-\frac{1}{m\kappa }\frac{\partial V_{(q)}}{\partial q}$, leading to solution [13]

$$P(q,q_0|t-t_0,t_0)=\left(exp{\displaystyle \underset{q_0}{\overset{q}{\int }}\frac{1}{2D}K(q^{\prime })d{q}^{\prime }}\right){\displaystyle \underset{q_0}{\overset{q}{\int }}Dq}exp-\frac{1}{4D}{\displaystyle \underset{t_0}{\overset{t}{\int }}dt\left({\dot{q}}^2+K^2(q)+2D{\partial }_{q}K(q)\right)}$$

(104)

As far as it concerns ${{<\dot{q}>}^{(\infty )}}_{(q,t)}$ in quantum case (102), it cannot be expressed in a closed form, unlike (103), because it is contingent on the particular relaxation path ${\rho }_{(q,t)}$, which the system follows toward the steady state. This path is significantly influenced by the initial conditions, namely the MDD ${{|\psi |}^2}_{(q,t_0)}={\rho }_{(q,t_0)}$ as well as $<\dot{q}{>}_{(q,t_0)}$, and, consequently, by the initial time $t_0$, at which the quantum superposition of states is subjected to fluctuations.

In addition, from (90), we can see that $q_{t_k}$ depends on the exact sequence of inputs of stochastic noise, since, in classically chaotic systems, very small differences can lead to relevant divergences of the trajectories in a short time. Therefore, in principle, different stationary configurations ${\rho }_{(q,t=\infty )}$ (analogues of quantum eigenstates) can be reached whenever they start from an identical superposition of states. Therefore, in classically chaotic systems, Born’s rule can also be applied to the measurement of a single quantum state.

Even if $L\ll {\lambda }_c\cup {\lambda }_{qu}$, it is worth noting that, to have finite quantum lengths ${\lambda }_c$ and ${\lambda }_{qu}$ (necessary to have quantum stochastic dynamics) and the quantum decoupled (classical) environment or measuring apparatus, the nonlinearity of the overall system (system–environment) is necessary: quantum decoherence, leading to the decay of superposition states, is significantly promoted by the widespread classical chaotic behavior observed in real systems.

On the other hand, a perfect linear universal system would maintain quantum correlations on a global scale and would never allow for quantum decoupling between the system and the experimental apparatus performing the measure. Merely assuming the existence of separate systems and environments subtly introduces the classical condition (${\lambda }_c,{\lambda }_{qu}<\infty$) into the nature of the overall supersystem.

Furthermore, given that Equation (24) (see Equations (A31) and (A38), in ref. [19]) is valid only in the leading order of approximation of $\dot{q}$ (i.e., during a slow relaxation process with small amplitude fluctuations), in instances of large fluctuations occurring on a timescale much longer than the relaxation period of ${\rho }_{(q,t)}$, transitions may occur to ${\tilde{n}}_{(q,t)}$ that are not captured by (102), potentially leading from a stationary eigenstate to a new superposition of states.

In this case, relaxation will follow again toward another stationary state. ${\rho }_{(q,t)}$ (100) describes the relaxation process occurring in the time interval between two large fluctuations rather than the system evolution toward a statistical mixture. Due to the extended timescales associated with these jumping processes, a system comprising a significant number of particles (or independent subsystems) undergoes a gradual relaxation towards a statistical mixture. The statistical distribution of this mixture is dictated by the temperature-dependent behavior of the diffusion coefficient.

2.7. EPR Paradox and Pre-Existing Reality

The SQHM highlights that conventional quantum theory, despite its well-defined reversible deterministic theoretical framework, remains incomplete with respect to its foundational postulates. Specifically, the SQHM underscores that the measurement process is not explicated within the deterministic ‘Hamiltonian’ framework of standard quantum mechanics. Instead, it manifests as a phenomenon comprehensively described within the framework of a quantum stochastic generalized approach.

The SQHM reveals that quantum mechanics represents the deterministic (zero noise) limit of a broader quantum–stochastic theory induced by spacetime gravitational background fluctuations.

From this standpoint, zero-noise quantum mechanics defines the deterministic evolution of the ‘probabilistic wave’ of the system. Moreover, the SQHM suggests that the term ‘probabilistic’ is inaccurately introduced, since it arises from the inherent probabilistic nature of the measurement process outside the theory framework. Given the capacity of the SQHM to describe both wavefunction decay and the measurement process, thereby achieving a comprehensive quantum theory, the term ‘state wave’ is a more appropriate substitute for the expression ‘probabilistic wave’. The SQHM theory reinstates the principle of determinism into conventional quantum theory, emphasizing that it delineates the deterministic evolution of the ‘state wave’ of the system. It elucidates the probabilistic outcomes as a consequence of the fluctuating gravitational background.

Furthermore, it is noteworthy to observe that the SQHM addresses the lingering question of pre-existing reality before measurement. In contrast, the Copenhagen interpretation posits that only the measurement process allows the system to decay into a stable eigenstate, establishing a persistent reality over time. Consequently, it remains indeterminate within this framework whether a persistent reality exists prior to measurement. The SQHM rejects the anthropocentric notion that the act of measurement induces the collapse of the wavefunction, in line with the viewpoint of Penrose: ‘It takes place in the physics, and it is not because somebody comes and looks at it’.

About this point, the SQHM introduces a simple and natural innovation showing that the world is capable of self-decaying through macroscopic-scale decoherence, wherein only the stable macroscopic stationary states (very close to eigenstates, or coherent states) persist. These states, being stable with respect to fluctuations, establish an enduring reality that exists prior to measurement.

Regarding the EPR paradox, the SQHM demonstrates that, in a perfect quantum deterministic (coherent) universe, it is not feasible to achieve the complete decoupling between the subparts of the system, namely the measuring apparatus and the measured system, and carry out the measurement in a finite time interval. Instead, this condition can only be realized within a large-size classical supersystem—a quantum system in 4D spacetime with fluctuating background—where the quantum entanglement, due to the quantum potential, extends up to a finite distance [19]. Under these circumstances, the SQHM shows that it is possible to restore local relativistic causality with a finite speed of transmission of interactions and information, compatible with the precision of measurements that are confined outside quantum non-local domains with lengths smaller than $\frac{{\lambda }_c}{2\sqrt{2}}$.

If the Lennard–Jones inter-particle potential yields a sufficiently weak force, resulting in a microscopic range of quantum non-local interaction and a large-scale classical phase, photons, as demonstrated in reference [19], maintain their quantum behavior at the macroscopic level due to their infinite quantum potential range of interaction. Consequently, they represent the optimal particles for conducting experiments aimed at demonstrating the characteristics of quantum entanglement over a distance.

In order to clearly describe the standpoint of the SQHM on this argument, we can analyze the output of two entangled photon experiment traveling in opposite directions in the state

$$|\psi >=\frac{1}{\sqrt{2}}|H_1,H_2>+e^{i\phi }|V_1,V_2>$$

(105)

Vertical and horizontal polarizations are denoted as $V$ and $H$ respectively, while $\varphi$ represents a constant phase coefficient.

Photons ‘one’ and ‘two’ encounter polarizers $P_a$ (Alice) and $P_b$ (Bob), with their polarization axes positioned at angles $\alpha$ and $\beta$ relative to the horizontal axis, respectively. For the sake of our analysis, we can assume $\varphi =0$.

The likelihood of photon ‘two’ successfully traversing Bob’s polarizer is $P\left(\alpha ,\beta \right)=\frac{1}{2}{\cos }^2\left(\alpha -\beta \right)$.

According to the prevailing view in quantum mechanics in the scientific community, when photon ‘one’ traverses polarizer $P_a$ at an angle of $\alpha$ relative to its axes, the state of photon ‘two’ immediately collapses to a linearly polarized state at the same angle $\alpha$, leading to the composite state $|{\alpha }_1,{\alpha }_2>=|{\alpha }_1>|{\alpha }_2>$.

On the other hand, within the framework of SQHM, which can elucidate the dynamics of wavefunction collapse, the collapse process is not instantaneous. Following the Copenhagen interpretation of quantum mechanics, it is imperative to assert rigorously that the state of photon ‘two’ remains undefined until its measurement at the polarizer $P_b$.

Hence, when photon ‘one’ traverses polarizer $P_a$, according to the SQHM perspective, we must consider the composite state as $|{\alpha }_1,S>=|{\alpha }_1>|Q{P}_1,S_2>$, where $|Q{P}_1,S_2>$ signifies the state of photon ‘two’ in interaction with the residual tail field $Q{P}_1$ generated by the quantum potential of photon ‘one’ at polarizer $P_a$.

The spatial extension of the field $|Q{P}_1,S_2>$, in the case where the photons travel in opposite direction, is the double of the one crossed by photon one before its adsorption. In this regard, it is noteworthy that the quantum potential is not proportional to the intensity of the tail field of photon one. Instead, it is proportional to its second derivative. Therefore, a minimal residual tail field with a high frequency interacting with photon two can result in a notable quantum potential interaction originating from the tail field $Q{P}_1$.

When the residual part of the two entangled photons $|Q{P}_1,S_2>$ also passes through Bob’s polarizer, it undergoes the transition $|Q{P}_1,S_2>\to |{\beta }_2>$ with probability $P\left(\alpha ,\beta \right)=\frac{1}{2}{\cos }^2\left(\alpha -\beta \right)$. The duration of the photon two adsorption (wavefunction decay and measurement) due to its spatial extension, and finite light speed, it is just the time necessary to transfer the information about the measure of photon one to the place of photon two measurement. A possible experiment is proposed in ref. [19].

Summarizing, the SQHM reveals the following key points:

• The SQHM posits that quantum mechanics represents the deterministic limit of a broader quantum stochastic theory.
• Classical reality emerges at the macroscopic level, constituting a pre-existing reality before measurement.
• The measurement process is feasible in a classical macroscopic world, because we can have really quantum decoupled and independent systems, namely the system and the measuring apparatus.
• Determinism is acknowledged within standard quantum mechanics under the condition of zero GBN.
• Locality is achieved at the macroscopic scale, where quantum non-local domains condense to punctual domains.
• Determinism is retrieved in quantum mechanics representing the zero-noise limit of the SQHM. The probabilistic nature of quantum measurement is introduced by GBN.
• The maximum light speed of the propagation of information and the local relativistic causality align with quantum uncertainty.
• The SQHM addresses GBN as playing the role of the hidden variable in the Bohm non-local hidden variable theory: the Bohm theory ascribes the indeterminacy of the measurement process to the unpredictable pilot wave, whereas stochastic quantum hydrodynamics attributes its probabilistic nature to the fluctuating gravitational background. This background is challenging to determine due to its predominantly early-generation nature during the Big Bang, characterized by the weak force of gravity without electromagnetic interaction. In the context of Santilli’s non-local hidden variable approach in IsoRedShift Mechanics, it is possible to demonstrate the direct correspondence between the non-local hidden variable and GBN [21]. Furthermore, it must be noted that the consequent probabilistic nature of the wavefunction decay, and its measured output, is also compounded by the inherently chaotic nature of the classical law of motion and the randomness of GBN, further contributing to the indeterminacy of measurement outcomes.

2.8. The SQHM and the Objective-Collapse Theories

The SQHM well inserts itself into the so-called objective-collapse theories [37,38,39,40]. In collapse theories, the Schrödinger equation is augmented with additional nonlinear and stochastic terms, referred to as spontaneous collapses, that serve to localize the wavefunctions in space. The resulting dynamics ensures that, for microscopic isolated systems, the impact of these new terms is negligible, leading to the recovery of usual quantum properties with only minute deviations.

An inherent amplification mechanism operates to strengthen the collapse in macroscopic systems comprising numerous particles, overpowering the influence of quantum dynamics. Consequently, the wavefunction for these systems is consistently well-localized in space, behaving practically like a point in motion following Newton’s laws.

In this context, collapse models offer a comprehensive depiction of both microscopic and macroscopic systems, circumventing the conceptual challenges linked to measurements in quantum theory. Prominent examples of such theories include the Ghirardi–Rimini–Weber model [38], the continuous spontaneous localization model [39] and the Diósi–Penrose model [40,41].

While the SQHM aligns well with existing objective-collapse models, it introduces an innovative approach that effectively addresses critical aspects within this class of theories. One notable achievement is the resolution of the ‘tails’ problem by incorporating the quantum potential length of interaction, in addition to the De Broglie length. Beyond this interaction range, the quantum potential cannot maintain the coherent Schrödinger quantum behavior of wavefunction tails.

The SQHM also highlights that there is no need for an external environment, demonstrating that the quantum stochastic behavior responsible for wavefunction collapse can be an intrinsic property of the system in a spacetime with fluctuating metrics due to the gravitational background. In principle, gravitons, a manifestation of dark energy within the gravitational field, can be thought of as external environment. However, there exists a nuanced distinction from conventional concepts. While an external system or environment typically exists separately from the physical system of interest, gravitational vibrations within the reference system represent something distinct: There is no additional physical system per se, but rather, the external system is inherently integrated into the specific type of reference system under consideration. While the concept remains largely the same, there are subtle, yet fundamentally important differences. Thus, rather than rejecting existing concepts outright, it can be seen as an enhancement or refinement of them. Furthermore, situated within the framework of relativistic quantum mechanics, which aligns seamlessly with the finite speed of light and information transmission, the SQHM establishes a clear connection between the uncertainty principle and the invariance of light speed.

The theory also derives, within a fluctuating quantum system, the indeterminacy between energy and time—an aspect not expressible in conventional quantum mechanics—providing insights into measurement processes that cannot be completed within a finite time interval in a truly quantum global system. Notably, the theory finds support in the confirmation of the Lindemann constant for the melting point of solid lattices and the transition of ${}^4\mathrm{H}\mathrm{e}$ from fluid to superfluid states. Additionally, it can possibly propose a potential explanation for the measurement of entangled photons through a Earth–Moon–Mars experiment [19].

3. Simulation Analogy: Complexity in Achieving Future States

The discrete spacetime structure derived by (80) ${\Delta x}_{\mathit{min}}>\frac{\hslash }{2m_{u}c}=\frac{\hslash c}{2E_u}$ (where $E_u$ is the total energy of the universe) that comes from the finite speed of light together with the minimum discrete measurable distance (69) allows for the implementation of a discrete simulation of the universe’s evolution.

In this case, the programmer of such universal simulation has to face the following problems:

• One key argument revolves around the inherent challenge of any computer simulation, namely the finite nature of computer resources. The capacity to represent or store information is confined to a specific number of bits. Similarly, the availability of floating-point operations per second is limited. Regardless of effort, achieving a truly ‘continuous’ simulated reality in the mathematical sense becomes unattainable due to these constraints. In a computer-simulated universe, the existence of infinitesimals and infinities is precluded, necessitating quantization, which involves defining discrete cells in spacetime.
• The speed of light must be finite. Despite real time and simulation time being disconnected from each other, computing the evolution of a system where interactions propagate infinitely fast necessitates the simultaneous computation of all interactions within a single timeframe. However, it is a practical impossibility for any computer with finite computing power to execute such a task. The limitation arises from the fact that any computer can only achieve a finite speed of propagation in a simulation, as this is the sole feasible method of integration. Therefore, a common issue in computer-simulation arises from the inherent limitation of computing power in terms of the speed of executing calculations. Objects within the simulation cannot surpass a certain speed, as doing so would render the simulation unstable and compromise its progression. Any propagating process cannot travel at an infinite speed, as such a scenario would require an impractical amount of computational power. Therefore, in a discrete representation, the maximum velocity for any moving object or propagating process must conform to a predefined minimum single-operation calculation time. This simulation analogy aligns with the finite speed of light c as a motivating factor.
• Discretization must be dynamic. The use of fixed-size discrete grids is clearly a huge dispersion of computational resource in spacetime regions where there are no bodies and there is nothing to calculate (so that we can fix there just one big cell, saving computational resources). On the one hand, the need to increase the size of the simulation requires lowering the resolution; on the other hand, there is the need to achieve better resolution within smaller domains of the simulation where mass is present. This dichotomy is already present to those creating vast computerized cosmological simulations [42]. This problem is attacked by varying the mass quantization grid resolution as a function of the local mass density and other parameters, leading to the so-called automatic tree refinement (ATR). The adaptive moving mesh method, an approach similar to ATR [43], would vary the size of the cells of the quantized mass grid locally, as a function of kinetic energy density while at the same time varying the size of the local discrete time-step, which should be kept per-cell as a 4th parameter of space, in order to better distribute the computational power where it is needed the most. By doing so, the grid would become distorted having different local sizes. In a 4D simulation, this effect would also involve the time being perceived as flowing differently in different parts of the simulation: faster for regions of space where there is more local kinetic energy density, and slower where there is less. [Additional consequences are reported and discussed in Section 3.3].

In principle, there are two instruments or methods for computing the future states of a system. One involves utilizing a classical apparatus composed of conventional computer bits. Unlike Qbits, these classical bits cannot create, maintain, or utilize the superposition of their states, rendering them classical machines. On the other hand, quantum computation employs a quantum system of Qbits and utilizes the quantum law of evolution for calculations.

However, the capabilities of the classical and quantum approaches to predict the future state of a system differ. This distinction becomes evident when considering the calculation of the evolution of many-body system. In the classical approach, computer bits must compute the position and interactions of each element of mass at every calculation step. This becomes increasingly challenging (and less precise) due to the chaotic nature of classical evolution. In principle, the classical N-body simulations are straightforward, as they primarily entail integrating the 6N ordinary differential equations that describe particle motions. However, in practice, the sheer magnitude of particles, N, is often exceptionally large (of order of millions or tens of billions like in the Millennium simulation [43]). Moreover, the computational expense becomes prohibitive due to the four-power increase $N^4$ in the number of particle–particle interactions that need to be computed. Consequently, direct integration of the differential equations requires an exponential increase of calculation and data storage resources for large scale simulations.

On the other hand, quantum evolution does not require defining the state of each particle at every step. It addresses the evolution of the global wave of superposition of states for all particles. Eventually, when needed or when decoherence is induced or spontaneously occurs, the classical state of each particle at a specific instant is obtained through the wavefunction decay (under this standpoint, calculated is the analogous of ‘measured’ or ‘collapsed’). This represents a form of optimization: sacrificing the knowledge of the classical state at each time step, but being satisfied with knowing the classical state of each particle at discrete time intervals, specifically after a large number of calculation steps. This approach allows for a quicker computation of the future state of reality with a lesser use of resources. Moreover, since the length of quantum coherence ${\lambda }_{qu}$ is finite, the group of entangled particles undergoing to the common wavefunction decay, are of smaller finite number, further simplifying the algorithm of the simulation.

The advantage of quantum calculus over classical calculus can be metaphorically demonstrated by addressing the challenge of finding the global minimum. When using classical methods like maximum descent gradient or similar approaches, the pursuit of the global minimum—such as in the determination of prime numbers—results in an exponential increase in the calculation time as the maximum value of the prime numbers rises.

In contrast, employing the quantum method allows us to identify the global minimum in linear or, at least, polynomial time. This can be loosely conceptualized as follows: in the classical case, it is akin to having a ball fall into each hole to find a minimum, and then the values of each individual minimum must be compared with all possible minima before determining the overall minimum. The utilization of the quantum method involves using an infinite number of balls, spanning the entire energy spectrum. Consequently, at each barrier between two minima (thanks to quantum tunneling), some of the balls can explore the next minimum almost simultaneously. This simultaneous exploration (quantum computing) significantly shortens the time needed to probe the entire set of minima, then wavefunction decay allows us to measure (or detect) the outcome of the process (measure).

If we aim to create a simulation on a scale comparable to the vastness of the universe, we must find a way to address the many-body problem. Currently, solving this problem remains an open challenge in the field of computer science. Just recently in December 2023, a new quantum algorithm for simulating coupled harmonic oscillators in polynomial time has been uncovered [44], showing that quantum mechanics appears to be a promising candidate for making the many-body problem manageable. This is achieved through the utilization of the entanglement process, which encodes coherent particles and their interaction outcomes as a wavefunction. The wavefunction evolves without explicit solving, and, when coherence diminishes, the wavefunction collapse leads to calculate (as well as determine) the essential classical properties of the system given by the underlying physics at discrete time steps.

This sheds light on the reason why physical properties remain undefined until measured; from the standpoint of the simulation analogy, it is a direct consequence of the quantum optimization algorithm, where, in each local quantum-correlate domain, the classical state remains uniquely defined only at few discrete times, unlike the continuous description given by classical evolution. In this way, the determination of reality properties is achieved solely through the utilization of the minimal amount of computational power. In accordance with [44], quantum computing demonstrates the capability to solve classical problems in polynomial time that would otherwise require exponential time, thereby optimizing the simulation. Moreover, the combination of the coherent quantum evolution with the wavefunction collapse has been proven to constitute a Turing-complete computational process, as evidenced by its application in quantum computing for performing computations.

An even more intriguing aspect of the possibility that reality can be virtualized as a computer simulation is the existence of an algorithm capable of solving the intractable many-body problem, challenging classical algorithms. Consequently, the entire class of problems characterized by a phenomenological representation, describable by quantum physics, can be rendered tractable through the application of quantum computing. However, it is worth noting that very abstract mathematical problems, such as the ‘lattice problem’ [45], may still remain intractable. Currently, the most well-known successful examples of quantum computing include Shor’s algorithm [46] for prime number discovery and Grove’s algorithm [47] for inverting ‘black box functions’.

Classical computation categorizes the determination of prime numbers as an NP (non-polynomial) problem, whereas quantum computation classifies it as a P (polynomial) problem with Shor’s algorithm. However, not all problems considered NP in classical computation can be reduced to P problems by utilizing quantum computation. This implies that quantum computing may not be universally applicable in simplifying all problems but only a certain limited class.

The possibility of acknowledging the universe’s many-body problem as a computer simulation requires that the NP problem of N-body is tractable [44]. In such a scenario, it becomes theoretically feasible to utilize universe-like particle simulations for solving NP problems by embedding the problem within specific assigned particle behavior. This concept implies that the laws of physics are not inherently given but are rather formulated to represent the solution of specific problems.

To clarify further: if various instances of universe-like particle simulations were employed to tackle distinct problems, each instance would exhibit different laws of physics governing the behavior of its particles. This perspective opens up the opportunity to explore the purpose of the universe and inquire about the underlying problem it seeks to solve.

In essence, it prompts the question: What is the fundamental problem that the universe is attempting to address?

3.1. How the universe Computes the Next State: The Unraveling of the Meaning of Time and Free Will

At this point, to examine the universal simulation and generate evolution akin to SQHM characteristics within a flat space (excluding gravity except for gravitational background noise contributing to quantum decoherence), let us focus on the local evolution within a spacetime cell of a few De Broglie lengths or quantum coherence lengths ${\lambda }_{qu}$ [19]. After a certain characteristic time, the superposition of states in a local quantum-entangled domain, evolving following the motion Equation (24), decays into one of its eigenstates and leads to a stable state that, surviving fluctuations, constitutes a lasting state over time: we can define it as reality since, for its stability, it gives the same result even after repeated measurements. Moreover, given macroscopic decoherence, the local domain in different places are quantum disentangled from each other. Therefore, their decay to a stable eigenstate is unlikely to happen at the same time. Due to the perceived randomness of GBN, this process can be assumed to be stochastically distributed into the space, leading to a foam-like classical reality in spacetime that, in this way, results in cells that are locally quantum but globally classic.

Furthermore, after an interval of time much larger than the wavefunction decay one, each domain is perturbed by a large fluctuation that is able to let it to jump to a quantum superposition that re-starts evolving following the quantum law of evolution for a while, before new wavefunctions collapse, and so on.

From the standpoint of the SQHM, the universal computation method exploits the quantum evolution for a while and then, by decoherence, derives the classical N-body state at certain discrete instants by the wavefunction collapse exactly like a universal quantum computer. Then it goes to the next step by computing the evolution of the quantum entangled wavefunction evolution, saving on classically calculating the state of the N-bodies repeatedly, deriving it only when the quantum state decays into the classical one (as in a measure).

Practically, the universe realizes a sort of computational optimization to speed up the derivation of its future state by utilizing a Qbits-like quantum computation.

Free Will

Following the pigeonhole principle, which states that any computer that is a subsystem of a larger one cannot handle the same information (and thus cannot produce a greater power of calculation in terms of speed and precision) as the larger one, and considering the inevitable information loss due to compression, we can infer that a human-made computer, even utilizing a vast system of Q-bits, cannot be faster and more accurate than the universal quantum computer.

Therefore, the temporal horizon of predicting the future states, before they happen, is by force limited inside reality. Hence, among the many future states possible, we can infer that we can determine or choose the future output within a certain temporal horizon and that free will is limited. Moreover, since the decision of what reality state we want to realize is not connected to the previous events before a certain preceding interval of time (4D disentanglement), we can also say that such a decision is not predetermined.

Nevertheless, other than stating that the will is free but limited, from the present analysis, there is an additional aspect of the concept of free will that needs to be analyzed. Specifically, it pertains to whether many possible states of reality exist in future scenarios, providing us with the genuine opportunity to choose which of them to attain.

In this context, within the deterministic quantum evolution framework, or even in classical scenarios, with precisely defined initial conditions in 4D spacetime, such a possibility is effectively prohibited, since the future states are predetermined. Time in this context does not flow but merely serves as a ‘coordinate’ of the 4D spacetime where reality is located, losing the significance it holds in real life.

In the absence of GBN, knowing the initial condition of the universe at initial instant of the Big Bang and the laws of physics precisely, the future of the universe remains defined.

This is because, unless you introduce noise into the simulation, the basic quantum laws of physics are deterministic.

Actually, in the context of SQHM evolution, the random nature of GBN plays an important role in shaping the future states of the universe. From the standpoint of the simulation analogy, the nature of GBN presents important informational aspects.

The randomness introduced by GBN renders the simulation inherently unpredictable to an internal observer. Even if the internal observer employs an identical algorithm to the simulation to forecast future states, the absence of access to the same noise source results in rapid divergence in their predictions of future states. This is due to the critical influence of each individual fluctuation in the wavefunction decay (see Section 2.6.3). In other words, to the internal observer, the future would be encrypted by such noise. Furthermore, if the noise that would be used in the simulation analogy evolution were a pseudo-random noise with enough unpredictability, only someone who is in possession of the seed would in fact be able to predict the future or invert the arrow of time. Even if the noise is pseudo-random, the problem of deriving the encryption key is practically intractable. Therefore, in presence of GBN, the future outcome of the computation is ‘encrypted’ by the randomness of GBN.

Moreover, if the simulation makes use of a pseudo-random routine to generate GBN and it appears truly random inside reality, it follows that the seed ‘encoding GBN’ is kept outside the simulated reality and is unreachable to us. In this case, we are in front of an instance of a ‘one-time pad’, effectively equating to deletion, which is proven unbreakable. Therefore, in principle, the simulation could effectively conceal information about the key used to encrypt GBN noise in a manner that remains unrecoverable.

From this perspective, the renowned Einstein quote, ‘God does not play dice with the universe,’ is aptly interpreted. In this context, it implies that the programmer of the universal simulation does not engage in randomness, as everything is predetermined for him. However, from within this reality, we remain unable to ascertain the seed of the noise, and the noise manifests itself as genuinely random. Furthermore, even if from inside this reality, we would be able to detect the pseudo-random nature of GBN, featuring a high level of randomness, the challenge of deciphering the key remains insurmountable [48] and the encryption key practically irretrievable.

Thus, we would never be able to trace back to the encryption key and completely reproduce the outcomes of the simulation, even knowing the initial state and all the laws of physics perfectly, since simulated evolution depends on the form of each single fluctuation.

This universal behavior emphasizes the concept of ‘free will’ as a constrained capability, unable to access information beyond a specific temporal horizon. Furthermore, the simulation analogy delves deeper into this idea, portraying free will as a faculty originating in macroscopic classical systems characterized by foam-like dimensions in spacetime. As a result, our consciousness lacks a perfect definition of free will; we desire something without a full precise understanding of what it is. Nonetheless, through the exercise of our free will, we can impact the forthcoming macroscopic state, albeit with a certain imprecision and ambiguity in our intentions, yet not predetermined by preceding states of reality beyond a specific interval of time.

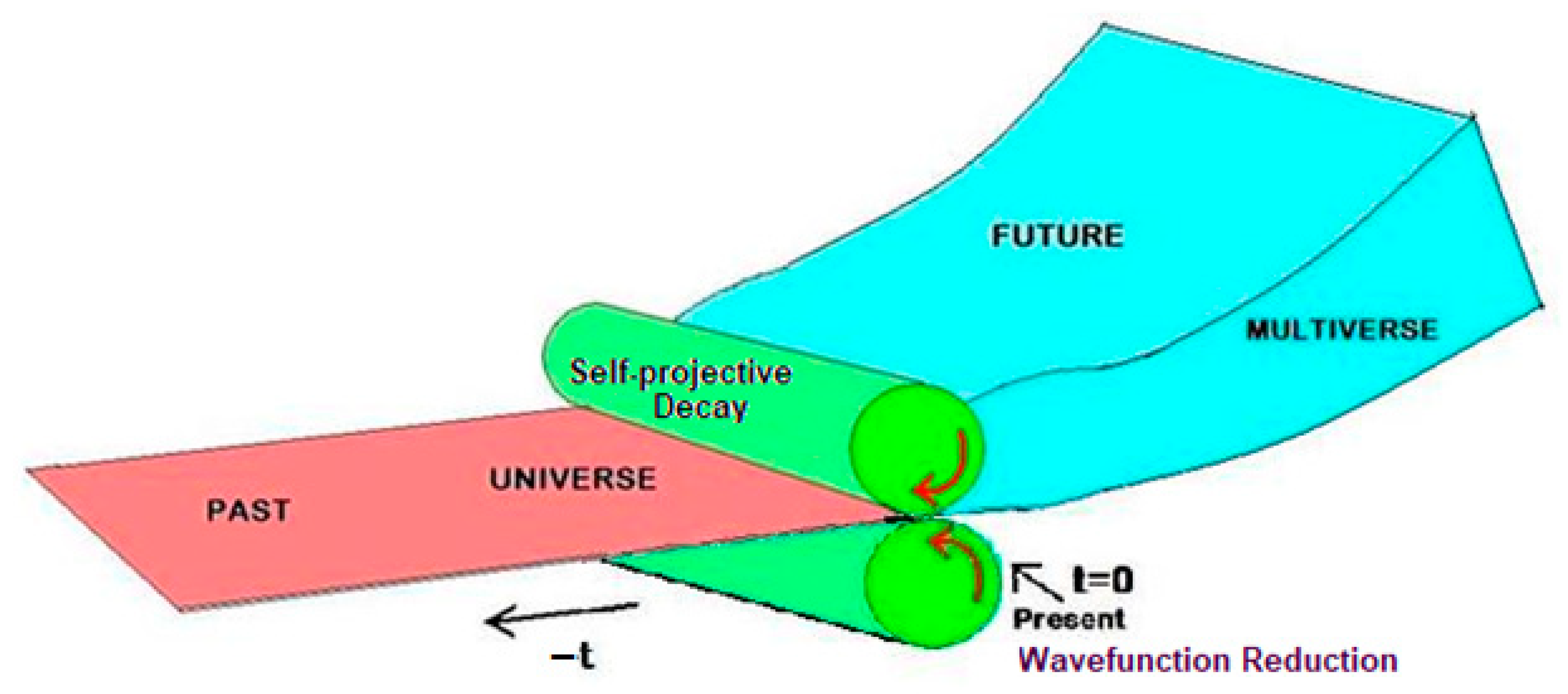
3.2. The Universal ‘Pasta Maker’ and the Actual Time in 4D Spacetime

Working with a discrete spacetime offers advantages that are already supported by lattice gauge theory [49]. This theory demonstrates that in such a scenario, the path integral becomes finite-dimensional and can be assessed using stochastic simulation techniques, such as the Monte Carlo method.

In our scenario, the fundamental assumption is that the optimization procedure for universal computation has the capability to generate the evolution of reality. This hypothesis suggests that the universe evolves quantum mechanics in polynomial time, efficiently solving the many-body problem and transitioning it from NP to P. In this context, quantum computers, employing Q-bits with wavefunction decay that both produces and effectively computes the result, utilize a method inherent to the physical reality itself.

From a global spacetime perspective, aside from the collapses in each local domain, it is important to acknowledge a second fluctuation-induced effect. Larger fluctuations taking place over extended time intervals can induce a jumping process in the wavefunction configuration, leading to a generic superposition of states. This prompts a restart in its evolution following quantum laws. As a result, after each local wavefunction decay, a quantum resynchronization phenomenon occurs, propelling the progression towards the realization of the next local classical state of the universe.

Furthermore, with quantum synchronization, at the onset of the subsequent moment, the array of potential quantum states (in terms of superposition) encompasses multiple classical states of realization. Consequently, in the current moment, the future states form a quantum multiverse where each individual classical state is potentially attainable depending on events (such as the chain of wave–function decay processes) occurring beforehand. As the present unfolds, marked by the quantum decoherence process leading to the attainment of a classical state, the past is generated, ultimately resulting in the realization of the singular (foam-like) classical reality: the universe.

Moreover, if all possible configurations of the realizable universe exist in the future (extending past our ability to determine or foresee over a finite temporal extent), the past is comprised of fixed events (universe) that we are aware of but unable to alter.

In this context, we can metaphorically illustrate spacetime and its irreversible universal evolution as an enormous pasta maker. In this analogy, the future multiverse is represented by a blob of unshaped flour dough, inflated because it contains all possible states. This dough, extending up to the surface of the present, is then pressed into a thin pasta sheet, representing the quantum superposition reduction to the classical state realizing the universe.

The 4D surface boundary (see Figure 1) between the future multiverse and the past universe marks the instant of present time. At this point, the irreversible process of decoherence occurs, entailing the computation or reduction to the present classical state. This specific moment defines the current time of reality, a concept that cannot be precisely located within the framework of relativistic spacetime. The SQHM aligns with the gravitational decoherence hypothesis [50]. It agrees with Roger Penrose’s point of view that dispels the anthropocentric idea that the act of measurement triggers the collapse: ‘It takes place in the physics, and it is not because somebody comes and looks at it’.

3.3. Quantum and Gravity

Until now, we have not adequately discussed how gravity arises from the discrete nature of the universal ‘calculation’. Nevertheless, it is interesting to provide some insights into the issue because, viewed through this perspective, gravity naturally emerges as quantized.

Considering the universe as an extensive quantum computer operating on a predetermined space-time grid does not yet represent the most optimized simulation. Indeed, the optimization of the simulation has not taken into account the possibility of adjusting the fixed dimensions of the elemental grid. This becomes apparent when we realize that maintaining constant elemental cell dimensions leads to a significant dispersion of computational resources in spacetime regions devoid of bodies or any need for calculation. In such regions, we could simply allocate one large cell, thereby conserving computational resources.

This perspective aligns with a numerical algorithm employed in numerical analysis known as adaptive mesh refinement (AMR). This technique dynamically adjusts the accuracy of a solution within specific sensitive or turbulent regions during the calculation of a simulation. In numerical solutions, computations often occur on predetermined, quantified grids, such as those on the Cartesian plane, forming the computational grid or ‘mesh’. However, many issues in numerical analysis do not demand uniform precision across the entire computational grid as, for instance, used for graph plotting or computational simulation. Instead, these issues would benefit from selectively refining the grid density only in regions where enhanced precision is required.

The local adaptive mesh refinement (AMR) creates a dynamic programming environment enabling the adjustment of numerical computation precision according to the specific requirements of a computation problem, particularly in areas of multidimensional graphs that demand precision. This method allows for lower levels of precision and resolution in other regions of the multidimensional graphs. The credit for this dynamic technique of adapting computation precision to specific requirements goes to Marsha Berger, Joseph Oliger, and Phillip Colella [42,51,52], who developed an algorithm for dynamic gridding known as AMR. The application of AMR has subsequently proven to be widely beneficial and has been utilized in the investigation of turbulence problems in hydrodynamics, as well as the exploration of large-scale structures in astrophysics, exemplified by its use in the Bolshoi Cosmological Simulation [53].

An intriguing variation of AMR is the adaptive moving mesh method (AMMM) proposed by Huang Weizhang and Russell Robert [43,54]. This method employs an r-adaptive (relocation adaptive) strategy to achieve outcomes akin to those of adaptive mesh refinement. Upon reflection, an r-adaptive strategy, grounded in local energy density as a parameter, bears resemblance to the workings of curved space-time in our universe.

Conceivably, a more sophisticated cosmological simulation could leverage an advanced iteration of the AMMM algorithm. This iteration would involve relocating space grid cells and adjusting the local delta time for each cell. By moving cells from regions of lower energy density to those of higher energy density at the system’s speed of light and scaling the local delta time accordingly, the resultant grid would appear distorted and exhibit behavior analogous to curved space-time in general relativity.

Furthermore, as cell relocation induces a distortion in the grid mesh, updating the grid at the speed of light, as opposed to simultaneous updating, would disperse computations across various timeframes. In this scenario, gravity, time dilation, and gravitational waves would spontaneously manifest within the simulated universe, mirroring their emergence from curved space-time in our universe.

A criterion for reducing the grid step is based on providing a more detailed description in regions with higher mass density (more particles or energy density) with a higher amplitude of induced quantum potential fluctuations that reduces the De Broglie length of quantum coherence.

This point of view finds an example in the Lagrangian approach, as outlined in ref. [55], where the computational mesh dynamically moves with the matter being simulated. This results in an increased resolution, characterized by smaller mesh cells, in regions of high mass/energy density, while decreasing resolution in other areas. While this approach holds significant potential, it is not without its challenges and limitations, as highlighted in the work of Gnedin and Bertschinger [56].

The variability of the mesh introduces noticeable apparent forces, which are deemed undesirable in the method [57] due to their tendency to violate energy conservation. Consequently, countermeasures are implemented to eliminate or rectify this inconvenience.

From the standpoint of the simulation analogy, the field of force that naturally emerges [56,57], due to grid mesh distortion caused by cell relocation methods [53,54], is not as problematic as it might appear. The force field, resulting from this optimization process in the calculation, may simulate gravity induced by discretization of the spacetime, as an ‘apparent’ force arising from lattice cell distortion. On this ansatz, the 4D non-uniform lattice network of the universal algorithm replicates reality by depicting 3D space incorporating the gravity. The universal algorithm includes rules (spacetime geometrization) for modulating the variable density of the computational grid to simulate the gravity observed in reality. This approach naturally results in discretized gravity that is quantum from its inception.

From this perspective, gravity arises as an apparent force resulting from the optimization process of AMMM to streamline the advancement of the reality simulation as shown in references [54,55,56,57], and the emergence of gravity can be attributed to the algorithmic optimization. The theoretical framework for transitioning from the variable mesh of the computer simulation to the discrete 4D curved spacetime with gravity has the potential to provide insights into the quantum gravity. The causal dynamical triangulation theory [58] closely aligns with the perspective of simulating physics through discrete computations, representing a theoretical framework. However, challenges emerge when attempting to reconcile this approach with the continuum classical limits of general relativity (see Section 3.3.1).

From this line of reasoning, an intriguing observation emerges: dynamically enlarging grid cells in regions where less computational power is needed inevitably results in the creation of vast cells corresponding to empty spacetime. The constraint of limited resources makes it impossible to achieve an infinitely large grid cell, preventing the realization of completely flat space within any cell.

In the context of the quantum geometrization of spacetime [33], leading to a quintessence-like interpretation of the cosmological constant that diminishes with the universe’s expansion, the finite maximum size of the simulation cell implies that the cosmological constant can be arbitrarily small but not zero. This aligns with the implications of pure quantum gravity, which posits that a vacuum with zero cosmological constant collapses into a polymer-branched phase devoid of physical significance.

Moreover, assuming the discrete nature of spacetime, the cosmological constant is also discrete, and the smallest discrete value before zero decreases as the universe expands. This raises the question: is there a minimal critical value for the cosmological constant (at a certain degree of universe inflation) below which the vacuum will collapse to the polymer-branched phase prompting an envisioning of the ultimate fate of the universe?

On the opposite side, if achieving a zero-grid dimension is deemed impossible, the inquiry into the minimum elemental size of spacetime naturally arises. In this context, as highlighted in [19], the SQHM emphasizes the existence of a finite minimum discrete element of distance. Consequently, spacetime can be conceptualized as a lattice composed of elemental cells of discrete size. It is noteworthy to observe that the discreteness of spacetime deduced by the SQHM is many orders of magnitude smaller than the minimum geometric quantity of LQG. This minimum discrete distance renders spacetime akin to a fabric with sparse threads, rather than a continuous plastic layer. It should not be conflated with the minimum geometric quantity of LQG, which is due to the discrete spectrum of area and volume operators where the ground state is linked to the Planck length and implicitly incorporates the concept of detectability. This is because revealing this ground state would require an energy equal to or greater than that of the Planck mass, inevitably forming a black hole that overshadows it.

To establish the order of magnitude for the elemental size of spacetime, we can assert that the volume of such an elemental cell must not exceed the volume within which the matter of the pre-big-bang black hole collapses [33,59]. This condition ensures the presence of a quantum potential repulsive force equal to the attractive gravitational force, establishing the black hole equilibrium configuration, leading to the expression:

$$\Delta x_{\min }=\frac{\hslash }{2m_{\max }c}=\frac{\hslash }{2m_{u}c}=\frac{\hslash c}{2E_u}$$

(106)

where $m_u$ is the mass equivalent to the total universe energy of the universe $E_u\cong {10}^{53÷60}\mathrm{j}$ [60], leading to

$$\Delta x_{\min }=\frac{\hslash c}{2E_u}\approx \frac{6.62\times {10}^{-34}\times 3\times {10}^8}{2\times {10}^{53÷60}}\approx {10}^{-\left(78÷85\right)}m$$

(107)

where, being $c$, $\hslash$, $E_u$, physical constants, make also $\Delta x_{\min }$ a physical universal constant. Furthermore, for the time coordinate this requires that

$$\Delta t_{\min }=\frac{\hslash c}{2c{E}_u}\approx 3\times {10}^{-\left(87÷94\right)}s$$

(108)

3.3.1. The Classical Limit Problem in Quantum Loop Gravity (QLG) and Causal Dynamical Triangulation (CDT)

Even if from the standpoint of the simulation analogy both CDT [58] and QLG [61] take support and endorsement, also a contradictory aspect emerges in the procedure to achieve the classical limit of the theories, namely the general relativity.

About this point, the SQHM asserts that achieving classical macroscopic reality requires not only imposing the condition $li{m}_{\hslash \to 0}$, but enforcing the double conditions

$${\mathit{lim}}_{macro}\equiv {\mathit{lim}}_{dec}{\mathit{lim}}_{\hslash \to 0}={\mathit{lim}}_{\hslash \to 0}{\mathit{lim}}_{dec}$$

(109)

where the subscript ‘dec’ stands for decoherence defined as

$$\begin{array}{ll}{\mathit{lim}}_{dec}\psi ={\mathit{lim}}_{dec}& {\displaystyle \sum _{k=k_{\mathit{min}}}^{k=k_{\mathit{max}}}{b}_k|{\psi }_k|exp[\frac{i{S}_{(k)}}{\hslash }]}\\ & =b_{\tilde{k}}|{\psi }_{\tilde{k}}|exp[\frac{i{S}_{{(}_{\tilde{k}})}}{\hslash }]\end{array}.$$

(110)

where $k_{\mathit{min}}<\tilde{k}<k_{\mathit{max}}$ is one of the $k_{\mathit{max}}-k_{\mathit{min}}$ eigenstates and holding.

The SQHM demonstrates that in the so-called semiclassical limit, attained by the condition $li{m}_{\hslash \to 0}$, applied to the (zero-noise) quantum mechanics, the quantum entanglement between particles persists and influences interactions even at infinite distances. Thus, rather than a genuine classical limit, it portrays a large-scale quantum description. This approach implicitly supports the wrong idea that the properties of the vacuum at a macroscopic large-scale replicate those at a small scale, which is not true due to the breaking of scale invariance symmetry in the SQHM by the De Broglie length.

This aspect can be analytically examined by exploring the least action principle [19,32], generalized in the Madelung hydrodynamic formulation.

In the quantum hydrodynamic approach, the quantum equation of motion for the complex wavefunction is separated into two equations involving real variables. These equations pertain to the conservation of mass density distribution and its evolution, which is described by a Hamilton-Jacobi-like equation. This evolution can be expressed through a generalized hydrodynamic Lagrangian function that adheres to a generalized stationary action condition principle [32].

By utilizing the quantum hydrodynamic Lagrangian, the variation of the quantum hydrodynamic action for a general quantum superposition of states can be expressed as [32] (Greek indexes run from 0 to 3)

$$\begin{array}{ll}\delta S=& -\frac{1}{c}{\displaystyle \int {\displaystyle \iiint {|\psi |}^2{\displaystyle \sum _k\left(\left({\tilde{p}}_{(k)}{\partial }_{\mu }{\dot{q}}_{(k)\nu }\right)\delta q^{\mu }-\left(\frac{\partial {\tilde{L}}_{(k)}}{\partial |{\psi }_k|}-{\partial }^{\mu }\frac{\partial {\tilde{L}}_{(k)}}{\partial {\partial }_{\mu }|{\psi }_k|}\right)\delta |{\psi }_k|\right)}}}d\Omega \\ & =\delta \left(\Delta S_{Q_{mix}}+\Delta S_Q\right)\ne 0\end{array}$$

(111)

where

$$\Delta S_Q=\frac{1}{c}{\displaystyle \int {\displaystyle \iiint |\psi {|}^2{\displaystyle \sum _k\left(\frac{\partial {\tilde{L}}_{(k)}}{\partial |{\psi }_k|}-{\partial }^{\mu }\frac{\partial {\tilde{L}}_{(k)}}{\partial {\partial }_{\mu }|{\psi }_k|}\right)\delta |{\psi }_k|}}}d\Omega$$

(112)

is the variation of the action generated by quantum effects and where

$$\delta \left(\Delta S_{Q_{mix}}\right)=-\frac{1}{c}{\displaystyle \int {\displaystyle \iiint |\psi {|}^2{\displaystyle \sum _k{\tilde{p}}_{(k)}\frac{\partial {\dot{q}}_{(k)\nu }}{\partial q^{\mu }}\delta |{\psi }_k|}}}d\Omega$$

(113)

is the variation of the action generated by the mixing hat happens within the quantum superposition of states.

The expression (113) is typical of superposition states, since the variation of the action solely due to eigenstates is represented by:

$$\begin{array}{ll}\delta S& ={\displaystyle \int {\displaystyle \iiint |\psi {|}^2\left({\displaystyle \sum _k\frac{\partial {\tilde{L}}_{(k)}}{\partial x_{{(k)}^{\mu }}}}\right)\delta x_{{(k)}^{\mu }}}}dVdt\\ & ={\displaystyle \int {\displaystyle \iiint |\psi {|}^2{\displaystyle \sum _k\left(\frac{\partial {\tilde{L}}_{(k)}}{\partial q^{\mu }}\delta q^{\mu }+\frac{\partial {\tilde{L}}_{(k)}}{\partial {\dot{q}}_{(k)}^{\mu }}\delta {\dot{q}}_{(k)}^{\mu }+\frac{\partial {\tilde{L}}_{(k)}}{\partial |{\psi }_k|}\delta |{\psi }_k|+\frac{\partial {\tilde{L}}_{(k)}}{\partial {\partial }_{\mu }|{\psi }_k|}\delta {\partial }^{\mu }|{\psi }_k|\right)}}}dVdt\\ & =\frac{1}{c}{\displaystyle \int {\displaystyle \iiint |\psi {|}^2{\displaystyle \sum _k\left(\left(\frac{\partial {\tilde{L}}_{(k)}}{\partial q^{\mu }}-\frac{d}{dt}\frac{\partial {\tilde{L}}_{(k)}}{\partial {\dot{q}}_{(k)}^{\mu }}\right)\delta q^{\mu }+\left(\frac{\partial {\tilde{L}}_{(k)}}{\partial |{\psi }_k|}-{\partial }^{\mu }\frac{\partial {\tilde{L}}_{(k)}}{\partial {\partial }_{\mu }|{\psi }_k|}\right)\delta |{\psi }_k|\right)}}}d\Omega \\ & =\delta \left(\Delta S_Q\right)\ne 0\end{array}.$$

(114)

Moreover, given that the quantum motion equations for the k-th eigenstate [31] satisfies the condition

$$\left(\frac{\partial {\tilde{L}}_{(k)}}{\partial q^{\mu }}-\frac{d}{dt}\frac{\partial {\tilde{L}}_{(k)}}{\partial {\dot{q}}_{(k)}^{\mu }}\right)=0,$$

(115)

the variation of the action $\delta S$ for the k-th eigenstates reads as

$$\delta S=\delta \left(\Delta S_{Q(k)}\right)=\frac{1}{c}{\displaystyle \int {\displaystyle \iiint |{\psi }_k{|}^2\left(\frac{\partial {\tilde{L}}_{(k)}}{\partial |{\psi }_k|}-{\partial }^{\mu }\frac{\partial {\tilde{L}}_{(k)}}{\partial {\partial }_{\mu }|{\psi }_k|}\right)\delta |{\psi }_k|}}d\Omega$$

(116)

and therefore by (115) it follows both that

$${\mathit{lim}}_{dec}\delta S=\left(\Delta S_{Q(k)}\right)$$

(117)

and that

$${\mathit{lim}}_{dec}\delta \left(\Delta S_{Qmix}\right)=0.$$

(118)

Furthermore, since in the semiclassical limit, for $\hslash \to 0$ and consequently $V_{qu}\to 0$, we have that

$$\frac{\partial \left({\mathit{lim}}_{\hslash \to 0}{L}_{(k)}\right)}{\partial |{\psi }_k|}=0,$$

(119)

$$\frac{\partial \left({\mathit{lim}}_{\hslash \to 0}{L}_{(k)}\right)}{{\partial }^{\mu }|{\psi }_k|}=0,$$

(120)

and finally, through the identity:

$${\mathit{lim}}_{\hslash \to 0}\delta \left(\Delta S_{Q(k)}\right)=0,$$

(121)

by utilizing (118) and (121), the classical least action condition

$${\mathit{lim}}_{\hslash \to 0}{\mathit{lim}}_{dec}\delta S=0.$$

(122)

The classical least action law is recovered when the quantum hydrodynamic equations transition into their classical form. In this context, the condition is rigorously achieved through a coarse-grained approach, where the minimum discrete length is larger than the range of interaction of the quantum potential. Within the minimal cell of this coarse-grained approach (representing a macroscopic point mass), where quantum physics dominates, the decay of the superposition of states leads to stationary configurations that are practically identical to eigenstates. Meanwhile, the macroscopic point masses move according to classical laws of motion since in their interaction $V_{qu}=0$.

From this perspective, it is not possible for any quantum gravity theory to achieve the classical limit of general relativity solely by imposing ${\mathit{lim}}_{\hslash \to 0}$. This limitation arises because the classical least action, a fundamental principle of general relativity, cannot be restored with a straightforward condition ${\mathit{lim}}_{\hslash \to 0}$.

This goes beyond a mere formal theoretical bottleneck; it is a genuine condition positing that spacetime at the macroscopic level undergoes decoherence and lacks quantum properties. This holds true, at least, in regions governed by Newtonian gravity. However, in high-gravity areas near black holes and within them, the strong gravitational interaction can give rise to macroscopic quantum entanglement over significant distances [58].

In this context, it is conceivable that quantum gravity approaches, such as QLG and CDT, might face substantial challenges in achieving the classical limit of general relativity solely by taking the limit of a null Planck constant. Although classical properties may be recovered in coherent states, this approach is not exempt from the influence of quantum potential (propelling quantum entanglement) on large-scale, as envisioned by Objective Collapse Theories, which in the framework of SQHM persists within the tail interaction of coherent states.

Furthermore, given that the quantum uncertainty and the finite speed of light rules out the existence of a continuum limit, deeming it devoid of physical significance, CDT could encounter difficulties in attempting to derive it.

3.3.2. The Simulation Analogy and the Holographic Principle

Even if the Holographic Principle and the Simulation Analogy support the idea that reality is a phenomenon stemming from a computing process encoding it, some notable differences arise. The simulation analogy portrays the real world as if it were being orchestrated by a computational procedure subject to various optimization methods. The macroscopic classical reality, characterized by foam-like patterns with short discrete time intervals in microscopic quantum domains, clearly shows that scale invariance is a broken symmetry in spacetime: The properties of the vacuum on a small scale are quite different from those on a macroscopic scale, subjected to low gravity conditions [19], where the De Broglie length defines the absolute scale.

Conversely, the holographic principle, based on the insightful observation that 3-D space can be traced back to an informatively equivalent 2D formulation, that allows for the development of a theory where gravity and quantum mechanics can be described together, implicitly assumes that the properties of the vacuum at a macroscopic scale replicate those at a small scale, which is not accurate. Essentially, the holographic principle takes a similar shortcut to quantum loop gravity and causal dynamical triangulation, facing challenges in describing macroscopic reality and general relativity.

To address this gap, the theory must integrate the decoherence process, which involves leakage of information. A sort of condition of bounded from below information loss should be introduced to ensure a more comprehensive understanding of classical reality and make the theory less abstract, potentially paving the way for experimental confirmations at classical scale.

However, for the sake of precision, it must be noted that in scenarios of high gravity, such as in black holes, where quantum entanglement can span significant distances [58], the Holographic Principle can yield accurate predictions, indicating that information about infalling mass remains encoded on the event horizon area of black holes.

4. Philosophical Breakthrough

The spacetime structure, governed by its laws of physical evolution that enable the modeling of reality as a computer simulation, eliminates the possibility of a continuous realization in both time and space. This applies both to quantum microscopic world and to classical objects with their dynamic behavior, encompassing living organisms and their information processing.

4.1. Extending Free Will

Although we cannot predict the ultimate outcome of our decisions beyond a certain point in time, it is feasible to develop methods that enhance the likelihood of achieving our desired results in the distant future. This forms the basis of ‘best decision-making’. It is important to highlight that having the most accurate information about the current state extends our ability to forecast future states. Furthermore, the farther away the realization of our desired outcome is, the easier it becomes to adjust our actions to attain it. This concept can be thought of as a preventive methodology. By combining information gathering and preventive methodology, we can optimize the likelihood of achieving our objectives and, consequently, expanding our free will.

Additionally, to streamline the evaluation process of ‘what to do’, in addition to the rational-mathematical calculations that dynamically exactly e detailed reconstruct the pathway to our final state, we can focus solely on the probability of a certain future state configuration being realized, adopting a faster evaluation (a sort of Monte Carlo approach). This allows us to potentially identify the best sequence of events to achieve our objective. States beyond the time horizon in a realistic context can be accessed through a multi-step tree pathway. A practical example of this approach is the widely recognized cardiopulmonary resuscitation procedure [62,63]. In this procedure, even though the early assurance of the patient’s rescue may not be guaranteed, it is possible to identify a sequence of actions that maximizes the probability of saving their life.

In the final scenario, free will is the ability to make the desired choice at each step, shaping the optimal path that enhances the probability of reaching the future desired reality. Considering the simulated nature of the universe, it becomes evident that utilizing powerful computers and software, such as those at the basis of artificial intelligence, for acquiring and handling information can significantly enhance the decision-making process. However, a comprehensive analysis and development of this argument extend beyond the scope of the current work and are deferred to future research.

4.2. Methodological Approaches, Emergent from the Darwinian Principle of Evolution, for the Best Future States Problem Solving

Considering intelligence as a function that, in certain circumstances, aids in finding the most effective way to achieve desired or useful outcomes, it is conceivable that methods beyond slow and burdensome rational calculations exist to attain results. This concept aligns with emotional intelligence, a basic mechanism that, as demonstrated by psychology and neuroscience, initiates subsequent purposeful rational evaluation.

The simulation nature of reality demonstrates a form of intelligence (with both emotional and rational components) that has evolved through a selection process favoring the ‘winner is the best solution’. Although this work does not delve into introducing another important aspect, the physical law governing matter self-assembling [64] leading to the appearance of life, it can already be asserted that two ‘methodologies of intelligence’ have emerged. The first one is ‘capturing intelligence’, where the subject acquires resources by overcoming and/or destroying the antagonist. The second one is ‘synergic intelligence’, which seeks collaborative actions to share gained resources or to construct a more efficient system or structure. The latter form of intelligence of the universal nature has played a crucial role in shaping organized systems (living organism) and social structures and their behaviors. However, a detailed examination of these dynamics goes beyond the scope of this work and is left for future analysis.

4.3. Dynamical Conscience

By adhering to the quantum but macroscopically classical dynamics of the SQHM, all objects, including living organisms, within the simulation analogy undergo fresh re-calculations at each time step. This process propels them forward into the future within the reality. The compilation of previous instant states, stored and processed within an energy-information handling system, such as the brain, encapsulates the dynamics of evolution and forms the foundation of consciousness in living organisms [65,66,67].

Neuroscience conceptualizes the consciousness of the biological mind as a three-level process. Starting from the outermost level and moving inward, we have the cognitive calculation, the orientative emotional stage, and, at the most fundamental level, the discrete time acquisition routine. This routine captures the present state, compares it with the anticipated state from the previous time step, and projects the future state for the next acquisition step. The comparison between the anticipated and realized states provides input for decision-making at higher levels. Additionally, this comparison generates awareness of changes in reality and the speed of those changes, allowing for adjustments in the adaptive time scan velocity. In situations where reality is rapidly evolving with the emergence of new elements or potential dangers, the scanning time velocity is increased. This process gives rise to the perception of time dilation, where a few moments appear as a significantly prolonged period in the subject’s mind.

Given the natural progression of universal time, which achieves optimal performance via quantum computation involving stepwise evolution and wavefunction decay for output extraction, it is inevitable that, due to selective processes like matter self-assembly and subsequent Darwinian evolution, living systems, optimized for efficiency, adopt the highest-performing intelligence for a subsystem (the minds of organisms) through replication of universal quantum computing methods. This suggests that groups of interconnected neurons implement quantum computing at the microscopic level of their structure, resulting in their output and/or overall state being the outcome of multiple local wavefunction decays.

The macroscopic classical reality, characterized by foam-like patterns and brief discrete time and microscopic space quantum domains, aligns with the Penrose–Hameroff theory [68] proposing that a quantum mechanical approach to consciousness can account for various aspects of human behavior, including free will. According to this theory, the brain utilizes the inherent property of quantum physical systems to exist in multiple superposed states, allowing it to explore a range of different options in the shortest possible period of time.

4.4. Intentionality of Conscience

Intentionality is contingent upon the fundamental function of intelligence, which empowers the intelligent system to respond to environmental situations. Following calculation or emotional evaluation, when potential beneficial objectives are identified, intentionality is activated to initiate action. However, this reliance is constrained by the underlying laws of physics explicitly defined in the simulation. Essentially, the intelligent system is calibrated to adhere to the physics of the simulation. In our reality, it addresses all needs essential for development of life and organized structures, encompassing basic requirements, for instance, such as the necessity to eat, freedom of movement, association, and protection from cold and heat and many others.

This problem-solving disposition is, however, constrained by the physics of the environment. When it comes to artificial machines, they cannot develop intentionality solely through calculations because they lack integration with the world. In biological intelligence, the ‘hardware’ is intricately linked with the physics of the environment. Not only it manages energy and information, but there is also an inverse influence: energy shapes and develops the hardware of the biological system.

In contrast, a computational machine lacks the capacity to autonomously modify its hardware and establish criteria for its safe maintenance or enhancement. In other words, intentionality, the driving force behind the pursuit of desired solutions, cannot be developed by computational procedure executed by hardware. Intentionality serves as a safety mechanism, or navigation system, for a continually evolving intelligent system whose hardware is seamlessly integrated into its functionality and continuously updated. To achieve this, a physically self-evolving wetware is necessary. At the level of artificial intelligence or autonomous machines, a partial improvement, aimed at better mimicking biological behavior, can be achieved by developing software that mimics biological self-modification, such as genetic programming.

4.5. Final Considerations

So far, the finite speed of information transmission has been merely postulated, the simulation analogy provides an explanation. Although real time and simulation time are disconnected, to compute the effects of infinite speed particles you would need to compute all the interactions all at once in one frame (requiring an infinite speed of computer calculation power). Since this is impossible, you need a finite speed of propagation in any simulation, because that is the only way you can integrate. This speed absolute value depends directly on the computing power you have and nothing else.

Furthermore, quantum physics, which underpins quantum computing, exponentially simplifies the evolution of classical physics, thereby practically enabling simulations that were previously unattainable. Quantum physics serves as the foundational framework of universe, while classical physics emerges on a macroscopic scale. The universe evolves through quantum computation, with classical states derived only at discrete intervals. This is less demanding than the computation of continuous classical evolution, highlighting the sophistication of such an approach.

This suggests that the hypothesis, proposed by a large number of scientists, as positing classical physics as fundamental while quantum physics arises from it through some ‘emergent’ mechanism, appears counterproductive and an unjustified complication from computational standpoint.

The SQHM agrees with Roger Penrose’s point of view that dispels the anthropocentric idea that the act of measurement triggers the collapse: ‘It takes place in the physics, and it is not because somebody comes and looks at it’. Penrose’s assertion that the intelligence (and the universe which inherently possesses it) is not classically computable aligns closely with the perspective presented in this work, which argues that the universal progression with integrated intelligence is achievable only through the foundation of its quantum computing.

Moreover, considering that the maximum entropy tendency is not universally valid [69,70,71], but rather the most efficient energy dissipation with order and living structures formation is the emergent law [64], we are positioned to narrow down the goal, motivating the simulation, to two possibilities: the generation of life and/or the realization of an efficient intelligent system.

Furthermore, as the physical laws, along with the resulting evolution of reality, are embedded in the problem that the simulation seeks to address, intentionality and free will are inherently manifested within the (simulated) reality to achieve the simulation’s objective.

5. Conclusions

The stochastic quantum hydrodynamic model achieves a significant advancement by incorporating the influence of the fluctuating gravitational background, akin to a form of dark energy, into quantum equations. This approach offers solutions that effectively tackle crucial aspects within the realm of objective-collapse Theories. A notable accomplishment lies in resolving the ‘tails’ problem through the definition of the quantum potential length of interaction, supplementing the De Broglie length. Beyond the quantum interaction range, the quantum potential is unable to sustain coherent Schrödinger quantum behavior of wavefunction tails.

The SQHM additionally emphasizes that an external environment is unnecessary, illustrating that the quantum stochastic behavior leading to wave–function collapse can be an intrinsic property of the system within a spacetime characterized by fluctuating metrics. Moreover, positioned within the framework of relativistic quantum mechanics, seamlessly aligning with the finite speed of light and information transmission, the SQHM establishes a distinct connection between the uncertainty principle and the invariance of light speed.

The theory further deduces, within a fluctuating quantum system, the indeterminacy relation between energy and time—an aspect not expressible in conventional quantum mechanics. This revelation offers insights into measurement processes that cannot be concluded within a finite time interval, particularly within a genuinely quantum global system. Remarkably, the theory garners experimental validation through the confirmation of the Lindemann constant concerning the melting point of solid lattices and the transition of ${}^4\mathrm{H}\mathrm{e}$ from fluid to superfluid states.

The self-consistency of the SQHM is guaranteed by its ability to depict the collapse of the wavefunction within its theoretical framework. This characteristic allows it to demonstrate the compatibility of the relativistic locality principle with the non-local property of quantum mechanics, specifically the finite speed of light and the uncertainty principle. Furthermore, by illustrating that large-scale systems naturally transition into decoherent stable states, the SQHM effectively resolves the ‘pre-existing’ reality problem in quantum mechanics.

Moving forward, the paper demonstrates that the physical dynamics of the SQHM can be analogized to a computer simulation where various optimization procedures are applied to bring it into realization. This conceptual framework leading to macroscopic reality of foam-like consistency, wherein microscopic domains with quantum properties coexist, helps in elucidating the meaning of time in our contemporary reality and deepens our understanding of free will. The overarching design, introducing irreversible processes influencing the manifestation of macroscopic reality in the present moment, posits that the multiverse exists solely in future states, with the past constituted by the formed universe after the present instant. The projective decay at the present time represents a kind of multiverse reduction to a universe.

The discrete simulation analogy lays the foundation for a profound understanding of several crucial questions. It addresses inquiries about, the emergence of gravity in a discrete spacetime evolution, and the recovery of the classical general relativity limit in Quantum Loop Gravity and Causal Dynamical Triangulation.

The Simulation Analogy reveals a strategy that minimizes the amount of information to be processed, thereby facilitating the operation of the simulated reality in attaining the solution of its predefined founding problem. From the perspective within, reality is perceived as the manifestation of simulation-specific physical laws. In the scenario under consideration, the simulation appears to employ an entropic optimization strategy, minimizing information loss while achieving maximum useful data compression and maintenance. All this in alignment with the simulation’s intended purpose of life as well as intelligence generation.