Research Trends in Quantum Computers by Focusing on Qubits as Their Building Blocks
Abstract
:1. Quantum Technology
2. Quantum Computer Hardware
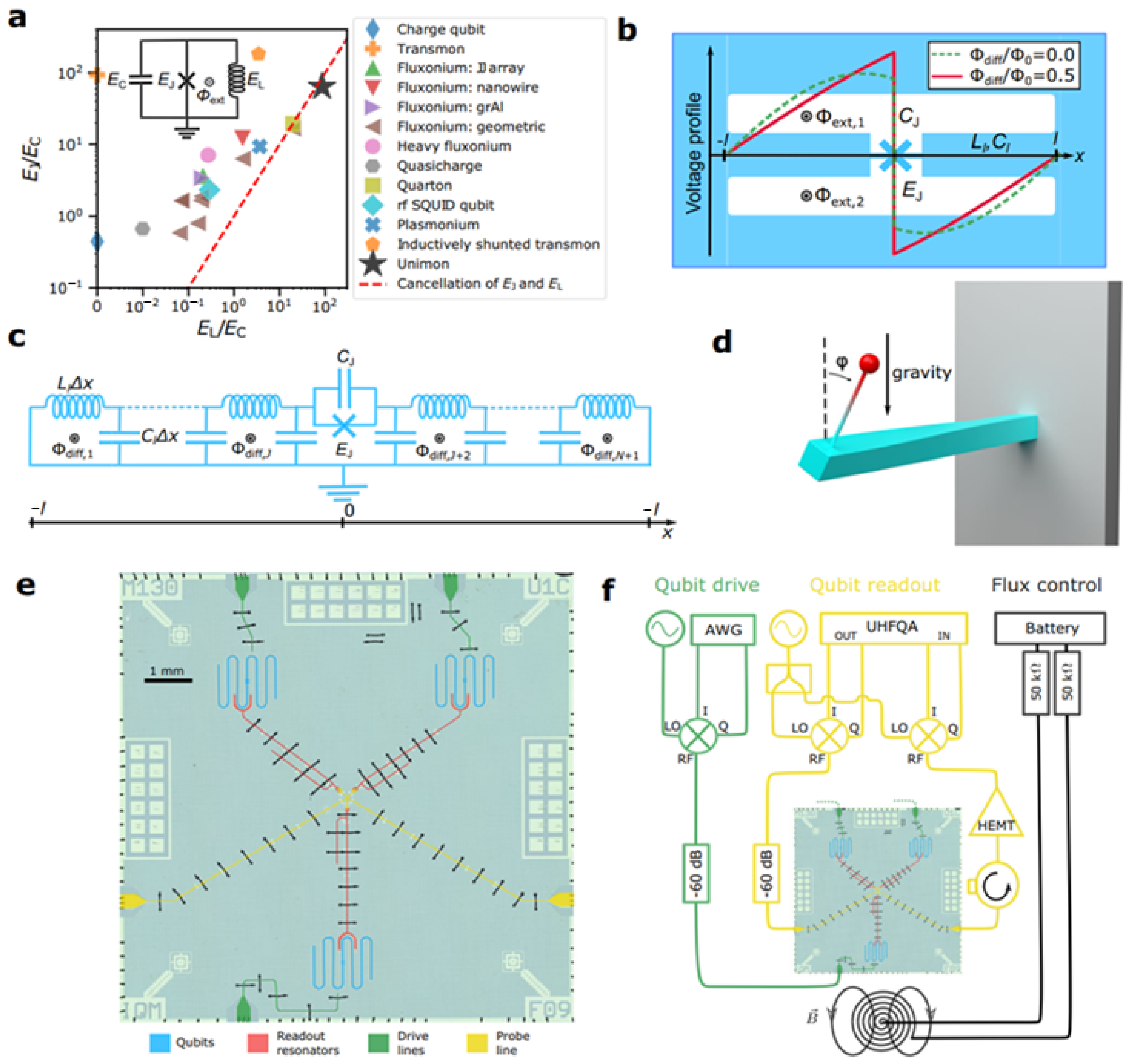
2.1. Superconducting Qubits
2.2. Trapped Ion Qubits
2.3. Neutral Atom Qubits
2.4. Other Types of Qubits
- Semiconductor qubits: the field of semiconductor qubits is quite diverse, encompassing various systems, materials, and techniques. The semiconductor qubits demonstrated so far differ from each other in many ways. They range from systems that operate at mill kelvin temperatures, which can only be achieved inside dilution refrigerators, to systems that are suitable for room-temperature operation. They can be artificially engineered potential wells that confine quantized electronic states or single-atom impurities in a lattice. They exploit nuclear or electronic degrees of freedom. Despite these differences, however, they share specific properties, such as the potential for high-density integration on a large scale. This feature arises from the well-established nanofabrication technology of the semiconductor industry [53].
- Nuclear magnetic resonance (NMR) qubits: While nuclear magnetic resonance (NMR) has demonstrated impressive control, it is not a practical candidate for quantum computers due to scalability issues. As the number of qubits grows beyond a dozen, the ratio of gate time to decoherence becomes too small. Therefore, there is a need for other technologies that can handle larger systems.
- Topological qubits: Topological qubits utilize anyons, which are exotic quasiparticles. Anyons have unique properties in fundamental physics as they generalize the statistics of bosons and fermions. Due to their exotic statistical behavior, they exhibit non-trivial quantum evolutions described by their topology. This means that they are abstracted from local geometrical details. When anyons are used to encode and process quantum information, this topological behavior provides much-desired resilience against control errors and perturbations [54].
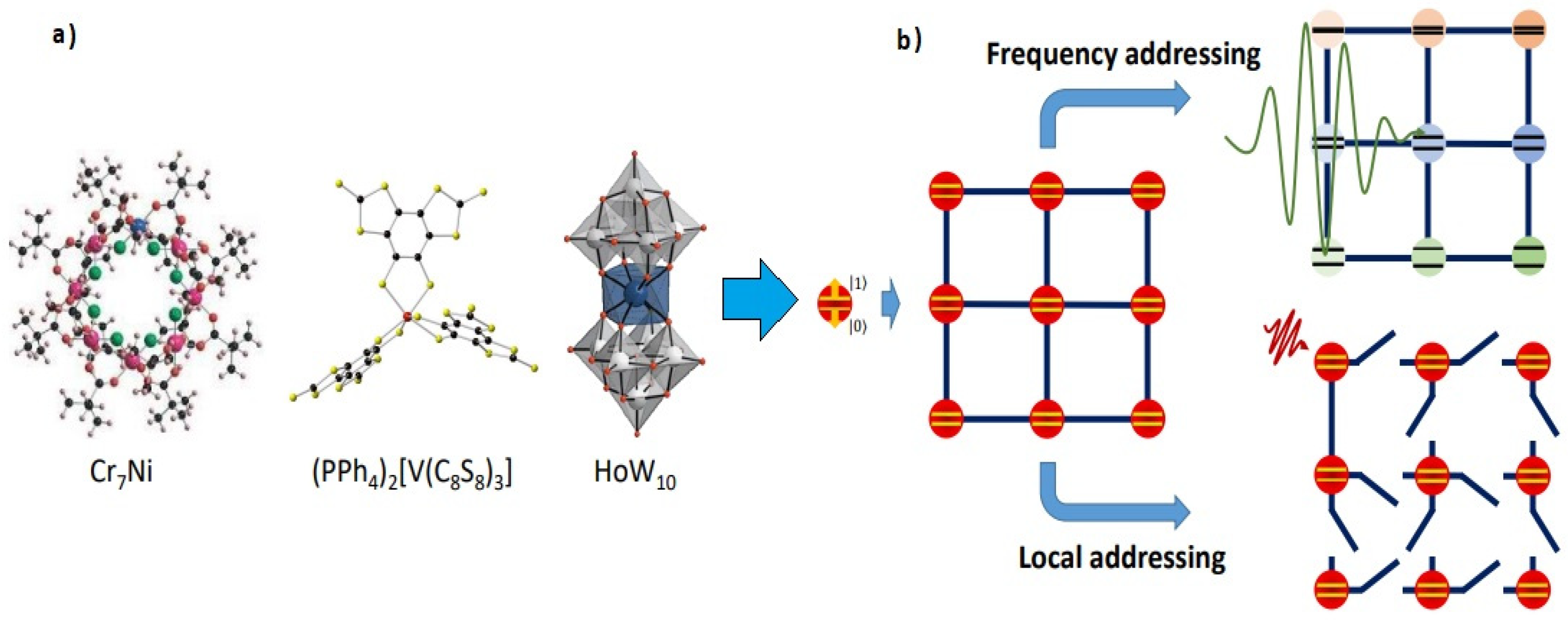
- Molecular spins: Artificial magnetic molecules can contribute to the achievement of large-scale quantum computation by (a) integrating multiple quantum resources and (b) reducing the computational cost of some applications. Chemical design, guided by theoretical proposals, facilitates the embedding of nontrivial quantum functionalities in each molecular unit, which then act as a microscopic quantum processor able to encode error-protected logical qubits or to implement quantum simulations. Scaling up even further requires “wiring-up” multiple molecules. Recently, this goal was achieved by coupling to on-chip superconducting resonators. The potential advantages of this hybrid approach and the challenges that still lay ahead have been critically reviewed. Figure 4 demonstrates the molecular structures of three molecular spin qubits and the scaling-up process [55].
3. Looking Ahead
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ellerhoff, B.M. The Basic Building Blocks of Quantum Computing. In Calculating with Quanta: Quantum Computer for the Curious; Springer: Berlin/Heidelberg, Germany, 2022; pp. 9–20. [Google Scholar]
- Golestan, S.; Habibi, M.; Mousavi, S.M.; Guerrero, J.M.; Vasquez, J.C. Quantum computation in power systems: An overview of recent advances. Energy Rep. 2023, 9, 584–596. [Google Scholar] [CrossRef]
- National Academies of Sciences, Engineering and Medicine. Quantum Computing: Progress and Prospects; National Academies of Sciences, Engineering and Medicine: Washington, DC, USA, 2019. [Google Scholar]
- Roffe, J. Quantum error correction: An introductory guide. Contemp. Phys. 2019, 60, 226–245. [Google Scholar] [CrossRef]
- Google Quantum AI. Suppressing quantum errors by scaling a surface code logical qubit. Nature 2023, 614, 676–681. [Google Scholar] [CrossRef]
- Kim, Y.; Eddins, A.; Anand, S.; Wei, K.X.; Van Den Berg, E.; Rosenblatt, S.; Nayfeh, H.; Wu, Y.; Zaletel, M.; Temme, K. Evidence for the utility of quantum computing before fault tolerance. Nature 2023, 618, 500–505. [Google Scholar] [CrossRef]
- Preskill, J. Quantum computing in the NISQ era and beyond. Quantum 2018, 2, 79. [Google Scholar] [CrossRef]
- Martinis, J.M.; Osborne, K. Superconducting qubits and the physics of Josephson junctions. arXiv 2004, arXiv:cond-mat/0402415. [Google Scholar]
- Manucharyan, V.E.; Koch, J.; Glazman, L.I.; Devoret, M.H. Fluxonium: Single cooper-pair circuit free of charge offsets. Science 2009, 326, 113–116. [Google Scholar] [CrossRef]
- Nguyen, L.B.; Lin, Y.-H.; Somoroff, A.; Mencia, R.; Grabon, N.; Manucharyan, V.E. High-coherence fluxonium qubit. Phys. Rev. X 2019, 9, 041041. [Google Scholar] [CrossRef]
- Zhang, G.; Liu, Y.; Raftery, J.J.; Houck, A.A. Suppression of photon shot noise dephasing in a tunable coupling superconducting qubit. NPJ Quantum Inf. 2017, 3, 1. [Google Scholar] [CrossRef]
- Wang, Z.; Shankar, S.; Minev, Z.; Campagne-Ibarcq, P.; Narla, A.; Devoret, M.H. Cavity attenuators for superconducting qubits. Phys. Rev. Appl. 2019, 11, 014031. [Google Scholar] [CrossRef]
- Serniak, K.; Hays, M.; De Lange, G.; Diamond, S.; Shankar, S.; Burkhart, L.; Frunzio, L.; Houzet, M.; Devoret, M. Hot nonequilibrium quasiparticles in transmon qubits. Phys. Rev. Lett. 2018, 121, 157701. [Google Scholar] [CrossRef] [PubMed]
- Pop, I.M.; Geerlings, K.; Catelani, G.; Schoelkopf, R.J.; Glazman, L.I.; Devoret, M.H. Coherent suppression of electromagnetic dissipation due to superconducting quasiparticles. Nature 2014, 508, 369–372. [Google Scholar] [CrossRef] [PubMed]
- Place, A.P.; Rodgers, L.V.; Mundada, P.; Smitham, B.M.; Fitzpatrick, M.; Leng, Z.; Premkumar, A.; Bryon, J.; Vrajitoarea, A.; Sussman, S. New material platform for superconducting transmon qubits with coherence times exceeding 0.3 milliseconds. Nat. Commun. 2021, 12, 1779. [Google Scholar] [CrossRef] [PubMed]
- Rigetti, C.; Gambetta, J.M.; Poletto, S.; Plourde, B.L.; Chow, J.M.; Córcoles, A.D.; Smolin, J.A.; Merkel, S.T.; Rozen, J.R.; Keefe, G.A. Superconducting qubit in a waveguide cavity with a coherence time approaching 0.1 ms. Phys. Rev. B 2012, 86, 100506. [Google Scholar] [CrossRef]
- Zhang, H.; Chakram, S.; Roy, T.; Earnest, N.; Lu, Y.; Huang, Z.; Weiss, D.; Koch, J.; Schuster, D.I. Universal fast-flux control of a coherent, low-frequency qubit. Phys. Rev. X 2021, 11, 011010. [Google Scholar] [CrossRef]
- Wang, C.; Axline, C.; Gao, Y.Y.; Brecht, T.; Chu, Y.; Frunzio, L.; Devoret, M.; Schoelkopf, R.J. Surface participation and dielectric loss in superconducting qubits. Appl. Phys. Lett. 2015, 107, 162601. [Google Scholar] [CrossRef]
- Jurcevic, P.; Javadi-Abhari, A.; Bishop, L.S.; Lauer, I.; Bogorin, D.F.; Brink, M.; Capelluto, L.; Günlük, O.; Itoko, T.; Kanazawa, N. Demonstration of quantum volume 64 on a superconducting quantum computing system. Quantum Sci. Technol. 2021, 6, 025020. [Google Scholar] [CrossRef]
- Paladino, E.; Galperin, Y.; Falci, G.; Altshuler, B. 1/f noise: Implications for solid-state quantum information. Rev. Mod. Phys. 2014, 86, 361. [Google Scholar] [CrossRef]
- Klimov, P.; Kelly, J.; Chen, Z.; Neeley, M.; Megrant, A.; Burkett, B.; Barends, R.; Arya, K.; Chiaro, B.; Chen, Y. Fluctuations of energy-relaxation times in superconducting qubits. Phys. Rev. Lett. 2018, 121, 090502. [Google Scholar] [CrossRef]
- Schlör, S.; Lisenfeld, J.; Müller, C.; Bilmes, A.; Schneider, A.; Pappas, D.P.; Ustinov, A.V.; Weides, M. Correlating decoherence in transmon qubits: Low frequency noise by single fluctuators. Phys. Rev. Lett. 2019, 123, 190502. [Google Scholar] [CrossRef]
- Andersen, C.K.; Remm, A.; Lazar, S.; Krinner, S.; Lacroix, N.; Norris, G.J.; Gabureac, M.; Eichler, C.; Wallraff, A. Repeated quantum error detection in a surface code. Nat. Phys. 2020, 16, 875–880. [Google Scholar] [CrossRef]
- Hertzberg, J.B.; Zhang, E.J.; Rosenblatt, S.; Magesan, E.; Smolin, J.A.; Yau, J.-B.; Adiga, V.P.; Sandberg, M.; Brink, M.; Chow, J.M. Laser-annealing Josephson junctions for yielding scaled-up superconducting quantum processors. NPJ Quantum Inf. 2021, 7, 129. [Google Scholar] [CrossRef]
- Sung, Y.; Ding, L.; Braumüller, J.; Vepsäläinen, A.; Kannan, B.; Kjaergaard, M.; Greene, A.; Samach, G.O.; McNally, C.; Kim, D. Realization of high-fidelity cz and z z-free iswap gates with a tunable coupler. Phys. Rev. X 2021, 11, 021058. [Google Scholar] [CrossRef]
- Spring, P.A.; Cao, S.; Tsunoda, T.; Campanaro, G.; Fasciati, S.; Wills, J.; Bakr, M.; Chidambaram, V.; Shteynas, B.; Carpenter, L. High coherence and low cross-talk in a tileable 3D integrated superconducting circuit architecture. Sci. Adv. 2022, 8, eabl6698. [Google Scholar] [CrossRef] [PubMed]
- Koch, J.; Terri, M.Y.; Gambetta, J.; Houck, A.A.; Schuster, D.I.; Majer, J.; Blais, A.; Devoret, M.H.; Girvin, S.M.; Schoelkopf, R.J. Charge-insensitive qubit design derived from the Cooper pair box. Phys. Rev. A 2007, 76, 042319. [Google Scholar] [CrossRef]
- Barends, R.; Kelly, J.; Megrant, A.; Sank, D.; Jeffrey, E.; Chen, Y.; Yin, Y.; Chiaro, B.; Mutus, J.; Neill, C. Coherent Josephson qubit suitable for scalable quantum integrated circuits. Phys. Rev. Lett. 2013, 111, 080502. [Google Scholar] [CrossRef]
- Hyyppä, E.; Kundu, S.; Chan, C.F.; Gunyhó, A.; Hotari, J.; Janzso, D.; Juliusson, K.; Kiuru, O.; Kotilahti, J.; Landra, A. Unimon qubit. Nat. Commun. 2022, 13, 6895. [Google Scholar] [CrossRef]
- Bruzewicz, C.D.; Chiaverini, J.; McConnell, R.; Sage, J.M. Trapped-ion quantum computing: Progress and challenges. Appl. Phys. Rev. 2019, 6, 021314. [Google Scholar] [CrossRef]
- Barends, R.; Kelly, J.; Megrant, A.; Veitia, A.; Sank, D.; Jeffrey, E.; White, T.C.; Mutus, J.; Fowler, A.G.; Campbell, B. Superconducting quantum circuits at the surface code threshold for fault tolerance. Nature 2014, 508, 500–503. [Google Scholar] [CrossRef]
- Levine, H.; Keesling, A.; Omran, A.; Bernien, H.; Schwartz, S.; Zibrov, A.S.; Endres, M.; Greiner, M.; Vuletić, V.; Lukin, M.D. High-fidelity control and entanglement of Rydberg-atom qubits. Phys. Rev. Lett. 2018, 121, 123603. [Google Scholar] [CrossRef]
- Harty, T.; Allcock, D.; Ballance, C.J.; Guidoni, L.; Janacek, H.; Linke, N.; Stacey, D.; Lucas, D. High-fidelity preparation, gates, memory, and readout of a trapped-ion quantum bit. Phys. Rev. Lett. 2014, 113, 220501. [Google Scholar] [CrossRef] [PubMed]
- Ballance, C.; Harty, T.; Linke, N.; Sepiol, M.; Lucas, D. High-fidelity quantum logic gates using trapped-ion hyperfine qubits. Phys. Rev. Lett. 2016, 117, 060504. [Google Scholar] [CrossRef] [PubMed]
- Gaebler, J.P.; Tan, T.R.; Lin, Y.; Wan, Y.; Bowler, R.; Keith, A.C.; Glancy, S.; Coakley, K.; Knill, E.; Leibfried, D. High-fidelity universal gate set for be 9+ ion qubits. Phys. Rev. Lett. 2016, 117, 060505. [Google Scholar] [CrossRef] [PubMed]
- Erhard, A.; Wallman, J.J.; Postler, L.; Meth, M.; Stricker, R.; Martinez, E.A.; Schindler, P.; Monz, T.; Emerson, J.; Blatt, R. Characterizing large-scale quantum computers via cycle benchmarking. Nat. Commun. 2019, 10, 5347. [Google Scholar] [CrossRef] [PubMed]
- Schäfer, V.; Ballance, C.; Thirumalai, K.; Stephenson, L.; Ballance, T.; Steane, A.; Lucas, D. Fast quantum logic gates with trapped-ion qubits. Nature 2018, 555, 75–78. [Google Scholar] [CrossRef]
- Lekitsch, B.; Weidt, S.; Fowler, A.G.; Mølmer, K.; Devitt, S.J.; Wunderlich, C.; Hensinger, W.K. Blueprint for a microwave trapped ion quantum computer. Sci. Adv. 2017, 3, e1601540. [Google Scholar] [CrossRef]
- Wong-Campos, J.D.; Moses, S.A.; Johnson, K.G.; Monroe, C. Demonstration of two-atom entanglement with ultrafast optical pulses. Phys. Rev. Lett. 2017, 119, 230501. [Google Scholar] [CrossRef]
- Akhtar, M.; Bonus, F.; Lebrun-Gallagher, F.; Johnson, N.; Siegele-Brown, M.; Hong, S.; Hile, S.; Kulmiya, S.; Weidt, S.; Hensinger, W. A high-fidelity quantum matter-link between ion-trap microchip modules. Nat. Commun. 2023, 14, 531. [Google Scholar] [CrossRef]
- Mazzanti, M.; Schüssler, R.; Espinoza, J.A.; Wu, Z.; Gerritsma, R.; Safavi-Naini, A. Trapped ion quantum computing using optical tweezers and electric fields. Phys. Rev. Lett. 2021, 127, 260502. [Google Scholar] [CrossRef]
- Pagano, G.; Hess, P.; Kaplan, H.; Tan, W.; Richerme, P.; Becker, P.; Kyprianidis, A.; Zhang, J.; Birckelbaw, E.; Hernandez, M. Cryogenic trapped-ion system for large scale quantum simulation. Quantum Sci. Technol. 2018, 4, 014004. [Google Scholar] [CrossRef]
- Jaksch, D.; Cirac, J.I.; Zoller, P.; Rolston, S.L.; Côté, R.; Lukin, M.D. Fast quantum gates for neutral atoms. Phys. Rev. Lett. 2000, 85, 2208. [Google Scholar] [CrossRef] [PubMed]
- Barredo, D.; De Léséleuc, S.; Lienhard, V.; Lahaye, T.; Browaeys, A. An atom-by-atom assembler of defect-free arbitrary two-dimensional atomic arrays. Science 2016, 354, 1021–1023. [Google Scholar] [CrossRef] [PubMed]
- Lukin, M.D.; Fleischhauer, M.; Cote, R.; Duan, L.; Jaksch, D.; Cirac, J.I.; Zoller, P. Dipole blockade and quantum information processing in mesoscopic atomic ensembles. Phys. Rev. Lett. 2001, 87, 037901. [Google Scholar] [CrossRef]
- Saffman, M.; Walker, T.G.; Mølmer, K. Quantum information with Rydberg atoms. Rev. Mod. Phys. 2010, 82, 2313. [Google Scholar] [CrossRef]
- Hulet, R.G.; Kleppner, D. Rydberg atoms in “circular” states. Phys. Rev. Lett. 1983, 51, 1430. [Google Scholar] [CrossRef]
- Kleppner, D. Inhibited spontaneous emission. Phys. Rev. Lett. 1981, 47, 233. [Google Scholar] [CrossRef]
- Hulet, R.G.; Hilfer, E.S.; Kleppner, D. Inhibited spontaneous emission by a Rydberg atom. Phys. Rev. Lett. 1985, 55, 2137. [Google Scholar] [CrossRef]
- Xia, T.; Zhang, X.; Saffman, M. Analysis of a controlled phase gate using circular Rydberg states. Phys. Rev. A 2013, 88, 062337. [Google Scholar] [CrossRef]
- Graham, T.; Song, Y.; Scott, J.; Poole, C.; Phuttitarn, L.; Jooya, K.; Eichler, P.; Jiang, X.; Marra, A.; Grinkemeyer, B.; et al. Demonstration of multi-qubit entanglement and algorithms on a programmable neutral atom quantum computer. arXiv 2021, arXiv:2112.14589. [Google Scholar]
- Cong, I.; Levine, H.; Keesling, A.; Bluvstein, D.; Wang, S.-T.; Lukin, M.D. Hardware-efficient, fault-tolerant quantum computation with rydberg atoms. Phys. Rev. X 2022, 12, 021049. [Google Scholar] [CrossRef]
- Chatterjee, A.; Stevenson, P.; De Franceschi, S.; Morello, A.; de Leon, N.P.; Kuemmeth, F. Semiconductor qubits in practice. Nat. Rev. Phys. 2021, 3, 157–177. [Google Scholar] [CrossRef]
- Lahtinen, V.; Pachos, J.K. A short introduction to topological quantum computation. SciPost Phys. 2017, 3, 021. [Google Scholar] [CrossRef]
- Carretta, S.; Zueco, D.; Chiesa, A.; Gómez-León, Á.; Luis, F. A perspective on scaling up quantum computation with molecular spins. Appl. Phys. Lett. 2021, 118, 240501. [Google Scholar] [CrossRef]
- Available online: https://thequantuminsider.com/quantum-research/ (accessed on 16 May 2022).
- Krastanov, S.; Heuck, M.; Shapiro, J.H.; Narang, P.; Englund, D.R.; Jacobs, K. Room-temperature photonic logical qubits via second-order nonlinearities. Nat. Commun. 2021, 12, 191. [Google Scholar] [CrossRef] [PubMed]
- Head-Marsden, K.; Krastanov, S.; Mazziotti, D.A.; Narang, P. Capturing non-Markovian dynamics on near-term quantum computers. Phys. Rev. Res. 2021, 3, 013182. [Google Scholar] [CrossRef]
- Papaj, M.; Fu, L. Creating Majorana modes from segmented Fermi surface. Nat. Commun. 2021, 12, 577. [Google Scholar] [CrossRef]
- Head-Marsden, K.; Flick, J.; Ciccarino, C.J.; Narang, P. Quantum information and algorithms for correlated quantum matter. Chem. Rev. 2020, 121, 3061–3120. [Google Scholar] [CrossRef]
- Krylov, A.I.; Doyle, J.; Ni, K.-K. Quantum computing and quantum information storage. Phys. Chem. Chem. Phys. 2021, 23, 6341–6343. [Google Scholar] [CrossRef]
- Daiss, S.; Langenfeld, S.; Welte, S.; Distante, E.; Thomas, P.; Hartung, L.; Morin, O.; Rempe, G. A quantum-logic gate between distant quantum-network modules. Science 2021, 371, 614–617. [Google Scholar] [CrossRef]
- Malz, D.; Smith, A. Topological two-dimensional Floquet lattice on a single superconducting qubit. Phys. Rev. Lett. 2021, 126, 163602. [Google Scholar] [CrossRef]
- Borjans, F.; Mi, X.; Petta, J. Spin digitizer for high-fidelity readout of a cavity-coupled silicon triple quantum dot. Phys. Rev. Appl. 2021, 15, 044052. [Google Scholar] [CrossRef]
- Tang, W.; Tomesh, T.; Suchara, M.; Larson, J.; Martonosi, M. Cutqc: Using small quantum computers for large quantum circuit evaluations. In Proceedings of the 26th ACM International conference on architectural support for programming languages and operating systems, Virtual Event, 19–23 April 2021; pp. 473–486. [Google Scholar]
- Bourassa, J.E.; Alexander, R.N.; Vasmer, M.; Patil, A.; Tzitrin, I.; Matsuura, T.; Su, D.; Baragiola, B.Q.; Guha, S.; Dauphinais, G. Blueprint for a scalable photonic fault-tolerant quantum computer. Quantum 2021, 5, 392. [Google Scholar] [CrossRef]
- Shikano, Y.; Watanabe, H.C.; Nakanishi, K.M.; Ohnishi, Y.-y. Post-Hartree–Fock method in quantum chemistry for quantum computer. Eur. Phys. J. Spec. Top. 2021, 230, 1037–1051. [Google Scholar] [CrossRef]
- Terashi, K.; Kaneda, M.; Kishimoto, T.; Saito, M.; Sawada, R.; Tanaka, J. Event classification with quantum machine learning in high-energy physics. Comput. Softw. Big Sci. 2021, 5, 1–11. [Google Scholar] [CrossRef]
- Available online: https://www.precedenceresearch.com/quantum-computing-market (accessed on 31 November 2022).


| Institutions | Projects |
|---|---|
| Massachusetts Institute of Technology | |
| Harvard University | |
| Max Planck Society | |
| Princeton University | |
| University of Tokyo |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dejpasand, M.T.; Sasani Ghamsari, M. Research Trends in Quantum Computers by Focusing on Qubits as Their Building Blocks. Quantum Rep. 2023, 5, 597-608. https://doi.org/10.3390/quantum5030039
Dejpasand MT, Sasani Ghamsari M. Research Trends in Quantum Computers by Focusing on Qubits as Their Building Blocks. Quantum Reports. 2023; 5(3):597-608. https://doi.org/10.3390/quantum5030039
Chicago/Turabian StyleDejpasand, Mohamad Taghi, and Morteza Sasani Ghamsari. 2023. "Research Trends in Quantum Computers by Focusing on Qubits as Their Building Blocks" Quantum Reports 5, no. 3: 597-608. https://doi.org/10.3390/quantum5030039
APA StyleDejpasand, M. T., & Sasani Ghamsari, M. (2023). Research Trends in Quantum Computers by Focusing on Qubits as Their Building Blocks. Quantum Reports, 5(3), 597-608. https://doi.org/10.3390/quantum5030039






