Abstract
This paper discusses the fundamental assumptions and background of the consistent histories (CH) approach to quantum mechanics. The focus of the paper is on the concept of frameworks. It is proposed that frameworks should be interpreted objectively as observer-independent realities. Two further options are considered: a hidden-variables variant of the CH approach, and a many-worlds version, which considers each individual history belonging to a given family as describing a separate world. The latter interpretation is subsequently compared and contrasted with the standard many-worlds interpretation. Finally, the solution to the measurement problem offered by the many-worlds variant of CH is analyzed and amended.
1. Introduction
The consistent histories (CH) interpretation of quantum mechanics is relatively less well-known than the major contenders in the area: the many-worlds interpretation, Bohmian mechanics, or the spontaneous localization theory. Yet, it deserves to be thoroughly evaluated and contrasted with other interpretations. So far, there have been only a handful of papers that directly and critically analyzed this conception in its entirety, its ontological presuppositions, and consequences. The consistent histories approach was first proposed in [1], and then developed in [2,3,4]. The fullest exposition of this interpretation can be found in [5], while [6,7] contain a very useful condensed survey of its main assumptions. Early critiques of the CH approach can be found in [8,9,10], while [11] is one of the most recent polemics focusing on the measurement problem.
While the formalism of consistent histories is occasionally used outside its narrow circle of followers, the specifics of this approach remain obscure for the majority of the philosophers of physics. In this article, I will analyze the basic tenets of the consistent histories approach, as presented in the works of one of its major and most vocal proponents, Robert Griffiths (mostly in [5,6]). The focus of this survey will be on the concept of framework and its possible interpretations. I will defend the claim that the best interpretation of frameworks is in terms of distinct worlds. I will compare the many-worlds variant of consistent histories with the standard many-worlds interpretation, pointing out some of the most crucial differences. Finally, I will address the central issue that prompted the emergence of various interpretations of quantum mechanics in the first place, namely the measurement problem. I will argue that the way the consistent histories interpretation deals with this problem presupposes a weak conception of scientific explanation. For this solution to work, we have to rely on some variant of the anthropic principle.
2. Basic Formalism of Consistent Histories
The fundamental concept of the consistent histories approach is that of a framework. Formally, a framework is constituted by a projective decomposition of the identity, that is a set of projectors in a Hilbert space such that and . Adding to the set (a sample space) all linear combinations of the form , we obtain a Boolean algebra (or, generally, a σ-algebra), on which a classical probability function Pr can be defined. Two frameworks and are compatible if for all α, β; otherwise the frameworks are incompatible. As is well known, there is no joint probability function satisfying Kolmogorov’s axioms that could be defined on incompatible frameworks (sample spaces). This fact forms the basis for the central postulate of CH, according to which all quantum reasoning involving probabilities has to be done within a single framework (the so-called single framework rule). It is prohibited to combine two incompatible frameworks in one quantum description. For instance, we cannot attribute to a quantum system the conjunction of two properties represented by non-orthogonal projectors (and thus belonging to different, incompatible frameworks), even though each property taken separately may be attributable to the system within a particular framework.
In standard applications, a particular Hilbert space is assumed to contain momentary states of a system taken at a certain instance. If we consider a tensor product of k such spaces, we can represent states taken at k successive instances, and thus constituting a history of a system. A history is formally defined as a tensor product of N + 1 projection operators: . This operator represents a straightforward situation, in which the system possesses property at time t0, property at t1, and so on. It is also possible to consider histories that are nontrivial superpositions of the projectors of the above kind, even though their physical interpretation is somewhat intricate. A family of histories contains orthogonal projectors of the above kind that sum up to unity, exactly as explained in the previous paragraph. Histories Yα are called “elementary”, and they constitute a sample space. In what follows, we will drop the distinction between families of histories and families of elementary histories (sample spaces) if this does not lead to confusion. Thus, such a family constitutes a framework, for which it is possible to define a classical probability function.
In order to introduce probabilities into the formalism, we have to take into account the physical dynamics of the system. The evolution from time ta to tb is assumed to be governed by a unitary operator T(tb, ta), which depends on the Hamiltonian of the system. Next, we define for any history its corresponding chain operator , as follows:
Defining the inner product on the set of chain operators:
we can introduce the probability function Pr to any family of histories, in the standard manner:
However, when we want to extend the probability function Pr to all linear combinations of histories, a problem occurs. The probability of a linear combination should equal , but when we apply Formula (3) and use the (anti)linearity of the inner product, we will obtain cross products . In order to eliminate this possibility, the condition of consistency is imposed on families of histories:
In other words, consistent families are built out of histories whose corresponding chain operators are mutually orthogonal. It may be added that the condition of orthogonality depends on the underlying dynamics, and is not a property of a family simpliciter (since the chain operators contain the evolution operator T). That is, it is possible to have one and the same family that is consistent under one dynamics and inconsistent under another (for an example see [5], p. 145).
The general Formula (3) for probability reduces to the familiar Born rule in the case when we consider only two moments t0, t1 and limit ourselves to histories with a fixed initial state . That is, the selected family of histories consists of the following:
where , , and are mutually orthogonal and span the entire single-moment Hilbert space 1. When we apply Formula (2), we can quickly calculate that
In the subsequent discussions, we will limit ourselves to histories with fixed initial states, however with an arbitrary number of times N ≥ 1. That is, we will consider any histories of the form
A typical misconception associated with the notion of histories is that the above operator (7) should represent a possible evolution of the system that starts with the state and then develops according to a particular unitary operator. This is incorrect, because, as we can see in the simple two-time example (5), the states at time t1 will generally not be the result of a unitary evolution applied to the initial state . We will return to the question of the proper ontological interpretation of histories later, but for now we can use a conceptual crutch, in the form of a Copenhagen-style explanation, with its irreducible use of measurements. A history of the form (7) may be provisionally interpreted as resulting from a series of measurements, each of which is associated with a particular projector . In other words, at every moment ti where i > 0, we ask the experimental question whether the system is in a state corresponding to . If the answer each time is “yes”, we have physically selected the history (7) out of many alternative possibilities. The probability associated with a particular history is precisely the probability that appropriate measurements will reveal a string of yes-answers to questions . However, we have to stress that the CH approach does not admit the concept of measurement understood as a special physical process different from the standard unitary evolution prescribed by the Schrödinger equation. We will discuss this issue shortly.
Among the families of histories with a fixed initial state, we may of course distinguish a special history that satisfies the above-mentioned intuition. That is, we may consider the following history:
where for i = 1, …, N. For obvious reasons this history is called unitary, and together with its complementary histories (built out of all remaining combination of projectors and ), it constitutes a unitary family. A characteristic feature of this family is that its elements receive only probabilities 0 or 1 under the assumed dynamics. However, as Griffiths stresses, other than that, there is nothing special regarding unitary histories in comparison to other histories. In particular, Griffiths rejects the view that only unitary histories and unitary wave functions (“uniwaves”) are ontologically real. A unitary family provides us with one framework within which we can describe a particular system, but alternative frameworks are still available and have no lesser reality. Thus, we should abandon the standard view that a quantum system develops uniquely via the evolution of its wave function, and that at any moment of its evolution the only physical reality associated with this system is its unitarily evolved wave function.
3. Example of a Consistent Family
It should be rather obvious how to use families of histories as frameworks that enable us to consider all sorts of questions regarding the conditional and unconditional probabilities of various quantum events. Given a particular dynamics, each element in a selected family of histories receives its classical probability, according to Formula (3). Then, we can calculate various probabilities of particular occurrences at selected times, on the condition that, at other times, the system has such and such properties. The procedure should be as follows: if we are interested in calculating specific probabilities of some outcomes conditionally on some other outcomes obtained at different times, we should first select a family of histories that contains these outcomes, apply the underlying dynamics, and compute the probabilities. It has to be stressed that this procedure can be executed only within an appropriate framework (family). Selecting an alternative, incompatible framework, we cut ourselves off from the possibility of answering the question of interest.
Let us use a simple example to illustrate this method. Consider a spin-half particle (an electron) entering a Stern–Gerlach magnet that was aligned with the z axis, and select three points in time: t0 and t1 before entering the magnet, and t3 after leaving the magnet (see Figure 1). The initial state at t0 is assumed to be , where is the spatial wave function associated with the particle at t0. We assume the standard dynamics in the following form:
where indicate the appropriate wave functions, whose spatial supports are depicted on Figure 1, and are eigenvectors of the z-spin operator corresponding to eigenvalues +1/2 and −1/2. This case, which Griffiths calls “microscopic measurement” is taken from his book [5], pp. 230–233.
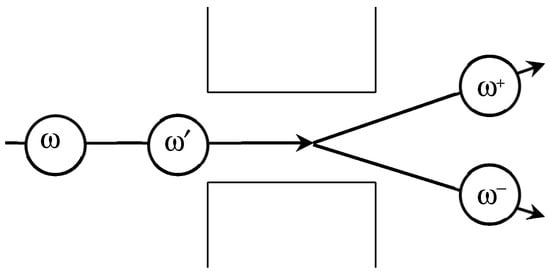
Figure 1.
A spin-half particle passing through a Stern–Gerlach apparatus.
A typical way to describe the evolution of the system is by applying the transformations (9) to the initial state and thus obtaining the successive states at t1 and t2. That way we will arrive at the following unitary history:
which together with its complement will constitute one possible family of histories (let us symbolize it with 0). The probability assigned to this history is obviously 1. On the other hand, if we wanted to calculate the probabilities of obtaining definite values of z-spin at time t2, we would have to use a different family 1, consisting of the following two histories (plus their complement, which I will ignore):
The algorithm for calculating probabilities produces the straightforward result: each of the above histories has an equal one-half probability. Thus, the conditional probability of finding that the particle has its z-spin “up” at t2 equals ½, as expected. However, we may be interested in asking a similar question regarding the z-spin at t1, before the particle enters the magnet. In order to answer this question, we have to select yet another family (let us call it 2):
Again, the probabilities associated with these histories equal ½. Thus, the likelihood of finding the z-spin “up” at t1, conditional on the initial state being , is one-half. However, if we conditionalize on the later values of spins at t2, the result will be different: the probability of the z-spin being “up” at t1, given that at t2 it was “up”, equals one.
This conclusion may come as a surprise. Traditionally, we believe that it is the interaction with the magnet that produces the “splitting” of the electrons into two beams with different values of spin. Whether this splitting is treated as a symptom of a mysterious non-unitary “collapse”, or as a result of a physical process of decoherence, it remains the case that before the interaction with the magnet, the z-spin is not supposed to be well-defined. However, when we interpret the above probabilistic reasoning literally, it seems that it makes perfect sense to expect that there will be two possible and equally probable ways for the system to evolve, each of which involves a definite value of the z-spin, even before the electron enters the magnet. At least this is true from the perspective of a particular framework. Yet, this is baffling. It seems that we cannot make any progress in our attempt to understand the CH interpretation without delving deeper into the concept of a framework and its role in this interpretation.
4. Frameworks and Worlds
What are frameworks, ontologically speaking, and what exactly is their role? Let us approach this problem by following Griffiths’ formulation of the fundamental principles governing the use of frameworks in [6] (p. 98). We have already mentioned the single-framework rule, which states that every instance of quantum reasoning should be performed within one specific framework. To that, Griffiths adds the principle of liberty, which prescribes that the scientist can use any framework he or she deems appropriate. That no framework is better than any other is encompassed in the principle of equality. However, frameworks can be more or less useful for some purposes, and this fact is reflected in the principle of utility: we should use the framework that best suits our goals. Finally, Griffiths mentions the principle of incompatibility, which seems to be a variant of the single-framework rule, since it prohibits the simultaneous use of two incompatible frameworks. As we already know that only one framework can be used in any particular reasoning, this principle appears to be redundant.
It is difficult to shake off the feeling that all these rules and principles have a strongly pragmatic and instrumentalist character. They do not say what frameworks are or what they are supposed to represent, but instead they tell us merely how to use them and what we may or may not do with them. Observe, for example, that the single-framework rule, central to the CH approach, has the form of an unconditional command “you must not use two incompatible frameworks in one reasoning”. However, there is no explanation of the source of this postulate (a divine decree?). What would happen if we obstinately ignored this rule? Would we end up with a logical contradiction? Most certainly not, since the rules of the CH interpretation do not have the status of logical laws. Perhaps there would be some other unpleasant consequences, such as consistently losing bets (the Dutch book argument). Alternatively, there may be some ontological reasons for not mixing up different frameworks, if they turn out to describe distinct realities, as will be suggested in what follows.
The emphasis put on the rules of reasoning within particular frameworks seems to show an affinity with quantum Bayesianism (or operationalism) and its antirealist attitude towards quantum theory [12,13,14]. It is no wonder then that David Wallace has voiced his doubts about whether CH is a realist theory in the conventional sense of the word [15] (p. 39). Griffiths seem to be less pessimistic in regards to this issue, but his clarifications are rather nebulous. First off, he stresses that the choice of a particular framework does not in any way influence reality. This is little consolation to a realist, unless we specify what reality truly consists of and what its relation to the multitude of incompatible frameworks is. Griffiths uses a series of classical analogies that are supposed to throw some light on this problem [6] (p. 99). Unfortunately none of these analogies are complete, since in the classical case there is no analogue of the quantum concept of incompatibility. For instance, he compares the choice of a quantum framework to the selection of an inertial frame of reference in special relativity, only to observe that in the latter case all inferences performed in one frame of reference can be translated into inferences in any other frame, which is not true in the quantum case. Another incomplete analogy drawn by Griffiths likens frameworks to different perspectives adopted when observing an object (for instance viewing a mountain from different sides). However, he quickly admits that these observations can be combined together into a consistent description, in contrast to the case of quantum frameworks. As we can see, it is very difficult, if not outright impossible, to explicate the concept of frameworks under the assumption of the existence of one, unified reality.
It seems to me that the only realist, objectual interpretation of a framework is that frameworks refer to some observer-independent and distinct realities. It is hopefully not too far-fetched to call these realities “worlds”. Adopting this interpretation, we can immediately explain the single-framework rule, or its cognate, the principle of incompatibility. Any reasoning has to be done in exactly one framework, because separate worlds do not overlap, and thus their descriptions cannot be combined into one consistent story. This interpretation also accounts for the principle of equality, since among alternative worlds we do not distinguish more or less real ones. The remaining principles (liberty and utility) of course will have to retain their pragmatic character, but this should not be particularly worrying for the realist (pragmatic choices regarding which world we wish to consider do not threaten the objective character of the framework-selected worlds). It may be worth noting that alternative worlds corresponding to distinct and incompatible frameworks do not have to be mutually contradictory, in the sense that there is a quantum-mechanical statement which is true in one of them and false in another. Nevertheless, they are still distinct. Their distinctness may follow from the fact that there are some properties that may be used to characterize objects in one world but not in the other. In other words, different worlds are characterized by different sets of available properties (for instance, in one world, these properties may include spin in the z direction, and in another, spin in the x direction).
In order to explain these things further, we have to delve deeper into the structure of the worlds picked out by appropriate frameworks. As we remember, in the CH approach, frameworks are identified with consistent families of histories. What is the relation between alternative histories from a particular family and the world represented by this family? We can find one possible answer to this question in [6], p. 102, where Griffiths writes:
“[…] if a single framework, a single consistent family, of histories is in view, the sample space, represented mathematically by an appropriate PD of the history identity, is a collection of mutually-exclusive possibilities, one and only one of which actually occurs.”[italics mine]
This rather stunning admission seems to indicate that each framework-world contains only one out of the multitude of alternative histories, even if other histories receive non-zero quantum probabilities. To my knowledge, this suggestion has never been worked out in detail, but it definitely looks like a variant of the hidden variable hypothesis. The standard version of this hypothesis asserts that each measurable parameter characterizing a physical system possesses in actuality a well-defined, precise value, which is nevertheless not known to us, hence the use of the probability distribution. This hypothesis is famously vulnerable to a number of no-go theorems, in particular the Bell and Kochen–Specker theorems. However, in combination with the CH approach, the hidden variables escape these problems. The key point is that no framework-world assigns precise values to incompatible observables. Each framework admits only orthogonal projectors that are mutually compatible, and out of these projectors exactly one is selected to represent the actually possessed property. Thus, no violation of Bell’s inequalities follows, since all known variants of these inequalities require an assignment of precise values to incompatible properties (such as spins in different directions). For the same reason, the Kochen–Specker “coloring” theorem is not violated [16] (pp. 119–138). Consequently, the hidden-variable version of the CH approach does not need to admit strong non-locality or contextuality.
The Many-Worlds Variant of CH
In spite of the above-mentioned advantage over the standard version, the hidden-variable interpretation of CH may still not be the first choice for many philosophers. It presupposes the existence of a fundamental rift between what is (the actually obtaining history) and what can be known (the probability distribution over alternative histories). Those who prefer not to introduce elements of reality that cannot be known, even in principle, may be compelled to follow a different route. Alternative histories whose probabilities under a given dynamics are non-zero may be assumed to represent distinct and parallel realities, in line with the many-worlds interpretation (MWI) of quantum mechanics. Griffiths himself makes a disparaging remark regarding this approach, but without giving any deeper reason for his preference [6] (p. 102). However, on some occasions he slips into language that may suggest an objectivist interpretation of distinct frameworks. For instance, in [7], he spells out the thesis of unicity, which he subsequently rejects, as follows: “at any point in time there is one and only one state of the universe which is “true”, and with which every true statement about the world must be consistent”. By negation, if we reject this claim, we have to assume that there are more than one “true” states of the universe, which we may call “worlds”. It seems to me that the many-worlds variant of CH (henceforth abbreviated as MWCH) is rather natural, so I will try to analyze it further, in spite of Griffiths’ reservations, contrasting it with the well-known Everettian interpretation of quantum mechanics.
According to MWCH, there is not a single world associated with a given family of histories, but a collection of mutually exclusive worlds (except in the case of unitary families). Thus the set of all worlds can be partitioned into families, which then divide up further into individual worlds. We can illustrate this with the help of the example from the previous section. Family 0 includes just one possible world (let us call it ) with the unitary history (10), since this is the only history in this family that receives a non-zero probability. However, another group of worlds contains equally probable histories from family 1. In one of these worlds (), the electron has a well-defined x-spin before entering the magnet and then acquires the value “up” of the z-spin, while simultaneously travelling along the upper trajectory. The alternative world () differs, in that the electron leaves the magnet following the lower trajectory and possesses the “down” value of spin in the z direction. The third considered family 2, which—it has to be stressed—is equally acceptable, also separates into two worlds. One world contains an electron that already exhibits the “up” value of its z-spin before entering the magnet, and consequently follows the upper trajectory, while in the other world the electron consistently possesses z-spin “down” from the moment t1. All in all, in our simple example we have five distinct worlds , , , , and grouped into three families 0, 1, and 2.
Let us observe that worlds belonging to the same family differ with respect to the specific values possessed by the same measurable parameter (z-spin in our example). However, the differences between worlds belonging to distinct families are more subtle. For instance, worlds and diverge due to the fact that in at time t2 the electron is in a superposition with no well-defined z-spin, while in it possesses a definite value z+. On the other hand, worlds , diverge with respect to the definite values of z-spin at t2, as well as regarding the state of the electron at t1. In world , the electron has a definite value of x-spin at t1, whereas in the electron is characterized by a definite z-spin at the same moment t1. In worlds and there are no differences regarding the possessed values of the same parameter, but nevertheless the worlds are different due to their incompatible characterizations of the electron’s state at t1.
We may contrast the MWCH approach with the standard many-worlds interpretation ([17,18,19]). According to the latter, the evolution of the system is given by the unitary history (10) from family 0. No other histories are admissible; they do not represent any real physical processes. However, MWI interprets the superposition characterizing the system at time t2 as describing two independent realities: one in which the electron has spin “up” in the z direction, and the other in which the z-spin of the electron is “down”. Thus, MWI admits the existence of two worlds and , even though no history corresponding to these worlds represents a genuine quantum-mechanical process, since these histories clearly violate the universal law of quantum mechanics, i.e., the Schrödinger equation.
This point is rarely made, so it bears repeating. Even though “officially” MWI insists that the Schrödinger equation is universally valid with no exceptions, individual worlds clearly violate it. The law of the unitary evolution applies to the entire multiverse and not the separate worlds constituting it. Observe that, in contrast to MWCH, MWI does not admit the world as a separate entity. The unitary history refers to the collection of worlds and rather than a distinct world. For the proponent of MWI there is no single world in which the electron after leaving the magnet would still be in a superposition of states with distinct locations. Superpositions of states with well-defined locations, by necessity, refer to distinct realities.
Incidentally, we may observe that many authors have combined the assumption of the fundamental reality of the wave function and its unitary evolution with the formalism of CH ([15,20]). That is, they admit a family of histories corresponding to the components of the universal wave function writtenin the preferred basis with respect to which the splitting into separate worlds occurs. However, this is not a full CH (at least not according to Griffiths), since it ignores other available histories. This explains a remark made in [6], p. 95 ft. 2, that “the discussion of consistent histories presented in (Wallace 2008) bears little resemblance to what is found in (Griffiths 2002)”.
How about worlds and ? Here, the thorny issue of the exact moment of the splitting of the worlds comes into view. The “traditional” variant of MWI assumes that the splitting occurs at the precise moment of measurement (I am tempted to call this variant the Copenhagen version of the many-worlds interpretation), when macroscopic outcomes are revealed to us. However, this solution relies on the concept of measurements being fundamentally distinct from other types of physical interactions. An alternative, rather popular view is that the splitting is a result of a physical process of decoherence, which is a physical interaction with the environment possessing a huge number of degrees of freedom (see [21] for a comprehensive physical and philosophical analysis of decoherence). Given some specifics of this interaction, the components of the superposition corresponding to states with distinct spatial locations become “recorded” in approximately orthogonal states of the environment, which leads to the suppression of the interference (“non-diagonal”) coefficients in the density operator used to calculate the probabilities of finding the system in particular states. In our simplified example, we assume that the decohering interactions (for instance with air molecules) occur after the electron leaves the magnet and that its unitarily evolved state decomposes into parts with distinct locations. Consequently, the splitting takes place at moment t2, which eliminates the worlds and , since they seem to move the moment of splitting back in time to point t1.
On the other hand, the many-worlds variant of CH does not require any objective process leading to the splitting of the initial world into several copies, whether in the form of an interaction with a measuring device or as a result of the decoherence with the environment. For the proponent of MWCH, it just does not make sense to ask generally when exactly the electron whose initial state is splits into a number of copies corresponding to the different outcomes of the measurement down the line. There is one framework in which the splitting seems to occur at the last possible moment, and another in which from the very beginning, the electron evolves in the form of distinct copies associated with the later recorded outcomes. To make matters even more interesting, there is also a framework in which no splitting takes place at all, and the electron is always in the state of superposition. Thus, ultimately, we can get rid of the objective branching of the actual world, replacing it with the multitude of different worlds grouped in various frameworks.
Another related difference between MWI and MWCH that is worth emphasizing is that the latter easily circumvents the problem of the preferred basis that affects earlier versions of MWI. As is well known, MWI requires that there be a unique decomposition of the unitary wave function into mutually orthogonal states that define appropriate worlds. Since formally there is an infinity of ways we can decompose any vector, there has to be an additional rule selecting the preferred orthogonal basis with respect to which the decomposition is made. On the other hand, MWCH admits any decomposition of that sort, according to the principle of liberty. Any decomposition of the unitary wave function corresponds to a set of objectively existing worlds, and no decomposition is considered to be privileged.
It may be asked what is to be gained by introducing the ontologically extravagant hypothesis of the existence of a myriad of distinct worlds, far surpassing the number of the worlds admitted in the standard MW interpretation. My answer to that question would not be in terms of an immediate gain but rather in terms of the lack of a satisfactory alternative. The CH interpretation derives its flexibility from admitting an infinite number of incompatible but equally admissible frameworks in which we can describe a particular quantum process. However, from a realist perspective, these frameworks must correspond to some objective, observer-independent reality. Since incompatible frameworks cannot be combined into a consistent story, the corresponding realities must be in some sense distinct. Calling these realities “worlds” merely reflects the fact that they cannot be summed up to obtain a consistent whole. I do not see any other way to uphold the central postulates of CH while retaining the basic assumptions of scientific realism. The only alternative is to admit that quantum facts are in some sense created by the observer by the very act of selecting a particular framework.
5. The Measurement Problem and Quasi-Classicality
The biggest test of the consistent histories approach is how well it deals with the measurement problem. Here, by the measurement problem I understand the question of how to explain the occurrence of definite macroscopic outcomes in the light of the fact that the unitary evolution of the system consisting of the measured object and the measuring device typically produces a superposition of states involving different outcomes. We may add that, in the literature on the subject, one can find mentions of more than one measurement problem. For instance, [6] distinguishes two measurement problems: one as stated above, and the other expressed by the question of how to relate the alternative positions of the pointer with the earlier microscopic situation that is supposed to be measured. Tim Maudlin, in [22], adds to this a third problem, which he calls the problem of effects. Roughly, it is the question of how to explain that future repeated measurements of the same observable will yield the same results. Maximilian Schlosshauer, on the other hand, mentions two separate but related problems: the nonobservability of interference, and the preferred basis problem ([21], p. 50).
The MWI approach solves the problem of definite outcomes by adopting the many-worlds reading of the final superposition of the combined system. Definite outcomes occur in separate worlds, corresponding to the components of the superposed state with well-defined macroscopic locations of the measuring instrument (the pointer). However, as we have seen, the MWCH approach admits many more possible histories than MWI, and this creates a potential problem. Griffiths optimistically announces that the measurement problem finds its solution in CH, because there is an admissible framework in which measurements indeed produce definite outcomes ([6], p. 105). This specific framework involves the decomposition of the identity in the orthogonal basis corresponding to the states with well-defined positions of the pointer. In this framework it is indeed the case that each history contains a definite outcome, and moreover the probabilities associated with these histories correspond precisely to the observed frequencies of appropriate outcomes.
The problem is, though, that there are many alternative frameworks and alternative worlds in which there are patently no definite outcomes. One such world is the familiar unitary world in which the initial superposition persists even after the interaction with the measuring device. As Elias Okon and Daniel Sudarsky point out in their critique of CH [11], there has to be an additional rule that eliminates all frameworks except the one in which measurements indeed have definite outcomes. However, such a rule is not present in the standard version of CH and, therefore, must be brought in from outside this interpretation. Griffiths seems to disagree with this conclusion. Is there any way to solve this controversy?
One way to reconcile the conflicting positions of Griffiths on the one hand, and Okon and Sudarsky on the other, is to observe that they tacitly base their arguments on different standards of scientific explanations. Okon and Sudarsky seem to presuppose a stronger notion of explanation, according to which, in order to explain a given occurrence, we have to derive it from the applicable laws and assumed initial conditions (this resembles the well-known deductive-nomological conception of explanation of Carl Hempel and Paul Oppenheim [23]). In other words, we explain a particular happening when we show that it must occur in a given situation (we can definitely predict it). On the other hand, for Griffiths it is sufficient that there is an available framework within which measurements can be assigned definite outcomes. That is, he most probably would subscribe to the weaker interpretation of explanation: for an occurrence to be explained we should show that it may happen given the laws and the circumstances (it is consistent with the laws and the initial conditions).
Typically, such weak explanations are employed when we deal with indeterministic events whose occurrences do not follow from the laws and earlier conditions. However, in the case of the many-worlds variant of CH the situation is more subtle. It is not the case that there is some single-world probability that the definite outcomes will occur and some probability that they will not, but rather that they are certain to occur in some but not all of the admissible worlds. Seen from this perspective, a complete explanation of a particular observed phenomenon that occurs only in some worlds requires that we answer the question why we as observers occupy those precise worlds. In our currently considered problem, the question is how to explain that we do not happen to inhabit worlds in which systems, after measurements, continue to occupy superposed states (as is the case in the unitary worlds).
A broad answer to this question may be provided in the form of a familiar anthropic principle of sorts. We may speculate that the effective suppression of macroscopic superpositions is necessary for the emergence of living organisms possessing appropriate cognitive abilities. However, this solution presupposes that we can definitively exclude the possibility of the existence of sentient beings in a universe that admits macroscopic superpositions of positions and other related parameters. While we do not have a satisfactory account of cognitive processes and functions, such as perceptions, in superposed states, the lack of such an account does not, by itself, constitute proof that cognition in the universe without the definite outcomes of experiments is impossible. As Okon and Sudarsky correctly observe, it would be circular to simply start with the thesis that macroscopic objects in our world possess well-defined locations, and then to use this thesis to eliminate all the alternative worlds admissible by our theory. To break this circularity, I suggest that we should propose a general theory of consciousness and cognition which would entail that sentient beings cannot exist in a world with macroscopic superpositions.
A related problem that admits a similar solution to CH is the question of how to generally explain the classical appearance of the macroscopic world. Here, an answer is provided in the form of the so-called quasi-classical frameworks ([5], pp. 356–359; [6], p. 103). These are histories and families of histories, describing possible evolutions of systems with a huge number of particles that, when appropriately coarse-grained, recover classical properties and their approximately classical dynamics. Griffiths suggests that there will be many such families that will give rise to the same classical description. Moreover, he claims that thanks to the process of decoherence some of these quasi-classical frameworks will be consistent. Even though he does not offer a strict proof for this contention, his plausibility argument relies on the formal similarity between the condition of decoherence (the lack of off-diagonal elements in an appropriate density matrix) and the consistency condition (4).
Griffiths is aware of the fact that, typically, there will be many non-classical and yet consistent families of histories in addition to the quasi-classical ones ([5], p. 367). He cites a much-discussed result by Dowker and Kent [8] showing that for any consistent, quasi-classical history of a system up to a certain point, there is an infinity of alternative continuations that do not satisfy the condition of quasi-classicality. Thus, the persistence of the quasi-classical behavior is not guaranteed. Griffiths’s answer to this challenge takes us back to his “pragmatic” stance, as constituted by the principle of liberty. The scientist is free to choose whatever framework suits him/her best, and in order to describe the evolution of a macroscopic system, it is most useful to choose a quasi-classical framework. From this perspective, the CH interpretation would be threatened only if Dowker and Kent could prove that there is a quasi-classical history that cannot be extended to preserve its quasi-classicality. However, as long as there is a complete family of histories that retain their quasi-classicality, no problem arises.
However, again the argument by Okon and Sudarsky applies here. The choice of a quasi-classical family seems circular, since we assume from the outset what the result should be—the approximately classical features of the macroscopic world—and we cherry-pick the framework that will achieve this, ignoring the other, equally acceptable frameworks. Again, the main bone of contention here is the standards of scientific explanation. Adopting the many-worlds perspective on CH, we ask whether it is sufficient to explain the observable features of the macroscopic world by pointing out that in some possible worlds these features are guaranteed to occur, or should we find a way to eliminate all non-classical worlds on the basis of some further principles. As in the case of measurements, one way to defend the weaker concept of explanation is to argue that conscious observers cannot exist in worlds where macroscopic objects behave non-classically (persist in macroscopic superpositions).
6. Conclusions
The consistent histories approach to quantum mechanics is based on the concept of a framework, formally identified as a consistent family of histories (sequences of projectors which are mutually orthogonal and sum up to the identity). In this paper, I have suggested interpreting frameworks as referring to distinct worlds rather than to the enigmatic and epistemic “perspectives” or “aspects” of the actual world. Then, there are two further options to consider. One option is to follow the suggestion that in every consistent family of histories exactly one history is selected as actually occurring. This leads to a variant of the hidden variables theory that avoids the known no-go theorems without the necessity of accepting non-locality or contextuality. An alternative proposal, explored in this paper, is to associate each possible history within a given family with a separate world, in a fashion resembling the many-worlds interpretation. According to this approach, there is typically more than one world corresponding to a given family of histories. The many-worlds variant of CH differs in many important respects from the standard many-worlds interpretation: it does not accord a special status to unitary evolution and the universal wave function; it postulates many more alternative worlds than MWI; it does not rely on the special role of measurements or decoherence in bringing about the branching of the actual world; as a matter of fact, it dispenses altogether with the concept of world branching (splitting).
The solution of the measurement problem offered by MWCH is such that the existence of the worlds in which there are definite outcomes of measurements is guaranteed by the fact that decoherence renders appropriate families consistent. This also secures the existence of the worlds in which macroscopic objects display approximately classical behavior (the property of quasi-classicality). The main problem with this solution is that it also admits worlds that do not contain well-defined outcomes of measurements, and do not display classical behavior at the macroscopic level. I have suggested that the proponents of the many-worlds variant of CH may reply that they use a weaker notion of explanation in regard to the observability of the classical behavior of the macroscopic world. However, for this answer to work, we need to offer an argument that sentient, conscious beings can only exist in quasi-classical worlds.
Funding
This research was partly funded by the National Science Center, Poland, grant number 2021/43/B/HS1/01399.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The author declares no conflict of interest.
References
- Griffiths, R.B. Consistent histories and the interpretation of quantum mechanics. J. Stat. Phys. 1984, 36, 219–272. [Google Scholar] [CrossRef]
- Omnès, R. The Interpretation of Quantum Mechanics; Princeton University Press: Princeton, NJ, USA, 1994. [Google Scholar]
- Omnès, R. Understanding Quantum Mechanics; Princeton University Press: Princeton, NJ, USA, 1998. [Google Scholar]
- Gell-Mann, M.; Hartle, J.B. Quantum mechanics in the light of quantum cosmology. In Complexity, Entropy and the Physics of Information; Zurek, W.H., Ed.; Addison-Wesley: Redwood City, CA, USA, 1990; pp. 425–458. [Google Scholar]
- Griffiths, R.B. Consistent Quantum Theory; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Griffith, R.B. A consistent quantum ontology. Stud. Hist. Phil. Mod. Phys. 2013, 44, 93–114. [Google Scholar] [CrossRef]
- Griffiths, R.B. The Consistent Histories Approach to Quantum Mechanics. In Stanford Encyclopedia of Philosophy; Stanford University: Stanford, CA, USA, 2019; Available online: https://plato.stanford.edu/entries/qm-consistent-histories/ (accessed on 15 December 2022).
- D’Espagnat, B. Consistent histories and the measurement problem. Phys. Lett. A 1987, 124, 204–206. [Google Scholar] [CrossRef]
- Dowker, F.; Kent, A. On the consistent histories approach of quantum mechanics. J. Stat. Phys. 1996, 82, 1575–1646. [Google Scholar] [CrossRef]
- Bassi, A.; Ghirardi, G. Can the decoherent histories description of reality be considered satisfactory? Phys. Lett. A 1999, 257, 247–263. [Google Scholar] [CrossRef]
- Okon, E.; Sudarsky, D. Measurements according to Consistent Histories. Stud. Hist. Phil. Mod. Phys. 2014, 48, 7–12. [Google Scholar] [CrossRef]
- Peres, A. Quantum Theory: Concepts and Methods; Kluwer: Dordrecht, The Netherlands, 1995. [Google Scholar]
- Fuchs, C.A. Quantum mechanics as quantum information, mostly. J. Mod. Opt. 2003, 50, 987–1023. [Google Scholar] [CrossRef]
- Timpson, C.G. Philosophical aspects of quantum information theory. In The Ashgate Companion to Contemporary Philosophy of Physics; Rickles, D., Ed.; Ashgate Publishing: Aldershot, UK, 2008; pp. 197–261. [Google Scholar]
- Wallace, D. Philosophy of quantum mechanics. In The Ashgate Companion to Contemporary Philosophy of Physics; Rickles, D., Ed.; Ashgate Publishing: Aldershot, UK, 2008; pp. 16–98. [Google Scholar]
- Redhead, M. Incompleteness, Non-Locality and Realism. A Prolegomenon to the Philosophy of Quantum Mechanics; Clarendon Press: Oxford, UK, 1987. [Google Scholar]
- Vaidman, L. Many-worlds interpretation of quantum mechanics. In The Stanford Encyclopedia of Philosophy, Fall 2021 ed.; Zalta, E.N., Ed.; Stanford University: Stanford, CA, USA, 2021; Available online: https://plato.stanford.edu/archives/fall2021/entries/qm-manyworlds/ (accessed on 15 December 2022).
- Vaidman, L. Why the Many-Worlds Interpretation? Quantum Rep. 2022, 4, 264–271. [Google Scholar] [CrossRef]
- Wallace, D. The Emergent Multiverse: Quantum Theory according to the Everett Interpretation; Oxford University Press: Oxford, UK, 2012. [Google Scholar]
- Saunders, S. Many worlds? An introduction. In Many Worlds? Everett, Quantum Theory and Reality; Saunders, S., Barrett, J., Kent, A., Wallace, D., Eds.; Oxford University Press: Oxford, UK, 2010; pp. 1–50. [Google Scholar]
- Schlosshauer, M. Decoherence and the Quantum-to-Classical Transition; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 2007. [Google Scholar]
- Maudlin, T. Three measurement problems. Topoi 1995, 4, 7–15. [Google Scholar] [CrossRef]
- Hempel, C.; Oppenheim, P. Studies in the logic of explanation. Phil. Sci. 1948, 15, 135–175. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).