A Potential-Based Quantization Procedure of the Damped Oscillator

Abstract

Today, two of the most prosperous fields of physics are quantum computing and spintronics. In both, the loss of information and dissipation play a crucial role. In the present work, we formulate the quantization of the dissipative oscillator, which aids the understanding of the abovementioned issues, and creates a theoretical frame to overcome these issues in the future. Based on the Lagrangian framework of the damped spring system, the canonically conjugated pairs and the Hamiltonian of the system are obtained; then, the quantization procedure can be started and consistently applied. As a result, the damping quantum wave equation of the dissipative oscillator is deduced, and an exact damping wave solution of this equation is obtained. Consequently, we arrive at an irreversible quantum theory by which the quantum losses can be described.

1. Introduction

The existence of oscillator motion and the wave propagation mode are the necessary conditions for signal transmission, and consequently, information transfer. In a realistic quantum operation, the dissipation of a signal appears due to the loss of energy from a quantum system, for example, a single atom coupled to a single mode of electromagnetic radiation undergoes spontaneous emission [1]. This may happen in an ion trap quantum computation, as proposed by Cirac and Zoller [2]. Similarly, in spin-wave interconnects, spin-wave memories, or spin-wave transducers, and the attenuation reduces the efficiency, the lossy spin-wave propagation leads to fundamental limitations [3]. In the construction of quantum computers and further quantum information systems, the qubits are responsible for information transfer. A single electron on a solid neon surface provides the experimental realization of a new qubit platform [4]. In this realization, the limited coherent time is due to the energy and phase loss originating from the material surface deficiency and the noise of the environment.

These experiments and their theoretical discussions suggest the deeper understanding of dissipation of a single quantum package. The key to wave propagation is the oscillator; thus, it is worth dealing with the description of the quantized damped oscillator. The idea of quantizing the damped oscillator and the description of non-conserving energy subsystems coincide with the birth of quantum theory itself [5,6]. Based on their original idea of quantum dissipation, the description has been strongly developed [7]. In other research, the explicit time-dependent formulation can also provide a successful deduction of the dissipative oscillator [8,9]. However, the uncertainty principle is incompatible with the time-dependent mathematical structure [10]. The dissipative quantum systems can be modeled by the sets of decoupled harmonic oscillators in a reservoir [11,12,13]. The considered systems have a statistical behavior, so the observed dynamics differ from the motion of a single damped quantum oscillator.

Generally, the lack of success of the solution was due to several stumbling blocks in the construction. The first difficulty was immediately in the formulation of the Lagrangian; consequently, it was not possible to deduce the canonical variables, the Hamiltonian, and the Poission bracket expressions. Thus, the commutation rules, required for the quantization procedure, could not be formulated at all.

The problem of the missing Lagrangian structure of the dissipative systems was much older than the elaboration of the quantization procedure of conservative systems; it went back to Rayleigh [14]. The equation of motion (EOM) of the harmonic oscillator

$$\ddot{x}+{\omega }^{2}x=0$$

(1)

is deduced from the Lagrangian of

$$L=\frac{1}{2}{\dot{x}}^2-\frac{1}{2}{\omega }^2{x}^2,$$

(2)

where the related Euler–Lagrange equation is

$$\frac{\mathrm{d}}{\mathrm{d}t}\frac{\mathrm{d}L}{\mathrm{d}\dot{x}}-\frac{\mathrm{d}L}{\mathrm{d}x}=0.$$

(3)

To describe the damped oscillator, Rayleigh introduced the so-called dissipation potential—pertaining to the drag force $F=-C\dot{x}$—

$$\mathrm{\Phi }=\frac{1}{2}C{\dot{x}}^2,$$

(4)

by which the EOM could be recovered in the following way:

$$\frac{\mathrm{d}}{\mathrm{d}t}\frac{\mathrm{d}L}{\mathrm{d}\dot{x}}-\frac{\mathrm{d}L}{\mathrm{d}x}=\frac{\mathrm{d}\mathrm{\Phi }}{\mathrm{d}\dot{x}}.$$

(5)

It is easy to check that the correct EOM appears:

$$\ddot{x}+C\dot{x}+{\omega }^{2}x=0.$$

(6)

However, it can be proven that the added term on the right side in Equation (5) is not from the least action principle, and the related variational calculus, i.e., the Lagrangian frame is lost. Much later Bateman [15] suggested a mirror image description in which a complementary equation appears due to the introduced function y. Here, the variation problem is

$$\delta \int y\left(\ddot{x}+C\dot{x}+{\omega }^{2}x\right)dt=0.$$

(7)

In addition to the damped oscillator equation, the mirror image equation is

$$\ddot{y}-C\dot{y}+{\omega }^{2}y=0.$$

(8)

While the equation of x relates to the damping solution, the equation of y pertains to an exponentially increasing amplitude motion. The calculated Hamiltonian includes both of these functions at the same time. It may cause a cumbersome explanation and elaboration of canonical variable pairs. A few years ago, Bagarello et al. proved that the canonical quantization for the damped harmonic oscillator using the Bateman Lagrangian did not work [16]. Similarly, Morse and Feshbach [17] used the variable duplication method for the diffusion problem. In this case, the diffusion variable was considered a complex quantity, and its complex conjugate pair was the duplicated variable. Here, interpretation was cumbersome, due to the complex diffusion functions and the related canonical formulation.

The application of the complex absorbing potentials—firstly used for the description of scattering processes [18,19,20,21,22,23,24,25,26]—may provide an opportunity for the description of dissipation and ireversibility in quantum theory. The method is that the Schrődinger equation is formulated by a complex potential $V_r\left(x\right)+\mathrm{i}{V}_c\left(x\right)$, where $V_r\left(x\right)$ represents the conservative potential, and $V_c\left(x\right)$ pertains to the damping. Therefore, the EOM for this system is

$$\frac{\hslash }{\mathrm{i}}\frac{\partial \mathrm{\Psi }}{\partial t}-\frac{{\hslash }^2}{2m}{\nabla }^2\mathrm{\Psi }+\left(V_r+\mathrm{i}{V}_c\right)\mathrm{\Psi }=0.$$

(9)

The deduced balance equation for ${\mathrm{\Psi }}^{\ast }\mathrm{\Psi }$ is

$$\frac{\partial \left({\mathrm{\Psi }}^{\ast }\mathrm{\Psi }\right)}{\partial t}+\frac{\mathrm{i}\hslash }{2m}\nabla \left(\mathrm{\Psi }\nabla {\mathrm{\Psi }}^{\ast }-{\mathrm{\Psi }}^{\ast }\nabla \mathrm{\Psi }\right)-\frac{2}{\hslash }{V}_c{\mathrm{\Psi }}^{\ast }\mathrm{\Psi }=0,$$

(10)

where just the complex part of the potential remains, generating the loss of the system. An obvious choice is to describe the motion of the quantum damped oscillator by the complex harmonic potential introduced by real-valued angular frequencies ${\omega }_r$ and ${\omega }_c$ [26]

$$V\left(x\right)=\frac{1}{2}m\left({\omega }_r^2-\mathrm{i}{\omega }_c^2\right)x^2.$$

(11)

The solution can be obtained by the application of the Feynman path integral method [27,28,29,30], as it was shown previously [26]. We see that this method stands on the complex generalization of the acting potential, and the dissipation appears as a consequence of this non-hermitian potential. However, we miss the direct—introduced by an “equation-level”—formulation of the dissipation.

An explicit time-dependent Lagrangian method using the WKB approximation in the quantization procedure was developed by Serhan et al. [31,32]. Despite the exponentially decreasing time-dependence of the wave function, it describes a standing solution in space.

A path integral method with a dynamical friction term was suggested for quantum dissipative systems by El-Nabulsi [33]. Here, Stokes’ drag force introduced the loss. However, the equation did not contain the velocity-dependent term. It contrasts with the standard EOM, which yields the usual exponential relaxation in time.

Presently, we apply the canonical quantization method for the damped harmonic oscillator. We point out this classically developed procedure works in dissipative cases not only with conservative potentials. We start from the EOM, and we formulate the Lagrangian and the Hamiltonian of the problem in general in Section 2. As a particular case, the Hamiltonian of the underdamped oscillator is expressed in Section 3. The canonical quantization procedure is described in Section 4, and the damping wave function is calculated by the path integral method in Section 5. The results are summarized in a short conclusion in Section 6.

The present technique has multiple advantages compared to the previous approaches. (i) The canonical expressions and the quantization steps are similar to the usual procedure. Thus, the developed description can be considered a generalization. (ii) The solving methods, such as the path integral method, can be applied without radical changes. (iii) The required necessary difference in the interpretation of the damped wave function can be interpreted.

2. The Lagrangian and Hamiltonian of a Damped Harmonic Oscillator

The quantization procedure requires the formulation of the complete Lagrangian–Hamiltonian frame first. To achieve this aim, we begin our examination with the EOM for the damped harmonic oscillator

$$\ddot{x}+2\lambda \dot{x}+{\omega }^{2}x=0,$$

(12)

where m is the mass, $\lambda$ is a specific damping factor, and $\omega$ is the angular frequency. For the measurable quantity x, we define a generator potential q characterizing the underlying degrees of freedom, i.e., the definition equation can be obtained as in [34,35,36],

$$x=\ddot{q}-2\lambda \dot{q}+{\omega }^{2}q.$$

(13)

A suitable Lagrangian can be formulated by the potential

$$L=\frac{1}{2}{\left(\ddot{q}-2\lambda \dot{q}+{\omega }^{2}q\right)}^2.$$

(14)

The equations of motion can be calculated from a Lagrangian of the general form

$$L\left(q,\dot{q},\ddot{q},\cdots ,q^{\left(n\right)},\cdots ,q^{\left(N\right)},t\right)$$

$q^{\left(n\right)}$ denotes the nth order time derivative) [37,38]:

$$0=\sum _{n=0}^N{(-1)}^n\frac{{\mathrm{d}}^n}{\mathrm{d}{t}^n}\frac{\partial L}{\partial q^{\left(n\right)}}.$$

(15)

This method results in the EOM of the harmonic oscillator for the potential as the Euler–Lagrange equation. In general, Hamiltonian formalism requires canonical coordinate and momentum pairs

$$\begin{array}{ccc}\hfill q_n& =& q^{(n-1)}\hfill \end{array}$$

(16)

$$\begin{array}{ccc}\hfill p_n& =& \sum _{k=0}^{N-n}{(-1)}^k\frac{{\mathrm{d}}^k}{\mathrm{d}{t}^k}\frac{\partial L}{\partial q^{(n+k)}},\hfill \end{array}$$

(17)

where $\left(n=1,\cdots ,N\right)$. The Hamiltonian can be deduced from the abovementioned general Lagrangian as

$$H=\sum _{n=0}^N{p}_n\frac{\mathrm{d}{q}_n}{\mathrm{d}t}-L.$$

(18)

For the present particular case, $N=2$ and $n=1,2$, we obtain the relevant coordinates as

$$q_1:=q,$$

(19)

and

$$q_2:=\dot{q}.$$

(20)

Moreover, the general expression for the momentum $p_1$ is

$$p_1:=\sum _{k=0}^1{(-1)}^k\frac{{\mathrm{d}}^k}{\mathrm{d}{t}^k}\frac{\partial L}{\partial q^{(1+k)}}=\frac{\partial L}{\partial \dot{q}}-\frac{\mathrm{d}}{\mathrm{d}t}\frac{\partial L}{\partial \ddot{q}},$$

(21)

by which we calculate the particular case as

$$p_1:=4{\lambda }^2\dot{q}-\stackrel{⃛}{q}-{\omega }^2\dot{q}-2\lambda {\omega }^{2}q.$$

(22)

Similarly, we formulate the momentum $p_2$

$$p_2:=\sum _{k=0}^0{(-1)}^k\frac{{\mathrm{d}}^k}{\mathrm{d}{t}^k}\frac{\partial L}{\partial q^{(2+k)}}=\frac{\partial L}{\partial \ddot{q}},$$

(23)

i.e.,

$$p_2:=\ddot{q}-2\lambda \dot{q}+{\omega }^{2}q.$$

(24)

The Hamiltonian can be calculated by Equation (18). As a first step, we obtain it by the potential function q

$$\begin{array}{c}\hfill H=p_1{\dot{q}}_1+p_2{\dot{q}}_2-L\\ \hfill =2{\lambda }^2{\dot{q}}^2-\stackrel{⃛}{q}\dot{q}-{\omega }^2{\dot{q}}^2+\frac{1}{2}{\ddot{q}}^2-\frac{1}{2}{\omega }^4{q}^2.\end{array}$$

(25)

The following step is to substitute the potential function with the coordinates and the momenta. We arrive at the canonical formulation of the Hamiltonian as

$$H=\frac{1}{2}{p}_2^2-{\omega }^2{p}_2{q}_1+p_1{q}_2+2\lambda p_2{q}_2.$$

(26)

To preserve the energy-like unit of the Hamiltonian, we transform the coordinates and the momenta. The transformation means a simple product by $\omega$, $m\omega$, and $m{\omega }^2$. Thus, we obtain new coordinates, $Q_1$ and $Q_2$, and new momenta, $P_1$ and $P_2$.

$$\begin{array}{ccc}\hfill p_2& ⟶& P_2=m\omega p_2,\left[P_2\right]=\mathrm{kg}\frac{\mathrm{m}}{\mathrm{s}},\hfill \end{array}$$

(27)

$$\begin{array}{ccc}\hfill q_2& ⟶& Q_2=\omega q_2,\left[Q_2\right]=\mathrm{m},\hfill \end{array}$$

(28)

$$\begin{array}{ccc}\hfill p_1& ⟶& P_1=m\omega p_1,\left[P_1\right]=\mathrm{kg}\frac{\mathrm{m}}{{\mathrm{s}}^2},\hfill \end{array}$$

(29)

$$\begin{array}{ccc}\hfill q_1& ⟶& Q_1=\omega q_1,\left[Q_1\right]=\mathrm{m}\mathrm{s}.\hfill \end{array}$$

(30)

The meaning of the canonical moment $P_2$ and the canonical coordinate $Q_2$ is the same as the mechanical momentum and the spatial coordinate. Moreover, the Hamiltonian, $H^{\prime }$, is obtained

$$H⟶H^{\prime }=m{\omega }^{2}H,\left[H\right]=\mathrm{kg}\frac{{\mathrm{m}}^2}{{\mathrm{s}}^2}=\mathrm{J}.$$

(31)

The units of the quantities are denoted by the bracket $\left[\right]$. Finally, the Hamiltonian of the damped oscillator is

$$H^{\prime }=\frac{1}{2m}{P}_2^2-{\omega }^2{P}_2{Q}_1+P_1{Q}_2+2\lambda P_2{Q}_2.$$

(32)

Before we turn to the quantization procedure, it is worth examining a further property of this Hamiltonian. Since this Hamiltonian pertains to a dissipative process, we expect that this is a non-hermitian operator. The reason is that the probability does not conserve during dissipation. We will see later that the operators that belong to the first three terms are hermitian, but the fourth term is not. The fourth term operator will generate the dissipation in the description. Furthermore, the appearance of $\lambda$ in the term similarly shows this fact.

3. The Devil Is in the Details

Since the formulation of the Lagrangian does not contain explicit time dependence, the Hamiltonian must be a constant value, i.e., the Hamiltonian expresses a conservation law. At this point, there is an open question of what the Hamiltonian exactly means. Here, we try to clarify the role of the Hamiltonian in this theory.

We focus just on the solutions that pertain to the underdamped and overdamped cases. As was shown previously by Szegleti et al. [34], the $q\left(t\right)$ solution holds

$$q\left(t\right)=a_1{\mathrm{e}}^{-(\lambda +\gamma )t}+a_2{\mathrm{e}}^{-(\lambda -\gamma )t}+b_1{\mathrm{e}}^{(\lambda +\gamma )t}+b_2{\mathrm{e}}^{(\lambda -\gamma )t},$$

(33)

where $\gamma =\sqrt{{\lambda }^2-{\omega }^2}$. The last two terms are proportional to the exponentially increasing ${\mathrm{e}}^{\lambda t}$, so they have non-physical meaning. Consequently, they could not have a role in the measurable $x\left(t\right)$. After the fit of the initial conditions for the measurable quantities, the position, and the velocity, $x\left(0\right)=x_0$ and $\dot{x}\left(0\right)=v_0$, keeping the physical solutions, the relevant potential is

$$q\left(t\right)=\frac{(\gamma -\lambda )x_0-v_0}{8\gamma \lambda (\lambda +\gamma )}{\mathrm{e}}^{-(\lambda +\gamma )t}+\frac{(\gamma +\lambda )x_0+v_0}{8\gamma \lambda (\lambda -\gamma )}{\mathrm{e}}^{-(\lambda -\gamma )t}.$$

(34)

Now, we are ready to substitute this generator’s potential function into the expression of the Hamiltonian in Equation (25). The mathematical calculation results in

$$H=0,$$

(35)

and similarly,

$$H^{\prime }=0$$

(36)

by Equation (32). Since there is no explicit time dependence in the Lagrangian, the Hamiltonian must be constant. Generally, the Hamiltonian is the energy of the oscillating mass point. However, now the energy of the damped oscillator dissipates during the vibration. So, the non-zero energy cannot be the constant of motion. This strange result means that this zero value Hamiltonian is the conserved quantity of the damped oscillator. We may say there is no contradiction in the theory. However, the Hamiltonian loses the meaning of the “total energy of the system”. Despite this situation, we consider the Hamiltonian as an energy-like quantity. We will see that this zero value Hamiltonian in Equation (50) (see below) enables us to elaborate on the quantization formulation of the dissipative oscillator.

4. The Quantization Procedure

To achieve the state equation of the quantized damped oscillator, we need to identify the canonical momenta in the Hamiltonian, $H^{\prime }$, in Equation (32). In the case of the canonical pair $(P_2,Q_2)$ from Equations (27) and (28), we introduce into the transformed space the spatial coordinate y

$$P_2\left(=mv=m\frac{\mathrm{d}y}{\mathrm{d}t}=\right)=\hslash k,Q_2=y.$$

(37)

The momentum $P_2$ and the coordinate $Q_2$ are the usual canonically conjugated pairs. The construction of the momentum $P_1$ and the coordinate $Q_1$ are based on Equations (29) and (30) and a comparison with the momentum $P_2$ and the coordinate $Q_2$ in Equation (37). The appearing time factor in Equations (29) and (30) can be associated with Fourier transformed pairs, i.e.,

$$P_1=-\mathrm{i}\hslash k\omega ,Q_1=\frac{y}{\mathrm{i}\omega }.$$

(38)

$$\begin{array}{c}\hfill \frac{\partial }{\partial y}=\mathrm{i}k,\frac{\partial }{\partial t}=-\mathrm{i}\omega ,\\ \hfill \frac{1}{-\mathrm{i}\omega }=\int ...\mathrm{d}t,ky⟶\frac{1}{\mathrm{i}}.\end{array}$$

(39)

The terms of the Hamiltonian can be expressed in the operator formulation applying the above rules. The calculation of $P_2$ and $P_2^2$ proceeds as is usual.

$$\left[P_2,Q_2\right]=\frac{\hslash }{\mathrm{i}}.$$

(40)

Applying the above Fourier formulations, we can obtain the commutation rules

$$\left[P_1,Q_1\right]=-\frac{\hslash }{\mathrm{i}},$$

(41)

$$\left[P_2,Q_1\right]=0,$$

(42)

$$\left[P_1,Q_2\right]=0.$$

(43)

We take $P_2$ from Equation (37) and the first Fourier transform in Equation (39); then, we obtain

$$P_2=\hslash k=\frac{\hslash }{\mathrm{i}}\frac{\partial }{\partial y}⟶P_2^2=-{\hslash }^2\frac{{\partial }^2}{\partial y^2}.$$

(44)

The second term includes the $P_2{Q}_1$ product. Now, we consider $P_2$ from Equation (37) and $Q_1$ from Equation (38); then, we apply the third Fourier transform in Equation (39). The detailed steps are shown one by one

$$\begin{array}{ccc}\hfill P_2{Q}_1& =& \hslash k\frac{y}{\mathrm{i}\omega }=\underset{-\int ...\mathrm{d}t}{\underbrace{\frac{1}{\mathrm{i}\omega }}}\underset{mv}{\underbrace{\hslash k}}y=-\int mvy\mathrm{d}t\hfill \\ & =& -\int my\frac{\mathrm{d}y}{\mathrm{d}t}\mathrm{d}t=-\frac{1}{2}m{y}^2,\hfill \end{array}$$

(45)

by which we obtain the second term of the Hamiltonian in the operator formalism

$$-{\omega }^2{P}_2{Q}_1=\frac{1}{2}m{\omega }^2{y}^2.$$

(46)

We continue with the $P_1{Q}_2$ term. We take $P_1$ from Equation (38) and $Q_2$ from Equation (37), and we apply the second and fourth Fourier transform, i.e.,

$$P_1{Q}_2=-\mathrm{i}\hslash k\omega y=-\mathrm{i}\hslash \underset{1/\mathrm{i}}{\underbrace{ky}}\underset{\mathrm{i}\frac{\partial }{\partial t}}{\underbrace{\omega }}=\frac{\hslash }{\mathrm{i}}\frac{\partial }{\partial t}.$$

(47)

The last term of the Hamiltonian includes the $P_2{Q}_2$ product. The relevant substitutions come from Equation (37), and we consider the fourth Fourier transform

$$P_2{Q}_2=\hslash ky=\hslash \underset{1/\mathrm{i}}{\underbrace{ky}}=\frac{\hslash }{\mathrm{i}},$$

(48)

by which we write

$$2\lambda P_2{Q}_2=2\lambda \frac{\hslash }{\mathrm{i}}.$$

(49)

Taking the Hamiltonian in Equation (32), the fact that $H^{\prime }=0$ in Equation (36), and substituting these expressions into it, the quantized state equation of the damped oscillator can be formulated as

$$0=\underset{\mathrm{frictionless}\mathrm{quantum}\mathrm{oscillator}}{\underbrace{-\frac{{\hslash }^2}{2m}\frac{{\partial }^2\psi }{\partial y^2}+\frac{1}{2}m{\omega }^2{y}^2\psi +\frac{\hslash }{\mathrm{i}}\frac{\partial \psi }{\partial t}}}+\underset{\mathrm{damping}\mathrm{term}}{\underbrace{2\lambda \frac{\hslash }{\mathrm{i}}\psi }}.$$

(50)

Now, we can recognize the importance of the zero-valued Hamiltonian. Similar to the complex absorbing potential in Equation (11), a non-hermitian term appears in the state equation. Its role is the same as the term that generates dissipation in the motion. However, the deduction of the damped state equation comes from a consequent calculation; the complex part of the potential in Equation (11) is an ad hoc assumption. We can divide the equation into the undamped quantum harmonic oscillator and the damping part. The damping term also includes the quantum action factor ℏ.

5. Solution of Damping Wave Equation

The oscillation starts from a normalized Gaussian shape initial wave function, which is the eigenfunction of the lowest-lying energy level of the frictionless case:

$${\mathrm{\Psi }}_0(y,0)=\sqrt[4]{\frac{m\omega }{\pi \hslash }}exp\left(-\frac{m\omega }{2\hslash }{(y-y_0)}^2\right)$$

(51)

with its center position $y_0$. The movement of the undamped oscillator (the frictionless part of Equation (50)) can be calculated by the Feynman path integral method [27,28,29,30]. Souriau pointed out a correction that is necessary beyond the first half-period of motion in the integration formula of Feynman [39]. However, a further detailed study was to refine the oscillator wave packet motion. Naqvi and Waldenstrøm [40] introduced a $\gamma \ne 1$ parameter by which the width of the Gaussian wave packet changes periodically in time around the origin (see Figure 2 in Ref. [26])

$${\left|\mathrm{\Psi }(y,t)\right|}^2=\frac{1}{{\sigma }_y\left(t\right)\sqrt{2}}\times exp\left\{-\frac{{\left[y-y_{0}cos\left(\omega t\right)\right]}^2}{2{\sigma }_y^2(y,t)}\right\},$$

(52)

where

$${\sigma }_y^2(y,t)=\frac{\hslash }{2\gamma m\omega }\left[{cos}^2\left(\omega t\right)+{\gamma }^2{sin}^2\left(\omega t\right)\right]$$

(53)

ensures the width change.

The first two terms in Equation (50) do not depend on the time, and since the third term includes a first-order time derivative, the damping effect can be extracted from the third and fourth terms (see Appendix A), i.e.,

$$0=\frac{\hslash }{\mathrm{i}}\frac{\partial {\psi }^{\prime }}{\partial t}+2\lambda \frac{\hslash }{\mathrm{i}}{\psi }^{\prime }.$$

(54)

The solution to this equation can be expressed as

$${\psi }^{\prime }\sim exp\left(-2\lambda t\right).$$

(55)

Finally, we obtain the exact solution of the quantum dissipative oscillator Equation (50) as

$${\left|\mathrm{\Psi }(y,t)\right|}^2=\frac{1}{{\sigma }_y\left(t\right)\sqrt{2}}exp\left\{-\frac{{\left[y-y_{0}cos\left(\omega t\right)\right]}^2}{2{\sigma }_y^2(y,t)}\right\}\times exp\left(-4\lambda t\right).$$

(56)

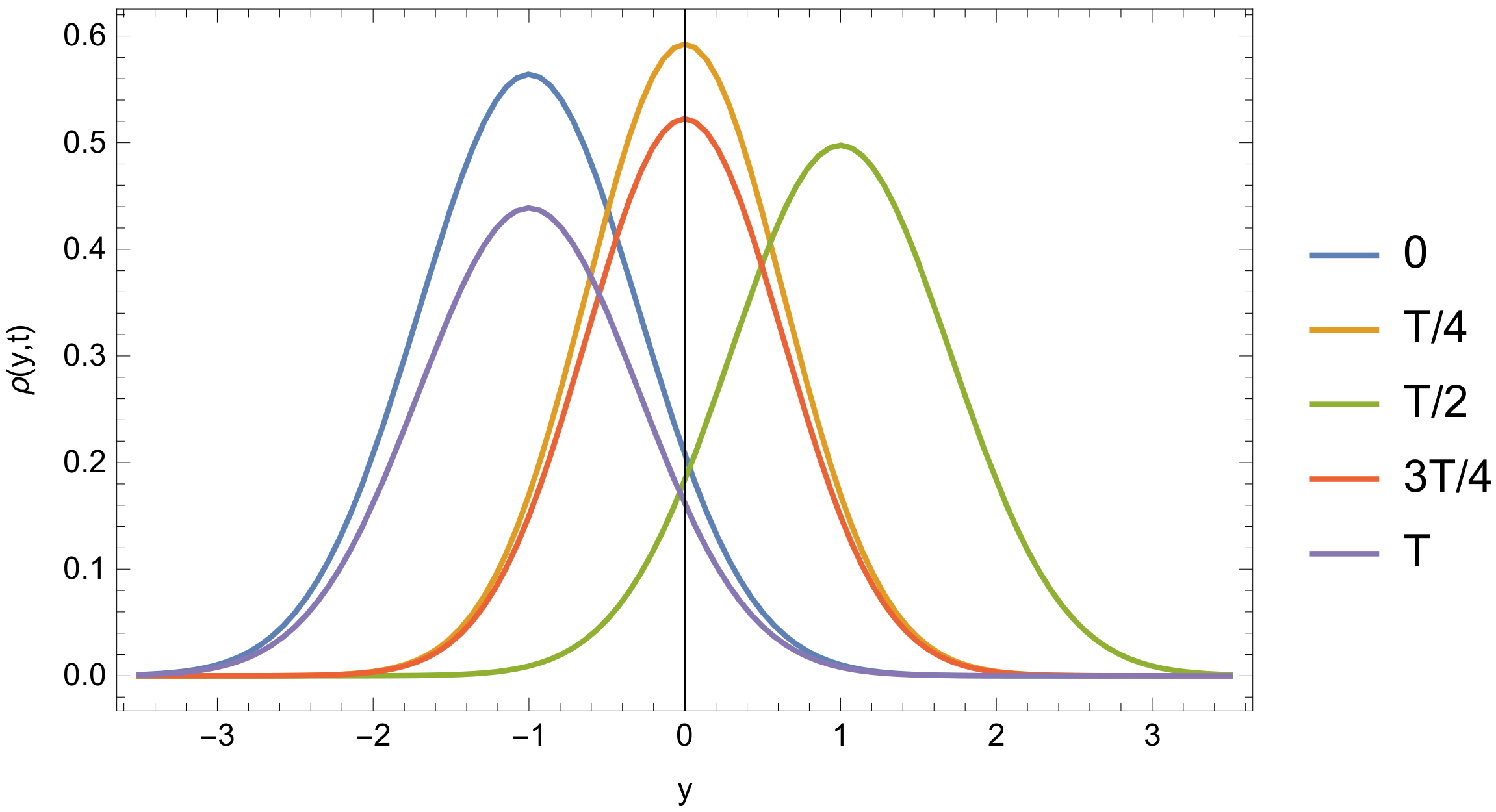
The time evolution of ${\left|\mathrm{\Psi }(y,t)\right|}^2$ is presented in Figure 1, as it is similarly experienced from the complex potential approximations in the description of dissipative quantum systems [18,26]. However, in the present quantization procedure, the damped oscillator frequency is identical to the frequency of the undamped oscillator. In contrast to the classic case, the damping does not modify the eigenfrequency $\omega$, i.e., the damping pertains to the energy and information loss. This fact suggests that the well-known Lorentz distribution in the scattering process does not relate to a frequency shift due to the damping effect on a quantum level. On the other hand, this result is in line with the second quantized solution in Ref. [41]. In this reference, Equation (A4.21) clearly shows that there is no frequency shift in the case of a damped quantum oscillator but just amplitude damping. The experimental and theoretical motivations for the quantum dissipation can be found in the early Refs. [42,43].

A time series of $\rho (y,t)$ with parameters set as $m=1$, $\hslash =1$, $\omega =1$, and $\lambda =0.01$ is shown in Figure 1 in which the evolution can be easily followed in one time period.

The damping of the quantum dissipative oscillator arises from the smooth function $exp\left(-4\lambda t\right)$, so the graph is similar for higher $\lambda$ values.

6. Conclusions

We presented a thorough investigation and a solution for the age-old problem, the quantization of the damped oscillator. The information loss is closely related to the signal distortion, i.e., the energy dissipation. Our method overcame the limitations of the previous formulations using several means to achieve the damping state equation. We returned to the fundamentals of quantum theory, such as (i) the Lagrangian formulation, (ii) the Hamiltonian canonical description, and (iii) the quantization procedure. Thus, we applied this mathematical framework to the damping oscillator. In possession of the correct Lagrangian description, the way opened toward the quantization procedure. As was shown, a remarkably understandable damping state equation energed. Finally, we calculated the exact solution of this quantum dissipative oscillator equation. We conclude that a consequent construction of the damping quantum oscillator equation is presented by the exact solution of this damped state equation. However, we emphasize that due to the non-hermitian complex potential, the probability meaning of the wave function is lost. The results bring us closer to the understanding of energy dissipation, information loss, and the maximal probability of the recovery of a signal on the microscopic level. Our studies in the area of quantum dissipation require further discussion and examination.