Equal Radiation Frequencies from Different Transitions in the Non-Relativistic Quantum Mechanical Hydrogen Atom

Abstract

Is it possible that two different transitions in the non-relativistic quantum mechanical model of the hydrogen atom give the same frequency of radiation? That is, can different energy level transitions in a hydrogen atom have the same photon radiation frequency? This question, which was asked during a Ph.D. oral exam in 1997 at the University of Colorado Boulder, is well-known among physics graduate students. We show a general solution to this question, in which all equifrequency transition pairs can be obtained from the set of solutions of a Diophantine equation. This fun puzzle is a simple yet concrete example of how number theory can be relevant to quantum systems, a curious theme that emerges in theoretical physics but is usually inaccessible to a general audience.

1. Introduction

For more than a century, quantum mechanics has been the fundamental theory that guides our understanding of how nature works at the scale of atoms and subatomic particles. The hydrogen atom is the simplest possible atom for theoretical investigation, consisting of only a single proton and a single electron orbiting around [1]. While the hydrogen atom has been intensively studied since the dawn of quantum mechanics (Figure 1), as a demonstration of what measurements can reveal about atoms, there are still surprises and hidden structures [2]. One example is the emergence of equifrequency transitions, in which many distinctive jumps between atomic levels can radiate identical photon energy. This question was raised during a Ph.D. oral exam in 1997 at the University of Colorado Boulder [3] and soon became well-known in the physics community, especially among graduate students. The answer is definitely yes, and an infinite number of transitions have been found [4]; however, to the best of our knowledge, a generalization is still lacking.

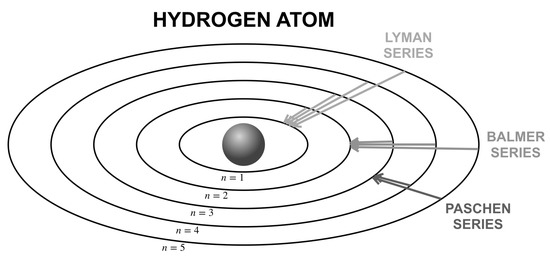
Figure 1. Energy-level transitions in the non-relativisitic quantum mechanical model of the hydrogen atom. An electron jumps from an outer ring $n_1$-th to an inner ring $n_2$-th, emits a photon with radiation energy $\mathsf{\Delta }E\propto n_2^{-2}-n_1^{-2}$.

Here, we show the connection between the above question and a Diophantine equation [5], and present a general solution, i.e., how all equifrequency transition pairs can be obtained. While this finding might not address any foundational issue or important problem in quantum mechanics, it definitely provides us with a more complete understanding of the most popular atom in all quantum mechanics textbooks, and the relationship between atomic levels (disregarding degeneracies due to angular momentum and spin). It is also a simple illustration of how number theory can be of relevance to physics [6], in a way that is accessible to non-experts.

2. A General Solution for All Equifrequency Transitions

In quantum mechanics, the n-th energy level of a hydrogen atom is given by $E\left(n\right)=-E_o/n^2$, where $n\in {\mathbb{Z}}^{+}$ is a positive integer and $E_o=13.6$ eV is the Rydberg energy [7]. For simplicity, we will not consider any relativistic effects [8] or other corrections (such as fine structure [9,10]) to this equation. The challenge is to find all transition pairs ($n_1\to n_2$, $n_3\to n_4$) with an equal radiation energy, which means:

$$\begin{array}{|c|}\hline \frac{1}{n_2^2}-\frac{1}{n_1^2}=\frac{1}{n_4^2}-\frac{1}{n_3^2}>0\\ \hline\end{array}.$$

(1)

Here, we will find a general solution to this equation, including trivial solutions where $n_1=n_3$ and $n_2=n_4$.

Consider the Diophantine equation [5] with a parameter $s\in {\mathbb{Z}}^{+}$ and unknowns $x,y,z\in {\mathbb{Z}}^{+}$,

$$x^2-y^2=s{z}^2.$$

(2)

With any two solutions $(x_1,y_1,z_1)$ and $(x_2,y_2,z_2)$ to this equation, for any positive integer pair $(t_1,t_2)$ that satisfies

$$x_1{y}_1{t}_1{z}_2=x_2{y}_2{t}_2{z}_1,$$

(3)

a solution to Equation (1) can be obtained:

$$(n_1,n_2,n_3,n_4)=(x_1{t}_1,y_1{t}_1,x_2{t}_2,y_2{t}_2),$$

(4)

which can be checked by direct substitution. To generate all solutions $(t_1,t_2)$ to Equation (3), we use any $k\in {\mathbb{Z}}^{+}$ and $G=\gcd (x_1{y}_1{z}_2,x_2{y}_2{z}_1)$,

$$t_1=k{x}_2{y}_2{z}_1/G,t_2=k{x}_1{y}_1{z}_2/G,$$

(5)

where the operation $\gcd (\alpha ,\beta )$ determines the greatest common divisor of $\alpha ,\beta \in {\mathbb{Z}}^{+}$ [11].

We can prove that the above procedure comprises all solutions of Equation (1). Starting from this equation, denote $t_1^{\prime }=\gcd (n_1,n_2)$ and $t_2^{\prime }=\gcd (n_3,n_4)$. Write $n_1=x_1^{\prime }{t}_1^{\prime },n_2=y_1^{\prime }{t}_1^{\prime },n_3=x_2^{\prime }{t}_2^{\prime },n_4=y_2^{\prime }{t}_2^{\prime }$. Note that $n_1>n_2$ and $n_3>n_4$ i.e., $x_1^{\prime }>y_1^{\prime }$ and $x_2^{\prime }>y_2^{\prime }$. Then, we rewrite (1) as,

$$\frac{x_1^{\prime 2}-y_1^{\prime 2}}{x_2^{\prime 2}-y_2^{\prime 2}}={\left(\frac{x_1^{\prime }{y}_1^{\prime }{t}_1^{\prime }}{x_2^{\prime }{y}_2^{\prime }{t}_2^{\prime }}\right)}^2$$

(6)

and put the fraction $x_1^{\prime }{y}_1^{\prime }{t}_1^{\prime }/x_2^{\prime }{y}_2^{\prime }{t}_2^{\prime }$ into irreducible form $z_1^{\prime }/z_2^{\prime }$ where $\gcd (z_1^{\prime },z_2^{\prime })=1$ and both are non-zero,

$$\frac{x_1^{\prime }{y}_1^{\prime }{t}_1^{\prime }}{x_2^{\prime }{y}_2^{\prime }{t}_2^{\prime }}=\frac{z_1^{\prime }}{z_2^{\prime }}.$$

(7)

Thus,

$$\frac{x_1^{\prime 2}-y_1^{\prime 2}}{x_2^{\prime 2}-y_2^{\prime 2}}=\frac{z_1^{\prime 2}}{z_2^{\prime 2}}$$

(8)

and hence there exists $s^{\prime }\in {\mathbb{Z}}^{+}$ such that,

$$x_1^{\prime 2}-y_1^{\prime 2}=s^{\prime }{z}_1^{\prime 2},x_2^{\prime 2}-y_2^{\prime 2}=s^{\prime }{z}_2^{\prime 2}.$$

(9)

Note here that condition (7) is exactly Equation (3) and condition (9) provides us two solutions (2). Combined with the above paragraph, we see that these two conditions (7) and (9) are both necessary and sufficient. This completes the proof.

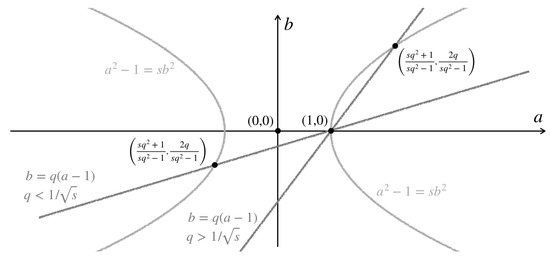
To generate the set of all non-zero integer solutions $(x,y,z)$ to Equation (2), we need the set of all non-zero rational solutions $(a,b)$ into their dehomogenized version (by dividing both sides of (2) by $1/y^2$):

$$a^2-1=s{b}^2.$$

(10)

This equation is very similar to the Pell equation [12], but can be solved using a much simpler method. By taking any $(a,b)=(a_1/a_2,b_1/b_2)$ that satisfies (10) and any $l\in \mathbb{Z}$, we obtain all triples,

$$(x,y,z)=\left(\frac{l{a}_1{b}_2}{G_2},\frac{l{a}_2{b}_2}{G_2},\frac{l{a}_2{b}_1}{G_2}\right),$$

(11)

of (2) where $G_2=\gcd (a_2,b_2)$.

The geometric way [13] of dealing with Equation (10) is to draw a line in the $ab$-plane passing through $(1,0)$ with a rational slope $q\in \mathbb{Q}$; for example, the line $b=q(a-1)$ (see Figure 2). For $q^2\ne 1/s$, this line will cut the curve (10) at another point,

$$(a,b)=\left(\frac{s{q}^2+1}{s{q}^2-1},\frac{2q}{s{q}^2-1}\right),$$

(12)

and, more importantly, all solutions of Equation (10) can be attained in this way by varying q. Note that $q=0$ gives $z=0\notin {\mathbb{Z}}^{+}$, and changing the sign of q changes the sign of $(a,b)$. Hence, if we let $q=q_1/q_2$ where $q_1\in \mathbb{Z}\backslash \left\{0\right\}$, $q_2\in {\mathbb{Z}}^{+}$; then, $a=a_1/a_2$, $b=b_1/b_2$, where

$$\begin{array}{c}\hfill a_1=s{q}_1^2+q_2^2,a_2=s{q}_1^2-q_2^2,\end{array}$$

(13)

$$\begin{array}{c}\hfill b_1=2q_1{q}_2,b_2=s{q}_1^2-q_2^2.\end{array}$$

(14)

The positive triple $(x,y,z)$ can be obtained from (11) with the correct sign choice.

Figure 2. The geometric representation of curve Equation (10) and line equation $b=q(a-1)$ in the a-b plane. The intersection in the first quadrant provides a solution to Equation (10).

In summary, we can generate a solution $(x,y,z)$ to Equation (2) with parameter $s\in {\mathbb{Z}}^{+}$ from any number $q=q_1/q_2\ne 0$. Given the pair, we go through Equations (13) and (), pick a value $l\in \mathbb{Z}$ and use Equation (11) to arrive at $(x,y,z)$. Then, with two such solutions, say, $(x_1,y_1,z_1)$ and $(x_2,y_2,z_2)$, we choose a value $k\in {\mathbb{Z}}^{+}$ and use Equation (5) to obtain $(t_1,t_2)$ before plugging in Equation (4) to obtain a pair $(n_1\to n_2,n_3\to n_4)$. See Figure 3 for a demonstration. The key difference in our approach compared to previous ones is using (2), where we can generate all possible rational solutions, which enables us to find all possible solutions to the puzzle (1).

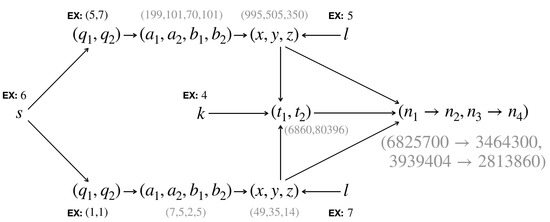
Figure 3. A demonstration for the procedure to obtain an equifrequency transition pair. Here we start by selecting $s=6$, then from $(q_1,q_2)=(5,7)$ and $l=5$ we get $(x_1,y_1,z_1)=(995,505,350)$, from $(q_1,q_2)=(1,1)$ and $l=7$ we get $(x_2,y_2,z_2)=(49,35,14)$. Then, with $k=4$, we arrive at $(n_1\to n_2,n_3\to n_4)=(6825700\to 3464300,$$3939404\to 2813860)$, which can be checked as satisfying Equation (1).

3. Families of Equifrequency Transitions

Perondi [4] found an infinite number of solutions to the generalization of (1):

$$\begin{array}{|c|}\hline \frac{1}{{\beta }_1^2}-\frac{1}{{\alpha }_1^2}=\frac{1}{{\beta }_2^2}-\frac{1}{{\alpha }_2^2}=\cdots =\frac{1}{{\beta }_n^2}-\frac{1}{{\alpha }_n^2}\\ \hline\end{array},$$

(15)

for any $n\in {\mathbb{Z}}_{\ge 2}$. His approach is to start with a set of k primes $S_k=\{{\mu }_1,\dots ,{\mu }_k\}$, for some $k\in {\mathbb{Z}}_{\ge 2}$, and then try to find an integer $\mathsf{\Delta }$, for which

$$\frac{1}{{\beta }_1^2}-\frac{1}{{\alpha }_1^2}=\frac{1}{{\beta }_2^2}-\frac{1}{{\alpha }_2^2}=\cdots =\frac{1}{{\beta }_n^2}-\frac{1}{{\alpha }_n^2}=\frac{4{\mu }_1\cdots {\mu }_k}{{\mathsf{\Delta }}^2}$$

(16)

has a solution. By partitioning [14], the set of indices $\{1,\dots ,k\}$ into two sets $I,J$ and denoting ${\gamma }_I={\prod }_{i\in I}{\mu }_i,{\gamma }_J={\prod }_{j\in J}{\mu }_j$, he found that if ${\gamma }_I\ne {\gamma }_J$ and ${\mathsf{\Delta }}_{I,J}$ is divisible by ${\gamma }_I-{\gamma }_J$ and ${\gamma }_I+{\gamma }_J$, then $(\alpha ,\beta )=(\frac{{\mathsf{\Delta }}_{I,J}}{{\gamma }_I-{\gamma }_J},\frac{{\mathsf{\Delta }}_{I,J}}{{\gamma }_I+{\gamma }_J})$ is a solution to

$$\frac{1}{{\beta }^2}-\frac{1}{{\alpha }^2}=\frac{4{\mu }_1\dots {\mu }_k}{{\mathsf{\Delta }}_{I,J}^2},$$

(17)

which, again, using the identity ${(\alpha +\beta )}^2-{(\alpha -\beta )}^2=4\alpha \beta$. Now, by enlarging (or shrinking) $S_k$ if necessary, and splitting the set of indices differently, he found n distinct pairs $({\gamma }_I-{\gamma }_J,{\gamma }_I+{\gamma }_J)$. Then, he chose a positive integer $\mathsf{\Delta }$, which is divisible by n ${\mathsf{\Delta }}_{I,J}$’s, and found n pairs $({\alpha }_{I,J},{\beta }_{I,J})=(\frac{\mathsf{\Delta }}{{\gamma }_I-{\gamma }_J},\frac{\mathsf{\Delta }}{{\gamma }_I+{\gamma }_J})$ solution to (16).

Similar to the above, we can find all solutions to the generalized Equation (15) of Perondi by simply solving the first equation, which is equal to the ith equation, for all i, using the method we found in the previous section. First, choose $s\in {\mathbb{Z}}^{+}$ and n distinct triple $(x_i,y_i,z_i)$, satisfying:

$$\left\{\begin{array}{c}{x}_1^2-y_1^2=s{z}_1^2\hfill \\ x_2^2-y_2^2=s{z}_2^2\hfill \\ \cdots \hfill \\ x_n^2-y_n^2=s{z}_n^2.\hfill \end{array}\right.$$

(18)

Then, we want to find $t_i$, such that

$$\left\{\begin{array}{c}{x}_1{y}_1{t}_1{z}_2=x_2{y}_2{t}_2{z}_1\hfill \\ x_1{y}_1{t}_1{z}_3=x_3{y}_3{t}_3{z}_1\hfill \\ \cdots \hfill \\ x_1{y}_1{t}_1{z}_n=x_n{y}_n{t}_n{z}_1.\hfill \end{array}\right.$$

(19)

It suffices that $t_1$ is divisible by

$$\left\{\frac{x_i{y}_i{z}_1}{\gcd (x_1{y}_1{z}_i,x_i{y}_i{z}_1)}\mathrm{for}\mathrm{all}2\le i\le n\right\}.$$

(20)

and the remaining $t_i$ are deduced from (19). The final solution to the generalized Equation (15) is:

$$({\beta }_i,{\alpha }_i)=(y_i{t}_i,x_i{t}_i)\mathrm{for}\mathrm{all}1\le i\le n.$$

(21)