Complex Deep Learning with Quantum Optics

Abstract

The rapid evolution towards future telecommunications infrastructures (e.g., 5G, the fifth generation of mobile networks) and the internet is renewing a strong interest for artificial intelligence (AI) methods, systems, and networks. Processing big data to infer patterns at high speeds and with low power consumption is becoming an increasing central technological challenge. Electronics are facing physically fundamental bottlenecks, whilst nanophotonics technologies are considered promising candidates to overcome the limitations of electronics. Today, there are evidences of an emerging research field, rooted in quantum optics, where the technological trajectories of deep neural networks (DNNs) and nanophotonics are crossing each other. This paper elaborates on these topics and proposes a theoretical architecture for a Complex DNN made from programmable metasurfaces; an example is also provided showing a striking correspondence between the equivariance of convolutional neural networks (CNNs) and the invariance principle of gauge transformations.

1. Introduction

The techno-economic drivers steering the evolution towards future telecommunications (e.g., 5G) and the internet are boosting a new growing interest for artificial intelligence (AI). As a matter of fact, the deployment of ultra-broadband communications infrastructures and the availability of huge processing and storage capabilities at affordable costs are creating the opportunity of developing a pervasive artificial nervous system [1] embedded into the reality.

One of the most demanded tasks of AI is extracting patterns and features directly from collected big data. Among the various most promising approaches for accomplishing this goal, deep neural networks (DNNs) [2] are outperforming.

The reason for the efficiency of DNNs is not fully explained, but one possible explanation, elaborated in literature, is that DNNs are based on an iterative coarse-graining scheme, which reminds us of an important tool in theoretical physics, called the renormalization group (RG) [3]. In fact, in a DNN, each high-level layer learns increasingly abstract higher-level features, providing a useful, and at times reduced, representation of the features to a lower-level layer. This similarity, and other analysis described in literature [4], suggests the intriguing possibility that the principles of DNNs are deeply rooted in quantum physics.

Today, the gauge theory, the mathematical framework at the basis of the standard model, finds remarkable applications in several other fields: Mathematics, economics, finance, and biology [5,6]. Common to most of these contexts, there is a formulation of the problems in terms of the variational free energy principle. In view of this reasoning, it seems promising to explore how this reasoning could be further extended for the development of future DNNs and more in general AI systems, based on quantum optics.

In line with Moore’s law, electronics starts facing physically fundamental bottlenecks, whilst nanophotonics technologies are considered promising candidates to overcome the limitations of electronics. In fact, the operations of DNNs are mostly matrix multiplications, and nanophotonic circuits can make such operations almost at the speed of light and very efficiently, due to the nature of photons.

Nanophotonics includes several domains [7], such as photonic crystals [8], plasmonics [9], metamaterials, metasurfaces [10,11,12], and other materials performing photonic behaviors [13]. This paper provides a short review of these domains and explores the emerging research field where DNNs and nanophotonics are converging. This field is still in its infancy, so it has been considered useful to provide this work in order to meditate the directions of future research and innovation. Specifically, this paper doesn’t address the application of DNNs to the nanophotonic inverse design [6], which is another interesting application area, where the photonic functionalities are obtained by optimization in a design parameter space by seeking a solution that minimizes (or maximizes) an objective or fitness function; the paper focusses on the design and implementation of DNNs with nanophotonics technologies.

In summary, the main contributions of this paper include:

• An overview highlighting the emergence of a research and innovation field where the technological trajectories of DNNs and nanophotonics are crossing each other;
• The possibility that DNN principles are deeply rooted in quantum physics, and therefore encouraging the design and development of complex deep learning with nanophotonics technologies;
• A proposal for a theoretical architecture for a complex DNN made of programmable metasurfaces and a description of an example showing the correspondence between the equivariance of convolutional neural networks (CNNs) and the invariance principle of gauge transformations.

The paper is structured as follows. After the introduction, Section 2 describes the basic principles of DNNs and why their functioning is showing similarities with the RG of quantum physics. Section 3 provides an overview of the basic principles of the quantum field theory (QFT) and its relations with nanophotonics. Section 4 describes the high-level architecture of a complex DNN made with metasurfaces and illustrates an example showing the correspondence between the equivariance principle of CNNs and the invariance of gauge transformations. Plans for future works and conclusions and are closing the paper.

2. Deep Neural Networks

DNNs are networks made of multiple and hierarchical layers of neurons. Any DNN has at least two layer which are hidden, where the neurons of one layer receiving inputs from ones in the layer below. The number of layers is just one of the characteristics of the complexity of a DNN; some other ones are, for instance, the numbers of neurons, the numbers of the connections and the related weights.

A DNN can be supervised or unsupervised. Both paradigms require a training phase with some sort of information: In case of supervised learning, for instance, humans provide correct labels for images; in case of an unsupervised DNN, for instance with reinforcement learning, rewards are provided for successful behavior. The former class includes models such as convolutional neural networks (CNN), fully connected DNNs (FC DNNs), and hierarchical temporal memory (HTM). The latter class, the unsupervised DNNs, includes models such as stacked auto-encoders, restricted Boltzmann machines (RBMs), and a deep belief network (DBN) [14].

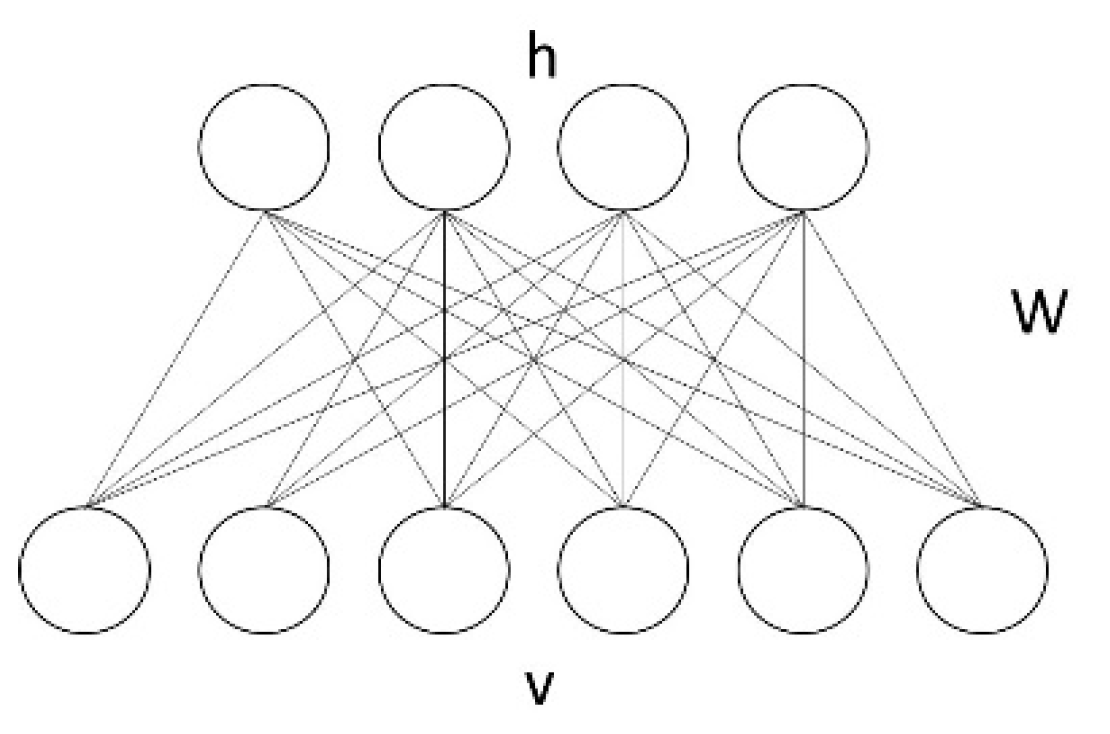
For instance, let’s focus the attention on RBMs which can be interpreted as a specific type of deep neural network (DNN). A RBM consists of two layers of neurons. The visible layer receives the input examples while the other hidden layer builds an internal representation of the input, as shown in Figure 1. No lateral connections exist within each layer (therefore, they are called “restricted”) for computational efficiency.

The V units of the first layer, denoted by the vector v = (v₁, … v_V), correspond to the components related to an observation, and are therefore called “visible”, while the H units in the second layer h = (h₁, …, h_H) represent “hidden” variables. The term “restricted”, in the name RBM, refers to the connections between the units: Each unit is connected with all hidden units, but there are no connections between units of the same kind. w_ij is the symmetric connection weight between the units.

In analogy with statistical physics, a RBM models the configuration of visible and hidden units (v, h) in terms of an energy function:

$$E\left(v,h\right)={\displaystyle \sum }_i{b}_i{v}_i+{\displaystyle \sum }_i{c}_j{h}_j+{\displaystyle \sum }_i{w}_{ij}{v}_i{h}_j$$

(1)

A RBM assigns a probability to each joint configuration (v, h), which, by convention, is high when the energy of the configuration is low (Gibbs distribution):

$$p_{\lambda }\left(v, h\right)=\frac{e^{-E\left(v, h\right)}}{Z}$$

(2)

where λ ≡ {b_i, c_j, w_ij} is the variational parameters and Z the partition function:

$$Z={\displaystyle \sum }_{vϵV}{\displaystyle \sum }_{hϵH}{e}^{-E_{\lambda }\left(v, h\right)}$$

(3)

In a RBM, the probability distribution of data is dealt with via an energy-based model with hidden units. This generative modeling shows deep connections to statistical physics [15].

Interestingly, [16] describes a one-to-one mapping between RBM-based DNNs and the variational RG [3], while in [4] they conjecture even possible similarities between the principles of QFT and RBM-based DNN. The question becomes even more intriguing in a recent publication [17] where deep reinforcement learning has been demonstrated to show its effectiveness in discovering control sequences for a tunable quantum system whose time evolution starts far from its final equilibrium, without any a priori knowledge. These simple considerations, and other analyses described in literature, are suggesting the possibility that DNN principles are deeply rooted in quantum physics.

2.1. Convolutional Neural Networks

Another very interesting type of DNN is the CNN.

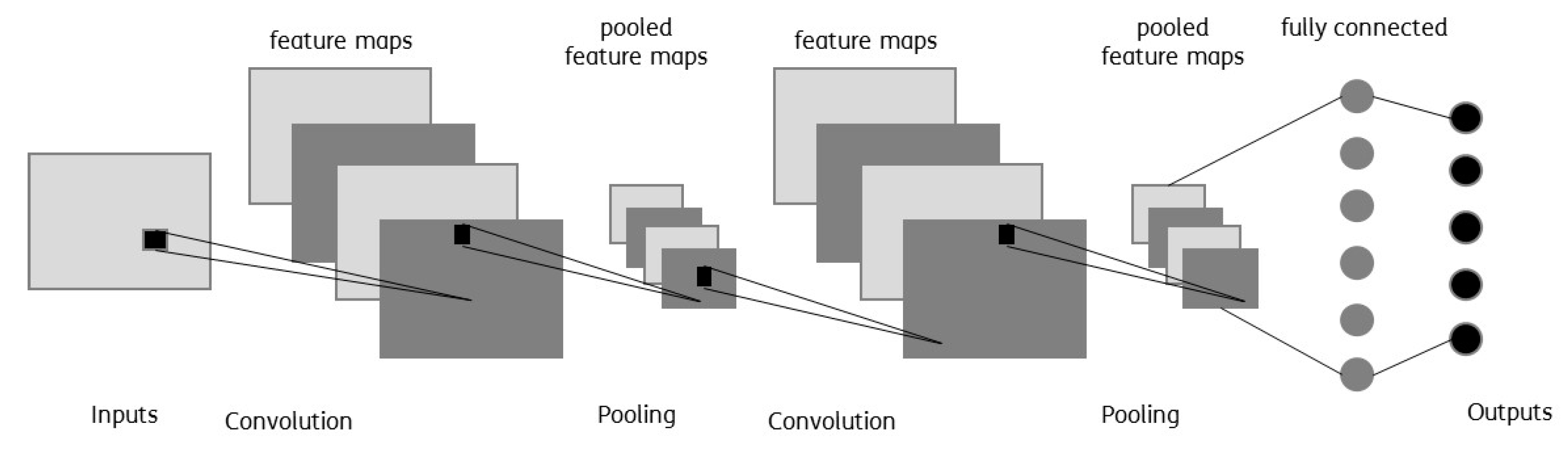
CNNs make use of convolutional filters or kernels, which allow the detection of local patterns regardless of their position, for example, in an image. With the use of convolutional layers, CNNs create feature maps, using a filter or kernel, which are trained to recognize relevant features: In other words, during forward propagation of the signal, feature maps convert the images, leaving only those features which are associated with a given kernel. Figure 2 shows the high level architectural model of a CNN.

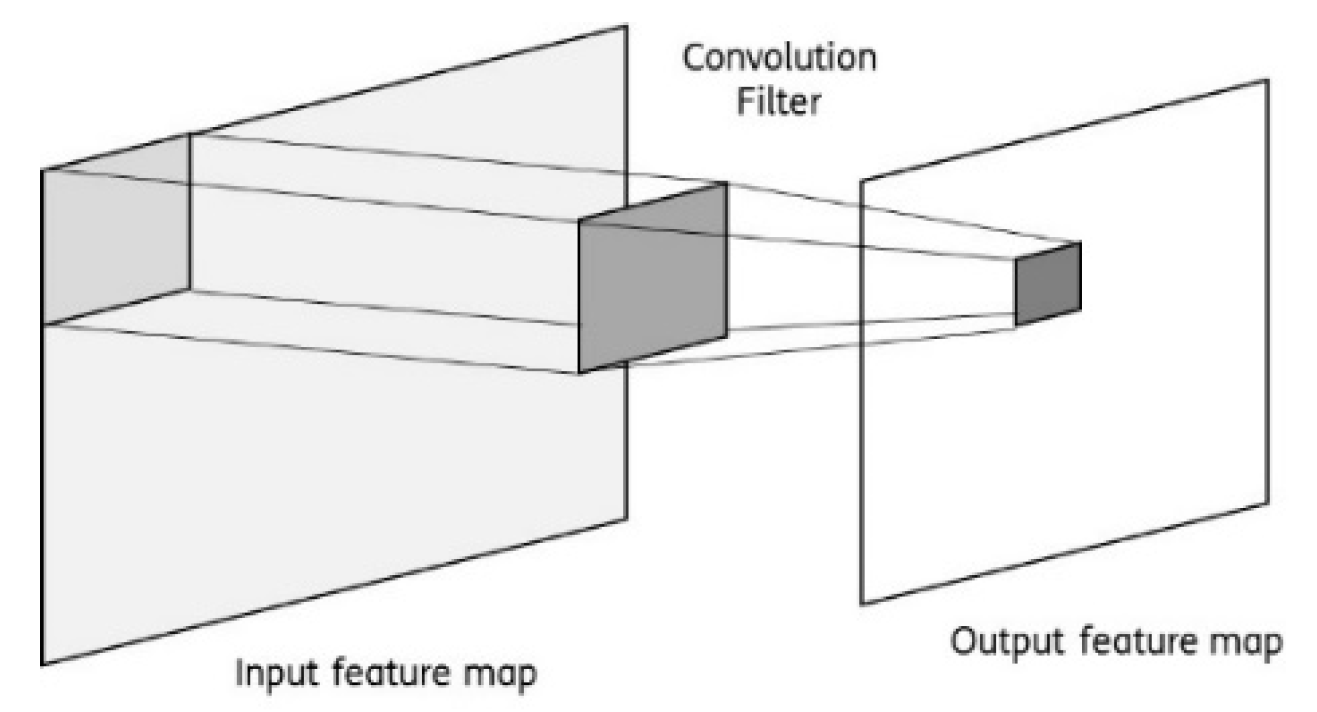
The convolution operation (Figure 3) makes the sum of the element-wise product of a filter and a portion of the input feature map. During the training, the filter parameters (e.g., weights of the element-wise product) are tuned to extract meaningful information (e.g., patterns) from data, r images. The pooling layer is then applied to the output feature map produced by the convolution (e.g., by taking the maximum value from a given array of numbers). In other words, during this operation, a feature map is split into bunch boxes and the maximum value from each box is taken.

CNNs are very efficient in recognizing patterns in two-dimensional (2D) images, but they are not directly applicable to three-dimensional (3D) spaces and, in general, manifold signals. Some examples of use cases where CNNs should work on data collected over spherical surfaces include: The analysis of proteins, medical imaging, omnidirectional vision with multiple cameras (for drones, self-driving cars, VR/AR), astro-physics, or climate science. The design of the CNN for these use cases is by far more complicated: In fact, when a certain pattern moves around on the sphere, we must deal with 3D rotations instead of simple translation (as in the planar case). Rotation of a spherical signal cannot be emulated by a translation of its planar projection, but it will result in distortions.

In this case, it might be useful extending the principle of equivariance for CNNs: Practically, the value of the output feature map should be given by an inner product between the input feature map and a rotated filter (i.e., functions) on the geometric surface spaces. For example, the paper [18] demonstrated that the spherical correlation satisfies a generalized Fourier theorem, thus allowing us to compute it (the convolution kernel) efficiently with the generalized fast Fourier transform (FFT).

The problem is even more complicated when dealing with signals on manifolds. In fact, manifolds do not have global symmetries, but they might have some local symmetries and it is not altogether clear how to develop the convolution-like operations for the CNNs. The requirement is that the convolution-like operations should be equivariant, which means that the CNNs should be capable of recognizing the effects of any transformation of an input frame in the output frame. The next paragraphs describe an example of how the gauge theory could be used to design the kernels of CNNs.

2.2. Examples of Applications for Telecommunicvations and the Internet

The ongoing digital transformation of telecommunications and the internet will radically increase the flexibility of network and service platforms while ensuring the levels of programmability, reliance, and performance required by the fifth generation of mobile networks (5G) scenarios and applications (e.g., the internet of things, the tactile internet, immersive communications, automotive, industry 4.0, smart agriculture, omics, and E-Health, etc.).

On the other hand, the management complexity of such future telecommunication infrastructures will overwhelm human-made operations, thus posing urgent needs of designing and deploying management systems with AI features. As a matter of fact, the use of the huge data lake generated by a telecommunications infrastructure will allow automating processes by introducing cognitive capabilities at various levels. Examples of cognitive capabilities include: understanding application needs and automating the dynamic provisioning of services; monitoring and maintaining network states; dynamically allocating virtual network resources and services; ensuring network reliability and enforcing security policies. Moreover, although we cannot yet fully grasp how pervasive AI will be, it is likely that it will also enable innovative features when provisioning future digital cognitive services for homes, businesses, transportation, manufacturing, and other industry verticals, included smart cities.

3. Quantum Field Theory and Nanophotonics

3.1. Quantum Field Theory

Quantum field theory (QFT) is a fundamental theory of quantum physics, well recognized for the countless empirical demonstrations offering a successful re-interpretation of quantum mechanics (QM). In fact, QFT opens a new point of view in quantum physics, where particles are excited states of underlying fields. The concept of “the field” is rather well-known: Intuitively, a field, for example an electromagnetic field, is defined as a property of spacetime which could be represented by a scalar, a vector, a complex number, etc. Therefore, QFT defines an excited state of a field as any state with energy greater than the ground state, called a vacuum: For example, photons are excited states of an underneath electromagnetic field.

Further technical details about QFT are outside the scope of the paper, but, interestingly, we noted that in [14] the author describes a potential relationship between QFT and DNN principles. This explains the correspondence of the Euclidean QFT in a flat spacetime with d+1 dimensions and statistical mechanics in d+1 dimensional flat space using an imaginary time. This might open some interesting considerations for developing DNNs based on complex number operations.

In general, the gauge theory is a type of QFT, in which the Lagrangian of a system (defined as the difference between kinetic and potential energy) is kept invariant under continuous symmetry transformations (called gauge transformation) [19].

One of the most quoted examples of gauge theory is electrodynamics, as described by the Maxwell equations. In electrodynamics, the structure of the field equations is such that the electric field E(t, x) and the magnetic field H(t, x) can be expressed in terms of a scalar field A₀(t, x) (scalar electric potential) and a vector field A(t, x) (vector magnetic potential).

In many aspects, the so-called four-potential A^µ = (A₀, A) describes the electromagnetic field at a more fundamental level than the electric and magnetic field themselves. However, the four-potential definition is not unique: In other words, different choices of an arbitrary scalar field are consistent with given observable electric and magnetic fields, E and H. This is essentially a symmetry property, i.e., an example of gauge invariance.

This symmetry or gauge invariance is then a guiding principle for modeling electrodynamics in media and thus in transformation optics based on a variational approach. This means that we can formulate Maxwell’s equations in an inherently covariant manner so to permit the description of electromagnetic phenomena on pseudo-Riemannian manifolds independent of the choice of coordinate frame. Mathematical details are reported in [20]. In this paper, we explain why this is important for designing equivariant CNNs.

Another remarkable aspect is that gauge theories are used in physics, mathematics, economics, finance, and biology [5]. Common to most contexts, there is a formulation in terms of the free energy principle. For instance, in biology and neuroscience, the free energy principle proposes a unified approach of action, perception, and learning of any self-organizing system, in equilibrium with its environment.

This is well elaborated, for example, in [21] and [22], where the free energy principle has been proved valid for describing several aspects of functional brain architectures. In this case, the system is the brain with its Lagrangian (reflecting neuronal or internal states), while the environment (with external states) is producing local sensory perturbations (appearing as local symmetry breakings or gauge transformations). Attention, perception, and action are compensatory gauge fields, restoring the symmetry of the Lagrangian [4]. If this reasoning applies for the brain, or for the nervous system, it might also be applicable for an AI system, such as a DNN; another clue that reinforces the initial work hypothesis.

It is also well known that the propagation of the electromagnetic field propagations/interactions, for instance in a certain material, is the expression of a natural tendency of the overall system to assume a configuration with the minimum free energy (Hamilton’s path of least action).

3.2. Quantum Optics and Nanophotonics

As mentioned, there are growing evidences of an emerging research field, rooted in quantum optics, where the technological trajectories of DNNs and nanophotonics technologies are intercepting each other. In fact, photonic crystals, plasmonics, metamaterials, metasurfaces, and other materials performing photonic behaviors have already been considered for developing DNNs. This paragraph will provide only a short introduction to the readers who are not familiar with the subject of nanophotonics: For further reading on this subject, we advise the readers turn to more comprehensive reviews [23,24,25,26,27,28,29,30,31,32,33,34].

First, we will recall some basic principles, then the attention will be focused on metamaterials and metasurfaces. It is well known that Maxwell’s equations are form-invariant under arbitrary spatial coordinate transformations: This means that the effects of a coordinate transformation can be absorbed by the properties of the material crossed by electromagnetic (EM) waves [35]. Therefore, in general, transformation optics offer great versatility for controlling EM waves: A spatially changing refractive index can be used to lead to changes in EM waves propagation characteristics.

Metamaterials are structures designed and artificially engineered to manipulate EM waves in unconventional ways. For instance, EM waves propagation characteristics depends on the nanoresonators introduced into the material, its morphology, the geometry of the array, the surrounding media, etc. Remarkably, it is possible to develop metamaterial with refractive indexes not present in nature (e.g., 0 or negative refraction), therefore producing devices with anomalous reflection and transmission of EM waves [29].

Examples of resonators include various split rings structures up to metallic nanoparticles, supporting resonances associated with free electron motion, i.e., localized surface plasmon resonances. For instance, if a metamaterial is properly engineered with nanoparticles and is fired with high intensity light pulses, injecting energy into the electrons in gold particles, the refractive index of the material will change.

Additionally, metasurfaces, which are two-dimensional slices of 3D bulk metamaterials, are recently attracting a growing interest. In metasurfaces, each pixel can be engineered to emit a certain EM wave with specific amplitude, phase, radiation pattern, and polarization. Low conversion efficiencies remain a challenge, which is partly overcome by using, for example, metasurfaces integrated in quantum wells or multilayered devices.

Remarkably, Yu et al. [35] proposed the idea of designing metasurfaces characterized by abrupt phase shifts, which could be used to control EM fields patterns. This is recalling the approach adopted in the design of reconfigurable transmit-arrays antenna. As a matter of fact, metasurfaces can be seen as arrays of nano-antennas: By shifting the resonant frequency through the nanoantenna designs, it is possible to effectively control the amount of the phase shifted in the scattered signal.

As another example, in [36], the authors realized a prototype of a so-called information metasurface, controlled by a field-programmable gate array, which implements the harmonic beam steering via an optimized space-time coding sequence. In [37], a new architecture for a fully-optical neural network is proposed, using an optical field-programmable gate array based on Mach–Zehnder interferometers.

Nonlinearities can also be used to manipulate EM waves, thus establishing connections between optics and other areas of physics: Consider, for example, the EM pattern formation in nonlinear lattices. The design of photonic lattices can leverage procedures that are analogous to RGs in condensed matter or quantum physics when the microscopic details of the material get encoded in the values of a limited number of coefficients for minimizing the effective free energy.

To conclude this paragraph, we mention the interesting analysis developed in [38], where it is argued that the existence of a perturbation of the phase of a certain material can be interpreted as a Nambu–Goldstone bosons condensation. It is, in fact, demonstrated how finite size propagating nonlinear beams inside a photonic lattice can act as effective meta-waveguides for Nambu–Goldstone phase waves. Furthermore, the propagation properties of the phase wave depend on characteristics of the underlying nonlinear beams, behaving as an optical metamaterial. This explanation of a phase perturbation of a material, in terms of Nambu–Goldstone bosons condensation, has remarkable applications in biological intelligence.

4. Complex Deep Learning with Quantum Optics

In [39], an interesting example of an all-optical diffractive deep neural network (D²NN) is described.

A D²NN is made of a set of diffractive layers, where each point (equivalent of a neuron) acts as a secondary source of an EM wave directed to the following layer. The amplitude and phase of the secondary EM wave are determined by the product of the input EM wave and the complex-valued transmission or reflection coefficient at that point (following the laws of transformation optics).

In this example, the transmission/reflection coefficient of each point of a layer is a learnable network parameter, which is iteratively adjusted during the training process (e.g., performed in a computer) using a classical error back-propagation method. After the training, the design of the layer is fixed as the transmission/reflection coefficients of all the neurons of all layers are determined.

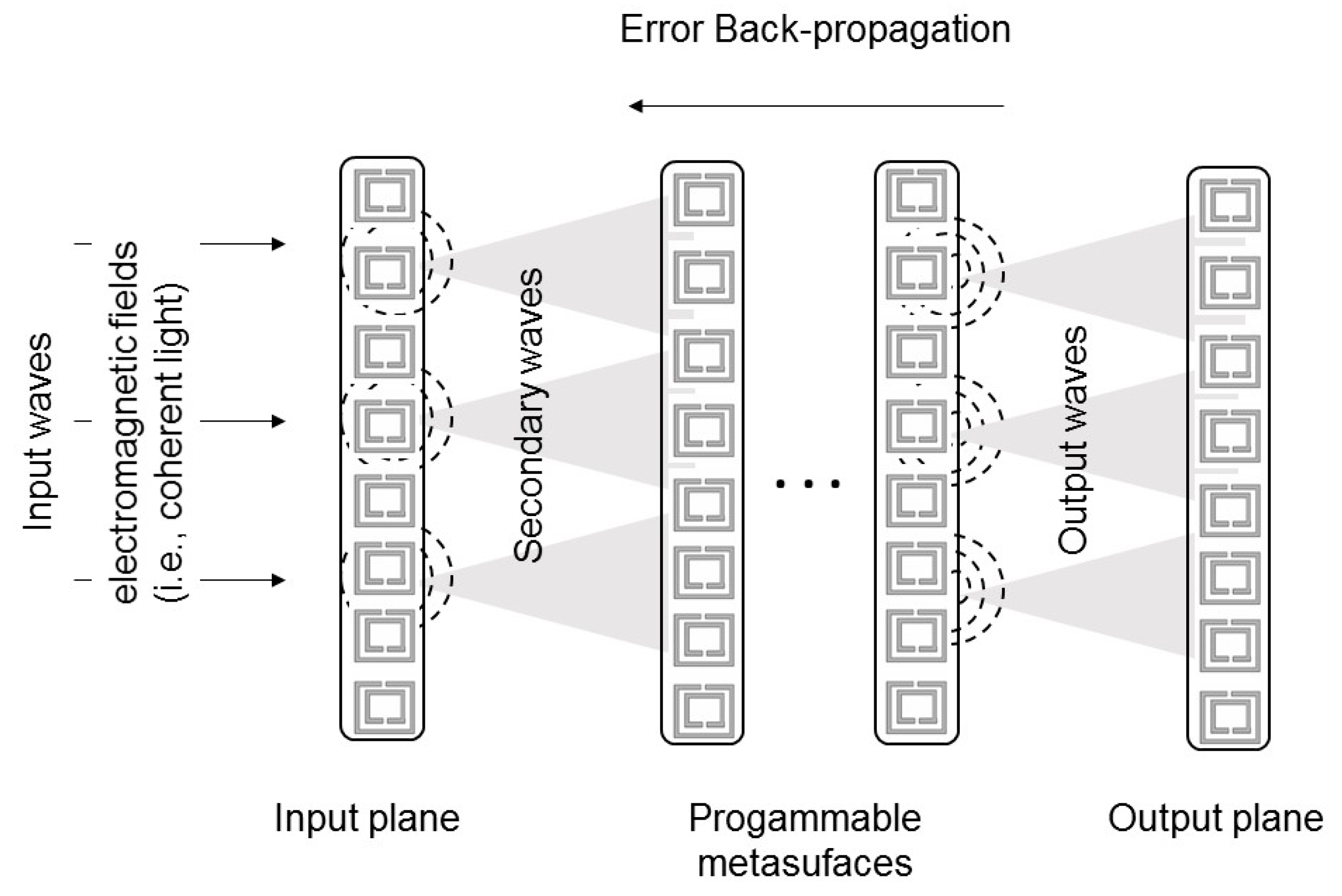
One can imagine an ideal nanophotonic DNN (Figure 4), generalizing the model of the D²NN, where the neural layers are physically formed by multiple layers of programmable metasurfaces. Additionally, in this case, each point on a given metasurface represents a neuron that is connected to other neurons of the following metasurface through the transformation optics principles. On the other hand, the programmability of the metasurface allows a change in the refractive index of each point of the metasurface, dynamically.

A training phase is still required to iteratively adjust the refractive indices, but these indices are not fixed (as in D²NN). As mentioned, there are already examples of programmable metasurfaces with switching diodes and mechanical micro/nano-systems [37,38,39]. It should be mentioned that, in this first example, the electronic control for metasurface programming is still required. In the future, we may consider other challenging alternatives, for instance, all-optical control, using plasmomic modern techniques.

There are some key differences between this type of nanophotonic DNN and the traditional DNNs, such as:

• The inputs are electromagnetic waves which bring us to the processing with complex numbers (rather than with the real numbers);
• The functions of any neuron is the expression of wave interference phenomena and electromagnetic interactions with the metamaterial oscillators (rather than sigmoid, linear, or non-linear neuron functions);
• Coupling of neurons is based on the principles of wave propagation and interference.

The first aspect is particularly important: It should be mentioned that, today, most DNNs are based on real number operations and representations. However, recent studies show that the use of complex numbers could have richer representational characteristics and facilitate noise-robust memory retrieval mechanisms [40]. In fact, the phase (in complex number elaborations) is not only important from a biological point of view [41], but also from a signal processing viewpoint [42,43]: The phase provides a detailed description of objects as it encodes shapes, edges, and orientations.

Consider the example of the design of an equivariant CNN, which is a specific case of DNN. In our multi-layered architecture, a learned feature of a CNN can be seen as an EM wave, providing a convolution operation at the following layer.

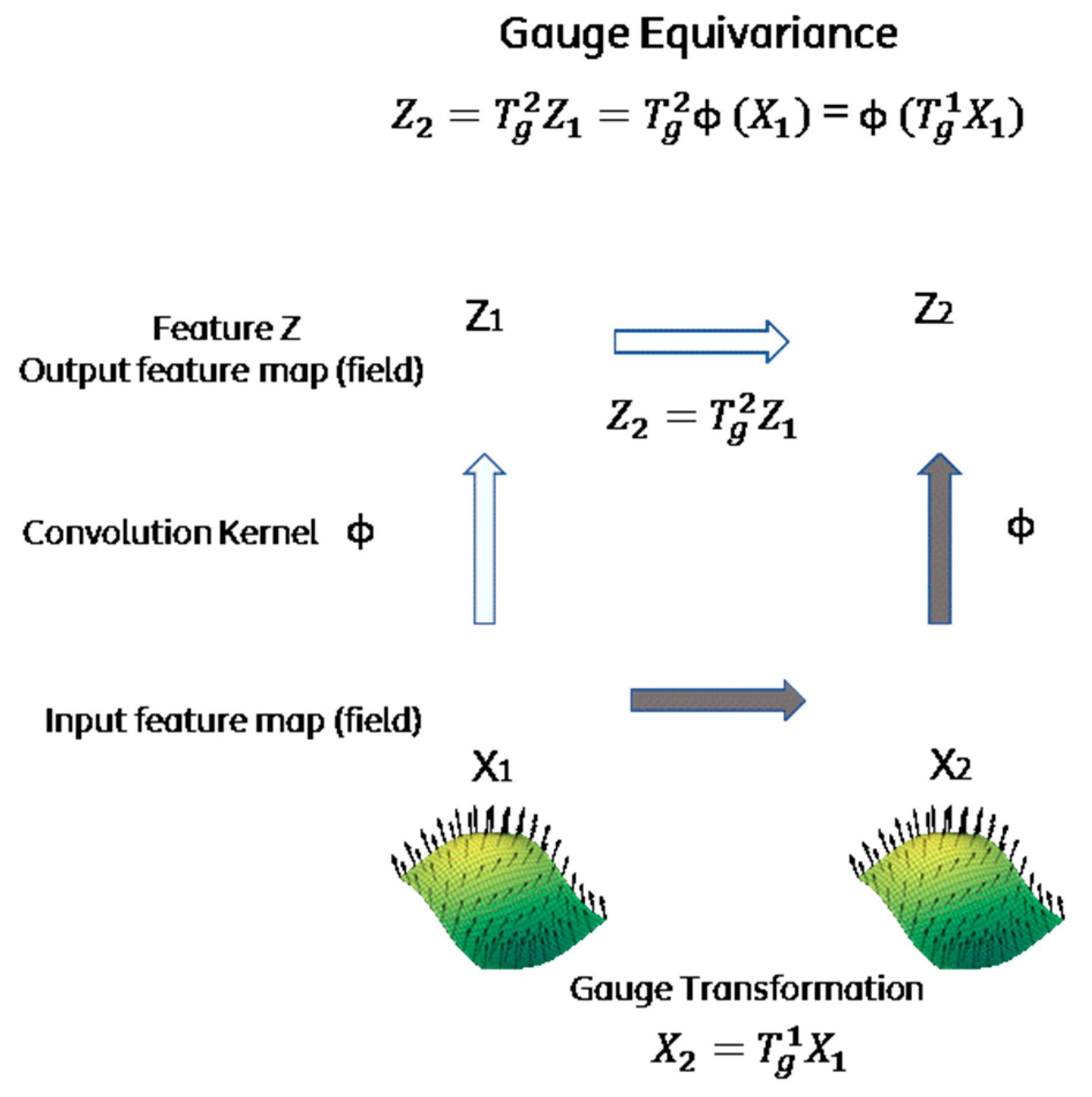
In this direction, the gauge theory could help in designing equivariant convolution-like operations of a CNN on general manifolds. In a nutshell, we describe an analogy with physics: The gauge equivariant convolution for CNN on manifolds takes, as the input, feature “fields” and produces, as the output, new feature “fields”; each “field” is given by a number of feature maps, whose activations can be seen as the coefficients of a geometrical object (e.g., scalar, vector, tensor, etc.) relative to a spatially varying frame (i.e., the gauge transformation). Figure 5 is showing an example of equivariance, where the mapping preserves the algebraic structure of the transformation (Z₁ ≠ Z₂$)$ but keeps the relationship (${\mathrm{Z}}_2={\mathrm{T}}_{\mathrm{g}}^2{\mathrm{Z}}_1={\mathrm{T}}_{\mathrm{g}}^2\mathsf{\phi }\left({\mathrm{X}}_1\right)$ =$\mathsf{\varphi }\left({\mathrm{T}}_{\mathrm{g}}^1{\mathrm{X}}_1\right))$.

This is more formally described in [44], where it is demonstrated that, to maintain equivariance, certain linear constraints must be placed in the convolution kernel [45]. In our example, the EM convolution kernels are implemented with metasurfaces, whereby the transformation optics allow us to achieve the design criteria of equivariance. Furthermore, operating with complex numbers allows us to perform a complex convolution, as described in [42], which has very useful implications.

Further investigations are required whether or not such a physical CNN architecture can provide real practical advantages over traditional implementations of CNN in computers. This paper represents a tentative step in this research avenue in order to stimulate further activities in the broader scope of optical DNNs.

As a future work, it is planned to simulate (and then experimentally validate) a prototype of complex DNN based on metasurfaces. The idea is then to test its performances with the Modified National Institute of Standards and Technology (MNIST) database [46], which is a collection of hand-written digits that is widely used in the deep learning community (Figure 6). The images of the digits are very small (784 = 28 × 28 pixels), so the DNN in them must have 784 input nodes on the visible layer.

Each visible node receives one-pixel value for each pixel in one image: The approach encodes the digits into amplitudes and phases of the input field to the DNN prototype. The training is aimed at mapping input digits into digits detectors (0, 1, …, 9) of the output layer. In order to get the maximum optical signal at the output detectors, the phase at each point of the metasurfaces are properly tuned. A preliminary model includes five metasurfaces, each one equipped with xxx neurons. Initial results show a classification accuracy of around 90%, but this still needs further study and refinements.

Another challenging question requiring future research concerns the parallel understanding of classical wave optics and quantized light (photons) interactions in nanostructures. This is an exciting area of research, where the combination of quantum optics with nanophotonics might have far-reaching impacts for the telecommunications industry, the future of the internet, sensing and metrology systems, and any related energy-efficiency technology.

5. Conclusions

In the evolution towards future telecommunications infrastructures (e.g., 5G) and the internet, the processing of big data at high speeds and with low power for innovative AI systems is becoming an increasingly central technological challenge.

If electronics, on the one hand, start facing physically fundamental bottlenecks, nanophotonics technologies, on the other hand, are considered promising candidates for the above future requirements. Interestingly, DNN principles seem to be deeply rooted in quantum physics, showing correspondences, for instance, with QFT and gauge theory principles. As a matter of fact, a gauge theory mathematical framework has already been used for modeling biological intelligence and nervous systems: If these principles are applicable for the brain, or for the nervous system, they might also be applicable for an AI system, such as a DNN.

This paper elaborated on that theory, which is even more motivated by the evidences of the emergence of research fields where the trajectories of DNNs and nanophotonics are crossing each other. This led us first to develop an ideal architecture of a complex DNN made of programmable metasurfaces and then to draw a practical example showing the correspondence between the equivariance principle of CNNs and the invariance of a gauge transformation. Further theoretical studies, numerical simulations, and experiments are necessary, but this work aims at stimulating the integration of the two communities of AI and quantum optics.