A Cooperative Car-Following Eco-Driving Strategy for a Plug-In Hybrid Electric Vehicle Platoon in the Connected Environment
Abstract
1. Introduction
2. Methodology
2.1. Hypothesis
2.2. Vehicle Powertrain Modeling
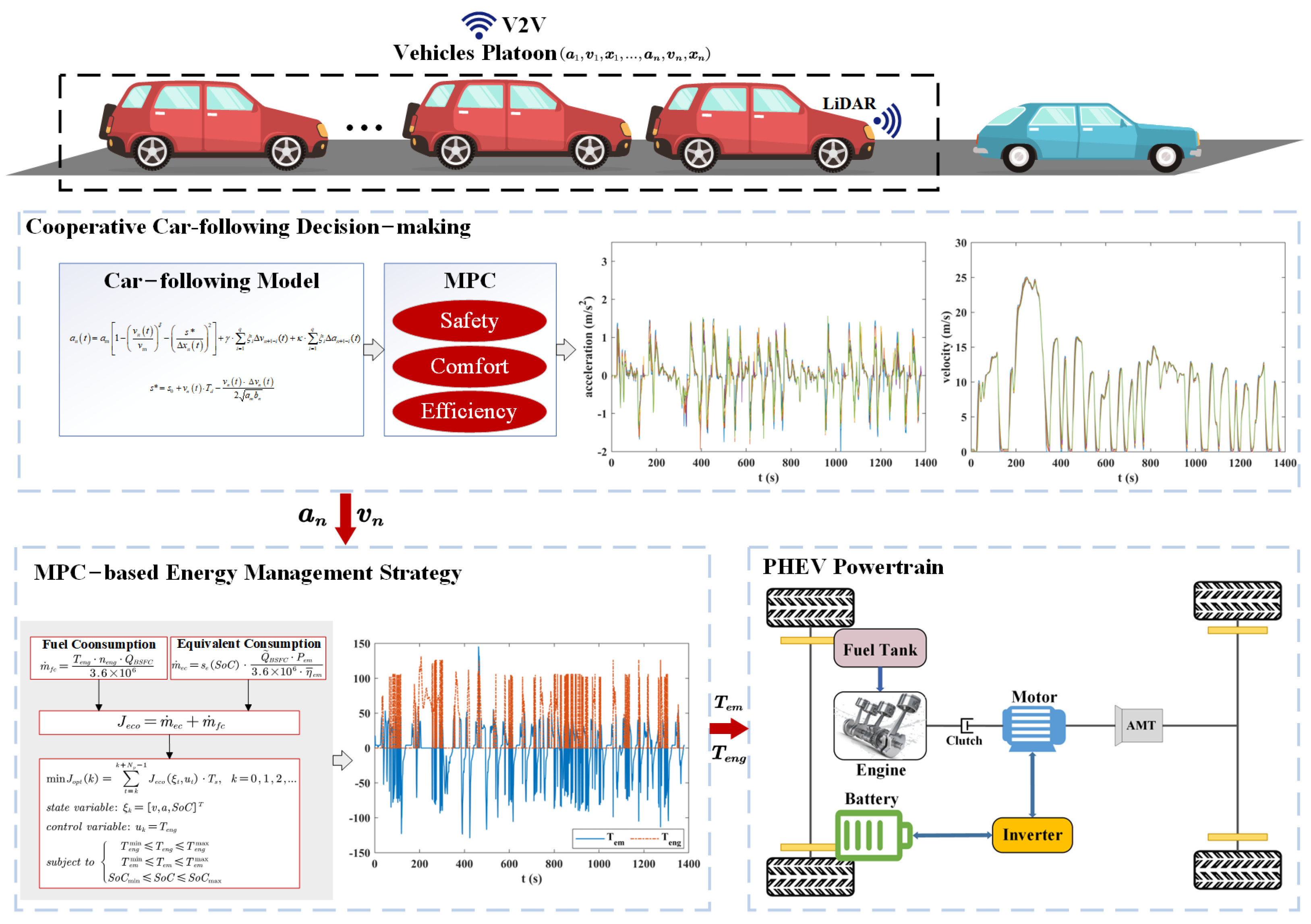
2.3. Hierarchical Eco-Driving Strategy
2.3.1. Cooperative Car-Following Decision-Making for CAPHEV Platoon
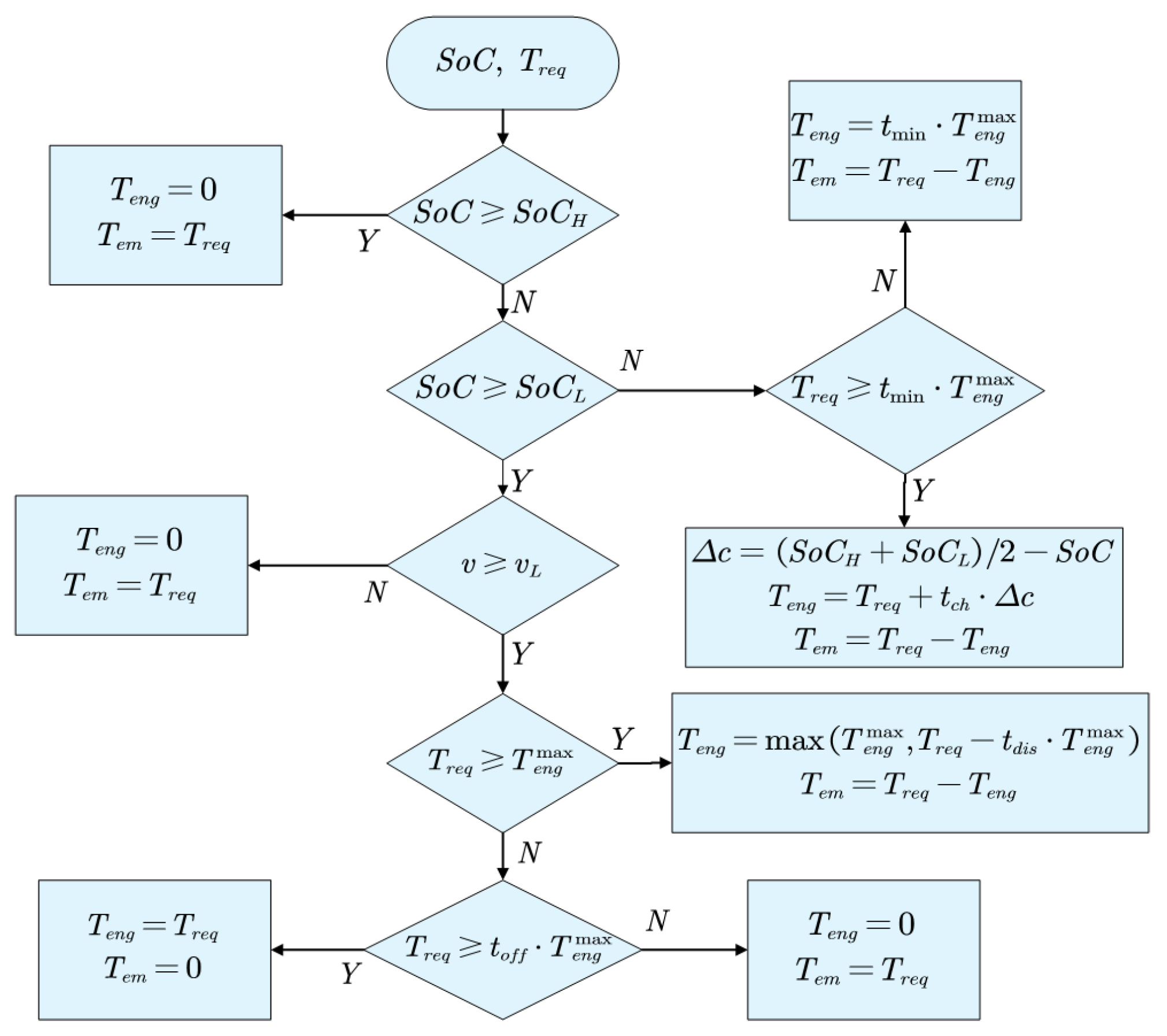
2.3.2. Distributed Energy Management Strategy
3. Results and Discussion
3.1. Simulation Experiment Parameter Configuration
3.2. Rule-Based Eco-Driving Strategy
3.3. Simulation Results
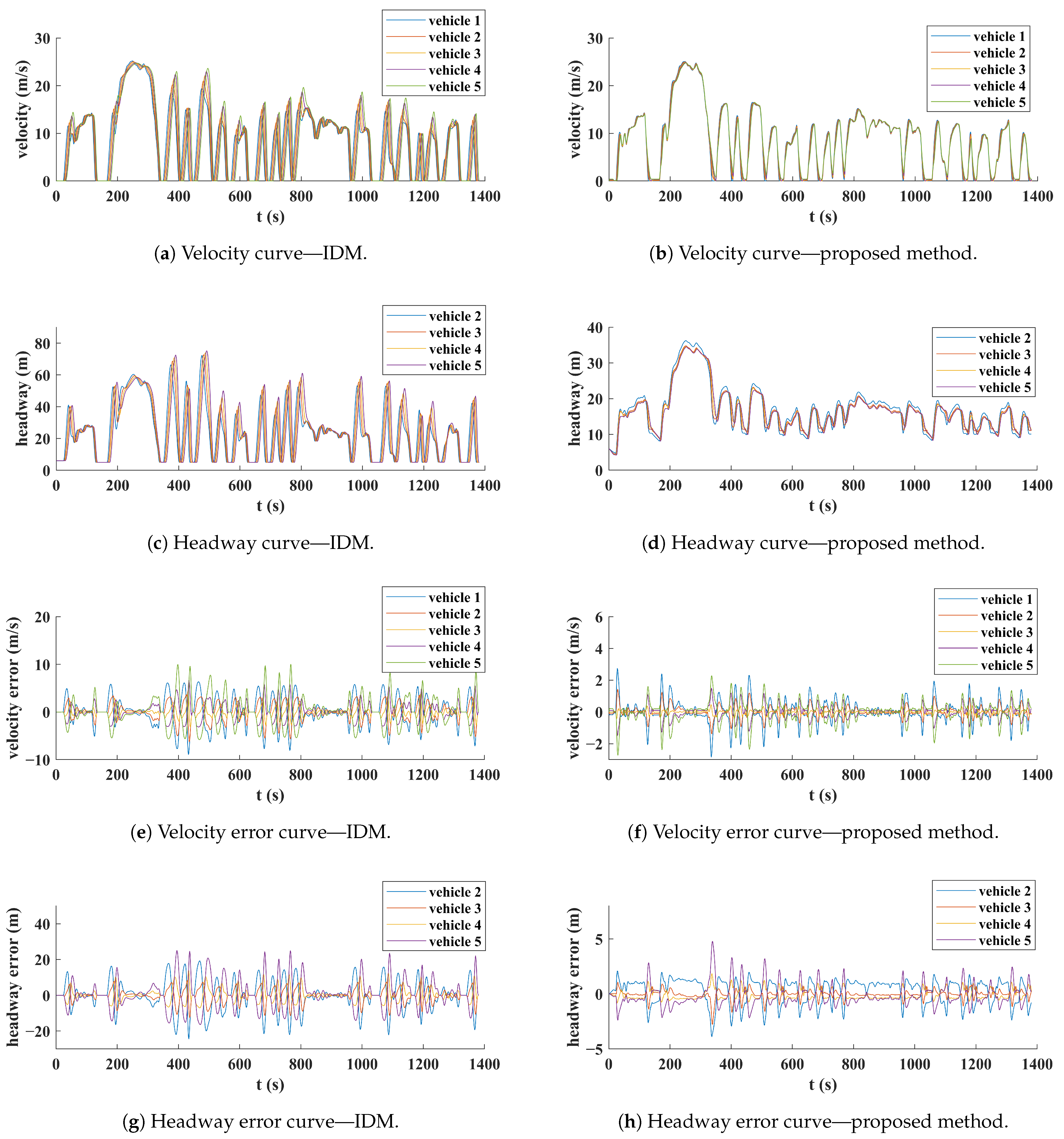
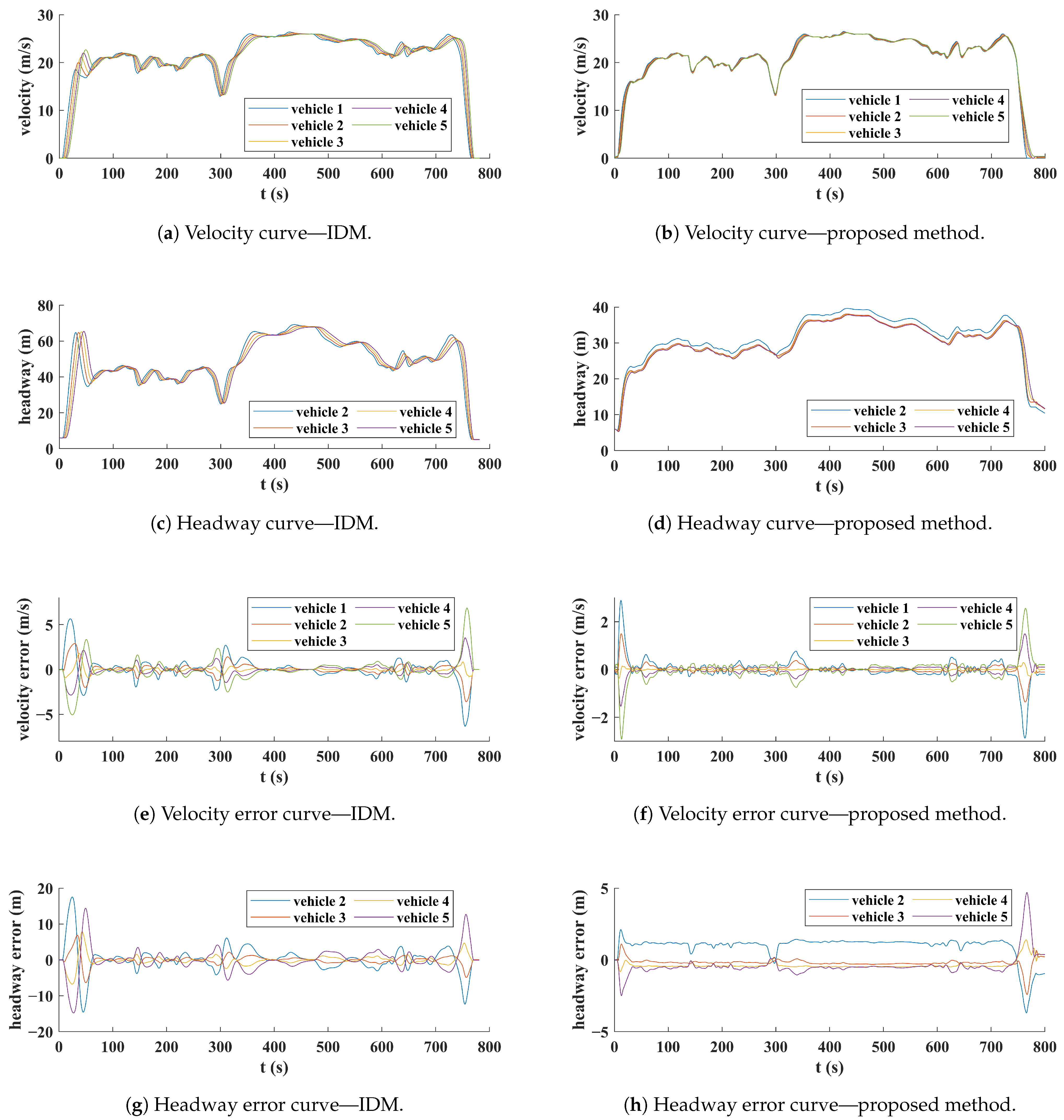
3.3.1. Analysis of Car-Following Performance
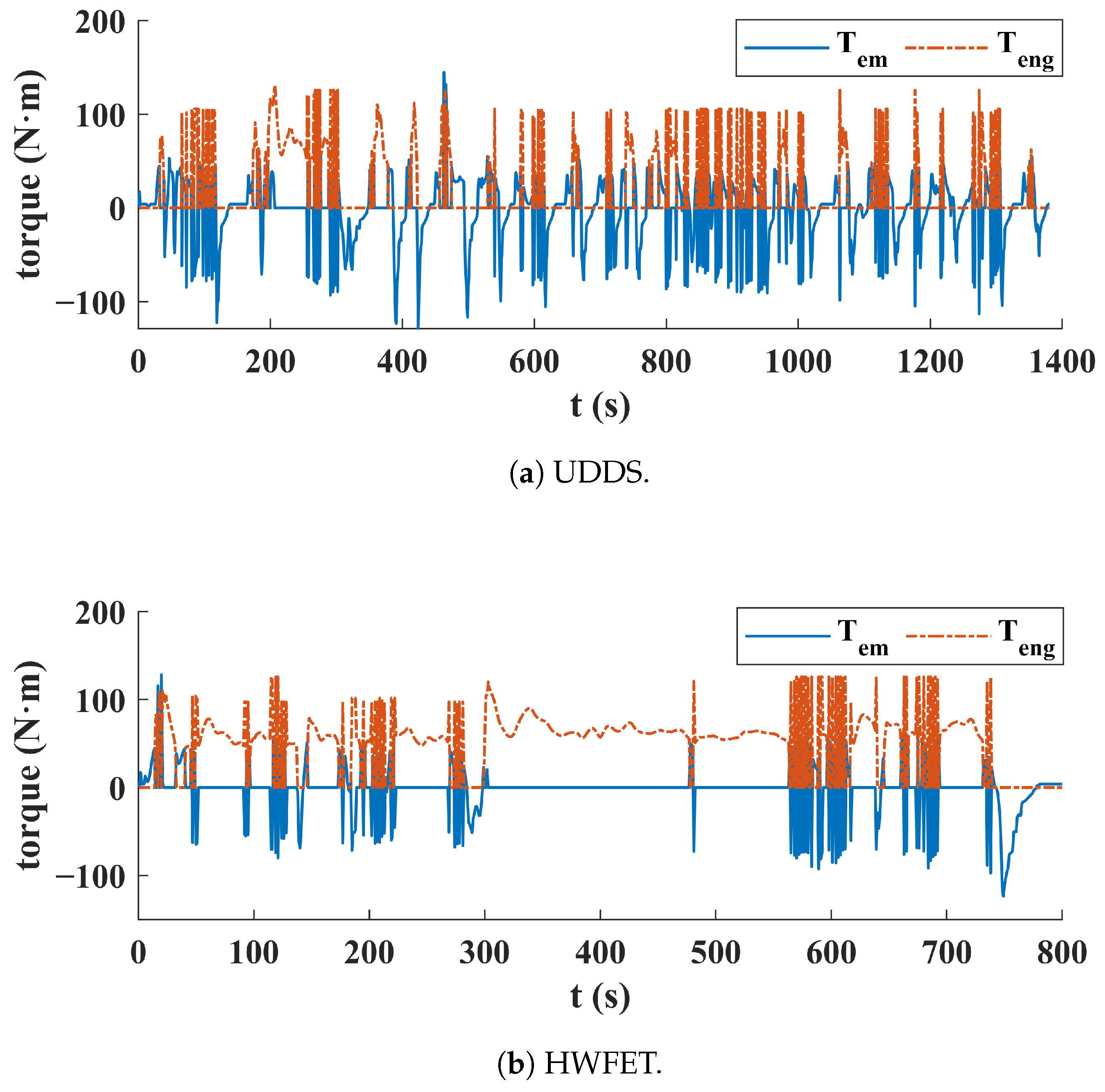
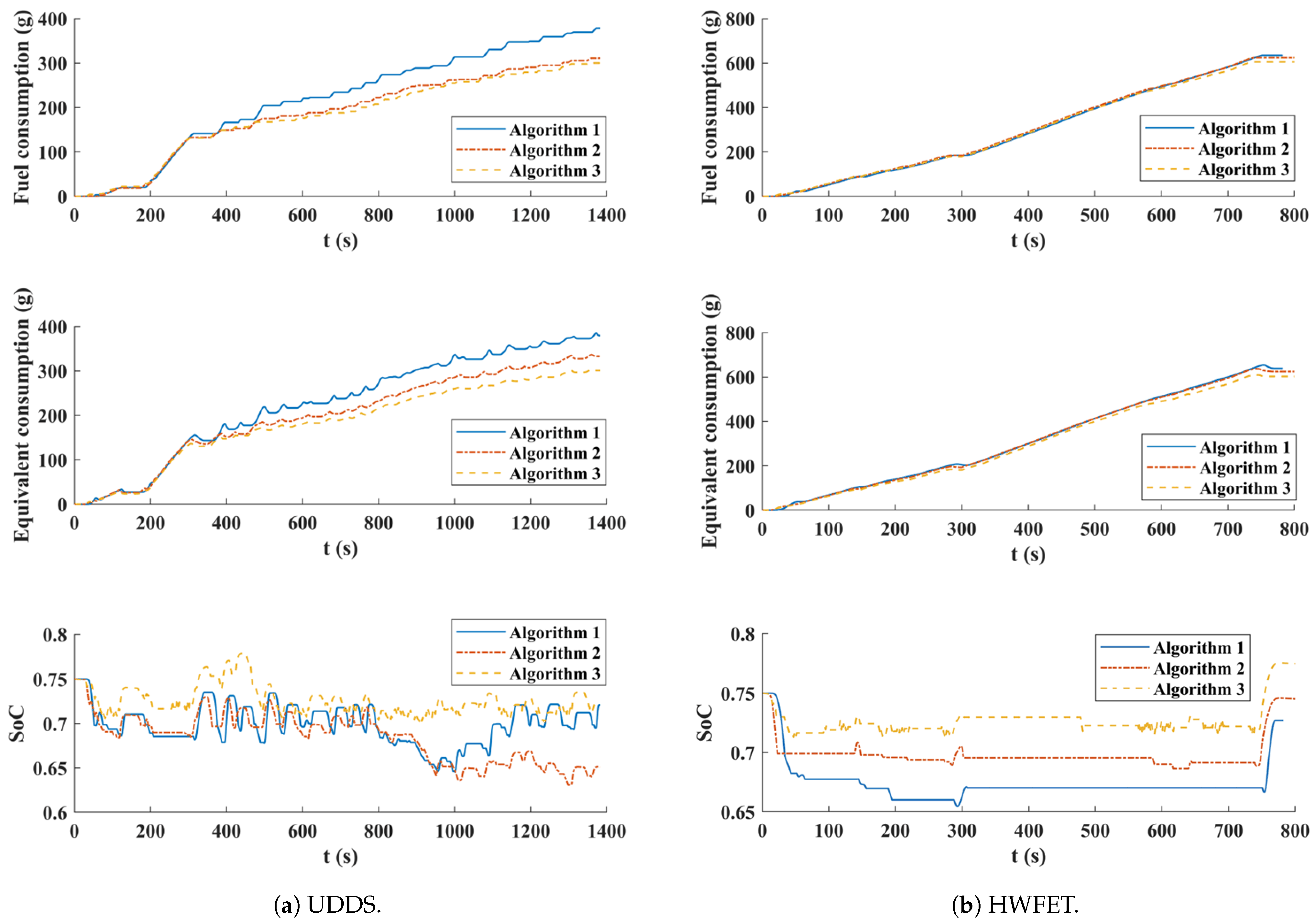
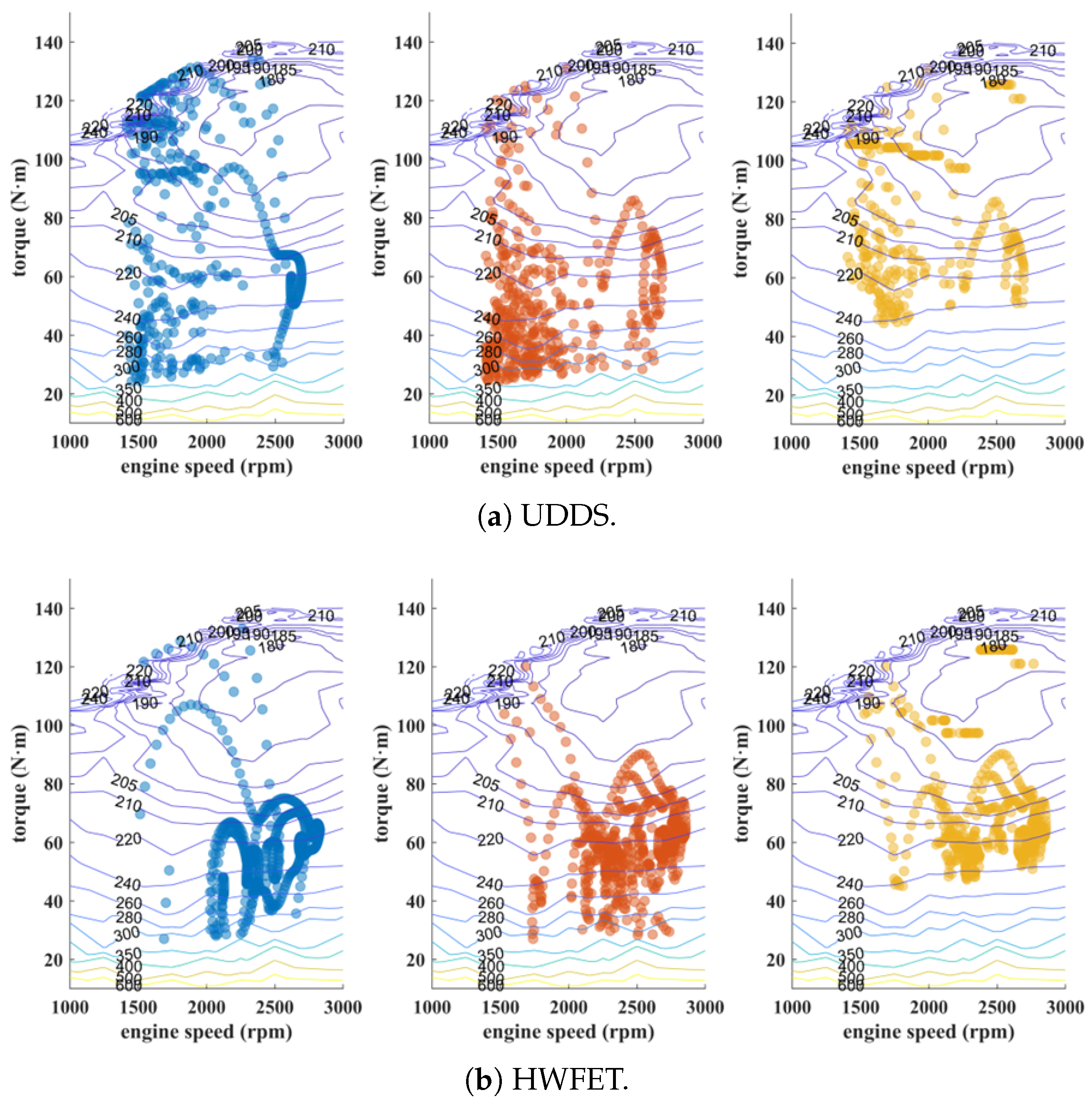
3.3.2. Analysis of Energy Management Performance
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, F.; Hu, X.; Langari, R.; Cao, D. Energy management strategies of connected HEVs and PHEVs: Recent progress and outlook. Prog. Energy Combust. Sci. 2019, 73, 235–256. [Google Scholar] [CrossRef]
- Han, J.; Wang, X.; Shi, H.; Wang, B.; Wang, G.; Chen, L.; Wang, Q. Research on the Impacts of Vehicle Type on Car-Following Behavior, Fuel Consumption and Exhaust Emission in the V2X Environment. Sustainability 2022, 14, 5231. [Google Scholar] [CrossRef]
- Yu, S.; Shi, Z. An extended car-following model considering vehicular gap fluctuation. Measurement 2015, 70, 137–147. [Google Scholar] [CrossRef]
- Guo, L.; Zhao, X.; Yu, S.; Li, X.; Shi, Z. An improved car-following model with multiple preceding cars’ velocity fluctuation feedback. Phys. A Stat. Mech. Its Appl. 2017, 471, 436–444. [Google Scholar] [CrossRef]
- Han, J.; Zhang, J.; Wang, X.; Liu, Y.; Wang, Q.; Zhong, F. An Extended Car-Following Model Considering Generalized Preceding Vehicles in V2X Environment. Future Internet 2020, 12, 216. [Google Scholar] [CrossRef]
- Wen, J.; Wang, S.; Wu, C.; Xiao, X.; Lyu, N. A longitudinal velocity CF-MPC model for connected and automated vehicle platooning. IEEE Trans. Intell. Transp. Syst. 2022, 24, 6463–6476. [Google Scholar] [CrossRef]
- Wang, X.; Han, J.; Bai, C.; Shi, H.; Zhang, J.; Wang, G. Research on the Impacts of Generalized Preceding Vehicle Information on Traffic Flow in V2X Environment. Future Internet 2021, 13, 88. [Google Scholar] [CrossRef]
- Zhao, W.; Ngoduy, D.; Shepherd, S.; Liu, R.; Papageorgiou, M. A platoon based cooperative eco-driving model for mixed automated and human-driven vehicles at a signalised intersection. Transp. Res. Part Emerg. Technol. 2018, 95, 802–821. [Google Scholar] [CrossRef]
- Viadero-Monasterio, F.; Gutiérrez-Moizant, R.; Meléndez-Useros, M.; López Boada, M.J. Static output feedback control for vehicle platoons with robustness to mass uncertainty. Electronics 2024, 14, 139. [Google Scholar] [CrossRef]
- Bertoni, L.; Guanetti, J.; Basso, M.; Masoero, M.; Cetinkunt, S.; Borrelli, F. An adaptive cruise control for connected energy-saving electric vehicles. IFAC-PapersOnLine 2017, 50, 2359–2364. [Google Scholar] [CrossRef]
- Kim, Y.; Tay, S.; Guanetti, J.; Borrelli, F. Eco-driving with learning model predictive control. arXiv 2019, arXiv:1907.04990. [Google Scholar] [CrossRef]
- Kim, H.; Choi, E.Y.; Joa, E.; Lee, H.; Lim, L.; Moura, S.; Borrelli, F. Energy-Aware Lane Planning for Connected Electric Vehicles in Urban Traffic: Design and Vehicle-in-the-Loop Validation. arXiv 2025, arXiv:2503.23228. [Google Scholar]
- Viadero-Monasterio, F.; Meléndez-Useros, M.; Jiménez-Salas, M.; Boada, B.L. Robust Adaptive Control of Heterogeneous Vehicle Platoons in the Presence of Network Disconnections With a Novel String Stability Guarantee. IEEE Trans. Intell. Veh. 2025, 1–13. [Google Scholar] [CrossRef]
- Zhai, C.; Luo, F.; Liu, Y.; Chen, Z. Ecological cooperative look-ahead control for automated vehicles travelling on freeways with varying slopes. IEEE Trans. Veh. Technol. 2018, 68, 1208–1221. [Google Scholar] [CrossRef]
- Zhang, X.; Fang, S.; Shen, Y.; Yuan, X.; Lu, Z. Hierarchical velocity optimization for connected automated vehicles with cellular vehicle-to-everything communication at continuous signalized intersections. IEEE Trans. Intell. Transp. Syst. 2023, 25, 2944–2955. [Google Scholar] [CrossRef]
- Sharma, N.K.; Hamednia, A.; Murgovski, N.; Gelso, E.R.; Sjöberg, J. Optimal eco-driving of a heavy-duty vehicle behind a leading heavy-duty vehicle. IEEE Trans. Intell. Transp. Syst. 2020, 22, 7792–7803. [Google Scholar] [CrossRef]
- Lu, K.; Chen, Y.; Tong, Y.; Zhang, J.; Luo, Y.; Wang, J. Eco-driving control for CAVs at signalized intersections: Adapting to traffic uncertainties. Transp. Res. Part D Transp. Environ. 2024, 132, 104270. [Google Scholar] [CrossRef]
- Deshpande, S.R.; Jung, D.; Bauer, L.; Canova, M. Integrated approximate dynamic programming and equivalent consumption minimization strategy for eco-driving in a connected and automated vehicle. IEEE Trans. Veh. Technol. 2021, 70, 11204–11215. [Google Scholar] [CrossRef]
- Zhou, Q.; Du, C.; Yan, Y. A multi-layer predictive energy management strategy for intelligent hybrid electric trucks collaborated with eco-driving control. Energy 2024, 308, 132848. [Google Scholar] [CrossRef]
- Maino, C.; Misul, D.; Musa, A.; Spessa, E. Optimal mesh discretization of the dynamic programming for hybrid electric vehicles. Appl. Energy 2021, 292, 116920. [Google Scholar] [CrossRef]
- Shi, D.; Liu, S.; Cai, Y.; Wang, S.; Li, H.; Chen, L. Pontryagin’s minimum principle based fuzzy adaptive energy management for hybrid electric vehicle using real-time traffic information. Appl. Energy 2021, 286, 116467. [Google Scholar] [CrossRef]
- Yang, C.; Du, X.; Wang, W.; Yang, L.; Zha, M. A rolling convergent equivalent consumption minimization strategy for plug-in hybrid electric vehicles. IEEE Trans. Veh. Technol. 2023, 73, 3340–3353. [Google Scholar] [CrossRef]
- Li, L.; Wang, X.; Song, J. Fuel consumption optimization for smart hybrid electric vehicle during a car-following process. Mech. Syst. Signal Process. 2017, 87, 17–29. [Google Scholar] [CrossRef]
- Li, B.; Zhuang, W.; Zhang, H.; Zhao, R.; Liu, H.; Qu, L.; Zhang, J.; Chen, B. A comparative study of energy-oriented driving strategy for connected electric vehicles on freeways with varying slopes. Energy 2024, 289, 129916. [Google Scholar] [CrossRef]
- Wang, S.; Lin, X. Eco-driving control of connected and automated hybrid vehicles in mixed driving scenarios. Appl. Energy 2020, 271, 115233. [Google Scholar] [CrossRef]
- Xue, J.; Jiao, X.; Yu, D.; Zhang, Y. Predictive hierarchical eco-driving control involving speed planning and energy management for connected plug-in hybrid electric vehicles. Energy 2023, 283, 129058. [Google Scholar] [CrossRef]
- Hu, X.; Zhang, X.; Tang, X.; Lin, X. Model predictive control of hybrid electric vehicles for fuel economy, emission reductions, and inter-vehicle safety in car-following scenarios. Energy 2020, 196, 117101. [Google Scholar] [CrossRef]
- Dehkordi, S.G.; Larue, G.S.; Cholette, M.E.; Rakotonirainy, A.; Rakha, H.A. Ecological and safe driving: A model predictive control approach considering spatial and temporal constraints. Transp. Res. Part D Transp. Environ. 2019, 67, 208–222. [Google Scholar] [CrossRef]
- Hu, M.; Li, C.; Bian, Y.; Zhang, H.; Qin, Z.; Xu, B. Fuel economy-oriented vehicle platoon control using economic model predictive control. IEEE Trans. Intell. Transp. Syst. 2022, 23, 20836–20849. [Google Scholar] [CrossRef]
- Zhu, Z.; Gupta, S.; Gupta, A.; Canova, M. A deep reinforcement learning framework for eco-driving in connected and automated hybrid electric vehicles. IEEE Trans. Veh. Technol. 2023, 73, 1713–1725. [Google Scholar] [CrossRef]
- Viadero-Monasterio, F.; Meléndez-Useros, M.; Jiménez-Salas, M.; Boada, M.J.L. Fault-Tolerant Robust Output-Feedback Control of a Vehicle Platoon Considering Measurement Noise and Road Disturbances. IET Intell. Transp. Syst. 2025, 19, e70007. [Google Scholar] [CrossRef]
- Nie, Z.; Farzaneh, H. Real-time dynamic predictive cruise control for enhancing eco-driving of electric vehicles, considering traffic constraints and signal phase and timing (SPaT) information, using artificial-neural-network-based energy consumption model. Energy 2022, 241, 122888. [Google Scholar] [CrossRef]
- Chada, S.K.; Görges, D.; Ebert, A.; Teutsch, R.; Subramanya, S.P. Evaluation of the driving performance and user acceptance of a predictive eco-driving assistance system for electric vehicles. Transp. Res. Part C Emerg. Technol. 2023, 153, 104193. [Google Scholar] [CrossRef]
- Bian, Y.; Du, C.; Hu, M.; Li, S.E.; Liu, H.; Li, C. Fuel economy optimization for platooning vehicle swarms via distributed economic model predictive control. IEEE Trans. Autom. Sci. Eng. 2021, 19, 2711–2723. [Google Scholar] [CrossRef]
- Du, W.; Murgovski, N.; Ju, F.; Gao, J.; Zhao, S.; Zheng, Z. Real-time Eco-driving control with mode switching decisions for electric trucks with dual electric machine coupling propulsion. IEEE Trans. Veh. Technol. 2023, 72, 15477–15490. [Google Scholar] [CrossRef]
- Shieh, S.Y.; Ersal, T.; Peng, H. Pulse-and-glide operations for hybrid electric vehicles in the car-following scenario. IEEE Trans. Veh. Technol. 2023, 72, 9922–9937. [Google Scholar] [CrossRef]
- Wingelaar, B.; da Silva, G.R.G.; Lazar, M. Model predictive eco-driving control for heavy-duty trucks using branch and bound optimization. IEEE Trans. Intell. Transp. Syst. 2023, 24, 15178–15189. [Google Scholar] [CrossRef]
- Zhu, Z.; Gupta, S.; Pivaro, N.; Deshpande, S.R.; Canova, M. A GPU implementation of a look-ahead optimal controller for eco-driving based on dynamic programming. In Proceedings of the 2021 European Control Conference (ECC), Delft, The Netherlands, 29 June–2 July 2021; pp. 899–904. [Google Scholar]
- Viadero-Monasterio, F.; Meléndez-Useros, M.; Zhang, H.; Boada, B.L.; Boada, M.J.L. Signalized Traffic Management Optimizing Energy Efficiency Under Driver Preferences for Vehicles With Heterogeneous Powertrains. IEEE Trans. Consum. Electron. 2025, 71, 3454–3464. [Google Scholar] [CrossRef]
- Liu, C.Z.; Li, L.; Yong, J.W.; Muhammad, F.; Cheng, S.; Wang, X.Y.; Li, W.B. The bionics and its application in energy management strategy of plug-in hybrid electric vehicle formation. IEEE Trans. Intell. Transp. Syst. 2020, 22, 7860–7874. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Mohamed, R.; Jameel, M.; Abouhawwash, M. Nutcracker optimizer: A novel nature-inspired metaheuristic algorithm for global optimization and engineering design problems. Knowl.-Based Syst. 2023, 262, 110248. [Google Scholar] [CrossRef]
- Mitschke, M.; Wallentowitz, H. Dynamik der Kraftfahrzeuge; Springer: Berlin/Heidelberg, Germany, 1972; Volume 4. [Google Scholar]
- Ma, F.; Yang, Y.; Wang, J.; Liu, Z.; Li, J.; Nie, J.; Shen, Y.; Wu, L. Predictive energy-saving optimization based on nonlinear model predictive control for cooperative connected vehicles platoon with V2V communication. Energy 2019, 189, 116120. [Google Scholar] [CrossRef]
- Coppola, A.; Lui, D.G.; Petrillo, A.; Santini, S. Eco-driving control architecture for platoons of uncertain heterogeneous nonlinear connected autonomous electric vehicles. IEEE Trans. Intell. Transp. Syst. 2022, 23, 24220–24234. [Google Scholar] [CrossRef]
- Ma, F.; Yang, Y.; Wang, J.; Li, X.; Wu, G.; Zhao, Y.; Wu, L.; Aksun-Guvenc, B.; Guvenc, L. Eco-driving-based cooperative adaptive cruise control of connected vehicles platoon at signalized intersections. Transp. Res. Part D Transp. Environ. 2021, 92, 102746. [Google Scholar] [CrossRef]
- Treiber, M.; Hennecke, A.; Helbing, D. Congested traffic states in empirical observations and microscopic simulations. Phys. Rev. E 2000, 62, 1805. [Google Scholar] [CrossRef]
- Han, J.; Wang, X.; Wang, G. Modeling the Car-Following Behavior with Consideration of Driver, Vehicle, and Environment Factors: A Historical Review. Sustainability 2022, 14, 8179. [Google Scholar] [CrossRef]
- Han, J.; Shi, H.; Chen, L.; Li, H.; Wang, X. The Car-Following Model and Its Applications in the V2X Environment: A Historical Review. Future Internet 2022, 14, 14. [Google Scholar] [CrossRef]
- Mayne, D.Q.; Rawlings, J.B.; Rao, C.V.; Scokaert, P.O. Constrained model predictive control: Stability and optimality. Automatica 2000, 36, 789–814. [Google Scholar] [CrossRef]
- Guo, L.; Gao, B.; Gao, Y.; Chen, H. Optimal energy management for HEVs in eco-driving applications using bi-level MPC. IEEE Trans. Intell. Transp. Syst. 2016, 18, 2153–2162. [Google Scholar] [CrossRef]
- Liu, Y.; Huang, Z.; Li, J.; Ye, M.; Zhang, Y.; Chen, Z. Cooperative optimization of velocity planning and energy management for connected plug-in hybrid electric vehicles. Appl. Math. Model. 2021, 95, 715–733. [Google Scholar] [CrossRef]



| Component | Parameter | Value |
|---|---|---|
| Engine | Maximum power (kw) | 63 |
| Maximum torque (N·m) | 145 | |
| Motor | Maximum power (kw) | 49 |
| Maximum torque (N·m) | 250 | |
| Transmission | Final transmission ratio | 4.55 |
| AMT transmission ratio | [3.79 2.17 1.41 1.00 0.86] | |
| Battery pack | Maximum battery capacity (Ah) | 13 |
| Nominal voltage (V) | 288 |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| (m/s2) | 2 | (m/s) | 30 |
| (m/s) | 3 | (s) | 1.5 |
| (m/s2) | 3 | 0.2 | |
| 0.1 |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Vehicle Mass m (kg) | 1500 | Air Resistance Coefficient | 0.44 |
| Frontal Area A (m2) | 2.66 | Air Density (kg/m3) | 1.206 |
| Road Slope (°) | 0 | Road Resistance Coefficient | 0.0125 |
| Tire Radius (m) | 0.343 | Sampling Time (s) | 0.1 |
| Transmission Efficiency (%) | 90 | Control Horizon | 1 |
| Initial | 0.75 | Prediction Horizon | 10 |
| (m/s) | 90 | (m/s) | 30 |
| (m/s2) | 2 | (m/s3) | 1.5 |
| (m/s2) | −3 | (m/s3) | −1.5 |
| Driving Cycle | Time (s) | Average Velocity (m/s) | Maximum Velocity (m/s) | Mileage (km) |
|---|---|---|---|---|
| UDDS | 1370 | 8.8 | 25.3 | 12.0 |
| HWFET | 765 | 21.5 | 26.8 | 16.5 |
| Parameter | Description | Value |
|---|---|---|
| The highest SoC allowed | 0.7 | |
| The lowest SoC allowed | 0.5 | |
| The threshold of velocity | 4 m/s | |
| The threshold factor for the ICE to charge | 0.5 | |
| The charging factor | 50 | |
| The threshold factor for the ICE to shut off | 0.2 | |
| The discharging factor | 0.2 |
| Algorithm | Driving Cycle | Fuel Consumption (g) | Equivalent Energy Consumption (g) | SoC (%) | Average Running Time (ms) |
|---|---|---|---|---|---|
| Algorithm 1 | UDDS | 378.5 | 379.7 | 72.1 | - |
| Algorithm 2 | 310.8 (−17.9%) | 333.0 (−12.3%) | 65.1 (−9.7%) | 385 | |
| Algorithm 3 | 300.1 (−20.7%) | 301.1 (−20.7%) | 72.3 (+0.3%) | 422 | |
| Algorithm 1 | HWFET | 635.1 | 638.4 | 72.7 | - |
| Algorithm 2 | 624.5 (−1.7%) | 624.6 (−2.2%) | 74.5 (+2.5%) | 398 | |
| Algorithm 3 | 605.7 (−4.6%) | 603.0 (−5.5%) | 77.5 (+6.6%) | 430 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lv, Z.; Chen, T.; Han, J.; Feng, K.; Shen, C.; Wang, X.; Wang, J.; Wang, Q.; Chen, L.; Zhang, H.; et al. A Cooperative Car-Following Eco-Driving Strategy for a Plug-In Hybrid Electric Vehicle Platoon in the Connected Environment. Vehicles 2025, 7, 111. https://doi.org/10.3390/vehicles7040111
Lv Z, Chen T, Han J, Feng K, Shen C, Wang X, Wang J, Wang Q, Chen L, Zhang H, et al. A Cooperative Car-Following Eco-Driving Strategy for a Plug-In Hybrid Electric Vehicle Platoon in the Connected Environment. Vehicles. 2025; 7(4):111. https://doi.org/10.3390/vehicles7040111
Chicago/Turabian StyleLv, Zhenwei, Tinglin Chen, Junyan Han, Kai Feng, Cheng Shen, Xiaoyuan Wang, Jingheng Wang, Quanzheng Wang, Longfei Chen, Han Zhang, and et al. 2025. "A Cooperative Car-Following Eco-Driving Strategy for a Plug-In Hybrid Electric Vehicle Platoon in the Connected Environment" Vehicles 7, no. 4: 111. https://doi.org/10.3390/vehicles7040111
APA StyleLv, Z., Chen, T., Han, J., Feng, K., Shen, C., Wang, X., Wang, J., Wang, Q., Chen, L., Zhang, H., & Jiang, Y. (2025). A Cooperative Car-Following Eco-Driving Strategy for a Plug-In Hybrid Electric Vehicle Platoon in the Connected Environment. Vehicles, 7(4), 111. https://doi.org/10.3390/vehicles7040111








