Optimization of Operations in Bus Company Service Workshops Using Queueing Theory
Abstract
1. Introduction
2. Materials and Methods
- -
- Arrival of users,
- -
- Queue of waiting users,
- -
- Service,
- -
- Departure of users.
- -
- Single-server queueing system,
- -
- Multi-server queueing system,
- -
- Closed queueing system,
- -
- Multi-server closed queueing system.
- The probability Pn(t) depends on the length of the time interval and the number of Arrivals
- The probability Pn(t) is independent of the number of arrivals before the time interval t,
- In a sufficiently small time interval, two or more arrivals cannot occur simultaneously.
- Utilization factor per server:
- Utilization factor of the system:
- The probability that there are no users in the system:
- Probability that there are n users in the system:
- Average number of users being served:
- Average number of users waiting for service:
- Average number of users in the system (waiting + being served):
- Average waiting time of a user before service:
- Average time a user spends in the system (waiting + being served):
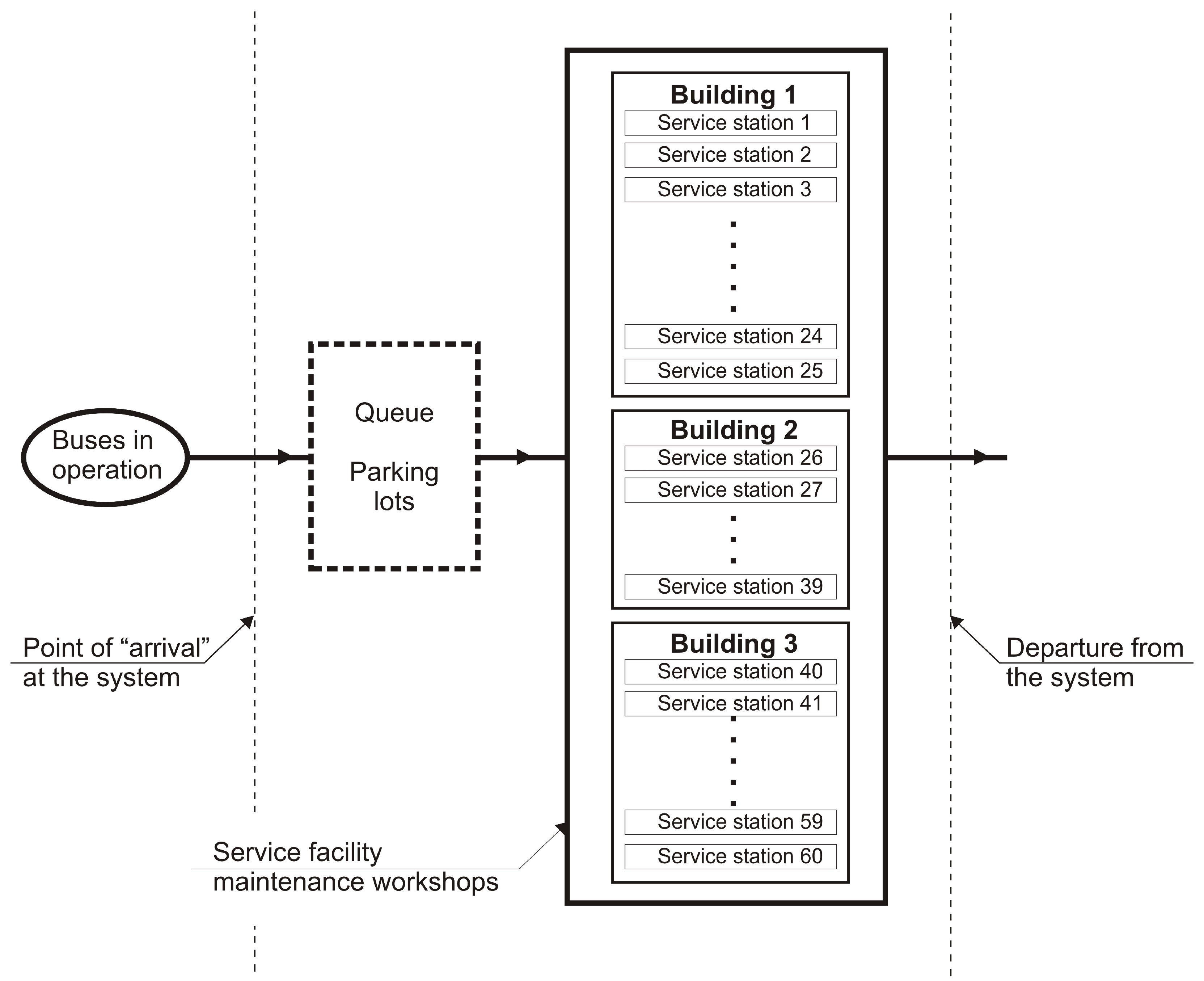
3. Results—Solving a Real-World Case of Queueing Theory in the Bus Company’s Maintenance Workshops
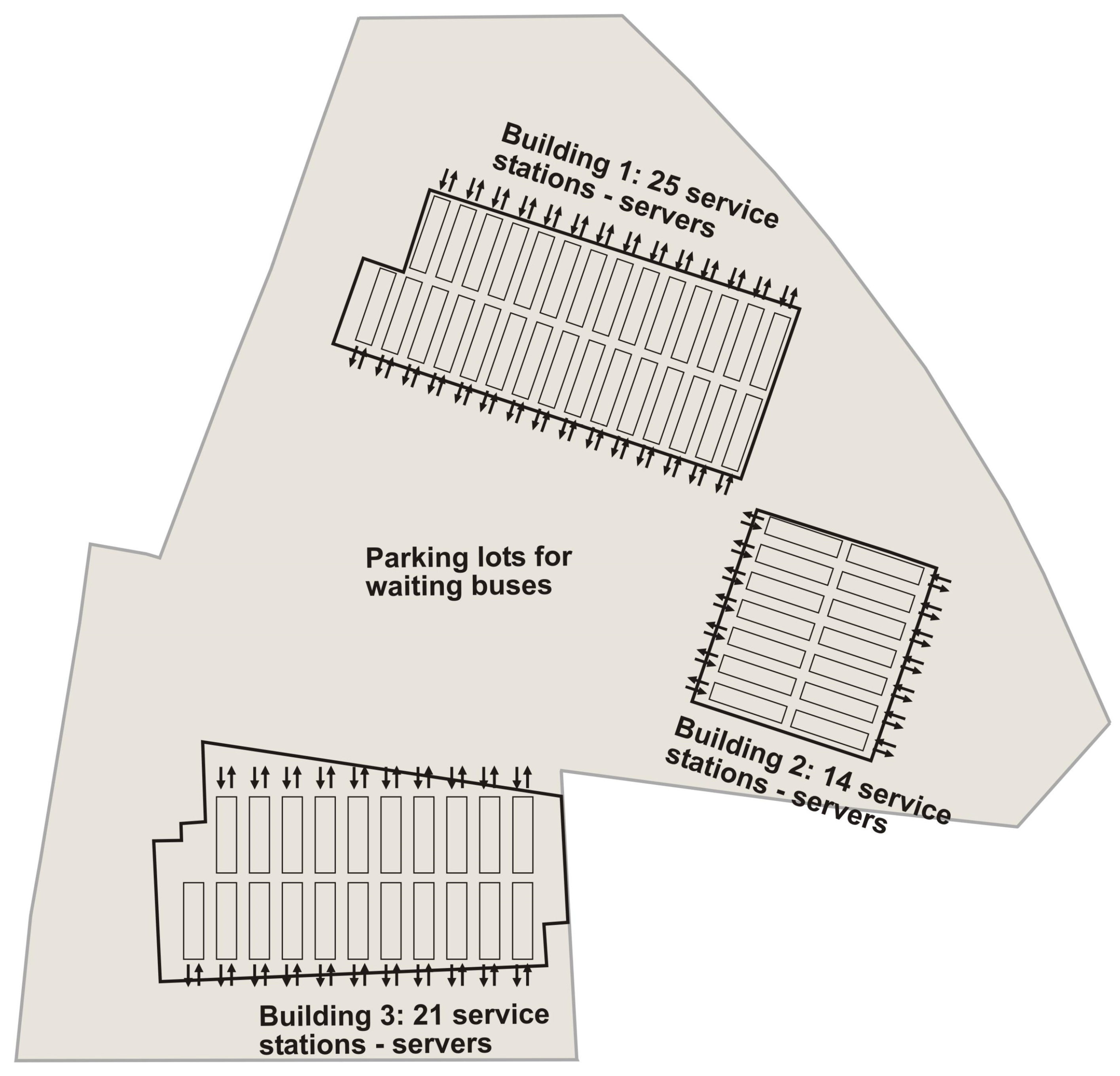
3.1. Problem Description
3.2. Analysis of the Current Situation
- Number of service stations (servers): k = 60
- Number of workers per service station: d = 2
- Number of company buses: m = 220
- Number of city buses: m1 = 57
- Number of suburban or intercity buses: m2 = 163
- Number of working hours required for the maintenance, servicing, and repair of a city bus: hd1 = 1350 h/year
- Number of working hours required for the maintenance, servicing, and repair of a suburban or intercity bus: hd2 = 950 h/year
- Average number of visits for company buses: λd = 65 visits/day
- Workshop working hours: td = 12 h/day
- Number of working hours performed for external clients: hdz = 60,000 h/year
- Number of working days per year: l = 252 days
- Profit loss if a bus is out of service: j = 580 EUR/day
- Average number of working hours per bus:
- Average number of hours a bus spends on maintenance, servicing, and repair in the workshops:
- Number of workshop hours occupied by 220 in-house buses:
- Service time per one bus visit:
- Number of working hours completed in the workshops in one year:
- Arrival rate (for internal and external buses):
- Service rate (service intensity) per service station (server):
- Service factor per service station: ρ = 48.16
- System service factor: ρ* = 0.802
- Average number of buses waiting for service: Q = 0.268
- The average number of buses currently being serviced: S = 48.135
- Average number of buses in the system: T = 48.403
- Average waiting time for service: W* = 2 min, 22 s
- Average time a customer (bus) spends in the system (waiting + service): W = 7 h, 5 min, 48 s
- Utilization of working time:
- If one bus operates on average 16 h a day, the loss of profit for one bus per hour is: 580/16 = 36.25 EUR. Based on this, the loss of profit can be calculated if there are on average S = 48.1353 buses in the service workshops with an average W = 7.058 h.
3.3. Analysis of the Future State with Possible Solutions
- Arrival rate (for internal and external buses): λ = 81.83 visits/day
- Service rate (service intensity) per service station: μ = 1.7 visits/day
- Number of service stations in the queuing system: k = 39
- Calculation of the system service factor:
- Increase μ by increasing the number of working hours per day,
- Reduce λ by not accounting for the 60,000 working hours performed for external clients. The workshops will service and repair only domestic buses.
- Increase the productivity of the worker. This reduces the annual number of standard working hours required for repairs, servicing, and maintenance of the bus (which is not recommended as it may reduce the safety of the completed work),
- Combine individual operations in servicing or repairing buses at each service station. This allows multiple workers to perform different tasks simultaneously at each service station, thereby reducing the time the bus spends in the service workshops.
3.3.1. Increase in the Number of Working Hours per Day
- Arrival rate (for internal and external buses): λ = 81.83 visits/day
- Service rate (service intensity) per service station:
- Number of service stations (servers) in the queuing system: k = 39
3.3.2. Workshops Serve Only Domestic Buses
3.3.3. Increasing the Productivity of the Service Station (Server)
- Number of service stations (servers): k = 39
- Number of workers per service station: d = 2
- Number of company buses: m = 220
- Number of city buses: m1 = 57
- Number of suburban or intercity buses: m2 = 163
- Workshop working hours: td = 12 h/day
- Number of working hours performed for external clients: hdz = 60,000 h/year
- Number of working days per year: l = 252 days
- Profit loss if a bus is out of service: j = 580 EUR/day
4. Discussion
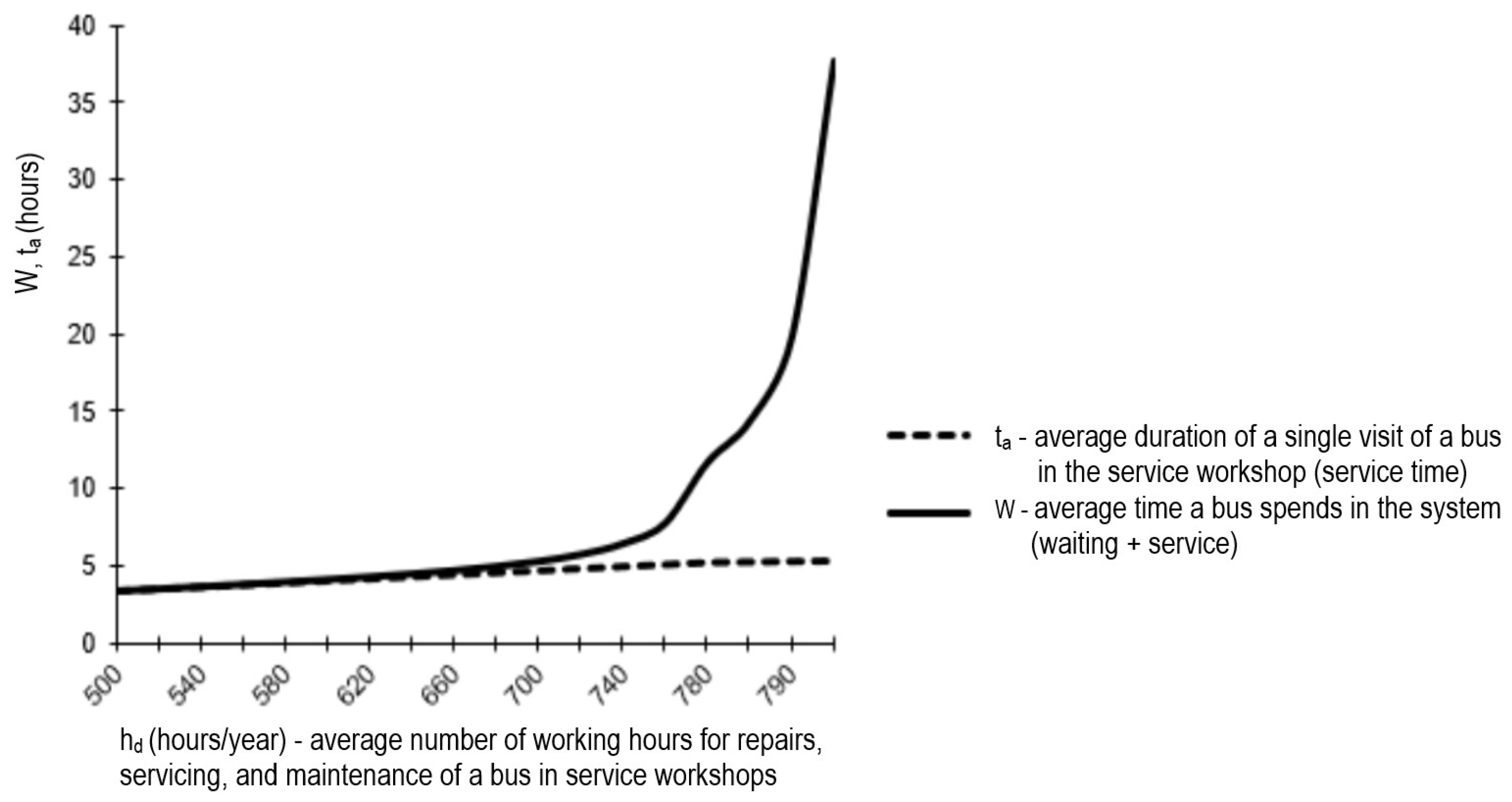
- A high utilization of working hours does not necessarily lead to the best solution, as high utilization also increases waiting times for service (see Table 2 and Table 3). From this perspective, the first solution (increasing the number of working hours per day) is better than the second (servicing only internal buses).
- The second solution, in which the company forfeits 60,000 working hours per year due to workshop downsizing (cost reduction), is not optimal. Why should workshops not also serve external clients if there is demand?
- If the value of the system service factor ρ* is close to 1, even a small reduction in service time (ta) significantly reduces the waiting time for a bus to receive service. Therefore, it is more reasonable to optimize the service station workflow.
- In the case of merging service operations at individual service stations, the throughput of the queuing system increases, and as a result, profit losses due to buses being out of service decrease.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Savsar, J. Modeling and simulation of maintenance operations at Kuwait public transport company. Kuwait J. Sci. 2013, 40, 115–129. [Google Scholar]
- Hangani, A.; Shafahi, Y. Bus maintenance systems and maintenance scheduling: Model formulations and solutions. Transp. Res. Part A Policy Pract. 2002, 36, 453–482. [Google Scholar] [CrossRef]
- Maze, T.H.; Cook, A.R. Theory and Practice of Transit Bus Maintenance Performance Measurement. Transp. Res. Rec. 1987, 1140, 18–29. [Google Scholar]
- Landowski, B. Method of modelling operation and maintenance processes in public transport systems using a certain class of stochastic processes. MATEC Web Conf. 2021, 332, 01005. [Google Scholar] [CrossRef]
- Xu, J.; Qiao, Q.; Wu, R.; Zhou, Z. Advanced maintenance cycle optimization of urban rail transit vehicles. Adv. Mech. Eng. 2019, 11, 1687814019827113. [Google Scholar] [CrossRef]
- Buyukkaramikli, N.; Ooijen, H.; Bertrand, J. Integrating inventory control and capacity management at a maintenance service provider. Ann. Oper. Res. 2015, 231, 185–206. [Google Scholar] [CrossRef]
- Han, Q.T.; Cao, W.J.; Zhang, Y. Research on Maintenance Resources Distribution Based on Queuing Theory. Appl. Mech. Mater. 2012, 239–240, 1428–1431. [Google Scholar] [CrossRef]
- Bebic, D.; Stazic, L.; Komar, I. Ships Shore Service Optimization Using the Queueing Theory. Int. J. Simul. Model. 2019, 18, 596–607. [Google Scholar] [CrossRef]
- Antoniol, G.; Cimitile, A.; Di Lucca, G.A.; Di Penta, M. Assessing staffing needs for a software maintenance project through queuing simulation. IEEE Trans. Softw. Eng. 2004, 30, 43–58. [Google Scholar] [CrossRef]
- Son, J. Developing a model for estimating delays at two-lane highway work zones. KSCE J. Civ. Eng. 1999, 3, 81–88. [Google Scholar] [CrossRef]
- Cassidy, M.J.; Haan, L.D. Proposed Model for Predicting Motorist Delays at Two-Lane Highway Work Zones. J. Transp. Eng. 1993, 119, 27–42. [Google Scholar] [CrossRef]
- Sihotang, E.; Sugito; Mustafid; Ispriyanti, D.; Prahutama, A.; Rachman, A. Analysis of queue and performance of automatic toll booths with a normal distribution (case study: Automatic booths toll gate muktiharjo). J. Phys. Conf. Ser. 2020, 1524, 012093. [Google Scholar] [CrossRef]
- Petrović, A.; Nikolić, M.; Bugarić, U.; Delibašić, B.; Lio, P. Controlling highway toll stations using deep learning, queuing theory, and differential evolution. Eng. Appl. Artif. Intell. 2023, 119, 105683. [Google Scholar] [CrossRef]
- Zahedieh, F.; Lee, C. Impacts of a Toll Information Sign and Toll Lane Configuration on Queue Length and Collision Risk at a Toll Plaza with a High Percentage of Heavy Vehicles. Vehicles 2024, 6, 1249–1267. [Google Scholar] [CrossRef]
- Wang, T.; Huang, L.; Tian, J.; Zhang, J.; Yuan, Z.; Zheng, J. Bus dwell time estimation and overtaking maneuvers analysis: A stochastic process approach. Transp. Res. Part E Logist. Transp. Rev. 2024, 186, 103577. [Google Scholar] [CrossRef]
- Yongzheng, K.; Aixin, C.; Zhen, Z. Optimization Research of Bus Stops that Are Based on Berths. In Proceedings of the 2015 International Conference on Electrical and Information Technologies for Rail Transportation; Lecture Notes in Electrical Engineering; Springer: Berlin/Heidelberg, Germany, 2016; Volume 378. [Google Scholar] [CrossRef]
- Wang, C.; Chen, W.; Xu, Y.; Ye, Z. Modeling Bus Capacity for Bus Stops Using Queuing Theory and Diffusion Approximation. Transp. Res. Rec. J. Transp. Res. Board 2021, 1524, 012093. [Google Scholar] [CrossRef]
- Sun, F.; Sun, L.; Sun, S.; Wang, D. Study on the Calculation Models of Bus Delay at Bays Using Queueing Theory and Markov Chain. Comput. Intell. Neurosci. 2015, 2015, 750304. [Google Scholar] [CrossRef]
- Liu, Z.; Ma, X.; Zhou, S.; Liu, X. Optimizing shared charging services at sustainable bus charging hubs: A queue theory integration approach. Renew. Energy 2024, 237, 121860. [Google Scholar] [CrossRef]
- Chen, W.; Qui, K.; Zhang, S.; Zhou, J.; Zhang, W. Queuing theory guided performance evaluation and energy optimization for a reconfigurable high speed device interconnected bus. Sustain. Comput. Inform. Syst. 2019, 22, 179–190. [Google Scholar] [CrossRef]
- Meng, F.; Pei, W.; Zhang, Q.; Zhang, Y.; Ma, B.; Li, L. Research on the capacity of charging stations based on queuing theory and energy storage scheduling optimization sharing strategy. J. Energy Storage 2024, 96, 112673. [Google Scholar] [CrossRef]
- Najafi, A.; Gao, K.; Parishwad, O.; Tsaousoglou, G.; Jin, S.; Yi, W. Integrated optimization of charging infrastructure, electric bus scheduling and energy systems. Transp. Res. Part D Transp. Environ. 2025, 141, 104664. [Google Scholar] [CrossRef]
- Pourvaziri, H.; Sarhadi, H.; Azad, N.; Afshari, H.; Taghavi, M. Planning of electric vehicle charging stations: An integrated deep learning and queueing theory approach. Transp. Res. Part E Logist. Transp. Rev. 2024, 186, 103568. [Google Scholar] [CrossRef]
- Wu, H.; Calderon, A.D. A Study on the Construction of Charging Stations on Freeways Using a Road Section Power Consumption Model. In Proceedings of the 8th International Conference on Green Energy and Applications (ICGEA), Singapore, 14–16 March 2024; pp. 72–79. [Google Scholar] [CrossRef]
- Kumar, N.; Kumar, T.; Nema, S.; Thakur, T. A comprehensive planning framework for electric vehicles fast charging station assisted by solar and battery based on Queueing theory and non-dominated sorting genetic algorithm-II in a co-ordinated transportation and power network. J. Energy Storage 2022, 49, 104180. [Google Scholar] [CrossRef]
- Saldarini, A.; Miraftabzadeh, S.M.; Brenna, M.; Longo, M. Strategic Approach for Electric Vehicle Charging Infrastructure for Efficient Mobility along Highways: A Real Case Study in Spain. Vehicles 2023, 5, 761–779. [Google Scholar] [CrossRef]
- Varshney, S.; Panda, K.P.; Gupta, G.; Shah, M.; Srinivas, B.A.; Bajaj, M.; Blazek, V.; Prokop, L. Stochastic modeling of electric vehicle infrastructure using queueing-theoretical approach. Results Eng. 2025, 25, 104149. [Google Scholar] [CrossRef]
- Sun, L.; Song, R. Improving Efficiency in Congested Traffic Networks: Pareto-Improving Reservations through Agent-Based Timetabling. Sustainability 2022, 14, 2211. [Google Scholar] [CrossRef]
- Wang, X.; Wu, X.; Liu, J. Optimization Models of Actuated Control Considering Vehicle Queuing for Sustainable Operation. Sustainability 2022, 14, 8998. [Google Scholar] [CrossRef]
- Wang, W.; Ji, Y.; Zhao, Z.; Yin, H. Simulation Optimization of Station-Level Control of Large-Scale Passenger Flow Based on Queueing Network and Surrogate Model. Sustainability 2024, 16, 7502. [Google Scholar] [CrossRef]
- Jia, W.; Huang, Y.; Zhao, Q.; Qi, Y. Modeling taxi drivers’ decisions at airport based on queueing theory. Res. Transp. Econ. 2022, 92, 101093. [Google Scholar] [CrossRef]
- Yang, M. Security Check Model Based on Queuing Theory. In Proceedings of the 7th International Conference on Education, Management, Information and Computer Science (ICEMC 2017), Shenyang, China, 16–18 June 2017. [Google Scholar] [CrossRef][Green Version]
- Wen, S.W.; Tang, T.Q.; Zhang, J.; Qin, M.X.; Huang, H.J. Information-based taxi-passenger matching management in transportation hubs: A double-ended queuing perspective. Transp. Res. Part E Logist. Transp. Rev. 2025, 197, 104096. [Google Scholar] [CrossRef]
- Król, A.; Król, M. A Stochastic Simulation Model for the Optimization of the Taxi Management System. Sustainability 2019, 11, 3838. [Google Scholar] [CrossRef]
- Flesser, M.; Shalaby, A.; Friedrich, B. Integration of urban aerial cable cars into public transit: Operational capacity limits due to passenger queuing at stations. J. Public Transp. 2024, 26, 100094. [Google Scholar] [CrossRef]
- Drent, M.; Arts, J. Expediting in Two-Echelon Spare Parts Inventory Systems. Manuf. Serv. Oper. Manag. 2020, 23, 6. [Google Scholar] [CrossRef]
- Ademujimi, T.; Prabhu, V. Model-Driven Bayesian Network Learning for Factory-Level Fault Diagnostics and Resilience. Sustainability 2024, 16, 513. [Google Scholar] [CrossRef]
- Larson, R.C.; Odoni, A.R. Urban Operations Research. Prentice-Hall, New York 1981, Massachusetts Institute of Technology. Available online: https://web.mit.edu/urban_or_book/www/book/ (accessed on 11 April 2025).
- Benjamin, J.R.; Cornell, C.A. Probability, Statistics and Decision for Civil Engineers; McGraw-Hill, Cop.: New York, NY, USA, 1970. [Google Scholar]
- Bronson, R. Schaum’s Outline of Theory and Problems of Operations Research; McGraw-Hill, Cop.: New York, NY, USA, 1982. [Google Scholar]
- Pauše, Ž. Vjerojatnost (Informacija, Stohastični Procesi); Školska Knjiga: Zagreb, Croatia, 1985. [Google Scholar]
- Petrić, J.; Šarenac, L.; Kojić, Z. Operaciona Istraživanja II (Zbirka Rešenih Zadataka); Naučna Knjiga: Beograd, Serbia, 1984. [Google Scholar]

| ρ= | 48.13529 | ||||||
| ρ*= | 0.802254 | ||||||
| n | n! | ρn | (ρn)/n! | Pn | n.Pn | ||
| 0 | 1 | 1 | 1 | 1.29152× 10−16 | 0 | ||
| 1 | 1 | 1 | 1 | 1.29152 × 10−16 | 0 | ||
| 2 | 1 | 36.2079646 | 36.2079646 | 4.67632 × 10−15 | 4.67632 × 10−15 | ||
| 3 | 2 | 1311.016701 | 655.5083503 | 8.46599 × 10−14 | 1.6932 × 10−13 | ||
| 4 | 6 | 47,469.24629 | 7911.541048 | 1.02179 × 10−12 | 3.06536 × 10−12 | ||
| 5 | 24 | 1,718,764.789 | 71,615.19955 | 9.24922 × 10−12 | 3.69969 × 10−11 | ||
| 6 | 120 | 62,232,974.65 | 518,608.1221 | 6.69791 × 10−11 | 3.34895 × 10−10 | ||
| 7 | 720 | 2,253,329,343 | 3,129,624.088 | 4.04196 × 10−10 | 2.42518 × 10−9 | ||
| 8 | 5040 | 81,588,469,092 | 16,188,188.31 | 2.09073 × 10−9 | 1.46351 × 10−8 | ||
| 9 | 40,320 | 2.95415 × 1012 | 73,267,668.67 | 9.46263 × 10−9 | 7.57011 × 10−8 | ||
| 10 | 362,880 | 1.06964 × 1014 | 294,763,683.7 | 3.80692 × 10−8 | 3.42623 × 10−7 | ||
| 11 | 3,628,800 | 3.87294 × 1015 | 1,067,279,303 | 1.37841 × 107 | 1.37841 × 10−6 | ||
| 12 | 39,916,800 | 1.40231 × 1017 | 3,513,091,928 | 4.53721 × 10−7 | 4.99093 × 10−6 | ||
| 13 | 479,001,600 | 5.07749× 1018 | 10,600,159,015 | 1.36903 × 10−6 | 1.64283 × 10−5 | ||
| 14 | 6,227,020,800 | 1.83846× 1020 | 29,523,860,185 | 3.81305 × 10−6 | 4.95697 × 10−5 | ||
| 15 | 8.7178 × 1010 | 6.65668 × 1021 | 76,357,063,177 | 9.86163 × 10−6 | 0.000138063 | ||
| 16 | 1.3077 × 1012 | 2.41025 × 1023 | 1.84316 × 1011 | 2.38046 × 10−5 | 0.00035707 | ||
| 17 | 2.0923 × 1013 | 8.72702 × 1024 | 4.17106 × 1011 | 5.38699 × 10−5 | 0.000861918 | ||
| 18 | 3.5569 × 1014 | 3.15988 × 1026 | 8.88385 × 1011 | 0.000114736 | 0.001950518 | ||
| 19 | 6.4024 × 1015 | 1.14413 × 1028 | 1.78703 × 1012 | 0.000230798 | 0.00415437 | ||
| 20 | 1.2165 × 1017 | 4.14265 × 1029 | 3.40552 × 1012 | 0.000439828 | 0.008356738 | ||
| 21 | 2.4329 × 1018 | 1.49997 × 1031 | 6.16535 × 1012 | 0.000796264 | 0.015925289 | ||
| 22 | 5.1091 × 1019 | 5.43108 × 1032 | 1.06302 × 1013 | 0.00137291 | 0.028831115 | ||
| 23 | 1.124 × 1021 | 1.96648 × 1034 | 1.74954 × 1013 | 0.002259558 | 0.049710285 | ||
| 24 | 2.5852 × 1022 | 7.12024 × 1035 | 2.75423 × 1013 | 0.003557131 | 0.081814011 | ||
| 25 | 6.2045 × 1023 | 2.57809 × 1037 | 4.15521 × 1013 | 0.00536652 | 0.12879647 | ||
| 26 | 1.5511 × 1025 | 9.33475 × 1038 | 6.01807 × 1013 | 0.00777243 | 0.194310751 | ||
| 27 | 4.0329 × 1026 | 3.37992 × 1040 | 8.38085 × 1013 | 0.010823995 | 0.281423872 | ||
| 28 | 1.0889 × 1028 | 1.2238 × 1042 | 1.1239 × 1014 | 0.014515364 | 0.39191483 | ||
| 29 | 3.0489 × 1029 | 4.43114 × 1043 | 1.45336 × 1014 | 0.018770421 | 0.525571789 | ||
| 30 | 8.8418 × 1030 | 1.60442 × 1045 | 1.8146 × 1014 | 0.023435819 | 0.67963874 | ||
| 31 | 2.6525 × 1032 | 5.80929 × 1046 | 2.1901 × 1014 | 0.028285443 | 0.848563291 | ||
| 32 | 8.2228 × 1033 | 2.10343 × 1048 | 2.55803 × 1014 | 0.033037365 | 1.02415832 | ||
| 33 | 2.6313 × 1035 | 7.61608 × 1049 | 2.89441 × 1014 | 0.037381742 | 1.196215749 | ||
| 34 | 8.6833 × 1036 | 2.75763 × 1051 | 3.17578 × 1014 | 0.041015661 | 1.353516797 | ||
| 35 | 2.9523 × 1038 | 9.98481 × 1052 | 3.38201 × 1014 | 0.043679223 | 1.485093584 | ||
| 36 | 1.0333 × 1040 | 3.6153 × 1054 | 3.49874 × 1014 | 0.045186736 | 1.581535762 | ||
| 37 | 3.7199 × 1041 | 1.30903 × 1056 | 3.51895 × 1014 | 0.045447771 | 1.636119739 | ||
| 38 | 1.3764 × 1043 | 4.73971 × 1057 | 3.44362 × 1014 | 0.044474899 | 1.645571267 | ||
| 39 | 5.2302 × 1044 | 1.71615 × 1059 | 3.28122 × 1014 | 0.042377515 | 1.610345573 | ||
| 39 | 2.0398 × 1046 | 6.21384 × 1060 | 3.04632 × 1014 | 0.039343681 | 1.534403565 | ||
| ∑ | 2.094 × 1046 | 6.39033 × 1060 | 3.79228 × 1015 | 0.489779171 | 16.30935228 | ||
| Q= | 7.1269197 | ||||||
| S= | 36.207964 | ||||||
| T= | 43.334884 | ||||||
| W* | 0.0870942 | ||||||
| W= | 0.5295720 |
| hd | h | h220 | ta | hdl | λ | μ | ρ* | Cp (%) | Ct (%) |
|---|---|---|---|---|---|---|---|---|---|
| 500 | 250 | 55,000 | 3.3578 | 170,000 | 100.455 | 3.5738 | 0.7207 | 110.72 | 52.5437 |
| 520 | 260 | 57,200 | 3.4921 | 174,400 | 99.0909 | 3.4364 | 0.7394 | 102.615 | 50.6454 |
| 540 | 270 | 59,400 | 3.6264 | 178,800 | 97.8283 | 3.3091 | 0.758 | 95.1111 | 48.7472 |
| 560 | 280 | 61,600 | 3.7607 | 183,200 | 96.6558 | 3.1909 | 0.7767 | 88.1429 | 46.8489 |
| 580 | 290 | 63,800 | 3.895 | 187,600 | 95.5643 | 3.0809 | 0.7953 | 81.6552 | 44.9506 |
| 600 | 300 | 66,000 | 4.0293 | 192,000 | 94.5455 | 2.9782 | 0.814 | 75.6 | 43.0524 |
| 620 | 310 | 68,200 | 4.1636 | 196,400 | 93.5924 | 2.8821 | 0.8327 | 69.9355 | 41.1541 |
| 640 | 320 | 70,400 | 4.2979 | 200,800 | 92.6989 | 2.792 | 0.8513 | 64.625 | 39.2559 |
| 660 | 330 | 72,600 | 4.4322 | 205,200 | 91.8595 | 2.7074 | 0.87 | 59.6364 | 37.3576 |
| 680 | 340 | 74,800 | 4.5665 | 209,600 | 91.0695 | 2.6278 | 0.8886 | 54.9412 | 35.4594 |
| 700 | 350 | 77,000 | 4.7009 | 214,000 | 90.3247 | 2.5527 | 0.9073 | 50.5143 | 33.5611 |
| 720 | 360 | 79,200 | 4.8352 | 218,400 | 89.6212 | 2.4818 | 0.9259 | 46.3333 | 31.6629 |
| 740 | 370 | 81,400 | 4.9695 | 222,800 | 88.9558 | 2.4147 | 0.9446 | 42.3784 | 29.7646 |
| 760 | 380 | 83,600 | 5.1038 | 227,200 | 88.3254 | 2.3512 | 0.9632 | 38.6316 | 27.8664 |
| 780 | 390 | 85,800 | 5.2381 | 231,600 | 87.7273 | 2.2909 | 0.9819 | 35.0769 | 25.9681 |
| 785 | 393 | 86,350 | 5.2717 | 232,700 | 87.5825 | 2.2763 | 0.9866 | 34.2166 | 25.4935 |
| 790 | 395 | 86,900 | 5.3053 | 233,800 | 87.4396 | 2.2619 | 0.9912 | 33.3671 | 25.019 |
| 795 | 398 | 87,450 | 5.3388 | 234,900 | 87.2985 | 2.2477 | 0.9959 | 32.5283 | 24.5444 |
| 799 | 400 | 87,890 | 5.3657 | 235,780 | 87.1868 | 2.2364 | 0.9996 | 31.8648 | 24.1648 |
| 800 | 400 | 88,000 | 5.3724 | 236,000 | 87.1591 | 2.2336 | 1.0005 | 31.7 | 24.0699 |
| 1054 | 527 | 101,159 | 7.0755 | 291,792 | 81.8254 | 1.696 | 1.2371 | 0 | 0 |
| hd | hd1 | hd2 | Q | S | T | W* | W | h | J |
|---|---|---|---|---|---|---|---|---|---|
| 500 | 640.6606 | 450.8352 | 0.0893 | 28.1084 | 28.1978 | 0.0106 | 3.368 | 0.7207 | 3471.19 |
| 520 | 666.287 | 468.8686 | 0.1374 | 28.8385 | 28.9739 | 0.0166 | 3.5087 | 0.7393 | 3715.293 |
| 540 | 691.9134 | 486.9021 | 0.2078 | 29.584 | 29.7721 | 0.0254 | 3.6519 | 0.785 | 3973.445 |
| 560 | 717.5399 | 504.9355 | 0.3096 | 30.291 | 30.6007 | 0.0384 | 3.7991 | 0.7766 | 4248.655 |
| 580 | 743.1663 | 522.9689 | 0.4563 | 31.0192 | 31.4756 | 0.0573 | 3.9532 | 0.7953 | 4546.366 |
| 600 | 768.7927 | 541.0023 | 0.666 | 31.7468 | 32.4129 | 0.0845 | 4.1139 | 0.814 | 4873.141 |
| 620 | 794.4191 | 559.0357 | 0.9657 | 32.4736 | 33.4394 | 0.1238 | 4.2874 | 0.8328 | 5239.491 |
| 640 | 820.0456 | 577.0691 | 1.373 | 33.2015 | 34.5989 | 0.1808 | 4.4788 | 0.8513 | 5663.221 |
| 660 | 845.672 | 595.1025 | 2.025 | 33.929 | 35.954 | 0.2643 | 4.6963 | 0.8699 | 6171.386 |
| 680 | 871.2984 | 613.1359 | 2.9566 | 34.6561 | 37.6128 | 0.3895 | 4.9561 | 0.8886 | 6812.587 |
| 700 | 896.9248 | 631.1693 | 4.3892 | 35.3839 | 39.7732 | 0.5831 | 5.284 | 0.9072 | 7680.474 |
| 720 | 922.5513 | 649.2027 | 6.7132 | 36.1113 | 42.8245 | 0.8988 | 5.734 | 0.9259 | 8974.025 |
| 740 | 948.1777 | 667.2361 | 10.8515 | 36.8392 | 47.6907 | 1.4638 | 6.4334 | 0.9445 | 11212.62 |
| 760 | 973.8041 | 685.2696 | 19.6036 | 37.5676 | 57.1713 | 2.6633 | 7.7673 | 0.9632 | 16228.69 |
| 780 | 999.4305 | 703.303 | 47.1572 | 38.2937 | 85.451 | 6.4505 | 11.689 | 0.9818 | 36501.66 |
| 785 | 1005.837 | 707.8113 | 66.222 | 38.475 | 104.698 | 9.0732 | 14.345 | 0.9865 | 54887.78 |
| 790 | 1012.244 | 712.3197 | 105.59 | 38.6575 | 144.248 | 14.491 | 19.796 | 0.9912 | 104358.3 |
| 795 | 1018.65 | 716.828 | 235.082 | 38.8398 | 273.922 | 32.315 | 37.654 | 0.9958 | 376938.6 |
| 799 | 1023.776 | 720.4347 | 2650.63 | 38.9853 | 2689.61 | 364.82 | 370.19 | 0.9996 | 36386766 |
| 800 | 1025.057 | 721.3364 | |||||||
| 1054 | 1350 | 950 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Težak, S.; Sever, D. Optimization of Operations in Bus Company Service Workshops Using Queueing Theory. Vehicles 2025, 7, 82. https://doi.org/10.3390/vehicles7030082
Težak S, Sever D. Optimization of Operations in Bus Company Service Workshops Using Queueing Theory. Vehicles. 2025; 7(3):82. https://doi.org/10.3390/vehicles7030082
Chicago/Turabian StyleTežak, Sergej, and Drago Sever. 2025. "Optimization of Operations in Bus Company Service Workshops Using Queueing Theory" Vehicles 7, no. 3: 82. https://doi.org/10.3390/vehicles7030082
APA StyleTežak, S., & Sever, D. (2025). Optimization of Operations in Bus Company Service Workshops Using Queueing Theory. Vehicles, 7(3), 82. https://doi.org/10.3390/vehicles7030082






