Research on the Active Suspension Control Strategy of Multi-Axle Emergency Rescue Vehicles Based on the Inverse Position Solution of a Parallel Mechanism

Abstract

Aiming at the problems of complex control processes, strong model dependence, and difficult engineering application when the existing active suspension control strategy is applied to multi-axle vehicles, an active suspension control strategy based on the inverse position solution of a parallel mechanism is proposed. First, the active suspension of the three-axle emergency rescue vehicle is grouped and interconnected within the group, and it is equivalently constructed into a 3-DOF parallel mechanism. Then, the displacement of each equivalent suspension actuating hydraulic cylinder is calculated by using the method of the inverse position solution of a parallel mechanism, and then the equivalent actuating hydraulic cylinder is reversely driven according to the displacement, thereby realizing the effective control of the attitude of the vehicle body. To verify the effectiveness of the proposed control strategy, a three-axis vehicle experimental platform integrating active suspension and hydro-pneumatic suspension was built, and a pulse road experiment and gravel pavement experiment were carried out and compared with hydro-pneumatic suspension. Both types of road experimental results show that compared to hydro-pneumatic suspension, the active suspension control strategy based on the inverse position solution of a parallel mechanism proposed in this paper exhibits different degrees of advantages in reducing the peak values of the vehicle vertical displacement, pitch angle, and roll angle changes, as well as suppressing various vibration accelerations, significantly improving the vehicle’s driving smoothness and handling stability.

1. Introduction

The multi-axle emergency rescue vehicle (Figure 1) is the main equipment for land rescue, and it also serves as a critical subject of investigation within the field of emergency rescue equipment research [1,2,3]. Usually, the road surface after the disaster will be damaged and become unstructured. If the emergency rescue vehicle can maintain good ride comfort and handling stability in such complex and changeable road conditions, it is of great significance to ensure the rapidity and effectiveness of the rescue operation. This is mainly because, on the one hand, for the wounded in urgent need of rescue, if the attitude of the vehicle changes during the moving process, resulting in severe turbulence, it is very likely to pose a significant risk of exacerbating existing trauma through re-injury, which may further compromise subsequent medical interventions. On the other hand, the violent turbulence and vibration will also pose a potential threat to the on-board precision rescue equipment, resulting in equipment damage or functional failure, which will significantly weaken the response speed and operation efficiency of the rescue team.

As a core component influencing vehicle ride comfort and handling stability, the suspension system plays a decisive role in maintaining body attitude stability while ensuring driving smoothness through the synergistic action of elastic elements and damping components. Based on different force mechanisms, suspensions can be categorized into three types: passive, semi-active, and active. Among them, passive suspensions, with fixed stiffness and damping parameters, are unable to adapt to varying road conditions and thus fail to meet the dynamic adaptation requirements of multi-axle emergency rescue vehicles operating on unstructured terrains [4,5,6]. Although semi-active suspensions can improve dynamic responses through adjustable damping, their actuation mechanism remains constrained to passive adaptive regulation. In scenarios requiring active force intervention—such as mitigating body roll during emergency obstacle avoidance or pitch under braking—they still lack real-time active control capability for vehicle attitude regulation [7,8,9]. In contrast, active suspensions utilize actuators to directly generate controllable forces, enabling real-time dynamic compensation for road-induced disturbances [10,11,12]. This configuration demonstrates significant technological advantages in terrain adaptability and attitude control precision, making it fully capable of satisfying the demanding requirements for the ride comfort and handling stability of multi-axle emergency rescue vehicles operating on unstructured roads.

Driven by breakthroughs in digital signal processing and sensor fusion, active suspension technology has gradually moved from theoretical research to practical application [13,14,15]. The dynamic performance of an active suspension system primarily hinges on two core factors: the actuators and the control strategies. As the “brain” of the system, the control strategies are responsible for processing multidimensional information and calculating the action instructions of the actuator. The efficiency, accuracy, and adaptability of control strategies are directly related to the dynamic response characteristics of the active suspension system. Therefore, compared to actuators, control strategies play a more critical role in active suspension systems.

Over the past few decades, numerous researchers have thoroughly investigated the control strategies of active suspension and proposed a variety of advanced control strategies. Jeong et al. [16] proposed an angle damping active suspension control strategy for 8 × 8 armored combat vehicles, which reduced the vertical acceleration, pitch angle and roll angle of the sprung mass and improved the ride comfort. Zhang et al. [17] proposed a suspension travel tracking preview control algorithm for multi-axle vehicle suspension with large travel space, and the simulation results show that the algorithm can significantly improve the attitude motion of the vehicle body under deterministic and stochastic road excitation. Wang et al. [18] proposed a new low-complexity, fixed-time, prescribed performance control method for the nonlinearity of the hydraulic active suspension system, and this method does not need a function approximator, which can not only avoid a large amount of computational costs but also effectively improve the vehicle’s attitude stability. Khan et al. [19] designed an adaptive, proportional, integral, and differential control strategy for the vehicle active suspension system, and the simulation results show that the ride comfort and handling stability can be improved by using this active control scheme. Kumar et al. [20] proposed an active vehicle suspension dynamic controller based on fuzzy logic, which monitors the front and rear wheel speeds and accelerations in real time to output the main driving force for optimizing ride comfort. Zhang et al. [21] proposed an adaptive neural network optimization control strategy based on the backstepping control framework for the nonlinear control of vehicle active suspensions, and simulation results demonstrate that this strategy can significantly enhance ride comfort while effectively suppressing suspension stroke overruns. Na et al. [22] proposed a new control method for the fully active suspension system with unknown nonlinear dynamics, which does not rely on any function approximation method but can effectively deal with the inevitable uncertainty and nonlinearity in the suspension system. Lin et al. [23] developed a backstepping-based controller for active suspensions, integrating a deep deterministic policy gradient to streamline computations, and simulations confirm enhanced ride comfort under random roads, an improved transient response, and robustness. Kim et al. [24] developed a static output feedback active suspension controller using only vertical velocity, roll rate, and pitch rate measurements to overcome the measurability limitations of full-state feedback, with experimental results demonstrating significant improvements in ride comfort and motion sickness reduction.

The above research results on active suspension control strategies have improved the performance of active suspension systems at different levels, but the common practice of these control strategies is to treat each active suspension actuator as an independent control unit and assign an independent control variable to it. For the two-axle passenger car with fewer axles and a relatively simple structure, this control strategy shows good applicability. However, with the increase in the number of axles, when the two-axle vehicle becomes a multi-axle vehicle, the number of actuators increases linearly, and the number of control variables also rises sharply. This change will greatly increase the computing resources required for data processing and control algorithm implementation, which will greatly increase the difficulty of control algorithm implementation and also cause the response delay of the control system, weakening the control accuracy and system efficiency. In addition, with the increase in the complexity of the control system, the sensitivity of the system to external disturbances and parameter changes is significantly improved, and the robustness of the system is significantly reduced. Furthermore, most active suspension control strategies are highly dependent on accurate vehicle dynamics models, but in practical engineering, obtaining all parameters of the model comprehensively and accurately through system identification will face many challenges. Due to this limitation, many advanced control strategies are limited to theoretical simulation, and it is difficult to achieve effective engineering applications in active suspension systems for multi-axle vehicles. Moreover, existing research on active suspension control strategies reveals a prevalent focus on solving for the actuator’s active control force to enhance vehicle ride comfort and handling stability, with force-control methodologies dominating current approaches. However, for hydraulic actuators—the dominant execution mechanism in heavy-duty emergency rescue vehicles—their operational chamber experiences severe pressure fluctuations when encountering road disturbances, making precise force tracking extremely challenging and significantly limiting the performance of force-control strategies. In contrast, displacement control demonstrates stronger engineering applicability, as hydraulic actuators exhibit more physically feasible displacement responses compared to the transient force output characteristics. Despite its practical advantages, displacement-based active suspension control remains underexplored in current academic investigations. Therefore, it is necessary to further explore a simple, efficient, robust, and less dependent active suspension control strategy suitable for multi-axle emergency rescue vehicles.

Aiming at the complexity and particularity of active suspension control for multi-axle emergency rescue vehicles, this paper proposes an active suspension control strategy based on the inverse position solution of a parallel mechanism (ASCS-IPSPM) for multi-axle emergency rescue vehicles. Based on the geometric principle of determining a plane from three points, the actuating hydraulic cylinders of the active suspension system of the multi-axis emergency rescue vehicle are divided into three groups. Each group’s hydraulic cylinders are interconnected, effectively configuring the multi-axis emergency rescue vehicle as a parallel mechanism with 3-DOF. By using the method of calculating the inverse position solution of a parallel mechanism, the vehicle attitude change is solved as the displacement of each hydraulic cylinder. Subsequently, the hydraulic cylinders implement reverse actuation based on real-time displacement parameters, forming a closed-loop control for vehicle attitude. Through these dynamic compensation mechanisms, the driving performance of multi-axle emergency rescue equipment will be enhanced.

The contributions of this study can be summarized as follows:

(1)

To tackle the problem that the control complexity of the active suspension in multi-axle vehicles scales linearly with the number of actuators, by dividing the active suspension actuator hydraulic cylinders into three groups and interconnecting the hydraulic cylinders within each group, the multi-point support for the vehicle body has been successfully transformed into the virtual three-point support for the vehicle body. This conversion significantly reduces the workload of control, shifting from the independent control of each hydraulic cylinder to the integrated control of the hydraulic cylinder group. The calculation of the expansion and contraction amounts of multiple actuators in the past control strategy has been transformed into the calculation of only three virtual actuators’ expansion and contraction amounts, greatly improving the calculation efficiency and significantly enhancing the control efficiency. The ASCS-IPSPM also has broad applicability, not limited by the number of active suspension actuators, and can achieve efficient control through reasonable grouping.

(2)

The interconnected design between the hydraulic cylinders within the group enables the load self-balancing and self-adjustment functions of the active suspension system for multi-axle vehicles. Without relying on external control, the load balance of the suspension within the group can be maintained and effectively controlled, significantly reducing the difficulty of control while improving the stability and reliability of the system.

(3)

This article innovatively proposes a method for abstract complex multi-axle vehicle chassis as a 3-DOF parallel mechanism. By utilizing the inverse position solution of the parallel mechanism, the control quantities of actuators are calculated, achieving the efficient decoupling of complex active suspension systems and the precise control of vehicle attitude. This innovative approach provides a new perspective and tool for research on active suspension control methods in multi-axle vehicles.

This paper is organized into four sections. Section 2 details the principle of the ASCS-IPSPM, the methodology for simplifying a three-axle vehicle into a 3-DOF parallel mechanism, and derives the inverse position solution for this mechanism. Section 3 constructs an experimental platform for the three-axle vehicle, conducts comparative experiments, and analyzes the resulting data. Section 4 presents the discussion and concluding remarks.

2. Active Suspension Control Strategy Based on the Inverse Kinematics of a Parallel Mechanism

Before elaborating on the ASCS-IPSPM proposed in this paper, it is necessary to explain the research object and the applicability of the control strategy. The ASCS-IPSPM proposed in this paper has wide applicability and can be applied to all multi-axle vehicles in theory. However, considering the research focus, project requirements, and actual experimental conditions of the project, this paper selects a representative three-axis, six-wheel emergency rescue vehicle as the specific research object.

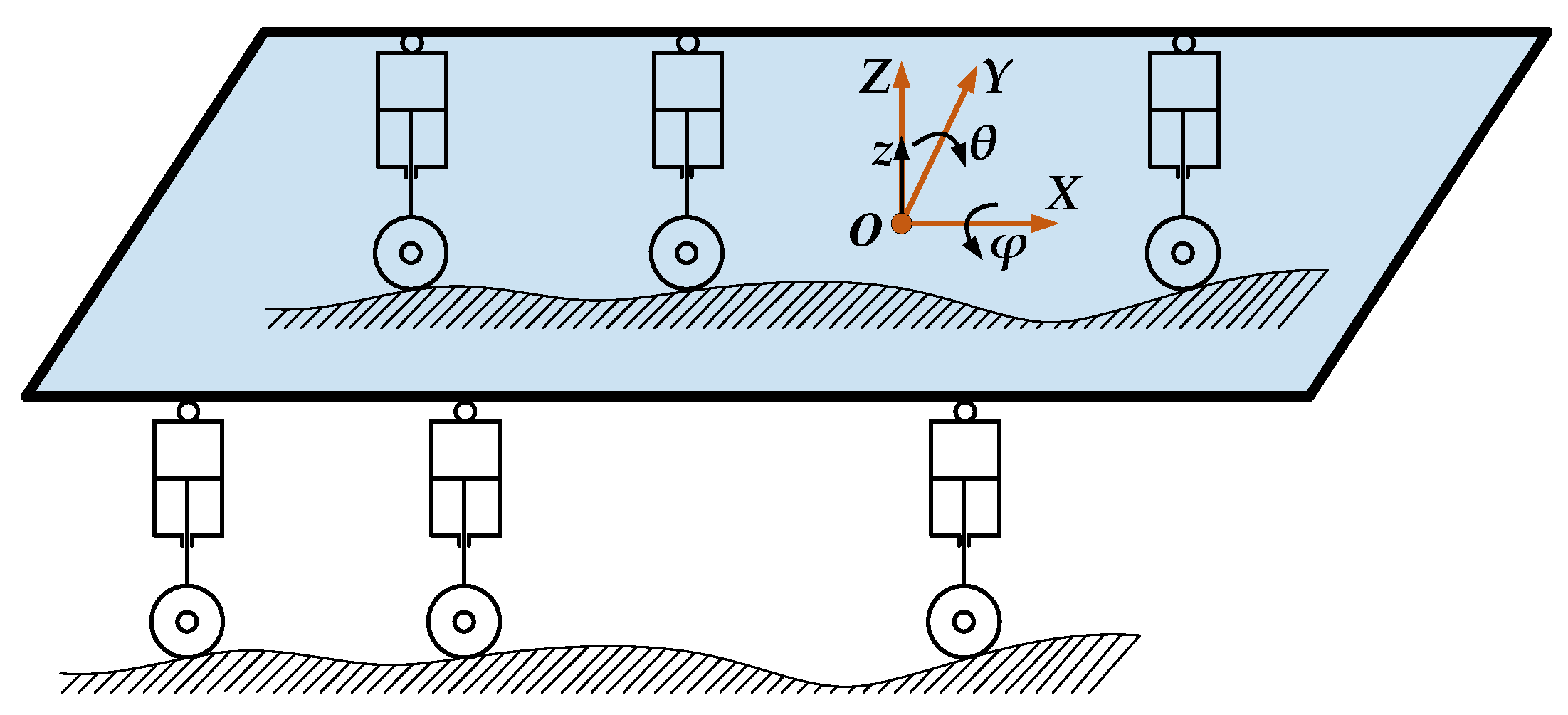
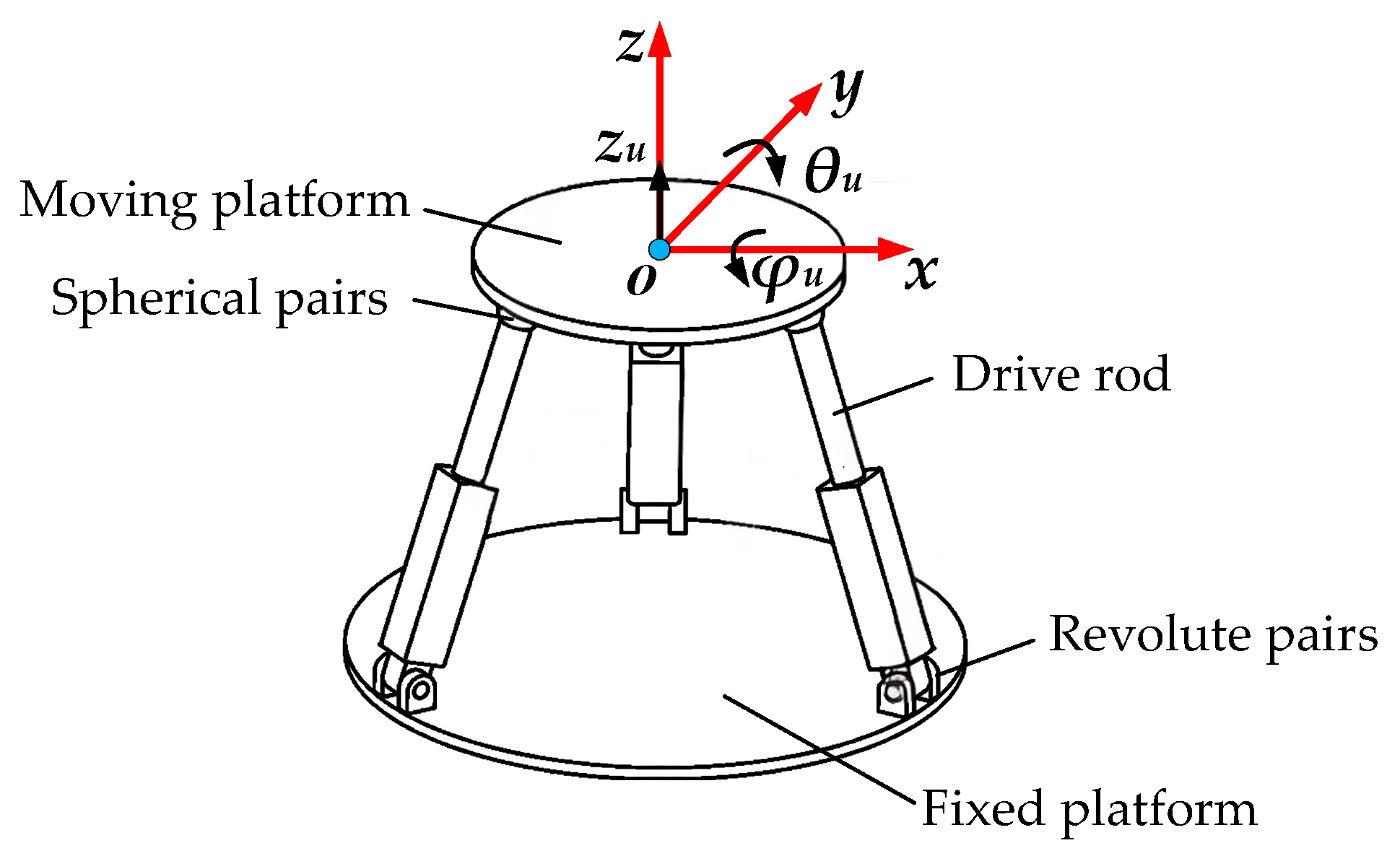
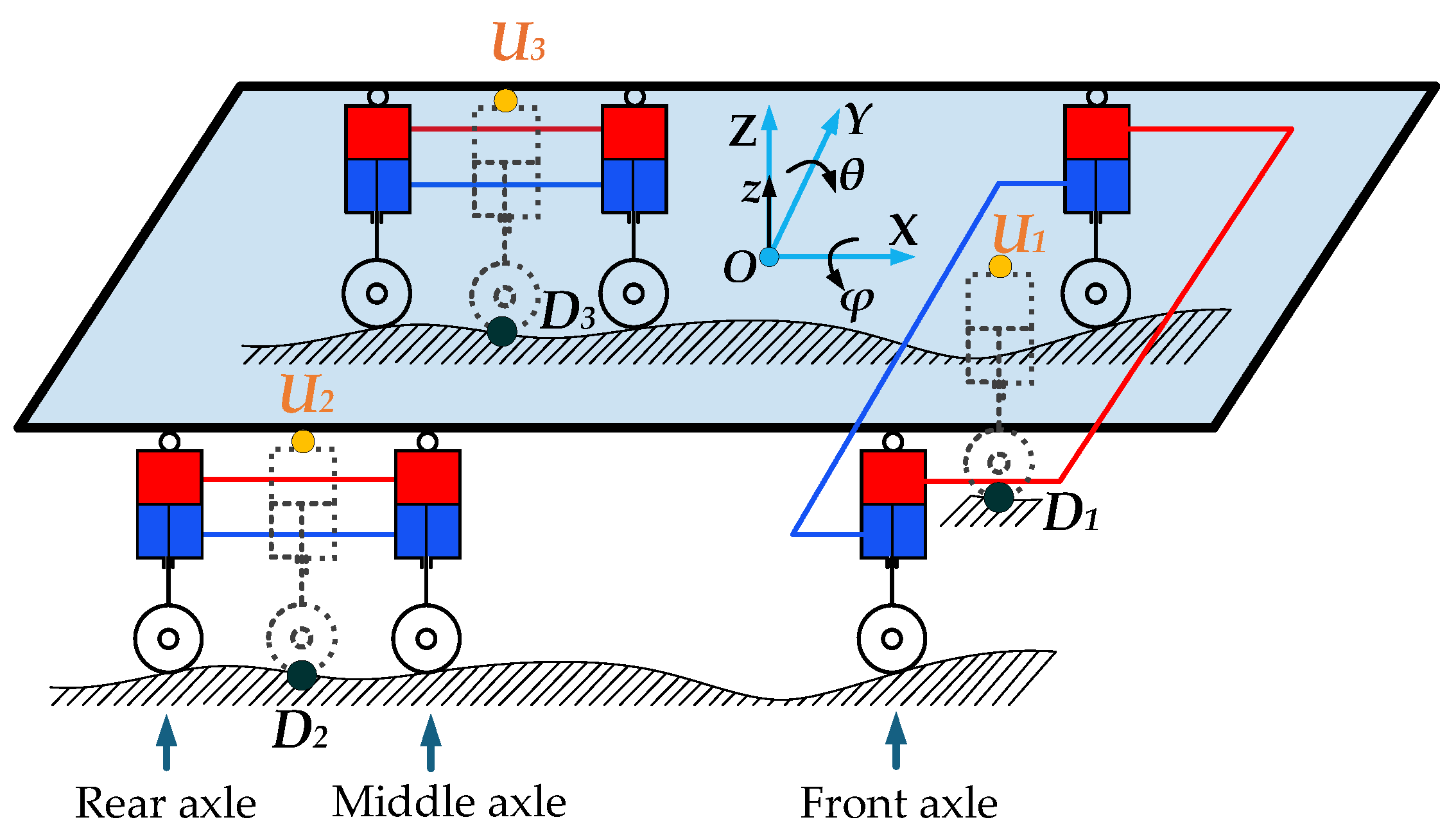
2.1. Construction of an Equivalent 3-DOF Parallel Mechanism for Three-Axis Vehicles

During off-road driving (as shown in Figure 2), the multi-axle emergency rescue vehicle exhibits three motion states relative to the ground level, namely, two rotations and one movement, under the action of road surface excitation. These three motion states are roll rotation, pitch rotation, and translational motion along the direction perpendicular to the earth’s horizontal plane. It is worth noting that in the field of parallel mechanisms, there is a parallel mechanism called 3-RPS [25], as diagrammatically illustrated in Figure 3. Its moving platform also possesses two rotational freedoms about the x/y axis, in addition to a single translational freedom along the z-axis. Its degree of freedom and type of motion are the same as the vehicle’s motion state. The 3-RPS parallel mechanism consists of a moving platform, a fixed platform, and three extendable drive rods connecting them. Spherical pairs connect the moving platform to the drive rods, while the fixed platform is articulated to these rods using revolute pairs. If the vehicle body is regarded as the moving platform, the horizontal plane is regarded as the fixed platform, and the active suspension actuating cylinder is regarded as the driving rod, then to a certain extent, the chassis of the multi-axle emergency rescue vehicle can be equivalent to a 3-DOF parallel mechanism similar to the 3-RPS mechanism. When considering the vehicle chassis as the moving platform, the horizontal plane as the fixed platform, and the hydraulic actuators as the driving rod, the multi-axle emergency rescue vehicle’s undercarriage can be analogously represented by a 3-DOF parallel mechanism resembling the 3-RPS configuration. By imitating the control methodology of the 3-RPS parallel mechanism’s moving platform, precise control of vehicle attitude can be realized, thereby ensuring handling stability through attitude adjustment while simultaneously enhancing ride quality

In the 3-RPS parallel mechanism, the actuator rods interface with the moving platform through three mounting points and connect to the fixed platform via an equivalent number of three joints. By contrast, the three-axle vehicle system illustrated in Figure 2 employs a six-point contact patch distribution through its tires, while its hydraulic suspension actuators establish six corresponding connection points with the vehicle chassis. If we want to construct the entire vehicle as a 3-DOF parallel mechanism, the first step is to equivalently convert the six support points of the suspension actuating hydraulic cylinder and the six tire grounding points to three.

Based on the hydro-pneumatic balanced suspension system’s design principle and dynamic operational characteristics [26,27,28], when the rodless chambers of a group of suspension hydraulic cylinders, as shown in Figure 4, are interconnected and the rod chambers are also interconnected, this group of hydraulic cylinders forms a balanced suspension system. The two support points, P₁ and P₂, originally scattered on the vehicle body, can be equivalently simplified as a single support point P_o in mechanical analysis. When the suspension hydraulic cylinders within the assembly share identical geometric and mechanical specifications, point P_o is located at the geometric midpoint of the straight line connecting all hydraulic cylinders in the group. It can also be inferred that there is a virtual suspension cylinder at the equivalent support point P_o, which can serve as a representative of the overall mechanical performance of the suspension hydraulic cylinder group.

Based on the hydraulic cylinder interconnection scheme presented in Figure 4, the six hydraulic cylinders of the three-axle vehicle (as depicted in Figure 2) are partitioned into three groups, as shown in Figure 5. The front axle’s left and right hydraulic cylinders constitute Group 1. Group 2 consists of the two right-side hydraulic cylinders mounted on both the middle and rear axles. Correspondingly, Group 3 integrates the two left-side hydraulic cylinders from the middle and rear axles. If the rodless chambers of the two hydraulic cylinders in each group are connected to the rodless chambers, and the rodless chambers are connected to the rodless chambers, the six support points can be equivalently simplified as three equivalent support points, U₁, U₂, and U₃.

U₁, U₂, and U₃ are located at the midpoint of the line connecting the two support points within each group. Aligned with each equivalent support point, D₁ is the midpoint of the connecting line between the left and right tire grounding points on the front axle, D₂ is the midpoint of the connecting line between the two tire grounding points located at the right lateral positions of both the middle and rear axles, and D₃ is the midpoint of the connecting line between the two tire grounding points located at the left lateral positions of both the middle and rear axles.

Employing the plane Δ U₁U₂U₃, which is spanned by the three equivalent support points, as the moving platform component of the parallel mechanism, taking the plane Δ D₁D₂D₃ determined by the three equivalent tire ground points D₁, D₂, and D₃,as the fixed platform of the parallel mechanism, and taking the line segments D₁U₁, D₂U₂, and D₃U₃ as the retractable drive rods of the parallel mechanism, the three-axle vehicle demonstrated in Figure 2 can be theoretically transformed into a 3-DOF parallel mechanism configuration, with the equivalent model presented in Figure 6.

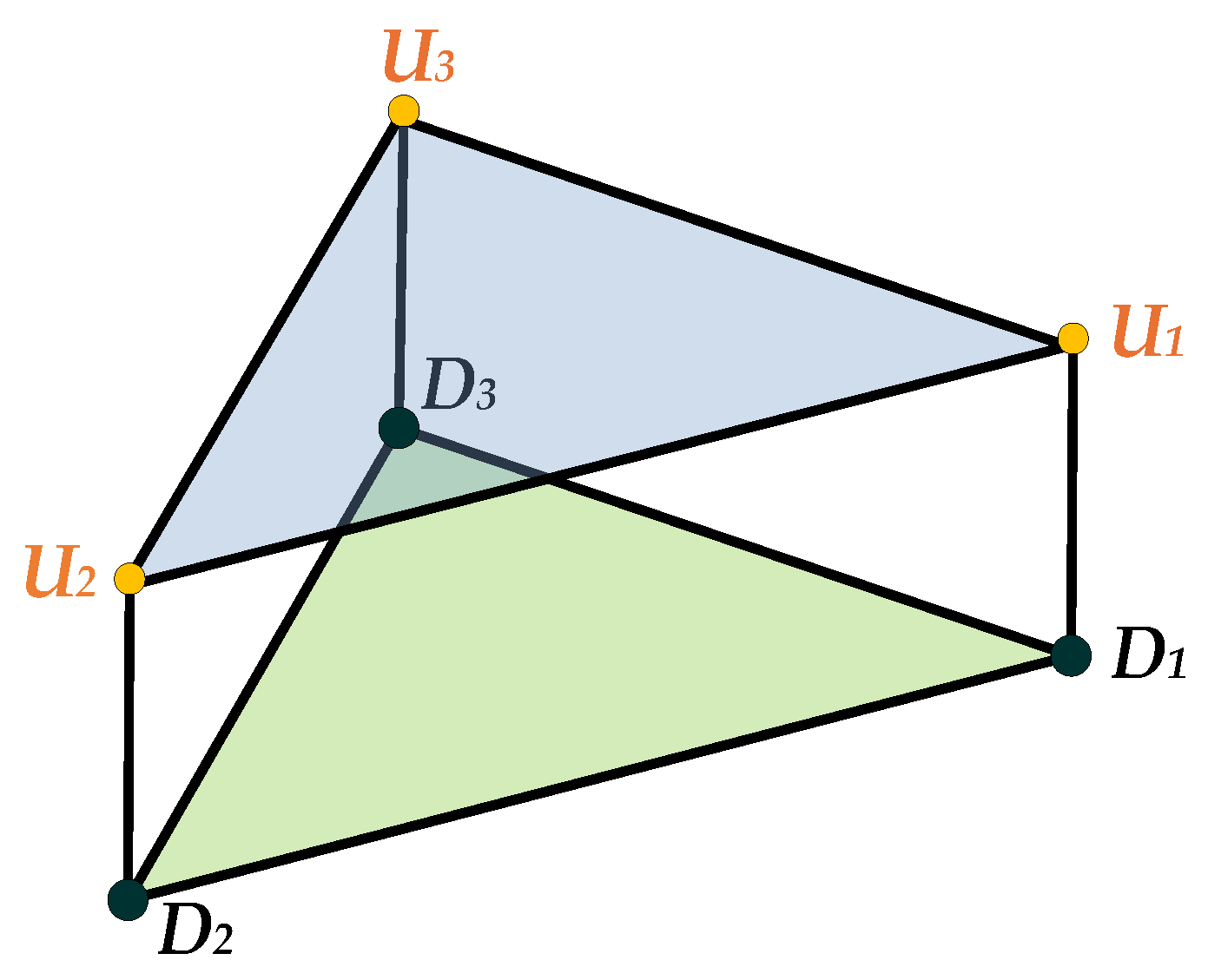
2.2. Inverse Position Solution of the Equivalent 3-DOF Parallel Mechanism

The determination of driving rod length, based on the predefined position and orientation of the moving platform, is defined as the inverse kinematic solution for the parallel mechanism’s positional analysis [29,30]. However, the conventional inverse kinematic solution methods developed for traditional 3-RPS parallel mechanisms cannot be directly applied to the equivalent 3-DOF parallel mechanism under study. The reason is that the moving platform and the fixed platform of the equivalent 3-DOF parallel mechanism are both isosceles-triangular, rather than equilateral-triangular like the traditional 3-RPS parallel mechanism. Additionally, due to the complex structure of vehicles, the installation position of sensors for measuring the attitude of the vehicle body usually cannot coincide with the center point of the mobile platform, so it is necessary to obtain the attitude data of the center of the mobile platform through coordinate transformation. Therefore, the inverse solution of the position for the equivalent 3-DOF parallel mechanism of three-axle vehicles needs to be newly derived.

When the vehicle is stationary on a horizontal plane with each suspension system’s hydraulic actuator maintained at its mid-stroke equilibrium position, the coordinate systems O_U-X_UY_UZ_U and O_D-X_DY_DZ_D are respectively established with the outer centers of the moving platform and the fixed platform as the origins, as shown in Figure 7.

The Z_U axis within the coordinate system of the moving platform is oriented orthogonally to the platform’s surface and extends vertically upward along its normal direction. The X_U axis is determined by the ball hinge U₁ and along the O_UU₁ direction, and the Y_U axis direction is determined by the right hand rule. The Z_D axis of the rectangular coordinate system of the fixed platform is perpendicular to the fixed platform and points directly upward, the X_D axis passes through point D₁ and along the direction of O_DD₁, and the direction of the Y_D axis is determined by the right hand rule. ${\phi }_U$ is the roll angle of the moving platform, ${\theta }_U$ is the pitch angle of the moving platform, $z_U$ is the vertical displacement of the moving platform; N_U is the midpoint of U₂U₃; and N_D is the midpoint of D₂D₃.

It can be seen in Figure 7 that the line segment D₁N_D = U₁N_U, and D₁N_D = U₁N_U = a. Because the actuating hydraulic cylinder is not perpendicular to the vehicle chassis, but there is a certain angle, the line segment D₂D₃ ≠ U₂U₃, set $D_2{D}_3=b_D$, and set $U_2{U}_3=b_U$. The circumscribed circle of the isosceles triangle of the moving platform and the fixed platform are $r_U$ and $r_D$, respectively. According to the geometric relationship, the coordinates of each point of the moving platform in the coordinate system O_U-X_UY_UZ_U are

$${}^{U}P{\phantom{,}}_{U_1}=\left[\begin{array}{c}{r}_U\\ 0\\ 0\end{array}\right],{}^{U}P{\phantom{,}}_{U_2}=\left[\begin{array}{c}{r}_U-a\\ -{\displaystyle \frac{b_U}{2}}\\ 0\end{array}\right],{}^{U}P{\phantom{,}}_{U_3}=\left[\begin{array}{c}{r}_U-a\\ {\displaystyle \frac{b_U}{2}}\\ 0\end{array}\right]$$

(1)

The coordinates of each point of the fixed platform in the coordinate system O_D-X_DY_DZ_D are

$${}^{D}P{\phantom{,}}_{D_1}=\left[\begin{array}{c}{r}_D\\ 0\\ 0\end{array}\right],{}^{D}P{\phantom{,}}_{D_2}=\left[\begin{array}{c}{r}_D-a\\ -{\displaystyle \frac{b_D}{2}}\\ 0\end{array}\right],{}^{D}P{\phantom{,}}_{D_3}=\left[\begin{array}{c}{r}_D-a\\ {\displaystyle \frac{b_D}{2}}\\ 0\end{array}\right]$$

(2)

The homogeneous transformation matrix of coordinate system O_U-X_UY_UZ_U relative to coordinate system O_D-X_DY_DZ_D is

$$T=\left[\begin{array}{cc}R& {}^{D}P{\phantom{,}}_{O_U}\\ 0& 1\end{array}\right]$$

(3)

where

$$R=\left[\begin{array}{ccc}c\gamma & -s\gamma & 0\\ s\gamma & c\gamma & 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{ccc}c\theta & 0& s\theta \\ 0& 1& 0\\ -s\theta & 0& c\theta \end{array}\right]\left[\begin{array}{ccc}1& 0& 0\\ 0& c\phi & -s\phi \\ 0& s\phi & c\phi \end{array}\right]$$

(4)

$${}^{D}P{\phantom{,}}_{O_U}=\left[\begin{array}{c}{}^{D}x{\phantom{,}}_{O_U}\\ {}^{D}y{\phantom{,}}_{O_U}\\ {}^{D}z{\phantom{,}}_{O_U}\end{array}\right]$$

(5)

where R is the posture rotation matrix of coordinate system O_U-X_UY_UZ_U relative to coordinate system O_D-X_DY_DZ_D. sγ, sθ, and sφ are the sine values of γ, θ, and φ, respectively. cγ, cθ, and cφ are the cosine values of γ, θ, and φ, respectively. The vector ${}^{D}P{\phantom{,}}_{O_U}$ is the position vector of the origin O_U in the coordinate system O_U-X_UY_UZ_U. ${}^{D}x{\phantom{,}}_{O_U}$, ${}^{D}y{\phantom{,}}_{O_U}$, and ${}^{D}z{\phantom{,}}_{O_U}$ are the coordinate values of origin O_U in the coordinate system O_U-X_UY_UZ_U.

The coordinate ${}^{D}P{\phantom{,}}_{U_i}$ of each point of the moving platform relative to the coordinate system O_D-X_DY_DZ_D can be expressed by the homogeneous transformation matrix T and the coordinate ${}^{U}P{\phantom{,}}_{U_i}$ of each point of the moving platform in the coordinate system O_U-X_UY_UZ_U as

$$\left[\begin{array}{c}{}^{D}P{\phantom{,}}_{U_i}\\ 1\end{array}\right]=T\left[\begin{array}{c}{}^{U}P{\phantom{,}}_{U_i}\\ 1\end{array}\right]\left(i=1,2,3\right)$$

(6)

Combining Equations (1) and (3) with Equation (6), the coordinates of each point of the moving platform in the coordinate system O_D-X_DY_DZ_D are

$${}^{D}P{\phantom{,}}_{U_1}=\left[\begin{array}{c}{}^{D}x{\phantom{,}}_{O_U}+r_{U}c\theta c\gamma \\ {}^{D}y{\phantom{,}}_{O_U}+r_{U}s\gamma c\theta \\ {}^{D}z{\phantom{,}}_{O_U}-r_{U}s\theta \end{array}\right]$$

(7)

$${}^{D}P{\phantom{,}}_{U_2}=\left[\begin{array}{c}{}^{D}x{\phantom{,}}_{O_U}+{\displaystyle \frac{b_U}{2}}\left(c\phi s\gamma -c\gamma s\phi s\theta \right)+\left(r_U-a\right)c\gamma c\theta \\ {}^{D}y{\phantom{,}}_{O_U}-{\displaystyle \frac{b_U}{2}}\left(c\phi c\gamma +s\phi s\gamma s\theta \right)+\left(r_U-a\right)c\theta s\gamma \\ {}^{D}z{\phantom{,}}_{O_U}-\left(r_U-a\right)s\theta -{\displaystyle \frac{b_U}{2}}c\theta s\phi \end{array}\right]$$

(8)

$${}^{D}P{\phantom{,}}_{U_3}=\left[\begin{array}{c}{}^{D}x{\phantom{,}}_{O_U}-{\displaystyle \frac{b_U}{2}}\left(c\phi s\gamma -c\gamma s\phi s\theta \right)+\left(r_U-a\right)c\gamma c\theta \\ {}^{D}y{\phantom{,}}_{O_U}+{\displaystyle \frac{b_U}{2}}\left(c\phi c\gamma +s\phi s\gamma s\theta \right)+\left(r_U-a\right)c\theta s\gamma \\ {}^{D}z{\phantom{,}}_{O_U}-\left(r_u-a\right)s\theta +{\displaystyle \frac{b_U}{2}}c\theta s\phi \end{array}\right]$$

(9)

It can be seen in Figure 7 that the special arrangement of each revolute pair limits the movement of each spherical pair of the moving platform, so the spherical pair U₁ can only move in the ${}^{D}y=0$ plane, and the spherical pairs U₂ and U₃ can only move in the plane of ${}^{D}x=r_D-a$. From this, the constraint equation can be obtained as follows

$${}^{D}y{\phantom{,}}_{O_U}+r_{U}s\gamma c\theta =0$$

(10)

$${}^{D}x{\phantom{,}}_{O_U}+{\displaystyle \frac{b_U}{2}}\left(c\phi s\gamma -c\gamma s\phi s\theta \right)+\left(r_U-a\right)c\gamma c\theta =r_D-a$$

(11)

$${}^{D}x{\phantom{,}}_{O_U}-{\displaystyle \frac{b_U}{2}}\left(c\phi s\gamma -c\gamma s\phi s\theta \right)+\left(r_U-a\right)c\gamma c\theta =r_D-a$$

(12)

Combining Equations (10)–(12), it can be obtained that

$${}^{D}x{\phantom{,}}_{O_U}=r_D-a-\left(r_U-a\right)c\gamma c\theta$$

(13)

$${}^{D}y{\phantom{,}}_{O_U}=-r_{U}s\gamma c\theta$$

(14)

$$\left\{\begin{array}{l}s\gamma ={\displaystyle \frac{s\phi s\theta }{\sqrt{s^2\phi s^2\theta +c^2\phi }}}\\ c\gamma ={\displaystyle \frac{c\phi }{\sqrt{s^2\phi s^2\theta +c^2\phi }}}\end{array}\right.$$

(15)

Substituting Equations (13)–(15) into Equations (7)–(9), we can obtain

$${}^D\mathit{P}{\phantom{,}}_{U_1}=\left[\begin{array}{c}{r}_D-a+{\displaystyle \frac{ac\phi c\theta }{\sqrt{s^2\phi s^2\theta +c^2\phi }}}\\ 0\\ {}^{D}z{\phantom{,}}_{O_U}-r_{U}s\theta \end{array}\right]$$

(16)

$${}^{D}P{\phantom{,}}_{U_2}=\left[\begin{array}{c}{r}_D-a\\ -{\displaystyle \frac{b_U}{2}}\sqrt{s^2\phi s^2\theta +c^2\phi }-{\displaystyle \frac{as\phi s\theta c\theta \sqrt{s^2\phi s^2\theta +c^2\phi }}{s^2\phi s^2\theta +c^2\phi }}\\ {}^{D}z{\phantom{,}}_{O_U}-\left(r_U-a\right)s\theta -{\displaystyle \frac{b_U}{2}}c\theta s\phi \end{array}\right]$$

(17)

$${}^{D}P{\phantom{,}}_{U_3}=\left[\begin{array}{c}{r}_D-a\\ {\displaystyle \frac{b_U}{2}}\sqrt{s^2\phi s^2\theta +c^2\phi }-{\displaystyle \frac{ac\theta s\phi s\theta \sqrt{s^2\phi s^2\theta +c^2\phi }}{s^2\phi s^2\theta +c^2\phi }}\\ {}^{D}z{\phantom{,}}_{O_U}-\left(r_U-a\right)s\theta +{\displaystyle \frac{b_U}{2}}c\theta s\phi \end{array}\right]$$

(18)

The length $L_i\left(i=1,2,3\right)$ of each driving rod is

$$L_i=\left|{}^{D}P{\phantom{,}}_{U_i}-{}^{D}P{\phantom{,}}_{D_i}\right|$$

(19)

Therefore, according to Equations (7)–(9) and (16)–(18), $L_i\left(i=1,2,3\right)$ can be expressed as

$$L_1=\sqrt{{\left[{\displaystyle \frac{ac\phi c\theta }{\sqrt{s^2\phi s^2\theta +c^2\phi }}}-a\right]}^2+{\left[{}^{D}z{\phantom{,}}_{O_U}-{\displaystyle \frac{4a^2+b_U^2}{8a}}s\theta \right]}^2}$$

(20)

$$L_2=\sqrt{{\left[{\displaystyle \frac{b_D}{2}}-{\displaystyle \frac{b_U}{2}}\sqrt{s^2\phi s^2\theta +c^2\phi }-{\displaystyle \frac{as\phi s\theta c\theta }{\sqrt{s^2\phi s^2\theta +c^2\phi }}}\right]}^2+{\left[{\displaystyle \frac{b_U}{2}}c\theta s\phi -{\displaystyle \frac{b_U^2-4a^2}{8a}}s\theta +{}^{D}z{\phantom{,}}_{O_U}\right]}^2}$$

(21)

$$L_3=\sqrt{{\left[-{\displaystyle \frac{b_D}{2}}+{\displaystyle \frac{b_U}{2}}\sqrt{s^2\phi s^2\theta +c^2\phi }-{\displaystyle \frac{ac\theta s\phi s\theta }{\sqrt{s^2\phi s^2\theta +c^2\phi }}}\right]}^2+{\left[{\displaystyle \frac{b_U}{2}}c\theta s\phi -{\displaystyle \frac{b_U^2-4a^2}{8a}}s\theta +{}^{D}z{\phantom{,}}_{O_U}\right]}^2}$$

(22)

2.3. Principle of the ASCS-IPSPM

Based on the established foundation of the equivalent 3-DOF parallel mechanism and inverse kinematic position development for the three-axle vehicle, this section proposes the ASCS-IPSPM and provides a detailed explanation of its control principle.

The sensors used to measure the attitude of the vehicle body are installed on the vehicle body, and the rectangular coordinate system O_S-X_SY_SZ_S is established with the center point O_S of its installation position as the origin, as shown in Figure 8. The vertical displacement measured by sensors is $z_S$, the roll angle is ${\phi }_S$, and the pitch angle is ${\theta }_S$.

Due to the complex structure of the vehicle body, the sensors installation position O_S generally cannot coincide with the center point O_U of the moving platform. Therefore, it is necessary to convert the sensors attitude measurement value into the attitude at the center point O_U through coordinate conversion. The coordinate of the center point O_U in the coordinate system O_S-X_SY_SZ_S is set to be (${}^{S}x{\phantom{,}}_{O_U},{}^{S}y{\phantom{,}}_{O_U},{}^{S}z{\phantom{,}}_{O_U}$), and according to the coordinate transformation relationship, the attitude measurement value ($z_U$, ${\phi }_U$, ${\theta }_U$) at the center point O_U can be expressed as

$$\left\{\begin{array}{l}{z}_U=z_S+{}^{S}y{\phantom{,}}_{O_U}\sin {\phi }_S-{}^{S}x{\phantom{,}}_{O_U}\sin {\theta }_S\\ {\phi }_U={\phi }_S\\ {\theta }_U={\theta }_S\end{array}\right.$$

(23)

Based on Equation (25), the schematic diagram of the ASCS-IPSPM principle is drawn as shown in Figure 9.

Combined with Figure 9, the control strategy steps of the ASCS-IPSPM are explained as follows

(1)

At the initial time t₀, the vertical displacement, roll angle, and pitch angle measured by sensors at the point O_S are $z_{S_{t_0}}$, ${\phi }_{S_{t_0}}$, and ${\theta }_{S_{t_0}}$, respectively. After coordinate transformation, the vertical displacement, roll angle, and pitch angle at the center point O_U are $z_{U_{t_0}}$, ${\phi }_{U_{t_0}}$, and ${\theta }_{U_{t_0}}$, respectively, which are the input signals in Figure 9. At the current time t, the vehicle is driving on an unstructured road. At this time, the vertical displacement, roll angle, and pitch angle measured by sensors at the point O_S are $z_{S_t}$, ${\phi }_{S_t}$, and ${\theta }_{S_t}$, respectively. The vertical displacement, roll angle, and pitch angle at the point O_U are $z_{U_t}$, ${\phi }_{U_t}$, and ${\theta }_{U_t}$, respectively, which are the output signals in Figure 9.

(2)

The attitude variation of the moving platform at time t is $\Delta z=z_{U_t}-z_{U_{t_0}}$, $\Delta \phi ={\phi }_{U_t}-{\phi }_{U_{t_0}}$, and $\Delta \theta ={\theta }_{U_t}-{\theta }_{U_{t_0}}$ relative to that at time t₀.

(3)

Taking $-\Delta z$, $-\Delta \phi$, and $-\Delta \theta$ as the relative attitude correction of the equivalent 3-DOF parallel mechanism moving platform of the three-axis vehicle, and replacing the attitude parameters ${}^{D}z{\phantom{,}}_{O_U}$, $\phi$, and $\theta$ in Equations (20)–(22) with $-\Delta z$, $-\Delta \phi$, and $-\Delta \theta$ respectively, and then combining with Equation (23), the inverse position solution L₁, L_2, and L₃ directly mapped to the sensors measurement can be derived, as shown in Equations (24)–(26). Equations (24)–(26) are the expansion amount of each equivalent driving rod. Then, L₁, L₂, and L₃ are used as displacement commands to perform displacement servo control on the equivalent drive rods U₁D₁, U₂D₂, and U₃D₃ (the control of the equivalent drive rod is achieved by controlling the average displacement of the two suspension actuating hydraulic cylinders in each group). The control target of the vehicle body attitude can be realized, so the vertical displacement, pitch angle, and roll angle of the vehicle body can be kept as stable as possible. This part is the position inverse solution module in Figure 9.

$$L_1=\sqrt{\begin{array}{l}{\left[{\displaystyle \frac{ac\left({\phi }_{S_t}-{\phi }_{S_{t_0}}\right)c\left({\theta }_{S_t}-{\theta }_{S_{t_0}}\right)}{\sqrt{s^2\left({\phi }_{S_t}-{\phi }_{S_{t_0}}\right)s^2\left({\theta }_{S_t}-{\theta }_{S_{t_0}}\right)+c^2\left({\phi }_{S_t}-{\phi }_{S_{t_0}}\right)}}}-a\right]}^2\\ +{\left[\begin{array}{l}{\displaystyle \frac{4a^2+b_U^2}{8a}}s\left({\theta }_{S_t}-{\theta }_{S_{t_0}}\right)+z_{S_{t_0}}-z_{S_t}+{}^{S}y{\phantom{,}}_{O_U}\sin {\phi }_{S_{t_0}}-{}^{S}y{\phantom{,}}_{O_U}\sin {\phi }_{S_t}\\ +{}^{S}x{\phantom{,}}_{O_U}\sin {\theta }_{S_t}-{}^{S}x{\phantom{,}}_{O_U}\sin {\theta }_{S_{t_0}}\end{array}\right]}^2\end{array}}$$

(24)

$$L_2=\sqrt{\begin{array}{l}{\left[\begin{array}{l}{\displaystyle \frac{b_D}{2}}-{\displaystyle \frac{b_U}{2}}\sqrt{s^2\left({\phi }_{S_t}-{\phi }_{S_{t_0}}\right)s^2\left({\theta }_{S_t}-{\theta }_{S_{t_0}}\right)+c^2\left({\phi }_{S_t}-{\phi }_{S_{t_0}}\right)}\\ -{\displaystyle \frac{as\left({\phi }_{S_t}-{\phi }_{S_{t_0}}\right)s\left({\theta }_{S_t}-{\theta }_{S_{t_0}}\right)c\left({\theta }_{S_t}-{\theta }_{S_{t_0}}\right)}{\sqrt{s^2\left({\phi }_{S_t}-{\phi }_{S_{t_0}}\right)s^2\left({\theta }_{S_t}-{\theta }_{S_{t_0}}\right)+c^2\left({\phi }_{S_t}-{\phi }_{S_{t_0}}\right)}}}\end{array}\right]}^2\\ +{\left[\begin{array}{l}{\displaystyle \frac{b_U}{2}}c\left({\theta }_{S_t}-{\theta }_{S_{t_0}}\right)s\left({\phi }_{S_t}-{\phi }_{S_{t_0}}\right)-{\displaystyle \frac{b_U^2-4a^2}{8a}}s\left({\theta }_{S_t}-{\theta }_{S_{t_0}}\right)\\ +z_{S_t}-z_{S_{t_0}}+{}^{S}y{\phantom{,}}_{O_U}\sin {\phi }_{S_t}-{}^{S}y{\phantom{,}}_{O_U}\sin {\phi }_{S_{t_0}}+{}^{S}x{\phantom{,}}_{O_U}\sin {\theta }_{S_{t_0}}-{}^{S}x{\phantom{,}}_{O_U}\sin {\theta }_{S_t}\end{array}\right]}^2\end{array}}$$

(25)

$$L_3=\sqrt{\begin{array}{l}{\left[\begin{array}{l}-{\displaystyle \frac{b_D}{2}}+{\displaystyle \frac{b_U}{2}}\sqrt{s^2\left({\phi }_{S_t}-{\phi }_{S_{t_0}}\right)s^2\left({\theta }_{S_t}-{\theta }_{S_{t_0}}\right)+c^2\left({\phi }_{S_t}-{\phi }_{S_{t_0}}\right)}\\ -{\displaystyle \frac{ac\left({\theta }_{S_t}-{\theta }_{S_{t_0}}\right)s\left({\phi }_{S_t}-{\phi }_{S_{t_0}}\right)s\left({\theta }_{S_t}-{\theta }_{S_{t_0}}\right)}{\sqrt{s^2\left({\phi }_{S_t}-{\phi }_{S_{t_0}}\right)s^2\left({\theta }_{S_t}-{\theta }_{S_{t_0}}\right)+c^2\left({\phi }_{S_t}-{\phi }_{S_{t_0}}\right)}}}\end{array}\right]}^2\\ +{\left[\begin{array}{l}{\displaystyle \frac{b_U}{2}}c\left({\theta }_{S_t}-{\theta }_{S_{t_0}}\right)s\left({\phi }_{S_t}-{\phi }_{S_{t_0}}\right)-{\displaystyle \frac{b_U^2-4a^2}{8a}}s\left({\theta }_{S_t}-{\theta }_{S_{t_0}}\right)\\ +z_{S_t}-z_{S_{t_0}}+{}^{S}y{\phantom{,}}_{O_U}\sin {\phi }_{S_t}-{}^{S}y{\phantom{,}}_{O_U}\sin {\phi }_{S_{t_0}}+{}^{S}x{\phantom{,}}_{O_U}\sin {\theta }_{S_{t_0}}-{}^{S}x{\phantom{,}}_{O_U}\sin {\theta }_{S_t}\end{array}\right]}^2\end{array}}$$

(26)

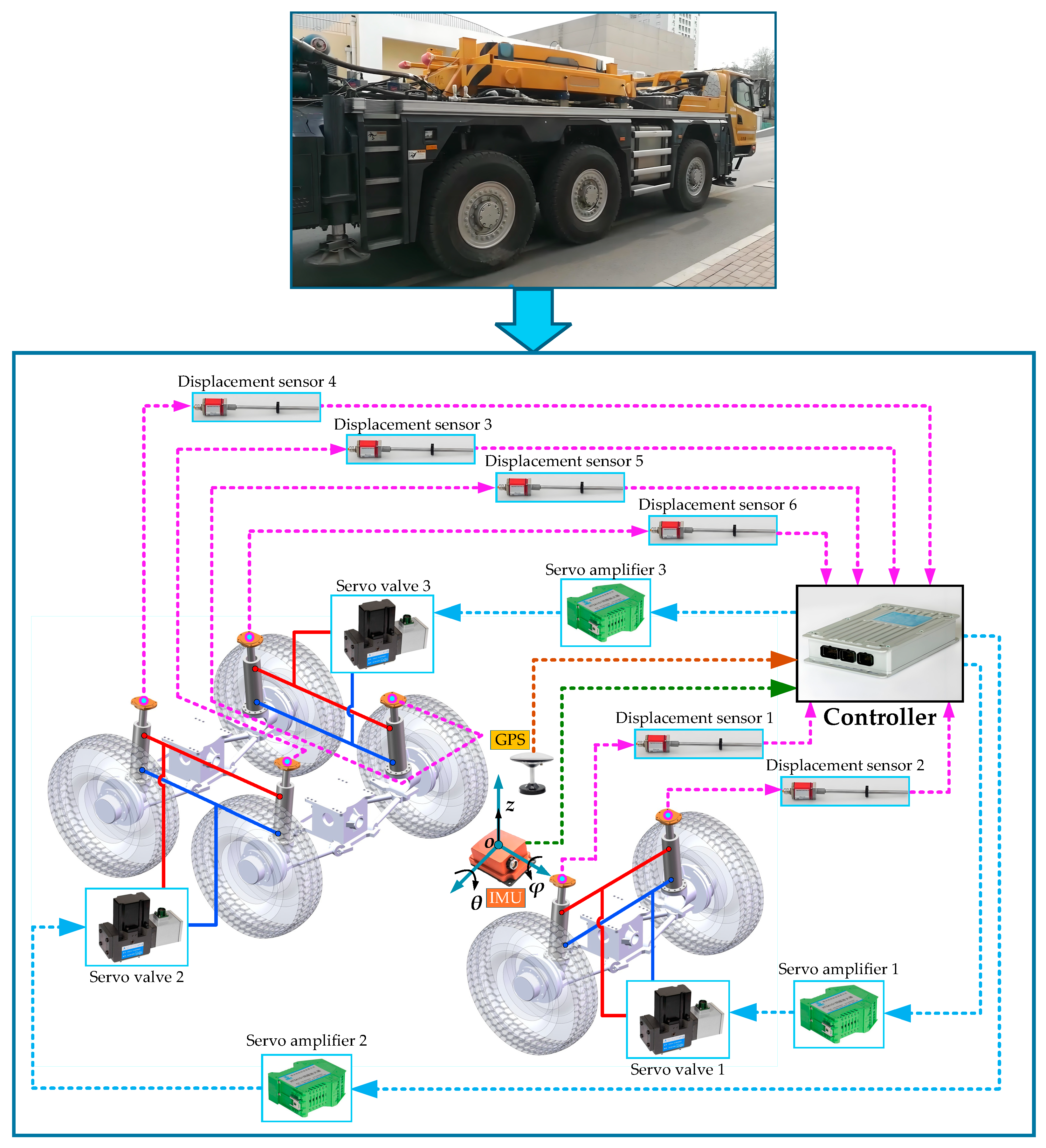
3. Construction of the Three-Axle Vehicle Experimental Platform and Experiments

3.1. Construction of the Three-Axle Vehicle Experimental Platform

In order to verify the application effect of the proposed ASCS-IPSPM in practical engineering, this paper selects a crane chassis produced by a company to build the vehicle suspension system experimental platform, and its structural composition and appearance are shown in Figure 10. The controller selects the PC/104 motherboard of SCM9022, produced by Shengbo Technology Embedded Computer Co., Ltd., Shenzhen, China, which is responsible for the realization of the control algorithm and the coordination of the solution modules of the system. The SysExpandModuleTM/ADT882-AT data acquisition card produced by the company is used for data signal acquisition and output. The electro-hydraulic servo valve adopts an SFD234 type electric feedback jet pipe servo valve and its supporting amplifier provided by Aerospace Junhe Technology Co., Ltd., and it receives the command signal from the controller. The displacement sensor adopts the MH100 magnetostrictive displacement sensor of the MTS company, which is used to measure the displacement of the suspension actuator cylinder in real time. The sensors used to measure the vehicle’s attitude are the combination of the Inertial Measurement Unit (IMU) and GPS. By fusing IMU and GPS measurement data through the Kalman filter, the cumulative error of a single sensor can be effectively compensated [31]. Among them, IMU uses an MTi 300-AHRS industrial grade unit produced by Xsens company in the Netherlands. The GPS system uses the professional measurement grade BD990 board provided by Trimble in the United States and the Zephyr-3 professional measurement grade full band antenna.

For comparative analysis, the vehicle experimental platform built in this study incorporates a dual-suspension architecture comprising both an active suspension system and hydro-pneumatic suspension (HPS). These two distinct suspension modalities achieve operational transition through precisely controlled valve group configurations.

3.2. Road Experiments

Based on the vehicle experimental platform built in Figure 10, the pulse road and random road experiments are carried out on the proposed ASCS-IPSPM, with the HPS as the comparison. The triangular deceleration strip shown in Figure 11a is selected as the pulse pavement, and the gravel pavement shown in Figure 11b is selected as the random pavement.

3.2.1. Pulse Road Experiment

• Experimental scheme

As the experimental field for the impulse road was indoors, to ensure the safety of the experiment, the vehicle speed was approximately 5.0 km/h during the experiment. Two sets of experiments were respectively conducted, one with a bilateral triangular deceleration strip and the other with a unilateral triangular deceleration strip.

(1)

The experimental scheme of bilateral triangular deceleration strips

Place two sets of triangular deceleration strips symmetrically according to the wheelbase in front of the vehicle. Start the active suspension system control program, drive the vehicle through the triangular deceleration strips, and record the vehicle’s body attitude and acceleration variations during the crossing process. Deactivate the active suspension system program, switch the suspension system to HPS, and drive the vehicle through the triangular deceleration strips at the same speed and manner, again recording the vehicle’s body attitude and acceleration changes. The bilateral deceleration strips experiment aims to evaluate the vertical motion and pitch motion of the vehicle during the crossing process.

(2)

The experimental scheme of the unilateral triangular deceleration strip

Start the active suspension system control program, drive the vehicle to traverse a deceleration strip with only one side wheel while maintaining the opposite wheels on the concrete pavement, and record the vehicle’s body attitude and acceleration variations during the crossing process. Deactivate the active suspension system program, switch the suspension system to HPS, and drive the vehicle through the triangular deceleration strip at the same speed and manner, again recording the vehicle’s body attitude and acceleration changes. The unilateral triangular deceleration strip experiment aims to evaluate the roll motion of the vehicle during the crossing process.

2.

Experimental results and analysis

Figure 12a and Figure 12b show the vertical displacement and pitch angle variations of the vehicle body when passing through the bilateral triangular deceleration strips under HPS and active suspension, respectively. Figure 12c demonstrates the roll angle changes when passing through the unilateral triangular deceleration strip under HPS and active suspension, respectively. Figure 12d and Figure 12e show the vertical acceleration and pitch angle acceleration variations of the vehicle body when passing through the bilateral triangular deceleration strips under HPS and active suspension, respectively. Figure 12f demonstrates the roll angle acceleration changes when passing through the unilateral triangular deceleration strip under HPS and active suspension, respectively.

Table 1. Peak values of the vehicle body attitude and attitude acceleration.

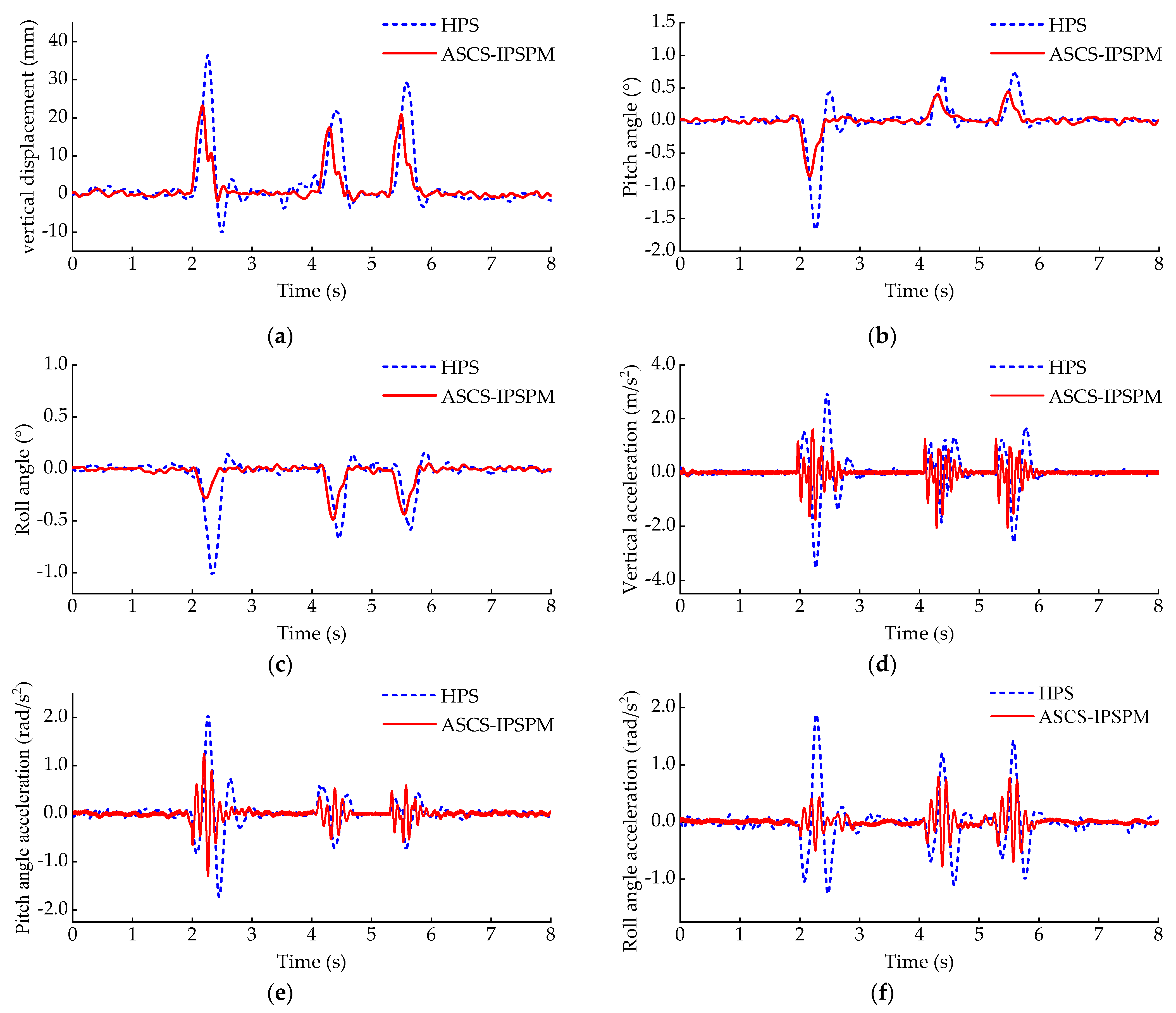
Body Attitude and Acceleration	HPS	ASCS-IPSPM
vertical displacement	36.1 (mm)	23.2 (mm)
pitch angle	1.69 (°)	0.88 (°)
roll angle	1.04 (°)	0.51 (°)
vertical acceleration	3.5351 (m·s−2)	2.0732 (m·s−2)
pitch angle acceleration	2.0563 (rad·s−2)	1.2952 (rad·s−2)
roll angle acceleration	1.8873 (rad·s−2)	0.7955 (rad·s−2)

summarizes the peak values of the vehicle attitude and attitude acceleration when passing through the triangular deceleration strips.

As shown in Figure 12a–c, whether passing over the bilateral triangular deceleration strips or the unilateral triangular deceleration strip, the HPS vehicle exhibits significant body attitude fluctuations. Notably, when the front axle of the vehicle traverses the deceleration strip, the attitude oscillation range reaches its maximum. In contrast, active suspension exhibits smaller fluctuations in vehicle body attitude, demonstrating a significant advantage in maintaining attitude stability. This advantage can be quantitatively demonstrated by the data presented in Table 1. According to the data shown in Table 1, compared with the HPS, the fluctuation peaks of the vertical displacement, pitch angle, and roll angle of the vehicle under active suspension are reduced by 35.73%, 48.31%, and 51.09%, respectively. Therefore, the ASCS-IPSPM proposed in this paper shows a good control effect in stabilizing the vehicle attitude.

As can be seen in Figure 12d,e, when subjected to instantaneous impact from triangular deceleration strips, the vertical acceleration, pitch angular acceleration, and roll angular acceleration of the vehicle body under a hydro-pneumatic suspension system exhibit significant variations. In contrast, the amplitude of the acceleration changes under the active suspension are relatively smaller, demonstrating notable suppression of vehicle body vibrations. The suppression effect on vehicle body vibration is quantitatively demonstrated by the data shown in Table 1. As calculated in Table 1, the peak values of the vertical acceleration, pitch angular acceleration, and roll angular acceleration under the active suspension are reduced by 41.35%, 37.01%, and 57.84%, respectively, compared with the HPS. These results indicate that the proposed ASCS-IPSPM can effectively suppress the vehicle body vibration, thereby improving the ride comfort and passenger comfort.

3.2.2. Gravel Pavement Experiment

• Experimental scheme

First, start the active suspension system control program, drive the vehicle over a designated path, and record the changes in body attitude and acceleration data. Then, deactivate the active suspension system program and switch to HPS. Maintain the same speed and path, and then record the body posture parameters and acceleration changes as well.

2.

Experimental results and analysis

Figure 13a–c show the curves of the vertical displacement, roll angle, and pitch angle of the vehicle body on the gravel pavement. Figure 13d–f show the curves of the vertical acceleration, pitch angle acceleration, and roll angle acceleration of the vehicle body under the gravel pavement.

It can be seen in the Figure 13a–c that during the driving process, the fluctuation range of the vehicle body attitude under the HPS is large, while the fluctuation range of the vehicle body attitude under the active suspension is significantly smaller than that under the HPS, and the stability of the vehicle attitude is greatly improved. It can be seen that the ASCS-IPSPM proposed in this paper shows good control performance in stabilizing the vehicle body attitude and improves the handling stability of the vehicle under the driving condition of gravel pavement.

In Figure 13d–f, it can be seen that compared with the HPS, the accelerations of the vertical vibration, pitch angle, and roll angle of the vehicle body under the active suspension are attenuated to a certain extent. The degree of attenuation can be determined based on the root mean square (RMS) values of each acceleration given in

Table 2. RMS value of the vehicle acceleration on gravel pavement.

Acceleration	HPS	ASCS-IPSPM
vertical acceleration	0.6581 (m·s−2)	0.4892 (m·s−2)
pitch angle acceleration	0.4262 (rad·s−2)	0.3311 (rad·s−2)
roll angle acceleration	0.4860 (rad·s−2)	0.3833 (rad·s−2)

. Compared with the HPS, the RMS values of the vertical acceleration, the pitch angular acceleration, and the roll angular acceleration under the active suspension are reduced by 25.66%, 22.31%, and 21.13% respectively. The ride comfort of the vehicle is greatly improved.

To further illustrate the effectiveness of the ASCS-IPSPM in suppressing vehicle body vibrations, a frequency-domain characteristic analysis based on power spectral density (PSD) [32] was conducted for the vertical, roll, and pitch three-directional acceleration responses. Figure 13g–i show the curves of the power spectral density of the vertical acceleration, pitch angle acceleration, and roll angle acceleration of the vehicle body. As shown in Figure 13g–i, compared with the HPS, the ASCS-IPSPM effectively suppresses the vibration amplitudes of vertical acceleration, roll angular acceleration, and pitch angular acceleration within the 0–10 Hz frequency band, which includes the 4–8 Hz range most sensitive to human perception. This indicates that the control strategy achieves superior vibration attenuation performance in the frequency range most sensitive to humans.

The experimental results of the gravel pavement verify again that the ASCS-IPSPM proposed in this paper can effectively stabilize the vehicle body attitude while improving the ride comfort and handling stability.

4. Discussion and Conclusions

The ASCS-IPSPM proposed in this paper simplifies the control complexity of active suspension systems for multi-axle emergency rescue vehicles by modeling the vehicle as a 3-DOF parallel mechanism and deriving its inverse kinematic solution. This approach enhances real-time control performance while demonstrating significant advantages in vehicle attitude stabilization and vibration suppression compared to the conventional HPS. Under the pulse road, active suspension reduces the peak fluctuations of the vertical displacement, pitch angle, and roll angle by 35.73%, 48.31%, and 51.09% compared to HPS. In terms of vibration suppression, the RMS values of vertical, pitch, and roll accelerations are reduced by 25.66%, 22.31%, and 21.13% compared with HPS under the gravel pavement. Moreover, ASCS-IPSPM effectively suppresses vibrations in the 0–10 Hz frequency band, especially in the most sensitive range of 4–8 Hz for humans, indicating the advantages of this strategy in alleviating human-sensitive vibrations and significantly improving ride comfort.

The active suspension control strategy proposed in this paper is not limited to three-axis vehicles, and it is equally effective for active suspension systems in four-axis and above vehicles equipped with hydraulic cylinder actuators. In addition, the controller and sensors adopted in the experimental platform constructed in this article exhibit excellent interchangeability and platform portability. When migrating the control system to alternative computing platforms, it is only necessary to ensure that the new platform meets equivalent computational performance requirements (such as real-time capability and computing power) and provides corresponding hardware interface drivers. This design facilitates the effective deployment of the control strategy across diverse hardware configurations.

The active suspension chassis developed based on this strategy is not only suitable for emergency rescue vehicles but also holds significant application value for special-purpose vehicles requiring high-precision stabilization of body posture, such as aerial ladder fire trucks, truck cranes, ambulances, and launch platforms.

Based on the experimental results, the proposed active suspension control strategy demonstrates excellent performance under low-speed driving conditions. However, due to the inherent phase lag characteristics of the hydraulic actuation system and the physical constraints of the vehicle powertrain’s output power, it is difficult to achieve real-time and precise compensation for road excitation at high-speed driving conditions. Therefore, the in-depth exploration of time-delay compensation mechanisms under high-speed conditions, the optimization of energy management strategies to overcome power limitations, and the enhancement of the overall dynamic response performance of the system will be the key focus areas for future research.