Robust Path Tracking Control with Lateral Dynamics Optimization: A Focus on Sideslip Reduction and Yaw Rate Stability Using Linear Quadratic Regulator and Genetic Algorithms
Abstract
1. Introduction
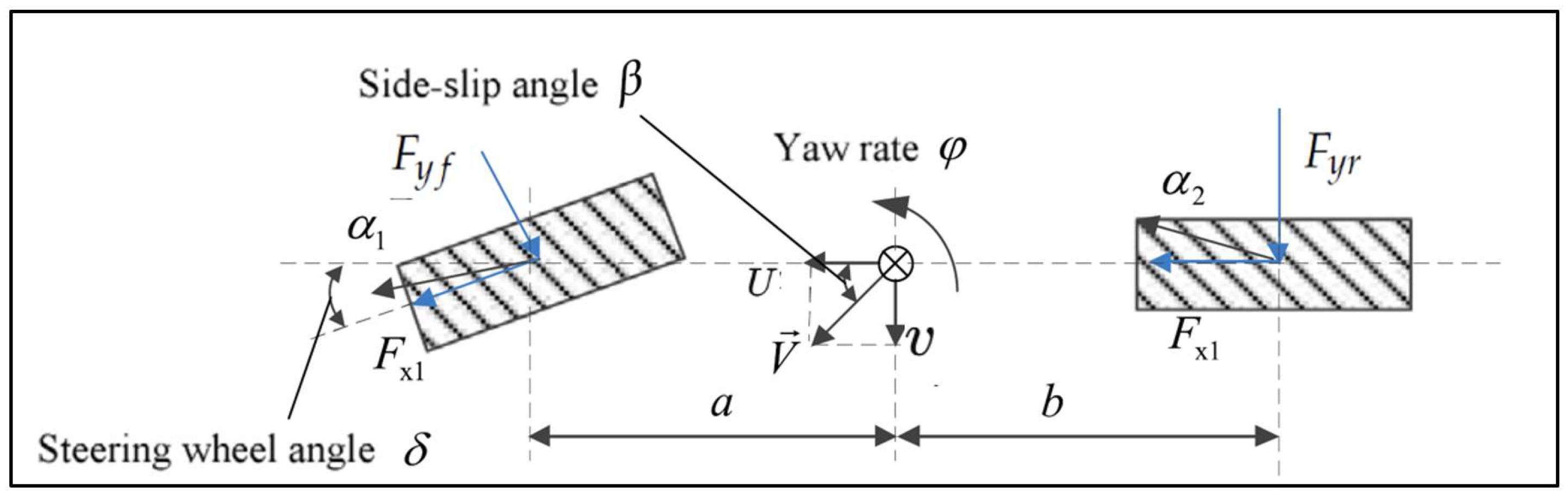
2. Vehicle Dynamics Modeling
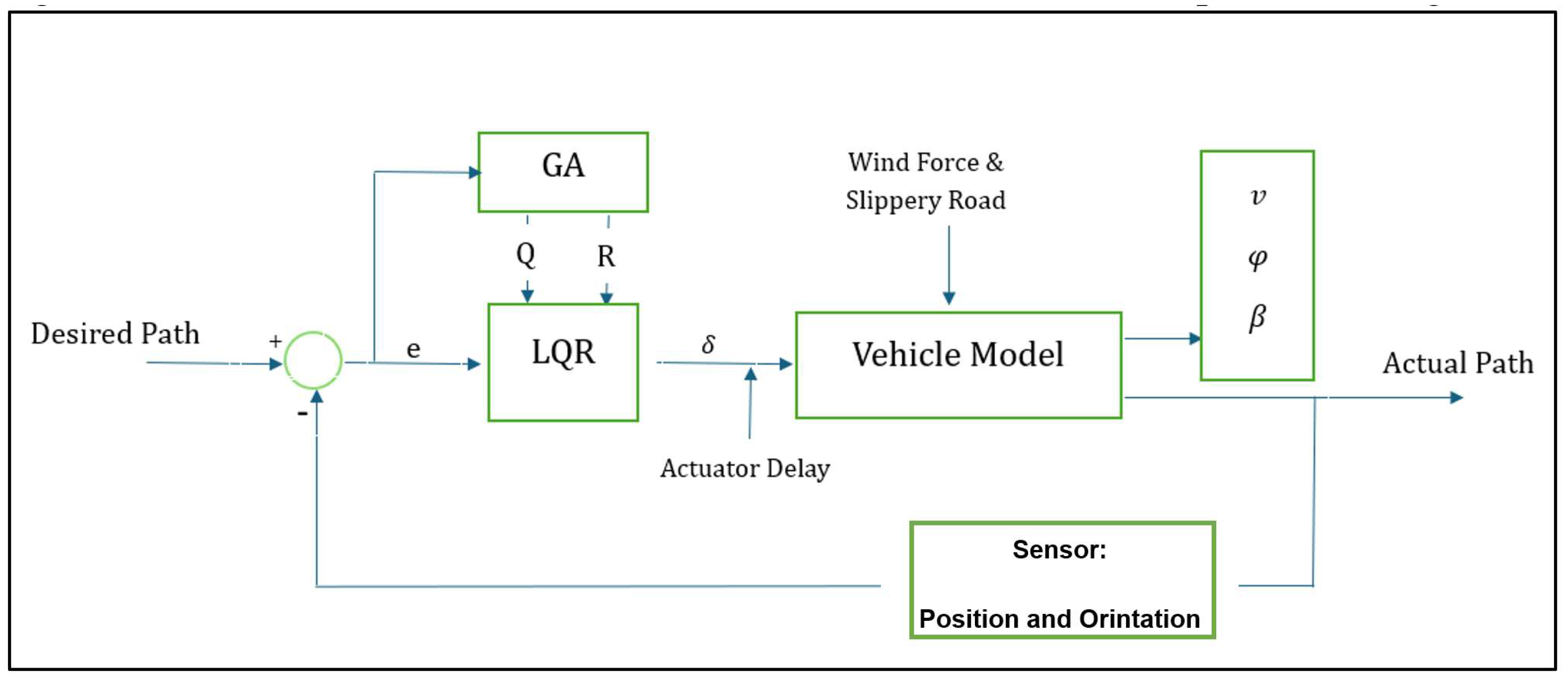
3. Control Design
3.1. Linear Quadratic Regulator (LQR)
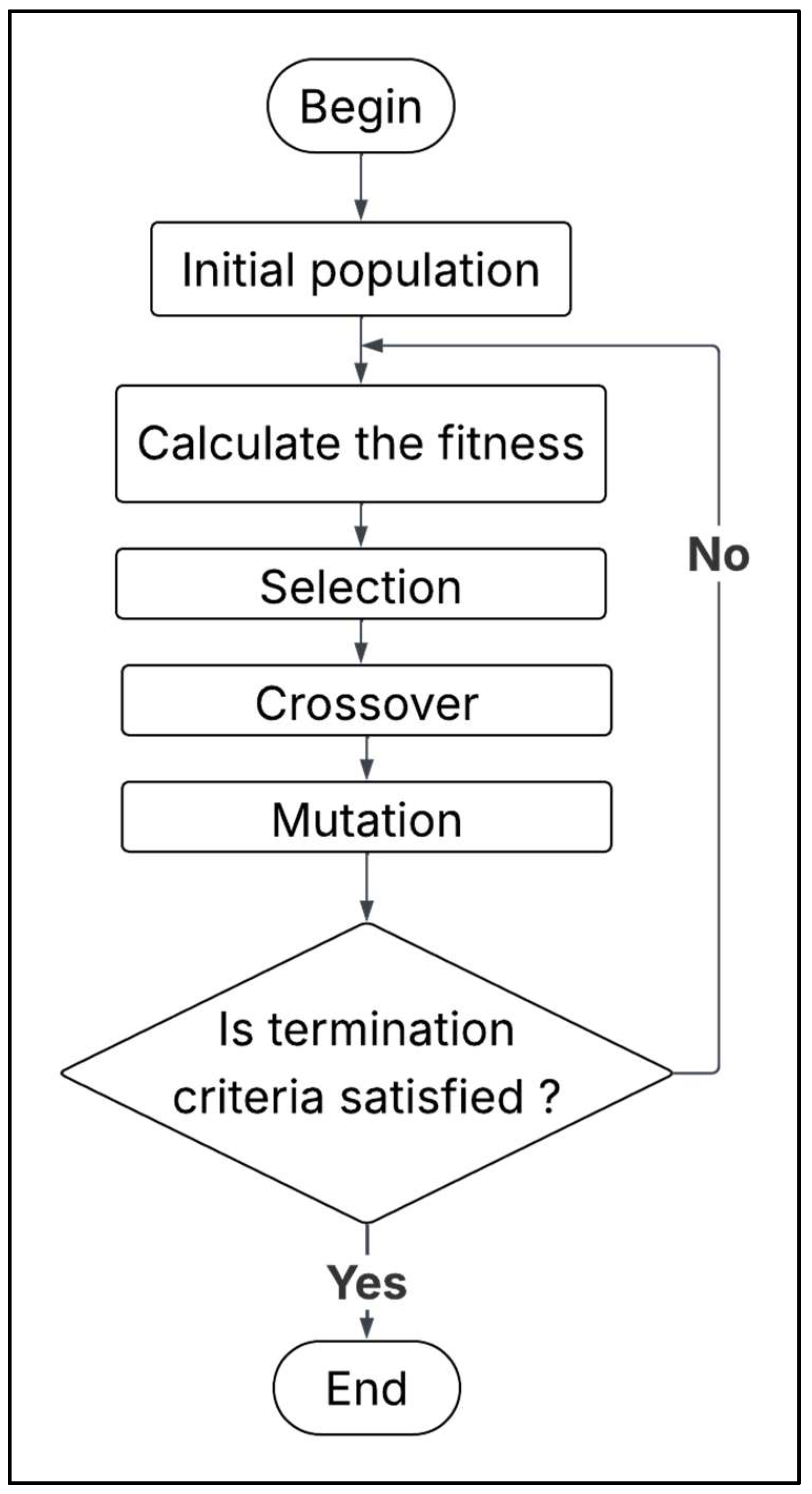
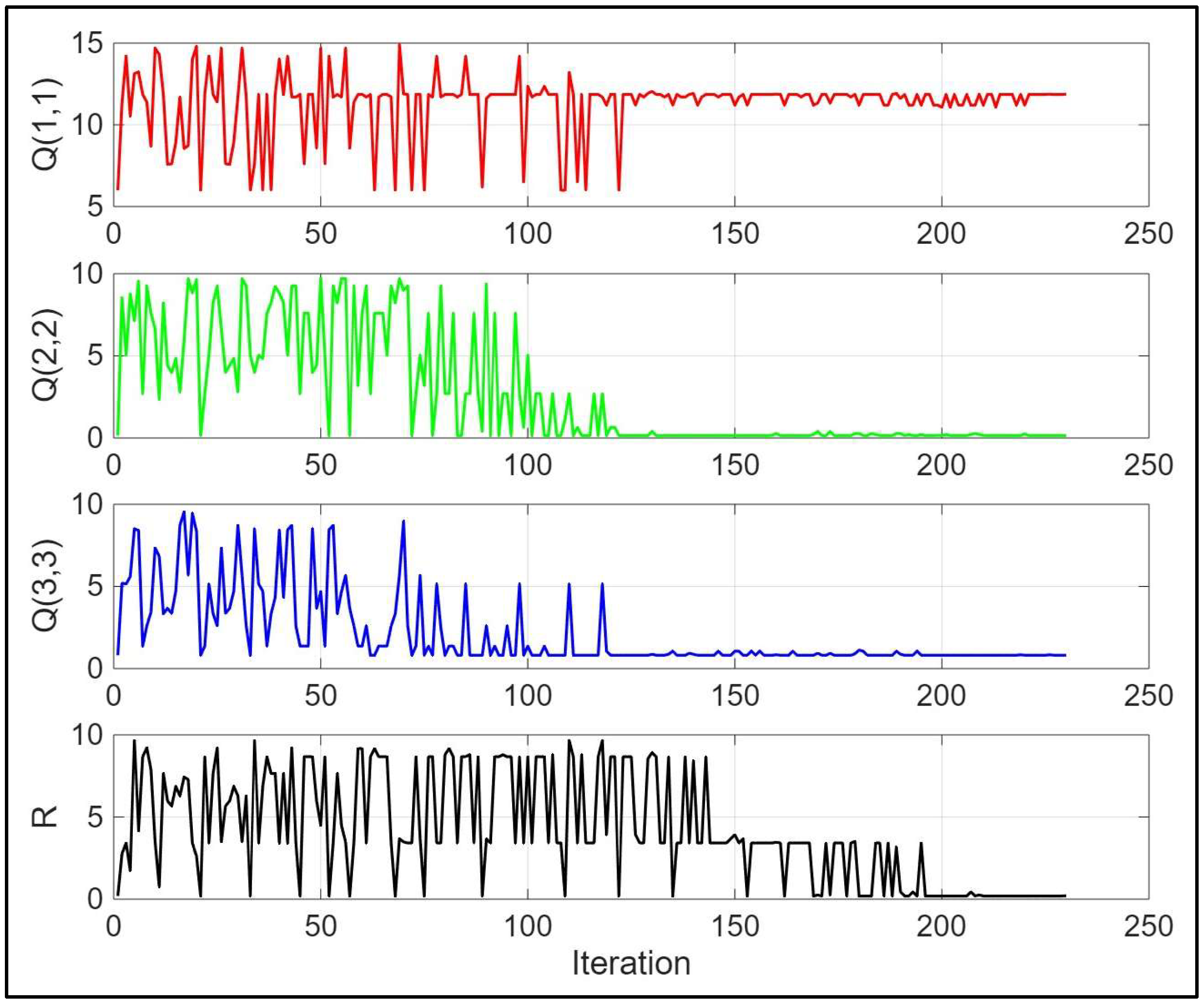
3.2. Genetic Algorithm Optimization
4. Simulation Setup
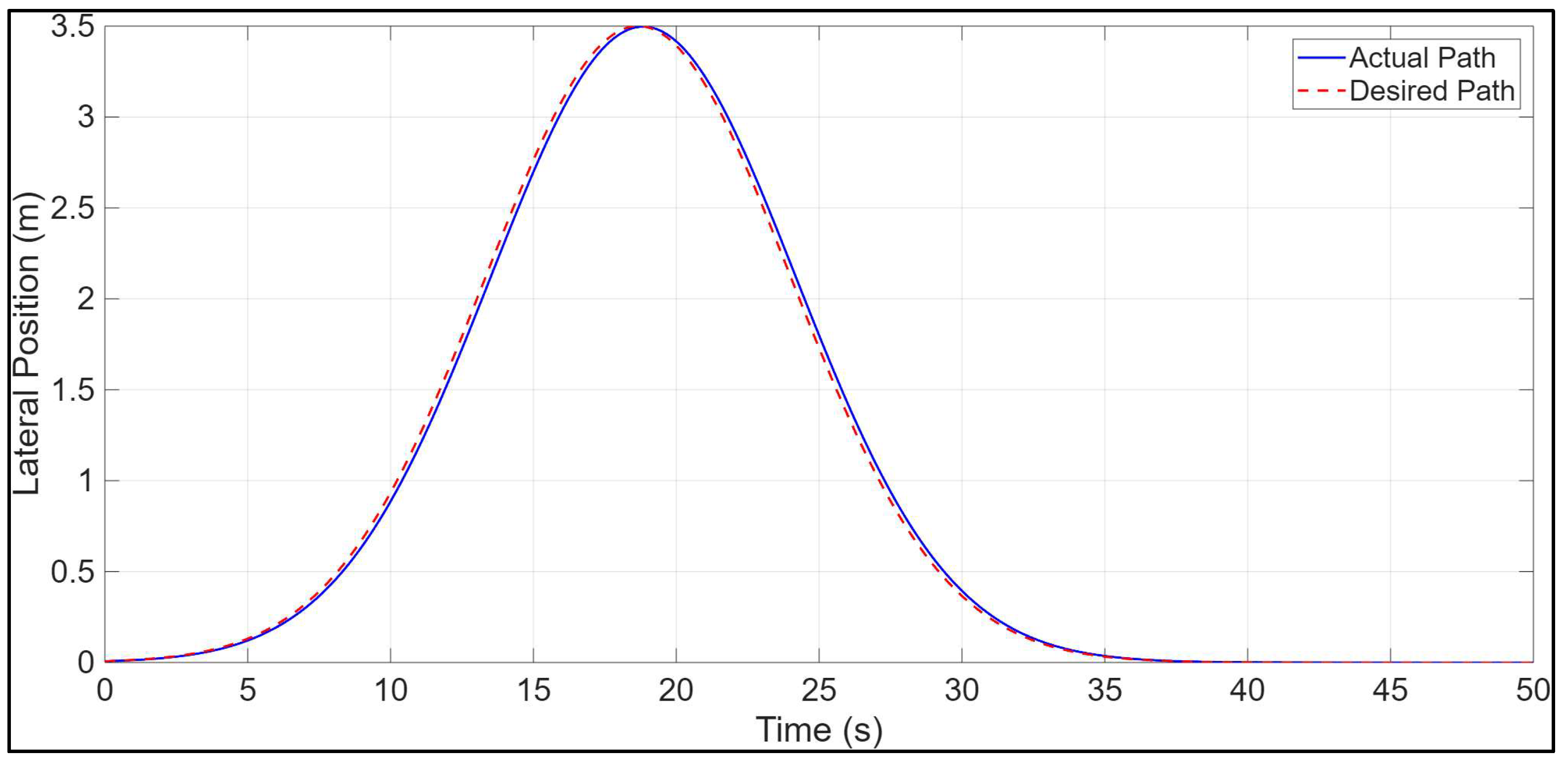
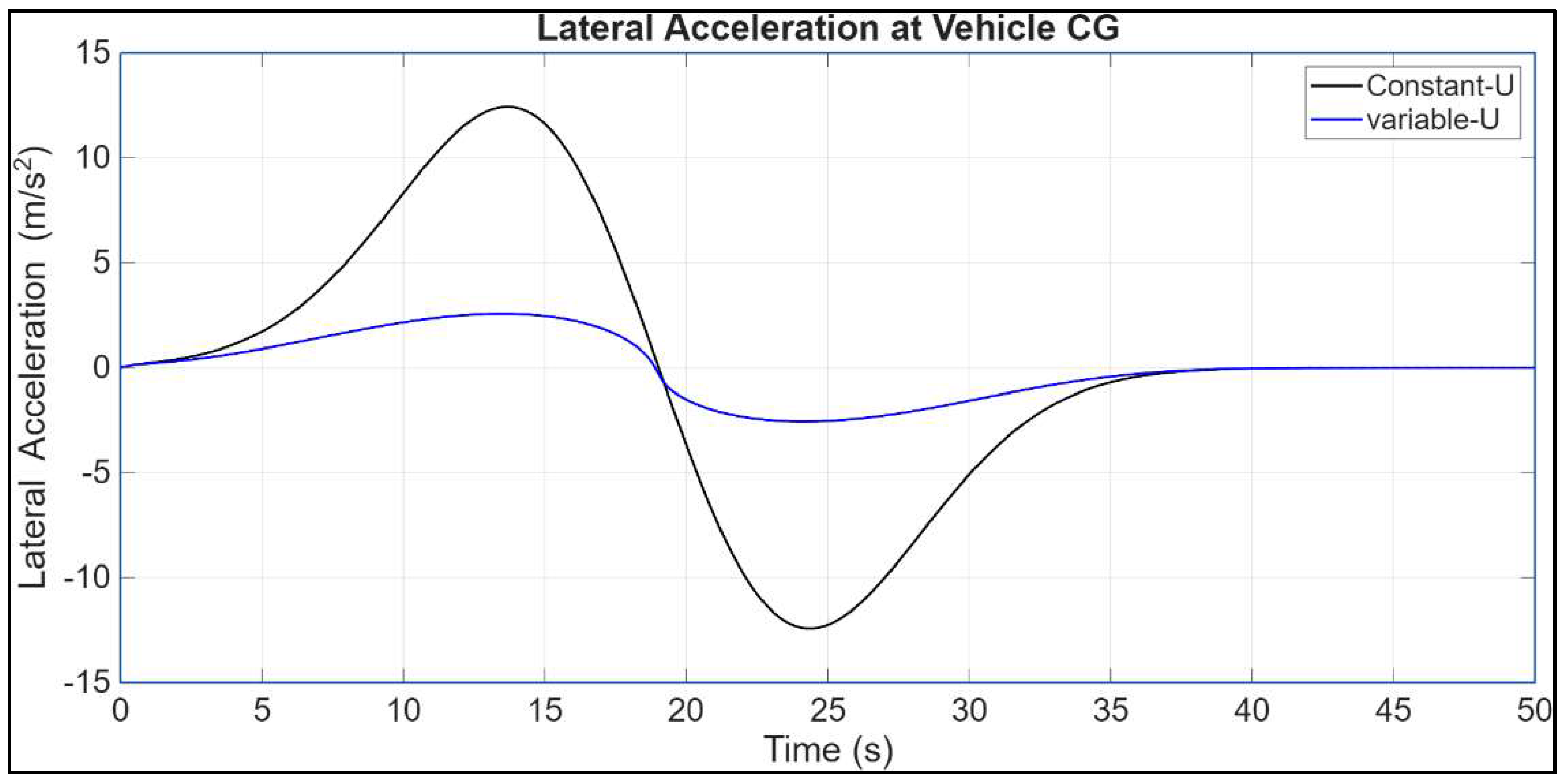
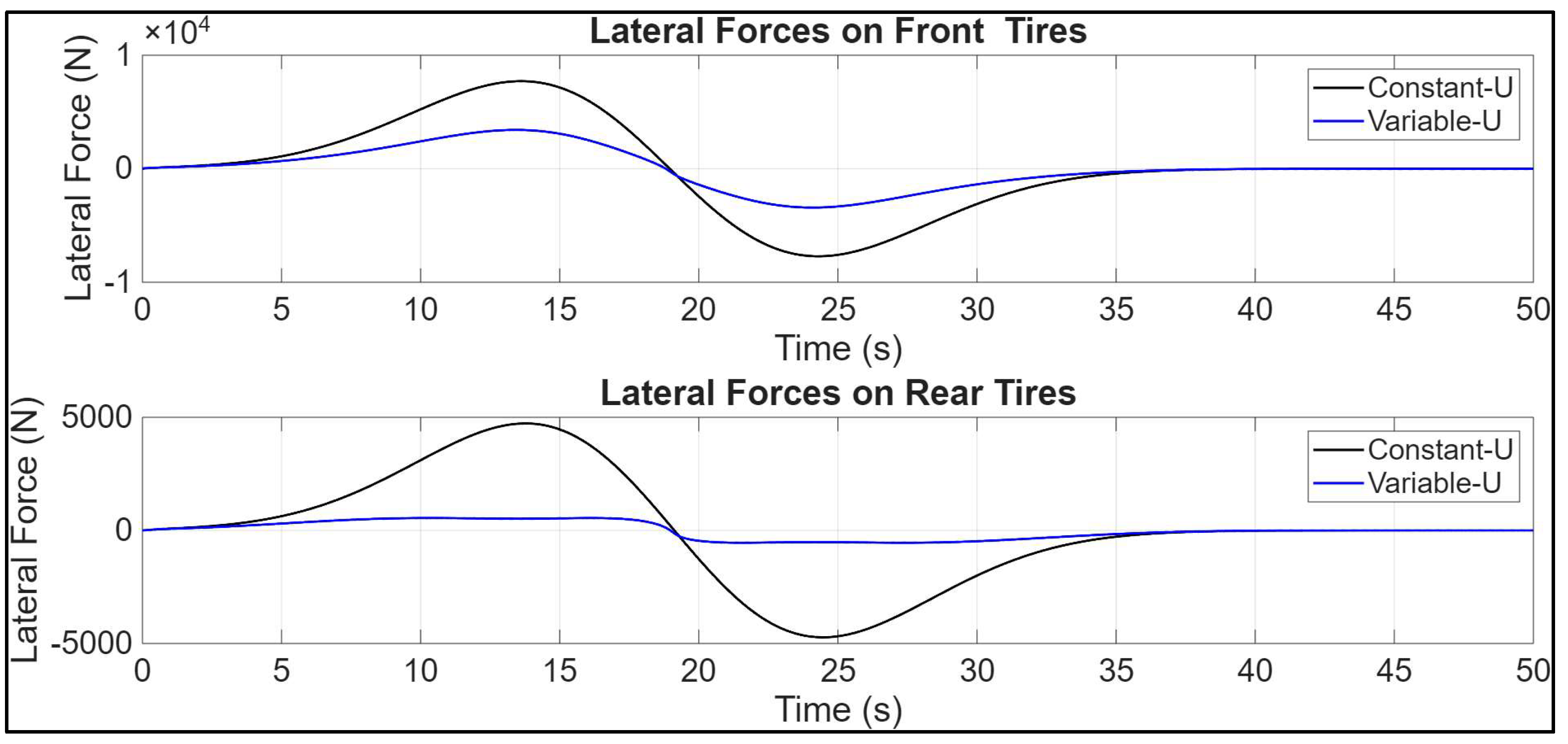
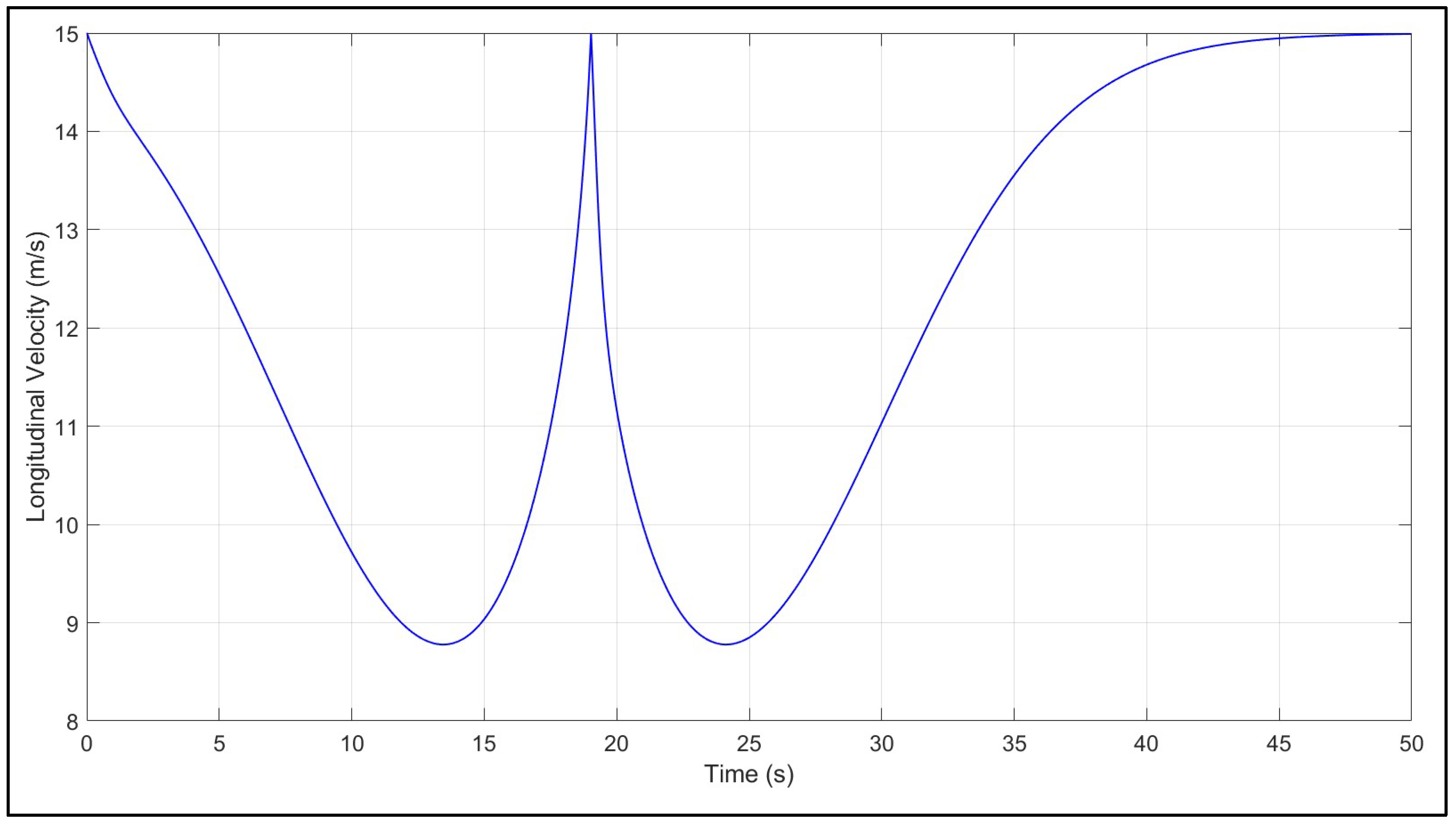
4.1. Constant vs. Variable Longitudinal Velocity U
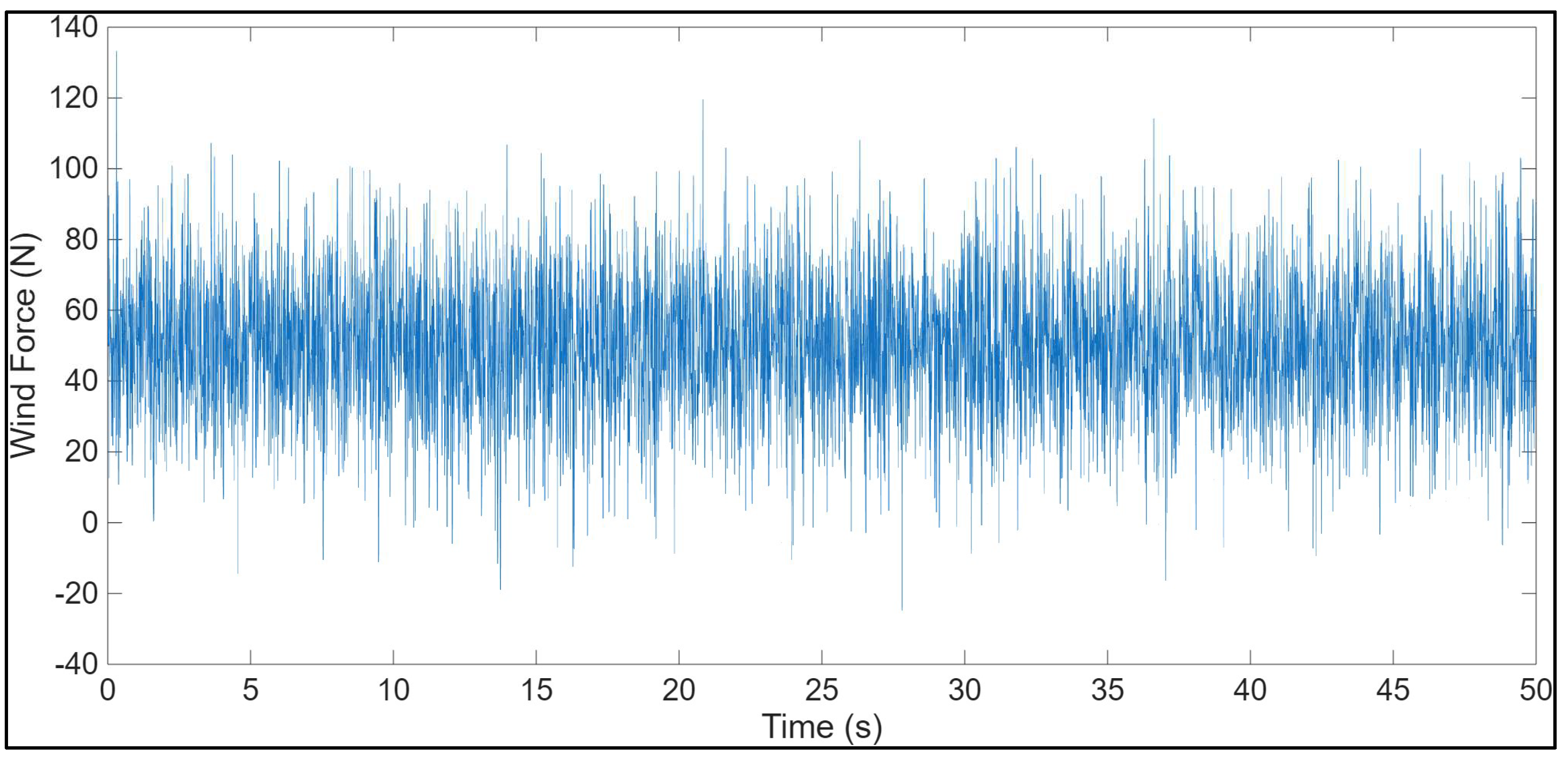
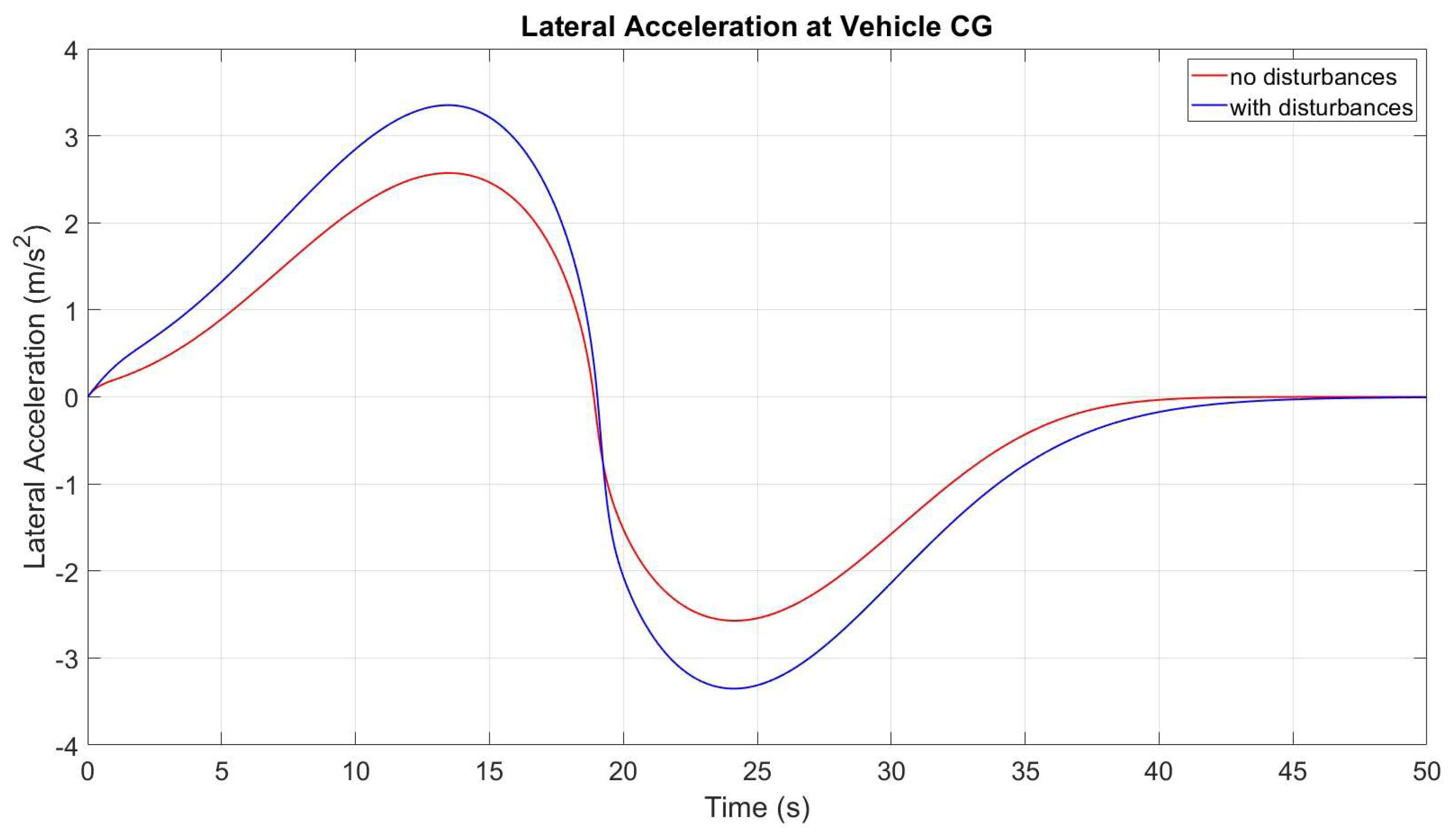
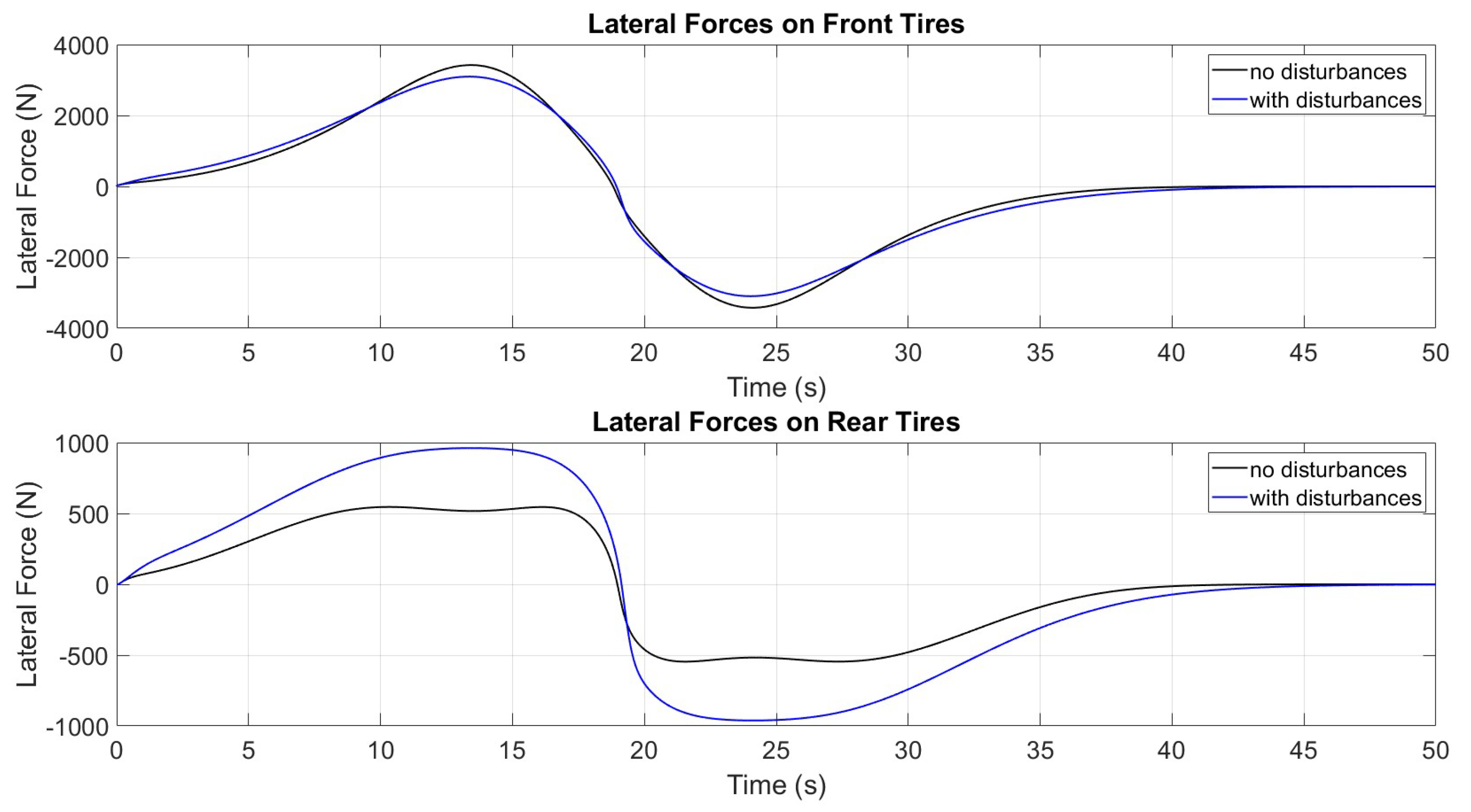
4.2. Disturbance and Delay in the Actuator Added to the System
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Faisal, A.; Kamruzzaman, M.; Yigitcanlar, T.; Currie, G. Understanding autonomous vehicles. J. Transp. Land Use 2019, 12, 45–72. [Google Scholar] [CrossRef]
- Booth, L.; Karl, C.; Farrar, V.; Pettigrew, S. Assessing the Impacts of Autonomous Vehicles on Urban Sprawl. Sustainability 2024, 16, 5551. [Google Scholar] [CrossRef]
- Bektache, D.; Ghoualmi-Zine, N. An artificial intelligence-based approach for avoiding traffic congestion in connected autonomous vehicles. Int. J. Veh. Auton. Syst. 2025, 18, 81–103. [Google Scholar] [CrossRef]
- Pappalardo, G.; Caponetto, R.; Varrica, R.; Cafiso, S. Assessing the operational design domain of lane support system for automated vehicles in different weather and road conditions. J. Traffic Transp. Eng. (Engl. Ed.) 2022, 9, 631–644. [Google Scholar] [CrossRef]
- Ma, B.; Pei, W.; Zhang, Q. Trajectory tracking control of autonomous vehicles based on an improved sliding mode control scheme. Electronics 2023, 12, 2748. [Google Scholar] [CrossRef]
- Rokonuzzaman, M.; Mohajer, N.; Nahavandi, S.; Mohamed, S. Review and performance evaluation of path tracking controllers of autonomous vehicles. IET Intell. Transp. Syst. 2021, 15, 646–670. [Google Scholar] [CrossRef]
- Tang, X.; Shi, L.; Wang, B.; Cheng, A. Weight adaptive path tracking control for autonomous vehicles based on PSO-BP neural network. Sensors 2022, 23, 412. [Google Scholar] [CrossRef]
- Deshmukh, D.; Kumutham, A.R.; Pratihar, D.K.; Deb, A.K. Accurate path tracing of a tracked robot: A modified PID approach with slip compensation. Eng. Res. Express 2025, 7, 015203. [Google Scholar] [CrossRef]
- He, Y.; Wu, J.; Xu, F.; Liu, X.; Wang, S.; Cui, G. Path tracking control based on TS fuzzy model for autonomous vehicles with yaw angle and heading angle. Machines 2024, 12, 375. [Google Scholar] [CrossRef]
- Tang, L.; Yan, F.; Zou, B.; Wang, K.; Lv, C. An improved kinematic model predictive control for high-speed path tracking of autonomous vehicles. IEEE Access 2020, 8, 51400–51413. [Google Scholar] [CrossRef]
- Ni, J.; Wang, Y.; Li, H.; Du, H. Path tracking motion control method of tracked robot based on improved LQR control. In Proceedings of the IEEE 2022 41st Chinese Control Conference (CCC), Hefei, China, 25–27 July 2022; pp. 2888–2893. [Google Scholar]
- Reda, A.; Benotsmane, R.; Bouzid, A.; Vásárhelyi, J. A hybrid machine learning-based control strategy for autonomous driving optimization. Acta Polytech. Hung. 2023, 20, 165–186. [Google Scholar] [CrossRef]
- Kovacs, A.; Vajk, I. Tuning parameter-free model predictive control with nonlinear internal model control structure for vehicle lateral control. Acta Polytech. Hung. 2023, 20, 185–204. [Google Scholar] [CrossRef]
- Zhang, X.; Li, J.; Ma, Z.; Chen, D.; Zhou, X. Lateral trajectory tracking of self-driving vehicles based on sliding mode and fractional-order proportional-integral-derivative control. Actuators 2023, 13, 7. [Google Scholar] [CrossRef]
- Zou, T.; Angeles, J.; Hassani, F. Dynamic modeling and trajectory tracking control of unmanned tracked vehicles. Robot. Auton. Syst. 2018, 110, 102–111. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, M.; Zhang, Y.; Guan, T.; Song, X.; Liu, J.; Zhen, Y.; Zhang, D. Driverless simulation of path tracking based on PID control. In Proceedings of the IOP Conference Series: Materials Science and Engineering, Hangzhou, China, 18–20 April 2020; Volume 892, No. 1. p. 012050. [Google Scholar]
- Lee, K.; Im, D.Y.; Kwak, B.; Ryoo, Y.J. Design of fuzzy-PID controller for path tracking of mobile robot with differential drive. Int. J. Fuzzy Log. Intell. Syst. 2018, 18, 220–228. [Google Scholar]
- Han, G.; Fu, W.; Wang, W.; Wu, Z. The lateral tracking control for the intelligent vehicle based on adaptive PID neural network. Sensors 2017, 17, 1244. [Google Scholar] [CrossRef]
- Debarshi, S.; Sundaram, S.; Sundararajan, N. Robust EMRAN-aided coupled controller for autonomous vehicles. Eng. Appl. Artif. Intell. 2022, 110, 104717. [Google Scholar] [CrossRef]
- Samak, C.V.; Samak, T.V.; Kandhasamy, S. Proximally optimal predictive control algorithm for path tracking of self-driving cars. In Proceedings of the 2021 5th International Conference on Advances in Robotics, Kanpur, India, 30 June–4 July 2021; pp. 1–5. [Google Scholar]
- Varma, B.; Swamy, N.; Mukherjee, S. Trajectory tracking of autonomous vehicles using different control techniques (pid vs lqr vs mpc). In Proceedings of the 2020 IEEE International Conference on Smart Technologies in Computing, Electrical and Electronics (ICSTCEE), Bengaluru, India, 9–10 October 2020; pp. 84–89. [Google Scholar]
- Wang, H.; Liu, B.; Ping, X.; An, Q. Path tracking control for autonomous vehicles based on an improved MPC. IEEE Access 2019, 7, 161064–161073. [Google Scholar] [CrossRef]
- Hu, J.; Peng, H.; Gao, H. Trajectory Tracking Control Based on Fuzzy-MPC for Autonomous Vehicles. In Proceedings of the 2024 IEEE 6th International Conference on Industrial Artificial Intelligence (IAI), Shenyang, China, 21–24 August 2024; pp. 1–6. [Google Scholar]
- Tavan, N.; Tavan, M.; Hosseini, R. An optimal integrated longitudinal and lateral dynamic controller development for vehicle path tracking. Lat. Am. J. Solids Struct. 2015, 12, 1006–1023. [Google Scholar] [CrossRef]
- Vivek, K.; Sheta, M.A.; Gumtapure, V. A comparative study of Stanley, LQR and MPC controllers for path tracking application (ADAS/AD). In Proceedings of the 2019 IEEE International Conference on Intelligent Systems and Green Technology (ICISGT), Visakhapatnam, India, 29–30 June 2019; pp. 67–674. [Google Scholar]
- Zhao, F.; An, J.; Chen, Q.; Li, Y. Integrated path following and lateral stability control of distributed drive autonomous unmanned vehicle. World Electr. Veh. J. 2024, 15, 122. [Google Scholar] [CrossRef]
- Wang, Z.; Sun, K.; Ma, S.; Sun, L.; Gao, W.; Dong, Z. Improved linear quadratic regulator lateral path tracking approach based on a real-time updated algorithm with fuzzy control and cosine similarity for autonomous vehicles. Electronics 2022, 11, 3703. [Google Scholar] [CrossRef]
- Nagariya, A.; Saripalli, S. An iterative lqr controller for off-road and on-road vehicles using a neural network dynamics model. In Proceedings of the 2020 IEEE Intelligent Vehicles Symposium (IV), Las Vegas, NV, USA, 19 October–13 November 2020; pp. 1740–1745. [Google Scholar]
- Zhao, W.; Gu, L. Hybrid particle swarm optimization genetic LQR controller for active suspension. Appl. Sci. 2023, 13, 8204. [Google Scholar] [CrossRef]
- Cheng, S.; Li, L.; Yan, B.; Liu, C.; Wang, X.; Fang, J. Simultaneous estimation of tire side-slip angle and lateral tire force for vehicle lateral stability control. Mech. Syst. Signal Process. 2019, 132, 168–182. [Google Scholar] [CrossRef]
- Ma, Y.J.; Zhou, X.L.; Ran, M.P. Estimation of Sideslip Angle Based on the Combination of Dynamic and Kinematic Methods. Int. J. Automot. Technol. 2024, 26, 785–798. [Google Scholar] [CrossRef]
- Stano, P.; Montanaro, U.; Tavernini, D.; Tufo, M.; Fiengo, G.; Novella, L.; Sorniotti, A. Model predictive path tracking control for automated road vehicles: A review. Annu. Rev. Control 2023, 55, 194–236. [Google Scholar] [CrossRef]
- Jneid, M.S.; Harth, P. Integrated Torque Vectoring Control Using Vehicle Yaw Rate and Sideslip Angle for Improving Steering and Stability of All Off-Wheel-Motor Drive Electric Vehicles. Acta Polytech. Hung 2024, 21, 87–106. [Google Scholar] [CrossRef]
- Das, S.; Pan, I.; Halder, K.; Das, S.; Gupta, A. LQR based improved discrete PID controller design via optimum selection of weighting matrices using fractional order integral performance index. Appl. Math. Model. 2013, 37, 4253–4268. [Google Scholar] [CrossRef]
- Das, S.; Pan, I.; Halder, K.; Das, S.; Gupta, A. Impact of fractional order integral performance indices in LQR based PID controller design via optimum selection of weighting matrices. In Proceedings of the 2012 IEEE International Conference on Computer Communication and Informatics, Coimbatore, India, 10–12 January 2012; pp. 1–6. [Google Scholar]
- Athuraliya, N.; De Silva, H.; Dasanayake, D.; Fernando, K.; Haddela, P.S.; Gunarathne, A. Classification of Documents and Images Using an Enhanced Genetic Algorithm. In Proceedings of the 2022 IEEE 4th International Conference on Advancements in Computing (ICAC), Colombo, Sri Lanka, 9–10 December 2022; pp. 405–410. [Google Scholar]
- Lambora, A.; Gupta, K.; Chopra, K. Genetic algorithm-A literature review. In Proceedings of the 2019 IEEE International Conference on Machine Learning, Big Data, Cloud and Parallel Computing (COMITCon), Faridabad, India, 14–16 February 2019; pp. 380–384. [Google Scholar]
- Lifeth, A. Modeling Epigenetic Evolutionary Algorithms: An Approach Based on the Epigenetic Regulation Process. Master’s Thesis, Universidad Nacional de Colombia, Engineering School, Computer Systems Engineering, Bogotá, DC, USA, 14 December 2020. [Google Scholar]
- Abdullah, A.; Mahmood, A.; Thanoon, M. Design of Linear Quadratic Regulator Based on Genetic Model Reference Adaptive Control. J. Autom. Mob. Robot. Intell. Syst. 2022, 16, 75–81. [Google Scholar] [CrossRef]
- Mahmood, A.; Al-bayati, K.Y.; Szabolcsi, R. Comparison between Genetic Algorithms of Proportional–Integral–Derivative and Linear Quadratic Regulator Controllers, and Fuzzy Logic Controllers for Cruise Control System. World Electr. Veh. J. 2024, 15, 351. [Google Scholar] [CrossRef]
- Dawood, Y.S.; Mahmood, A.K.; Ibrahim, M.A. Comparison of PID, GA and fuzzy logic controllers for cruise control system. Int. J. Com. Dig. Sys. 2018, 7, 311–319. [Google Scholar]
- Reymond, G.; Kemeny, A.; Droulez, J.; Berthoz, A. Role of lateral acceleration in curve driving: Driver model and experiments on a real vehicle and a driving simulator. Hum. Factors 2001, 43, 483–495. [Google Scholar] [CrossRef] [PubMed]
- NHTSA. Federal Motor Vehicle Safety Standards: Electronic Stability Control Systems; Controls and Displays. 2007. Available online: https://www.nhtsa.gov/document/final-rule-federal-motor-vehicle-safety-standards-electronic-stability-control-systems-0?utm_source=chatgpt.com (accessed on 9 February 2025).



| Parameters | Values |
|---|---|
| Vehicle mass (m) | 1500 (kg) |
| Yaw moment of inertia (Iz) | 3000 (kg·m2) |
| Distance from CG to front axle | 1.2 (m) |
| Distance from CG to rear axle | 1.6 (m) |
| Front cornering stiffness | 80,000 (N/rad) |
| Rear cornering stiffness | 80,000 (N/rad) |
| Height of the center of gravity (hg) | 510 (mm) |
| Rotational Inertia of the wheel (J) | 1 (kg·m2) |
| Radius of the front and rear wheels (RF/RR) | 307 (mm) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-bayati, K.Y.A.; Mahmood, A.; Szabolcsi, R. Robust Path Tracking Control with Lateral Dynamics Optimization: A Focus on Sideslip Reduction and Yaw Rate Stability Using Linear Quadratic Regulator and Genetic Algorithms. Vehicles 2025, 7, 50. https://doi.org/10.3390/vehicles7020050
Al-bayati KYA, Mahmood A, Szabolcsi R. Robust Path Tracking Control with Lateral Dynamics Optimization: A Focus on Sideslip Reduction and Yaw Rate Stability Using Linear Quadratic Regulator and Genetic Algorithms. Vehicles. 2025; 7(2):50. https://doi.org/10.3390/vehicles7020050
Chicago/Turabian StyleAl-bayati, Karrar Y. A., Ali Mahmood, and Róbert Szabolcsi. 2025. "Robust Path Tracking Control with Lateral Dynamics Optimization: A Focus on Sideslip Reduction and Yaw Rate Stability Using Linear Quadratic Regulator and Genetic Algorithms" Vehicles 7, no. 2: 50. https://doi.org/10.3390/vehicles7020050
APA StyleAl-bayati, K. Y. A., Mahmood, A., & Szabolcsi, R. (2025). Robust Path Tracking Control with Lateral Dynamics Optimization: A Focus on Sideslip Reduction and Yaw Rate Stability Using Linear Quadratic Regulator and Genetic Algorithms. Vehicles, 7(2), 50. https://doi.org/10.3390/vehicles7020050








