Pragmatic and Effective Enhancements for Stanley Path-Tracking Controller by Considering System Delay

Abstract

The Stanley controller is a proven approach for path tracking control in automated vehicles. If time delays occur, for example, in signal processing and steering angle control, precision and stability decrease. In this article, enhancements for the Stanley controller are proposed to achieve stable behavior with improved tracking accuracy. The approach uses the curvature of the path as feedforward, whereby the reference point for the feedforward input differs from that of the controller setpoints. By choosing a point further along the path, the negative effects of system delay are reduced. First, the parameters of the Stanley controller are calibrated using a straight line and circle maneuver. Then, the newly introduced feedforward parameter is optimized on a dynamic circuit. The approach was evaluated in simulation and validated on a demonstrator vehicle. The validation tests with the demonstrator vehicle on the dynamic circuit revealed a reduction of the root-mean-square cross-track error from 0.11 m to 0.03 m compared to the Stanley controller. We proved that the proposed approach optimizes the Stanley controller in terms of compensating for the negative effects of system delay. This allows it to be used in a wider range of applications that would otherwise require a more complex control approach.

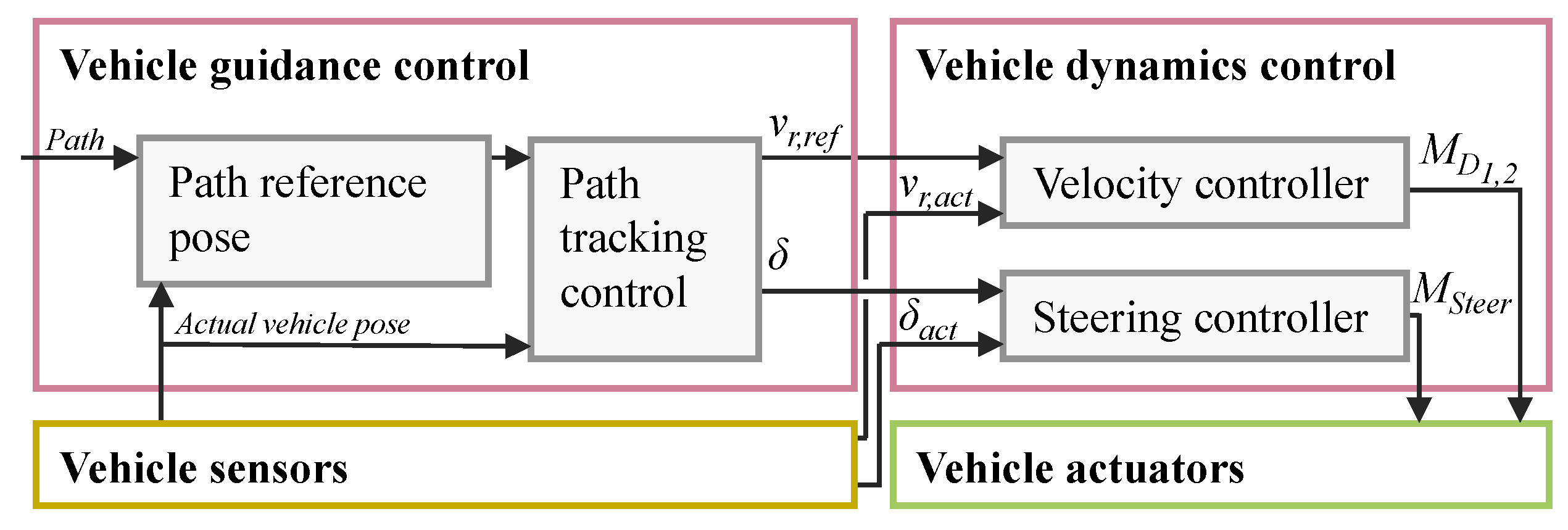
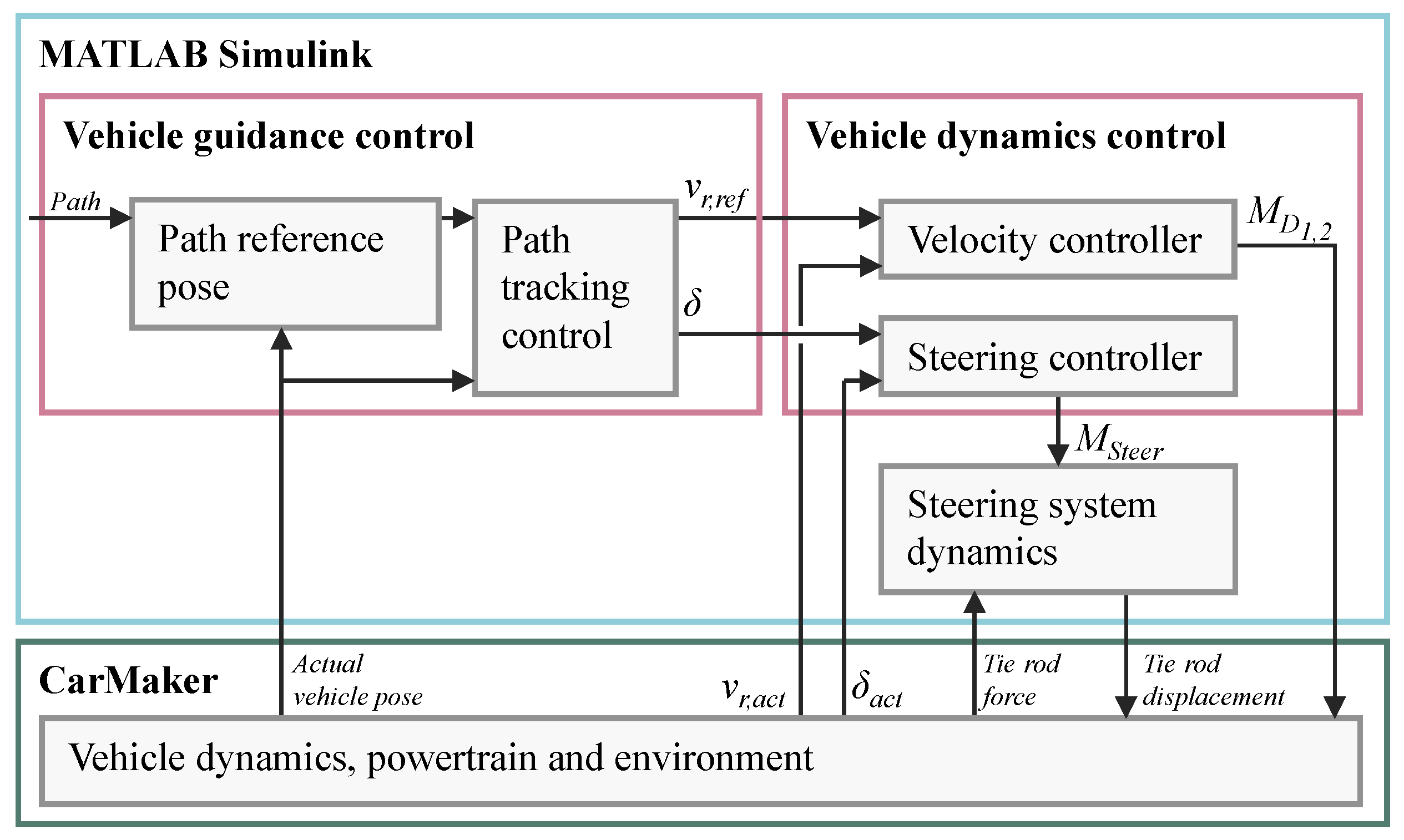
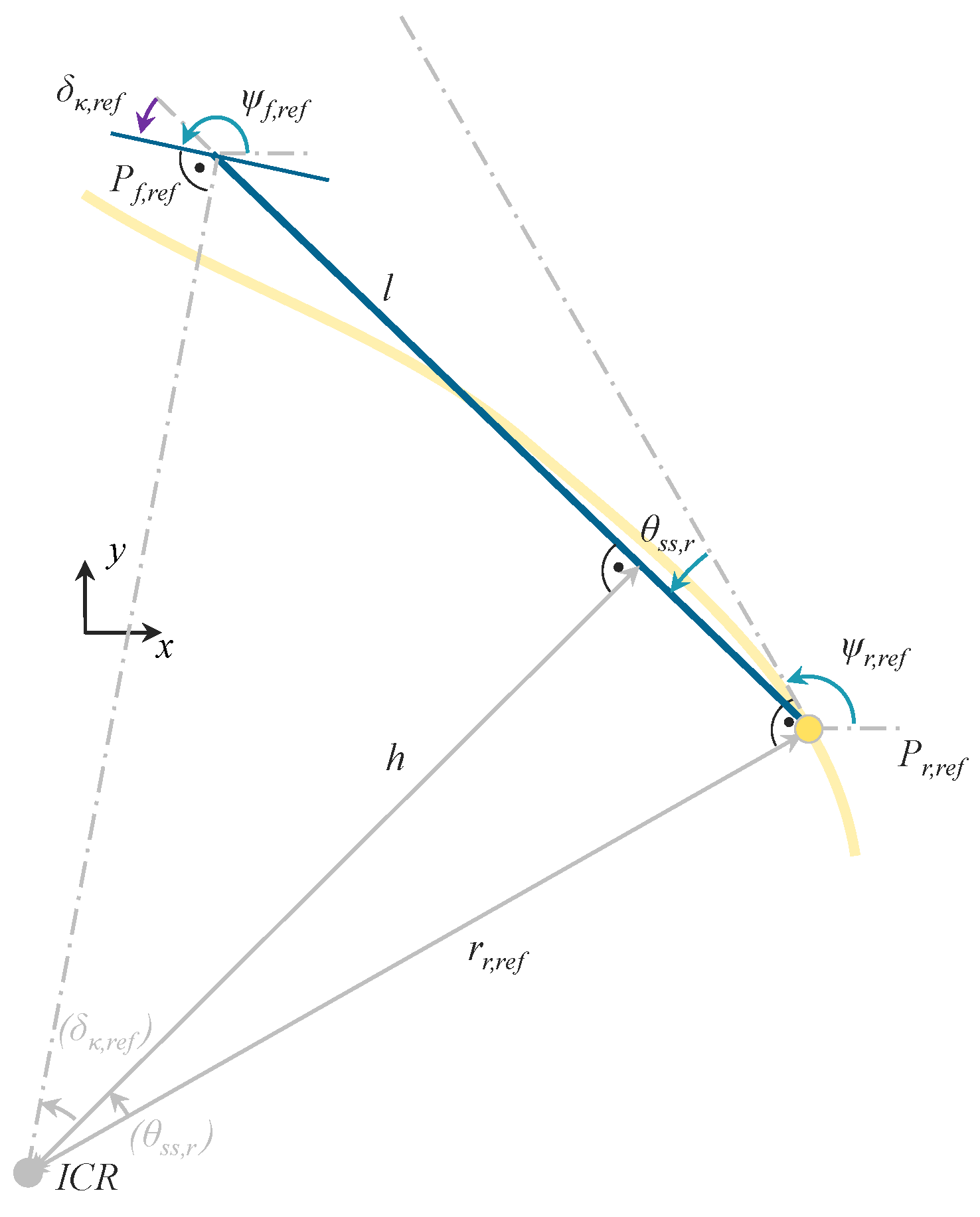
1. Introduction

Automated driving is currently one of the most important development goals in automotive research, not only in the field of passenger cars and public transport [1]. Driverless operation also represents a major benefit for future commercial vehicles [2] or automated guided vehicles [3]. The interface between the automated driving functions and the drive-by-wire chassis mechatronics is the path-tracking controller. Its task is to follow the path planned by the automation layer by adjusting the steering angle (lateral control) and the drive and braking torque (longitudinal control). Different control approaches are available depending on the requirements for control accuracy, velocity, and disturbances to be considered [4,5,6,7,8]. Among a number of different approaches of varying complexity, the Stanley controller [4], which belongs to the category of geometric path-tracking controllers, has been established for lateral control. The Stanley controller is a simple, efficient, and robust solution that provides sufficient control performance at moderate velocities [7,8,9,10]. Improving its accuracy, for example, by extending the approach or introducing methods for parameter tuning, is the subject of ongoing research [9,11]. More complex approaches, for example, model predictive controllers (MPCs), lead to comparatively better accuracy at higher velocities and in more dynamic driving situations but result in higher implementation complexity and often in higher computational effort [5,6,7]. Therefore, for applications that do not require higher velocity and high dynamics, the Stanley controller is a preferable solution.

As described by Xu et al. [12] and Zhang et al. [13], one major reason for the limitation of trajectory tracking accuracy and instability is the time delay within the whole vehicle system. Since it is not possible to avoid delays in most cases, solutions must be found to compensate for their effects on vehicle guidance control. The delays within the lateral control loop can be divided into input delay and steering delay, also called steering lag. Input delay results from reading sensor information, communication between sensors and control units, and processing and computation within control units. Steering lag is caused by the low-level controller design, communication delay from the control unit to the steering actuator, and hardware limits of the steering actuator system. In addition, steering lag is affected by the time it takes for the lateral tire force in the tire–road contact patch to be built up after the steering angle has reached the desired value [12,13].

The delay time depends on the characteristics of the sensor and actuator system. Zhang et al. [13] determined an input delay time of 0.1 s and a steering delay of 0.2 s. Other analysis found the steering delay time to be between 0.2 s and 0.5 s [14].

The challenge posed by system delay can be addressed using various advanced controller approaches. Delay compensation based on MPC or linear quadratic controller (LQR) approaches are described by, among others, Xu et al. [12], Luan et al. [15], and Zhang et al. [13]. Yu et al. [16] describe an MPC approach in which the actual position of the vehicle is predicted and the delay time is used as the prediction time to compensate for the effect of the delay. Based on the Stanley controller, AbdElmoniem et al. [17] propose a predictive Stanley lateral control approach in which the future driving states are considered to calculate the steering angle setpoints.

The advantages of these model-based extensions, or other more complex control approaches, become apparent at higher velocities and in more dynamic driving situations. For this reason, the Stanley controller is still widely used in practice for vehicles operating at lower velocities (e.g., mobile robots, indoor and outdoor logistics vehicles, and off-road applications). Its advantages include reduced implementation effort and less control engineering knowledge required compared to model-based solutions. However, there is also the challenge of steering lag compensation in these vehicle classes, especially since the performance of steer-by-wire systems may be limited due to their economic requirements, resulting in significant steering lag.

Therefore, for this article, we have analyzed the Stanley control law and propose a pragmatic adaptation of it that effectively increases its accuracy by reducing the negative effects of system delay. The goal was to find a solution that requires minimal additional implementation and parameterization effort compared to the original controller. We have achieved this improvement by feedforwarding the path curvature of a point along the path and selecting that point depending on the system delay time. Our approach extends the Stanley controller by only one additional parameter, keeping the implementation and parameter tuning effort at a comparable level.

With our solution, we target applications that are generally suitable (in terms of velocity and driving dynamics) for operation with a geometric path-tracking controller, such as the Stanley controller. For these applications, our proposed approach provides an improvement in accuracy without increasing the complexity of the approach and, thus, the required control engineering knowledge of the user. Due to the practice-oriented focus of our solution, we demonstrate a significant improvement in control accuracy compared to the Stanley control law not only with simulative but especially with real-world driving tests.

This article is organized as follows: Section 2 presents the methodology of this work, including the description of the demonstrator vehicle, the simulation model, and the maneuvers used for testing and validation. The path-tracking control approach and our proposed improvement to the Stanley controller are then derived, followed by a description of the testing and validation procedure, including the applied parameter optimization method. The results of both the simulation-based study and the driving tests with the demonstrator vehicle are presented and discussed in Section 3, followed by the conclusions in Section 4.

2. Materials and Methods

2.1. Demonstrator Vehicle

We used a demonstrator vehicle (scale 1:1.5) to validate the proposed control approach (Figure 1). The main functions of the cascaded control system of the vehicle include the path tracking controller, the steering angle controller, and the velocity controller. Thus, from the specified path and the actual position, the torque output signals for the drive motors and the steering actuator are determined (Figure 2). The localization is provided by a multi sensor RTK-GNSS module (Advanced Navigation Solutions – ANavS GmbH, Munich, Germany) which uses real-time kinematics (RTK) positioning techniques based on global navigation satellite systems (GNSS) signals. The controller runs on a dSPACE MicroAutoBox II (dSPACE GmbH, Paderborn, Germany), which allows a direct transfer of the control structures from the simulation model to the vehicle. The vehicle properties needed to configure the proposed control approach are listed in

Table 1. Vehicle properties relevant for the control approach: tire stiffness of the tire pair at the front axle $C_{y,f}$, tire stiffness of the tire pair at the rear axle $C_{y,r}$, vehicle mass m, distance from the center of gravity to front axle a, and distance from the center of gravity to rear axle b and the wheelbase l, which is the sum of a and b.

${\mathit{C}}_{\mathit{y},\mathit{f}}$ (kN/rad)	${\mathit{C}}_{\mathit{y},\mathit{r}}$ (kN/rad)	m (kg)	a (m)	b (m)	l (m)
28	26	394.4	0.91	1.16	2.07

.

Components involved in lateral vehicle guidance, thus contributing to the input delay, are the steering angle sensor, the yaw rate sensor, the RTK-GNSS module, and the dSPACE MicroAutoBox II. The controller algorithms are executed at 1000 Hz, with the steering angle sensor signal read at 100 Hz, the yaw rate sensor signals read at 200 Hz, and the RTK-GNSS module signals read at 50 Hz. The RTK-GNSS module calculates the vehicle position and orientation based on differential GPS measurements and predicts the actual position using acceleration and yaw rate measurement data. As a result, the delay caused by GNSS signal processing is already compensated for to a large extent in the localization signal provided.

The steering angle controller we have implemented on the vehicle control unit is based on the cascade control paradigm [18] with the aim of keeping the resulting steering lag as small as possible. In the outer loop, the desired steering angle is controlled with a proportional (P) controller, which outputs a target steering angle rate. The inner loop contains the measured steering angle rate as additional feedback and controls it with a proportional–integral–derivative (PID) controller. The target torque output calculated in this way is sent to the steering actuator at a frequency of 100 Hz. Steering lag measurements showed an average delay between target and actual steering angle signals of 0.1 s, indicating that the steering system of the demonstrator vehicle with the cascade control structure is less affected by steering lag compared to vehicles used in the literature [13,14].

2.2. Simulation Tools and Models

For the simulative development and optimization of the proposed control approach, the software tool CarMaker (Version 8.0, IPG Automotive GmbH, Karlsruhe, Germany) was used in co-simulation with MATLAB Simulink (Version R2018b, The MathWorks, Natick, MA, USA) based on the CarMaker extension CarMaker for Simulink [19]. The demonstrator vehicle is represented by corresponding CarMaker project files, and additional subsystems such as velocity and steering angle controllers are modeled in MATLAB Simulink. In the MATLAB Simulink model, the target velocity and target steering angle are converted into the CarMaker inputs motor torques and tie rod displacement. This co-simulation model of the demonstrator vehicle can be accessed from [20] including a more detailed description of the modeling. It also contains the modeling of the steering system dynamics, including the delay caused by steering lag as well as the modeling of the behavior of the real RTK-GNSS localization module with the frequency of the signals reduced to 50 Hz.

For the application in this work, the simulation model was extended to provide vehicle guidance control functionality based on predefined paths. This includes the calculation of the reference pose and the proposed path tracking controller, which are also implemented in the MATLAB Simulink model. Figure 3 shows the resulting overall simulation model. The vehicle guidance control submodule is also integrated into the control software of the demonstrator vehicle and is published along with this article (Supplementary Materials, Source Code S1).

2.3. Driving Maneuvers

We use two driving maneuvers to optimize and evaluate the path-tracking performance of the controller. The maneuvers are defined as paths describing the desired poses of the vehicle with the center of the rear axle as the reference point.

The first driving maneuver is used to optimize the controller parameters (Section 2.5.1). The vehicle first accelerates on a straight line to a constant velocity. Then, the path contains a sudden lateral offset of 0.5 m, causing a step in the setpoints of the control input, which can be used to investigate the step response of the controller. At 50 m after the starting point, a step-steer transitions the maneuver to a stationary circular maneuver with a radius of 12 m. The path is defined sequentially with two geometric straight-line equations and one equation of the circle.

The maneuver used for validation is a dynamic circuit on the test area used for the demonstrator vehicle tests in the course of this work. It is labeled “track_01” and can be accessed at [21]. The track is shown in Figure 4a supplemented by the course of desired vehicle velocity of the rear axle $v_{r,ref}$ Figure 4b and the resulting lateral acceleration Figure 4c. The points of the path (global coordinates $x_{r,ref}\left(s\right)$ and $y_{r,ref}\left(s\right)$) are described as functions of the path coordinate s. Besides the global coordinates, the path definition also includes the tangential orientation ${\psi }_{r,ref}\left(s\right)$ on each point of the path, the curvature of the path ${\kappa }_{ref}\left(s\right)$ (positive for left turns), and the desired vehicle velocity of the rear axle $v_{r,ref}\left(s\right)$. In the course of this work, the path was discretized with a list of points, each having a distance of 0.3 m from the other. To calculate the reference values with a higher resolution, a linear interpolation was applied between the two points in the list that are closest to the vehicle position. The algorithms for calculating the current reference values from the given path definition are included in the implementation published along with this article (Supplementary Materials, Source Code S1).

Alternative approaches may also be considered to provide appropriate maneuver input to the vehicle guidance controller. It is only crucial that the current setpoints for the coordinates $x_{r,ref}$ and $y_{r,ref}$ as well as the tangential orientation ${\psi }_{r,ref}$ and the curvature ${\kappa }_{ref}$ are given to the controller and that no sudden steps occur in the course of the tangential orientation ${\psi }_{r,ref}$ since the Stanley controller cannot handle them properly [6,17]. For example, the input can be a trajectory whose points are defined as a function of time t rather than as a function of the path coordinate s [7]. Instead of the specified velocity $v_{r,ref}$, the longitudinal guidance is implemented by specifying a longitudinal acceleration, which is required to reduce the longitudinal error.

2.4. Path Tracking Control Approaches

To derive the proposed control approach, we first describe the calculation of the reference vehicle pose, including the definition of the tracking error at the rear axle. A conversion of the reference values from the rear to the front axle is necessary to obtain the appropriate definition of the cross-track error and guiding angle of the front wheels for the control approach. Finally, we derive the proposed control equations on the basis of the Stanley path-tracking control approach.

2.4.1. Actual Vehicle Pose and Path Reference Pose

The task of the path-tracking controller is to guide the vehicle along a specified path. For this purpose, the center of the rear axle $P_r$ is selected as a reference to define the actual pose of the vehicle with its coordinates $x_r$ and $y_r$ and the orientation of the vehicle ${\psi }_r$ (Figure 5). With the wheelbase l, the coordinates of the center of the front axle $P_f$ are obtained using

$$\begin{array}{cc}\hfill x_f\left(t\right)& =x_r\left(t\right)+lcos{\psi }_r\left(t\right)\hfill \\ \hfill y_f\left(t\right)& =y_r\left(t\right)+lsin{\psi }_r\left(t\right)\hfill \end{array}$$

(1)

First, the point of the path $P_{r,ref}$ closest to $P_r$ must be found. The global coordinates $x_{r,ref}\left(s_{ref}\right)$ and $y_{r,ref}\left(s_{ref}\right)$ of the reference point $P_{r,ref}$ are obtained by choosing $s_{ref}$ such that the cross-track error at the rear axle $e_{lat,r}$ is minimized. We get

$$s_{ref}\left(t\right)=arg\underset{0\le s\le s_{max}}{min}\sqrt{{\left(x_{r,ref}\left(s\right)-x_r\left(t\right)\right)}^2+{\left(y_{r,ref}\left(s\right)-y_r\left(t\right)\right)}^2}$$

(2)

and the cross-track error at the rear axle $e_{lat,r}$ results in

$$e_{lat,r}\left(t\right)=\left(y_{r,ref}\left(t\right)-y_r\left(t\right)\right)cos{\psi }_{r,ref}\left(t\right)-\left(x_{r,ref}\left(t\right)-x_r\left(t\right)\right)sin{\psi }_{r,ref}\left(t\right)$$

(3)

with positive values for a deviation to the right of the path and negative values for a deviation to the left of the path.

2.4.2. Setpoints and Cross-Track Error at Front Axle

The proposed approach, as well as the Stanley controller, use the front wheels as guiding wheels [4], so the reference position of the front axle $P_{f,ref}$ needs to be known to obtain the appropriate cross-track error input for the controllers. The coordinates of $P_{f,ref}$ can be calculated by assuming that the vehicle follows exactly the desired path with its reference point in the center of the rear axle. Applying a dynamic bicycle model, the vehicle orientation deviates from the kinematic reference ${\psi }_{r,ref}$ by the slip angle of the rear axle ${\theta }_{ss,r}$ (Figure 6). For the coordinates of $P_{f,ref}$ we get

$$\begin{array}{cc}\hfill x_{f,ref}\left(t\right)& =x_{r,ref}\left(s_{ref}\left(t\right)\right)+lcos\left({\psi }_{r,ref}\left(t\right)+{\theta }_{ss,r}\left(t\right)\right)\hfill \\ \hfill y_{f,ref}\left(t\right)& =y_{r,ref}\left(s_{ref}\left(t\right)\right)+lsin\left({\psi }_{r,ref}\left(t\right)+{\theta }_{ss,r}\left(t\right)\right)\hfill \end{array}$$

(4)

Furthermore, the orientation ${\psi }_{f,ref}$ needs to be found, which is the direction of motion of the point $P_{f,ref}$. Therefore, in addition to already known quantities, the angle ${\delta }_{\kappa ,ref}$ is needed. This angle can also be understood as the kinematic reference steering angle, which results from the curvature of the vehicle motion. To derive ${\delta }_{\kappa ,ref}$, the instant center of rotation $ICR$ is considered. At this point, all lines perpendicular to the direction of motion of any fixed point of the vehicle intersect. The correlations in Figure 6 apply to the case of cornering, so ${\kappa }_{ref}\ne 0$ and ${\delta }_{\kappa ,ref}\ne 0$ are assumed for the following Equations (5) and (6). The distance between $ICR$ and $P_{r,ref}$ is the curve radius $r_{r,ref}$ which results from the curvature ${\kappa }_{ref}$.

$$r_{r,ref}\left(t\right)=\frac{1}{{\kappa }_{ref}\left(s_{ref}\left(t\right)\right)}$$

(5)

By applying trigonometric functions, the distance h can be expressed both by ${\delta }_{\kappa ,ref}$ and by means of ${\theta }_{ss,r}$.

$$\begin{array}{cc}\hfill h\left(t\right)& =r_{r,ref}\left(s_{ref}\left(t\right)\right)cos{\theta }_{ss,r}\left(t\right)\hfill \\ \hfill h\left(t\right)& =\frac{1}{tan{\delta }_{\kappa ,ref}\left(t\right)}\left(l-r_{r,ref}\left(s_{ref}\left(t\right)\right)sin{\theta }_{ss,r}\left(t\right)\right)\hfill \end{array}$$

(6)

Finally, ${\delta }_{\kappa ,ref}$ results in

$${\delta }_{\kappa ,ref}\left(t\right)=\mathit{arctan}\frac{l{\kappa }_{ref}\left(s_{ref}\left(t\right)\right)-sin{\theta }_{ss,r}\left(t\right)}{cos{\theta }_{ss,r}\left(t\right)}$$

(7)

which is also valid for the case of a straight path (${\kappa }_{ref}=0$), and we get the required orientation ${\psi }_{f,ref}$ as

$${\psi }_{f,ref}\left(t\right)={\psi }_{r,ref}\left(s_{ref}\left(t\right)\right)+{\theta }_{ss,r}\left(t\right)+{\delta }_{\kappa ,ref}\left(t\right)$$

(8)

With the reference values serving as setpoints for the controller, the cross-track error at the front axle $e_{lat,f}$ and the guiding angle of the front wheels ${\theta }_f$ (Figure 7) become

$$e_{lat,f}\left(t\right)=\left(y_{f,ref}\left(t\right)-y_f\left(t\right)\right)cos{\psi }_{f,ref}\left(t\right)-\left(x_{f,ref}\left(t\right)-x_f\left(t\right)\right)sin{\psi }_{f,ref}\left(t\right)$$

(9)

and

$${\theta }_f\left(t\right)={\psi }_{f,ref}\left(t\right)-{\psi }_r\left(t\right)$$

(10)

2.4.3. Stanley Control Approach

In this section, we describe the equations of the Stanley controller by Hoffmann et al. [4], which serve as the reference approach in this article. The labels of the variables are adapted to the definitions used in this work as well as the definition of the positive direction of the steering angle. A positive curvature of the path ${\kappa }_{ref}$ (left turn) leads to a positive yaw rate ${\dot{\psi }}_r$ and requires a positive steering angle $\delta$. In the same sense, a positive cross-track error $e_{lat,f}$ as well as a positive guiding angle of the front wheels ${\theta }_f$ lead to a steering angle adjustment in a positive direction.

The Stanley control law is given with

$${\delta }_{Stanley}\left(t\right)={\theta }_f\left(t\right)+\mathit{arctan}\frac{k{e}_{lat,f}\left(t\right)}{k_{soft}+v_r\left(t\right)}+{\delta }_{add}\left(t\right)$$

(11)

The first term ${\theta }_f$ makes the steered wheels turn according to the desired direction of travel. Assuming ideal vehicle behavior, no further terms would be required for the vehicle to follow the path. If a cross-track error $e_{lat,f}$ occurs, the second term adjusts the steering angle to reduce the cross-track error. The intensity of the correction can be adjusted with the parameter k and is automatically reduced when the actual velocity at the rear axle $v_r$ increases. To avoid aggressive corrections at low velocities, $k_{soft}$ is added to the denominator. The arctan function limits the second term to $\pm 0.5\pi$, which allows the vehicle to compensate for large cross-track errors. If $e_{lat,f}$ is getting large, the first and second terms are approximately equal in amount ($0.5\pi$) but have opposite signs, allowing the vehicle to travel vertically towards the desired path until the cross-track error is significantly reduced and ${\theta }_f$ leads to turning into the direction of the path. For dynamic driving situations, Hoffmann et al. [4] propose additional terms, which are summarized in this work by ${\delta }_{add}$.

$$\begin{array}{cc}\hfill {\delta }_{add}\left(t\right)=& k_{d,yaw}\left({\dot{\psi }}_{\kappa ,ref}\left(t\right)-{\dot{\psi }}_r\left(t\right)\right)\hfill \\ \hfill +& k_{d,steer}\left(\delta \left(i\right)-\delta (i+1)\right)\hfill \\ \hfill +& {\theta }_{ss,f}\left(t\right)\hfill \end{array}$$

(12)

The first part of the additional terms in (12) is based on the difference of the actual yaw rate ${\dot{\psi }}_r$ and the expected yaw rate ${\dot{\psi }}_{\kappa ,ref}$ multiplied by the parameter $k_{d,yaw}$. The expected yaw rate ${\dot{\psi }}_{\kappa ,ref}$ results from the curvature of the path ${\kappa }_{ref}$ and the actual velocity of the rear axle $v_r$ with

$${\dot{\psi }}_{\kappa ,ref}\left(t\right)=v_r\left(t\right){\kappa }_{ref}\left(s_{ref}\left(t\right)\right)$$

(13)

To avoid the instability caused by delays and overshoots of the steering actuator, Hoffmann et al. [4] add the second line of (12) where $\delta (i+1)$ is the current measured steering angle and $\delta \left(i\right)$ the measured steering angle one time period earlier. Using $k_{d,steer}$, the effect of this term can be parameterized.

The output of the Stanley controller is a steering angle which is assumed to be the direction of motion of the vehicle at the front axle. This applies only to kinematic behavior at low velocity. At higher velocity, it is necessary to add the slip angle of the front axle ${\theta }_{ss,f}$ to the output steering angle to achieve the desired direction of motion. According to Hoffmann et al. [4], the slip angle is given by the steady state yaw angle resulting from vehicle parameters (Table 1), the actual velocity $v_r$, and the expected yaw rate ${\dot{\psi }}_{\kappa ,ref}$

$${\theta }_{ss,f}\left(t\right)=\frac{m}{C_{y,f}\left(1+\frac{a}{b}\right)}{v}_r\left(t\right){\dot{\psi }}_{\kappa ,ref}\left(t\right)$$

(14)

Consequently, we define the slip angle of the rear axle ${\theta }_{ss,r}$ required in (4) and (8) as

$${\theta }_{ss,r}\left(t\right)=\frac{m}{C_{y,r}\left(1+\frac{b}{a}\right)}{v}_r\left(t\right){\dot{\psi }}_{\kappa ,ref}\left(t\right)$$

(15)

2.4.4. Proposed Approach for Enhancing the Stanley Controller

The derivation of the proposed control approach starts with the reformulation of the Stanley control law. Using (8), we reformulate (10) and obtain

$$\begin{array}{cc}\hfill {\theta }_f\left(t\right)& ={\psi }_{r,ref}\left(s_{ref}\left(t\right)\right)+{\theta }_{ss,r}\left(t\right)-{\psi }_r\left(t\right)+{\delta }_{\kappa ,ref}\left(t\right)\hfill \\ \hfill & ={\theta }_r^{*}\left(t\right)+{\delta }_{\kappa ,ref}\left(t\right)\hfill \end{array}$$

(16)

with

$${\theta }_r^{*}\left(t\right)={\psi }_{r,ref}\left(s_{ref}\left(t\right)\right)+{\theta }_{ss,r}\left(t\right)-{\psi }_r\left(t\right)$$

(17)

Here, ${\theta }_r^{*}$ can be interpreted as the actual orientation error of the vehicle considering the steady-state error. With (16), the Stanely control law (11) becomes

$$\begin{array}{cc}\hfill {\delta }_{Stanley}\left(t\right)=& {\delta }_{\kappa ,ref}\left(t\right)\hfill \\ \hfill +& {\theta }_r^{*}\left(t\right)\hfill \\ \hfill +& \mathit{arctan}\frac{k{e}_{lat,f}\left(t\right)}{k_{soft}+v_r\left(t\right)}\hfill \\ \hfill +& {\delta }_{add}\left(t\right)\hfill \end{array}$$

(18)

Considering (7), (15), and (13), we see that ${\delta }_{\kappa ,ref}$ depends only on constant vehicle parameters, current velocity $v_r$, and path curvature ${\kappa }_{ref}\left(s_{ref}\right)$. Since it is independent of the current vehicle position relative to the path, the term ${\delta }_{\kappa ,ref}$ can be considered to be feedforward of the Stanley control law. ${\theta }_r^{*}$ takes into account the orientation error and, as before, the $arctan$ term compensates for the cross-track error, while ${\delta }_{add}$ provides stabilization of the vehicle motion. Thus, for driving without major initial deviations along a curved path, the term ${\delta }_{\kappa ,ref}$ contributes most to the controller output ${\delta }_{Stanley}$.

The idea of the proposed enhancement of the Stanley approach is to use the feedforward term ${\delta }_{\kappa ,ref}$ to compensate for all delay effects within the entire lateral control loop of the vehicle system. For this purpose, ${\delta }_{\kappa ,ref}$ is replaced by ${\delta }_{\kappa ,ff}$, which considers the curvature of the path at a position offset by $s_{ff}$ along the path in the direction of travel. With (7) we get

$${\delta }_{\kappa ,ff}\left(t\right)=\mathit{arctan}\frac{l{\kappa }_{ref}(s_{ref}\left(t\right)+s_{ff}\left(t\right))-sin{\theta }_{ss,r}\left(t\right)}{cos{\theta }_{ss,r}\left(t\right)}$$

(19)

We assume a constant delay time, which must be compensated by a corresponding feedforward time $t_{ff}$. The path coordinate offset $s_{ff}$ results from the distance traveled within $t_{ff}$ and becomes

$$s_{ff}\left(t\right)=v_r\left(t\right)t_{ff}$$

(20)

For the purpose of keeping the approach simple, we have assumed that, in Equations (19) and (20), $v_r$ and ${\theta }_{ss,r}$ are constant during the time interval $t_{ff}$. For a more precise consideration, the course of the two quantities during $t_{ff}$ would have to be predicted.

Finally, the proposed enhancement of the Stanley control law is given with

$$\begin{array}{cc}\hfill {\delta }_{Stanley,enh}\left(t\right)=& {\delta }_{\kappa ,ff}\left(t\right)\hfill \\ \hfill +& {\theta }_r^{*}\left(t\right)\hfill \\ \hfill +& \mathit{arctan}\frac{k{e}_{lat,f}\left(t\right)}{k_{soft}+v_r\left(t\right)}\hfill \\ \hfill +& {\delta }_{add}\left(t\right)\hfill \end{array}$$

(21)

It further results from the derivation that both control laws “enhanced Stanley” (${\delta }_{Stanley,enh}$) and Stanley (${\delta }_{Stanley}$) are identical when $t_{ff}=0\mathrm{s}$ is chosen or ${\kappa }_{ref}$ is constant in the path segment considered.

An adaptation of the control law for reverse driving can be found in Appendix A.

Correspondingly, for longitudinal dynamics, a compensation of the delay in the course of the velocity can be implemented by choosing the velocity reference as $v_{r,ref}(s_{ref}\left(t\right)+s_v\left(t\right))$ with

$$s_v\left(t\right)=v_r\left(t\right)t_v$$

(22)

In this paper, however, this is not considered further, and therefore $t_v=0\mathrm{s}$ is chosen.

2.5. Test and Validation Procedure

The test and validation procedure comprises three main steps, which are described in the following subsections. First, the parameters of the control approaches were identified, followed by a comparison of the two control approaches in the simulation environment, and finally, the application and validation on the real demonstrator vehicle. In summary, we obtained six test runs for both the simulation and the real vehicle tests, which are shown in

Table 2. Test plan for parameter tuning, comparison of control approaches, and validation on the real demonstrator vehicle. Test runs with the index “S” are carried out in the simulation, while the index “DV” refers to test runs with the demonstrator vehicle.

No.	Environment	Maneuver	Path Tracking Controller
$1.1_S$/$1.1_{DV}$	Simulation/Demo. vhcl	Step-steer (3 m/s)	Stanley
$1.2_S$/$1.2_{DV}$	Simulation/Demo. vhcl	Step-steer (3 m/s)	Enh. Stanley
$2.1_S$/$2.1_{DV}$	Simulation/Demo. vhcl	Step-steer (8 m/s)	Stanley
$2.2_S$/$2.2_{DV}$	Simulation/Demo. vhcl	Step-steer (8 m/s)	Enh. Stanley
$3.1_S$/$3.1_{DV}$	Simulation/Demo. vhcl	Circuit “track_01”	Stanley
$3.2_S$/$3.2_{DV}$	Simulation/Demo. vhcl	Circuit “track_01”	Enh. Stanley

.

2.5.1. Parameter Tuning

In addition to the vehicle-specific parameters (Table 1), the control laws (11) and (21) contain further parameters that have to be adjusted to optimize the control behavior. Both approaches share the parameters k, $k_{soft}$, $k_{d,yaw}$, and $k_{d,steer}$. For the enhanced approach, the parameter $t_{ff}$ is additionally required. To find appropriate parameters, we followed the recommendations and procedure described by Hoffmann et al. [4]. According to the suggestion, we chose $k_{soft}=1$ m/s. We initially set $k_{d,steer}=0$, following the recommended approach of keeping the value as small as possible and increasing it only to avoid instabilities caused by delays in the steering control response.

For the adjustment of k and $k_{d,yaw}$, within the scope of this work, the following procedure has proven to be effective in order to achieve the best possible control performance while maintaining stability. The parameters are determined by analyzing the step response of the controller when the vehicle is moving on a straight track with a sudden offset of the path of 0.5 m. We have defined the optimization objective to reduce the cross-track error at the rear axle $e_{lat,r}$ as quickly as possible without causing overshoots or dynamic oscillations. Increasing k makes the vehicle respond faster to a cross-track error, but a too-large k causes overshoot and oscillation. These can be compensated for by increasing $k_{d,yaw}$. However, if k is too large, no $k_{d,yaw}$ can be found that sufficiently compensates for the oscillations. So the objective is to find the largest possible k for which there is a suitable $k_{d,yaw}$ that results in a stable step response without overshoot.

By increasing k step by step and adjusting $k_{d,yaw}$ accordingly, a suitably optimized combination is found. We first applied this for the maximum vehicle velocity 8 m/s (test run 2.1, maximum yaw rate 0.67 rad/s, and maximum lateral acceleration 5.33 m/s²) and then checked whether these values also led to the desired behavior at a velocity of 3 m/s (test run 1.1, maximum yaw rate 0.25 rad/s, and maximum lateral acceleration 0.75 m/s²). If not, k was further reduced, and $k_{d,yaw}$ was adjusted accordingly.

It should be noted that slight oscillations in the cross-track error should always be expected when driving straight due to system delay. Sufficient compensation of the oscillations is given if they occur immediately after the step response to the same extent as when driving straight ahead without step excitation.

The proposed enhanced control approach uses the same parameter setting as the Stanley reference control approach. In order to find the additionally needed optimized parameter of the feedforward time $t_{ff}$, we consider the tracking performance on the circuit (test run 3.2). We choose the root-mean-square cross-track error $e_{lat,r_{RMSE}}$ as the metric for evaluating the performance. The evaluation includes a whole lap on the circuit, whereas the segment marked in red in Figure 4a was excluded from the evaluation because it features a curvature that is larger than the maximum drivable curvature of the vehicle, causing an unavoidable cross-track error.

To find the feedforward time $t_{ff}$ that minimizes the root-mean-square cross-track error $e_{lat,r_{RMSE}}$, we started with $t_{ff}=0\mathrm{s}$, then increased it in steps of 0.1 s for each repetition of the test run execution as long as $e_{lat,r_{RMSE}}$ was decreasing, and stopped when the minimum was reached. To fine-tune $t_{ff}$, we continued the procedure in steps of 0.01 s around the previously found value.

2.5.2. Comparison of the Control Approaches in the Simulation Environment

The controller approaches differ with respect to the consideration of the variation of the path curvature. The different behavior is most obvious when a sudden step in curvature occurs. Therefore, a first comparison is made using the step-steer maneuver where the curvature changes from 0 m⁻¹ to 1/12 m⁻¹ at the transition from the straight line to the circular movement. For velocities of 3 m/s and 8 m/s, we consider how large the respective maximum cross-track error ${\widehat{e}}_{lat,r}$ of the two approaches is after the curvature step and how it affects the stability (test runs $1.1_S$, $1.2_S$, $2.1_S$, and $2.2_S$).

In addition, the tracking performance of the test runs $3.1_S$ and $3.2_S$ on the test circuit is compared, taking into account not only the maximum cross-track error ${\widehat{e}}_{lat,r}$, but also the root-mean-square cross-track error $e_{lat,r_{RMSE}}$.

2.5.3. Application and Validation on the Real Demonstrator Vehicle

For the real demonstrator vehicle, parameter tuning is conducted as described in Section 2.5.1. The test runs $3.1_{DV}$ and $3.2_{DV}$ on the test circuit provide results to evaluate the benefits of the proposed approach on a real demonstrator vehicle. Additionally, comparisons can be made with the corresponding simulative test runs $3.1_S$ and $3.2_S$.

3. Results and Discussion

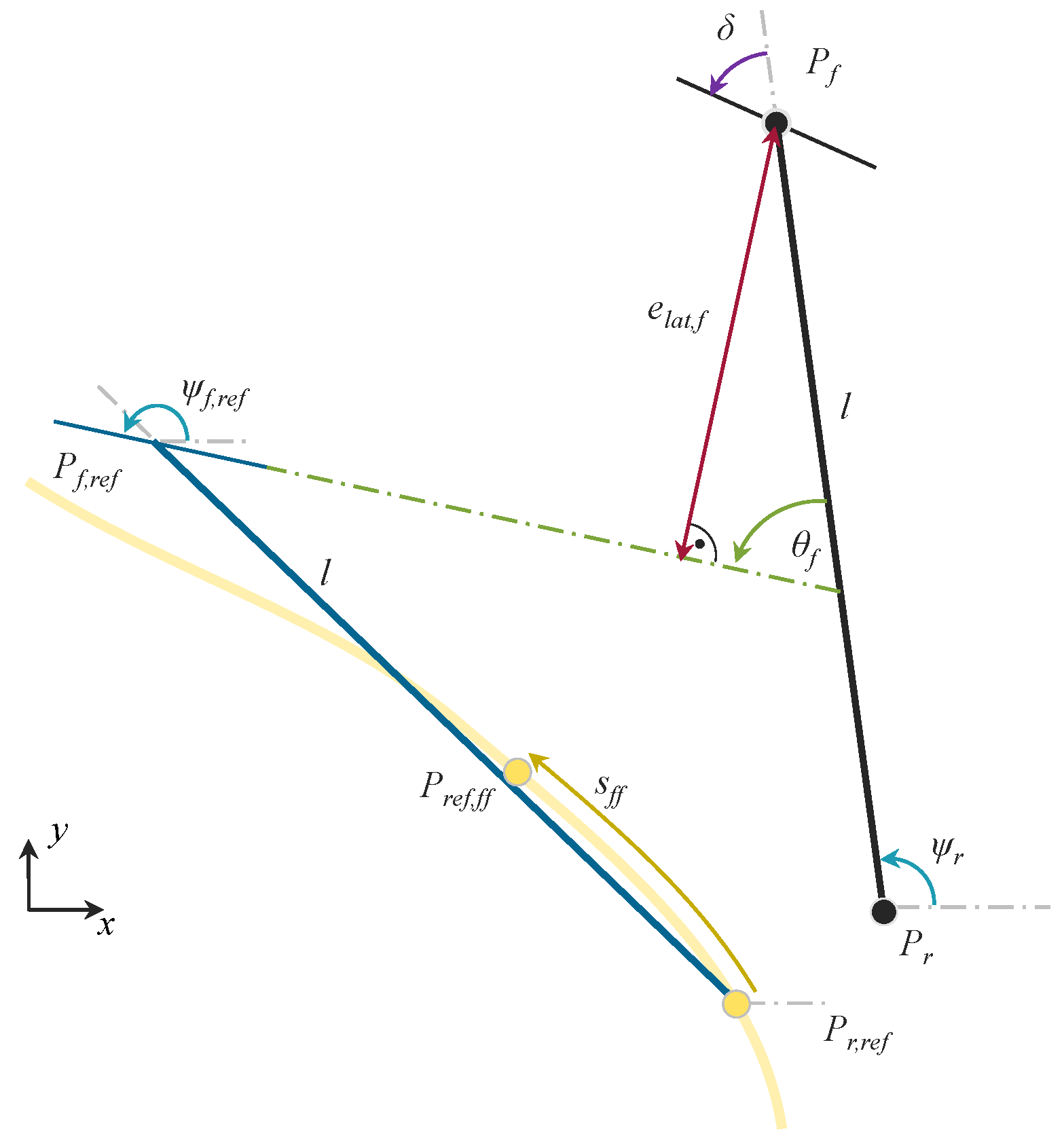
According to the test and validation procedure, the analysis and discussion of the results are also divided into three subsections. First, we discuss the results of the parameter tuning, followed by the simulative results, and finally, the validation on the demonstrator vehicle. Overall, the focus is on the comparison of the Stanley approach with the proposed enhanced Stanley approach. In the diagrams, the results labeled “Stanley” refer to results using the steering angle input $\delta ={\delta }_{Stanley}$ from (11) and, correspondingly, the label “enh. Stanley” refers to results using $\delta ={\delta }_{Stanley,enh}$ based on (21).

3.1. Parameter Tuning Results

Parameter tuning was conducted following the procedure in Section 2.5.1 for both the simulation vehicle model and the real demonstrator vehicle and yielded the parameters listed in

Table 3. Parameters for both control approaches identified in the simulation study and for the real demonstrator vehicle.

Environment	k (s−1)	${\mathit{k}}_{\mathit{soft}}$ (m/s)	${\mathit{k}}_{\mathit{d},\mathit{yaw}}$ (s)	${\mathit{k}}_{\mathit{d},\mathit{steer}}$	${\mathit{t}}_{\mathit{ff}}$ (s)
Simulation	3.0	1	0.125	0	0.18
Demo. vhcl.	0.8	1	0.150	0	0.20

. In both cases, $k_{soft}$ was chosen as recommended, and $k_{d,steer}$ remained at its default value since no instabilities due to delays in steering behavior occurred. The optimal parameters for k and $k_{d,yaw}$ differed between the simulation and the real demonstrator vehicle. For the real demonstrator vehicle, k could not be chosen to be as large as it had been in the simulation (0.8 s⁻¹ instead of up to 3.0 s⁻¹) because for larger k there was no suitable $k_{d,yaw}$ that met the objective of sufficient compensation of the oscillations after the step response. We see one reason for this in the fact that the yaw rate sensor signal had to be filtered on the real demonstrator vehicle to obtain a smooth signal. This resulted in a delay of the signal and, thus, a reduced stabilization effect on the vehicle guidance behavior. Model errors and other effects of the real vehicle that are not represented in the simulation model could also be among the reasons. These include sensor noise that is not part of the simulation model and insufficiently detailed modeling of the steering system behavior. On the real demonstrator vehicle, for example, small steering angle corrections are executed with a delay, especially during direction changes, because the system has a breakaway torque that must first be exceeded by a correspondingly large controller output before a movement is initiated. As a result, the oscillations around the setpoint are amplified when traveling on tracks with constant curvature, for example, on a straight line or on a stationary circular track.

Both in the simulation and on the demonstrator vehicle, the optimization of $t_{ff}$ leads to similar results (0.18 s in the simulation and 0.2 on the real demonstrator vehicle). The purpose of $t_{ff}$ is to read the vehicle curvature of the point on the path that the vehicle will reach after a time of $t_{ff}$. From this, the feedforward component of the steering angle output is calculated. This compensates for all delay effects within the feedforward loop so that, in the best case, the response of the vehicle to the feedforward output corresponds to the current curvature of the path. Delay effects (Section 1) include the delayed signal from the localization input, the delayed realization of the steering angle target, delays due to the build-up of lateral tire force and thus a delayed yaw rate response, and other delays due to communication between control units. The exact quantification of the delay effects is not part of this work; nevertheless, in the following, we will try to plausibilize the found value for $t_{ff}$. The RTK-GNSS module used has a prediction for the vehicle’s position and thus compensates for most of the delay effects that occur within the module. Only the reduced frequency of 50 Hz compared to the controller output frequency of 100 Hz has a delaying effect; we assume an average value of 0.01 s here. The realization of the steering angle using the steering angle controller was determined to be 0.1 s as described above (Section 2.1). The vehicle response (yaw rate) follows the steering angle with a delay of about 0.05 s on average, which was obtained from the evaluation of the measurement data on the test track. Based on the total delay of 0.2 s, this leaves 0.04 s for further delays in communication and effects that are not taken into account in this analysis.

3.2. Simulation Study Results

First, the results of the step-steer test runs are considered, followed by the results from the circuit test runs.

3.2.1. Step-Steer Maneuver

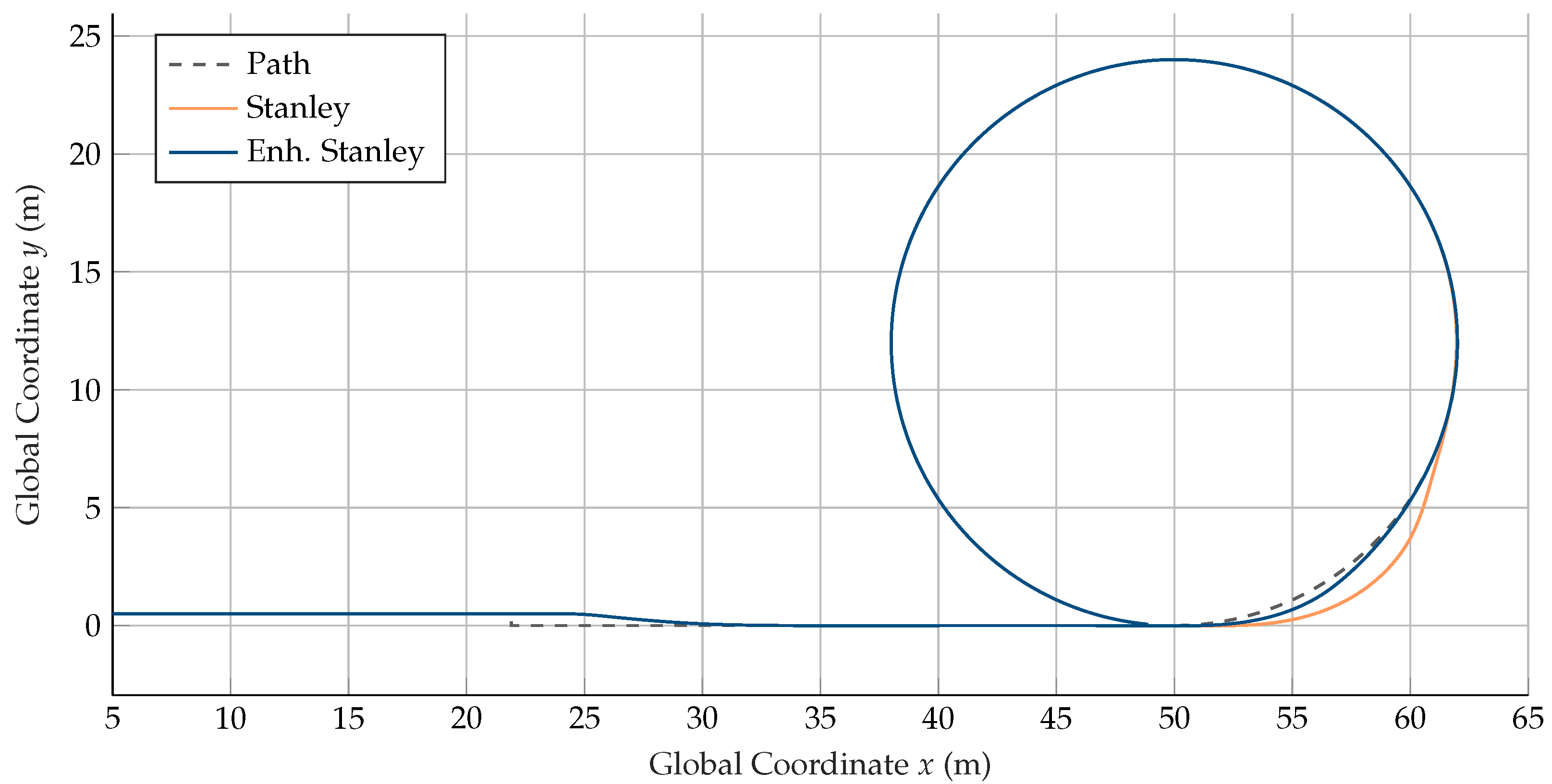
Figure 8 shows the course of the vehicle position and the reference path for the two controller approaches during the step-steer maneuver with 8 m/s. During straight-line driving and the lateral step, the courses of the two controller approaches are identical since, at constant curvature, the two approaches do not differ. After the transition to circular motion, differences appear in the course of the steering angle ${\delta }_{act}$ and consequently also in the vehicle position and the cross-track error $e_{lat,r}$ as shown in Figure 9b.

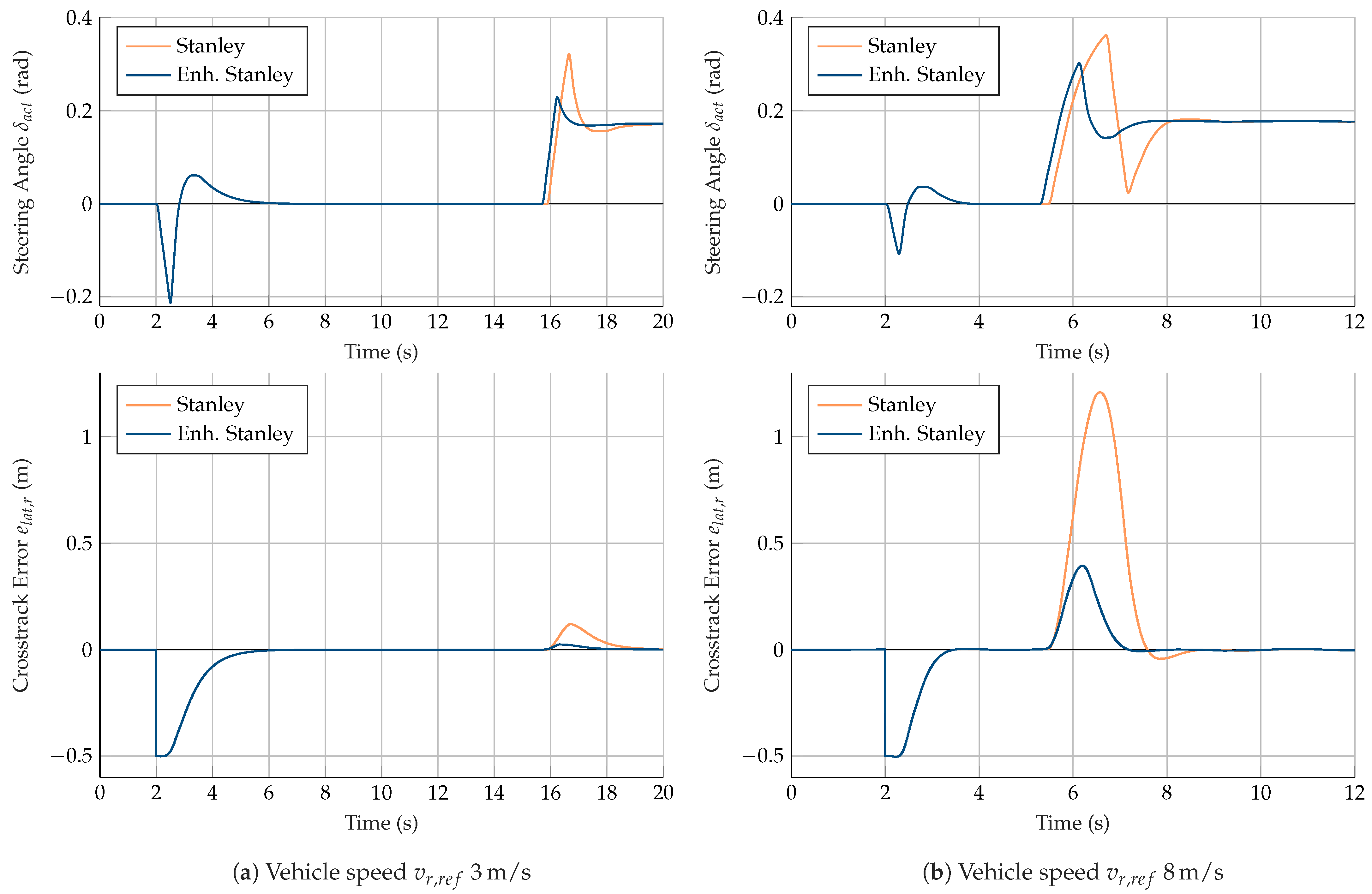
When using the Stanley approach, a deviation of 1.21 m occurs as a result of the transition to circular motion since steering into the circle is conducted too late. The deviation induced leads to further oscillations, which do not fade until half of the circular path has been completed. With the enhanced Stanley approach, overshooting also occurs, but it is smaller (0.39 m) and does not lead to oscillation. In the second half of the circle, the resulting paths of the two approaches are again congruent. The results confirm the desired functionality of the enhanced Stanley approach. With the enhanced approach, the vehicle follows the given path more precisely during changes in curvature. The maneuver presented here includes a step in the curvature and, thus, in the expected yaw rate at the transition to circular motion. The yaw rate of a vehicle, however, cannot change immediately due to rotational inertia and limited tire forces. Therefore the considered maneuver represents a corner case, which, however, allows us to show the limits of both approaches.

The courses of the actual steering angle ${\delta }_{act}$ and the cross-track error $e_{lat,r}$ for the test run with 3 m/s are shown in Figure 9a. The resulting maximum cross-track errors after the transition to circular motion occur to a smaller extent than for the test run with 8 m/s, and again the maximum deviation using the enhanced Stanley approach is smaller (0.02 m) than for the original Stanley approach (0.12 m). The dependency of the maximum deviation on the velocity is obvious since the vehicle with increasing velocity drives straight a longer distance during the delay time before the measured deviation can lead to a vehicle reaction.

3.2.2. Circuit Maneuver

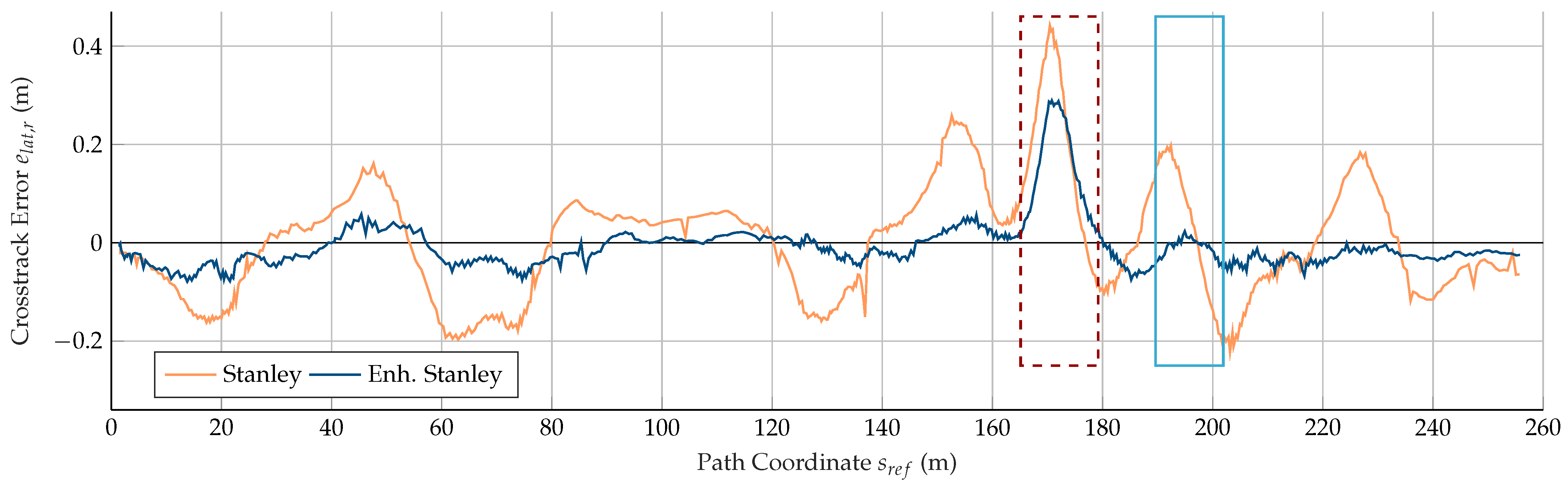
The results of the step-steer maneuver are also confirmed in the dynamic circuit maneuver. The course of the cross-track error of both controller approaches in Figure 10 shows that the enhanced Stanley approach leads to smaller deviations over the entire round of the circuit. The evaluation of the metrics (

Table 4. Evaluation of the two control approaches for the circuit maneuver test runs in simulation and with the demonstrator vehicle based on the metrics maximum cross-track error ${\widehat{e}}_{lat,r}$ and root-mean-square cross-track error $e_{lat,r_{RMSE}}$. The relative improvements of the metrics for the enhanced Stanley approach compared to the Stanley approach are given in parentheses.

	Simulation		Demonstrator Vehicle
Path Tracking Controller	${\mathit{e}}_{\mathit{lat},{\mathit{r}}_{\mathit{RMSE}}}$ (m)	${\widehat{\mathit{e}}}_{\mathit{lat},\mathit{r}}$ (m)	${\mathit{e}}_{\mathit{lat},{\mathit{r}}_{\mathit{RMSE}}}$ (m)	${\widehat{\mathit{e}}}_{\mathit{lat},\mathit{r}}$ (m)
Stanley	0.028 m	0.058 m	0.106 m	0.262 m
Enh. Stanley	0.004 m (−86%)	0.013 m (−77%)	0.033 m (−69%)	0.084 m (−68%)

) yields a maximum cross-track error ${\widehat{e}}_{lat,r}$ of 0.013 m, which corresponds to a reduction of 77% compared to the Stanley approach (0.058 m). The root-mean-square cross-track error $e_{lat,r_{RMSE}}$ is also reduced from 0.028 m to 0.004 m (−86%).

3.3. Demonstrator Vehicle Validation Results and Summary

To validate the simulated results, Figure 11 shows the course of the cross-track error on the circuit from the test runs with the real demonstrator vehicle. For the two controller approaches, the results are qualitatively comparable with the simulation results. However, the absolute cross-track errors are larger on the real vehicle. Using the Stanley approach, the maximum cross-track error ${\widehat{e}}_{lat,r}$ is 0.262 m and the root-mean-square cross-track error $e_{lat,r_{RMSE}}$ is 0.106 m and, thus, both metrics are about four times as large as in the simulation (Table 4). This is due to the different values obtained from the parameter tuning in the simulation compared to the demonstrator vehicle tests. By using a smaller value for k, cross-track errors on the real vehicle are corrected using smaller steering angle adjustments than in the simulation, resulting in larger deviations.

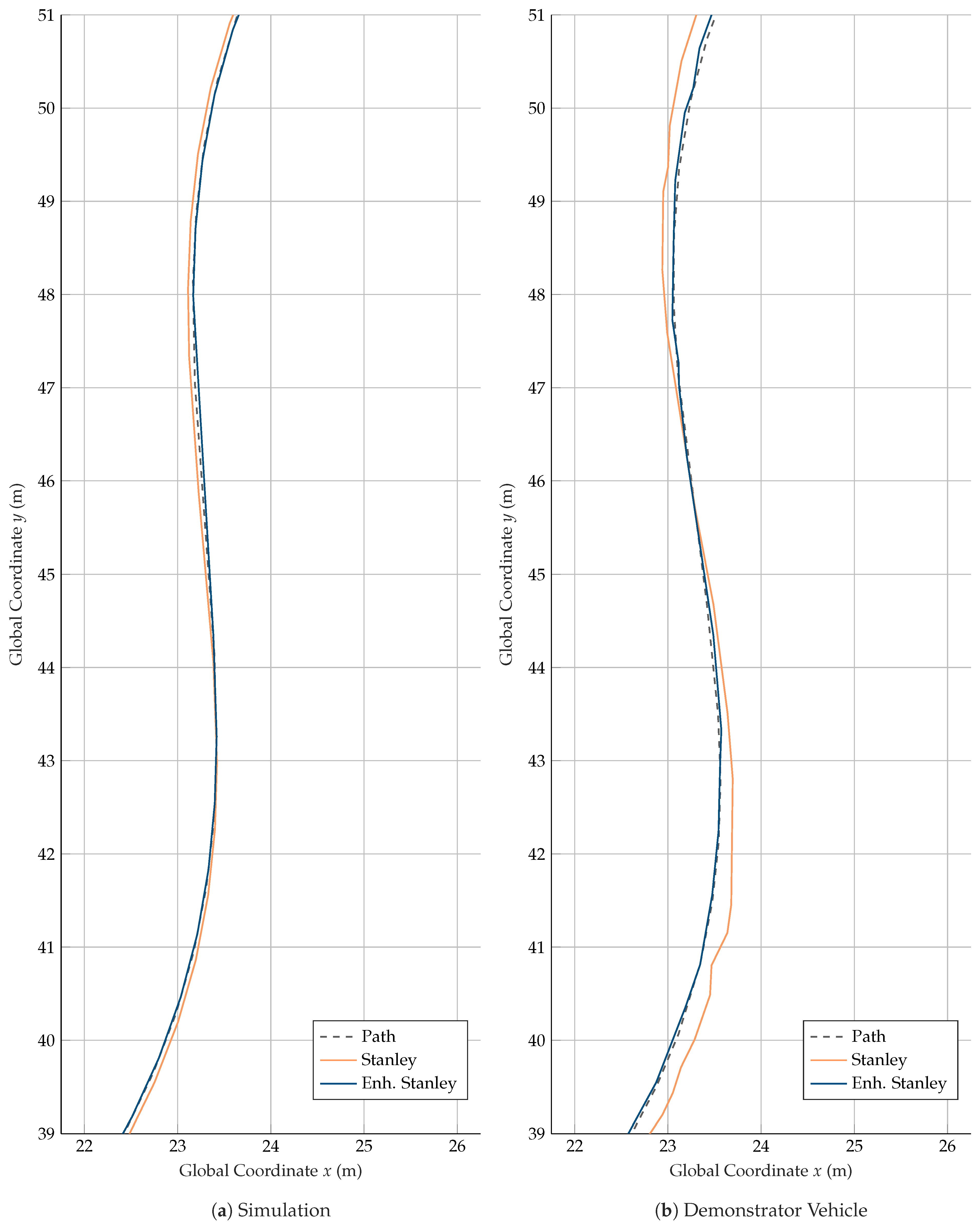
As in the simulation, the enhanced Stanley approach also leads to a reduction in the deviations for the real demonstrator vehicle, with the maximum cross-track error ${\widehat{e}}_{lat,r}$ decreasing by 68% to 0.084 m, and the root mean square cross-track error $e_{lat,r_{RMSE}}$ decreasing by 69% to 0.033 m. The improvement due to the enhanced approach is also clearly shown in Figure 12, where the same map segment of the simulated result and the real vehicle tests are compared. The course of the position, when using the Stanley approach, follows the path with a deviation that is on the outside of the curve. Using the enhanced Stanley approach, the course follows the nominal path with only minor deviations, partly on the outer and inner sides of the curve.

In summary, the described results demonstrate the improvement of the tracking accuracy of the Stanley approach by the proposed enhancement. This was the primary objective of this work. A comparison of the presented approach with other control approaches has been omitted since it was not the authors’ claim to achieve a better control performance than other state-of-the-art approaches. Rather, the focus was to demonstrate the significant effective improvement of the Stanley controller through a relatively minor modification. This is significant since the control approach is widely used because of its well-known simplicity, efficiency, and robustness.

The fields of application of the Stanley controller are moderate velocities and moderate vehicle dynamics, as indicated by the references [7,8,9,10] cited in the Introduction section. The proposed approach enhances the control performance by predictive feedforwarding the steering angle based on the path curvature. When the path curvature changes continuously, the feedforward component of the enhanced Stanley controller ensures that the resulting steering angle input matches the current path curvature better than it does with the original Stanley controller. This eliminates or reduces deviations from the path that would otherwise occur due to system delay. As a result, the control approach with predictive feedforward requires less control action to compensate for deviations, thus improving the robustness of the approach. At constant curvature, the controller dynamics of the proposed approach are identical to that of the Stanley controller (see Section 2.4.4). Therefore, it can be assumed that the fields of application in terms of driving dynamics and velocity of the controller remain unchanged by the enhancement and that the advantage is, therefore, mainly related to the increase in control accuracy.

To achieve robust behavior over the entire velocity range of the application, appropriate control parameters must be chosen. In none of the driving situations considered in our study, neither in the simulation nor in the driving tests with the demonstrator vehicle, did unstable behavior occur with either the Stanley or the proposed control method. This indicates that the approach we have chosen to identify suitable controller parameters is effective; however, no statement about the limits of stability at higher velocity can be made from this as the velocity of the investigated maneuvers was limited due to the vehicle’s maximum velocity of 8 m/s.

4. Conclusions and Outlook

We have proposed an enhancement to the Stanley path tracking controller that improves its tracking accuracy by mitigating the disturbing effects of system delay. We first reformulated the Stanley approach so that the reference path curvature appears explicitly in the equation. While the reference values of all other path inputs are read from the point on the path closest to the vehicle’s reference point, we chose a point on the path that is offset by the feedforward distance along the path to read the path curvature input. For the feedforward distance, we have chosen the distance that the vehicle travels at the current velocity during the constant specified feedforward time. The approach is designed pragmatically to avoid additional effort for implementation and application on a vehicle in order to retain one of the key advantages of the Stanley path-tracking controller approach. Nevertheless, the enhancement resulted in a significant reduction in cross-track error metrics. We have demonstrated this in this article both in the simulative study and with the real demonstrator vehicle.

With our solution, we address applications with moderate velocities and moderate vehicle dynamics on vehicles with sensors and steering systems affected by delays. By improving accuracy despite system delay with low computational cost, we provide a path-tracking solution that can contribute to the realization of economical, automated vehicle systems based on low-cost components. With the same input and output sizes as the Stanley controller, our solution can also be used as an easy-to-implement upgrade for existing applications using a Stanley controller without requiring structural changes or increased complexity.

In further investigations, the approach should be tested at higher velocities and, thus, more dynamic driving maneuvers to determine the limitations of the proposed controller. This requires the implementation of the device on a vehicle that allows higher velocities than the demonstrator vehicle used. Further insight can be gained by comparing the control performance of the proposed approach with the performance of other approaches, especially more complex approaches.