Abstract
Ground vibrations near railway lines are generated by the forces that are acting between wheel and rail. It seems to be a straight forward assumption that the vehicle dynamics are important for the level and the frequencies of the excitation forces. Different vehicle dynamics phenomena are analysed for their role in the excitation of ground vibrations: rigid body modes of the bogies, elastic (bending) modes of the car body, and elastic modes of the wheelset. The theoretical analyses use rigid body models, simplified elastic models, and detailed elastic models. Some of these problems are vehicle–track interaction problems where 3D finite-element boundary-element models have been used for the track and soil. It is shown that the rigid or flexible vehicle modes are well in the frequency range of ground vibrations (4 to 100 Hz). They have an influence on the excitation force but the additional forces are rather small and can be neglected in ground vibration prediction. The theoretical results are checked by experimental results of a simultaneous measurement of vehicle, track, and ground vibrations.
1. Introduction
This contribution is motivated by two research projects. The first project deals with the vehicle–track interaction in experiment and theory [1], the second project deals with the prediction of railway-induced vibration [2]. In the latter, a user-friendly prediction code has been developed which uses the simplest models with a minimum of parameters that sufficiently yield accurate predictions. In this article, more complex vehicle models are compared with the simplest model of a rigid wheelset to check if special vehicle dynamic effects yield considerable excitation forces for ground vibrations and must be added to the prediction code.
In the project of vehicle–track interaction, a complex measuring campaign was performed at the German high-speed line near Würzburg [1]. Vehicle, track, and soil vibrations have been measured simultaneously at a surface, bridge, and tunnel line during train runs with specified speeds and impact hammer excitation. The measurement results for the surface line are used here to confirm the theoretical analyses.
Most experimental studies on railway-induced ground vibrations concentrate on the measurements of the ground vibration, for example [3,4,5,6,7]. It is now almost a standard to determine the soil properties by wave measurements and analysis, see examples in [8,9,10,11,12]. Important additional information is obtained from measured track irregularities as in [13,14,15]. Even better are measurements of the vehicle vibration [16,17,18,19], namely axle-box measurements, but they are rarely combined with ground vibration measurements [20].
Vehicle dynamics are usually analysed as multi-body systems [21,22,23]. The simplest models would be multi-degree-of-freedom rigid body models. Much more complex multibody formalisms (including the complex wheel–rail contact mechanism) such as Gensys, SIMPACK, VAMPIRE, and NUCARS are in use to solve problems of running stability and wear [24]. Flexible vehicle components, namely car bodies [25] and wheelsets [26,27], are modelled for ride comfort, noise reduction, and wear control. These methods are usually too complex for the ground vibration problem. The interaction of the vehicle with the track and the underlying soil, however, is rarely found in vehicle dynamics.
The methods for the dynamics of the track and the train-induced ground vibrations are typically finite element methods with special boundaries [17,28], boundary element methods [11,29], wavenumber domain methods [13,30,31], and combined finite element and wavenumber methods (the so-called 2.5D method [14,15,32]). These methods allow us to calculate the propagation of waves travelling away from the track. The generation of the waves is often simplified. The interaction of the unsprung vehicle mass and the irregularities of the vehicle and track is widely accepted as excitation. More detailed vehicle models have been analysed for train-induced ground vibrations [33]. In [33,34], the additional influence of the bogie mass has been discussed, but later it has been found that it is of minimal effect [35]. To conclude, vehicle dynamics have rarely looked at the vehicle forces that generate train-induced ground vibrations [36], whereas ground vibration specialists have rarely examined the possible vehicle effects on the excitation of waves in the soil.
The aim of the present article is to cover the whole vehicle–track–soil interaction and the induced ground vibration. Vibration measurements of a railway vehicle are evaluated for the forces on the track (and the soil), which excite the ground vibration in the environment. The article is structured as follows: The measurement campaign about vehicle, track and ground vibrations at a surface, bridge, and tunnel line are presented in Section 2. The results of the vehicle, track, and ground measurements at the surface line are presented for different train speeds in Section 3. The theoretical analyses of the vehicle vibrations at frequencies below 40 Hz (rigid body modes of the vehicle and elastic modes of the car body) are done in Section 4. The high-frequency vehicle–track interaction (wheelset–track interaction) is analysed in Section 5. The application of the results to the prediction of train-induced ground vibrations is shown in Section 6. The novelty of the present article is the comparison of the measurement results with the results of simple vehicle models, which can be included in a fast prediction scheme and which can be used with a minimum of input parameters.
2. Simultaneous Measurement Campaign
Simultaneous measurements of the vehicle, track, and ground vibrations have been performed in 1994 on a 3 km long test section of the high-speed line near Würzburg [1]. The test train consisted of a locomotive E113, two carriages, a measuring car, two carriages, and a locomotive E111. The axle load of the measuring car is 100 kN, its wheelset mass is 1500 kg. Measurements have been performed simultaneously at three different track situations: at a surface line and a bridge with a ballasted track and at a tunnel with a slab track. The ballast track at the surface and the bridge consists of UIC60 rails on B60W sleepers with ZW687a rail pads. The high-speed track was in a good condition (low irregularities).
The vibration of the vehicle (the third carriage of the train) has been measured with accelerometers at 12 vertical and 3 horizontal measuring points (Figure 1a). Four accelerometers (A1 to A4) have been mounted on the axle boxes of two wheelsets, and four accelerometers (B1 to B4) have been mounted at the corresponding points of the bogie frame. Four accelerometers (C1 to C4) have been mounted at the car body above both bogies. At the bogie and car body points B2, B4, and C2 also have horizontal accelerations that have been measured. All measuring points are chosen symmetrically for the left and right side of the passenger car [37]. The vibrations of the three different tracks have been measured with geophones (velocity transducers) at 3 × 8 measuring points (2 rail and 6 sleeper points). The vibration of the ground has been measured with 14 geophones in a measuring line up to 100 m distance from the track, as per the layout of the measurements in Figure 2.
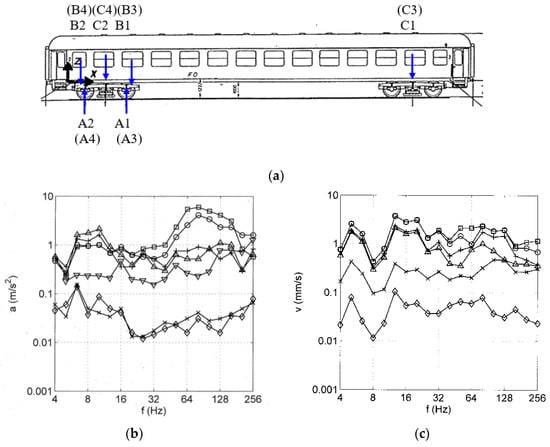
Figure 1.
(a) Measurement points of the railway vehicle (passenger car) for the test runs, axle boxes A1, A2, bogie B1 and B2, carriage C1 and C2, right hand side, A3, A4, B3, B4, C3, C4 symmetrically on the left hand side; (b) one-third octave band spectra of the accelerations of the railway vehicle running with vT = 160 km/h, 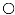 , ☐ wheelset A1 and A2, +, △ vertical bogie part B1 and B2, ▽ horizontal bogie part B1,
, ☐ wheelset A1 and A2, +, △ vertical bogie part B1 and B2, ▽ horizontal bogie part B1, 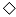 , ✕ car body part C1 and C2; (c) particle velocities of the track ☐,
, ✕ car body part C1 and C2; (c) particle velocities of the track ☐, 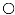 left and right rail, △, + sleeper 1 and 2, ✕, sleeper horizontal,
left and right rail, △, + sleeper 1 and 2, ✕, sleeper horizontal, 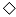 sub soil at 2.5 m distance.
sub soil at 2.5 m distance.
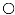 , ☐ wheelset A1 and A2, +, △ vertical bogie part B1 and B2, ▽ horizontal bogie part B1,
, ☐ wheelset A1 and A2, +, △ vertical bogie part B1 and B2, ▽ horizontal bogie part B1, 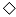 , ✕ car body part C1 and C2; (c) particle velocities of the track ☐,
, ✕ car body part C1 and C2; (c) particle velocities of the track ☐, 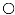 left and right rail, △, + sleeper 1 and 2, ✕, sleeper horizontal,
left and right rail, △, + sleeper 1 and 2, ✕, sleeper horizontal,  sub soil at 2.5 m distance.
sub soil at 2.5 m distance.
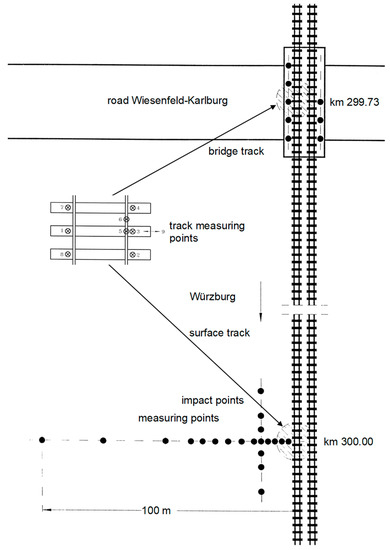
Figure 2.
Layout of the measurements at the surface line and the bridge with track, bridge, and soil measurement points.
The test train has run on the test section with the following train speeds
vT = 16, 25, 40, 63, 80, 100, 125, 140, 160 km/h.
A subset of these measurements, the train passages at the surface line, are used in the present manuscript to be compared with theoretical analyses. These measurements have been recorded using a 72-channel measuring system with programmable filters (here used for anti-aliasing), sample and hold amplifiers, and a 16-bit AD converter running at 2 kHz sampling rate. The measurements have been evaluated uniquely for a 2-s time record around the passage of the measuring car over the instrumented track section. The one-third octave band spectra in Section 3 are calculated from the corresponding Fourier spectra.
In addition to the train passages, each system has been characterized by impulse measurements (hammer impacts), the rigid and flexible modes of the railway vehicle, the flexible modes of the wheelset, the natural modes of the bridge, the receptances of the three tracks, and the transfer mobilities of the soil. The modes of the car body have been measured for 92 degrees of freedom and the results are shown in Section 4.2 together with the theoretical analysis. To assure that natural modes have been identified, an identifier function (phase resonance function) has been evaluated, as per the details in [38]. The measurements of the wheelset modes will be shown in Section 5 in comparison with the theoretical results.
3. Vehicle, Track, and Soil Vibrations Measured during Train Passages
At first, the measured vehicle, track, and soil vibrations are presented and compared for the train passage with 160 km/h. The accelerations of the vehicle have been measured for the different vehicle components (Figure 1a) and the corresponding accelerations are shown as one-third octave band spectra in Figure 1b. The bogie accelerations are almost constant over the whole frequency range of 4 to 256 Hz with amplitudes of 0.5 to 1.0 m/s2. The carriage has much lower amplitudes between 0.01 and 0.1 m/s2 where the higher values are for frequencies below 20 Hz and the lower amplitudes are for higher frequencies. The highest accelerations have been measured for the wheelsets, which are up to 5 m/s2 for frequencies between 50 and 160 Hz. At frequencies below 30 Hz, the wheelset accelerations are lower at about 1 m/s2, all wheelset spectra are the same and the wheelset and bogie spectra are quite similar. Some raised amplitudes occur between 6 and 10 Hz where the bogie has twice the amplitude compared to the wheelset. The horizontal accelerations of the bogie are smaller with 20–30% of the vertical amplitudes. All these trends will be explained with the models and calculations in Section 5.
Figure 1c shows the measurement results for the track, the one-third octave band spectra of the particle velocities of different track elements. These velocity spectra are almost constant over the whole frequency range and have values around 1 mm/s for the sleepers. The rail amplitudes are higher by a factor of 1.5 to 2 because of the elastic rail pads between sleeper and rail. The horizontal sleeper amplitudes are 10– 20% of the vertical sleeper amplitudes. These amplitudes are for a smooth curve of 5000 m radius and would be even smaller for a straight track. As a conclusion of the small horizontal amplitudes for the track, as well as for the vehicle (Figure 1b), the horizontal vibrations are neglected in the present analysis and in the prediction scheme. Finally, the subsoil amplitudes are very small, by a factor of 30 smaller than the sleeper amplitudes. All these track vibrations have the same characteristics of the spectra. There is a strong minimum at 8 Hz and a weak minimum at 25 Hz; a maximum is found at 5–6 Hz and for 12–20 Hz. The three raised thirds of the octaves are not the same as those of the vehicle between 6 and 10 Hz. The characteristics of the track spectra are caused by the sequence of the passing axles [38], which cannot be observed from the vehicle. Moreover, the track spectra up to 30 Hz are dominated by the passing static loads, and the response to the dynamic vehicle loads can only be observed at higher frequencies. It should be noted that at high frequencies, the left and right rails and sleeper ends have different spectra whereas they are the same for the low- and mid-frequency range. This trend can also be observed for the right and left axle-box accelerations in Figure 1b, and it will be explained by the different vibration modes of the wheelset at high frequencies.
The ground vibrations measured for the train speed of 160 km/h are presented as the one-third octave band spectra of the particle velocities at distances from 2.5 to 50 m (Figure 3a,b). The main amplitudes can be found between 10 and 80 Hz, whereas frequencies below 10 Hz and above 80 Hz are strongly reduced. Moreover, a strong attenuation with distance is observed in these frequency ranges. At low frequencies, there is an abrupt reduction from 2.5 m to 5 m distance. At high frequencies, there is a more regular reduction of two decades up to a distance of 50 m. The weakest attenuation of half a decade for 50 m can be found in the mid-frequency range at 10–16 Hz. These filter and attenuation effects lead to a dominant frequency of 12 or 16 Hz in the far field. This frequency peak (and a second weaker peak at 50–64 Hz) are even stronger for the passage of the locomotive in Figure 3a. The same shape of the spectra can also be found for lower train speeds of 63 and 25 km/h with lower amplitudes (Figure 3c,d).
Figure 3.
Vibration of the soil (one-third octave band spectra) at distances ☐ 2.5, ○ 7.5, △ 12.5, + 20, ✕ 30, 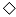 50 m, due to passage of (a) the locomotive with 160 km/h, the passenger car with (b) 160 km/h, (c) 63 km/h, and (d) 25 km/h.
50 m, due to passage of (a) the locomotive with 160 km/h, the passenger car with (b) 160 km/h, (c) 63 km/h, and (d) 25 km/h.
 50 m, due to passage of (a) the locomotive with 160 km/h, the passenger car with (b) 160 km/h, (c) 63 km/h, and (d) 25 km/h.
50 m, due to passage of (a) the locomotive with 160 km/h, the passenger car with (b) 160 km/h, (c) 63 km/h, and (d) 25 km/h.
The Influence of the train speed is further analysed with Figure 4 and Figure 5. The car body (Figure 4a) has low amplitudes, which increase with the train speed while the shape of the spectra with a typical decrease at 20 Hz remains constant. The bogie (Figure 4b) shows a similar increase of amplitudes with train speed mainly at low frequencies. For the wheelsets in Figure 4c–f, the accelerations increase clearly with the train speed as a~vT2, which means that the displacements of the wheels are speed independent in this low- and mid-frequency range and directly represent the track and vehicle irregularities. The somewhat greater high-frequency amplitudes increase less strongly with the train speed. The low- and mid-frequency wheelset and bogie spectra are shifted to higher frequencies with increasing train speed. This can be seen for the component between 6 and 10 Hz and for the maxima at 16 and 32 Hz for 160 km/h, which are the first and second out-of-roundness of the wheels [39]. At high frequencies, a specific maximum is shifted from 32 to 40, 50, 64, and 80 Hz (most clearly in Figure 4c), which is the frequency due to the distance of the sleepers [40]. The wheel A2 (Figure 4d) shows a fixed dominant frequency of 64 Hz, which hides the sleeper–distance maxima. Another fixed frequency, though weak, can be found at around 100 Hz, which could also be attributed to a vehicle or vehicle–track eigenfrequency. The specific speed-dependent or speed-independent frequencies are also analysed with narrow-band spectra in Appendix A, confirming the observations in the one-third octave band spectra with greater details.
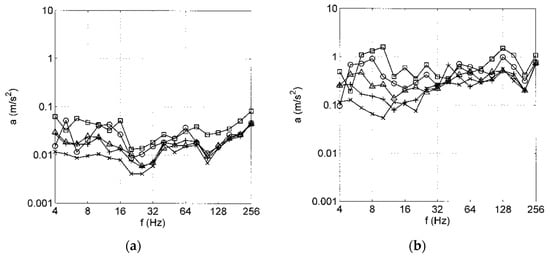
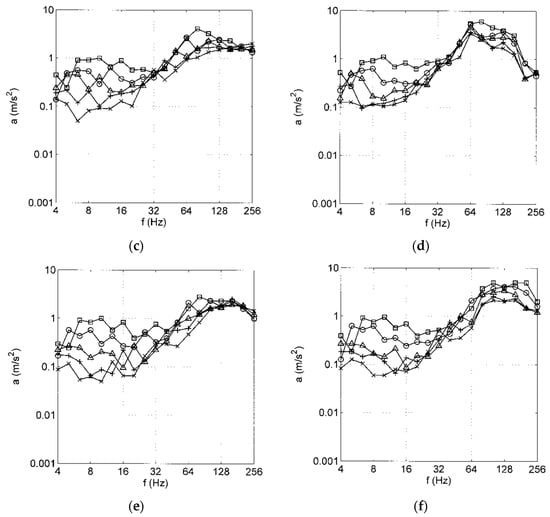
Figure 4.
Vibrations of the railway vehicle, one-third octave band spectra for different train speeds ☐ 160, ○ 125, △ 100, + 80, ✕ 63 km/h, (a) car body C1, (b) bogie B3, (c) wheel A1, (d) wheel A2, (e) wheel A3, (f) wheel A4.
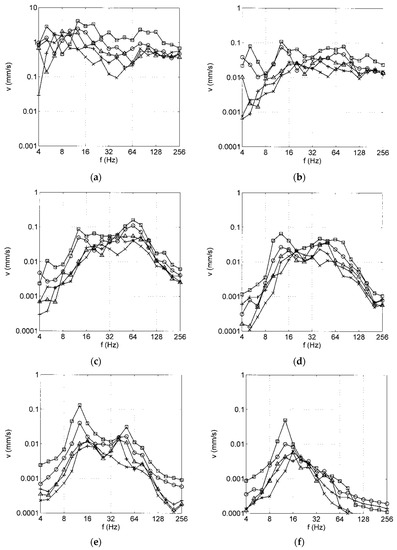
Figure 5.
Vibrations of the soil, one-third octave band spectra for different train speeds ☐ 160, ○ 125, △ 100, + 80, ✕ 63 km/h, at distances (a) 0 m (rail) (b) 2.5 m, (c) 5 m, (d) 17.5 m, (e) 30 m, (f) 100 m.
The influence of the train speed on the track and ground vibrations at different distances is presented in Figure 5. There is a general increase of velocity amplitudes with train speed, most clearly for the track (Figure 5a). The maximum rail amplitudes increase quite regularly as vmax~vT, which means that the rail displacements are almost the same for all train speeds. This maximum, comprising three thirds of octaves (10 to 16 Hz for 160 km/h), is also regularly shifted with train speed. Such a regular behaviour cannot be found for the soil measuring points. A frequency shift can be seen in Figure 5b for the lowest frequency of 4 and 5 Hz at 125 and 160 km/h, which belongs to the quasi-static response [38]. Another frequency shift can be followed at 5 m distance (Figure 5c) for the sleeper–distance frequency of 32 to 80 Hz. The more dominant maxima, however, are at 12 and 64 Hz. The high-frequency maximum at around 64 Hz loses its importance for the farer measuring points, and only the mid-frequency maximum of 12 Hz is left over at 100 m (Figure 5f). For this maximum, the clearest increase of amplitude can be observed for 125 and 160 km/h, where the amplitudes are up to 10 times higher than those of the lower speeds. The two speed-independent peak frequencies seem to be related to vehicle or soil resonances. Moreover, the specific shape of the spectra of different distances are strongly determined by the transfer function of the soil, which is so dominant that other vehicle and track characteristics are mostly hidden.
The following similarities can be observed between the vehicle, track, and soil vibrations. The low-frequency high-speed component can be found in the track and the near-field soil spectra, and it has been identified as the quasi-static response in [39]. The high-frequency maximum around 64 Hz can be found in the wheelset and in the mid-field ground vibrations. The most important maximum is around 12 Hz, which is dominant at the far field and has especially high amplitudes for the highest speeds and can also be found at the track at high speeds, but it is shifted to lower frequencies for lower train speeds. The layering of the soil at the measuring site yields an eigenfrequency at 12 Hz, but the resonance amplification is usually not so high. Finally, vehicle eigenfrequencies also occur in this mid-frequency range; for example, the bogie amplitudes are amplified at a slightly lower frequency range. The purpose of the following sections are to analyse possible vehicle resonances in the mid-frequency range around 12 Hz (below 40 Hz, Section 4) as well as in the high-frequency range around 64 Hz (above 40 Hz, Section 5) and their effects on the excitation forces of the ground vibrations.
4. Analyses of the Vehicle Dynamics at Frequencies below 40 Hz
The following sections analyse the influence of rigid bogie modes, flexible carriage modes, and flexible wheelset modes. The influence of the track has been analysed in detail by three-dimensional finite-element boundary-element models in [29]. The track stiffness has no influence on the vehicle–track interaction at low and mid frequencies, such as at the rigid bogie and the flexible carriage modes, which therefore are discussed for a rigid track. At higher frequencies, the compliance of the track is important, and it is included as a soil-dependent spring stiffness in the analysis of the flexible wheelset in Section 5. All analyses have been done by simple two- and three-degree-of-freedom systems, which could be introduced in the prediction software if necessary.
4.1. Rigid Body Modes of the Railway Vehicle at Frequencies below 40 Hz
The rigid vehicle model of Figure 6a is considered, which consists of two wheelset masses of 1700 kg (1550 kg), a bogie frame of mass 2800 kg (2500 kg), and the mass of half a car body of 16,500 kg (14,500 kg). The complete set of parameters of the ICExperimental mid car including the primary and secondary suspension can be found in [40], together with the measured ground vibration. The values in brackets are for the passenger car of the measuring campaign [1], for which similar results have been found. The parameters can be used to get the vertical and the pitching eigenfrequencies of the bogie
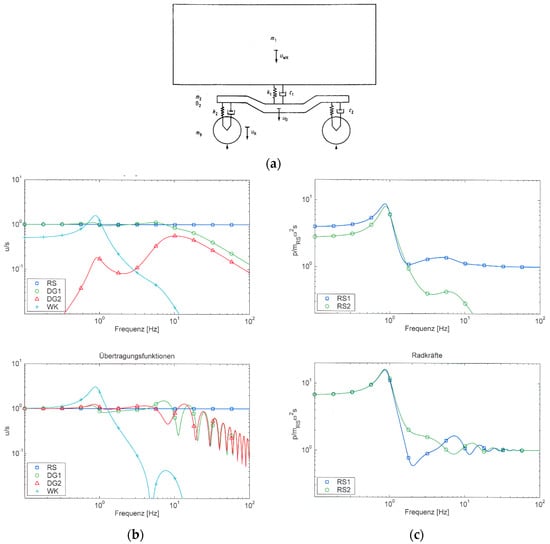
Figure 6.
(a) Four-mass vehicle model; (b) displacements of the ☐ wheelset A1, ○, △ bogie B1 and B2, + car body C2, (c) wheel–rail forces of wheelset ☐ A1 and ™ A2 related to the inertial force of a wheelset; excitation by track irregularities at wheelset A1 (top) or at both wheelsets travelling with 100 km/h (bottom).
The eigenfrequency of the car body can clearly be found at about 1 Hz as a resonance of the car body response, shown at the top of Figure 6b. The bogie resonances show little resonance amplification, the excited bogie part 1 shows the vertical eigenfrequency, the second not-excited bogie part has its maximum near the pitching eigenfrequency.
The displacements which are shown at the top of Figure 6b are calculated for a harmonic excitation s of one wheelset. At the very low frequencies below 1 Hz, the excited bogie part B1 exactly follows the excitation while bogie part B2 is almost at rest. The car body follows with half of the one-sided excitation. With increasing frequencies, the different components of the vehicle decouple from the excited wheelset. At first, the car body is decoupled above its eigenfrequency of 1 Hz, then the bogie above its vertical eigenfrequency of 7 Hz or above its pitching eigenfrequency of 14 Hz. In case of a flexible track, there is also a wheelset–track eigenfrequency between 50 to 100 Hz, above which the wheelset decouples from the excitation, as seen in Section 5. All of these trends can also be found in good agreement with the measurements in Figure 1b and Figure 4.
The one-sided excitation includes the symmetric and antimetric excitation of the bogie uniquely for all frequencies. Under real conditions, shown at the bottom of Figure 6b, both wheelsets of a bogie are excited by the same track irregularities, which have a certain time delay or a phase delay that increases linearly with frequency and is inverse to the train speed vT
ϕ = 2 π f lA/vT.
For the wheelset distance lA = 2.8 m and the train speed vT = 100 km/h, the phase delay is π at f = 5 Hz (anti-phase excitation), 2π at 10 Hz (in-phase excitation). More antimetric excitations follow at 15, 25, 35, … Hz. At low frequencies, the phase is close to zero. For this in-phase excitation, all masses follow the excitation (u/s = 1). Between 1 and 5 Hz, the second bogie part has higher amplitudes than the first bogie part. The antimetric excitation at 5 Hz yields identical amplitudes of both bogie parts and zero displacements of the car body due to the pure rotation of the bogie frame. For higher frequencies, there are regular variations of the bogie displacements due to the regular sequence of the symmetric and antimetric excitation. As the vertical mode has a lower eigenfrequency, it is more strongly reduced than the rotational mode at higher frequencies. Therefore, maxima are found for antimetric excitation and minima for symmetric excitation.
Corresponding results for the wheel–rail forces are shown in Figure 6c. For the one-sided excitation (Figure 6c top) the wheel–rail force of the excited first wheelset is higher than for the unexcited second wheelset. The difference is the inertial force of a wheelset. At frequencies below 1 Hz, the force is the inertial force of the whole (quarter) vehicle. At high frequencies, the force at the excited wheelset is the inertial force of this wheelset, while the force of the unexcited wheel tends to zero.
The bottom of Figure 6c shows the wheel–track forces for the realistic two-wheelset excitation with phase delay. For this realistic case, both wheelset forces tend to the inertial force of the wheelset for frequencies higher than 20 Hz. At very low frequencies below 1 Hz, the forces are the inertial forces of the whole vehicle, which are approximately seven times higher than the wheelset forces. The decrease of the forces follows immediately after the car body resonance, and the forces are close to the wheelset forces in the intermediate range of 5 to 20 Hz. For these frequencies, there are some differences between the first and the second wheelset and variations with frequency, which decrease rapidly with increasing frequency. It is observed that the force of the first wheelset is smaller than that of the second wheelset in the intermediate frequency range of 1 to 5 Hz. The possible amplification is not stronger than two, which would correspond to the mass of the wheelsets and the bogie frame. The restricted influence of the bogie resonances is due to the small inertia of the bogie frame and the strong damping of the primary suspension for the passenger cars considered here, and this conclusion was checked for other passenger cars and other train speeds.
The special bogie effects can also be found in the vehicle measurements (Figure 1b and Figure 4b) where a certain track irregularity is amplified by a factor of 1.5–2 for the bogie at 5–8 Hz (v = 125 km/h) and at 6–10 Hz (v = 160 km/h). These frequencies are not the frequencies of strong ground vibration, thus from the experimental view, accelerations of the bogie frame are not expected as a significant excitation of ground vibration.
4.2. Elastic Modes of the Car Body
A modal analysis of the measuring car, a typical passenger car of the German Railway, has been performed in a workshop in Würzburg [1,41]. The passenger car has been excited by hammer impacts so that the mode shapes could be established for 92 degrees of freedoms, 44 of the car body, 2 × 20 of the bogies, and 4 × 2 of the wheelsets. Besides rigid body modes in the range of 1.2 to 4 Hz, clearly separated elastic modes of the car body have been identified in Figure 7. The first bending mode is at 9 Hz, the lateral bending mode is at 11 Hz; the first torsional mode is at 14 Hz, and the second bending mode is at 18 Hz. Note that the two vertical eigenfrequencies have also been found during the test runs, as seen in Figure A1a in Appendix A. All of these elastic modes of the car body are in the frequency range of strong ground motion. The effect of these elastic modes on the excitation of ground vibration is analysed by a simple beam model on the support springs and dampers of the secondary suspension.
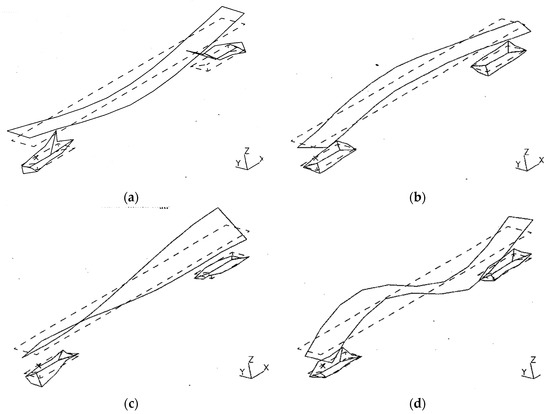
Figure 7.
Measured modes of a passenger car [38] at (a) 9 Hz (vertical bending 1), (b) 11 Hz (lateral bending 1), (c) 14 Hz (torsional 1), (d) 18 Hz (vertical bending 2).
The elastic support yields the rigid mode of the car body, which is at 1–5 Hz depending on the support stiffness (Figure 8a). A second maximum is found at 9 Hz for the displacement of the middle of the car, which is due to the first bending mode. The forces at the support (Figure 8b) show the rigid resonance below 5 Hz, but a minimum at the elastic eigenfrequency at 9 Hz. A maximum follows immediately, which has no considerable amplification for realistic support spring stiffnesses.
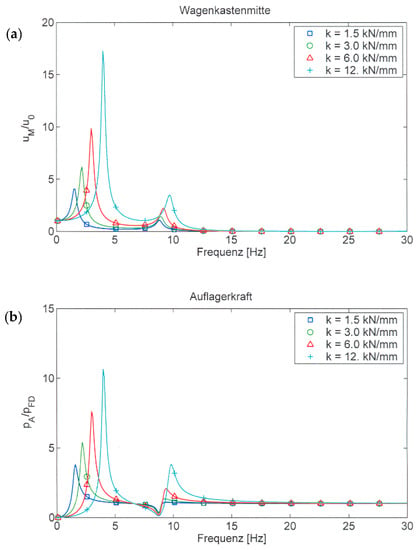
Figure 8.
Calculated (a) displacements at mid-car related to the in-phase support motion and (b) suspension forces compared to the suspension forces of a fixed car body, variation of the suspension stiffness.
These results can be generalised as follows: The elastic modes of the car body are almost the modes of the free and unsupported car body and occur at almost the free eigenfrequency. For the free modes, all inertial forces are balanced and no support forces appear. As the frequencies of the supported and unsupported modes are close together, the support forces are small at these eigenfrequencies. Under normal soft and medium support stiffnesses (secondary suspensions), the support forces have no important amplification in the “resonance region”.
Therefore, it can be concluded that the elastic modes of the car body, as well as the rigid bogie modes of Section 4.1, are not a reason for the pronounced ground vibration. Consequently, the forces below 40 Hz can be approximated by the rigid wheelset mass. Moreover, in this low- and mid-frequency range, the irregularities s of the wheel and track can be calculated directly from the axle-box accelerations a as s~a/ω2 without any influence of the vehicle model.
5. Wheelset–Track Analysis at Frequencies above 40 Hz
A typical wheelset of the passenger car, which has also been measured during the campaign, has been calculated as a finite-element model for different support conditions [42]. The most important eigenfrequencies of the wheelset are shown in Figure 9. The wheelset on a medium stiff support k = 5 × 108 N/m has an in-phase eigenfrequency at f1 = 62.7 Hz and an anti-phase eigenfrequency at f2 = 90.3 Hz, where the wheels and the mid-axle are in anti-phase. In addition to these coupled modes, there is the rolling mode at 84.7 Hz and the horizontal bending mode at 70.9 Hz, which is also the vertical free bending eigenfrequency of the wheelset.
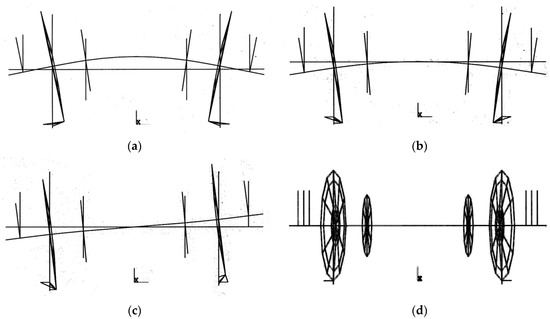
Figure 9.
Calculated modes of a wheelset on a track stiffness of kT = 5 × 108 N/m2 at (a) 62.7 Hz (vertical and bending in phase), (b) 90.3 Hz (vertical and bending out of phase), (c) 84.7 Hz (rolling), and (d) 70.9 Hz (horizontal bending).
The vertical modes vary with the support stiffness k. If the support is very stiff (k = 50 × 108 N/m, Figure 10a), the eigenfrequency f = 66.8 Hz approaches the eigenfrequency of the rigidly supported wheelset. If the support is very soft (k = 0.5 × 108 N/m, Figure 10d), the eigenfrequency f = 71.8 Hz tends to the eigenfrequency of the free wheelset. For realistic stiffness parameters, the eigenfrequencies are not so far from these two limit cases. For a medium stiff k = 10 × 108 N/m, the eigenfrequency f = 65.4 Hz is somewhat above the rigidly supported eigenfrequency (Figure 10b), and for a soft support with k = 2.5 × 108 N/m, the eigenfrequency f = 77.3 Hz is somewhat above the free eigenfrequency (Figure 10c). These somewhat contradictory results with a frequency jump between k = 2.5 and 10 × 108 N/m will be further explained at the end of this section.
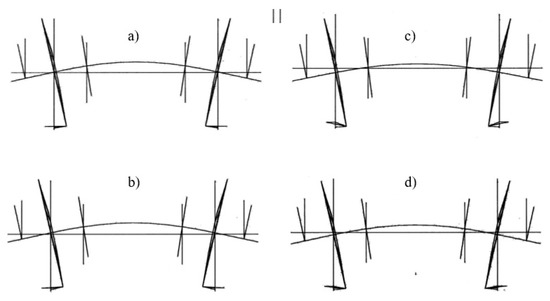
Figure 10.
Calculated elastic mode of a wheelset on different track stiffnesses (a) k = 50 × 108 N/m at 66.8 Hz, (b) k = 10 × 108 N/m at 65.4 Hz, (c) k = 2.5 × 108 N/m at 77.3 Hz, (d) k = 0.5 × 108 N/m at 71.8 Hz.
The calculated eigenfrequencies and mode shapes are confronted with an experimental modal analysis of a similar wheelset in a workshop [42], as seen in Figure 11. The wheelset was instrumented with 12 × 2 × 3 geophones around the two wheels and 7 × 3 geophones along the axle (all in three directions) and excited by a hammer vertically in the mid of the axle (shifted by 0.3 m) and horizontally at the upper end of one of the wheels (shifted by 30°). The horizontal excitation yields the mainly horizontal mode at 33.2 Hz, and the vertical excitation yields the mainly vertical mode at 79.3 Hz. The latter includes an anti-phase bending component. The free bending mode (in horizontal direction) has been found at 70.3 Hz for both excitations. The restrained bending mode (in vertical direction) lies at 107.5 Hz for both excitations. This eigenfrequency is higher than in the running train and in the calculation because of the stronger horizontal fixation at the contact point. The main conclusion of the comparison is the confirmation that the free bending mode is at approximately 70 Hz, and that the two coupled vertical and bending modes are close together.
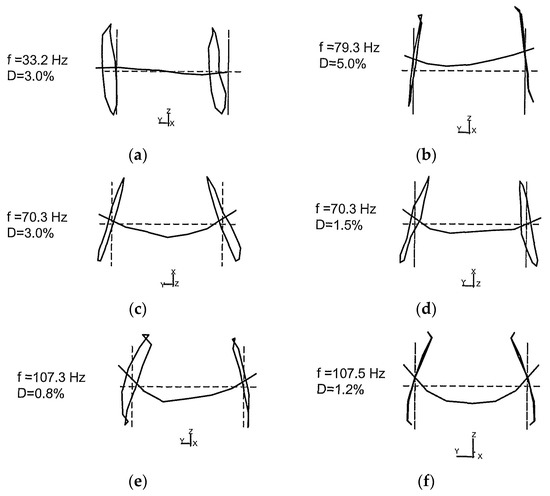
Figure 11.
Measured modes of the wheelset [42], horizontal hammer impact on the wheel (left) vertical hammer impact on the mid-axle, (a) horizontal at 32.3 Hz, (b) vertical (with out-of-phase bending) at 79.3 Hz, (c,d) horizontal (free) bending at 70.3 Hz, (e,f) vertical (restrained) bending at 107.5 Hz.
The frequency-dependent wheel and axle displacements are investigated by a simple two-mass model which is fitted to the known eigenfrequencies. It is given in full mathematical detail in Appendix B for possible inclusion in a fast prediction software. The results of the simple model are, in general, similar to the results of a more complex and detailed finite element model in [43]. In Figure 12a–d (top), the two vertical resonances of the wheelset can be found, but the amplifications are different for wheel and axle and vary with the support stiffness. The highest amplification is for the axle mass, whereas the wheel mass has a smaller resonance and even a zero at the eigenfrequency of the rigidly bounded wheelset.
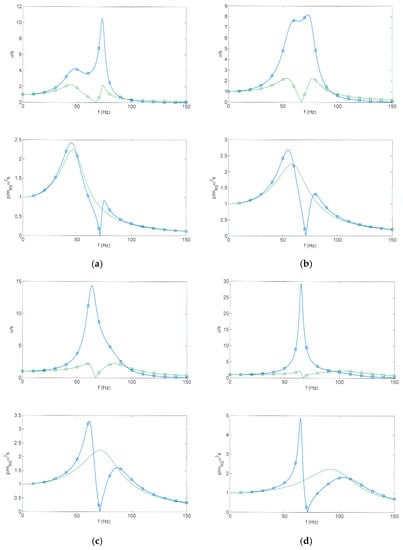
Figure 12.
The displacements u and wheel–rail forces p of a flexible wheelset excited by track and wheel irregularities s, with different track stiffness (a) 1.25 × 108 N/m2 (b) 2 × 108 N/m2 (c) 3 × 108 N/m2, (d) 5 × 108 N/m2, ☐ mid axle and  wheel displacements, forces of a ☐ flexible and − rigid wheelset.
wheel displacements, forces of a ☐ flexible and − rigid wheelset.
 wheel displacements, forces of a ☐ flexible and − rigid wheelset.
wheel displacements, forces of a ☐ flexible and − rigid wheelset.
The dynamic support forces (Figure 12a–d, bottom) also have a characteristic zero, which is at the eigenfrequency of the free wheelset. The first resonance is always stronger than the second resonance. The maximum amplification increases clearly with the stiffness of the support. Above the wheelset–track resonance, the force decreases compared to the inertial force of the wheelset. This is of importance for high-frequency excitations such as the sleeper–distance excitation for which the wheel–rail force increases according to
only for low train speeds and remains constant for high train speeds.
p ≈ mWω2~mWvT2
The variation of the response with the support stiffness is further demonstrated in Figure 13. The resonance frequencies show two crossing asymptotes (Figure 13a). One asymptote is the constant elastic eigenfrequency of the wheelset, the other asymptote is the rigid body eigenfrequency (the wheelset–track eigenfrequency), which increases with the support stiffness. Around the crossing of the asymptotes, the curves deviate from these asymptotes and the two eigenfrequencies change their role. The elastic eigenfrequency jumps from the upper curve to the lower curve and from the higher value of the free eigenfrequency to the lower value of the rigidly supported eigenfrequency.
Figure 13.
A flexible wheelset on a flexible track, variation of the track stiffness (a) eigenfrequencies, (b) modal damping, (c) maximum amplification of the wheel–rail force related to the rigid wheelset, (d) displacement difference mid axle-wheel; ☐ first, 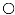 second mode.
second mode.
 second mode.
second mode.
The same things can be observed for the modal damping in Figure 13b. For low support stiffnesses, the low rigid body resonance has the strong support damping of D ≈ 0.25, and the higher elastic eigenfrequency has the low wheelset damping of D = 0.001. For high support stiffnesses, the eigenfrequencies have changed their position but kept their characteristic damping. The damping curves meet in the medium stiffness range and both eigenfrequencies have a medium damping of D ≈ 0.12.
The effect of the support stiffness on the maximum dynamic loads on the track is shown in Figure 13c. The resonance force is compared with the resonance force of a rigid wheelset. This “rigid” resonance amplitude occurs for soft support stiffnesses and for the first eigenfrequency. The second eigenfrequency, which consists of an anti-phase vibration, always has a smaller resonance force. For low support stiffnesses, the second mode is the almost free bending mode of the wheelset with very small support forces. For high support stiffnesses, the support mode is the second mode with support forces that are a little smaller than the “rigid” resonance forces. The elastic mode is then the first mode at nearly the fixed mode, and the resonance amplitude increases considerably with the increasing support stiffness. Similar effects can be read from the difference of the axle and wheel displacement (the elastic deformation) at resonance in Figure 13d. Once again, an increase of the elastic effects is found for the stiff support condition. Some explicit formula for the coupling of a flexible system with a track or a general support stiffness are derived for a two-mass system in Appendix B.
The conclusion for the excitation of ground vibration is that the flexibility of the wheelsets does not yield a considerable force increase on the track and ground. The only exceptions are very stiff support conditions where resonance amplifications of the force at the elastic eigenfrequency of the wheelset are possible. Note that the relevance of the elastic wheelset mode is further limited by the primary damping, which has not been included for simplicity. Usually, the most important mode of the wheelset is the vertical vehicle–track mode, which yields a resonance and a force reduction at higher frequencies, whereas the elastic and rocking wheelset modes can be measured at the axle boxes and have no effect on the ground vibration (see also [13,44]) and can be neglected in the prediction.
6. Prediction of Irregularities, Force Spectra, and Ground Vibrations
As a result of the analyses in Section 4 and Section 5, the effect of the irregularities on the dynamic forces and the ground vibrations can well be approximated by the model of a rigid wheelset. The irregularity amplitudes s decreases with frequency as s~f −2 for frequencies below 40 Hz and s~f −0.75 for frequencies above 40 Hz according to [40] (Figure 14a). As the force transfer function due to the inertia of the vehicle (the wheelset) increases with frequency at the same time, the resulting force spectrum (Figure 14b) is nearly constant with some increase around the vehicle–track resonance. Some similarities can be found between the predicted excitation forces in Figure 14b and the measured wheelset acceleration in Figure 4c–f. The present axle-box measurements confirm the general trend, the smooth almost constant force spectra with amplitudes of approximately 1 kN per axle and third of octave. This general trend has also been checked by many ground vibration measurements at different sites in [40]. The forces at higher frequencies, however, would be overestimated by the axle-box accelerations according to the analysis in Section 5.
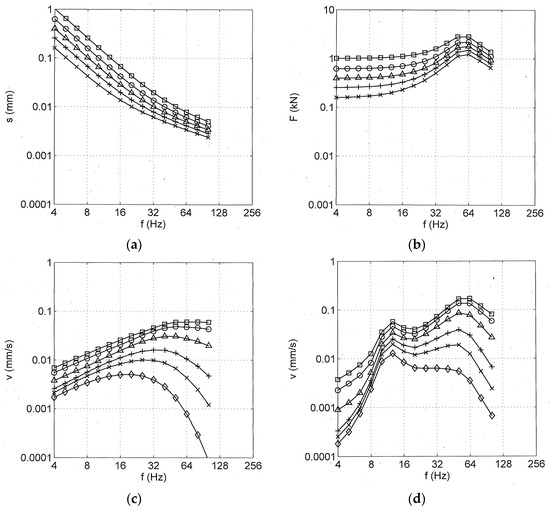
Figure 14.
Vehicle and track irregularities (a) and wheel–rail forces (b) for different train speeds from 63 to 160 km/h; ground vibrations at different distances from 3–50 m for (c) a homogeneous soil (vS1 = 270 m/s D = 5%) with a constant force of 1 kN, (d) for a layered soil (vS2 = 1000 m/s, h =10 m) with the force from (b), vT = 160 km/h.
The ground vibration for a train load with a constant force spectrum and for a homogeneous soil is shown in Figure 14c. The low-frequency velocity amplitudes increase systematically with frequency; the high-frequency amplitudes decrease due to the material damping of the soil. Therefore, the mid-frequency range between 16 and 64 Hz is dominant and these trends are in satisfactory agreement with the measurements. The prediction can be improved by using the calculated force spectrum and the transfer functions of the layered soil at the measuring site (Figure 14d). The layering of the soil yields an additional low-frequency cut-off, and the layer resonance at 12 to 16 Hz and the vehicle–track resonance at 50 to 64 Hz are now included. The even higher measured mid-frequency amplitudes for 160 km/h (Figure 3j) have been attributed to a scattering effect of the moving static loads, as seen in the detailed analyses in [45]. The whole simple, fast, and efficient prediction scheme is given with all details in [46].
7. Conclusions
The excitation of ground vibrations is due to forces on the track and on the ground. The excitation forces are mainly caused by the acceleration of the unsprung mass when it is passing over irregularities of the track or the wheel. Additional effects due to vehicle dynamics are shown to be of little importance in the relevant frequency range of 4 to 100 Hz. The car body is decoupled from the bogies and wheelsets starting from a very low frequency. Elastic modes of the car body are typically between 10 and 20 Hz, but they result in small support forces because they are almost free modes with balanced inertial forces. The rigid body modes of the bogies are at 7 to 15 Hz, but they are strongly damped for the passenger trains that have been analysed and measured. Moreover, the rotational modes of the bogie and the wheelset yield a couple of opposite forces which have no effect at some distance apart from the track. The elastic bending mode of the wheelset has little influence on the excitation force in most cases if its frequency lies above the fundamental vertical wheelset mode. The vertical wheelset mode, which is actually a wheelset–track–soil mode and is also called the P2 mode, yields a resonance amplification and a reduction of the excitation forces at higher frequencies. The theoretical analyses and the simultaneous measurements of the vehicle, track, and soil are generally in good agreement so that train-induced ground vibrations can be well predicted with the simplest vehicle model of a rigid wheelset on the dynamic track–soil stiffness in most cases. The specific prediction needs a realistic spectrum of the vehicle and track irregularities and the realistic transfer functions of the layered soil.
Funding
The research received no external funding.
Data Availability Statement
Data can be provided on request by the author.
Acknowledgments
The pleasant teamwork with my colleagues S. Said and W. Schmid during the complex measuring campaign is kindly appreciated.
Conflicts of Interest
The author declares no conflict of interests.
Appendix A. Fourier-Spectra of the Vehicle during Acceleration Runs of the Test Train
A test run has been measured where the train was accelerated from 40 to 110 km/h. The linear Fourier spectra are shown in Figure A1 for the whole test run as a spectrogram, which provides additional information about the vehicle modes and the excitation. The car body (Figure A1a) shows two strongly excited modes as horizontal lines at 2 Hz and at 10 Hz and a weak resonance at 14 Hz. The bogie (Figure A1b) shows a strongly excited region between 5 and 12 Hz, but with no clear peaks for the eigenfrequencies. All four measured axle boxes are presented in Figure A1c–f. The most dominant line is due to the sleeper distance excitation and runs from 20 to 50 Hz for all four wheels, most strongly in Figure A1c. More regular lines are clearly visible at all vehicle points, which are the wheel out-of-roundness lines of different orders. The first order is at 4–11 Hz, and the higher orders are integer multiples. These regular lines are most clearly at the two wheels of the wheelset in Figure A1d,f. Note that the fifth out-of-roundness is close to the sleeper-distance frequency and thus intensifies the corresponding effect. The eigenmodes of the wheelsets are difficult to find. There are some intensified frequency regions around 75 Hz for the wheels A1 and A2 (Figure A1c,d), which are on the inner side of the curve, and around 90 Hz for the wheels A3 and A4 on the outer side of the curve. The out-of-roundness lines are clearly intensified when they pass through the resonance region around 75 Hz (Figure A1d) and around 90 Hz (Figure A1f).
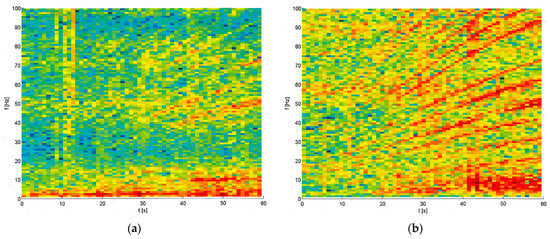
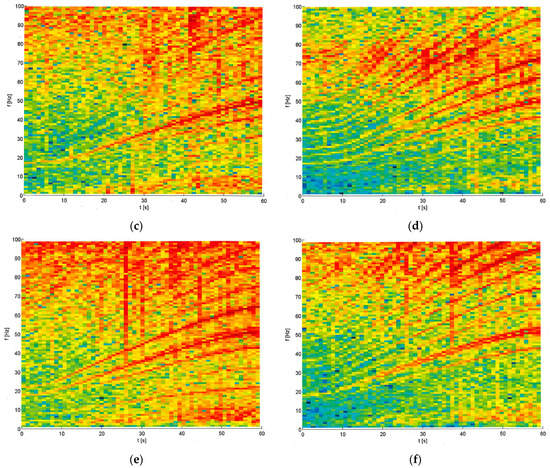
Figure A1.
Acceleration run from 40 to 120 km/h, spectrograms of (a) the car body C2, (b) the bogie B2, (c) the wheel A1, (d) wheel A2, (e) wheel A3, (f) wheel A4.
Appendix B. Influence of the Support Stiffness for a Two-Mass System
The two-mass system consists of two mass–spring systems in series (Figure A2). At the lower end of the lower system the harmonic displacement u0 is applied. The system equation reads
and the transfer functions for both masses can be derived
and
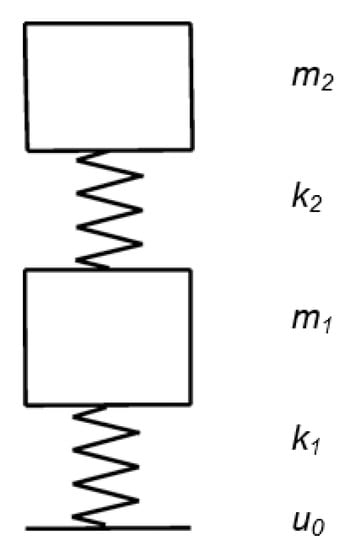
Figure A2.
The two-mass system.
The two eigenfrequencies follow from the zeros of the determinant
det K = 0 = m1m2ω4 − (k1m2 + k2m2+ k2m1)ω2 + k1k2
The following abbreviations are used when the influence of the support stiffness k1 is discussed
| ωA2 = k1/m1 support frequency, |
| ωS2 = k2/m2 structural frequency, |
| ωF2 = k2(1/m1 + 1/m2) free structural frequency, |
| ωF2 − ωS2 = k2/m1. |
The condition for the eigenfrequencies can be written as
and the solutions are
ω4 − (ωA2+ωF2–ωS2+ωS2)ω2 + ωS2ωA2 = 0
ω4 − (ωA2+ωF2)ω2 + ωS2ωA2 = 0,
If the second part of the root is negligible compared to 1, the approximations
hold. Therefore, it can be concluded for stiff and soft support [47]
| stiff support ωA2 →∞ ω1,22 = ωA2; ωS2 |
| soft support ωA2 →0 ω1,22 = ωF2; ωA2ωS2/ωF2. |
The stiff support yields the high support frequency ωA and the rigidly supported structural frequency ωS, whereas the soft support yields the free structural frequency and the low rigid body frequency
ωR2 = ωA2ωS2/ωF2 = k1/(m1 + m2).
The displacements and the support force can be written with the same abbreviations as
and
It follows that the support mass m1 has a zero at the (fixed) structural eigenfrequency ωS and that the support force has a zero at the free structural frequency ωF. For a soft support stiffness, there is also the eigenfrequency ω2 close to the free structural eigenfrequency ωF, and thus a pole-zero compensation for the support force. The force transfer function is close to that of a rigid mass with
The above formulas can be generalised for a hysteretically damped system by replacing the stiffnesses by complex stiffnesses ki* = ki(1 + i2Di) with the material damping values Di.
The conclusions can be applied to the flexible wheelset and the flexible car body. It is also used for the prediction of the floor responses in buildings due to ground vibration [46,47]. For continuous systems, the parameters can be adjusted to the fixed structural eigenmode v
or to the free structural eigenmode w
or to the ratio of the free and fixed structural eigenfrequencies
References
- Auersch, L.; Said, S.; Rücker, W. Das Fahrzeug-Fahrweg-Verhalten und die Umgebungserschütterungen bei Eisenbahnen; Research report 243; BAM: Berlin, Germany, 2001. [Google Scholar]
- Gerstberger, U.; Auersch, L.; Meinhardt, C.; Rücker, W. Ein Einfach Handhabbares Prognoseprogramm für Schienenverkehrserschütterungen; VDI-Berichte 1941 Baudynamik, VDI Verlag: Düsseldorf, Germany, 2006; pp. 19–28. [Google Scholar]
- Huber, G. Erschütterungsausbreitung Beim Rad/Schiene-System (Propagation of Ground Vibration due to the Wwheel/Rail System). Ph.D. Thesis, University Karlsruhe, Karlsruhe, Germany, 1988. [Google Scholar]
- Heckl, M.; Hauck, G.; Wettschurek, R. Structure-borne sound and vibration from rail traffic. J. Sound Vib. 1996, 193, 175–184. [Google Scholar] [CrossRef]
- Bahrekazemi, M. Train-Induced Ground Vibration and Its Prediction. Ph.D. Thesis, KTH Stockholm, Stockholm, Sweden, 2004. [Google Scholar]
- Zhai, W.; Wei, K.; Song, X.; Shao, M. Experimental investigation into ground vibrations induced by very high speed trains on a non-ballasted track. Soil Dyn. Earthq. Eng. 2015, 72, 24–36. [Google Scholar]
- Feng, S.; Zhang, X.; Wang, L.; Zheng, Q.; Du, F.; Wang, Z. In situ experimental study on high-speed train induced ground vibrations with the ballastless track. Soil Dyn. Earthq. Eng. 2017, 102, 195–214. [Google Scholar]
- Degrande, G.; Schillemanns, L. Free field vibrations during the passage of a Thalys high-speed train at variable speed. J. Sound Vib. 2001, 247, 131–144. [Google Scholar]
- Galvin, P. Analisis Numerico y Experimental de las Vibraciones Ocasionadas Por el paso de Trenes de Alta Velocidad en el Suelo y en Structuras Cercana a la via (Numerical and Experimental Analysis of the Vibrations at High Speed Railway Lines in the Soil and in Adjacent Structures). Ph.D. Thesis, University of Sevilla, Sevilla, Spain, 2007. [Google Scholar]
- Kouroussis, G. Modélisation des Effets Vibratoirs du Traffic Ferroviaire sur L’environnement (Modelling of the Vibratory Effects of Railway Traffic on the Environment). Ph.D. Thesis, Université de Mons, Mons, Belgium, 2009. [Google Scholar]
- Romero, A. Predicción, Medida Experimental y Evaluación de las Vibraciones Producidas Por el Tráfico Ferroviario (Prediction, Measurement and Evaluation of the Vibrations Produced by the Railway Traffic). Ph.D. Thesis, University of Sevilla, Sevilla, Spain, 2012. [Google Scholar]
- Connolly, D. Ground Borne Vibrations from High-Speed Trains. Ph.D. Thesis, University of Edinburgh, Edinburgh, UK, 2013. [Google Scholar]
- Maldonado, M. VVibrations Dues au Passage D’Un Tramway—Mesures Experimentales et Simulations Numériques (Vibrations due to the Passage of a Tram—Measurements and Numerical Simulations). Ph.D. Thesis, Ecole Centrale, Nantes, France, 2009. [Google Scholar]
- Alves Costa, P. Vibrações Do Sistema Via-Maciço Induzidas Por Tráfego Ferroviário—Modelação Numérica e Validação Experimental (Vibrations of the Track-Soil System Induced by Railway Traffic—Numerical Modelling and Experimental Validation). Ph.D. Thesis, University of Porto, Porto, Portugal, 2011. [Google Scholar]
- Triepaischajonsak, N. The Influence of Various Excitation Mechanisms on Ground Vibration From Trains. Ph.D. Thesis, University Southampton, Southampton, UK, 2012. [Google Scholar]
- Nielsen, J. Train/Track Interaction-Coupling of Moving and Statßionary Dynamic Systems-Theoretical and Experimental Analysis of Railway Structures Considering Wheel and Track Imperfections. Ph.D. Thesis, Chalmers University, Gothenburg, Sweden, 1993. [Google Scholar]
- Fröhling, R. Deterioration of Railway Track due to Dynamic Vehicle Loading and Spatially Varying Track Stiffness. Ph.D. Thesis, University of Pretoria, Pretoria, South Africa, 1997. [Google Scholar]
- Berggren, E. Railway Track Stiffness—Dynamic Measurements and Evaluation for Efficient Maintenance. Ph.D. Thesis, KTH, Stockholm, Sweden, 2009. [Google Scholar]
- Esveld, C. Modern Railway Track, 2nd ed.; MRT Production: Delft, The Netherland, 2011. [Google Scholar]
- Auersch, L.; Maldonado, M. Interaction véhicule-voie-sol et vibrations dues aux trains–Modélisation et vérifications expérimentales (Vehicle-track-soil interaction and vibrations due to trains—Modelling and experimental verification). Rev. Eur. De Mécanique Numérique 2011, 20, 257–280. [Google Scholar]
- Zhai, W.; Sun, X. A detailed model for investigating vertical interaction between railway vehicle and track. Veh. Syst. Dyn. 1994, 23, 603–615. [Google Scholar] [CrossRef]
- Iwnicki, S. (Ed.) Handbook of Railway Vehicle Dynamics; Taylor & Francis: London, UK, 2006. [Google Scholar]
- Knothe, K.; Stichel, S. Rail Vehicle Dynamics; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Iwnicki, S. (Ed.) The Manchester Benchmarks for Rail Vehicle Simulation; Routledge: London, UK, 1999. [Google Scholar]
- Tomioka, T.; Takigami, T. Reduction of bending vibration in railway vehicle carbodies using carbody- bogie dynamic interaction. Veh. Syst. Dyn. 2010, 48, 467–486. [Google Scholar] [CrossRef]
- Diana, G.; Cheli, F.; Bruni, S.; Collina, A. Experimental and numerical investigation on subway short pitch corrugation. Veh. Syst. Dyn. 1998, 29, 234–245. [Google Scholar] [CrossRef]
- Chaar, N. Wheelset Structural Flexibility and Vehicle-Track Dynamic Interaction. Ph.D. Thesis, KTH, Stockholm, Sweden, 2004. [Google Scholar]
- Ju, S. Finite element analysis of structure borne vibration from high-speed train. Soil Dyn. Earthq. Eng. 2007, 27, 259–273. [Google Scholar]
- Auersch, L. Dynamics of the railway track and the underlying soil: The boundary-element solution, theoretical results and their experimental verification. Veh. Syst. Dyn. 2005, 43, 671–695. [Google Scholar]
- Sheng, X.; Jones, C.; Petyt, M. Ground vibration generated by a harmonic load acting on a railway track. J. Sound Vib. 1999, 225, 3–28. [Google Scholar] [CrossRef]
- Auersch, L. Static and dynamic behaviours of isolated and un-isolated ballast tracks using a fast wavenumber domain method. Arch. Appl. Mech. 2017, 87, 555–574. [Google Scholar] [CrossRef]
- Takemiya, H. Simulation of track-ground vibrations due to high-speed train: The case of X-2000 at Ledsgard. J. Sound Vib. 2003, 261, 503–526. [Google Scholar] [CrossRef]
- Kouroussis, G.; Verlinden, O.; Conti, C. On the interest of integrating vehicle dynamics for the ground propagation of vibrations: The case of urban railway traffic. Veh. Syst. Dyn. 2010, 48, 1553–1571. [Google Scholar] [CrossRef]
- Alves Costa, P.; Calçada, R.; Silva Cardoso, A. Influence of train dynamic modelling strategy on the prediction of track–ground vibrations induced by railway traffic. Rail Rapid Transit. 2012, 226, 434–450. [Google Scholar] [CrossRef]
- Colaço, A.; Alves Costa, P.; Connolly, D. The influence of train properties on railway ground vibrations. Struct. Infrastruct. Eng. 2016, 12, 517–534. [Google Scholar] [CrossRef]
- Nielsen, J.; Mirza, A.; Cervello, S.; Huber, P.; Müller, R.; Nélain, B.; Ruest, G. Reducing train induced ground-borne vibration by vehicle design and maintenance. J. Rail Transp. 2015, 3, 17–39. [Google Scholar] [CrossRef]
- Zakel, H.; Willenbrink, L. Körperschallmessungen an Einem Bm 235-Wagen bei der Fahrt auf Verschiedenen Oberbauten der Neubaustrecke Fulda-Würzburg; Report to BAM; Deutsche Bahn AG Forschungs- und Technologiezentrum: München, Germany, 1997. [Google Scholar]
- Ulrich, H.; Weiland, M.; Schedlinski, C.; Link, M. Experimentelle Modalanalyse an Einem Schnellzugwagen der Deutschen Bahn AG; Report to BAM; Universität Kassel: Kassel, Germany, 1994. [Google Scholar]
- Auersch, L. Ground vibration due to railway traffic—The calculation of the effects of moving static loads and their experimental verification. J. Sound Vib. 2006, 293, 599–610. [Google Scholar]
- Auersch, L. Theoretical and experimental excitation force spectra for railway induced ground vibration—Vehicle-track soil interaction, irregularities and soil measurements. Veh. Syst. Dyn. 2010, 48, 235–261. [Google Scholar] [CrossRef]
- Auersch, L. Zur Parametererregung des Rad-Schiene-Systems: Berechnung der Fahrzeug-Fahrweg-Untergrund-Dynamik und experimentelle Verifikation am Hochgeschwindigkeitszug Intercity Experimental. Ing. -Arch. 1990, 60, 141–156. [Google Scholar]
- Krüger, M. Fahrzeugschwingungen und Dynamische Aufstandskräfte Eines Reisezugwagens; Report for BMBF-Project TV 9346; BAM: Berlin, Germany, 1998. [Google Scholar]
- Auersch, L. The role of vehicle dynamics in train-induced ground vibrations and the detection of irregular axle-pulse responses due to a varying track support stiffness. Rail Rapid Transp. 2022, 1–16, accepted. [Google Scholar]
- Ntotsios, E.; Thompson, D.; Hussein, M. The effect of track load correlation on ground borne vibration from railways. J. Sound Vib. 2017, 402, 142–163. [Google Scholar] [CrossRef]
- Auersch, L. Train-induced ground vibration due to the irregularities of the soil. Soil Dyn. Earthq. Eng. 2021, 140, 106438. [Google Scholar]
- Auersch, L. Simple and fast prediction of train-induced track forces, ground and building vibrations. Railw. Eng. Sci. 2020, 28, 232–250. [Google Scholar]
- Breitsamter, N. Ersatzmodelle zur Bestimmung der Schwingungsantwort von Gebäuden bei Anregung durch Bodenerschütterungen. Ph.D. Thesis, Technical University München, München, Germany, 1996. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).