Abstract
Wireless power transfer (WPT) is a power transfer technique widely used in many industrial applications, medical applications, and electric vehicles (EVs). This paper deals with the dynamic modeling of the resonant inverter employed in the WPT systems for EVs. To this end, the Generalized State-Space Averaging and the Laplace Phasor Transform techniques have been the flagship methods employed so far. In this paper, the modeling of the resonant inverter is accomplished by using the novel Modulated Variable Laplace Transform (MVLT) method. Firstly, the MVLT technique is discussed in detail, and then it is applied to model a study-case resonant inverter. Finally, a study-case resonant inverter is developed and utilized to validate the theoretical results with MATLAB/Simulink.
1. Introduction
The Wireless Power Transfer (WPT) system transmits electrical energy without any physical connection [1]. WPTs offer various benefits over wired ones, making them ideal for industrial applications: reducing danger from exposed wires, rendering the charging process easy, and reliable power transfer in rough weather conditions [2]. WPT is accomplished by inductively coupling the transmitter and receiver coils [3], thanks to Faraday’s law of electromagnetic induction. The receiver coil is deployed in the vehicle chases while the transmitter coils are buried under the ground. Further, due to better efficiency, resonant inductive WPT is used for EV charging [4].
The schematic of a WPT system is shown in Figure 1. It is composed of various power conversion stages [1]. On the transmitter side, it consists of a power factor correction circuit (PFC) and a high-frequency inverter, whereas on the receiver side, it has an uncontrolled bridge rectifier and a chopper cascaded with it. Moreover, on the transmitting side, the electromagnetic compatibility (EMC) filter ensures that the system meets the electromagnetic standards. The filtered low-frequency grid voltage is applied at the input of the PFC circuit for rectification. Typically, PFC stands for power factor correction, and it is carried out by either a simple uncontrolled diode rectifier [5] or a controlled rectifier [6]. The inverter converts DC voltage into AC voltage, feeding power to the transmitter coil. The induced high-frequency voltage on the receiver coil is conditioned by the diode rectifier and the chopper to regulate the voltage and current profile suitable for battery charging [7]. In addition, the compensation network on both sides improves the system efficiency and cancels the reactive power demand from the inverter.
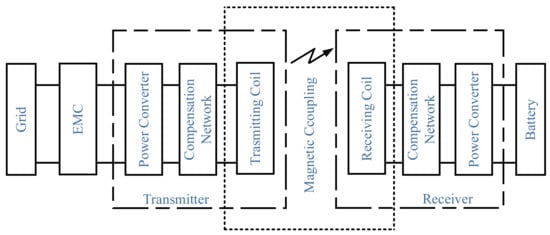
Figure 1.
General schematic of the WPT systems.
Usually, the steady-state analysis of a WPT system is carried out through the Fundamental Harmonic Approximation (FHA) technique [8]. For the transient analysis, instead, it is necessary to have a good dynamic model of the system available. To find the dynamic model of a WPT system, the traditional State-Space Averaging (SSA) method cannot be used because one prerequisite for its application is that the state variables of the system should be slowly time-variant compared to the converter switching period [9]. Furthermore, the transmitting power stage of a WPTS can be envisaged as a resonant converter. In resonant converters, the quantities in the resonant tanks exhibit predominantly oscillatory behavior. In WPTSs, the quantities involved in compensating networks are alternated signals pulsating at the inverter switching frequency. In other words, the switching period is equal to the natural time constant of the system. For this reason, SSA method applied to WPTSs and in general to resonant converters is not able to yield a useful dynamic model.
Therefore, other methods should be used to model the resonant inverter employed in the WPT systems, where its switching frequency is deliberately chosen to be close to the system natural frequency. To that end, the two main techniques that have gained success in the literature are the Generalized State-Space Averaging (GSSA) [10,11,12,13,14] and the Laplace Phasor Transform (LPT) [15,16,17,18,19]. These methods overcome the problem of the SSA technique by considering for the modeling of the AC quantities their slow-varying envelopes in place of their average values is refer [20,21]. A novel method called Modulated Variable Laplace Transform (MVLT) has been recently introduced by the author [22]. The method exploits the same averaging principle as the GSSA and the LPT techniques, and as demonstrated in [23], in the case of the modeling of a linear system, they are perfectly equivalent.
All the methods mentioned possess advantages and drawbacks. The GSSA method is the most general of the methods, but at the same time, it is relatively sophisticated due to the state-space representation of the system, which in some cases does not add any benefit to the analysis. The LPT is a circuit-based modeling technique that is relatively easy to apply, despite the usage of unconventional components such as complex resistors. In other words, the GSSA method applies the transformation to the state-space equations of the system, whereas the LPT method is based on transformations at the circuit level. The application of the LPT method starts with the conversion of the original circuit, substituting all the elementary components with their respective Laplace phasor-transformed counterparts. From the transformed circuit, it is easy to evaluate all the desired transfer functions.
This paper aims to show that in some situations, such as the modeling of the resonant inverter on the transmission side of the WPT systems, the MVLT technique could be the method to be preferred due to its simplicity and its straightforward application. The reason for the introduction of a new modeling method is that with both the GSSA and the LPT methods, the direct link between the instantaneous model and the envelope model is lost. This link is maintained by the MVLT method which thus can provide better insight into the envelope model.
This paper is organized as follows: Section 2 describes the WPT system to be modeled and the assumptions made to achieve this goal. Section 3 explains the MVLT method, and in Section 4, this method is applied to model the study-case resonant inverter. In Section 5, the model is verified by simulation. Finally, Section 6 concludes the paper.
2. System Description
The equivalent circuital diagram of the WPT system with a series–series compensation network is illustrated in Figure 2. Here, vs. is the source voltage; vt and vr are the voltages induced on the transmitter and receiver coils, respectively. The induced voltage in the coil is caused by a change in current in the coil, which may be explained by Faraday’s law of electromagnetic induction. Ct, Cr, and Lt, Lr are the transmitter and receiver side capacitors and inductances, respectively; the transmitter and receiver components are identical. Further, it and ir are the transmitter and receiver side currents, respectively, and M is the mutual inductance between the two coils. Rl is the resistance seen from the receiver coil. It is also referred to as load resistance.

Figure 2.
Equivalent circuital diagram of the series-series WPT system.
From the analysis carried out in [23], the entire receiver side can be replaced by a resistance R reflected to the transmitter side and is given by
Here, is the supply angular frequency in rad/sec, and is equal to , where f is the supply frequency in Hz. It should be noted that the voltage vs. is controlled by the phase-shift method, in which the frequency f remains fixed at 85 kHz. The supply frequency was chosen in accordance with the SAE J2954 standard, which recommended the operating frequency range of 79–90 kHz for the WPT system for EVs.
As may be observed from (1), that the receiver side reflects resistance to the transmitter side R depends on the values of M and Rl which vary with respect to the coil alignment and the battery state of charge, respectively. In this paper, for simplicity, M and Rl are considered to be fixed, thus giving a fixed value for R. In order to find an easy way to model the WPT system, the circuit of Figure 2 is redrawn in Figure 3, which can be represented as a simple series RLC network together with the load resistance R and source voltage vs, in which the following hypotheses are made: (i) the inverter switching frequency f is the resonant frequency of the LtCt tank which follows the relation ; (ii) due to the filtering action of the LtCt resonating tank, the current it is nearly sinusoidal; (iii) although the supply voltage is a quasi-square, only fundamental component contributes in the power transfer. Since the harmonic content of the resonant converter output is low, we used fundamental wave analysis in this paper.
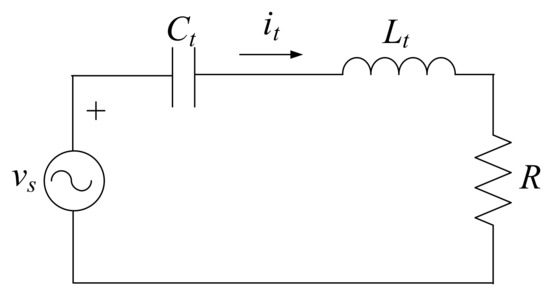
Figure 3.
Equivalent circuit of the transmission side of WPT system shown in Figure 2.
3. MVLT Modeling Method
The novel MVLT modeling method was first presented in [22], where the authors used this technique for the dynamic modeling of wireless power transfer systems. The technique can be applied to any circuit where the involved quantities are high-frequency sinusoidal signals with slowly varying amplitudes, like the ones illustrated in Figure 3. By applying a mathematical transformation, the MVLT method eliminates the high frequency and obtains a relationship between the envelopes. Supervising the envelopes of the quantities is easier due to their limited bandwidth, and at the same time, it is enough to maintain the system under control.
An amplitude modulated signal, e.g., can be written in the form of its dynamic phasor [22] as
Here is the real part operator and is the angular frequency of the carrier of the modulated signal . As an assumption of the MVLT technique, the frequency content of should be negligible at frequencies approaching , so that the modulating signal is much slower than the carrier. With this hypothesis, if is provided as the input signal to a system having a transfer function , the output signal can also be written in the form of (2). Hence, the relationship between the Laplace transforms of these two complex signals will be
where the operator is the Laplace transform of the argument. Using the “frequency shifting” property of the Laplace transform and with some additional mathematical steps, Equation (3) becomes
Here, the quantities and are the Laplace transforms of and , respectively. It is clear from (4) that the transfer function which links phasor quantities is nothing but the transfer function of the original signals with mapped into . The transfer function is a rational function of with complex coefficients. Nevertheless, it is always possible to break (4) into its real and the imaginary parts, as explained in the Appendix A, and it results in
where and are rational functions in with real coefficients in their numerators and denominators. Equation (4) gives the transfer function between the complex signals and . However, the target is to find the relationship between the envelopes. In this regard, the envelope of the output signal , which is , is given by
Here and are the real and imaginary parts of . Since (6) is not linear, it needs to be linearized to get the transfer function between the envelopes of the output and of the input . The linearization of (6) leads to
The graphical plot of Equation (6) for the linearization process of the output signal is shown in Figure 4. Indeed, the envelope of the output signal in linearized form is represented in Equation (7). Where subscripts i and f stand for the “initial” and “final” operating points, and are the real and imaginary parts of , where represent initial output of signal with blue phasor with angle, which coincides with the conventional phasor of the output before the perturbation that can be represented with a red phasor. The process of linearization can be better appreciated in Figure 4. The dynamic phasor moves from its initial value to the final value . During the transient, can be written as , where identifies its small variation around in the complex plane that can be represented with a black phasor. Assuming insignificant change in so that the phase of remains almost constant for all the transition, from Figure 4, the second equality of (7) appears more clear. Applying the Laplace transform to (7) and neglecting the tildes for the sake of lightening the notation, Equation (8) is obtained.

Figure 4.
Graphical explanation of the linearization process for Equation (6).
To link the Laplace transform of and to the Laplace transform of the small-signal input, let us consider the carrier of the signal as the reference of the phases. As a result, the dynamic phasor given by consists of the real part only. Therefore, with this frame of reference, the real part of also coincides with its envelope, and consequently is equal to in the -domain. When is applied to the dynamic phasor is obtained. Since the input of is real, the real part of is the output of and the imaginary part is the output of . With this consideration, Equation (8) becomes
Considering that the function enclosed in the square brackets can be obtained as , provided that is assumed to be real [14], the transfer function linking the envelopes can be finally written as
It is interesting to note that the angle of the phasor is also the phase of . From (10), it is easy to see that the MVLT method, applied to a linear system, directly relates the transfer functions for the modulated quantities and the transfer functions for the modulating signals (the envelopes). In the Appendix A, this relationship is further analyzed.
4. Method Application
As a first step for the MVLT method application, the transfer function between the original signals of the equivalent WPT system of Figure 3 is evaluated. For instance, the transfer function between current i and the input voltage source vs. is
As a second step, mapping into in (11) gives
It can be easily seen in (12) that the numerator and the denominator of are polynomials in with complex coefficients. As shown in (5), Equation (12) can be split into the real and the imaginary parts. The desired transfer function can be obtained by using (9). As per the hypotheses made for this case of study, the current it is in phase with the voltage source vs, therefore the angle in (9) is zero, and the envelope transfer function remains only the real part of (12) given by
Consider that when , which is another form of (1), Equation (13) can be further elaborated as
The transfer function in (14) links the current envelope with the supplying voltage envelope for the quantities in Figure 3. Equation (14) shows that the transfer function for the envelopes has all the coefficients that are real numbers.
5. Model Validation
To validate the model (14) obtained from the simplified circuit of Figure 3, an MATLAB/Simulink model of the resonant inverter has been developed. The values of the parameters considered in the realization of the resonant inverter and utilized to validate the theoretical results with MATLAB/Simulink are collected in Table 1. To corroborate the hypotheses made in the previous sections, firstly, the steady-state waveforms have been captured and shown in Figure 5a–f with two small perturbations at secondary load, i.e., receiver side-reflected resistances to the transmitter side R are 5 Ω, 10 Ω, and 15 Ω, respectively. Here, it is observed that although the inverter output voltage contains several harmonics, the current it is nearly sinusoidal. This means that the resonant tank is very selective and filters all of the harmonics except the fundamental one. The assumption made in Figure 3 of considering the inverter as a sinusoidal voltage source corresponding to the fundamental of the inverter output voltage is then verified. In Figure 5, it is also shown that at steady-state, the current it is in phase with the fundamental of the inverter output voltage, which means that the inverter switching frequency is perfectly tuned to the natural frequency of the LtCt circuit, i.e., the angle in (9) is zero. A MATLAB scope acquisition of the current and voltage wave forms has been evaluated with the three different loads set to 5 Ω, 10 Ω, and 15 Ω, with a small perturbation angle of αP = 45° in time interval 0.7–0.72 ms, as represented in Figure 5a–c, respectively. It is verified, through the voltage waveform, that the conduction angle of the converter output voltage is greater than α = 120° due to the addition of the perturbation angle. Additionally, the fundamental voltage of the converter output voltage also increases. For further demonstration, the simulation result of the current and voltage wave form with perturbation angle αP = 60° is shown in Figure 5d–f, where the voltage wave form for the full half-cycle is depicted.

Table 1.
Parameters of the Assembled Resonant Inverter.
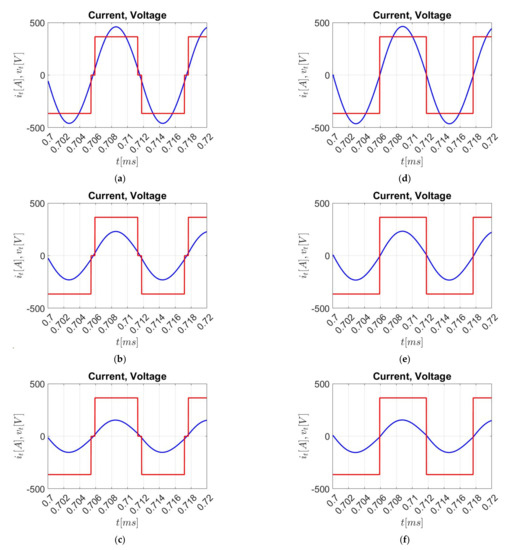
Figure 5.
Voltage (quasi-square wave) and current (sinusoidal waveform) for the realized resonant inverter. Current is a multiple of five. (a) αP = π/4, R = 5 Ω; (b) αP = π/4, R = 10 Ω; (c) αP = π/4, R = 15 Ω; (d) αP = π/3, R = 5 Ω; (e) αP = π/4, R = 10 Ω; (f) αP = π/3, R = 15 Ω.
To verify the dynamic model, a small perturbation to the system has been introduced. The inverter phase-shift angle α, which was initially set to 120°, is increased by 45°. Accordingly, the fundamental of the inverter output voltage has been also increased. Indeed, its amplitude started from a value of and has reached an approximate value of 460.5 V. A MATLAB scope acquisition of the current has been triggered by the step change in α at 0.5 ms. The acquired current is one that flows through the H-bridge inverter output of the current it, and thus they share the same positive envelope. Then, inverter current waveforms with small perturbations of phase shift angle α, with the three different loads set to 5 Ω, 10 Ω, and 15 Ω are shown in Figure 6a–c. The transfer function (14) has been implemented in Simulink. Since it places the envelopes in relation, a voltage step of 58 V (corresponding to a step of 45° in α) has been provided as its input. The resulting output with the three loads set to 5 Ω, 10 Ω, and 15 Ω., which is the small-signal envelope of inverter output current, has been superposed on the steady-state value of the amplitude of the current i that is around 80.5 A, 40.25 A, and 26.8 A, respectively. The total signal has been plotted in the three different graphs of the inverter output current as shown in Figure 6a–c. It can be noticed that the output of (14) matches very well with the real envelope of the inverter output current, thus validating the MVLT model. For further demonstration, the simulation was again carried out for α = 60°, where the sinusoidal and the envelope matched properly. The plots are shown in Figure 6d–f.

Figure 6.
Inverter output current (solid red line) obtained from MATLAB simulation and its envelope (dashed blue line) obtained in Simulink as the output of the model (14). (a) αP = π/4, R = 5 Ω; (b) αP = π/4, R = 10 Ω; (c) αP = π/4, R = 15 Ω; (d) αP = π/3, R = 5 Ω; (e) αP = π/4, R = 10 Ω; (f) αP = π/3, R = 15 Ω.
6. Conclusions
In this paper, the novel MVLT method is explicated. The method is used to obtain the dynamic model of the resonant inverter that feeds the load of a WPT system. The discussion begins by obtaining the equivalent circuit model of the WPT system and underlining the hypotheses made for its derivation. It continues with the MVLT method description and its application to the considered resonant inverter. It has been demonstrated that the sought dynamic model can be obtained from the system original transfer function followed by a simple remapping in -domain and a few additional mathematical steps. Unlike the existing GSSA and LPT methods, the MVLT technique emphasizes the link between the real signal transfer functions and the envelope transfer functions. Hence, the dynamic behavior of the envelopes can be directly assessed from the system transfer function. In this paper, the validity of the MVLT method has been verified by comparing the outcomes of the model implemented in Simulink. The result is satisfactory.
Author Contributions
Conceptualization, R.K.J., A.K. (Abhay Kumar), M.B. and M.F.; methodology, R.K.J., A.K. (Abhay Kumar), M.B. and M.F.; software, R.K.J. and A.K. (Abhay Kumar); validation, R.K.J., A.K. (Abhay Kumar) and M.F.; formal analysis, R.K.J., A.K. (Abhay Kumar), S.P., S.J., M.B., A.K. (Anand Kumar), B.P.J. and M.F.; investigation, R.K.J., A.K. (Abhay Kumar), M.B. and M.F.; resources, R.K.J., A.K. (Abhay Kumar), S.P., S.J., M.B., A.K. (Anand Kumar), B.P.J. and M.F.; data curation, R.K.J., A.K. (Abhay Kumar), S.P., S.J., M.B., A.K. (Anand Kumar), B.P.J. and M.F.; writing-original draft preparation, R.K.J., A.K. (Abhay Kumar), S.P., S.J., M.B., A.K. (Anand Kumar), B.P.J. and M.F.; writing-review and editing, R.K.J., A.K. (Abhay Kumar), S.P., S.J., M.B., A.K. (Anand Kumar), B.P.J. and M.F.; visualization, R.K.J., A.K. (Abhay Kumar), S.P., S.J., M.B., A.K. (Anand Kumar), B.P.J. and M.F.; supervision, R.K.J., A.K. (Abhay Kumar) and M.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Most of the data and the results are reported in the paper. Additional data can be requested from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
This appendix is used to show how the envelope transfer function can be split into its real and imaginary parts, as stated in Equation (5). Let be a rational function given by . The transfer function linking the dynamic phasors can be found as
In Equation (A1), , and are polynomials in with complex coefficients. These polynomials can be separated into their respective real and imaginary parts, obtaining
Introducing a polynomial , which is defined as the complex conjugate of , and multiplying the numerator and the denominator of Equation (A2) by it, Equation (A3) is obtained:
Equation (A3) is the expected result since it shows in the form of Equation (5). From Equation (9), it is clear that the transfer function that links the envelope is a linear combination (with the coefficients and ) of and . According to this and to Equation (A3), it can be stated that the denominator of has a degree that is twice the degree of . Thus, the transfer function for the envelopes has twice as many poles as the transfer function of the real system. By exploiting Equation (A3) with the help of some mathematical steps, it is also possible to find the relation between the poles of the two transfer functions. This interesting result is explained in detail in [18].
References
- Patil, D.; McDonough, M.K.; Miller, J.M.; Fahimi, B.; Balsara, P.T. Wireless Power Transfer for Vehicular Applications: Overview and Challenges. IEEE Trans. Transp. Electrif. 2018, 4, 3–37. [Google Scholar] [CrossRef]
- Chinthavali, M.; Onar, O.C. Tutorial on wireless power transfer systems. In Proceedings of the IEEE Transportation Electrification Conference and Expo (ITEC), Dearborn, MI, USA, 27–29 June 2016; pp. 1–142. [Google Scholar]
- Li, S.; Mi, C.C. Wireless power transfer for electric vehicle applications. IEEE J. Emerg. Sel. Top. Power Electron. 2015, 3, 4–17. [Google Scholar]
- Bertoluzzo, M.; Giacomuzzi, S.; Kumar, A. Design of a Bidirectional Wireless Power Transfer System for Vehicle-to-Home Applications. Vehicles 2021, 3, 406–425. [Google Scholar] [CrossRef]
- Pham, H.; Fujita, H.; Ozaki, K.; Uchida, N. Phase angle control of high-frequency resonant currents in a multiple inverter system for zone-control induction heating. IEEE Trans. Power Electron. 2011, 26, 3357–3366. [Google Scholar]
- Berger, A.; Agostinelli, M.; Vesti, S.; Oliver, J.A.; Cobos, J.A.; Huemer, M. A Wireless Charging System Applying Phase-Shift and Amplitude Control to Maximize Efficiency and Extractable Power. IEEE Trans. Power Electron. 2015, 30, 6338–6348. [Google Scholar] [CrossRef]
- Esteve, V.; Sanchis-Kilders, E.; Jordan, J.; Dede, E.J.; Cases, C.; Maset, E.; Ejea, J.B.; Ferreres, A. Improving the efficiency of IGBT series resonant inverters using pulse density modulation. IEEE Trans. Ind. Electron. 2011, 58, 979–987. [Google Scholar] [CrossRef]
- Vakacharla, V.R.; Rathore, A.K.; Tripathi, P.R.; Keshri, R.K. A comprehensive review of fundamental harmonic approximation analysis techniques for series-parallel resonant converters with capacitive filter. In Proceedings of the IECON 2019—45th Annual Conference of the IEEE Industrial Electronics Society, Lisbon, Portugal, 14–17 October 2019; pp. 2581–2585. [Google Scholar]
- Middlebrook, R.D.; Cuk, S. A general unified approach to modelling switching-converter power stages. In Proceedings of the IEEE Power Electronics Specialist Conference, Cleveland, OH, USA, 8–10 June 1976; pp. 18–34. [Google Scholar]
- Sanders, S.R.; Noworolski, J.M.; Liu, X.Z.; Verghese, G.C. Generalized averaging method for power conversion circuits. IEEE Trans. Power Electron. 1991, 6, 251–259. [Google Scholar] [CrossRef]
- Mahdavi, J.; Emaadi, A.; Bellar, M.D.; Ehsani, M. Analysis of power electronic converters using the generalized state-space averaging approach. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 1997, 44, 767–770. [Google Scholar] [CrossRef]
- Xu, J.; Lee, C.Q. Generalized state-space averaging approach for a class of periodically switched networks. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 1997, 44, 1078–1081. [Google Scholar]
- Gaviria, C.; Fossas, E.; Grino, R. Robust controller for a full-bridge rectifier using the IDA approach and GSSA modeling. IEEE Trans. Circuits Syst. I Reg. Papers. 2005, 52, 609–616. [Google Scholar] [CrossRef]
- Azer, P.; Emadi, A. Generalized state space average model for multi-phase interleaved buck boost and buck-boost DC-DC converters: Transient steady-state and switching dynamics. IEEE Access 2020, 8, 77735–77745. [Google Scholar] [CrossRef]
- Rim, C.T.; Cho, G.H. Phasor transformation and its application to the DC/AC analyses of frequency phase-controlled series resonant converters (SRC). IEEE Trans. Power Electron. 1990, 5, 201–211. [Google Scholar] [CrossRef]
- Rim, C.T. Unified general phasor transformation for AC converters. IEEE Trans. Power Electron. 2011, 26, 2465–2475. [Google Scholar] [CrossRef]
- Bertoluzzo, M.; Giacomuzzi, S.; Forato, M. Performance Analysis of Envelope Modelling Applied to Resonant Converters. IEEE Trans. Ind. Electron. 2022, 69, 4046–4055. [Google Scholar] [CrossRef]
- Yin, Y.; Zane, R.; Glaser, J.; Erickson, R.W. Small-signal analysis of frequency-controlled electronic ballasts. IEEE Trans. Circuits Syst. I. Fundam. Theory Appl. 2003, 50, 1103–1110. [Google Scholar] [CrossRef]
- Lee, S.; Choi, B.; Rim, C.T. Dynamics characterization of the inductive power transfer system for online electric vehicles by laplace phasor transform. IEEE Trans. Power Electron. 2013, 28, 5902–5909. [Google Scholar] [CrossRef]
- Yin, Y.; Zane, R.; Erickson, R.; Glaser, J. Direct modeling of envelope dynamics in resonant inverters. In Proceedings of the IEEE 34th Annual Power Electronics Specialists, Acapulco, Maxico, 15–19 June 2003; Volume 3, pp. 1313–1318. [Google Scholar]
- Forato, M.; Bertoluzzo, M.; Buja, G. Dynamic EV charging WPT system control based on Modulated Variable Laplace Transform. In Proceedings of the IEEE PELS Workshop on Emerging Technologies: Wireless Power Transfer, Wow, Montreal, QC, Canada, 3–7 June 2018; pp. 1–6. [Google Scholar]
- Forato, M. Dynamic Wireless Charging of Electric Vehicles. Ph.D. Thesis, University of Padova, Padova, Italy, 2018. Available online: http://paduaresearch.cab.unipd.it/11411/ (accessed on 28 November 2018).
- Han, W.; Chau, K.T.; Zhang, Z. Flexible induction heating using magnetic resonant coupling. IEEE Trans. Ind. Electron. 2017, 64, 1982–1992. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).