Autonomous Vehicle Control Comparison
Abstract
1. Introduction
- P+V Control (proportional control plus velocity negation);
- Open-loop optimal control (feedfoward);
- Real-Time Optimal Control (RTOC) (feedfoward plus feedback);
- Double-Integrator patching filter with P+V control;
- Double-integrator patching filter with gain-tuning for P+V control;
- Control law inversion patching filter with P+V control.
2. Materials and Methods
2.1. Classical Benchmark Control
2.2. Finding the Optimal Control
- Formulate the Hamiltonian;
- Minimize the Hamiltonian;
- Formulate the Adjoint Equations;
- Apply Terminal Transversality of the endpoint Lagrangian.
2.2.1. Formulate the Hamiltonian
2.2.2. Minimize the Hamiltonian
2.2.3. Formulate the Adjoint Equation
2.2.4. Terminal Transversality of the Endpoint Lagrangian
2.2.5. Real-Time Optimal Control (RTOC)
2.3. Patching Filters
2.3.1. Double-Integrator Patching Filter
2.3.2. Double-Integrator Patching Filter with Gain-Tuning
2.3.3. Control Law Inversion Patching Filter
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| P+V | Proportional and velocity |
| RTOC | Real-time optimal control |
| MAE | Mechanical and aerospace engineering |
| Quadratic cost | |
| Mean value of parameter x | |
| Standard deviation of parameter x | |
| F | Running cost |
| Endpoint cost | |
| State or angle (synonymous) | |
| Final state, or angle (synonymous) | |
| Rate or angular velocity (synonymous) | |
| Final rate or angular velocity (synonymous) | |
| Optimal value of parameter x | |
| Value of parameter x from sensor data | |
| Applied torque | |
| I | Moment of inertia of vehicle |
| Position gain | |
| Velocity gain | |
| Rise time | |
| Settling time | |
| u | Control parameter. In this case, . |
| Matrix of time coefficients for RTOC | |
| Optimal coefficients at each time step for RTOC | |
| Vector of current and final state and rate for RTOC |
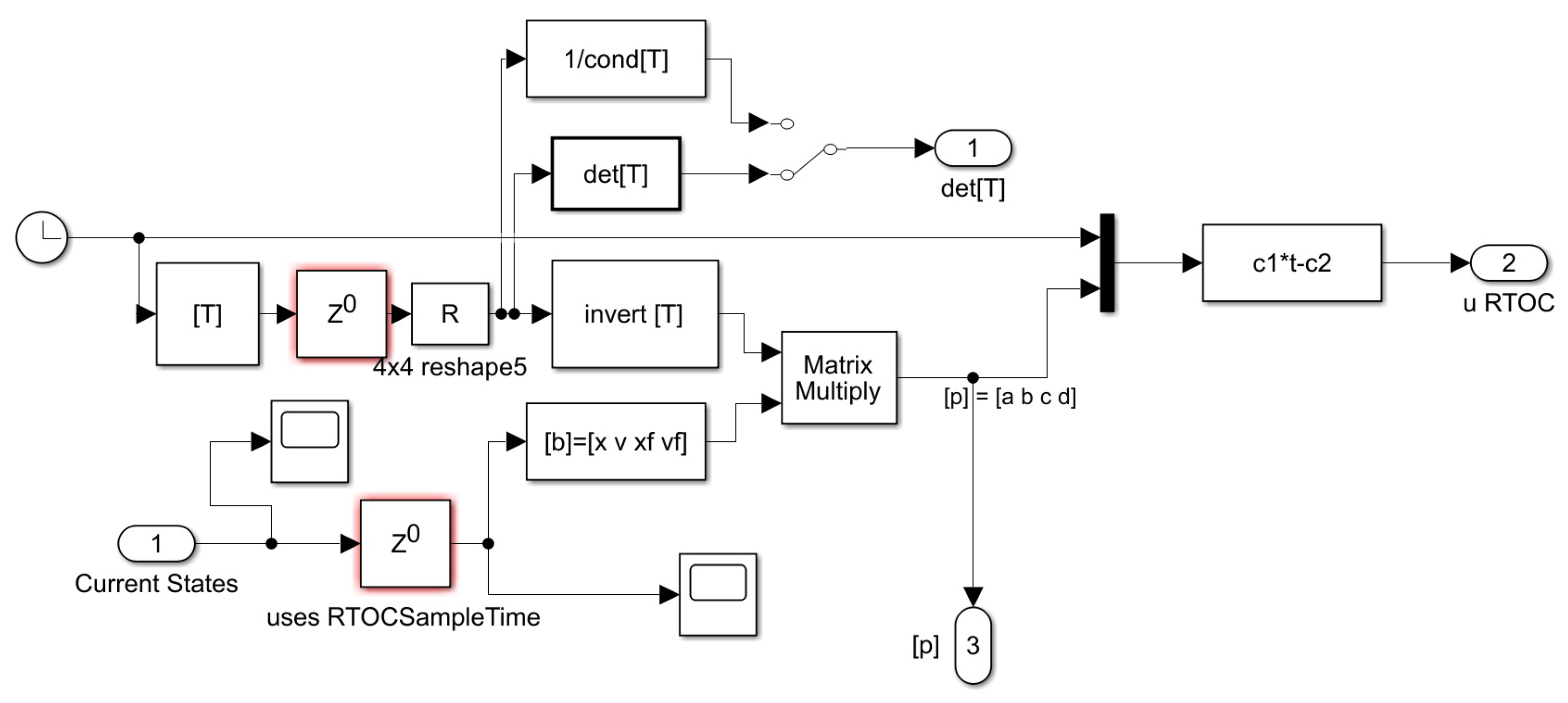
Appendix A. MATLAB Simulink Model







References
- Chasle, M. Note sur les propriétés générales du système de deux corps semblables entr’eux. Bull. Sci. Math. Astron. Phys. Chem. 1830, 14, 321–326. (In French) [Google Scholar]
- Euler, L. Formulae Generales pro Translatione Quacunque Corporum Rigidorum (General Formulas for the Translation of Arbitrary Rigid Bodies). Novi Comment Acad. Sci. Petrop. 1776, 20, 189–207. Available online: https://scholarlycommons.pacific.edu/euler-works/478/ (accessed on 31 August 2022).
- Newton, I. Principia, Jussu Societatis Regiæ; (Ac Typis Joseph Streater); Cambridge University Library: London, UK, 1687. [Google Scholar]
- Cooper, M.; Heidlauf, P.; Sands, T. Controlling Chaos—Forced van der pol equation. Mathematics 2017, 5, 70. [Google Scholar] [CrossRef]
- Smeresky, B.; Rizzo, A.; Sands, T. Optimal Learning and Self-Awareness Versus PDI. Algorithms 2020, 13, 23. [Google Scholar] [CrossRef]
- Baker, K.; Cooper, M.; Heidlauf, P.; Sands, T. Autonomous trajectory generation for deterministic artificial intelligence. Electr. Electron. Eng. 2018, 8, 59–68. [Google Scholar]
- Sands, T. Development of Deterministic Artificial Intelligence for Unmanned Underwater Vehicles (UUV). J. Mar. Sci. Eng. 2020, 8, 578. [Google Scholar] [CrossRef]
- Slotine, J.-J.E.; Weiping, L. Applied Nonlinear Control; Prentice-Hall: Hoboken, NJ, USA, 1991. [Google Scholar]
- Fossen, T. Comments on Hamiltonian adaptive control of spacecraft by Slotine, J.J.E. and Di Benedetto, M.D. IEEE Trans. Autom. Control. 1993, 38, 671–672. [Google Scholar] [CrossRef]
- Sands, T.; Kim, J.; Agrawal, B. Spacecraft Adaptive Control Evaluation. In Proceedings of the InInfotech@Aerospace, Garden Grove, CA, USA, 19–21 June 2012. [Google Scholar]
- University of Wisconsin. Staff-Authored News from College of Engineering. 2019. Available online: https://engineering.wisc.edu/news/ (accessed on 6 October 2022).
- Malecek, A. Robert Lorenz, Pioneer in Controls Engineering, Passes Away. 2019. Available online: https://engineering.wisc.edu/news/robert-lorenz-pioneer-controls-engineering-passes-away/ (accessed on 6 October 2022).
- Sands, T.; Lorenz, R. Physics-based automated control of spacecraft. In Proceedings of the AIAA Space 2009, Pasadena, CA, USA, 14–17 September 2009. [Google Scholar]
- Rätze, K.; Bremmer, J.; Biegler, L.; Sundmacher, K. Physics-Based Surrogate Models for Optimal Control of a CO2 Methanation Reactor. Comput. Aided Chem. Eng. 2017, 40, 127–132. [Google Scholar]
- Bukhari, A.; Raja, M.; Asif, Z.; Shoaib, M.; Kiani, A. Fractional order Lorenz based physics informed SARFIMA-NARX model to monitor and mitigate megacities air pollution. Chaos Solit. Fract. 2022, 161, 112375. [Google Scholar] [CrossRef]
- Sandberg, A.; Sands, T. Autonomous Trajectory Generation Algorithms for Spacecraft Slew Maneuvers. Aerospace 2022, 9, 135. [Google Scholar] [CrossRef]
- Cooper, M.; Heidlauf, P. Nonlinear Lyapunov control improved by an extended least squares adaptive feed forward controller and enhanced Luenberger observer. In Proceedings of the International Conference and Exhibition on Mechanical & Aerospace Engineering, Las Vegas, NV, USA, 2–4 October 2017. [Google Scholar]
- Cooper, M.; Heidlauf, P. Nonlinear feed forward control of a perturbed satellite using extended least squares adaptation and a luenberger observer. J. Aero. Aerosp. Eng. 2018, 7, 1. [Google Scholar] [CrossRef]
- Cooper, M.; Smeresky, B. An overview of evolutionary algorithms toward spacecraft attitude control. In Advances in Spacecraft Attitude Control; IntechOpen: London, UK, 2020. [Google Scholar]
- Chow, G.C. Analysis and Control of Dynamic Economic Systems; Krieger Publ.: Malabar, FL, USA, 1986; ISBN 0-89874-969-7. [Google Scholar]
- Borggaard, J.; Zietsman, L. The Quadratic-Quadratic Regulator Problem: Approximating feedback controls for quadratic-in-state nonlinear systems. In Proceedings of the 2020 American Control Conference (ACC), Denver, CO, USA, 1–3 July 2020; pp. 818–823. [Google Scholar]
- Kreindler, E. Contributions to the theory of time-optimal control. J. Frank. Inst. 1963, 275, 314–344. [Google Scholar] [CrossRef]
- Sciarretta, A.; Guzzella, L. Fuel-Optimal Control of Rendezvous Maneuvers for Passenger Cars (Treibstoffoptimale Annäherung von Straßenfahrzeugen). Automatisierungstechnik 2005, 53, 244–250. [Google Scholar] [CrossRef]
- Sensing and Controls Pioneer Lorenz Named to National Academy of Engineering. 2019. Available online: https://engineering.wisc.edu/blog/sensing-controls-pioneer-lorenz-named-national-academy-engineering/ (accessed on 1 September 2022).
- Raigoza, K.; Sands, T. Autonomous Trajectory Generation Comparison for De-Orbiting with Multiple Collision Avoidance. Sensors 2022, 22, 7066. [Google Scholar] [CrossRef]
- Sands, T. Treatise on Analytic Optimal Spacecraft Guidance and Control. Front. Robot. AI Robot. Control Syst. 2022, 9, 884669. [Google Scholar] [CrossRef]
- NASA Artemis. Available online: https://www.nasa.gov/specials/artemis/ (accessed on 1 September 2022).
- Media Usage Guidelines. Available online: https://www.nasa.gov/multimedia/guidelines/index.html (accessed on 1 September 2022).


| Variable | Definition | Variable | Definition |
|---|---|---|---|
| Desired state trajectory | Critical damping ratio | ||
| Proportional gain | Natural frequency | ||
| Velocity gain | Settling time | ||
| I | Moment of inertia | Rise time |
| Figure of Merit | pinv([T]) | |
|---|---|---|
| −0.6178 | 1.0014 | |
| 0.0035 | ||
| −1.9737 | 0.0029 | |
| 0.0094 | ||
| 3.1891 | 6.0167 | |
| 0.0218 |
| Figure of Merit | P+V Control: , | Open-Loop Optimal Guidance | RTOC | Double-Integrator Patching Filter , | Gain-Tuning with Double-Integrator Patching Filter , | Control Law Inversion Patching Filter , |
|---|---|---|---|---|---|---|
| 0.001 | 0.0002 | − | −0.0484 | |||
| 0.0101 | 0.099 | 0.0035 | 0.0021 | 0.0030 | 0.0020 | |
| 0.0075 | − | 0.6711 | 0.3322 | |||
| 0.0237 | 0.0100 | 0.0093 | 0.0224 | 0.0534 | 0.0224 | |
| 236.72 | 6.0110 | 6.0168 | 4.3251 | 9.1355 | 6.6956 | |
| 13.4524 | 0.6917 | 0.0213 | 0.1535 | 0.6566 | 1.660 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Banginwar, P.; Sands, T. Autonomous Vehicle Control Comparison. Vehicles 2022, 4, 1109-1121. https://doi.org/10.3390/vehicles4040059
Banginwar P, Sands T. Autonomous Vehicle Control Comparison. Vehicles. 2022; 4(4):1109-1121. https://doi.org/10.3390/vehicles4040059
Chicago/Turabian StyleBanginwar, Pruthvi, and Timothy Sands. 2022. "Autonomous Vehicle Control Comparison" Vehicles 4, no. 4: 1109-1121. https://doi.org/10.3390/vehicles4040059
APA StyleBanginwar, P., & Sands, T. (2022). Autonomous Vehicle Control Comparison. Vehicles, 4(4), 1109-1121. https://doi.org/10.3390/vehicles4040059







