Numerical Study of Longitudinal Inter-Distance and Operational Characteristics for High-Speed Capsular Train Systems
Abstract
:1. Introduction
2. High-Speed Capsular Vehicles and Related Works
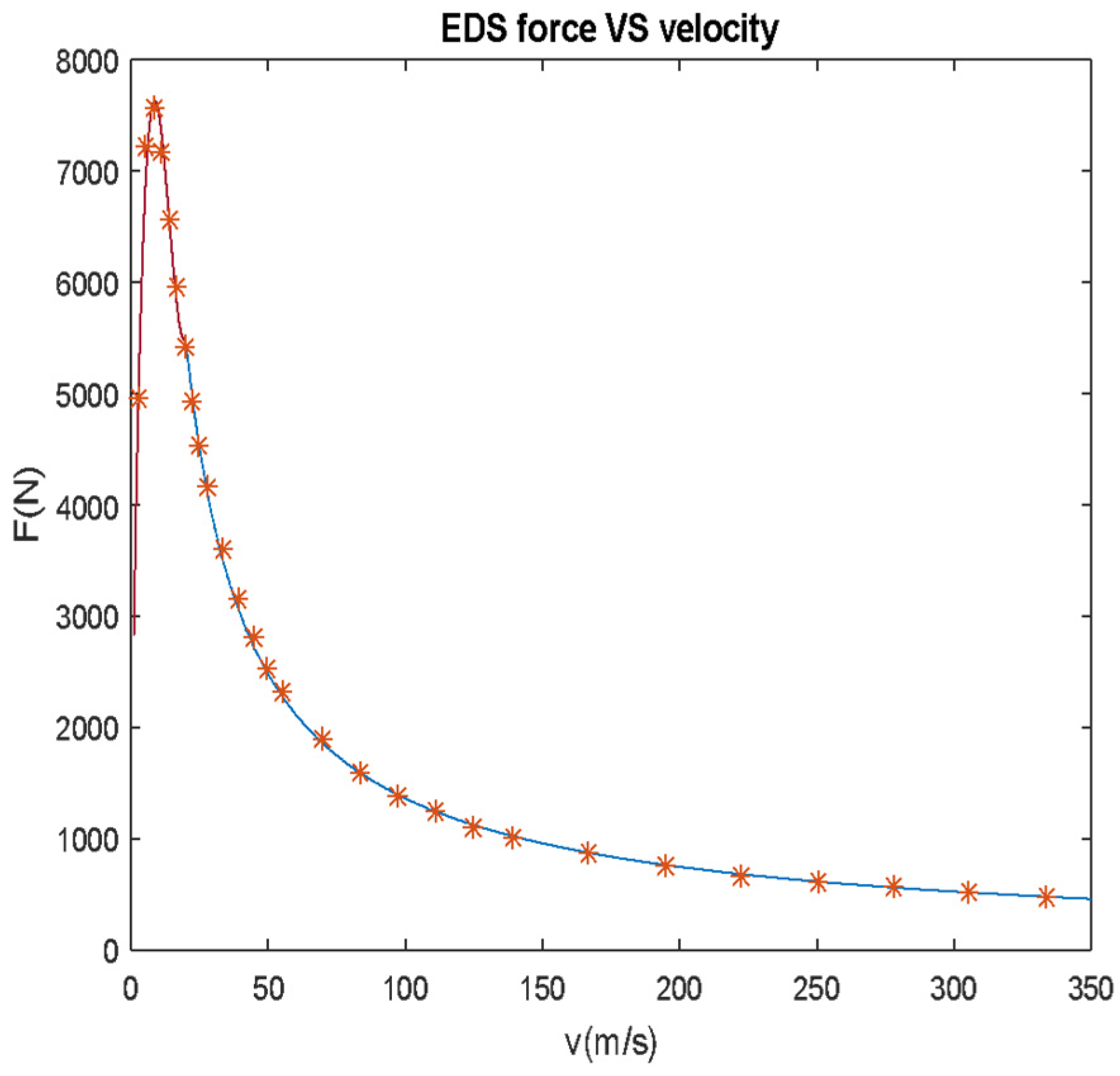
3. Systems Dynamic Model
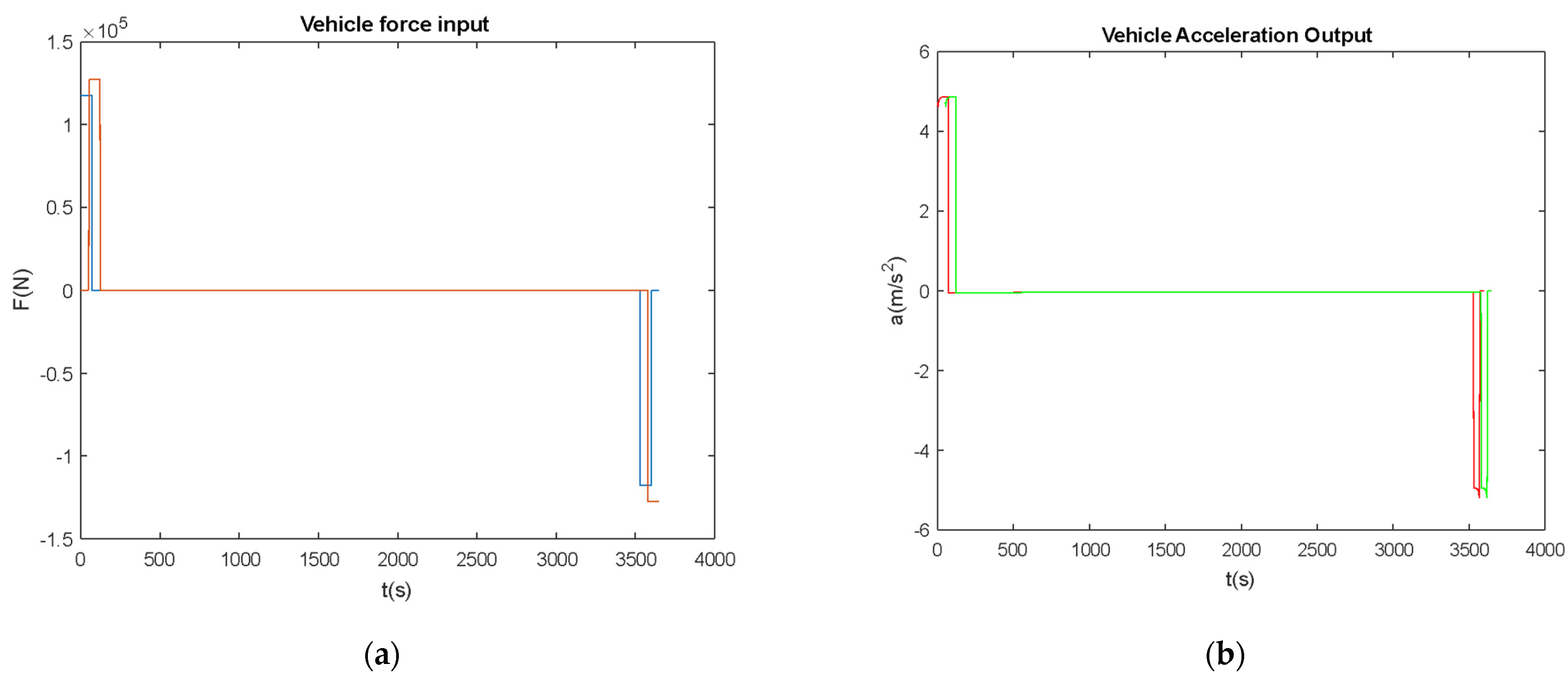
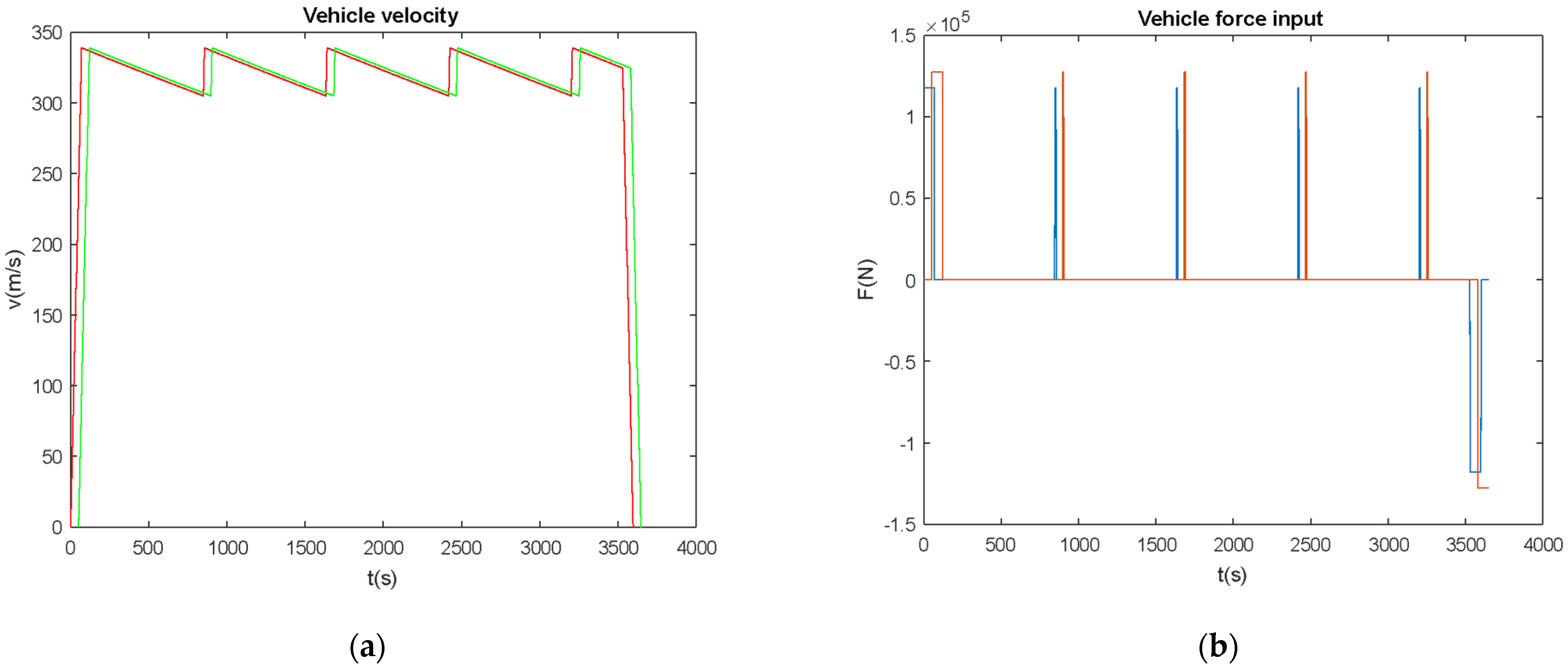
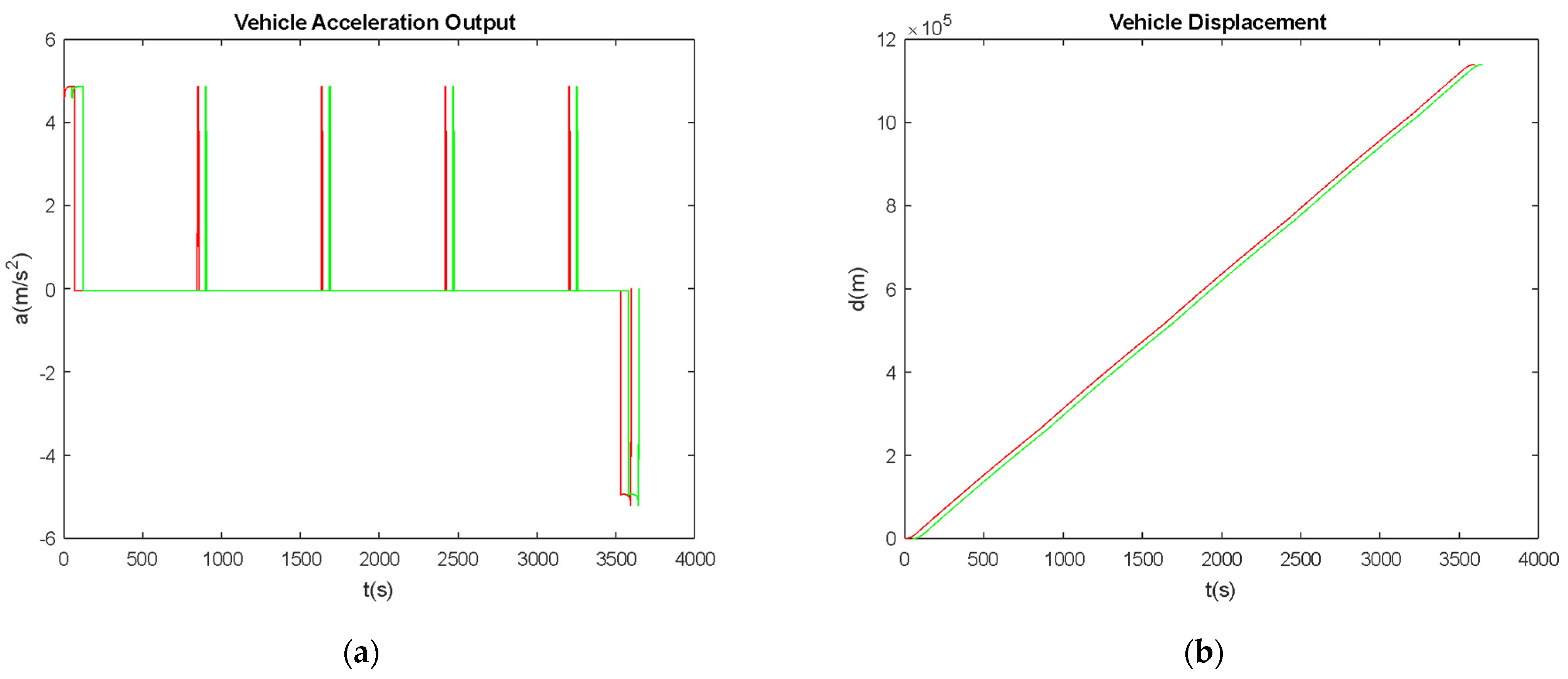
4. Numerical Analysis
5. Vehicle’s Actuation and Operation Aspects
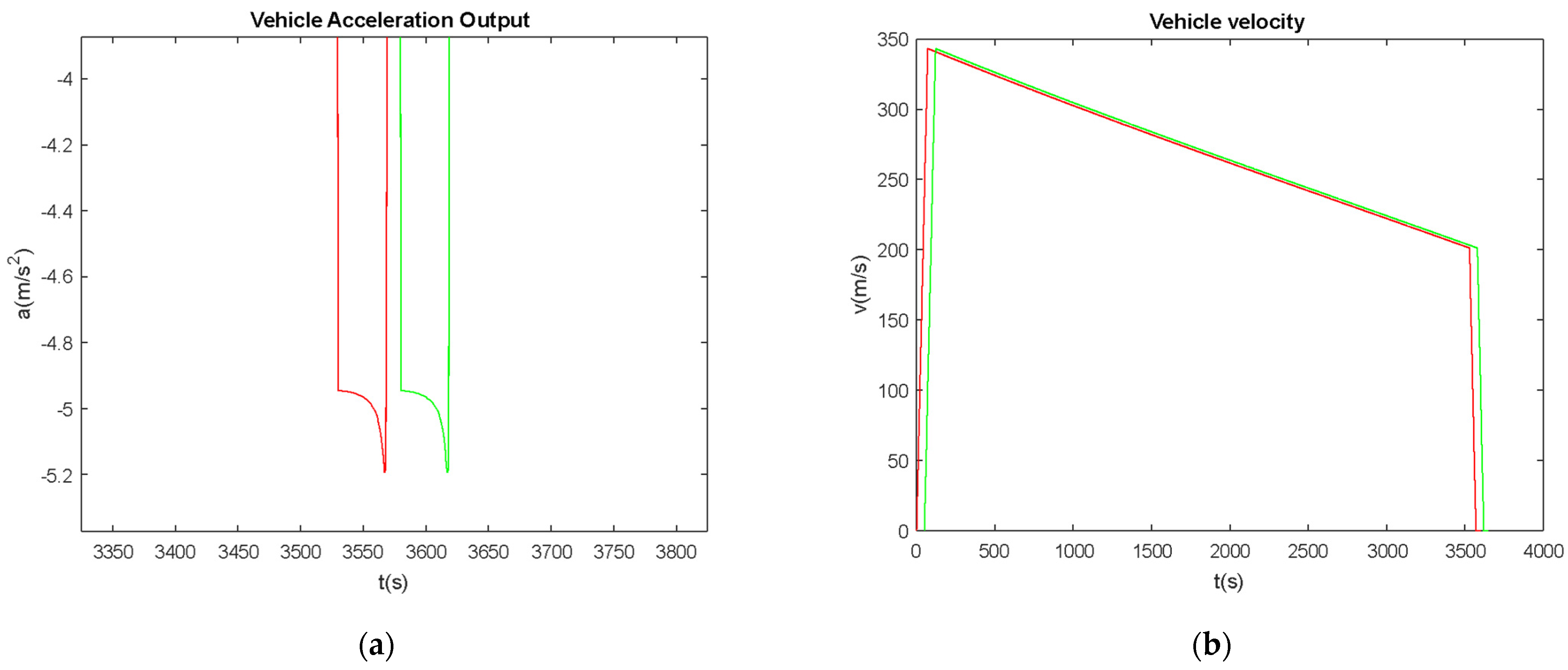
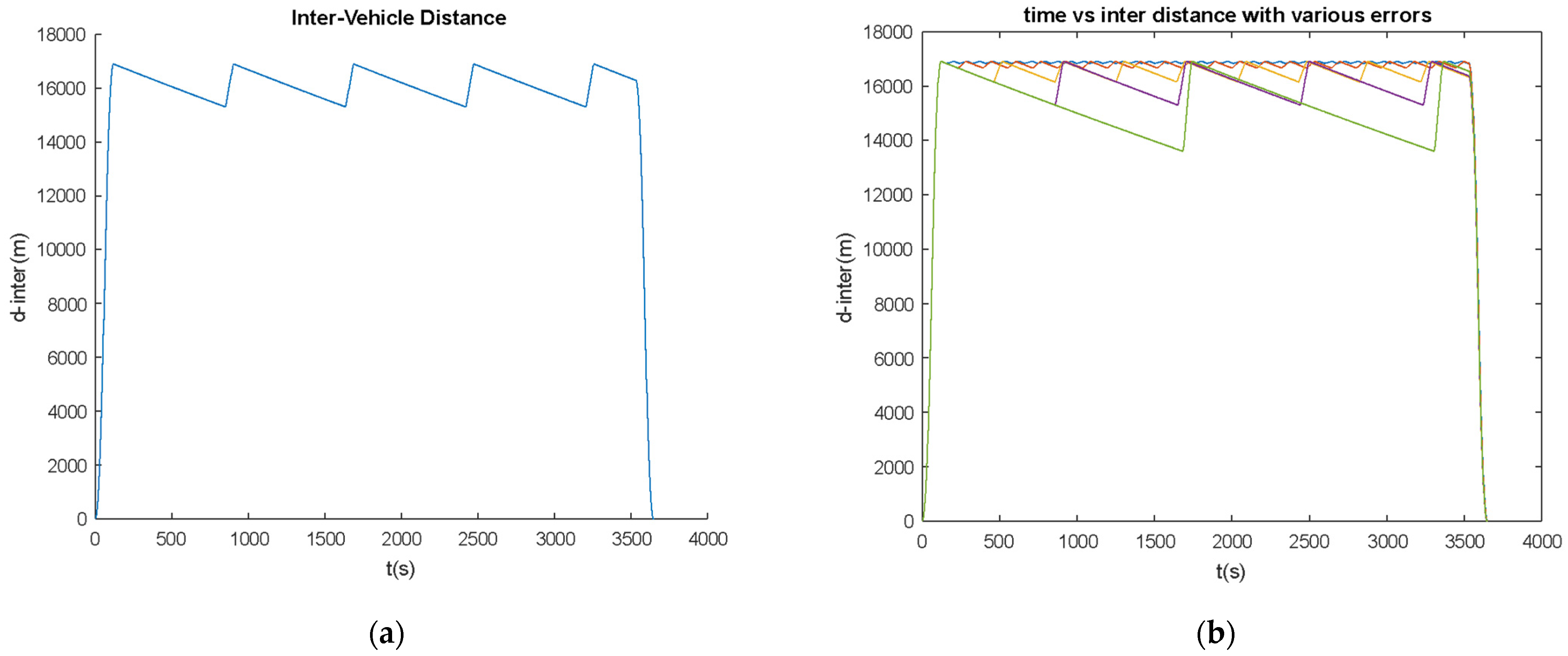
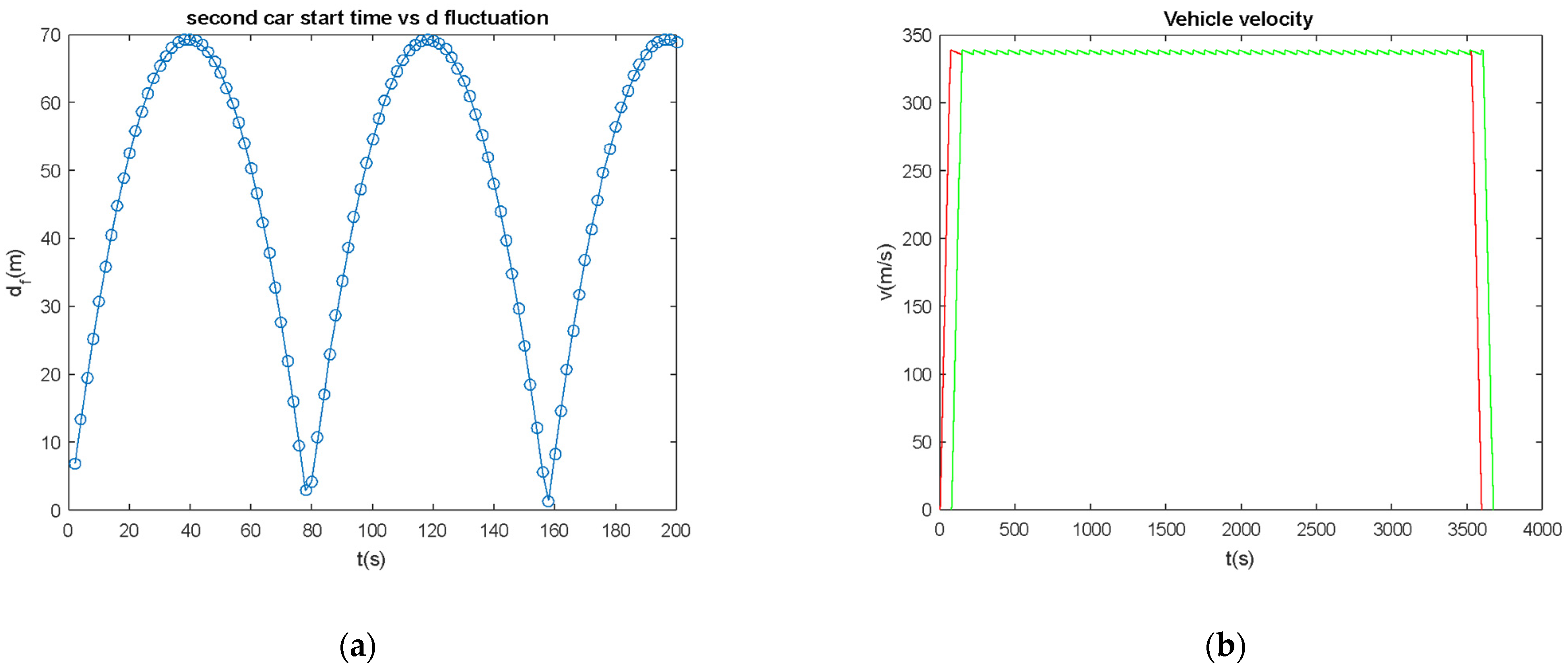
5.1. Minimizing the Flunctuation Distance
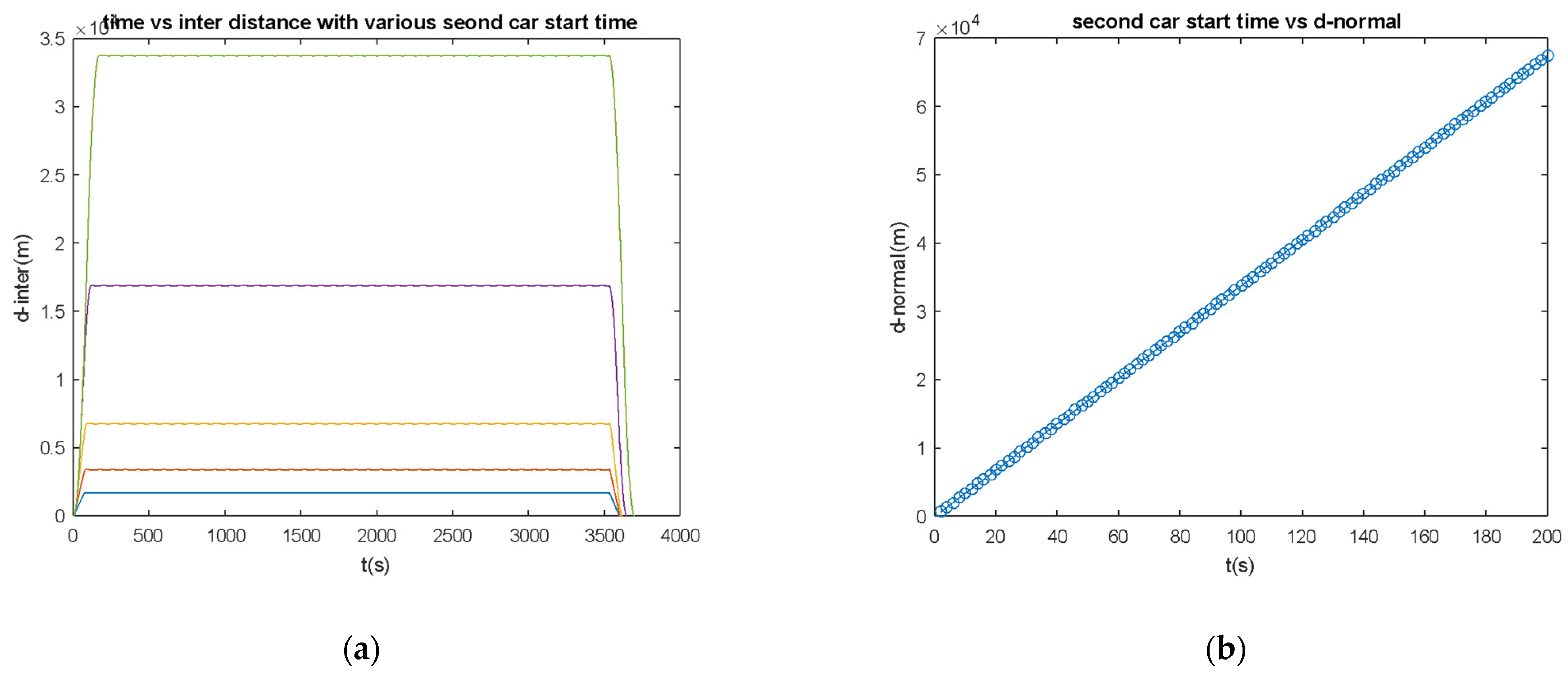
5.2. Second Vehicle Start Time Actuation and Characteristics
6. Conclusions
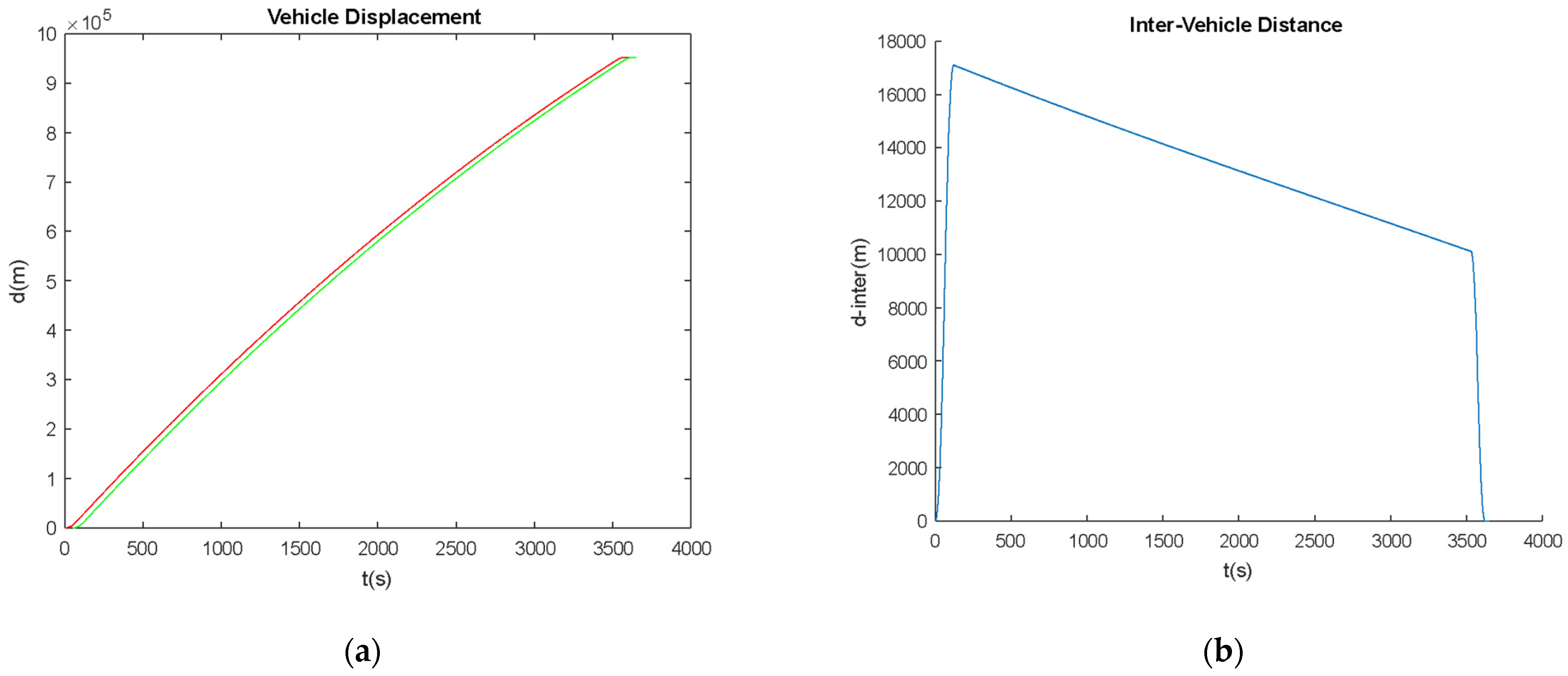
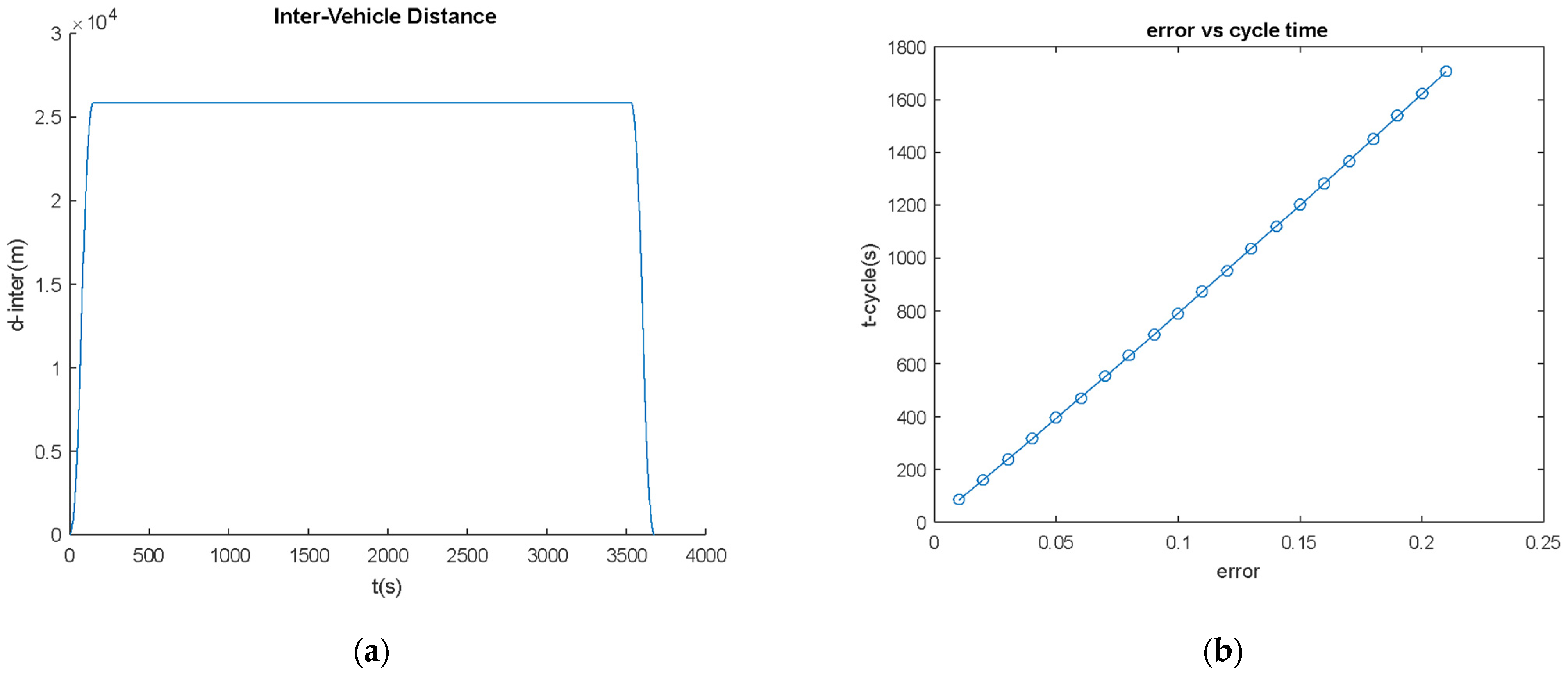
- Inter-distance is a function of error rate and second car start time, the magnitude range is determined by second car start time.
- Inter-distance fluctuation rate is a function of error rate and second car start time. However, it can be minimized by choosing the correct second car start time.
- If the second car start time is chosen as an integer number of push-down cycle times at a specific velocity error rate, the inter-distance fluctuation can be zero.
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xiangming, W. Experience in operation and maintenance of Shanghai Maglev demonstration line and further application of Maglev in China. In Proceedings of the Maglev’ 2006 Germany Proceedings, Dresden, Germany, 13–15 September 2006; Volume 1, pp. 17–19. [Google Scholar]
- Leheis, S. High-speed train planning in France: Lessons from the Mediterranean TGV-line. Transp. Policy 2012, 21, 37–44. [Google Scholar] [CrossRef] [Green Version]
- Hood, C. Shinkansen: From Bullet Train to Symbol of Modern Japan; Routledge: London, UK, 2006. [Google Scholar]
- Sunduck, D.; Keun-Yul, Y.A.N.G.; Jae-Hoon, L.E.E.; Byung-Min, A.H.N. Effects of Korean Train Express (KTX) operation on the national transport system. Proc. East. Asia Soc. Transp. Stud. 2005, 5, 175–189. [Google Scholar]
- Song, D.; Yang, C.H.; Hong, S.K.; Kim, S.B.; Woo, M.S.; Sung, T.H. Study on application of piezoelectricity to Korea Train eXpress (KTX). Ferroelectrics 2013, 449, 11–23. [Google Scholar] [CrossRef]
- Abdelrahman, A.S.; Sayeed, J.; Youssef, M.Z. Hyperloop Transportation System: Analysis, Design, Control, and Implementation. IEEE Trans. Ind. Electron. 2017, 65, 7427–7436. [Google Scholar] [CrossRef]
- Nar, P.; Narkar, B.; Subhash, S.; Palekar, L.S.; Ramchandra, Y. Review of Hyperloop Technology: A New Mode of Transportation. Int. J. Sci. Res. Dev. 2018, 6, 73–75. [Google Scholar]
- Nemchenko, A.; Boyarskaya, A. The Hyperloop High-Speed Train. 2017. Available online: https://rep.bntu.by/bitstream/handle/data/33629/The%20Hyperloop%20High-Speed%20Train.pdf?sequence=1 (accessed on 2 May 2019).
- Ross, P.E. Hyperloop: No Pressure. IEEE Spectr. 2015, 53, 51–54. [Google Scholar] [CrossRef]
- Singh, A.; Mahajan, A.; Mahajan, N.; Gaikwad, A. Hyperloop Transportation System. Int. Res. J. Eng. Technol. 2019, 6, 2554–2558. [Google Scholar]
- Dhandapani, C. A Review: Hyperloop Transportation System. Cikitusi J. Multidiscip. Res. 2019, 6, 5. [Google Scholar]
- Janzen, R. Transpod ultra-high-speed tube transportation: Dynamics of vehicles and infrastructure. Procedia Eng. 2017, 199, 8–17. [Google Scholar] [CrossRef]
- Ji, W.Y.; Jeong, G.; Park, C.B.; Jo, I.H.; Lee, H.W. A study of non-symmetric double-sided linear induction motor for Hyperloop All-In-One System (propulsion, levitation, and guidance). IEEE Trans. Magn. 2018, 54, 1–4. [Google Scholar] [CrossRef]
- Lluesma-Rodríguez, F.; González, T.; Hoyas, S. CFD simulation of a hyperloop capsule inside a closed environment. Results Eng. 2021, 9, 100196. [Google Scholar] [CrossRef]
- Oh, J.S.; Kang, T.; Ham, S.; Lee, K.S.; Jang, Y.J.; Ryou, H.S.; Ryu, J. Numerical analysis of aerodynamic characteristics of hyperloop system. Energies 2019, 12, 518. [Google Scholar] [CrossRef] [Green Version]
- Yang, Y.; Wang, H.; Benedict, M.; Coleman, D. Aerodynamic simulation of high-speed capsule in the Hyperloop system. In Proceedings of the 35th AIAA Applied Aerodynamics Conference, Denver, CO, USA, 5–9 June 2017. [Google Scholar]
- Opgenoord, M.M.J.; Merian, C.; Mayo, J.; Kirschen, P.; O’Rourke, C.; Izatt, G. MIT Hyperloop Final Report; Massachusetts Institute of Technology: Cambridge, MA, USA, 2017. [Google Scholar]
- Dudnikov, E. Advantages of a new Hyperloop transport technology. In Proceedings of the 2017 Tenth International Conference Management of Large-Scale System Development (MLSD), Moscow, Russia, 2–4 October 2017. [Google Scholar]
- Almujibah, H.; Kaduk, S.I.; Preston, J. Hyperloop—Prediction of Social and Physiological Costs. Transp. Syst. Technol. 2020, 6, 43–59. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, L.; Han, B.; Li, Z.; Zhou, T.; Wang, K.; Wang, D.; Ai, B. Concepts on Train-to-Ground Wireless Communication System for Hyperloop: Channel, Network Architecture, and Resource Management. Energies 2020, 13, 4309. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, L.; Wang, K.; Han, B.; Piao, Z.; Wang, D. Analysis of the Effective Scatters for Hyperloop Wireless Communications Using the Geometry-Based Model. In International Conference on Machine Learning for Cyber Security; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Nikolaev, R.; Idiatuallin, R.; Nikolaeva, D. Software system in Hyperloop pod. Procedia Comput. Sci. 2018, 126, 878–890. [Google Scholar] [CrossRef]
- Van Goeverden, K.; Milakis, D.; Janic, M.; Konings, R. Analysis and modelling of performances of the HL (Hyperloop) transport system. Eur. Transp. Res. Rev. 2018, 10, 41. [Google Scholar] [CrossRef]
- Lafoz, M.; Navarro, G.; Torres, J.; Santiago, Á.; Nájera, J.; Santos-Herran, M.; Blanco, M. Power supply solution for ultrahigh speed hyperloop trains. Smart Cities 2020, 3, 642–656. [Google Scholar] [CrossRef]
- Janić, M. Estimation of direct energy consumption and CO2 emission by high speed rail, transrapid maglev and hyperloop passenger transport systems. Int. J. Sustain. Transp. 2021, 15, 696–717. [Google Scholar] [CrossRef]
- Ahmadi, E.; Alexander, N.A.; Kashani, M.M. Lateral dynamic bridge deck–pier interaction for ultra-high-speed Hyperloop train loading. In Proceedings of the Institution of Civil Engineers-Bridge Engineering; Thomas Telford Ltd.: London, UK, 2020; Volume 13, pp. 198–206. [Google Scholar]
- Bose, A.; Viswanathan, V.K. Mitigating the Piston Effect in High-Speed Hyperloop Transportation: A Study on the Use of Aerofoils. Energies 2021, 14, 464. [Google Scholar] [CrossRef]
- Eichelberger, M.; Geiter, D.T.; Schmid, R.; Wattenhofer, R. High-Throughput and Low-Latency Hyperloop. In Proceedings of the 2020 IEEE 23rd International Conference on Intelligent Transportation Systems (ITSC), Rhodes, Greece, 20–23 September 2020. [Google Scholar]
- Sarin, M.; Overton, M. Complex Hyperloop Capsule Safety Requirements and Risk Mitigations. In Proceedings of the 36th International System Safety Conference, Phoenix, AZ, USA, 13–17 August 2018. [Google Scholar]
- Hyde, D.J.; Barr, L.C.; Taylor, C. Hyperloop Commercial Feasibility Analysis: High Level Overview; John, A., Ed.; Volpe National Transportation Systems Center (US): Cambridge, MA, USA, 2016.
- Alexander, N.A.; Kashani, M.M. Exploring Bridge Dynamics for Ultra-High-Speed, Hyperloop, Trains. Structures 2018, 14, 69–74. [Google Scholar]
- Mitropoulos, L.; Kortsari, A.; Koliatos, A.; Ayfantopoulou, G. The Hyperloop System and Stakeholders: A Review and Future Directions. Sustainability 2021, 13, 8430. [Google Scholar] [CrossRef]
- Gkoumas, K. Hyperloop Academic Research: A Systematic Review and a Taxonomy of Issues. Appl. Sci. 2021, 11, 5951. [Google Scholar] [CrossRef]




| Given System Specifications | |
|---|---|
| Pressure | 1/1000 [atm] |
| Max speed | 1220 [km/h] (339 [m/s]) |
| Weight | 24,000 [kg] (No passenger) |
| 26,000 [kg] (with full passenger) | |
| Dimension | 1.25 × 1.25 × 26 [m3] |
| Levitation gap | over 100 [mm] |
| Levitation | Superconductor EDS |
| Propulsion | LSM |
| Acceleration | (+,−) 0.5 g [m/(s^2)] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jo, B.W. Numerical Study of Longitudinal Inter-Distance and Operational Characteristics for High-Speed Capsular Train Systems. Vehicles 2022, 4, 30-41. https://doi.org/10.3390/vehicles4010002
Jo BW. Numerical Study of Longitudinal Inter-Distance and Operational Characteristics for High-Speed Capsular Train Systems. Vehicles. 2022; 4(1):30-41. https://doi.org/10.3390/vehicles4010002
Chicago/Turabian StyleJo, Bruce W. 2022. "Numerical Study of Longitudinal Inter-Distance and Operational Characteristics for High-Speed Capsular Train Systems" Vehicles 4, no. 1: 30-41. https://doi.org/10.3390/vehicles4010002
APA StyleJo, B. W. (2022). Numerical Study of Longitudinal Inter-Distance and Operational Characteristics for High-Speed Capsular Train Systems. Vehicles, 4(1), 30-41. https://doi.org/10.3390/vehicles4010002






