Abstract
Replacement heifers are regularly weighed to assess their health. These data also predict the milk yield in their first lactation (L). The first derivative of the growth curve represents the weight change rate at a given time. It is interesting to use the higher-order derivatives of one biological process, such as growth, to predict the outcome of another process, like lactation. With 78 records of grazing heifers, machine learning was used to predict the L based on variables calculated during the rearing period, from 3 to 21 months of age, every 3 months: body weight (P), first (1D), and second derivative (2D) of an individually modeled Fourier function. Other variables were the age at effective insemination (AI) and the season of the year when the heifer was born (E). The average deviance of the fitted models represented the goodness of fit. The models were trained using 85% of the records, and the fit was evaluated using the remaining data. The deviance was lower for the models including both derivatives in comparison to the models where the derivatives were not included (p = 0.022). The best models predicted the L using data of heifers at six months of age (r2 = 0.62) and the importance of the variables in the model was 35, 28, 21, and 16% for 1D, AI, 2D, and P, respectively. By utilizing this type of model, it would be possible to select and eliminate excess heifers early on, thereby reducing the financial and environmental costs.
1. Introduction
Replacement heifers are an important investment that will pay off through milk production. Productive cows are distinguished by their persistence in milk yield and longevity [1]. However, the costs incurred (financial and environmental) during heifer rearing must be offset by the future milk yield. Therefore, it is crucial to identify and select heifers with good productive potential as soon as possible [2]. Higher efficiency would result from efforts to achieve at least 88% of the mature milk yield in the first lactation and calve heifers younger than 22 months [1]. It is suggested that heifers reaching between 73% and 77% of their mature weight at the first calving can produce more milk in their first lactation without compromising the long-term milk yield and herd life [1]. However, farm-specific targets may be more useful than a “one-size-fits-all” approach [3]. In addition to attaining targets, an early retention strategy for heifers can help reduce feed costs, as opposed to retaining all the calves [2]; this requires suitable rearing management and selection criteria [4,5,6].
The first lactation milk yield is a performance indicator that is associated with other measures of lifetime performance [7,8,9]. Several studies have reported predictive models and correlations between the first lactation milk and body weight, average daily growth rate (ADG) or body condition score [10,11,12]. Particularly interesting is the use of derivatives of the weight curve models of growing heifers to detect negative breakpoints that explain differences in the first lactation milk associated with the number of breakpoints detected [13]. Informative breakpoints could occur at any time during the growing period. It is also possible that the body weight at a specific time better explains the first lactation milk on its own [11]. Detection of positive and negative breakpoints [13] could explain how grazing heifers with different growth trajectories (seasonal or linear) achieve similar outcomes [14].
Heifer growth during rearing is influenced by fluctuations in health and environmental conditions. Measures of heifer weights are a common practice used to monitor growth, calculate the ADG and determine management practices according to specific weight thresholds, such as the timing of the first insemination. The heifer’s target growth trajectory between body weights is predominantly linear, thus creating a mostly linear growth trajectory from 6 to 15 and 15 to 22 months of age [11,14]. Heifer growth curve models that predict the body weight at a specific point in the future can assist in cattle selection. Rather than a curve, the heifer’s growth during the rearing period has been characterized as linear [11,14].
Nonlinear growth models can represent patterns of acceleration and deceleration, such as periods of restriction and overfeeding; heifers that experience these oscillations experience a positive effect on the amount of secretory mammary tissue and its activity [15]. The effects of pre-pubertal and post-pubertal ADG on the future milk production and reproduction are inconsistent; while accelerated ADG reduces mammary development, there are also questions about whether periods of restriction and re-alimentation increase the amount and activity of mammary secretory tissue and if this is advantageous for grazing dairy [15]. Therefore, derivatives of Fourier transforms or splines would better represent fluctuations and changes in the ADG compared to growth curve models such as the Logistic, Brody, or Gompertz [16]. Additionally, these functions may not be entirely relevant for heifers, because the asymptotic value of the body weight is not reached until two or three lactations [13].
The approach of this study was to use the weight data of heifers during rearing to reveal oscillations that determine future milk performance. Fourier series are functions that consist of sums of trigonometric functions and are used to represent oscillatory components in a time series [17]. Transient or instantaneous growth rates may reveal growth spurts due to environmental factors [13]. As such, the instantaneous ADG is the first derivative of a growth curve at a given time [18]. The first derivatives of nonlinear functions can have maximum or minimum values representing points of inflexion at specific times. Changes in the heifer’s instantaneous growth rate could result from illness, changes in the nutritional plane or many management practices. Positive and negative changes in the instantaneous growth rate would accumulate and impact future performance. Because a derivative is a function, it can be derived to obtain a second derivative or higher-order derivatives [19]. The second derivative provides information about an inflection point and also indicates how the first derivative will change as the input varies. High-order derivatives are used to avoid local minima in multivariate optimization functions. They are especially valuable in machine learning for guiding the optimization search [20].
We proposed that the first and second derivatives of the growth curve provide valuable information for predicting the future milk yield. As far as we know, there are no reports on the use of the derivatives of a growth curve as explanatory variables in a predictive model. The closest approach was when the first derivative was used to detect breakdowns in the growth curves of heifers; there, the number of accumulated breakdowns during heifer rearing was then associated with milk production in the first lactation [13]. Handcock [21] utilized the weight of heifers up to 21 months of age to forecast the milk yield in their initial lactation and the first derivative proved valuable in determining the optimal weight for maximizing the milk yield. It also revealed that heifers with lower weights had a greater capacity to enhance their milk yield by increasing their weight in comparison to heavier heifers. In that study, the first derivative was not included as an explanatory variable in the model.
To generate the predictive model, we used artificial intelligence algorithms, specifically machine-learning algorithms. These algorithms are capable of identifying and associating patterns in the data, making them superior to ordinary least squares regression. This approach is supported by an increasing use of artificial intelligence algorithms to predict milk yields [22]. Machine learning (ML) takes advantage of parallel processing and a range of artificial intelligence algorithms such as neural networks, random forest, and generalized linear models, among many. There are ML frameworks such as H2O that solve classification or regression problems with streamlined workflows and easy model deployment [23]. Within the H2O platform, AutoML is a fully automated supervised learning algorithm that trains and cross-validates base models. It generates a stack of different models based on ML algorithms and also stacked ensembles. Model stacking is an ensemble modeling technique that involves training a model to combine the outputs of many models from the stack.
The present work used a small dataset of grazing heifers to model the first lactation milk yield based on a limited number of measurable variables early in the heifer’s life. The main objective was to determine if there was a specific age at which the heifer’s milk yield in her first lactation could be more accurately predicted. The hypothesis was that variables derived from a Fourier function representing the heifer’s growth during rearing were important in the modeling, particularly the first and second derivatives.
2. Materials and Methods
This exploratory and retrospective observational study was conducted at the National Autonomous University of Mexico station in Tequisquiapan, México (20°36′13.88″ N, 99°55′02.91″ W), at an altitude of 1913 m above sea level. Dairy production was in a year-round milk system of Holstein-Friesian, Jersey and their crosses on irrigated pasture with rotational grazing. The climate was semi-dry temperate, with 512 mm of precipitation and an average annual temperature of 17.5 °C. The predominant pasture species were alfalfa (Medicago sativa), cocksfoot (Dactylis glomerata), ryegrass (Lolium multiflorum), and tall fescue (Festuca arundinacea). The grazing area was allocated based on cuttings of the available forage before each grazing period, as well as the monthly values of the proximate analysis of the forage [24].
The management of the heifers was performed as follows: weighing at birth, repeatedly dosed with good-quality colostrum, and kept in individual housings. The heifers were fed whole milk, complemented with varying amounts of concentrate and ad libitum alfalfa hay, until they started grazing at around three months of age. After 12 months of age, their feeding consisted exclusively of grazing. We considered that the heifers between 12 and 18 months of age had altered food intake, probably because they spent a significant amount of time in management pens when heat detection, insemination procedures, and regrouping took place. After 18 months of age, when pregnancy was confirmed, the heifers were managed as a single group.
- Data
The body weight was recorded between 9 and 19 times during each heifer’s rearing. The individual growth curve was modeled using a 2 × 2 Fourier series (Equation (1)). Estimated values of the body weight (P, kg), first derivative (1D, kg d−1), and second derivative (2D, kg d−2) were calculated at a three-month interval from the third to the twenty-first month of age. P was used in the modeling instead of the measured body weight because the age of weighing was irregular among the heifers.
where y is the response variable, a0, a and b are the Fourier’s coefficients, t is the time, and i is the period and the π constant.
We used data from 78 Holstein-Friesian heifers with at least 293 days in milk. After calving, between 72 and 94 daily records were collected using proportional milk meters from Waikato LTD Co., Hamilton, New Zealand. Records of the 305-day milk yield were estimated from the daily milk weights by integrating a 2 × 2 Fourier function from day 1 to 305 (L, kg). The models were obtained using Table Curve 2D v5.01 software (Grafiti LLC, Palo Alto, CA, USA), and the normality of the residuals was tested using the Anderson–Darling test in the R program [25].
- 2.
- Modeling variables and scenarios
To model the future milk production, L was used as the response variable, while P, 1D, 2D, the age at effective artificial insemination (AI), and the season of the year in which the heifer was born (E) were used as explanatory variables. The milk yield in the first lactation, L, is an indicator of performance for other variables related to the productive life of the cow [7,8,9]. We hypothesized that P, 1D and 2D would predict L better at a certain heifer ages, because the heifer weight, ADG, and body condition are positively correlated with L [10,11,12]. The inclusion of 1D and 2D in the models was supported by the usefulness of higher-order derivatives in guiding the optimization search of multivariate functions solved by artificial intelligence [20]. In particular, we were interested in exploring whether the 1D and 2D variables contribute to improving the modeling compared to the variables P, E, or AI.
The following scenarios were generated based on the explanatory variables used: (a) all the variables, (b) except P, (c) without 1D and 2D, (d) except 1D, (e) except 2D, and (f) except AI. These scenarios were explored using estimates obtained at heifer ages of 3, 6, 9, 12, 15, 18, and 21 months. The database was divided into 85% of the records for training the models and 15% of the records for testing the model. Using bootstrapping [26], which is a sampling technique with replacement, six samples were taken from the database. Thus, there were 252 runs based on 6 scenarios, 7 ages of the heifer, and 6 samples.
- 3.
- Algorithms
Modeling was explored using multiple linear regression with the stepwise procedure; however, no model showed significance for any of the scenarios (p < 0.05). Therefore, we only report the modeling results performed with the AutoML function of the H2O package v.2.32.14 in R [27]. AutoML allows for the exploration of the database and the identification of patterns that enable the creation of a predictive model using various machine-learning algorithms, such as the random forest, neural networks, deep learning, and generalized linear models, among others. For each of the 252 runs, hundreds of predictive models were obtained, from which AutoML could generate an ensemble of models. Often, the ensemble had better predictive ability than the best model obtained using a specific machine-learning algorithm. Within each run, the models were ordered according to their deviance as a measure of the goodness of fit, which is a generalization of likelihood [28]. A model is considered a better fit if it has a lower numerical value for this statistic.
Overfitting and multicollinearity are conditions that limit the quality and usefulness of regression models. These issues can be addressed in machine learning [29]; the AutoML procedure reduces these conditions by thoroughly exploring the parameter values and conducting cross-validation through multiple runs of the algorithm [30]. Deviance was also used as a criterion to interrupt the processing of a run when no improvement was obtained in the cross-validation process. Only the best model from each run was chosen for further analysis.
- 4.
- Importance of variables and model interpretability
Deviance and the coefficient of determination (r2) were used to test the model by comparing the estimated values with the corresponding observed values from the records reserved for validation. For these two measures, the average and standard error (n = 6) were calculated for each scenario for the heifer’s age. For the heifer’s age when the deviance was lower, we tested the hypothesis of lower deviance for the scenario including all the available variables against the scenario when the derivatives were not included. Only this test was performed to control the type I error at a level significance of 0.05 using a one-tailed non-parametric Wilcoxon test.
The contribution of the explanatory variables to reducing the model’s deviance is determined by the importance in each model, but this is not possible for ensembles. Although machine-learning algorithms yield more accurate predictions, they are often referred to as black box models because they lack an explanation of the underlying process that led to those predictions. However, there is currently a growing focus on interpreting the models generated by machine learning [31]. The SHapley Additive exPlanations (SHAP) [32] values are an option for model interpretability; the SHAP values assist in post hoc agnostic interpretability of the variable importance in models. Each observed value is assigned a SHAP value, which represents its contribution to the value predicted by the model [33].
3. Results
The deviance was lower at six months of age when 1D was included as an explanatory variable in the model (Figure 1a,b,e,f). When 2D was used, but not 1D, the deviance decreased at 12 and 15 months compared to the other heifer ages (Figure 1d). When the derivatives were not included in the model, the deviance was high at any age (Figure 1c). When P was not included in the model, the deviance was only low at six months of age (Figure 1b). At six months of age, the deviance was lower in the scenario that included all the variables compared to the scenario where the derivatives were not included (p = 0.022). Interestingly, using all the variables, or excluding only AI, had low deviance when using data from six and nine months of age (Figure 1a,f). Furthermore, the models including all the variables consistently had the lowest deviance at any age.
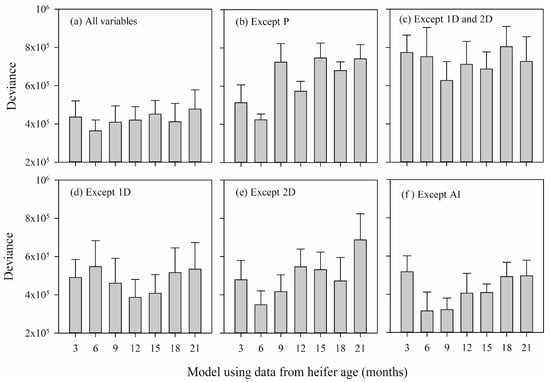
Figure 1.
Mean deviance of the milk yield (L) models in the first lactation of grazing heifers using variables corresponding to different ages of the heifer (3, 6, 9, 12, 15, 18, and 21 months of age). The scenarios were as follows: (a) all the variables, (b) all the variables except P, (c) all the variables except 1D and 2D, (d) all the variables except 1D, (e) all the variables except 2D, and (f) all the variables but AI. The error bars represent the standard error of the mean. A lower deviance value indicates a better training fit.
The r2 values were the lowest when 1D and 2D were unavailable for model building (Figure 2c). The r2 was consistently close to or slightly higher than 0.6 from three to twelve months of age when all the variables were included. At six months of age, the r2 value exceeded 0.6 only in the scenarios where P was not included (Figure 2b), 2D was not included (Figure 2e) or AI was not included (Figure 2f). Modeling without AI would be viable at early stages of heifer rearing since the r2 values were high when using data from 6 and 9 months of age.
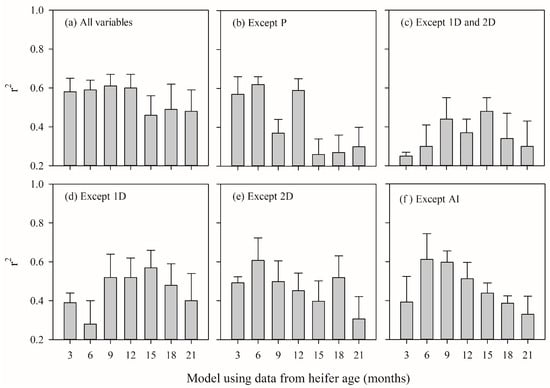
Figure 2.
Model validation of the milk yield in the first lactation (L) of grazing heifers using variables corresponding to different ages of the heifer (3, 6, 9, 12, 15, 18, and 21 months of age). Where the adjusted coefficient of determination (r2) represents the regression between the observed and estimated L of the 15% database not used for training. The scenarios were as follows: (a) all the variables, (b) all the variables except P, (c) all the variables except 1D and 2D, (d) all the variables except 1D, (e) all the variables except 2D, and (f) all the variables but AI. The error bars represent the standard error of the mean.
The obtained deviance and r2 values indicated that using all the variables from three to twelve months of age resulted in better models. In this case, 1D was the most important variable at six and nine months, while 2D was the most important at three and twelve months (Table 1). It is noteworthy that E was not utilized in the optimal model in any scenario or at any age. This result caught our attention because the production system under examination exhibits seasonal fluctuations in terms of forage availability. Additionally, heifers born in the autumn showed a slightly higher numerical value of L compared to those born in the spring (Table 2).

Table 1.
Importance of the variables (mean and standard error) used in the scenario when all the variables were available for modeling. Only shown are those heifer ages when the deviance was lower and the r2 was higher. The sum of importance is 1.

Table 2.
Mean and standard error of the mean of the productive and reproductive variables according to the heifer’s birth season.
Generally, the DL algorithm (70%) and XGBoost (16%) were the most commonly used in all the scenarios. The ensembles only produced a superior model in 4.7% of runs. Neural networks are well known for classification problems, while the XGBoost can be used directly for regression. Although machine-learning algorithms primarily focus on classification or regression problems, there is an overlap in their utility for solving these two types of problems [27]. The AutoML implementation does not provide SHAP values for DL models, but they are available for XGBoost and could offer insight into how the variables were important. The summary plot of the SHAP values (Figure 3) shows that 1D and AI in the XGBoost model using all the variables at six months of age were the most influential variables. High values for these variables had a negative impact on L; low values would contribute positively to L in the range of 200 to 300 kg. Although P had an average importance of 0.16 (Table 1), in this XGBoost model it was the least important.
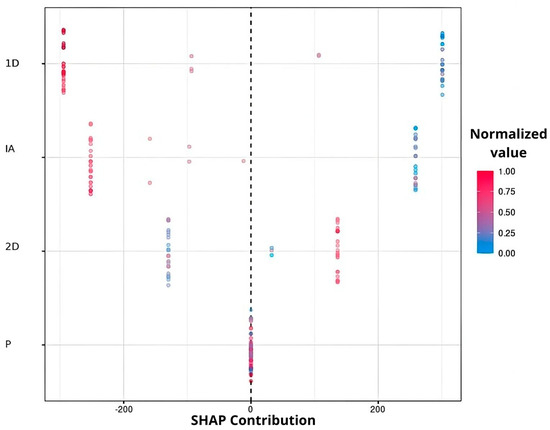
Figure 3.
SHAP values of the XGBoost model using the training database, including all the variables for heifers at six months of age. The importance of the variables in the model is shown in descending order. The red or blue tone indicates the normalized value of the variable. The higher color intensity represents the greater magnitude of the variable.
4. Discussion
The models using D1 and D2 had lower deviance at younger heifer ages, indicating the usefulness of these variables. All the explored models did not include interactions or quadratic effects to improve the relationship with L. Zanton and Heinrichs [34] showed that the average weight gain (ADG) before puberty explained the L in a quadratic model: y = ADG + ADG2 with r2 = 0.61; however, in a linear model, it was not significant: y = ADG with r2 = 0.06. With quadratic models, the relationship between the heifer weight and L was linear for weights at three months of age, but it was curvilinear for weights at six months or older for certain dairy racial groups, excluding Holstein-Friesian [11]. In a preliminary study, we used multiple regression analysis, but only identified non-significant relationships between the heifer weight and L as the main effect. Gelsiger et al. [35] used the ADG as a quadratic term, but they found that different management practices between barns had a greater effect on the L compared to nutrition or the ADG. In our study, the database was limited in terms of the number of heifers with complete records and the number of variables included. A predictive model for commercial applications would improve its accuracy by incorporating a larger number of records and variables, including those related to the environment, animal activity, management and parentage, among others. Aquilani et al. [36] reviewed the practical challenges of grassland agriculture to develop precision approaches involving the control, monitoring, and observation of livestock. Thus, there is potential to build more comprehensive databases as an alternative to exploring variable transformations that increase the model complexity.
AI was an important variable when using data from different ages and when all the variables were considered (Table 1). When relying on this kind of model, the decision to cull the heifer would have to wait until it reached 17 months of age and the pregnancy was confirmed. For models like the one shown in Figure 3, the low SHAP values when the days of AI increased indicate a negative contribution to milk production. This finding conflicts with the accepted practice of not exposing very young heifers to breeding [10]. However, using all the variables except AI from the data for the 6 and 9 months of age models with low deviance and high r2 contributes to our hypothesis that P, 1D, 2D can better predict L.
The naturally changing forage resource results in shifts in the feed intake and feed nutritional quality, but pasture-based conditions also lead to lower stress, improved hygiene, and better animal welfare compared to their pen-fed counterparts [37]. Overall, environmental conditions and their impact on phenotype can lead to fluctuations in the ADG. These fluctuations can be observed as changing values of 1D and 2D during the growth phase of heifers. In pen-fed animals, the fluctuations in the ADG may be different to those of grazing animals in terms of the magnitude, temporal occurrence, or frequency. In this sense, the modeling importance of the 1D, 2D, and potentially higher-order derivatives were encouraging, but their usefulness needs to be confirmed in other raising conditions for replacement heifers.
The modeling could be improved by increasing the execution time and reducing the number of algorithms included in the construction phase. It is possible that the solution space was not thoroughly explored due to the limited execution time of 200 s for completing a model. If the time limit was exceeded, the model would fail and be discarded.
Deep learning was the algorithm that provided the best solution in most runs. However, there were two main variants depending on how the model’s hyperparameters were optimized. The traditional method involved using a Cartesian grid, while the alternative method involved using a random search grid [27]. The average deviance for the Cartesian grid was 377,733, while for the random search grid it was 571,712. For XGBoost, something similar happened, with deviance values of 491,663 and 748,663. Possibly, the random search for hyperparameters was not efficient within the allocated time and the optimization of hyperparameters should be restricted to a Cartesian grid search.
5. Conclusions
The best prediction of the first lactation yield resulted from the models using 1D and 2D, particularly when using data from six to twelve months of the heifer’s growth period. For these models, 1D was the most important variable at six and nine months, while 2D was the most important at three and twelve months of age. The derivatives of the heifer growth curve were informative in predicting the milk yield, especially when the modeling did not incorporate the age at effective insemination. Models incorporating the derivatives of the growth curve would help producers make management decisions for heifers at early ages, optimizing resource investment.
Author Contributions
Conceptualization, A.G.-E. and M.C.-J.; data curation, A.G.-E.; formal analysis, A.G.-E.; investigation, V.L.-R., J.G.G.-M. and A.K.Y.O.; methodology, A.G.-E.; resources, V.L.-R. and A.K.Y.O.; validation, A.G.-E., M.C.-J., V.L.-R., J.G.G.-M. and A.K.Y.O.; writing—original draft, M.C.-J.; writing—review and editing, V.L.-R., J.G.G.-M. and A.K.Y.O. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data Availability Statements are available in the “Rights” section of the following links: The dataset is available at: https://zenodo.org/doi/10.5281/zenodo.10827559 (accessed on 25 April 2024). The code used is available at: https://zenodo.org/doi/10.5281/zenodo.10827726 (accessed on 25 April 2024).
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Heinrichs, A.J.; Jones, C.M.; Gray, S.M.; Heinrichs, P.A.; Cornelisse, S.A.; Goodling, R.C. Identifying Efficient Dairy Heifer Producers Using Production Costs and Data Envelopment Analysis. J. Dairy Sci. 2013, 96, 7355–7362. [Google Scholar] [CrossRef]
- Mohd Nor, N.; Steeneveld, W.; Mourits, M.C.M.; Hogeveen, H. The Optimal Number of Heifer Calves to Be Reared as Dairy Replacements. J. Dairy Sci. 2015, 98, 861–871. [Google Scholar] [CrossRef]
- Archer, S.C. An Observational Study of Growth Rate and Body Weight Variance Partition for United Kingdom Dairy Calves from Birth to 20 Weeks of Age. JDS Commun. 2021, 2, 248–252. [Google Scholar] [CrossRef]
- Cozler, Y.L.; Lollivier, V.; Lacasse, P.; Disenhaus, C. Rearing Strategy and Optimizing First-Calving Targets in Dairy Heifers: A Review. Animal 2008, 2, 1393–1404. [Google Scholar] [CrossRef]
- Miglior, F.; Fleming, A.; Malchiodi, F.; Brito, L.F.; Martin, P.; Baes, C.F. 100-Year Review: Identification and Genetic Selection of Economically Important Traits in Dairy Cattle. J. Dairy Sci. 2017, 100, 10251–10271. [Google Scholar] [CrossRef]
- Schuster, J.C.; Barkema, H.W.; De Vries, A.; Kelton, D.F.; Orsel, K. Invited Review: Academic and Applied Approach to Evaluating Longevity in Dairy Cows. J. Dairy Sci. 2020, 103, 11008–11024. [Google Scholar] [CrossRef]
- Van Vleck, L. First Lactation Performance and Herd Life. J. Dairy Sci. 1964, 47, 1000–1003. [Google Scholar] [CrossRef]
- Jairath, L.; Hayes, J.; Cue, R. Correlations between First Lactation and Lifetime Performance Traits of Canadian Holsteins. J. Dairy Sci. 1995, 78, 438–448. [Google Scholar] [CrossRef]
- Haworth, G.; Tranter, W.; Chuck, J.; Cheng, Z.; Wathes, D. Relationships between Age at First Calving and First Lactation Milk Yield, and Lifetime Productivity and Longevity in Dairy Cows. Vet. Rec. 2008, 162, 643–647. [Google Scholar] [CrossRef]
- Archbold, H.; Shalloo, L.; Kennedy, E.; Pierce, K.; Buckley, F. Influence of Age, Body Weight and Body Condition Score before Mating Start Date on the Pubertal Rate of Maiden Holstein–Friesian Heifers and Implications for Subsequent Cow Performance and Profitability. Animal 2012, 6, 1143–1151. [Google Scholar] [CrossRef]
- Handcock, R.C.; Lopez-Villalobos, N.; McNaughton, L.R.; Back, P.J.; Edwards, G.R.; Hickson, R.E. Positive Relationships between Body Weight of Dairy Heifers and Their First-Lactation and Accumulated Three-Parity Lactation Production. J. Dairy Sci. 2019, 102, 4577–4589. [Google Scholar] [CrossRef] [PubMed]
- Hayes, C.; McAloon, C.; Kelly, E.; Carty, C.; Ryan, E.; Mee, J.; O’Grady, L. The Effect of Dairy Heifer Pre-Breeding Growth Rate on First Lactation Milk Yield in Spring-Calving, Pasture-Based Herds. Animal 2021, 15, 100169. [Google Scholar] [CrossRef] [PubMed]
- Sauder, C.; Cardot, H.; Disenhaus, C.; Le Cozler, Y. Non-Parametric Approaches to the Impact of Holstein Heifer Growth from Birth to Insemination on Their Dairy Performance at Lactation One. J. Agric. Sci. 2013, 151, 578–589. [Google Scholar] [CrossRef]
- Handcock, R.C.; Jenkinson, C.M.C.; Laven, R.; McNaughton, L.R.; Lopez-Villalobos, N.; Back, P.J.; Hickson, R.E. Linear versus Seasonal Growth of Dairy Heifers Decreased Age at Puberty but Did Not Affect First Lactation Milk Production. N. Z. J. Agric. Res. 2021, 64, 83–100. [Google Scholar] [CrossRef]
- Roche, J.R.; Dennis, N.A.; Macdonald, K.A.; Phyn, C.V.C.; Amer, P.R.; White, R.R.; Drackley, J.K. Growth Targets and Rearing Strategies for Replacement Heifers in Pasture-Based Systems: A Review. Anim. Prod. Sci. 2015, 55, 902–915. [Google Scholar] [CrossRef]
- Brown, J.; Fitzhugh, H., Jr.; Cartwright, T. A Comparison of Nonlinear Models for Describing Weight-Age Relationships in Cattle. J. Anim. Sci. 1976, 42, 810–818. [Google Scholar] [CrossRef]
- Tolstov, G.P. Fourier Series; Courier Corporation: North Chelmsford, MA, USA, 2012; ISBN 978-0-486-14174-9. [Google Scholar]
- Berry, D.P.; Horan, B.; Dillon, P. Comparison of Growth Curves of Three Strains of Female Dairy Cattle. Anim. Sci. 2005, 80, 151–160. [Google Scholar] [CrossRef]
- Bos, H.J.M. Differentials, Higher-Order Differentials and the Derivative in the Leibnizian Calculus. Arch. Hist. Exact Sci. 1974, 14, 1–90. [Google Scholar] [CrossRef]
- Kochenderfer, M.J.; Wheeler, T.A.; Wray, K.H. Algorithms for Decision Making; MIT Press: Cambridge, MA, USA, 2022; ISBN 0-262-37023-9. [Google Scholar]
- Handcock, R.; Lopez-Villalobos, N.; McNaughton, L.; Edwards, G.; Hickson, R. Positive Relationship between Live Weight at First Calving and First Lactation Milk Production. In Proceedings of the World Congress on Genetics Applied to Livestock Production, Auckland, New Zealand, 11–16 February 2018; p. 126. [Google Scholar]
- Gocheva-Ilieva, S.; Yordanova, A.; Kulina, H. Predicting the 305-Day Milk Yield of Holstein-Friesian Cows Depending on the Conformation Traits and Farm Using Simplified Selective Ensembles. Mathematics 2022, 10, 1254. [Google Scholar] [CrossRef]
- LeDell, E.; Poirier, S. H2O Automl: Scalable Automatic Machine Learning. In Proceedings of the AutoML Workshop at ICML, San Diego, CA, USA, 12–18 July 2020; Volume 2020. [Google Scholar]
- Lemus, R.V.; Guevara-Escobar, A.; García, R.J.A.; Gaspar, S.D.; García, M.J.G.; Pacheco, R.D. Producción de Leche de Vacas En Pastoreo de Alfalfa (Medicago Sativa) En El Altiplano Mexicano. Rev. Mex. Cienc. Pecu. 2020, 11, 1–18. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Core Team: Vienna, Austria, 2013. [Google Scholar]
- Davison, A.C.; Hinkley, D.V.; Young, G.A. Recent Developments in Bootstrap Methodology. Stat. Sci. 2003, 18, 141–157. [Google Scholar] [CrossRef]
- Hall, P.; Gill, N.; Kurka, M.; Phan, W.; Bartz, A. Machine Learning Interpretability with H2O Driverless AI; Bartz, A., Ed.; H2O.ai Inc.: California, US, USA, 2019. [Google Scholar]
- McElreath, R. Statistical Rethinking: A Bayesian Course with Examples in R and STAN; CRC Press: Boca Raton, FL, USA, 2020; ISBN 978-0-429-63914-2. [Google Scholar]
- Chan, J.Y.-L.; Leow, S.M.H.; Bea, K.T.; Cheng, W.K.; Phoong, S.W.; Hong, Z.-W.; Chen, Y.-L. Mitigating the Multicollinearity Problem and Its Machine Learning Approach: A Review. Mathematics 2022, 10, 1283. [Google Scholar] [CrossRef]
- Mitchell, R.; Frank, E. Accelerating the XGBoost Algorithm Using GPU Computing. PeerJ Comput. Sci. 2017, 3, e127. [Google Scholar] [CrossRef]
- Rudin, C. Stop Explaining Black Box Machine Learning Models for High Stakes Decisions and Use Interpretable Models Instead. Nat. Mach. Intell. 2019, 1, 206–215. [Google Scholar] [CrossRef] [PubMed]
- Fryer, D.; Strümke, I.; Nguyen, H. Shapley Values for Feature Selection: The Good, the Bad, and the Axioms. IEEE Access 2021, 9, 144352–144360. [Google Scholar] [CrossRef]
- Baptista, M.L.; Goebel, K.; Henriques, E.M. Relation between Prognostics Predictor Evaluation Metrics and Local Interpretability SHAP Values. Artif. Intell. 2022, 306, 103667. [Google Scholar] [CrossRef]
- Zanton, G.; Heinrichs, A. Meta-Analysis to Assess Effect of Prepubertal Average Daily Gain of Holstein Heifers on First-Lactation Production. J. Dairy Sci. 2005, 88, 3860–3867. [Google Scholar] [CrossRef] [PubMed]
- Gelsinger, S.; Heinrichs, A.; Jones, C. A Meta-Analysis of the Effects of Preweaned Calf Nutrition and Growth on First-Lactation Performance. J. Dairy Sci. 2016, 99, 6206–6214. [Google Scholar] [CrossRef] [PubMed]
- Aquilani, C.; Confessore, A.; Bozzi, R.; Sirtori, F.; Pugliese, C. Precision Livestock Farming Technologies in Pasture-Based Livestock Systems. Animal 2022, 16, 100429. [Google Scholar] [CrossRef]
- Arnott, G.; Ferris, C.; O’connell, N. Welfare of Dairy Cows in Continuously Housed and Pasture-Based Production Systems. Animal 2017, 11, 261–273. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).