Estimation of Oral Exposure of Dairy Cows to the Mycotoxin Deoxynivalenol (DON) through Toxin Residues in Blood and Other Physiological Matrices with a Special Focus on Sampling Size for Future Predictions
Abstract
1. Introduction
2. Materials and Methods
2.1. Description of Data
2.1.1. Data for the Derivation of Prediction Equations and Internal Validation
2.1.2. Data for External Validation
2.2. Calculations and Statistics
2.2.1. Calculations
2.2.2. Statistics
Development of Prediction Equations
Internal and External Validation of Prediction Equations for DON Residues in Blood
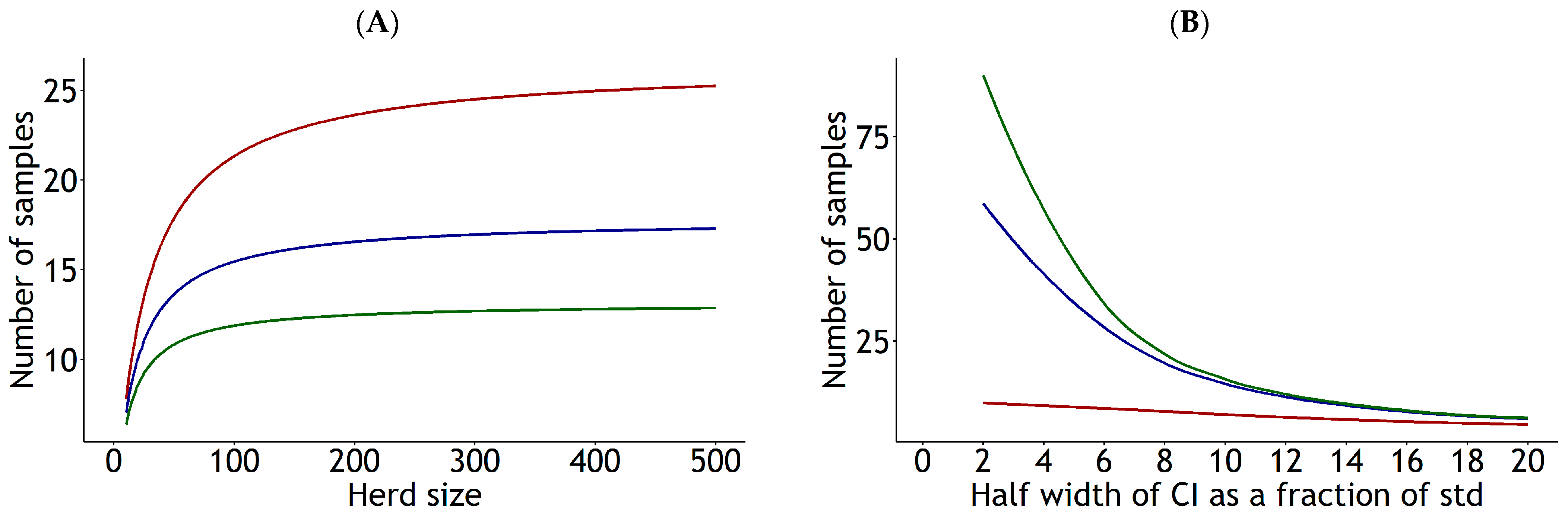
Estimation of Sample Size for Future Predictions
3. Results
3.1. Prediction Equations
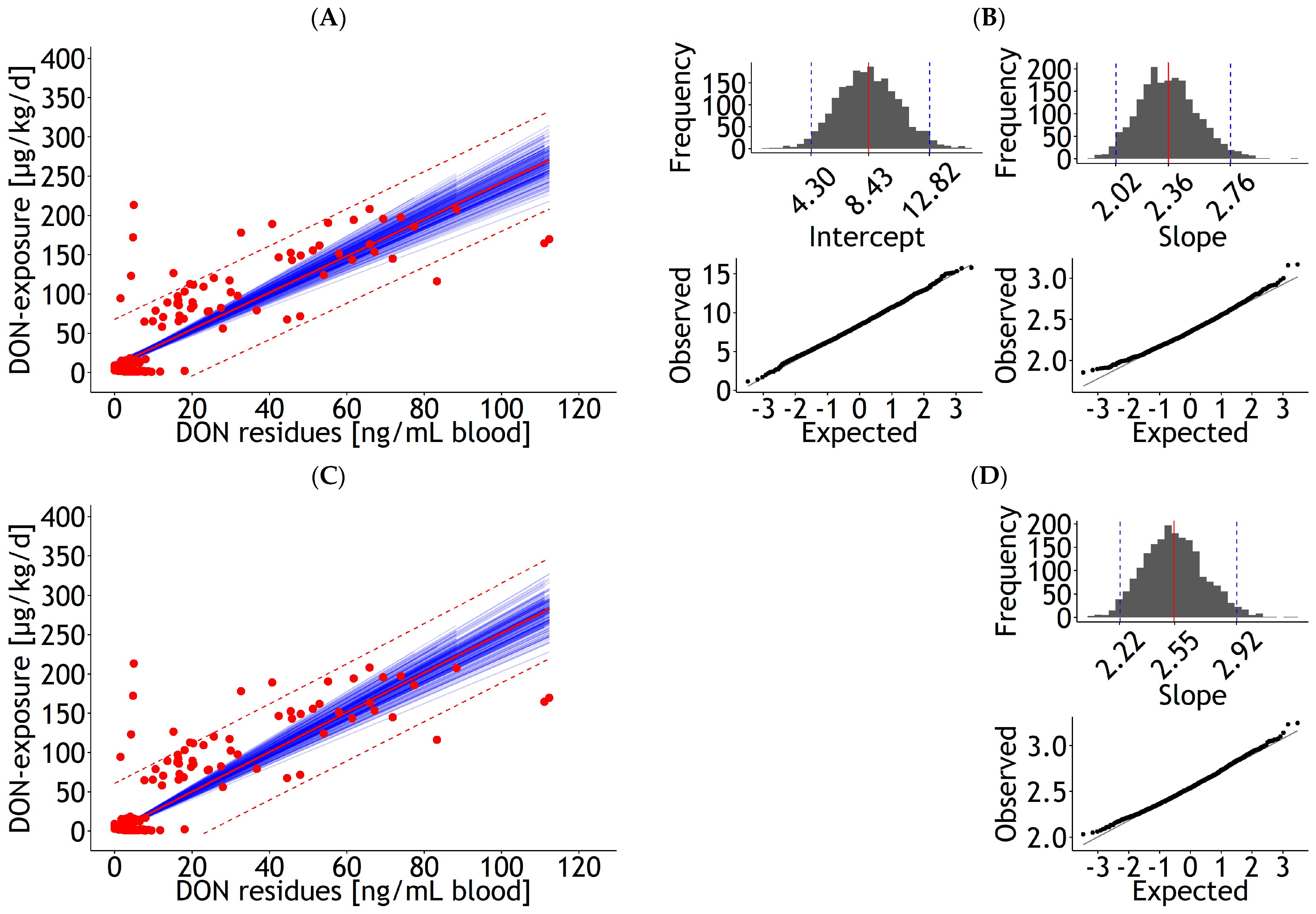
3.1.1. Blood
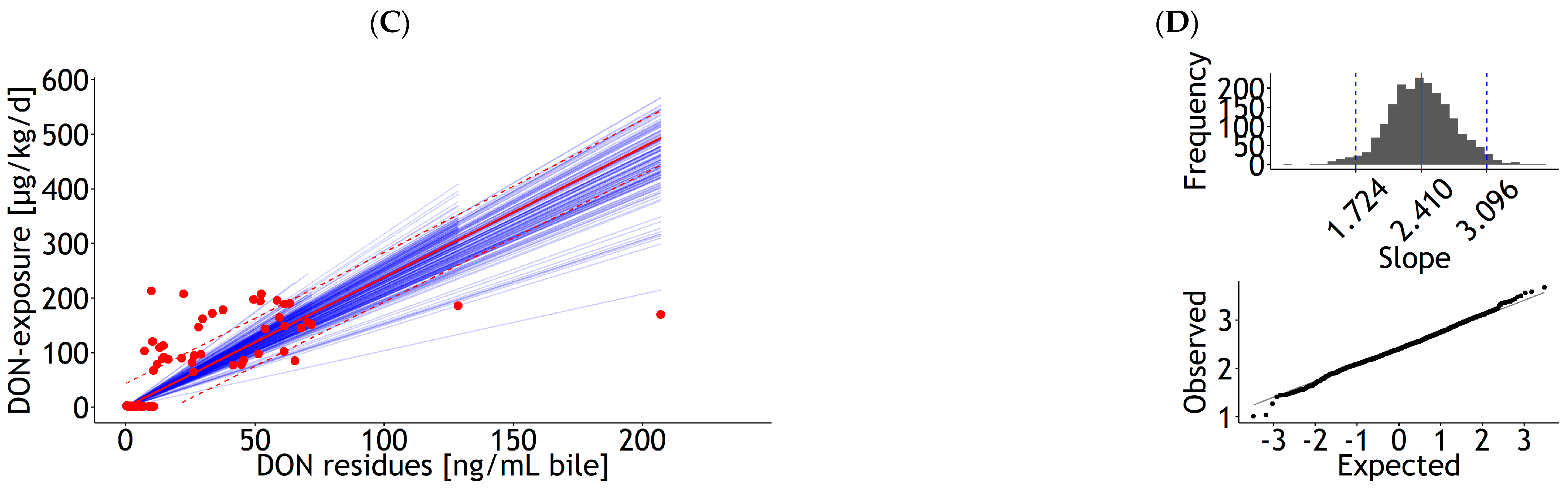
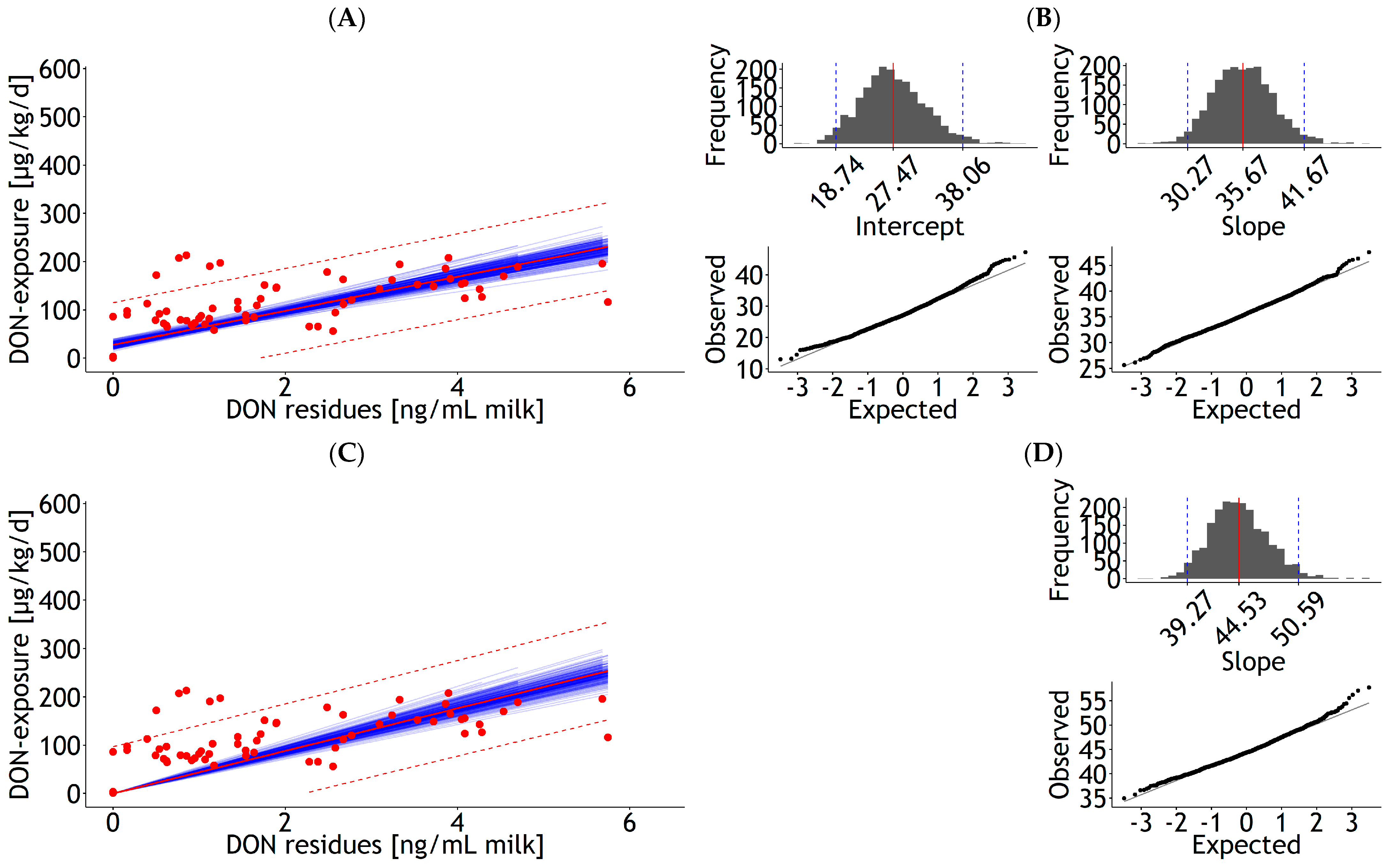
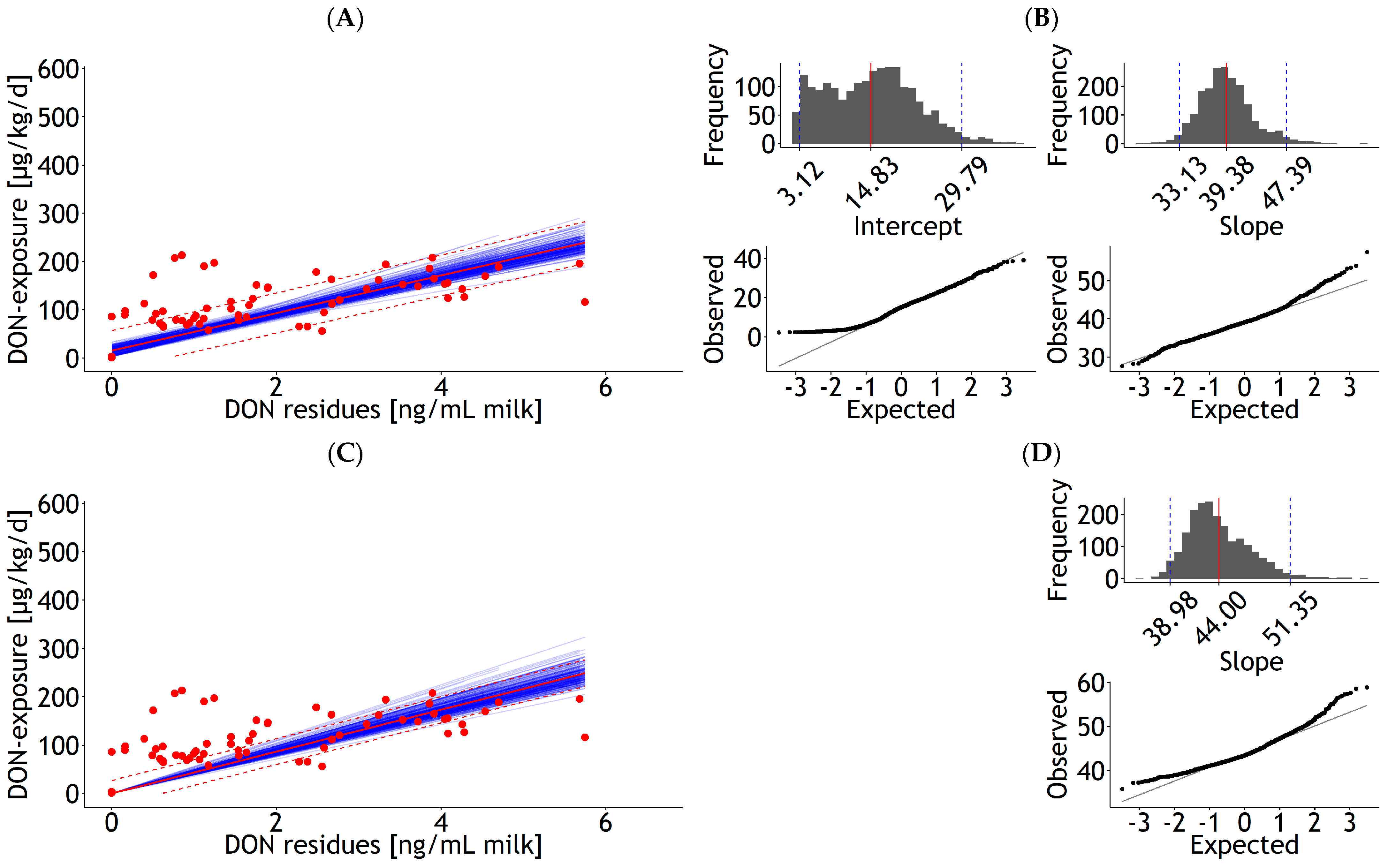
3.1.2. Urine, Bile, and Milk
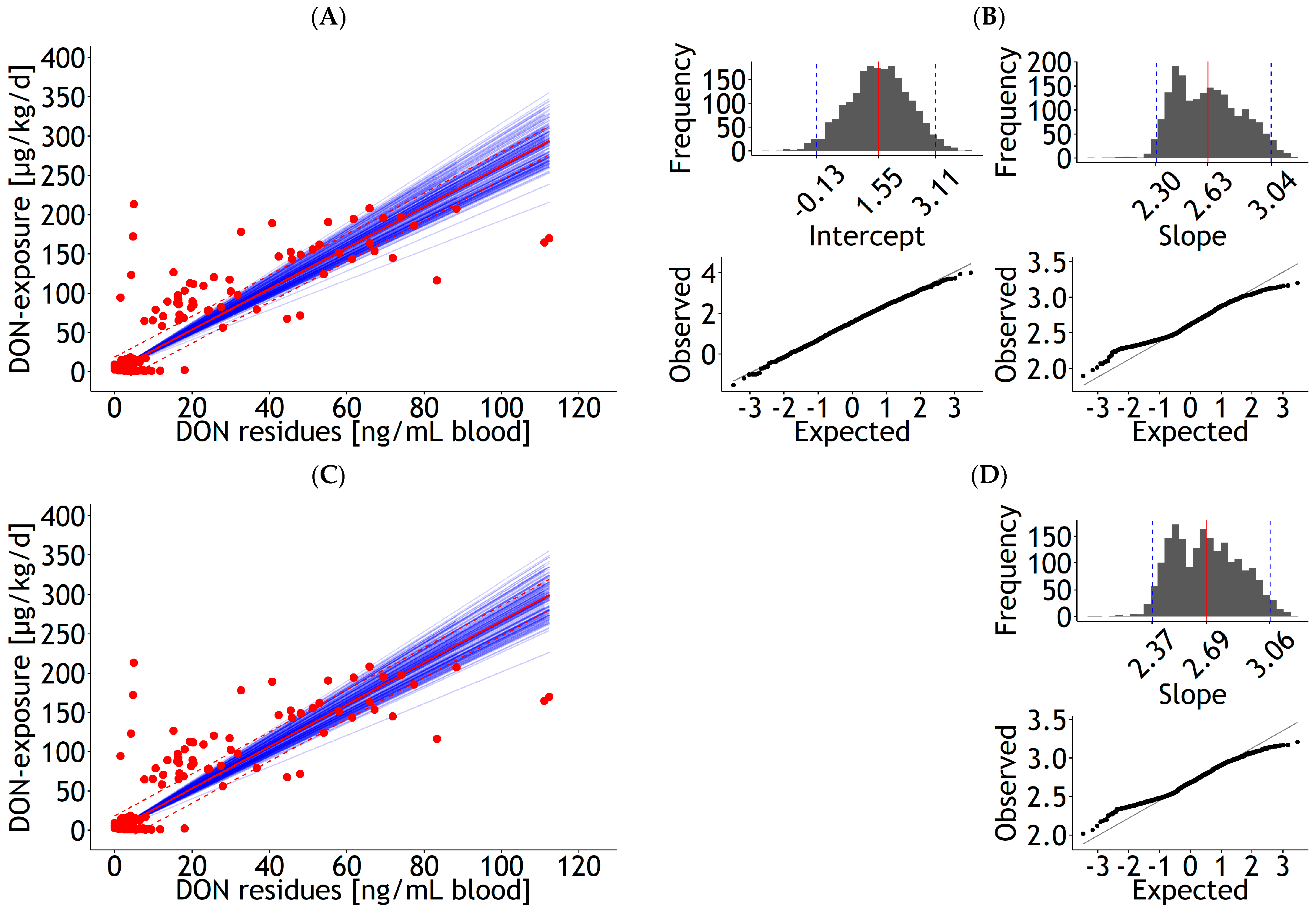
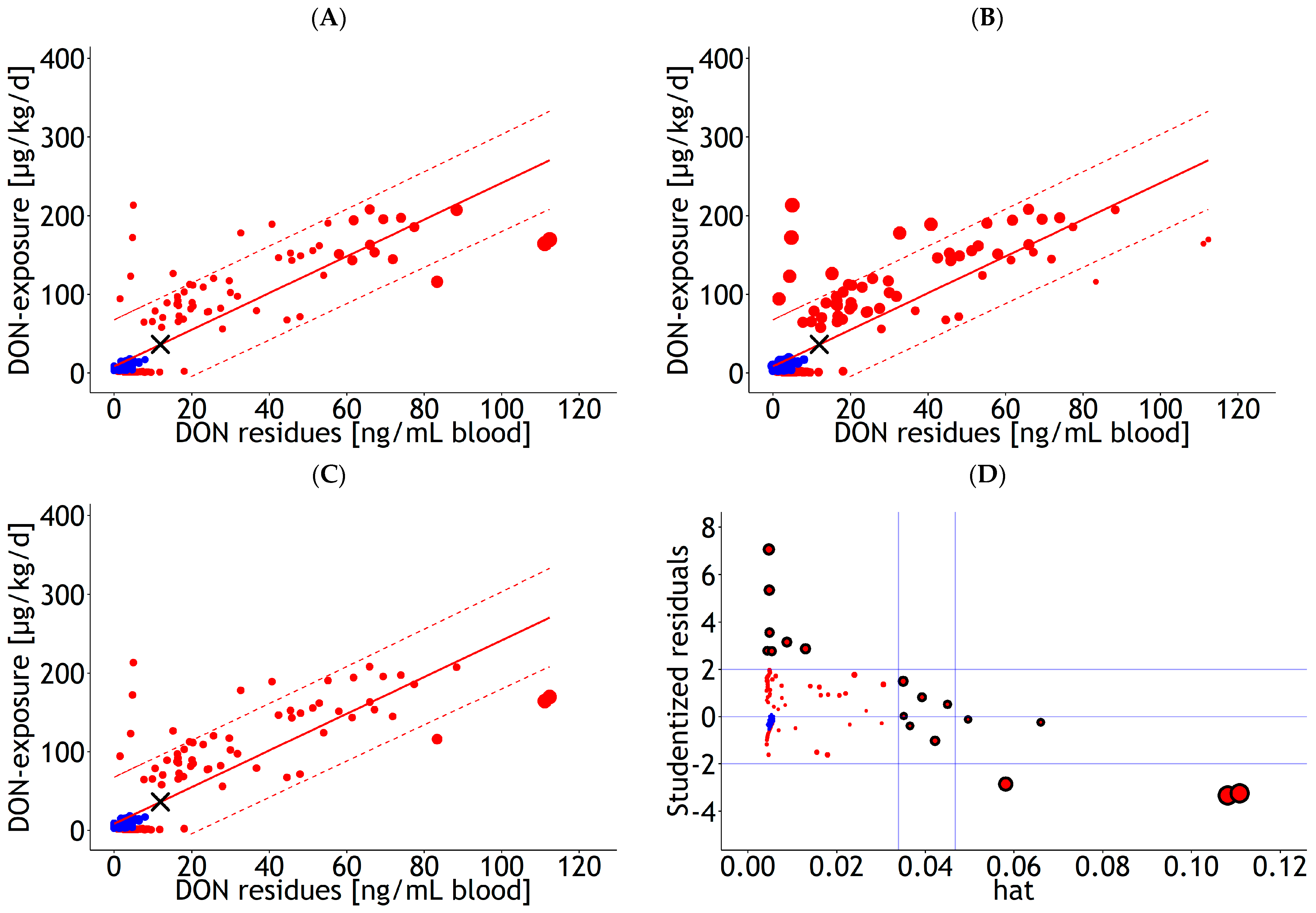
3.2. Influential Statistics
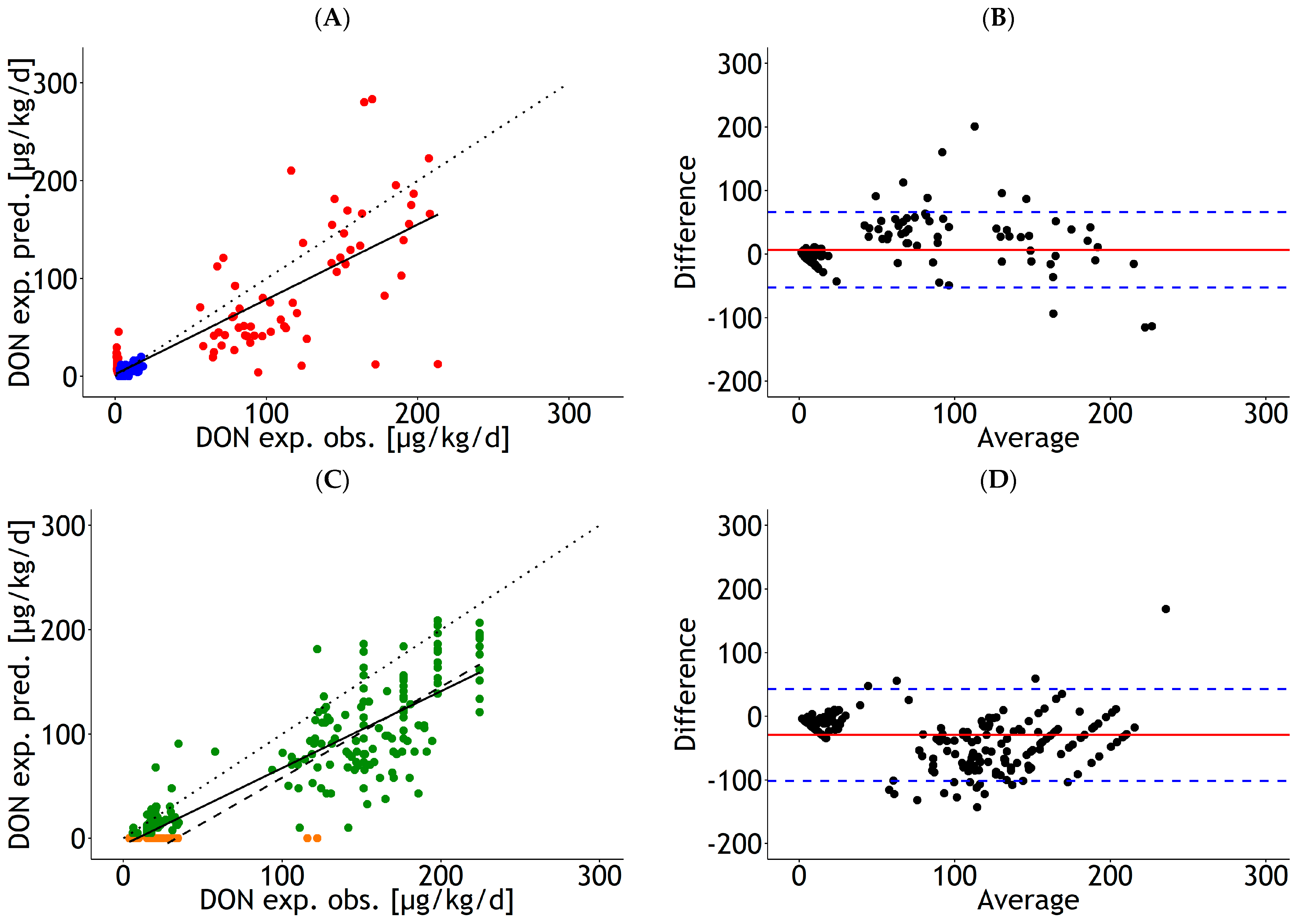
3.3. Internal and External Validation of Prediction Equations for DON Residues in Blood
3.4. Estimation of Sampling Size for Future Predictions
4. Discussion
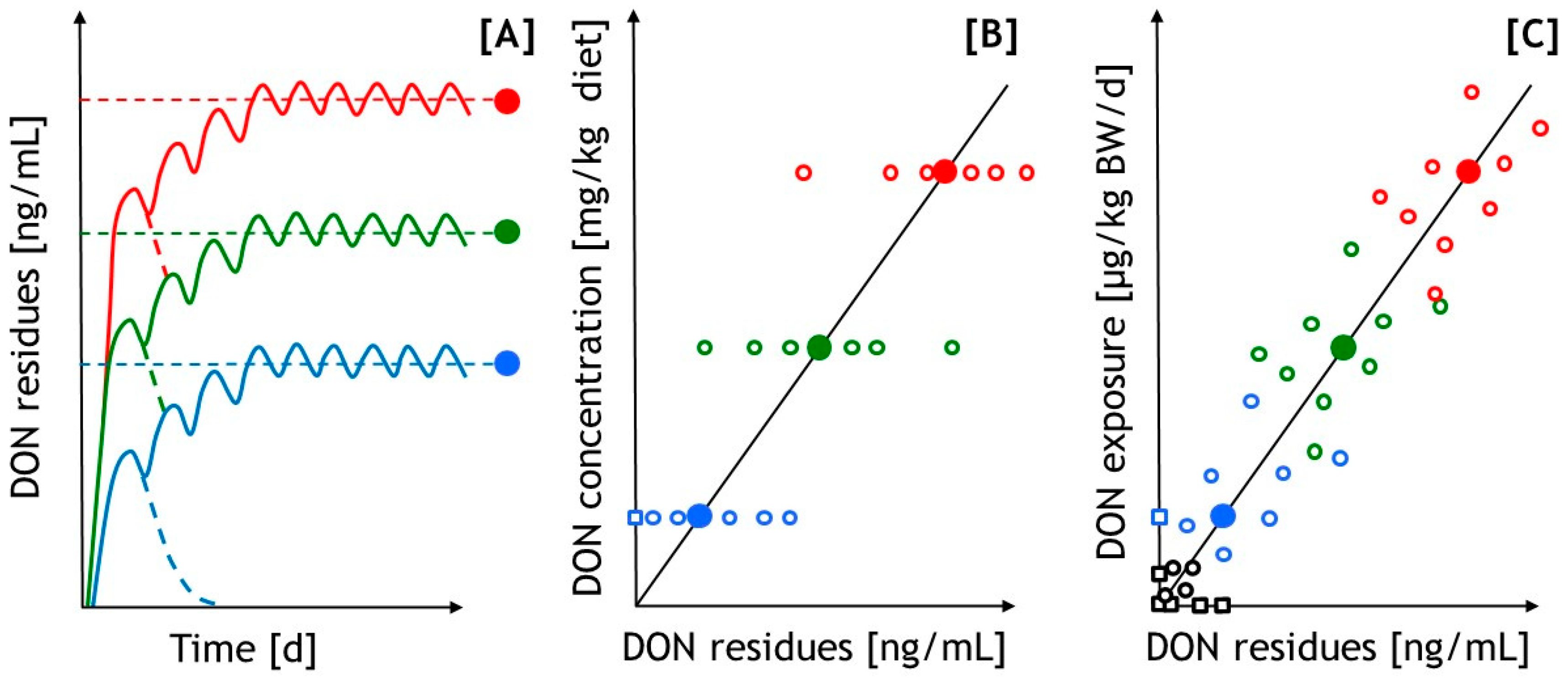
4.1. Toxicokinetic Aspects of DON as a Basis for Regressive Evaluation of the Data for Diagnostic Purposes
4.2. Handling of Influential Observations and Fitting Methods
4.3. Comparative Aspects on Suitability of Various Matrices as Predictors
4.4. Internal and External Validation of Prediction Equations for DON Residues in Blood
4.5. Recommendations for Appropriate Sampling Sizes for Future Predictions
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A



| Experiment | Matrix | Toxin | LOD (ng/mL) | LOQ (ng/mL) | Sample Clean-Up | Detection Method | Reference |
|---|---|---|---|---|---|---|---|
| 1 | Feed | DON | 0.03 mg/kg | IAC | HPLC-DAD | [48] | |
| Blood plasma | DON | 0.19 | 0.65 | SPE | HPLC-MS/MS | [11] | |
| DOM-1 | 0.09 | 0.31 | SPE | HPLC-MS/MS | |||
| Urine | DON | 0.25 | 0.80 | SPE | HPLC-MS/MS | [13] | |
| DOM-1 | 0.25 | 0.85 | SPE | HPLC-MS/MS | |||
| Milk | DON | 0.31 | 1.03 | SPE | HPLC-MS/MS | [14] | |
| DOM-1 | 0.17 | 0.58 | SPE | HPLC-MS/MS | |||
| Bile | DON | 0.16 | 0.53 | IAC | HPLC-MS/MS | [12] | |
| DOM-1 | 0.04 | 0.13 | IAC | HPLC-MS/MS | |||
| 2 | Feed | DON | 0.03 mg/kg | IAC | HPLC-DAD | [48] | |
| Blood plasma | DON | 0.22 | 0.72 | SPE | HPLC-MS/MS | [34] | |
| DOM-1 | 0.16 | 0.55 | SPE | HPLC-MS/MS | |||
| 3 | Feed | DON | 0.03 mg/kg | IAC | HPLC-DAD | [48] | |
| Blood serum | DON | 2.0 | IAC | HPLC-UVD | [16] | ||
| DOM-1 | 2.0 | IAC | HPLC-UVD |
| fr_SD | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | 1 |
| hw_CI | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 |
| N | ||||||||||
| 25 | 24 | 20 | 17 | 14 | 11 | 9 | 8 | 7 | 6 | 6 |
| 50 | 45 | 34 | 24 | 18 | 14 | 11 | 9 | 8 | 7 | 6 |
| 75 | 63 | 43 | 29 | 20 | 15 | 12 | 9 | 8 | 7 | 6 |
| 100 | 80 | 50 | 32 | 21 | 15 | 12 | 10 | 8 | 7 | 6 |
| 125 | 95 | 56 | 34 | 22 | 16 | 12 | 10 | 8 | 7 | 6 |
| 150 | 109 | 60 | 35 | 23 | 16 | 12 | 10 | 8 | 7 | 6 |
| 175 | 121 | 64 | 36 | 23 | 16 | 12 | 10 | 8 | 7 | 6 |
| 200 | 132 | 67 | 37 | 24 | 17 | 12 | 10 | 8 | 7 | 6 |
| 225 | 143 | 69 | 38 | 24 | 17 | 13 | 10 | 8 | 7 | 6 |
| 250 | 152 | 71 | 39 | 24 | 17 | 13 | 10 | 8 | 7 | 6 |
| 275 | 161 | 73 | 39 | 24 | 17 | 13 | 10 | 8 | 7 | 6 |
| 300 | 170 | 75 | 40 | 25 | 17 | 13 | 10 | 8 | 7 | 6 |
| 325 | 177 | 76 | 40 | 25 | 17 | 13 | 10 | 8 | 7 | 6 |
| 350 | 184 | 77 | 40 | 25 | 17 | 13 | 10 | 8 | 7 | 6 |
| 375 | 191 | 78 | 41 | 25 | 17 | 13 | 10 | 8 | 7 | 6 |
| 400 | 197 | 79 | 41 | 25 | 17 | 13 | 10 | 8 | 7 | 6 |
| 425 | 203 | 80 | 41 | 25 | 17 | 13 | 10 | 8 | 7 | 6 |
| 450 | 209 | 81 | 41 | 25 | 17 | 13 | 10 | 8 | 7 | 6 |
| 475 | 214 | 82 | 41 | 25 | 17 | 13 | 10 | 8 | 7 | 6 |
| 500 | 219 | 83 | 42 | 25 | 17 | 13 | 10 | 8 | 7 | 6 |
| 625 | 239 | 85 | 42 | 25 | 17 | 13 | 10 | 8 | 7 | 6 |
| 750 | 256 | 87 | 43 | 26 | 17 | 13 | 10 | 8 | 7 | 6 |
| 875 | 269 | 89 | 43 | 26 | 18 | 13 | 10 | 8 | 7 | 6 |
| 1000 | 279 | 90 | 43 | 26 | 18 | 13 | 10 | 8 | 7 | 6 |
References
- Gallo, A.; Mosconi, M.; Trevisi, E.; Santos, R.R. Adverse Effects of Fusarium Toxins in Ruminants: A Review of In Vivo and In Vitro Studies. Dairy 2022, 3, 474–499. [Google Scholar] [CrossRef]
- Zhao, L.; Zhang, L.; Xu, Z.; Liu, X.; Chen, L.; Dai, J.; Karrow, N.A.; Sun, L. Occurrence of Aflatoxin B1, deoxynivalenol and zearalenone in feeds in China during 2018-2020. J. Anim. Sci. Biotechnol. 2021, 12, 74. [Google Scholar] [CrossRef] [PubMed]
- Valenti, I.; Tini, F.; Sevarika, M.; Agazzi, A.; Beccari, G.; Bellezza, I.; Ederli, L.; Grottelli, S.; Pasquali, M.; Romani, R.; et al. Impact of Enniatin and Deoxynivalenol Co-Occurrence on Plant, Microbial, Insect, Animal and Human Systems: Current Knowledge and Future Perspectives. Toxins 2023, 15, 271. [Google Scholar] [CrossRef]
- Tolosa, J.; Rodríguez-Carrasco, Y.; Ruiz, M.J.; Vila-Donat, P. Multi-mycotoxin occurrence in feed, metabolism and carry-over to animal-derived food products: A review. Food Chem. Toxicol. 2021, 158, 112661. [Google Scholar] [CrossRef]
- Ogunade, I.M.; Martinez-Tuppia, C.; Queiroz, O.C.M.; Jiang, Y.; Drouin, P.; Wu, F.; Vyas, D.; Adesogan, A.T. Silage review: Mycotoxins in silage: Occurrence, effects, prevention, and mitigation. J. Dairy Sci. 2018, 101, 4034–4059. [Google Scholar] [CrossRef] [PubMed]
- Khatibi, P.A.; McMaster, N.J.; Musser, R.; Schmale, D.G. Survey of mycotoxins in corn distillers’ dried grains with solubles from seventy-eight ethanol plants in twelve States in the U.S. in 2011. Toxins 2014, 6, 1155–1168. [Google Scholar] [CrossRef] [PubMed]
- Dänicke, S.; Brezina, U. Invited Review: Kinetics and metabolism of the Fusarium toxin deoxynivalenol in farm animals: Consequences for diagnosis of exposure and intoxication and carry over. Food Chem. Toxicol. 2013, 60, 58–75. [Google Scholar] [CrossRef]
- Seeling, K.; Dänicke, S.; Ueberschär, K.H.; Lebzien, P.; Flachowsky, G. On the effects of Fusarium toxin-contaminated wheat and the feed intake level on the metabolism and carry over of zearalenone in dairy cows. Food Addit. Contam. 2005, 22, 847–855. [Google Scholar] [CrossRef]
- European Commission. Commission recommendation of 17 August 2006 on the presence of deoxynivalenol, zearalenone, ochratoxin A, T-2 and HT-2 and fumonisins in products intended for animal feeding. Off. J. Eur. Union 2006, 229, 7–9. [Google Scholar]
- Dänicke, S.; Winkler, J. Invited review: Diagnosis of zearalenone (ZEN) exposure of farm animals and transfer of its residues into edible tissues (carry over). Food Chem. Toxicol. 2015, 84, 225–249. [Google Scholar] [CrossRef]
- Winkler, J.; Kersten, S.; Meyer, U.; Engelhardt, U.; Dänicke, S. Residues of zearalenone (ZEN), deoxynivalenol (DON) and their metabolites in plasma of dairy cows fed Fusarium contaminated maize and their relationships to performance parameters. Food Chem. Toxicol. 2014, 65, 196–204. [Google Scholar] [CrossRef] [PubMed]
- Winkler, J.; Kersten, S.; Meyer, U.; Stinshoff, H.; Locher, L.; Rehage, J.; Wrenzycki, C.; Engelhardt, U.; Dänicke, S. Diagnostic opportunities for evaluation of the exposure of dairy cows to the mycotoxins deoxynivalenol (DON) and zearalenone (ZEN): Reliability of blood plasma, bile and follicular fluid as indicators. J. Anim. Physiol. Nutr. 2014, 99, 847–855. [Google Scholar] [CrossRef] [PubMed]
- Winkler, J.; Kersten, S.; Valenta, H.; Hüther, L.; Meyer, U.; Engelhardt, U.; Dänicke, S. Simultaneous determination of zearalenone, deoxynivalenol and their metabolites in bovine urine as biomarker of exposure. World Mycotoxin. J. 2015, 8, 63–74. [Google Scholar] [CrossRef]
- Winkler, J.; Kersten, S.; Valenta, H.; Meyer, U.; Engelhardt, G.; Dänicke, S. Development of a multi-toxin method for investigating the carry-over of zearalenone, deoxynivalenol and their metabolites into milk of dairy cows. Food Addit. Contam. 2015, 32, 371–380. [Google Scholar]
- Dänicke, S.; Krenz, J.; Seyboldt, C.; Neubauer, H.; Frahm, J.; Kersten, S.; Meyer, K.; Saltzmann, J.; Richardt, W.; Breves, G.; et al. Maize and Grass Silage Feeding to Dairy Cows Combined with Different Concentrate Feed Proportions with a Special Focus on Mycotoxins, Shiga Toxin (stx)-Forming Escherichia coli and Clostridium botulinum Neurotoxin (BoNT) Genes: Implications for Animal Health and Food Safety. Dairy 2020, 1, 91–126. [Google Scholar]
- Keese, C.; Meyer, U.; Valenta, H.; Schollenberger, M.; Starke, A.; Weber, I.A.; Rehage, J.; Breves, G.; Dänicke, S. No carry over of unmetabolised deoxynivalenol in milk of dairy cows fed high concentrate proportions. Mol. Nutr. Food Res. 2008, 52, 1514–1529. [Google Scholar] [CrossRef] [PubMed]
- R Core Team. R: A Language and Environment for Statistical Computing. 2021. Available online: https://www.R-project.org/ (accessed on 16 January 2023).
- Hadley Wickham. ggplot2: Elegant Graphics for Data Analysis; Springer: New York, NY, USA, 2016; ISBN 978-3-319-24277-4. [Google Scholar]
- Venables, W.N.; Ripley, B.D. Modern Applied Statistics with S, 4th ed.; Springer: New York, NY, USA, 2002. [Google Scholar]
- Efron, B. Bootstrap Methods: Another Look at the Jackknife. Ann. Statist. 1979, 7, 569–593. [Google Scholar] [CrossRef]
- Wright, D.B.; London, K.; Field, A.P. Using bootstrap estimation and the plug-in principle for clinical psychology data. J. Exp. Psychopathol. 2011, 2, 252–270. [Google Scholar] [CrossRef]
- Williamson, J.M.; Crawford, S.B.; Lin, H.-M. Resampling dependent concordance correlation coefficients. J. Biopharm. Stat. 2007, 17, 685–696. [Google Scholar] [CrossRef]
- Silge, J.; Chow, F.; Kuhn, M.; Wickham, H. rsample: General Resampling Infrastructure. 2021. Available online: https://CRAN.R-project.org/package=rsample (accessed on 16 January 2023).
- Zeileis, A.; Hothorn, T. Diagnostic Checking in Regression Relationships. R News 2002, 2, 7–10. [Google Scholar]
- Robinson, D.; Hayes, A. Simon Couch. Broom: Convert Statistical Objects into Tidy Tibbles. 2021. Available online: https://CRAN.R-project.org/package=broom (accessed on 16 January 2023).
- Kleiber, F.; Zeileis, A. Applied Econometrics with R; Springer: New York, NY, USA, 2008. [Google Scholar]
- Signorell, A.; Aho, K.; Alfons, A.; Anderegg, N.; Aragon, T.; Arppe, A.; Baddeley, A.; Barton, K.; Bolker, B.; Borchers, H.W. DescTools: Tools for Descriptive Statistics. 2022. Available online: https://cran.r-project.org/package=DescTools (accessed on 16 January 2023).
- Bland, J.M.; Altman, D.G. Statistical methods for assessing agreement between two methods of clinical measurement. Lancet 1986, 1, 307–310. [Google Scholar] [CrossRef] [PubMed]
- Rasch, D.; Herrendörfer, G.; Bock, J.; Busch, K. Verfahrensbibliothek Versuchsplanung und -Auswertung. Dtsch. Landwirtsch. Berl. 1978–1981, 1595 pp. Available online: https://library.wur.nl/WebQuery/wurpubs/65901 (accessed on 16 January 2023).
- Chatterjee, S.; Yilmaz, M. A Review of Regression Diagnostics for Behavioral Research. Appl. Psychol. Meas. 1992, 16, 209–227. [Google Scholar] [CrossRef]
- Riviere, J.E. Comparative Pharmacokinetics: Principles, Techniques, and Applications, 1st ed.; Iowa State Univ. Press/AMES: Ames, IA, USA, 1999. [Google Scholar]
- Ammer, S.; Lambertz, C.; von Soosten, D.; Zimmer, K.; Meyer, U.; Dänicke, S.; Gauly, M. Impact of diet composition and temperature-humidity index on water and dry matter intake of high-yielding dairy cows. J. Anim. Physiol. Anim. Nutr. 2018, 102, 103–113. [Google Scholar] [CrossRef] [PubMed]
- Lohölter, M.; Meyer, U.; Döll, S.; Manderscheid, R.; Weigel, H.J.; Erbs, M.; Höltershinken, M.; Flachowsky, G.; Dänicke, S. Effects of the thermal environment on metabolism of deoxynivalenol and thermoregulatory response of sheep fed on corn silage grown at enriched atmospheric carbon dioxide and drought. Mykotoxin Res. 2012, 28, 219–227. [Google Scholar] [CrossRef]
- Winkler, J.; Gödde, J.; Meyer, U.; Frahm, J.; Westendarp, H.; Dänicke, S. Fusarium toxin-contaminated maize in diets of growing bulls: Effects on performance, slaughtering characteristics, and transfer into physiological liquids. Mycotoxin Res. 2016, 32, 127–135. [Google Scholar] [CrossRef] [PubMed]
- Everitt, B. The Cambridge Dictionary of Statistics; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Faraway, J.J. Practical Regression and Anova Using R; University of Michigan: Ann Arbor, MI, USA, 2002. [Google Scholar]
- Romano, E.; Giraldo, R.; Mateu, J.; Diana, A. High leverage detection in general functional regression models with spatially correlated errors. Appl. Stoch. Model. Bus. Ind. 2022, 38, 169–181. [Google Scholar] [CrossRef]
- Arnold, J.B. Outliers and Robust Regression. Available online: https://uw-pols503.github.io/2016/outliers_robust_regression.html (accessed on 16 January 2023).
- Prelusky, D.B.; Trenholm, H.L.; Lawrence, G.A.; Scott, P.M. Nontransmission of Deoxynivalenol (Vomitoxin) to Milk Following Oral-Administration to Dairy-Cows. J. Environ. Sci. Health Part B 1984, 19, 593–609. [Google Scholar] [CrossRef]
- Horwitz, W.; Kamps, L.R.; Boyer, K.W. Quality assurance in the analysis of foods for trace constituents. J. Assoc. Off. Anal. Chem. 1980, 63, 1344–1354. [Google Scholar] [CrossRef]
- Maronna, R.A.; Martin, R.D.; Yohai, V.J. Robust Statistics: Theory and Methods; Wiley Series in Probability and Statistics: Chichester, Hoboken, USA, 2019. [Google Scholar] [CrossRef]
- Kwiecien, R.; Kopp-Schneider, A.; Blettner, M. Concordance analysis: Part 16 of a series on evaluation of scientific publications. Dtsch. Arztebl. Int. 2011, 108, 515–521. [Google Scholar] [CrossRef]
- Lin, L. A concordance correlation coefficient to evaluate reproducibility. Biometrics 1989, 45, 255. [Google Scholar] [CrossRef]
- Hilgers, R.-D.; Heussen, N.; Stanzel, S. Konkordanz-Korrelationskoeffizient nach Lin. In Lexikon der Medizinischen Laboratoriumsdiagnostik; Gressner, A.M., Arndt, T., Eds.; Springer: Berlin/Heidelberg, Germany, 2018; p. 1. ISBN 978-3-662-49054-9. [Google Scholar]
- Tobin, J. Estimation of Relationships for Limited Dependent Variables. Econometrica 1958, 26, 24. [Google Scholar] [CrossRef]
- Akoglu, H. User’s guide to correlation coefficients. Turk. J. Emerg. Med. 2018, 18, 91–93. [Google Scholar] [CrossRef] [PubMed]
- Altman, D.G. Practical Statistics for Medical Research, 1st ed.; Chapman & Hall/CRC: Boca Raton, FL, USA; London, UK; New York, NY, USA; Washington DC, USA, 1991; ISBN 0-412-27630-5. [Google Scholar]
- Oldenburg, E.; Bramm, A.; Valenta, H. Influence of nitrogen fertilization on deoxynivalenol contamination of winter wheat-experimental field trials and evaluation of analytical methods. Mycotoxin Res. 2007, 23, 7–12. [Google Scholar] [CrossRef] [PubMed]
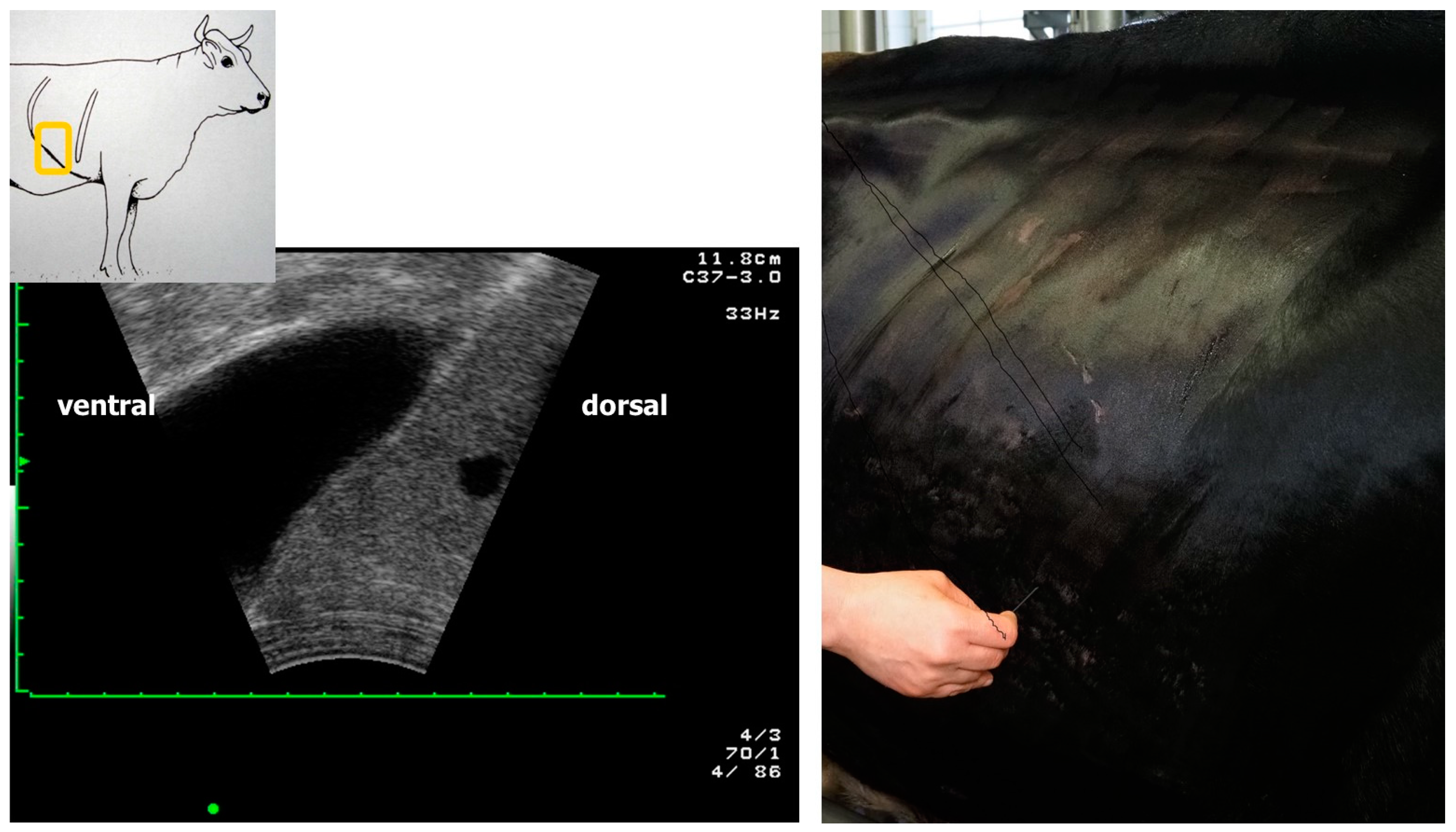
| DON (mg/kg Diet, 88% DM) | N | Mean | Standard Deviation | Median | Minimum | Maximum | |
|---|---|---|---|---|---|---|---|
| Experiment 1 | |||||||
| DON exposure (µg/kg BW/d) | 0.06–4.61 | 116 | 64.3 | 69.0 | 61.5 | 0.8 | 213.3 |
| 0.06 | 56 | 1.7 | 0.6 | 1.6 | 0.8 | 3.0 | |
| 2.31 | 30 | 83.5 | 16.3 | 82.0 | 56.2 | 120.2 | |
| 4.61 | 30 | 161.7 | 29.5 | 158.8 | 111.8 | 213.3 | |
| DON residue levels (ng/mL) | |||||||
| Blood plasma | 0.06–4.61 | 116 | 21.7 | 25.2 | 9.5 | 1.0 | 112.3 |
| 0.06 | 56 | 4.8 | 3.0 | 4.5 | 1.0 | 18.0 | |
| 2.31 | 30 | 20.9 | 10.1 | 18.8 | 2.5 | 48.0 | |
| 4.61 | 30 | 53.9 | 27.6 | 54.6 | 4.8 | 112.3 | |
| Urine | 0.06–4.61 | 99 | 1914.3 | 2839.6 | 609.5 | 39.9 | 13,555.0 |
| 0.06 | 44 | 184.7 | 147.3 | 121.0 | 39.9 | 664.5 | |
| 2.31 | 29 | 1772.5 | 1182.1 | 1690.0 | 422.7 | 5587.5 | |
| 4.61 | 26 | 4999.3 | 3849.6 | 4108.8 | 271.2 | 13,555.0 | |
| Bile | 0.06–4.61 | 85 | 22.5 | 32.2 | 9.1 | 0.3 | 207.0 |
| 0.06 | 45 | 3.2 | 2.9 | 2.5 | 0.3 | 11.0 | |
| 2.31 | 20 | 27.7 | 17.9 | 23.6 | 7.3 | 65.5 | |
| 4.61 | 20 | 61.0 | 42.3 | 56.3 | 9.9 | 207.0 | |
| Milk | 0.06–4.61 | 109 | 1.1 | 1.5 | 0.5 | 0 | 5.7 |
| 0.06 | 49 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | |
| 2.31 | 30 | 1.1 | 0.7 | 1.0 | 0.0 | 2.8 | |
| 4.61 | 30 | 3.0 | 1.4 | 3.3 | 0.5 | 5.7 | |
| Experiment 2 | |||||||
| DON exposure (µg/kg BW/d) | 0.14–0.2 | 121 | 9.8 | 4.5 | 10.1 | 2.8 | 18.4 |
| DON residue levels (ng/mL) | |||||||
| Blood plasma | 0.14–0.2 | 121 | 2.7 | 1.6 | 2.6 | 0.0 | 8.0 |
| Experiments 1 and 2 | |||||||
| DON exposure (µg/kg BW/d) | 0.06–4.61 | 237 | 36.5 | 55.5 | 10.6 | 0.8 | 213.3 |
| DON residue levels (ng/mL) | |||||||
| Blood plasma | 0.06–4.61 | 237 | 11.9 | 20.0 | 3.7 | 0.0 | 112.3 |
| Experiment 3 | |||||||
| DON exposure (µg/kg BW/d) | 0.35–4.66 | 267 | 88.2 | 75.4 | 34.8 | 3.8 | 224.5 |
| DON residue levels (ng/mL) | |||||||
| Blood serum | 0.35–4.66 | 267 | 23.3 | 25.2 | 12.0 | 0.0 | 127.0 |
| Speci-men | Me-thod | Experiment | y | a p-Value | SE | b p-Value | SE | Rainbow Test (p-Value) | RSE (µg/kg BW/d) | N | Exposure Threshold 1 (ng/mL) | Figure Equation |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Blood | lm | 1 | DON exposure | 17.36 | 5.157 | 2.17 | 0.156 | 0.012 | 42.1 | 116 | Figure A1A,B | |
| 0.001 | <0.001 | 1 | ||||||||||
| Blood | lm | 2 | DON exposure | 4.98 | 0.598 | 1.81 | 0.191 | 0.122 | 3.4 | 121 | Figure A1A,B | |
| <0.001 | <0.001 | 2 | ||||||||||
| Blood | lm | 1 | DON exposure | 2.52 | 0.123 | 0.039 | 44.0 | 116 | Figure A1C,D | |||
| <0.001 | 3 | |||||||||||
| Blood | lm | 2 | DON exposure | 3.17 | 0.125 | 0.043 | 4.3 | 121 | Figure A1C,D | |||
| <0.001 | 4 | |||||||||||
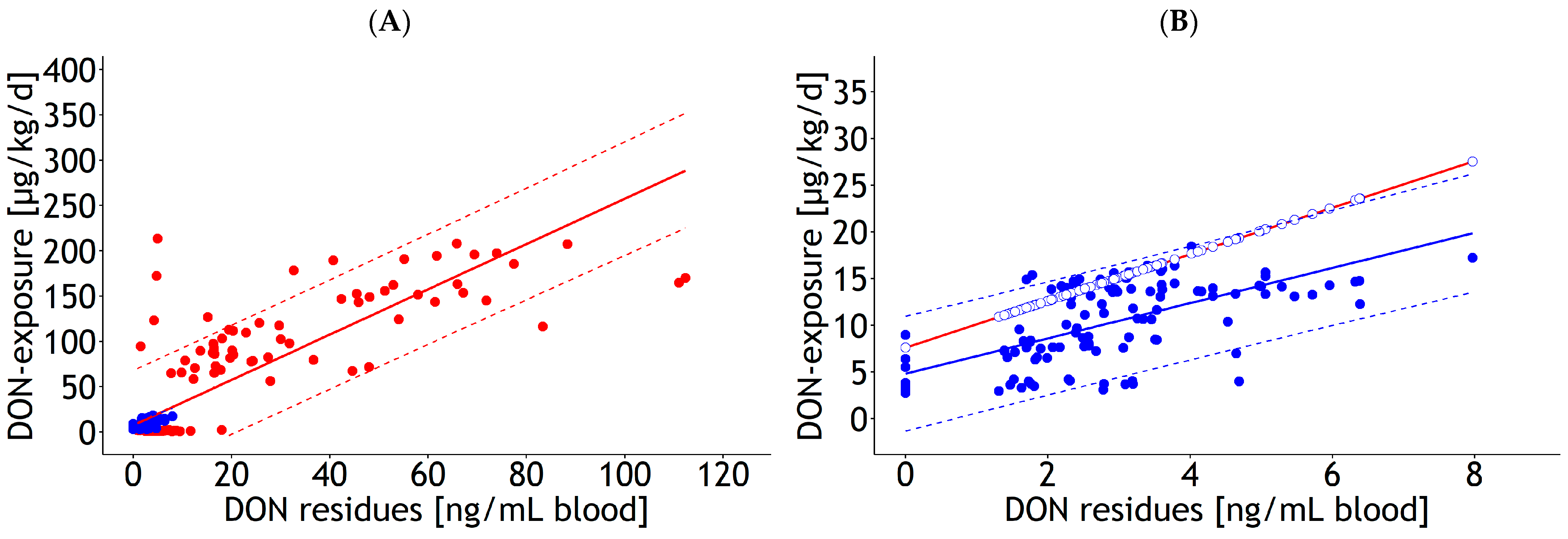
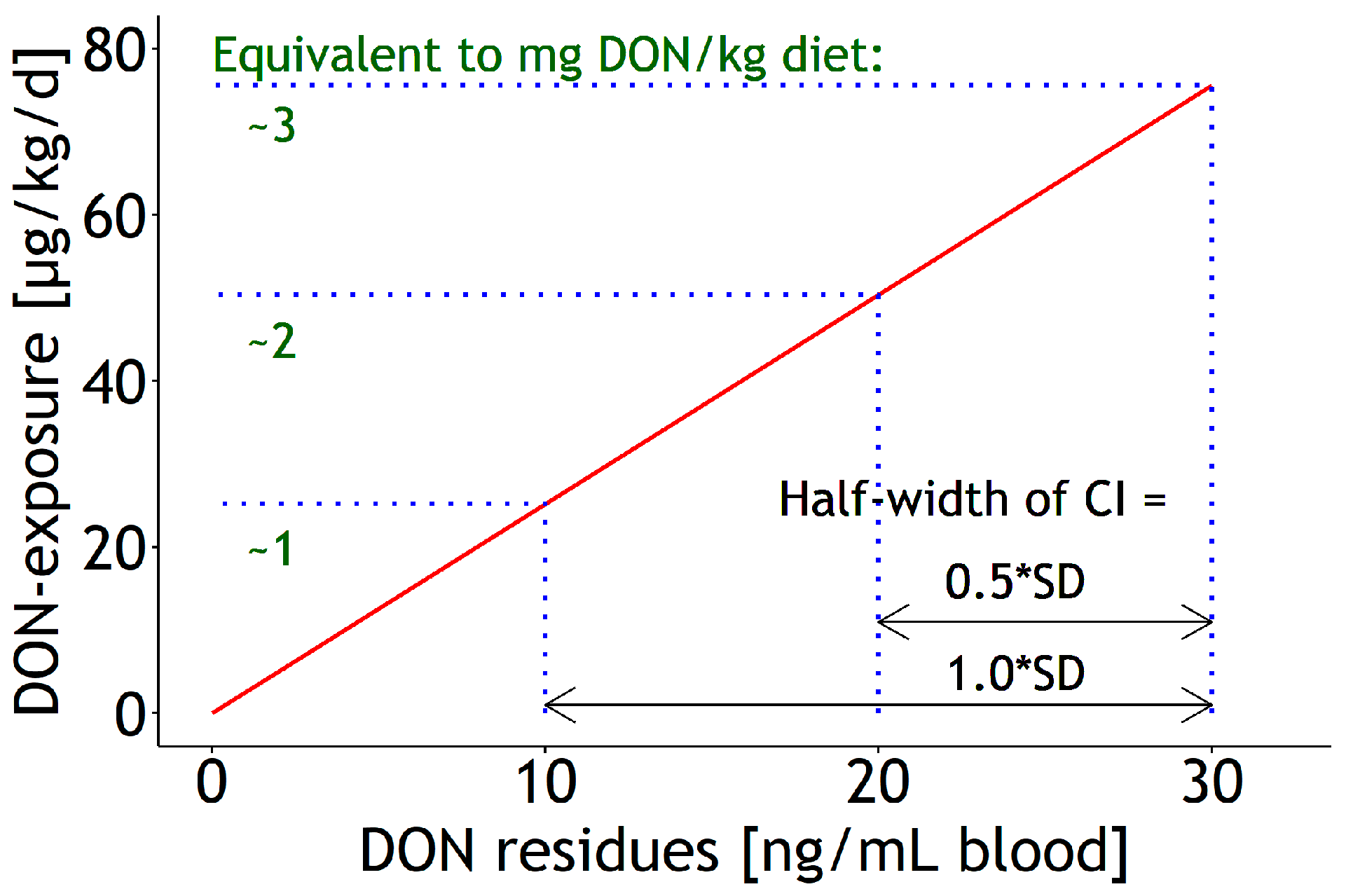
| Blood | lm | 1 and 2 | DON exposure | 8.68 | 2.272 | 2.33 | 0.098 | 1.000 | 30.0 | 137 | 21.8 | Figure 1A |
| <0.001 | <0.001 | 5 | ||||||||||
| Blood | lm | 1 and 2 | DON exposure | 2.52 | 0.086 | 1.000 | 30.9 | 137 | 24.3 | Figure 1C | ||
| <0.001 | 6 | |||||||||||
| Blood | rlm | 1 | DON exposure | 7.61 | 4.107 | 2.50 | 0.124 | 0.012 | 30.6 | 116 | Figure A2A,B | |
| 0.068 | <0.001 | 7 | ||||||||||
| Blood | rlm | 2 | DON exposure | 4.83 | 0.671 | 1.89 | 0.215 | 0.122 | 3.1 | 121 | Figure A2A,B | |
| <0.001 | <0.001 | 8 | ||||||||||
| Blood | rlm | 1 | DON exposure | 2.67 | 0.090 | 0.039 | 27.8 | 116 | Figure A2C,D | |||
| <0.001 | 9 | |||||||||||
| Blood | rlm | 2 | DON exposure | 3.20 | 0.131 | 0.043 | 4.6 | 121 | Figure A2C,D | |||
| <0.001 | 10 | |||||||||||
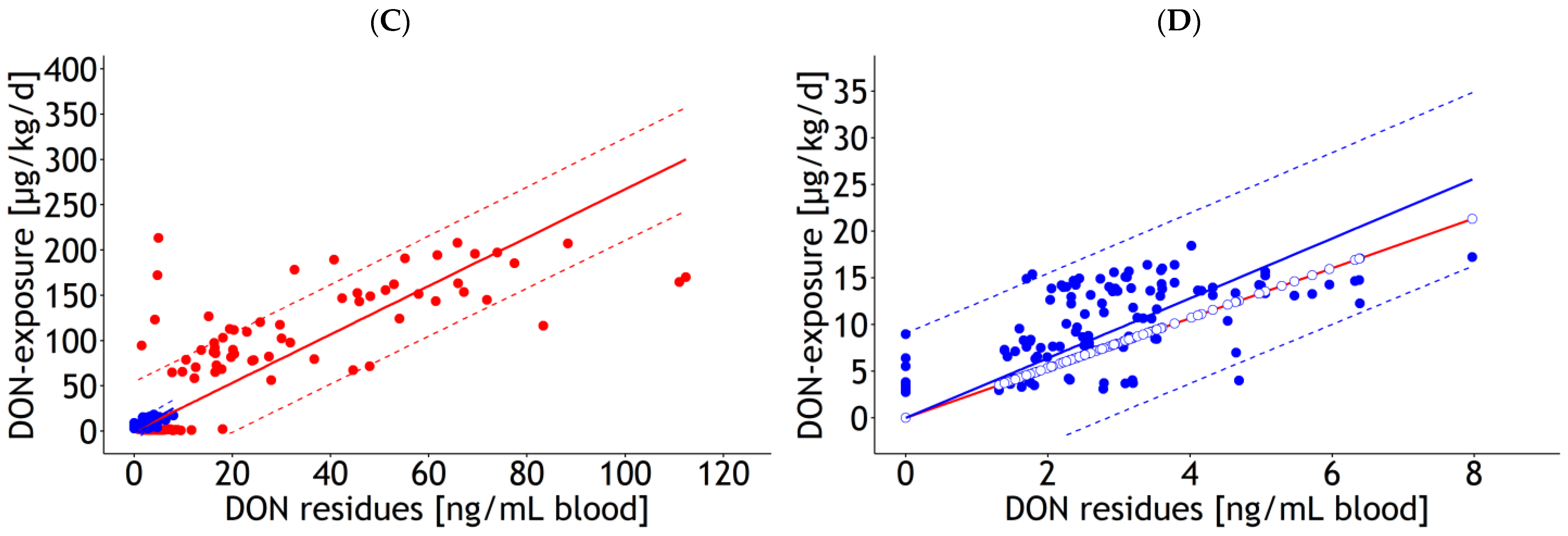
| Blood | rlm | 1 and 2 | DON exposure | 1.65 | 0.926 | 2.60 | 0.040 | 1.000 | 8.7 | 137 | 6.0 | Figure A3A |
| 0.066 | <0.001 | 11 | ||||||||||
| Blood | rlm | 1 and 2 | DON exposure | 2.67 | 0.034 | 1.000 | 9.4 | 137 | 6.9 | Figure A3C | ||
| <0.001 | 12 | |||||||||||
| Blood | lm | 1 | DON diet | 0.52 | 0.143 | 0.06 | 0.004 | <0.001 | 1.16 | 116 | Figure A4A,B | |
| <0.001 | <0.001 | 13 | ||||||||||
| Blood | lm | 2 | DON diet | 0.15 | 0.003 | 0.01 | 0.001 | 0.012 | 0.02 | 121 | Figure A4A,B | |
| <0.001 | <0.001 | 14 | ||||||||||
| Blood | lm | 1 | DON diet | 0.07 | 0.003 | <0.001 | 1.22 | 116 | Figure A4C,D | |||
| <0.001 | 15 | |||||||||||
| Blood | lm | 2 | DON diet | 0.05 | 0.002 | 0.176 | 0.08 | 121 | Figure A4C,D | |||
| <0.001 | 16 | |||||||||||
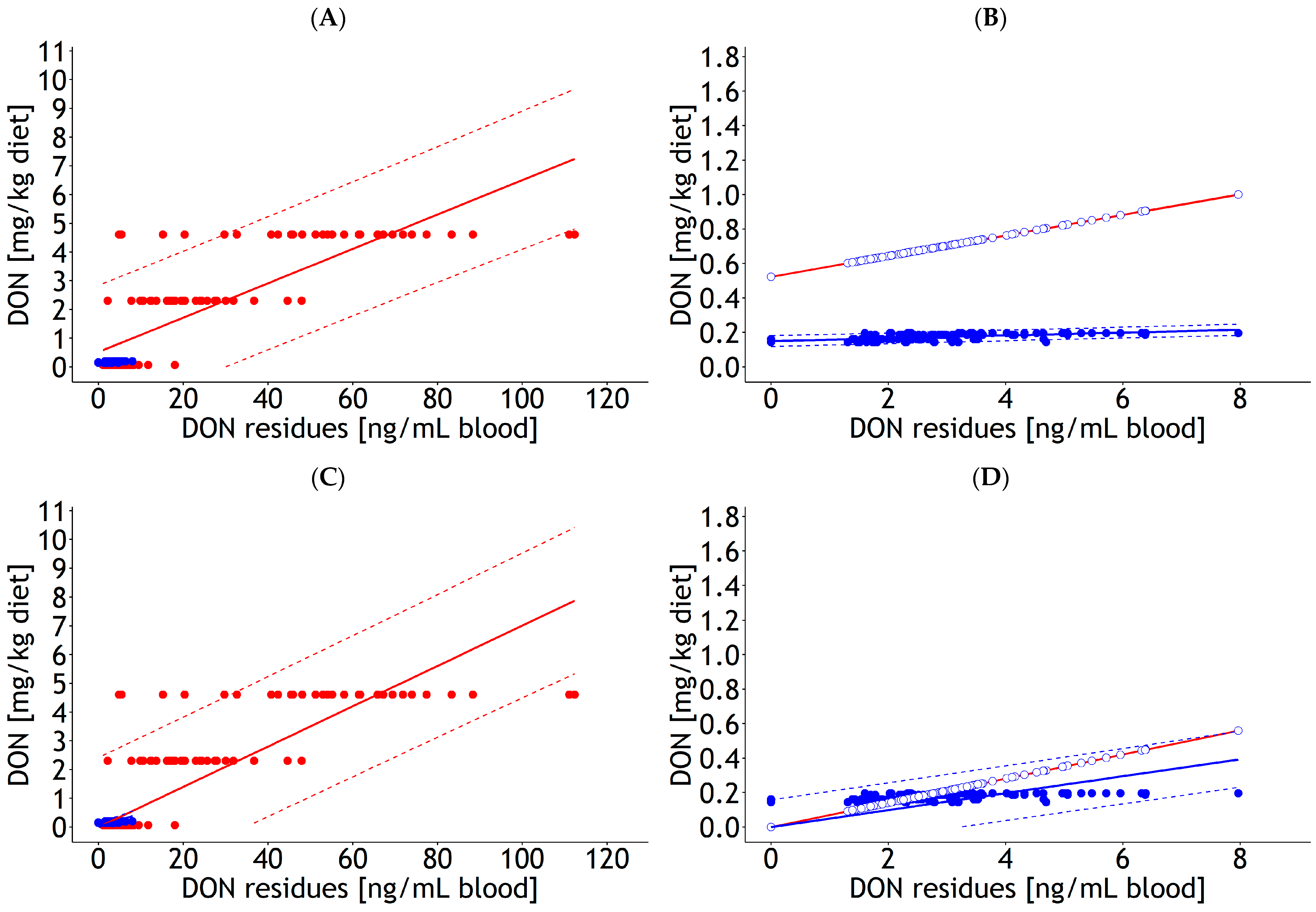
| Blood | lm | 1 and 2 | DON diet | 0.19 | 0.064 | 0.07 | 0.003 | 1.000 | 0.84 | 137 | 22.5 | Figure A5A |
| <0.001 | <0.001 | 17 | ||||||||||
| Blood | lm | 1 and 2 | DON diet | 0.07 | 0.002 | 1.000 | 0.86 | 137 | 24.3 | Figure A5C | ||
| <0.001 | 18 | |||||||||||
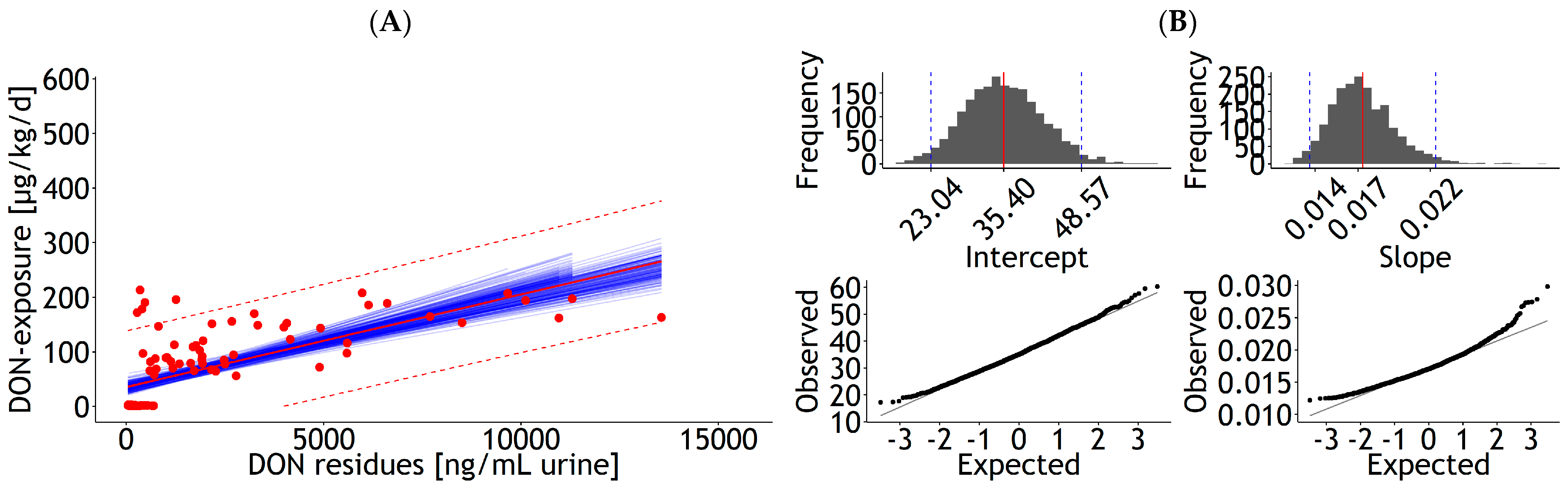
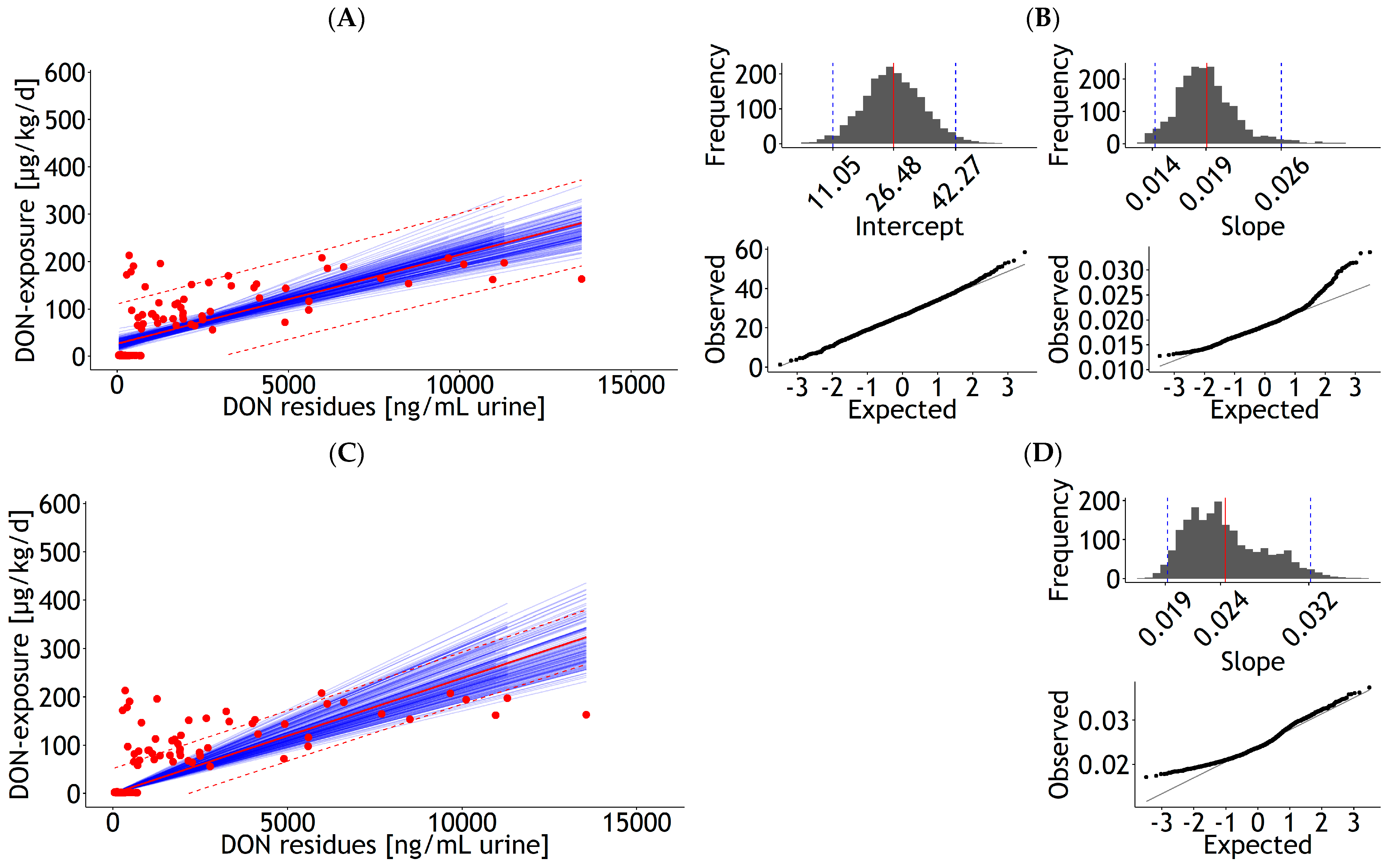
| Urine | lm | 1 | DON exposure | 35.67 | 6.249 | 0.017 | 0.002 | 0.937 | 51.5 | 99 | 4021 | Figure A6A |
| <0.001 | <0.001 | 19 | ||||||||||
| Urine | lm | 1 | DON exposure | 0.022 | 0.002 | 0.468 | 59.2 | 99 | 5237 | Figure A6C | ||
| <0.001 | 20 | |||||||||||
| Urine | rlm | 1 | DON exposure | 26.59 | 5.21 | 0.018 | 0.00 | 0.937 | 42.57 | 99 | 3083 | Figure A7A |
| <0.001 | <0.001 | 21 | ||||||||||
| Urine | rlm | 1 | DON exposure | 0.023 | 0.00 | 0.468 | 26.42 | 99 | 2179 | Figure A7C | ||
| 0.00 | 22 | |||||||||||
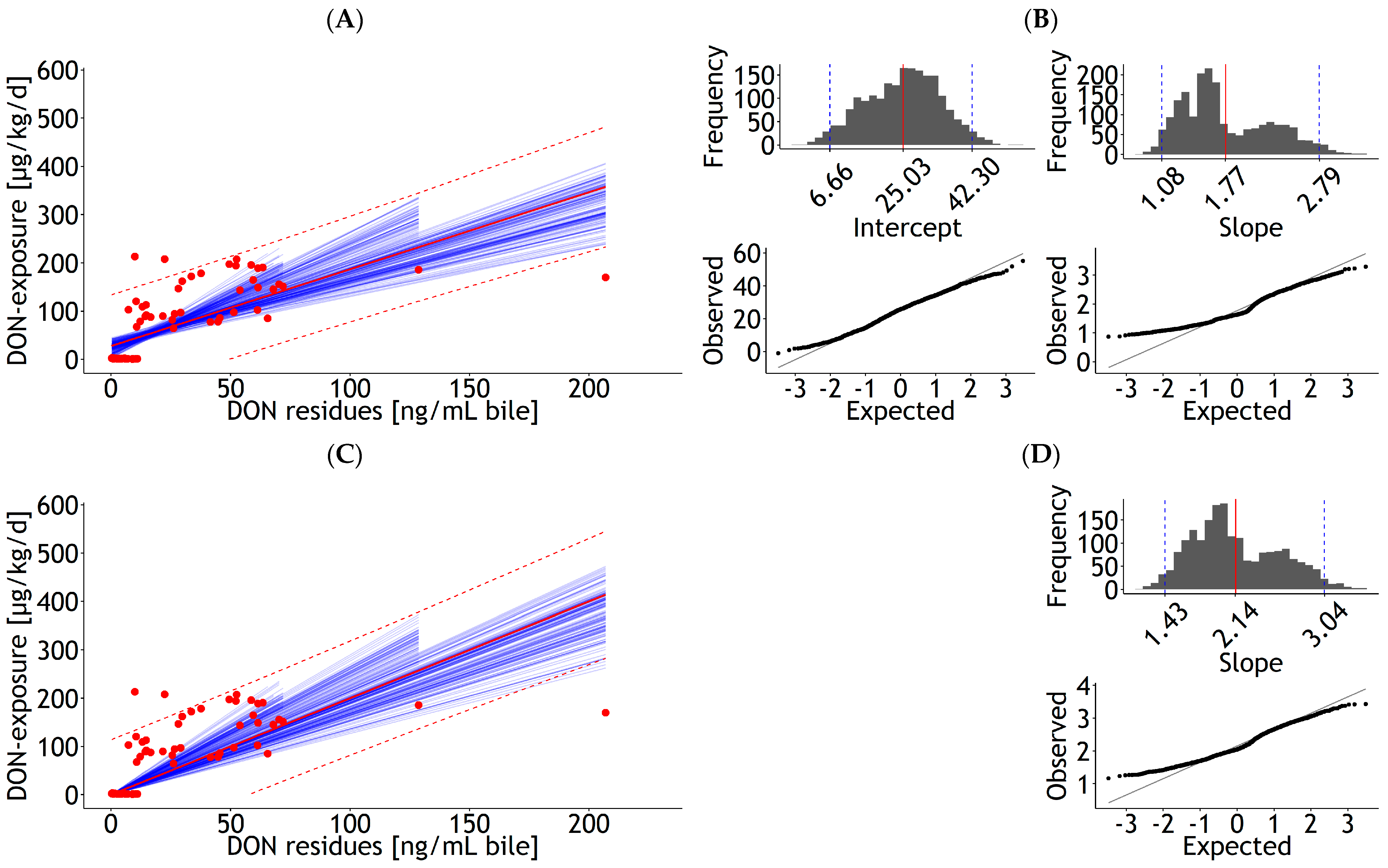
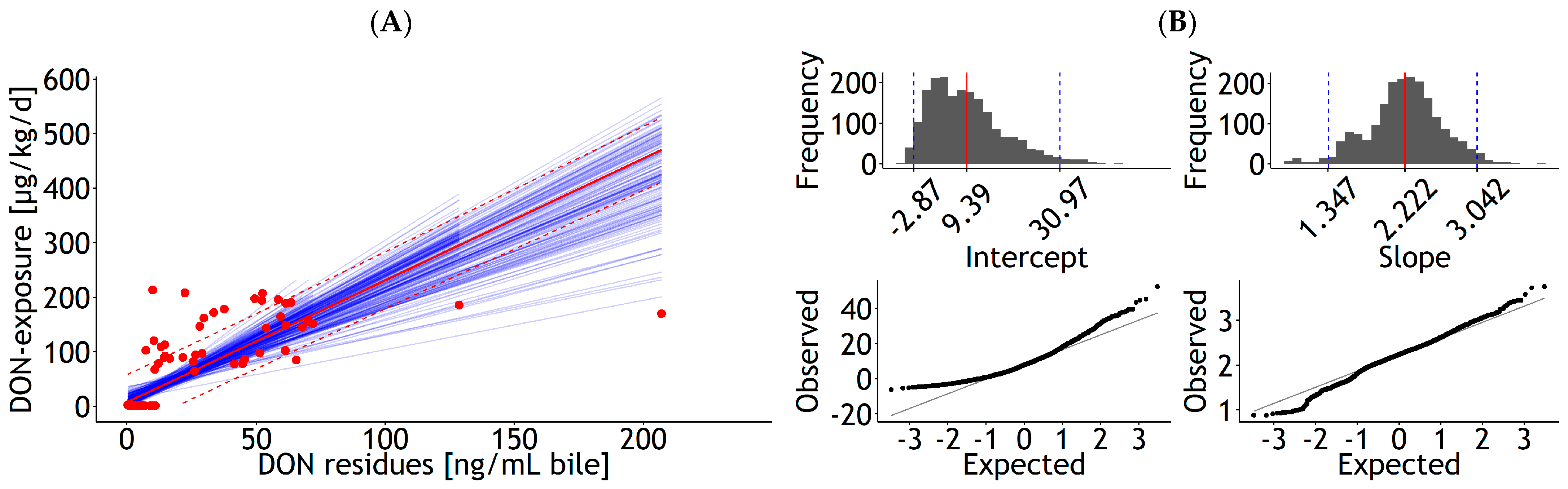
| Bile | lm | 1 | DON exposure | 27.71 | 7.00 | 1.59 | 0.18 | 0.026 | 52.82 | 85 | 50.1 | Figure A8A |
| <0.001 | <0.001 | 23 | ||||||||||
| Bile | lm | 1 | DON exposure | 2.00 | 0.16 | 0.003 | 57.24 | 85 | 58.2 | Figure A8C | ||
| 0.00 | 24 | |||||||||||
| Bile | rlm | 1 | DON exposure | 7.62 | 4.46 | 2.24 | 0.11 | 0.026 | 25.53 | 85 | 19.2 | Figure A9A |
| 0.098 | <0.001 | 25 | ||||||||||
| Bile | rlm | 1 | DON exposure | 2.38 | 0.08 | 0.003 | 22.16 | 85 | 18.3 | Figure A9C | ||
| 0.00 | 26 | |||||||||||
| Milk | lm | 1 | DON exposure | 27.46 | 5.30 | 35.40 | 2.79 | 0.576 | 43.99 | 109 | 1.7 | Figure A10A |
| <0.001 | <0.001 | 27 | ||||||||||
| Milk | lm | 1 | DON exposure | 44.17 | 2.47 | 0.300 | 48.97 | 109 | 2.2 | Figure A10C | ||
| 0.00 | 28 | |||||||||||
| Milk | rlm | 1 | DON exposure | 15.40 | 3.72 | 39.02 | 1.96 | 0.576 | 21.11 | 109 | 0.67 | Figure A11A |
| <0.001 | <0.001 | 29 | ||||||||||
| Milk | rlm | 1 | DON exposure | 43.39 | 1.16 | 0.300 | 13.57 | 109 | 0.61 | Figure A11C | ||
| <0.001 | 30 |
| Specimen | Urine | Blood | Bile | Milk |
|---|---|---|---|---|
| Expected DON residue levels | very high | low | low | very low |
| Specimen collection | non-invasive | minimally invasive | minimally invasive | non-invasive |
| Closeness to the inner (systemic) exposure | reasonable | good | poor | reasonable |
| Relationship to dietary exposure 1 | linear | linear | weakly linear | linear |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dänicke, S.; Kersten, S.; Billenkamp, F.; Spilke, J.; Starke, A.; Saltzmann, J. Estimation of Oral Exposure of Dairy Cows to the Mycotoxin Deoxynivalenol (DON) through Toxin Residues in Blood and Other Physiological Matrices with a Special Focus on Sampling Size for Future Predictions. Dairy 2023, 4, 360-391. https://doi.org/10.3390/dairy4020024
Dänicke S, Kersten S, Billenkamp F, Spilke J, Starke A, Saltzmann J. Estimation of Oral Exposure of Dairy Cows to the Mycotoxin Deoxynivalenol (DON) through Toxin Residues in Blood and Other Physiological Matrices with a Special Focus on Sampling Size for Future Predictions. Dairy. 2023; 4(2):360-391. https://doi.org/10.3390/dairy4020024
Chicago/Turabian StyleDänicke, Sven, Susanne Kersten, Fabian Billenkamp, Joachim Spilke, Alexander Starke, and Janine Saltzmann. 2023. "Estimation of Oral Exposure of Dairy Cows to the Mycotoxin Deoxynivalenol (DON) through Toxin Residues in Blood and Other Physiological Matrices with a Special Focus on Sampling Size for Future Predictions" Dairy 4, no. 2: 360-391. https://doi.org/10.3390/dairy4020024
APA StyleDänicke, S., Kersten, S., Billenkamp, F., Spilke, J., Starke, A., & Saltzmann, J. (2023). Estimation of Oral Exposure of Dairy Cows to the Mycotoxin Deoxynivalenol (DON) through Toxin Residues in Blood and Other Physiological Matrices with a Special Focus on Sampling Size for Future Predictions. Dairy, 4(2), 360-391. https://doi.org/10.3390/dairy4020024







