Tutorial on the Use of the regsem Package in R
Abstract
:1. Introduction
1.1. Regularized Regression
1.2. Regularized SEM
2. Implementation
3. Empirical Example
4. Extensions
4.1. Other Application Scenarios
4.1.1. Regression/Path Analysis Models
4.1.2. Factor Analysis Models
4.1.3. Longitudinal Models
4.1.4. Group-Based SEM
4.2. Problems of the Lasso Penalty and Its Remedies
4.3. Computational Methods
4.4. Missing Data
4.5. Categorical Predictors
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kline, R.B. Principles and Practice of Structural Equation Modeling, 4th ed.; Methodology in the Social Sciences; Guilford Press: New York, NY, USA, 2016; ISBN 978-1-4625-2300-9. [Google Scholar]
- Bentler, P.M.; Chou, C.-P. Practical Issues in Structural Modeling. Sociol. Methods Res. 1987, 16, 78–117. [Google Scholar] [CrossRef]
- Jacobucci, R.; Grimm, K.J.; McArdle, J.J. Regularized Structural Equation Modeling. Struct. Equ. Model. A Multidiscip. J. 2016, 23, 555–566. [Google Scholar] [CrossRef] [PubMed]
- Huang, P.-H.; Chen, H.; Weng, L.-J. A Penalized Likelihood Method for Structural Equation Modeling. Psychometrika 2017, 82, 329–354. [Google Scholar] [CrossRef] [PubMed]
- Hoerl, A.E.; Kennard, R.W. Ridge Regression: Biased Estimation for Nonorthogonal Problems. Technometrics 1970, 12, 55–67. [Google Scholar] [CrossRef]
- Tibshirani, R. Regression Shrinkage and Selection via the Lasso. J. R. Stat. Society. Ser. B Methodol. 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Zou, H.; Hastie, T. Regularization and variable selection via the elastic net. J. R. Stat. Soc. Ser. B Stat. Methodol. 2005, 67, 301–320. [Google Scholar] [CrossRef] [Green Version]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control. 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Schwarz, G. Estimating the Dimension of a Model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Hirose, K.; Yamamoto, M. Sparse estimation via nonconcave penalized likelihood in factor analysis model. Stat. Comput. 2014, 25, 863–875. [Google Scholar] [CrossRef] [Green Version]
- Yarkoni, T.; Westfall, J. Choosing Prediction over Explanation in Psychology: Lessons from Machine Learning. Perspect. Psychol. Sci. 2017, 12, 1100–1122. [Google Scholar] [CrossRef]
- Zhao, P.; Yu, B. On Model Selection Consistency of Lasso. J. Mach. Learn. Res. 2006, 7, 2541–2563. [Google Scholar]
- Zou, H. The Adaptive Lasso and Its Oracle Properties. J. Am. Stat. Assoc. 2006, 101, 1418–1429. [Google Scholar] [CrossRef] [Green Version]
- Fan, J.; Li, R. Variable Selection via Nonconcave Penalized Likelihood and its Oracle Properties. J. Am. Stat. Assoc. 2001, 96, 1348–1360. [Google Scholar] [CrossRef]
- Zhang, C.-H. Nearly unbiased variable selection under minimax concave penalty. Ann. Stat. 2010, 38, 894–942. [Google Scholar] [CrossRef] [Green Version]
- Kwon, K.; Kim, C. How to design personalization in a context of customer retention: Who personalizes what and to what extent? Electron. Commer. Res. Appl. 2012, 11, 101–116. [Google Scholar] [CrossRef]
- Jin, S.; Moustaki, I.; Yang-Wallentin, F. Approximated Penalized Maximum Likelihood for Exploratory Factor Analysis: An Orthogonal Case. Psychometrika 2018, 83, 628–649. [Google Scholar] [CrossRef]
- Jacobucci, R.; Brandmaier, A.M.; Kievit, R.A. A Practical Guide to Variable Selection in Structural Equation Modeling by Using Regularized Multiple-Indicators, Multiple-Causes Models. Adv. Methods Pract. Psychol. Sci. 2019, 2, 55–76. [Google Scholar] [CrossRef] [Green Version]
- Scharf, F.; Nestler, S. Should Regularization Replace Simple Structure Rotation in Exploratory Factor Analysis? Struct. Equ. Model. A Multidiscip. J. 2019, 26, 576–590. [Google Scholar] [CrossRef]
- Jacobucci, R.; Grimm, K.J.; Brandmaier, A.M.; Serang, S.; Kievit, R.A.; Scharf, F.; Li, X.; Ye, A. Regsem: Regularized Structural Equation Modeling. 2021. Available online: https://cran.r-project.org/web/packages/regsem/regsem.pdf (accessed on 29 September 2021).
- Rosseel, Y. lavaan: AnRPackage for Structural Equation Modeling. J. Stat. Softw. 2012, 48, 1–36. [Google Scholar] [CrossRef] [Green Version]
- Jacobucci, R. Regsem: Regularized Structural Equation Modeling. arXiv 2017, arXiv:1703.08489. [Google Scholar]
- McArdle, J.J.; McDonald, R.P. Some algebraic properties of the Reticular Action Model for moment structures. Br. J. Math. Stat. Psychol. 1984, 37, 234–251. [Google Scholar] [CrossRef]
- McArdle, J.J. The Development of the RAM Rules for Latent Variable Structural Equation Modeling. In Contemporary Psycho-Metrics: A Festschrift for Roderick P. McDonald; Multivariate Applications Book Series; Lawrence Erlbaum Associates Publishers: Mahwah, NJ, USA, 2005; pp. 225–273. ISBN 0-8058-4608-5. [Google Scholar]
- Kessler, R.C. National Comorbidity Survey: Baseline (NCS-1), 1990-1992; Inter-university Consortium for Political and Social Research: Ann Arbor, MI, USA, 2016. [Google Scholar] [CrossRef]
- Alegria, M.; Jackson, S.J.; Kessler, R.C.; Takeuchi, D. Collaborative Psychiatric Epidemiology Surveys (CPES), 2001–2003; Inter-university Consortium for Political and Social Research: Ann Arbor, MI, USA, 2016. [Google Scholar] [CrossRef]
- Jackson JSCaldwell, C.H.; Antonucci, T.C.; Oyserman, D.R. National Survey of American Life-Adolescent Supplement (NSAL-A); Inter-university Consortium for Political and Social Research: Ann Arbor, MI, USA, 2016. [Google Scholar] [CrossRef]
- Meinshausen, N. Relaxed Lasso. Comput. Stat. Data Anal. 2007, 52, 374–393. [Google Scholar] [CrossRef]
- Lüdtke, O.; Ulitzsch, E.; Robitzsch, A. A Comparison of Penalized Maximum Likelihood Estimation and Markov Chain Monte Carlo Techniques for Estimating Confirmatory Factor Analysis Models With Small Sample Sizes. Front. Psychol. 2021, 12, 5162. [Google Scholar] [CrossRef] [PubMed]
- Serang, S.; Jacobucci, R.; Brimhall, K.C.; Grimm, K.J. Exploratory Mediation Analysis via Regularization. Struct. Equ. Model. A Multidiscip. J. 2017, 24, 733–744. [Google Scholar] [CrossRef] [PubMed]
- Huang, P.-H. Penalized Least Squares for Structural Equation Modeling with Ordinal Responses. Multivar. Behav. Res. 2020, 13, 1–19. [Google Scholar] [CrossRef] [PubMed]
- Revelle, W. Psych: Procedures for Psychological, Psychometric, and Personality Research 2021. Psychol. Assess. 2021, 127, 294–304. [Google Scholar]
- Li, X.; Jacobucci, R. Regularized structural equation modeling with stability selection. Psychol. Methods 2021, 12, 28. [Google Scholar] [CrossRef]
- Jacobucci, R.; Grimm, K.J. Regularized Estimation of Multivariate Latent Change Score Models. Routledge 2018, 32, 109–125. [Google Scholar] [CrossRef]
- Ye, A.; Gates, K.M.; Henry, T.R.; Luo, L. Path and Directionality Discovery in Individual Dynamic Models: A Regularized Unified Structural Equation Modeling Approach for Hybrid Vector Autoregression. Psychometrika 2021, 86, 404–441. [Google Scholar] [CrossRef]
- Huang, P.-H. A penalized likelihood method for multi-group structural equation modelling. Br. J. Math. Stat. Psychol. 2018, 71, 499–522. [Google Scholar] [CrossRef]
- Bauer, D.J.; Belzak, W.C.M.; Cole, V.T. Simplifying the Assessment of Measurement Invariance over Multiple Background Variables: Using Regularized Moderated Nonlinear Factor Analysis to Detect Differential Item Functioning. Struct. Equ. Model. A Multidiscip. J. 2019, 27, 43–55. [Google Scholar] [CrossRef] [PubMed]
- Robitzsch, A. Regularized Latent Class Analysis for Polytomous Item Responses: An Application to SPM-LS Data. J. Intell. 2020, 8, 30. [Google Scholar] [CrossRef] [PubMed]
- Meinshausen, N.; Bühlmann, P. Stability selection. J. R. Stat. Soc. Ser. B Stat. Methodol. 2010, 72, 417–473. [Google Scholar] [CrossRef]
- Graham, J.W. Adding Missing-Data-Relevant Variables to FIML-Based Structural Equation Models. Struct. Equ. Model. A Multidiscip. J. 2003, 10, 80–100. [Google Scholar] [CrossRef]
- Huang, Y.; Montoya, A. Lasso and Group Lasso with Categorical Predictors: Impact of Coding Strategy on Variable Selection and Prediction. PsyArXiv 2020. [Google Scholar] [CrossRef]
- Huang, P.-H. Lslx: Semi-Confirmatory Structural Equation Modeling via Penalized Likelihood. J. Stat. Softw. 2020, 93, 1–37. [Google Scholar] [CrossRef]
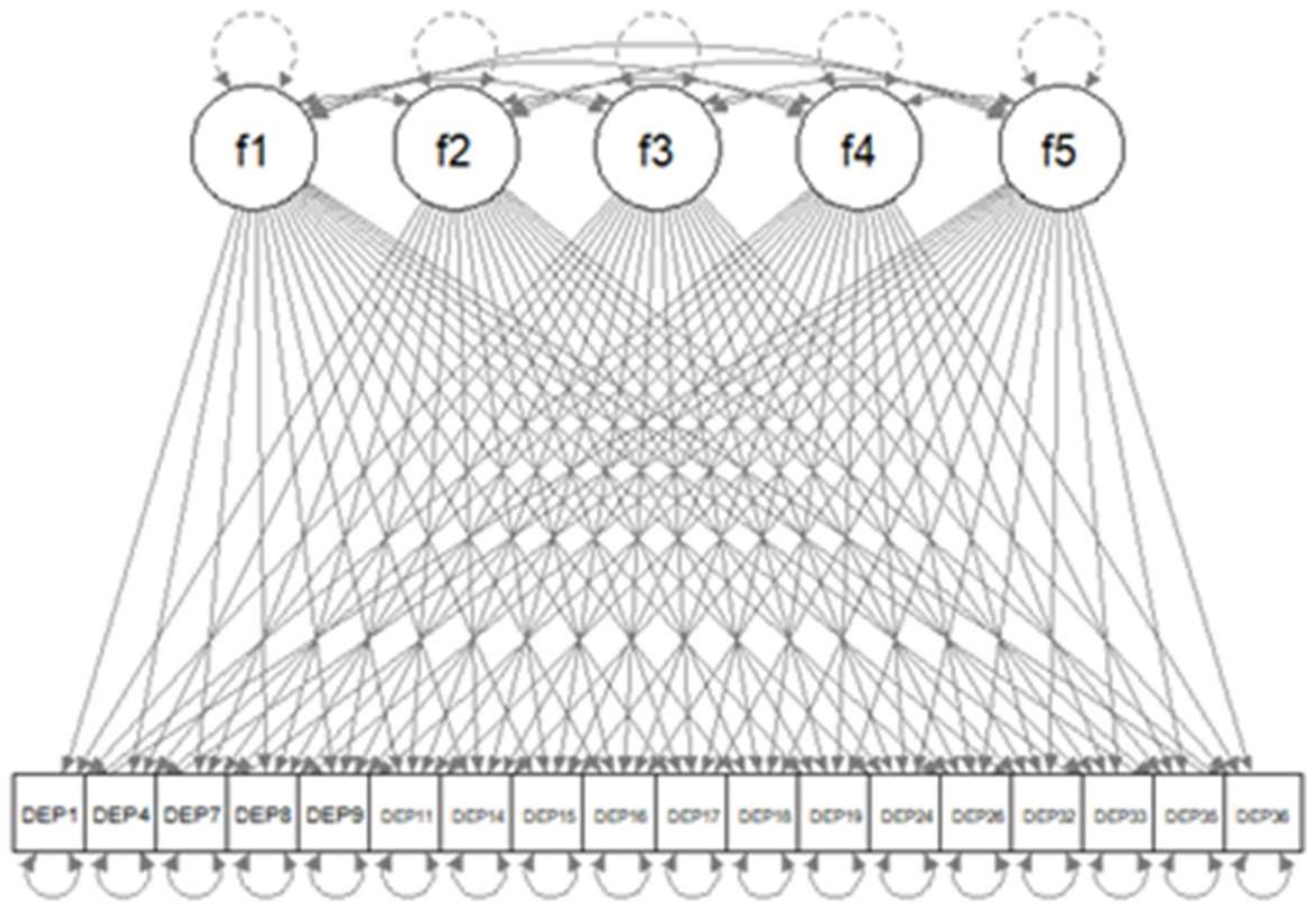
| R Code 1 |
|---|
| library(lavaan) lav.mod<-paste( “f1=~NA*”,paste(colnames(dat.sub2),collapse=“+”),”\n”, “f2=~NA*”,paste(colnames(dat.sub2),collapse=“+”),”\n”, “f3=~NA*”,paste(colnames(dat.sub2),collapse=“+”),”\n”, “f4=~NA*”,paste(colnames(dat.sub2),collapse=“+”),”\n”, “f5=~NA*”,paste(colnames(dat.sub2),collapse=“+”),”\n”, “f1~~1*f1; f2~~1*f2; f3~~1*f3; f4~~1*f4; f5~~1*f5”) dat.s<-scale(dat.sub2) lav.out<-cfa(dat.s,model=lav.mod,missing=“listwise”) |
| R code |
|---|
| library(regsem) A<-extractMatrices(lav.out)$A head(A[1:18,19:23]) |
| Output 1 |
| f1 f2 f3 f4 f5 DEP1 1 19 37 55 73 DEP4 2 20 38 56 74 DEP7 3 21 39 57 75 DEP8 4 22 40 58 76 DEP9 5 23 41 59 77 DEP11 6 24 42 60 78 |
| R code |
|---|
| pars.pen <- A[1:18,19:23][load.2<.5] pars.pen |
| Output |
| [1] 1 2 3 6 7 8 9 10 11 12 13 14 15 16 17 18 20 22 23 26 [21] 27 28 29 30 31 32 33 34 37 38 39 40 41 42 43 45 46 49 50 51 [41] 52 53 54 55 56 57 58 59 60 61 62 65 66 67 68 69 70 71 72 73 [61] 75 76 77 78 79 80 81 82 83 84 85 89 90 |
| R code 1 | |||||
|---|---|---|---|---|---|
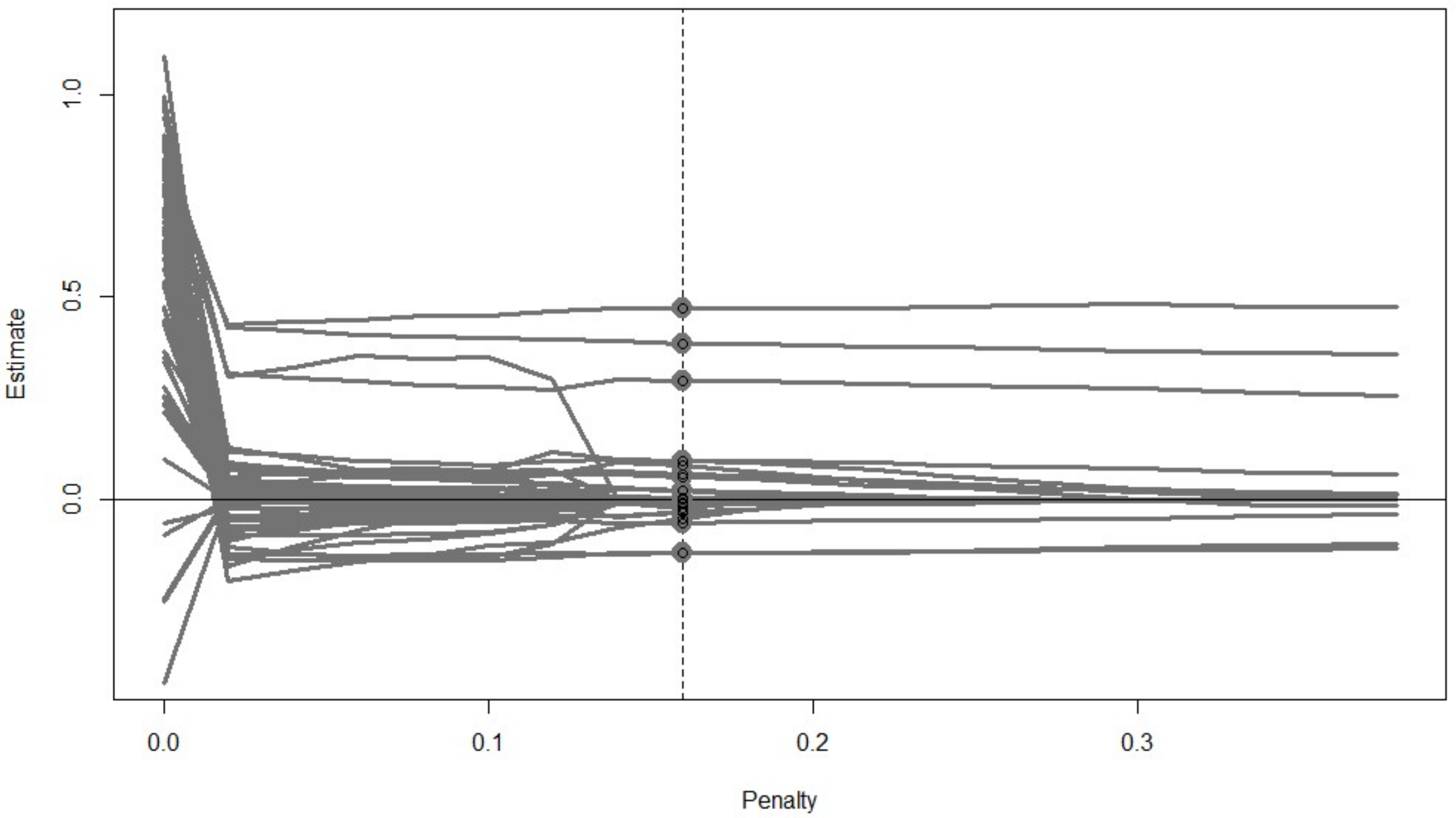
| out.reg<-cv_regsem(lav.out, type = “lasso”, pars_pen = pars.pen, n.lambda = 20, jump = 0.02) out.reg plot(out.reg, show.minimum=“BIC”) | |||||
| Output 2,3 | |||||
| out.reg$parameters | |||||
| f1 -> DEP1 | f1 -> DEP4 | f1 -> DEP7 | f1 -> DEP8 | ||
| [1,] | 0.816 | 0.675 | 0.869 | 0.012 | |
| [2,] | −0.004 | 0.000 | 0.425 | −0.557 | |
| [3,] | −0.005 | 0.000 | 0.416 | −0.554 | |
| [4,] | −0.004 | 0.000 | 0.407 | −0.550 | |
| [5,] | −0.004 | 0.000 | 0.403 | −0.550 | |
| [6,] | −0.002 | 0.000 | 0.398 | −0.548 | |
| ... | |||||
| out.reg$fits | |||||
| lambda | conv | rmsea | BIC | chisq | |
| [1,] | 0.00 | 0 | 0.12929 | 22002.41 | 6.828856e+02 |
| [2,] | 0.02 | 0 | 0.10402 | 21835.50 | 6.867450e+02 |
| ... | |||||
| [9,] | 0.16 | 0 | 0.09721 | 21787.29 | 8.027334e+02 |
| ... | |||||
| [11,] | 0.20 | 1 | 0.00000 | −14315219.42 | −1.433654e+07 |
| [12,] | 0.22 | 0 | 0.09851 | 21810.05 | 8.451946e+02 |
| ... | |||||
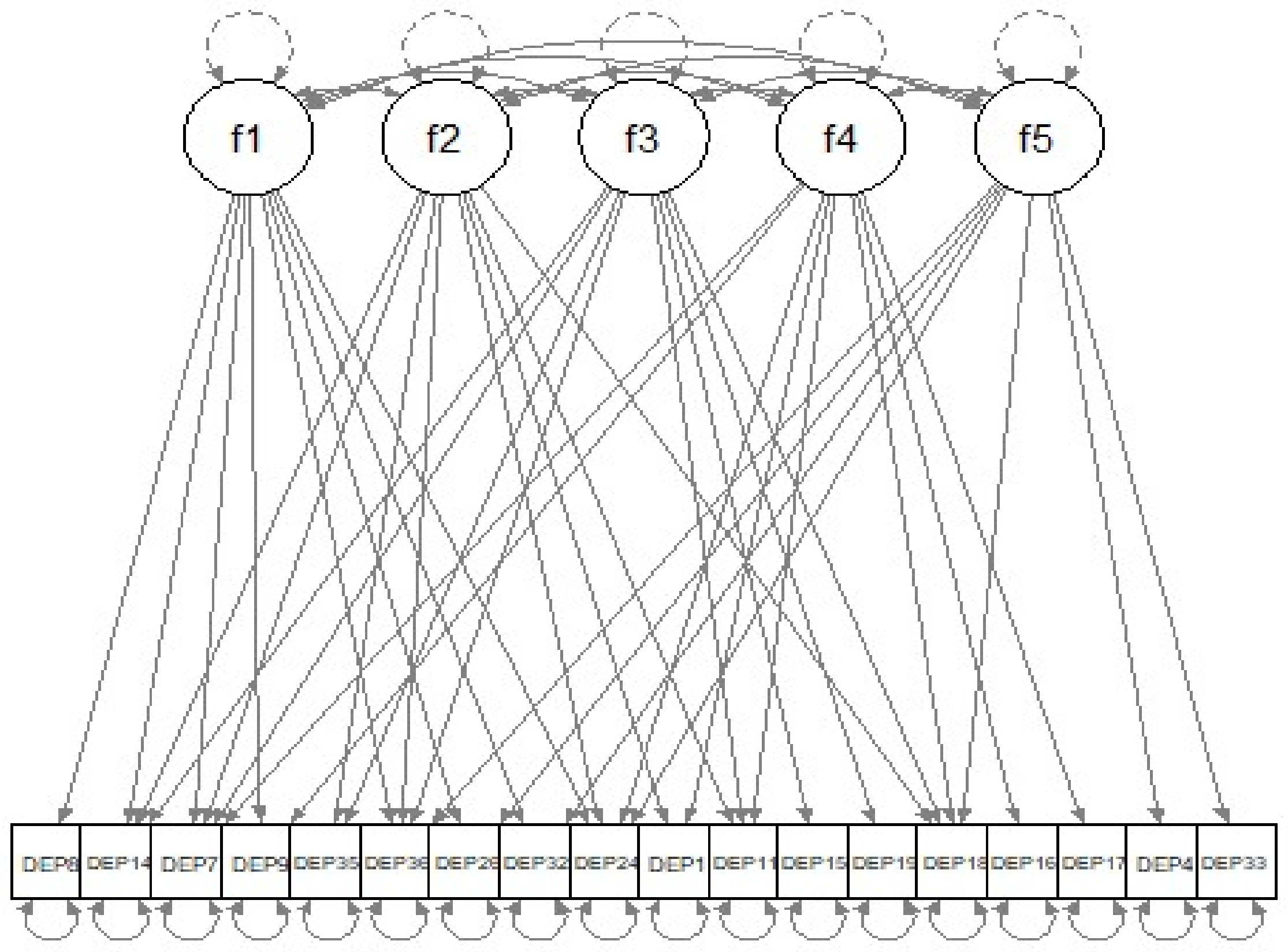
| out.reg$final_pars | |||||
| f1 -> DEP1 | f1 -> DEP4 | f1 -> DEP7 | f1 -> DEP8 | ||
| 0.000 | 0.000 | 0.384 | −0.548 | ||
| f1 -> DEP9 | f1 -> DEP11 | f1 -> DEP14 | f1 -> DEP15 | ||
| −0.902 | 0.000 | −0.009 | 0.000 | ||
| f1 -> DEP16 | f1 -> DEP17 | f1 -> DEP18 | f1 -> DEP19 | ||
| 0.000 | 0.000 | 0.000 | 0.000 | ||
| f1 -> DEP24 | f1 -> DEP26 | f1 -> DEP32 | f1 -> DEP33 | ||
| −0.058 | 0.002 | -0.010 | 0.000 | ||
| f1 -> DEP35 | f1 -> DEP36 | ... | |||
| 0.000 | 0.023 | ||||
| R code | ||||
|---|---|---|---|---|
| out.20 <- multi_optim(lav.out, type = “lasso”, pars_pen = pars.pen, lambda = 0.20) summary(out.20) | ||||
| Output1 | ||||
| Out.20$returnVals | ||||
| convergence | df | fit | rmsea | BIC |
| 0 | 92 | 0.7426382 | 0.12149 | 22120.89 |
| R code |
|---|
| stabsel.out<-stabsel(dat.sub22, model2, det.range = T, jump = 0.02, detr.nlambda = 20, times = 30, n.lambda = 10, n.boot = 100, pars_pen = pars.pen, p = 0.9) |
| #or equivalently: range<-det_range(dat.sub22, model2, jump = 0.02, detr.nlambda = 20, times = 30, pars_pen = pars.pen) stabsel.out2<-stabsel(dat.sub22, model2,det.range = F, from = range$lb, to = range$ub, n.lambda = 10, n.boot=100,pars_pen = pars.pen, p = 0.9) #can further tune the probability cutoff based on model fit: Stabsel.out3<-stabsel_thr(stabsel.out, from=0.8, to=1, method = “aic”) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Jacobucci, R.; Ammerman, B.A. Tutorial on the Use of the regsem Package in R. Psych 2021, 3, 579-592. https://doi.org/10.3390/psych3040038
Li X, Jacobucci R, Ammerman BA. Tutorial on the Use of the regsem Package in R. Psych. 2021; 3(4):579-592. https://doi.org/10.3390/psych3040038
Chicago/Turabian StyleLi, Xiaobei, Ross Jacobucci, and Brooke A. Ammerman. 2021. "Tutorial on the Use of the regsem Package in R" Psych 3, no. 4: 579-592. https://doi.org/10.3390/psych3040038
APA StyleLi, X., Jacobucci, R., & Ammerman, B. A. (2021). Tutorial on the Use of the regsem Package in R. Psych, 3(4), 579-592. https://doi.org/10.3390/psych3040038






