Abstract
The expectation–maximization (EM) algorithm is an important numerical method for maximum likelihood estimation in incomplete data problems. However, convergence of the EM algorithm can be slow, and for this reason, many EM acceleration techniques have been proposed. After a review of acceleration techniques in a unified notation with illustrations, three recently proposed EM acceleration techniques are compared in detail: quasi-Newton methods (QN), “squared” iterative methods (SQUAREM), and parabolic EM (PEM). These acceleration techniques are applied to marginal maximum likelihood estimation with the EM algorithm in one- and two-parameter logistic item response theory (IRT) models for binary data, and their performance is compared. QN and SQUAREM methods accelerate convergence of the EM algorithm for the two-parameter logistic model significantly in high-dimensional data problems. Compared to the standard EM, all three methods reduce the number of iterations, but increase the number of total marginal log-likelihood evaluations per iteration. Efficient approximations of the marginal log-likelihood are hence an important part of implementation.
1. Introduction
Item response theory (IRT) models have long been a staple in psychometric research, with applications in the investigation of test properties in smaller to medium samples (e.g., in personality, intelligence, or creativity research [1,2]), but also in large-scale assessments [3,4]. Especially popular—and the topic of the present work—are logistic IRT models for binary data, particularly the one-parameter (1PL; also: Rasch) and two-parameter (2PL) models. While conditional maximum likelihood is feasible for the 1PL model, marginal maximum likelihood (MML) estimation for IRT models is the predominant estimation approach, particularly for the 2PL model. MML estimation is usually performed with the help of the expectation–maximization (EM) algorithm (Refs. [5,6]; for a comprehensive introduction, see [7], and for implementation details, see [8]). The EM algorithm is well suited to carry out ML estimation for situations in which one can consider parts of the “complete data” to be unobserved. In IRT models, the unobserved data are identical to latent ability. The EM algorithm maximizes the expected complete-data log-likelihood using an iterative two-step approach [5,9] of estimating the current posterior distribution of latent variables given the data and current or initial parameter estimates by determining the expected complete-data log-likelihood function (expectation (E) step), and then maximizing this expected complete-data log-likelihood function to obtain parameter estimates (maximization (M) step) until convergence. However, one problem with the EM algorithm is that convergence can be slow [7]. This can pose a serious challenge to applied researchers employing the EM algorithm for IRT models in data-rich settings, such as large-scale assessments. In addition, simulation is a routine strategy to evaluate statistical decisions in the IRT context, so speeding up the EM algorithm speeds up methodology development.
Research into the acceleration of the EM algorithm has yielded several promising techniques, such as new quasi-Newton methods (QN) [10], squared iterative methods (SQUAREM) [11,12,13], and parabolic EM [14]. However, these recent methods have only been presented in isolation, and the way they work has not been compared in detail. Furthermore, they have not been previously presented and compared in the psychometric context of IRT models. In fact, to our knowledge, only one psychometric paper [15] from over twenty years ago has been dedicated to a comparison of EM accelerators in the context of IRT models. As several new methods have been developed since then and as data-rich settings are becoming increasingly more common, this work aims to provide a reasonably self-contained introduction to general-purpose EM accelerators and a systematic comparison of recent EM accelerators in a psychometric setting.
1.1. The EM Algorithm for Logistic IRT Models
The 2PL model models N participants’ dichotomous responses (with 1 for a correct and 0 for an incorrect response) to M items on a test, where the response of person i to an item j depends on the person’s ability and some item parameters [16]. Assuming follows a Bernoulli distribution, the 2PL model assumes that the probability of a correct response of person i with ability to item j is
with item discrimination (describing how well item j discriminates between persons of high and low ability) and item difficulty [16]. Equivalent but numerically advantageous is the slope-intercept parameterization [8,17], for which we replace the expression inside the exponential function with the expression , with the following relationships between the parameters: and . The 1PL model is nested within the 2PL model as a special case; it is obtained when for all items . Let for , denote the probability of observing the response vector ; i.e., the responses of person i to all M items if the person has ability is given by [8]:
Assuming that latent ability is normally distributed around 0 with variance , , and denoting the corresponding probability density function, the observed data or marginal likelihood (i.e., the responses of all N participants to all M items) is given by [8]:
Here, is the item parameter vector that characterizes the distribution of X and is to be estimated. In slope-intercept notation, it is given by . Note that , the variance of personal ability, is generally also unknown, i.e., it may also have to be estimated (1PL case) or may need to be fixed, usually to 1 in the 2PL model, for identification purposes [8].
The integral in Equation (3) proves difficult to evaluate and, thus, is usually approximated numerically. A common approach is Gauss–Hermite (GH) quadrature [8]; see [17] for other methods. GH quadrature approximates the continuous integral by a discrete sum over K discrete ability levels , each weighted with a weight that takes into account the distance between discrete ability levels and the height of the density function in the neighborhood of [8]. Rewriting Equation (3) in quadrature notation yields [8]:
By considering response patterns and how often they occur for each ability level across participants rather than considering participants’ responses individually, we obtain the complete-data likelihood
where denotes the total number of persons of ability level attempting item j, and denotes the total number of correct responses to item j for persons of ability level . Furthermore, represents the number of persons of each of the K ability levels attempting item j, and denotes the number of correct responses to item j by the persons at each of the K ability levels. The tuple can be said to contain “complete” information about an item j. The values of the and vectors are unobserved. For this reason, the posterior expected complete-data log-likelihood, conditional on the observed response data and current parameter estimates, is used instead ([8], Section 6.4.1), where we replace and with their posterior expected values ([8], Chapter 6):
for and . is the posterior probability of person i having ability , given that person’s observed response vector, , the item parameters , and the variance of ability in the population, . The posterior membership probabilities for and are unknown and must be estimated during each E-step of the EM algorithm, given the response data , as well as the and current item parameter estimates . The estimated posterior membership probabilities can then be used to compute estimates of and . Each E-step is then followed by an M-step, in which the posterior expected complete-data log-likelihood, that is, the logarithm of the term in Equation (5) with the estimates of posterior expected values and replacing the respective and terms, is maximized with respect to the vector of item parameters . This is done iteratively by finding the root of the derivatives of the posterior expected complete-data log-likelihood independently for each item, i.e., solving [8]
for . Here, , with and denoting the probabilities of getting a correct and incorrect answer, respectively. Please note that unless the ability variance is fixed, it also needs to be estimated during each M-step. E- and M-steps are then carried out in alternating fashion until convergence. It is worth noting that the convergence of the EM algorithm is not guaranteed if the IRT model employed is not an exponential family model ([8], Section 6.4.1). Only the 1PL (or Rasch) model is a member of the exponential family. However, empirical work suggests that the EM algorithm generally also converges for other IRT models [18].
1.2. EM Accelerators
Ref. [13] divides existing techniques into two broad classes: The first class, which they title monotone acceleration techniques, includes modifications of specific EM algorithms. These methods include data augmentation [19], parameter expansion EM (PX-EM) [20], Expectation/Conditional Maximization (ECM) [21], and Expectation/Conditional Maximization Either (ECME) [22]. These methods have been shown to substantially speed up convergence rates for the EM algorithm [7]. However, they have to be construed and implemented for each application of the EM algorithm, which means they are not feasible to use for applied researchers unless they have been specifically implemented for the model they are using. As this work aims to make recommendations for applied researchers, these methods will not be discussed here. Please see [7] for an introduction and an overview. The second class, referred to as non-monotone by [13], includes methods that are based on finding the root of a function and are universally applicable to applications of the EM algorithm. This class includes quasi-Newton methods [23,24], conjugate gradient methods [25], and multivariate Aitken’s procedure [26]. Only the quasi-Newton methods (QN1 and QN2 in the current paper’s terminology) were studied in a psychometric study on the topic [15]. In recent years, new acceleration methods of this class have been proposed and have shown promising performance: faster quasi-Newton methods (QN) [10,13], squared iterative methods (SQUAREM) [11,12,13], and parabolic EM (PEM) [14]. In the following, we will present these methods in unified notation for easy comparability and will compare their performances in a numerical simulation.
1.2.1. EM Accelerators and Fixed-Point Mappings
The recently proposed EM accelerators discussed and compared in this work take advantage of the fact that the EM algorithm can be considered a fixed-point mapping F from the parameter space onto itself [14],
By using the mapping iteratively, as the EM algorithm does, a sequence is generated from a starting point [14], where , . In other words, the mapping F corresponds to one evaluation of the E- and M-step of the EM algorithm. Under certain conditions [27], the sequence satisfies , , and thus converges to , which corresponds to either a saddle point or a local maximum of (and ) [5,7,27]. If F is differentiable, is a fixed point of F, i.e., . Linearization of F in a small neighborhood of yields [14]
where is the Jacobian matrix of F evaluated at . Usually, J cannot be expressed explicitly. The vector is the error after the th EM update. Equation (12) stresses that converges approximately linearly to . The rate of convergence depends on the eigenvalues of the rate matrix , with the latter having been shown to measure the fraction of missing information [5].
As explained above, the EM algorithm effectively creates a sequence that converges to . To accelerate convergence, another sequence, , has to be generated from the same starting point, but with a faster rate of convergence to , so that Faster convergence also implies that fewer evaluations of F are required until a convergence criterion, such as that or is met [14]. Here, denotes a small, fixed, positive, real number. Note that one could use either the observed or the complete-data log-likelihood because both are maximized by the same parameter estimates. The former is often easier to evaluate and is thus often used to probe for convergence. In the following, for simplicity, the symbol is used throughout instead of to indicate a member of the accelerated parameter estimation sequence.
1.2.2. Steffenson-Type Methods
Before giving a detailed description of the accelerators studied in the present work, we are going to provide a brief introduction to Quasi-Newton (QN) and, in particular, Steffenson-type methods (STEM), which form the basis for some of the more recently proposed accelerators and will thus be crucial in the understanding of them. For a more detailed description of these classes of methods, please consult [7] or [13]. Newton’s method for locating the fixed point of F is based on finding the root of a linear approximation of the residual function around , i.e., . Iteratively, this can be expressed as , [10,13], which we are going to refer to as a Newton update. If is unknown, it has to be approximated by a low-rank matrix, so that can be easily computed (leading to quasi-Newton methods). To find a good approximation for , secant constraints can be used [10,13]: If two successive iterations of the EM algorithm, , are performed close to the fixed point based on the current parameter estimate , Equation (11) yields , with and [13].
Steffenson-type (STEM) methods make use of a single secant constraint to obtain an approximation in the form of [13]. With this approximation for , the Newton update simplifies to a quasi-Newton update of , . The parameter is called the steplength [13]. The STEM update therefore consists of a step of length taken from in the direction of u (Figure 1). Because the direction is fixed, a single STEM update cannot account for curvature in trajectories to the fixed point (Figure 1). Instead, the direction is continually corrected in subsequent updates.
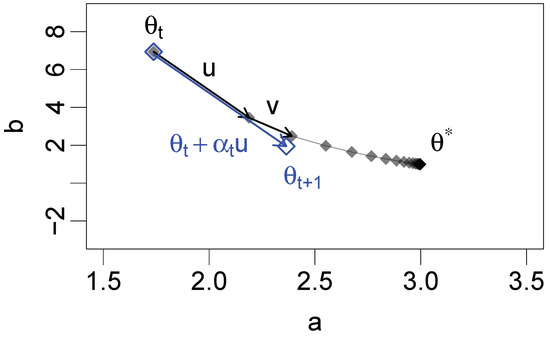
Figure 1.
Illustration of the Steffenson-type (STEM) method in two dimensions with . Blue: a STEM update with as a starting point. Gray: successive expectation–maximization (EM) updates from to . Black arrows: the vectors and .
The steplength must be chosen in such a way that the secant constraint is satisfied, resulting in as the constraint for . Ref. [13] provides three suggestions for the steplength, all satisfying the imposed secant constraint:
The STEM method with steplength S1 is also equivalent to first-order Reduced Rank Extrapolation (RRE1), a polynomial extrapolation method [12]. Similarly, STEM with S2 is equivalent to first order Minimal Polynomial Extrapolation (MPE1) [12]. In general, for a fixed and , [13]. Note, however, that for acceleration to occur, must be larger than 1 [13]; for , the quasi-Newton STEM update becomes a simple EM update, i.e., there is no acceleration.
A STEM update with one of the above steplengths does not necessarily increase the likelihood, i.e., STEM is not necessarily globally convergent. To obtain global convergence, the steplength may have to be adapted in such a way that the likelihood increases in every iteration. The strategy proposed by [13] for globally convergent STEM is as follows: If , is set to 1. If but , is decreased towards 1 until . If and , is accepted as the steplength.
1.2.3. Advanced Quasi-Newton Methods (QN)
Ref. [10] proposes a more advanced quasi-Newton method, which, instead of a single secant constraint, uses q secant constraints, yielding , with and , where and , for . For , this simplifies to (compare above). Note that U and V are both matrices, where p is the dimension of . For the matrices to have full rank, q must not be bigger than p [10].
An approximation is determined by minimizing the Frobenius norm under the secant constraints [10]. This yields with the inverse , as well as the quasi-Newton update
For , this simplifies to , , with . In other words, the case is similar to an STEM update with an additional EM update: One EM update is performed, and then a step of length is taken in the direction of v (Figure 2). The steplength used is S2 (14).
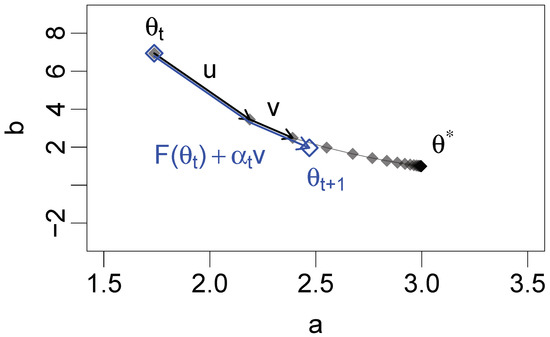
Figure 2.
Illustration of the quasi-Newton (QN) () method in two dimensions, with . Blue: a QN () update with as a starting point. Gray: successive EM updates from to . Black arrows: the vectors and .
Ref. [10] shows that QN methods can be very efficient: With these methods, the fixed point is reached in 10–100 times fewer iterations than with the standard (unaccelerated) EM algorithm. Furthermore, these methods are suitable for high-dimensional problems because of their minimal storage requirements. In contrast to earlier quasi-Newton methods [23,24], STEM and QN methods do not require the storage or manipulation of the observed information matrix or the Hessian of F. Combined with globalization strategies, they are globally convergent [10].
1.2.4. Squared Iterative Methods (SQUAREM)
In a small neighborhood of , STEM has the following error equation [13]:
where is the error after the th STEM update. Equation (18) shows that the rate matrix of STEM is . The squared iterative method proposed by [13] is derived from STEM by squaring this rate matrix and demanding that the error of the new method satisfies . From , it follows that and . This results in the SQUAREM update [13]:
Figure 3 shows a SQUAREM update consisting of two steps: one of length in the direction of u and one of length in the direction of . The second step can accommodate a change in direction between u and v, which allows SQUAREM to account for curvature in the trajectory to the fixed point. The sum of the steps can also be written as , i.e., as a weighted sum of u and v. The weights are positive if .
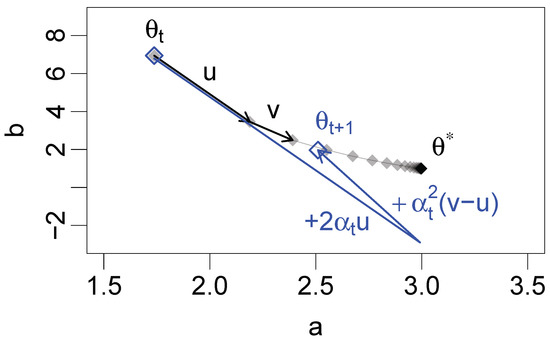
Figure 3.
Illustration of the squared iterative methods (SQUAREM) () method in two dimensions with . Blue: a SQUAREM () update with as a starting point. Gray: successive EM updates from to . Black arrows: the vectors and .
Together with the three steplengths proposed for in Equations (13)–(15) and in conjunction with globalization strategies, Expression (19) yields three SQUAREM methods: gSqS1, gSqS2, and gSqS3, where S1–S3 indicate which steplength is used [13]. Because of the squaring of the rate matrix, SQUAREM usually converges faster than STEM or QN with . Of the three global SQUAREM methods, both gSqS1 and gSqS3 perform better than gSqS2, and gSqS3 is consistently faster than gSqS1 [13]. However, QN methods with can be faster than SQUAREM [10].
The SQUAREM method described thus far is of the first order, . The order parameter, k, is related (but not equal) to the number of successive EM updates used during the accelerated update. Higher-order SQUAREM methods () can easily be derived from first-order SQUAREM methods [12]. Let denote the iteration of Fi times, with , and so on. Then, the SQUAREM update (19) of order can be rewritten as [12]:
with , and . Equation (20) can be generalized as follows to give rise to higher-order SQUAREM methods () [12]:
The coefficients and have to fulfill [12]:
See [12] for an alternative derivation and how higher-order SQUAREM methods relate to other acceleration methods, a discussion of which would be beyond the scope of this work. Like QN methods, SQUAREM methods are suitable for high-dimensional problems [12]. Combined with globalization strategies, they are globally convergent [13]. Furthermore, first-order SQUAREM () does not have additional storage costs compared to STEM or QN (). This means that first-order SQUAREM is highly competitive. However, higher-order SQUAREM methods () do require evaluations of F, which incurs additional cost, so k should be chosen as the smallest number for which reasonable acceleration can be achieved [13]. Note that first-order SQUAREM () can already accelerate the EM algorithm four- to ten-fold, depending on the problem studied [13].
1.2.5. Parabolic EM (PEM)
Unlike the QN and SQUAREM methods, parabolic EM is derived from purely geometric considerations. It is based on a Bezier parabola, a parametric curve controlled by three points; here, these are , and , and a parameter, s [14]. The Bezier parabola is given by , originally defined for [14]. For PEM, we choose , so that values beyond can be explored [14]. It passes through and through , and is tangent at these points to the line that passes through and and the line that passes through and (also see Figure 4). For ease of exposition, we assume that the Bezier parabola is a subspace of the parameter space, omitting a discussion of parameter constraints. The parameter subspace defined by the parabola is explored by means of either arithmetic or geometric search [14]. In either case, s is incremented from until the log-likelihood, , no longer increases. At this point, the search is stopped and the PEM update is performed [14]:
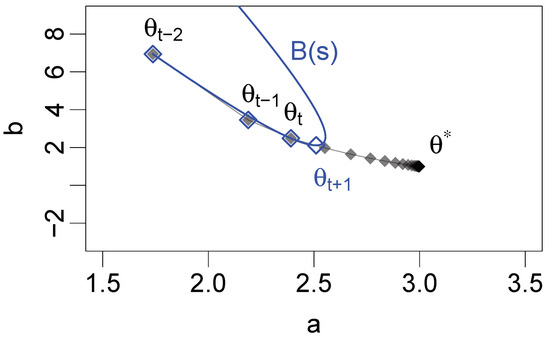
Figure 4.
Illustration of the parabolic expectation–maximization (PEM) method (19) in two dimensions with . Blue: a PEM update based on a Bezier parabola with , and as starting points. Gray: successive EM updates from to .
Each explored value of s prompts a log-likelihood evaluation, so log-likelihood evaluations are ideally cheap. Note that, if , , and lie on a straight line, PEM will simply explore that line [14]. This does not cause problems for the algorithm. A few EM updates are usually performed before starting PEM [14], as PEM tends to be more efficient closer to the fixed point. In contrast to the QN and SQUAREM methods, the parabola allows PEM to explore a larger parameter subspace for the best possible update (compare Figure 4).
The exploration of the parameter space by arithmetic or geometric search means that PEM has one or two tuning parameters: The mesh size h and the ratio a can be used to control the incrementation of s [14], with for the arithmetic and for the geometric search, where i is a dummy variable. Ref. [14] shows that large values for h or a can destabilize the algorithm and recommend the geometric search with and .
The Bezier parabola function can be re-written as , with and . This is very similar to the SQUAREM update (19) with . In fact, Ref. [14] shows that first-order SQUAREM is a special case of PEM using a single point on the Bezier parabola, , as the next update. Unlike SQUAREM, PEM does not use a predefined point, but instead explores the neighborhood of until a local maximum of has been found. For this reason, PEM is more stable than SQUAREM and can be faster, although this has only been measured in CPU time, not in terms of numbers of F and L evaluations [14].
Like the QN and SQUAREM methods, PEM has low storage requirements and is therefore suitable for high-dimensional problems. PEM may perform a much larger number of log-likelihood evaluations during the exploration step. However, this may not be too great of a disadvantage, as the evaluation of L is often not as costly. Ref. [13] shows that PEM can accelerate the EM algorithm four- to ten-fold depending on the problem studied.
1.2.6. Expected Results of the Numerical Comparison
Based on the detailed descriptions and considerations above, we expect SQUAREM () to perform better than QN () because of the squared rate matrix. PEM, in turn, should perform better than SQUAREM () because, instead of using a fixed update, it explores the parameter space for the best possible update during each iteration. However, it is important to keep in mind that the runtime of all three acceleration techniques is determined by a trade-off between a reduced number of iterations to the fixed point and an increased number of F and L evaluations per iteration. In particular, higher-order QN () and SQUAREM () methods may suffer from a large number of F evaluations, while PEM may suffer from a large number of log-likelihood evaluations.
2. Results
As item parameters can be optimized independently for each item during the M-step, we only visualize the results regarding the trajectories for item 1 (Figure 5 and Figure 6 for the six simulation conditions in conjunction with the start values provided by mirt; for the corresponding plots for the start values 0 and 1 for all difficulties and discriminations, respectively, see Appendix B; the overall pattern of results was comparable for both choices of start values). Figure 5 and Figure 6 show the cumulative relative steplength (left columns) and the angle between successive EM updates (right columns) in all six conditions for all 100 trials. Note that for each trial, the underlying true parameter value(s) for item 1 were sampled randomly and, therefore, different in every trial. Across the left-hand columns in Figure 5 and Figure 6, we can see that most trajectories approach the proximity of the fixed point in relatively few steps, with some, especially for the 1PL models, starting off very close to it, attesting to the choice of starting values provided by mirt. While others do take a few more steps to reach the proximity of the fixed point, all trajectories across all conditions show that before half the steps of the complete trajectory have been taken, the EM algorithm is already very close to the fixed point and only makes very small adjustments in the parameter estimates with each further EM cycle. The right-hand columns in Figure 5 and Figure 6 show that instabilities occur in some trajectories: The angle between successive iterations appears to switch from zero to and back. An angle of indicates that after a step in one direction, a step is taken in the opposite direction. It is unclear to the authors why these instabilities occur; however, they do not impede the ability of the trajectories to find the fixed point. If the angle is different from zero, the fixed point is approached on a curve. Such a pattern occurs most notably for the 2 PL model, both in conjunction with nine and with 100 items (see C′ in Figure 5 and Figure 6). In these cases, acceleration methods such as SQUAREM and PEM may be more suitable because they explicitly allow for changes in direction.
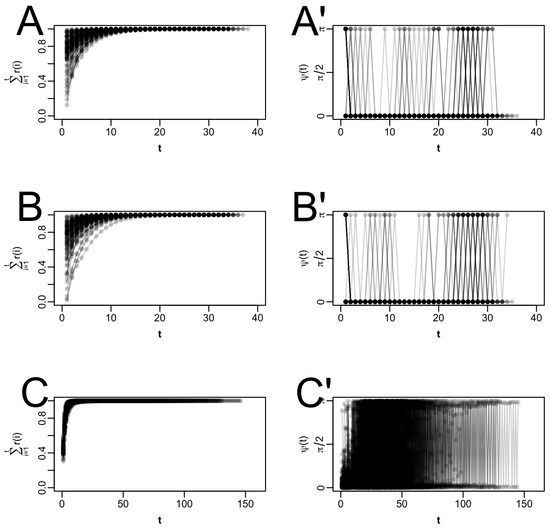
Figure 5.
Properties of F for conditions 1–3 (i.e., with nine items), with starting values as provided by mirt. For illustrative purposes, only the parameter spaces of item 1 are shown here. Note that the colors are transparent, so darker colors indicate that more trajectories pass through the same spot. For each trajectory, the cumulative relative steplength ((A) for condition 1 (one parameter (1PL)), (B) for condition 2 (1PL with fixed variance), (C) for condition 3 (two parameters (2PL))) and the angle between successive EM updates ((A′) for condition 1, (B′) for condition 2, (C′) for condition 3) are plotted as a function of the iteration index, t.
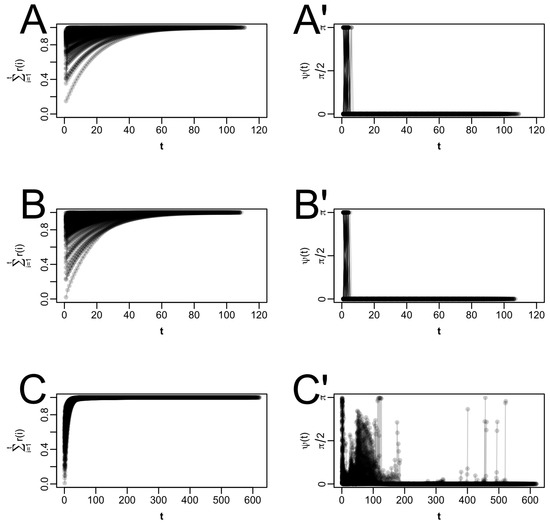
Figure 6.
Properties of F for conditions 4–6 (i.e., with 100 items), with starting values as provided by mirt. For illustrative purposes, only the parameter spaces of item 1 are shown here. Note that the colors are transparent, so darker colors indicate that more trajectories pass through the same spot. For each trajectory, the cumulative relative steplength ((A) for condition 4 (1PL), (B) for condition 5 (1PL with fixed variance), (C) for condition 6 (2PL)) and the angle between successive EM updates ((A′) for condition 4, (B′) for condition 5, (C′) for condition 6) are plotted as a function of the iteration index, t.
Table 1, Table 2, Table 3 and Table 4 show the average number of iterations from the starting value to the fixed point, the average number of F evaluations, the average number of log-likelihood evaluations, the fraction of converged trials, the average CPU time in ms, and the relative computing time as compared to the standard EM algorithm for all nine acceleration methods as well as the standard EM algorithm as a benchmark in all six conditions. The first three conditions, i.e., all models with nine items, are shown in Table 1 for the starting values provided by mirt and Table 3 for starting values set to 0 and 1 for all difficulties and all discriminations, respectively, and the other three conditions, i.e., all models with 100 items, are shown in Table 2 and Table 4 for the two different choices of starting values, respectively.

Table 1.
EM acceleration results for conditions 1, 2, and 3 (all with nine items), with starting values as provided by mirt. The numbers shown represent a rounded average over 100 simulation trials. : Average number of iterations from the starting value to the fixed point; Fevals: Average number of F evaluations; Levals: Average number of log-likelihood evaluations; Conv.: Fraction of converging runs; CPU: Average CPU time in milliseconds; Rel. time: Relative computing time as compared to standard EM.

Table 2.
EM acceleration results for conditions 4, 5, and 6 (all with 100 items), with starting values as provided by mirt. The numbers shown represent a rounded average over 100 simulation trials. : Average number of iterations from the starting value to the fixed point; Fevals: Average number of F evaluations; Levals: Average number of log-likelihood evaluations; Conv.: Fraction of converging runs; CPU: Average CPU time in milliseconds; Rel. time: Relative computing time as compared to standard EM.

Table 3.
EM acceleration results for conditions 1, 2, and 3 (all with nine items), with starting values 0 and 1 for all difficulties and discriminations, respectively. The numbers shown represent a rounded average over 100 simulation trials. : Average number of iterations from the starting value to the fixed point; Fevals: Average number of F evaluations; Levals: Average number of log-likelihood evaluations; Conv.: Fraction of converging runs; CPU: Average CPU time in milliseconds; Rel. time: Relative computing time as compared to standard EM.

Table 4.
EM acceleration results for conditions 4, 5, and 6 (all with 100 items), with starting values 0 and 1 for all difficulties and discriminations, respectively. The numbers shown represent a rounded average over 100 simulation trials. : Average number of iterations from the starting value to the fixed point; Fevals: Average number of F evaluations; Levals: Average number of log-likelihood evaluations; Conv.: Fraction of converging runs; CPU: Average CPU time in milliseconds; Rel. time: Relative computing time as compared to standard EM.
The performance of the accelerators varied considerably between conditions, with some drastic speed-ups and even some increases in computing time. For conditions with nine items (conditions 1–3, see Table 1 and Table 3), we only observe speed-ups in CPU time across all accelerators (except PEM, which even shows an increase in computing time) for condition 2, that is, for the 1PL model with the fixed latent variance, and some of the accelerators (i.e., higher-order QN and higher-order SQUAREM) when starting with the starting values provided by mirt. In the second condition, higher-order QN methods (especially ) as well as second-order SQUAREM show the best results in terms of CPU time decreases, with QN () taking first place and reducing the CPU time of standard EM to less than a third for the mirt starting values. With 0 or 1 as starting values, the pattern is overall similar for the second condition, where the best performing accelerators are QN () and QN (), which both reduce the computing time by nearly 60%. For condition 3 (2PL with nine items), we see consistently bad performance of all accelerators for both choices of starting values in terms of CPU time, with all of the increasing computing time. For condition 1 (1PL with nine items), results are mixed with regard to CPU time. Only SQUAREM (), SQUAREM (), and QN () show a (modest) decrease in CPU time, and that only for the mirt starting values. The other accelerators either just about match the CPU time of standard EM or even show increases. In terms of the average number of iterations from the starting value to the fixed items, all accelerators show notable reductions for both choices of starting values. The best performances with regard to the average number of iterations for nine items (i.e., across conditions 1–3) are exhibited by the higher-order SQUAREM methods in condition 2, reducing the number of iterations from 37 to only 3. PEM and higher-order QN also show competitive performances here. Again, the pattern of results is very similar for both choices of starting values. In terms of the number of F evaluations, the QN methods as well as first-order SQUAREM (but only for conditions 2–3) show the best results across conditions 1–3 for both choices of starting values. Across conditions 1–3 and starting values, PEM is characterized by a very high number of log-likelihood evaluations, which may explain its performance in terms of CPU time.
For the conditions with 100 items (conditions 4–6, see Table 2 and Table 4), only condition 4, that is, the 1PL model, showed similar unfortunate patterns of increased CPU time compared to standard EM, as we have seen in the first three conditions, regardless of the choice of starting values. Conditions 5 and 6 (i.e., the 1PL model with fixed latent variance and the 2PL model), however, showed very good results in terms of speed-up of CPU times for all accelerators. Out of all of them, first-order QN and PEM showed the least computing time reductions; however, they still exhibited notable speed-ups. Again, this pattern was exhibited for both choices of starting values. However, it should be pointed out that computing time decreases were overall greater for the less ideal starting values (as compared to the mirt starting values), with (nearly) all accelerators being able to halve computing times when used with less ideal starting values and, therefore, more able to show their full potential. For the 1PL model with fixed latent variance (condition 5) and both choices of starting values, higher-order SQUAREM and especially higher-order QN showed the best results in terms of computing time. For the 2PL model (condition 6) and both choices of starting values, higher-order QN methods still performed very well, but were beat by lower-order SQUAREM methods, in particular, first-order SQUAREM. In terms of the average number of iterations and the number of F evaluations, the pattern of results observed for 100 items is similar to the one outlined above for the conditions with nine items. PEM (and for conditions 5 and 6, also first-order QN) still suffers from a very high number of log-likelihood evaluations for both choices of starting values.
Even though the focus of our simulations was the application of IRT models in a large-assessment type setting as represented by the large sample of N = 10,000 in our simulations, we want to give an impression of how far our results are specific to such a setting or would also generalize to other settings. To gain such an impression, please consult Appendix C and Appendix D for a comparison of the accelerators in our six simulation conditions (each with the two sets of starting values) with and , respectively. Please note that when looking at the computation times, considering the relative computation times (as compared to standard EM) is generally more helpful (please also see the discussion section for more thoughts on this). To sum up the important patterns of the results, we observe that acceleration performance tends overall to be (qualitatively) similar for the first and fourth condition (1 PL, nine and 100 items, respectively) across all sample sizes examined, that is, we mostly observe de- rather than acceleration. However, note that an exception from this observation is the first condition in conjunction with ; here, we do actually observe acceleration for all or most accelerators, depending on the choice of starting values. Interestingly, the accelerators perform worse in the second condition (1 PL model with fixed variance, nine items) in the smaller samples, with most of them exhibiting deceleration instead of the acceleration observed for all accelerators in the large sample in this condition. In the fifth condition (1PL model with fixed variance, 100 items), accelerator performance becomes much more heterogeneous, both within the condition but also across different starting values and sample sizes. Please consult Appendix C and Appendix D for details. However, generally, higher-order QN and SQUAREM methods tended to perform better. Just as interesting is the change in the pattern of results in the third condition (2PL model, nine items). Here, we see considerably better performance of some of the accelerators, namely higher-order SQUAREM and PEM, which actually are able to show a decrease in computing time by up to a third in the smaller samples (instead of deceleration across all accelerators in the large sample); however, differences across starting values and between and can be noted. In condition 6, where we saw really good performances across all accelerators in the large-sample case, performance was more heterogeneous in the smaller samples, with some accelerators even showing deceleration. The acceleration methods that still performed consistently well in comparison to the others were the higher-order SQUAREM methods. Overall, the pattern of results does seem to depend on the sample size of the setting. In a similar vein, Appendix E shows some results from a small simulation with a variant of latent class models, namely the Gaussian Mixture Model (GMM). As our focus in this work is on the IRT setting, and, in particular, the 1PL and 2PL models, we are not going to go into detail here about these additional situations, but refer those readers who are interested in the performance of the accelerators in a different model class to Appendix E, as well as to our remarks upon the generalizability of our results beyond the 1PL and 2PL model in the discussion.
3. Discussion
In the present study, we numerically compared three recently proposed variants of model-independent EM accelerators, “squared” iterative methods (SQUAREM; ; [11,12,13]), advanced quasi-Newton (QN; ; [10]) methods, and parabolic EM (PEM; [14]), evaluated in large-sample psychometric settings with either few or a large number of items (nine vs. one hundred) for the 1PL and 2PL models. We used a constant sample size of N = 10,000 in our simulations, as, for one, the EM algorithm for the 1PL and 2PL models actually looks at frequency of response patterns, rather then individual responses, therewith factorizing the log-likelihood and resulting in the sample size having smaller leverage over the acceleration than the number of items (which increases the number of possible response patterns). Secondly, acceleration of the estimation of IRT models in large samples might be interesting not just for simulation studies (where the sample size can naturally be varied arbitrarily and the computational expense originates from the repetitions), but also in real-life large-assessment studies, which, in themselves, constitute a computationally expensive setting. Two sets of starting values were used in conjunction with each of the six resulting settings: (1) realistic starting values as provided by the R package mirt [17] and (2) less ideal starting values, which are more likely to enable the accelerators to show their full potential. The underlying idea of all three acceleration methods studied is to view the EM algorithm as a fixed-point mapping, which, applied iteratively, generates a sequence of parameter estimates from the starting value to—upon convergence—the fixed point. Acceleration is achieved by all three methods discussed here by creating another sequence of parameter estimates from the same starting point converging to the same fixed point, but with a faster rate of convergence. While all accelerators decreased the number of iterations as well as (for the most part) the number of EM cycles required to reach the fixed point many-fold, not all accelerators were able to achieve speed-ups in CPU time (as compared to standard EM) across all conditions. The most promising decreases in CPU time were observed for settings with 100 items and for models that did not estimate the latent ability variance (but instead had it fixed at 1). Higher-order QN and SQUAREM (depending on the model, either higher- or lower-order) methods performed the best in terms of reduction of CPU time. PEM did neither perform as well as expected, nor as well as the other methods. The pattern of results was similar for both choices of starting values. As is to be expected, the less ideal starting values allowed for stronger decreases in computing time (in those conditions in which decreases occurred), especially so for the settings with a large number of items. We include additional evaluations of the acceleration methods in different settings (e.g., smaller samples, different model class) in the appendices (see Appendix C, Appendix D and Appendix E) in order to give an impression of how far our findings generalize beyond the setting of IRT (in particular, 1PL and 2PL) models.
3.1. Properties of Trajectories for Standard EM
Studying the trajectories of the standard EM algorithm in our simulation study, we observed that, using starting values provided by mirt, the majority of trajectories found themselves in proximity of the fixed point right from the starting point. Naturally, this was more so the case for the starting values provided by mirt than for the less ideal starting values. Even those that started further away reached proximity of the fixed point in only relatively few iterations. Thus, quite the number of EM steps are actually rather small. This yields the opportunity for the accelerators to replace a number of small EM steps with one larger EM step. We also examined the angles between successive EM updates, in the course of which we observed some instabilities in the trajectories with angles indicating that the direction of the trajectory was changed into the opposite from one step to the next. This pattern occurred for several trajectories, more so for settings with nine compared to 100 items, and more so for the 2PL compared to the 1PL model, but for both choices of starting values. While such instabilities occurred at any point throughout the trajectories for only nine items, they only occurred early on for the 1PL model when 100 items were included and occurred predominantly early, and only occasionally later on for the 2PL model in conjunction with 100 items, again for both choices of starting values. However, since all trajectories reach the fixed point eventually, these instabilities are unlikely to affect the acceleration results. Apart from the backwards steps, the examination of the angles of successive EM steps indicates that some curvilinearity may be present in the trajectories for the 2PL model. This would suggest that in scenarios with the 2PL models, accelerators that explicitly take the non-linear shape of the trajectories into account, that is, SQUAREM and PEM, should show superior performance. It is important to point out that using the angles of successive EM steps in order to understand the EM trajectories is not an infallible solution. Especially in a multi-dimensional trajectory, they do not provide an unambiguous impression of what the corresponding trajectory might look like. Therefore, the observations made in this regard should be taken with a grain of salt.
3.2. Comparison of EM Accelerators
Contrary to what the observations made on the trajectories for standard EM led us to believe, we found that PEM did not provide competitive if any speed-ups of computing time in any of our simulation scenarios. In settings with nine items, we either observed roughly unaltered (1PL) or even decelerated (2PL) computing times as compared to standard EM. In settings with one hundred items, we found that PEM did achieve acceleration in computing times (except for when the latent variance was also estimated in the 1PL along with the item parameters—then, we again observed deceleration) and especially so for the less ideal starting values, but these still could not compete with the accelerations achieved by some of the other methods. This is unexpected because, for one, the Bezier parabola allows PEM to search the parameter space for the best possible update in each iteration. Additionally, especially the non-linear trajectories in conditions with the 2PL model should provide a setting in which PEM can shine, in particular compared to methods such as QN, which cannot account for the non-linearity in the trajectories. However, the number of evaluations of the fixed point function and of the log-likelihood is markedly increased, which incurs additional cost and increases the CPU time. It should be noted that these results are not consistent with previous studies, which applied PEM to the estimation of different models (a linear mixed model, a poisson mixture model, and a multivariate Student distribution), where the CPU time with PEM was reliably three to four times smaller than with standard EM [14]. Even when PEM did accelerate the EM algorithm in our simulations, the speed-up did not even manage to halve the computing time for the mirt starting values, and only just halved them for the less ideal starting values. This may certainly be explained by the large number of log-likelihood evaluations that PEM required. This number was consistently the greatest for PEM out of all accelerators and up to almost 10 times larger than that of the other methods. One possible explanation for the results is that we followed the generic recommendations of [14] for the choice of tuning parameters in our PEM implementation. While these performed well for models studied by [14], parameter values more optimally suited to IRT models may exist. This is still a good recommendation to derive from our simulations: Applied researchers might wish to tune parameters for PEM specifically to their application or choose another acceleration method rather than rely on the recommended parameters by [14].
For QN and SQUAREM, we found that performance depended (even more strongly) on the simulation setting. With regard to the choice of starting values, the pattern of results was mostly the same, just the magnitude of the computing time decreases (if they occurred) was greater for the less ideal starting values (as, of course, is to be expected). The performance in the settings with the 1PL for which the latent ability variance was estimated was generally rather poor across all acceleration methods. For nine items, only higher-order SQUAREM and QN methods provided acceleration in terms of CPU time (but note that first-order QN also provided deceleration). For 100 items, all methods showed decelerations. We attribute this impaired performance to the additional estimation of the latent ability variance, as we observed considerably better performances for conditions with the 1PL model for which the latent variance was fixed to 1. For nine items, we here saw the best results for higher-order QN () and second-order SQUAREM with CPU times. For 100 items, higher-order QN () still came out on top for the 1PL model with the fixed latent variance, but with more drastic reductions in computing time relative to standard EM. These magnitudes of the reduction in runtime are in line with results for other models [10,13]. Generally, the higher-order QN and SQUAREM methods performed better than the lower-order variants for the 1PL model with the fixed latent variance. For the 2PL model, all methods decelerated the EM algorithm when only nine items were used. The performance of the accelerators was considerably better for the 2PL model in conjunction with 100 items. Here, we observed the best performance for first-order SQUAREM, which reduced the CPU time to nearly a third of the CPU time for standard EM. While we still observed the pattern that higher-order QN methods performed better than lower-order QN methods in this condition, we observed the reversed pattern for SQUAREM.
Better performances of SQUAREM compared to QN, as we observed for the 2PL model with 100 items, are in line with our expectations, as SQUAREM is characterized by a “squared” rate matrix compared to QN. However, this pattern did not emerge consistently across conditions, with (higher-order) QN methods performing better than SQUAREM methods for the 1PL model (with a fixed latent ability variance). We observed a general tendency across conditions of SQUAREM requiring a more fixed-point function but less log-likelihood evaluations, and QN showed the reversed pattern. This may well provide an explanation for the different rank orders of methods for the 1PL and 2PL models: When the log-likelihood is more costly to evaluate, i.e., in our case, for the 2PL model, SQUAREM benefits more noticeably from the fewer evaluations of the log-likelihood, ranking in front of QN. This is much less of an advantage when log-likelihood evaluation is cheaper, as it is for the 1PL model.
3.3. Limitations and Avenues for Future Research
It is important to point out that the results discussed above apply first and foremost to the settings in which they were obtained, that is, in large-sample settings and to the 1PL and 2PL models. They do not necessarily generalize to other model classes or even just (considerably) smaller sample settings. In fact, our additional examinations indicated that this is likely the case. While it was beyond the scope of the present work to include model classes beyond the classic 1PL and 2PL models, it would certainly be an interesting and worthwhile endeavor for future research to evaluate the accelerators’ performances in the context of more complex model classes. One starting point in this regard may be our additional examinations of the Gaussian Mixture Model (GMM), which could be extended. More complex latent class or mixture models might also be interesting. Another angle from which extensions could build upon our results is to investigate multi- rather than unidimensional IRT models. As these models are much more complex, we could speculate that the corresponding EM trajectories are also increasingly more complex, perhaps providing better ground for PEM to unfold its potential.
Another important limitation of the present study constitutes the exclusive usage of default tuning parameters as provided by [28]. Our decision was motivated by our desire to closely mimic real applications of the EM algorithm and its accelerators in psychometric settings, where applied researchers would likely also rely on generically recommended tuning parameters. However, this may have also kept the accelerators, most notably PEM, from unfolding their full acceleration potential. It would therefore be interesting for future research to investigate which tuning parameter constellations are optimal for IRT models. Based on our results, which found differences in rank orders of the accelerators between the 1PL and 2PL models, we would also encourage future research to derive specific PEM tuning parameter recommendations for different IRT models. In the same vein, another interesting avenue for future research presents itself in the shape of exploring the possibility of self-tuning accelerators. This may be especially advantageous in the light of the observed differing performance for different IRT models and would provide general as well as user-friendly solutions for applied researchers.
Furthermore, the implementation of the accelerators in this simulation study via turboEM and an extracted EM cycle from mirt was not optimized for speed. In fact, it is not very efficient because single EM steps have to be passed from mirt to turboEM in every iteration. Thus, the absolute runtimes in our simulation are not necessarily comparable to, e.g., the runtime of standard EM as implemented and runtime optimized in mirt. This was mostly in order to ensure comparability between all acceleration methods, as they are not all available in mirt. However, it is worth pointing out that any runtime overhead due to our implementation was constant across all acceleration methods as well as standard EM, so our relative runtimes in particular are nonetheless informative and valid. An immediately following suggestion for future research certainly is the implementation of these accelerators directly in IRT software, including but not limited to mirt in R. This limitation also leads us down another avenue for future research: Exploring how to increase efficiency of the implementation of the different accelerators for IRT models. A problem to this end is the increased number of costly evaluations of the log-likelihood. One major reason for why the log-likelihood is so costly to evaluate is the integral over the latent ability, which requires some type of numerical approximation, e.g., via Gauss–Hermite (GH) quadrature. A worthwhile endeavor for future research might be to use GH quadrature with increasing numbers of quadrature points along the trajectory, starting out with cruder approximations in the beginning. This may help reduce the time cost of log-likelihood evaluations, at least for the earlier trajectory steps. To this end, further research is needed to find an optimal balance between the imprecision of approximation and speedup of the EM algorithm.
In terms of the examination of the trajectories of the EM algorithm, our results are limited to the trajectories for standard EM. It might be interesting for future research to examine the trajectories for the different accelerators in order to better understand their behavior. For example, it would be very interesting to see if accelerated trajectories are straighter and make larger steps per iteration than standard EM trajectories. Finally, our simulation study used 100 trials per simulation condition. This constituted a good trade-off between precision of average results and computational feasibility for us; however, as holds for any simulation study, results would be more reliable if the number of trials was larger. Lastly, as Ref. [29] stresses, any simulation studies comparing runtime of algorithms should be taken with (maybe a little more than) a grain of salt. We have already discussed that our implementation is likely not the most efficient, and naturally, any CPU times also depend on the CPU used. Thus, we would like to stress that attention should be paid more to the ranking of the accelerators rather than the absolute CPU times. However, even these might be different if all accelerators were implemented differently as well as run with the optimal choices for tuning parameters [29].
4. Materials and Methods
4.1. Simulation Conditions
We varied the IRT model used between a 1PL model with estimated ability variance , a 1PL model with fixed to 1, and a 2PL model ( fixed to 1 for identification purposes). Furthermore, we varied the number of items ( vs. ), focusing on more extreme ends of the spectrum to get a good idea of the behavior of the accelerators. Thus, we compared the accelerators, i.e., QN with , SQUAREM with , and PEM, in six different scenarios (see Table 5). We used two different sets of starting values in conjunction with each of the six conditions: (1) realistic starting values as provided by the R package mirt [17] and (2) less ideal starting values, which are more likely to enable the accelerators to show their full potential.

Table 5.
The six simulation conditions; var. = variance.
4.2. Generation of Item Responses
To generate the item parameters of the 2PL model in each trial, we used a bivariate truncated normal distribution to sample the discrimination () and difficulty () parameters, and then computed the intercept parameters as and slopes as for each item . This approach was inspired by but slightly adapted from [30]. As the correlation between difficulties and discriminations, we chose 0.35 (but note that this will only approximately be the underlying correlation, as we implemented the truncation via rejection sampling; see below) based on the application of a 2PL model to math achievement test data [31,32]. For the means and variances for the bivariate normal distribution, we used means of 0 and 1 for difficulties and discriminations, respectively, and variances of 1, again similarly to [30]. We also adopted their lower bounds of and for difficulties and discriminations, respectively, and upper bounds of 2 for both. We implemented the truncation by means of rejection sampling, that is, for each item , a pair of discrimination and difficulty was drawn and assigned as item parameters if both values were within the respective bounds, otherwise rejected and redrawn. For the 1PL model, item discrimination was fixed at 1 and difficulty drawn from a univariate truncated normal distribution with the same parameters and bounds as for the 2PL model (note that the respective intercept parameters are then given by ). Personal abilities were sampled randomly from a standard normal distribution. Using the slope-intercept parameterization of Equation (1) to calculate probabilities, response data for the N participants were generated from a binomial distribution in each trial. The R code used for the simulation is available as Supplementary Materials.
4.3. Simulation Procedure
In each condition and trial, we generated response data for N = 10,000 participants, as described above. We used a constant sample size across all conditions, as the EM algorithm for the 1PL and 2PL model actually looks at frequency of response patterns, rather than at individual responses, therewith factorizing the log-likelihood and resulting in the sample size having smaller leverage over the acceleration than the number of items (which increases the number of possible response patterns). What is more, acceleration of the estimation of IRT models in large samples might be interesting not just for simulation studies (where the sample size can naturally be varied arbitrarily), but also in real-life large-assessment studies that in themselves constitute a computationally expensive setting. We obtained the starting values for the EM algorithm either from the mirt::mirt function in each trial or set the starting values of all difficulties to 0 and those of all discriminations to 1 for less ideal starting values. We then used a combination of the mirt and turboEM packages [17,28], as described below, to fit the respective model of the condition with the EM algorithm in conjunction with the different accelerators. For the conditions in which the latent factor variance was estimated for the 1PL model, we used a parameter value constraint of in alignment with the mirt package. The R code used for the simulation is available as Supplementary Materials.
4.4. Implementation of Models and Accelerators
The EM accelerators, i.e., QN with , SQUAREM with , and PEM, were all implemented in our simulation study via the R package turboEM [28], which implements these methods in conjunction with globalization strategies in order to ensure global convergence if necessary (for an illustration, see Algorithms A1–A3 in Appendix A). To run the EM algorithm, we used a combination of the mirt and turboEM packages [17,28]. The mirt::mirt function implements the EM algorithm for IRT models [17]. A single (unaccelerated, i.e., standard) EM-step version of the mirt::mirt function for one EM update, i.e., the fixed-point function F, as well as the objective function (i.e., the observed log-likelihood for the current parameter estimates), was extracted from the mirt package. These functions were then used as inputs for the turboEM::turboem function, which is, in turn, used to run the EM algorithm with the various acceleration techniques as well as the standard EM algorithm (used as a benchmark in our numeric comparison). Note that this results in standard EM being implemented differently from how it is implemented in mirt, which is likely to be less efficient than the complete mirt implementation, but yields a perfectly comparable implementation of standard EM and all versions of accelerated EM. All acceleration methods were run with default tuning parameters [28]. The convergence criterion used is based on the parameter only, i.e., , in order to avoid additional evaluations of the log-likelihood. This is fairly strict, allowing the acceleration techniques the opportunity to show their full power. The maximum number of iterations was 1500, and the maximum running time was 60 s. Illustrative pseudo-code for (some of) the algorithms is provided in Appendix A (Algorithms A1–A3). The R code used for the simulation is available as Supplementary Materials.
4.5. Examination of Trajectories: Properties of F
Trajectories of F are sequences from initial starting values to the fixed point , as given by the standard EM algorithm. In order to be able to describe these for our different simulation conditions to better understand the latter, we used the following properties of F. The relative steplength is defined as the distance between successive EM updates relative to the total distance between the initial parameter estimates and the final maximum likelihood estimates :
where is the total number of iterations required to reach from the given . As approaches , approaches zero and approaches 1. The relative steplength can therefore be used to show how fast approaches the fixed point. The normalization to the total length of the trajectory, , ensures that the quantity is comparable for different starting points and models. We further define the curvature of F as the angle between successive iterations,
where and . The angle is zero if the vectors and point in the same direction, i.e., if the fixed point is approached in a straight line. If the angle is different from zero, the fixed point is approached on a curve.
5. Conclusions
To summarize, in what is, to our knowledge, the first comparison of recently proposed acceleration methods for the EM algorithm in an IRT context, we have found good performance of higher-order QN as well as higher-order SQUAREM for the 1PL model, and of first-order SQUAREM as well as higher-order QN for the 2PL model. Surprisingly, PEM neither performed as well as expected nor was able to compete with the other acceleration methods. Generally, acceleration was more successful when the latent ability variance was fixed rather than estimated. Speed-ups in computing time were more substantial in settings with one hundred than with nine items.
Supplementary Materials
The following are available online at https://www.mdpi.com/2624-8611/2/4/18/s1: R code for the simulation.
Author Contributions
Conceptualization, O.W. and P.D.; methodology, O.W., P.D., and M.B.; software, O.W. and M.B.; validation, O.W., P.D., and M.B.; formal analysis, O.W. and M.B.; investigation, O.W. and M.B.; resources, P.D.; data curation, O.W. and M.B.; writing—original draft preparation, O.W. and M.B.; writing—review and editing, P.D.; visualization, O.W. and M.B.; supervision, P.D.; project administration, P.D.; funding acquisition, not applicable. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Algorithm A1 shows pseudocode for the QN method, based on a simplified representation of the QN implementation within the turboEM:::accelerate and turboEM::: bodyQuasiNewton methods [28]. The algorithm starts with initial parameters . First, the q columns of matrix U are created from a sequence of EM updates (F; Algorithm A1, lines 1–11). Then, matrix V is created based on U and a further EM update (Algorithm A1, lines 12–16). Finally, QN updates are performed until convergence (Algorithm A1, lines 17–27). Algorithm A1 only shows a skeleton of the QN method. The implementation of the QN update in turboEM:::bodyQuasiNewton is a little more complex. For instance, parameter constraints can be supplied by the user to keep the parameter updates in turboEM:::bodyQuasiNewton within certain bounds [28]. Perhaps more importantly, there is an additional check that the negative log-likelihood is decreased (i.e., the log-likelihood is increased) by the QN update compared to the last EM update . If , the value of is set to instead [28]. This modification is used to ensure global convergence.
| Algorithm A1: Pseudocode for QN |
 |
Algorithm A2 shows pseudocode for the first-order SQUAREM method, based on [13]. It is consistent with the SQUAREM implementation within the turboEM:::accelerate and turboEM:::bodySquarem1 methods [28]. The algorithm operates on an input of initial parameter estimates . Based on these parameters, the algorithm is run until convergence. First, two successive EM updates are performed (Algorithm A2, lines 2–3) to calculate u and v (Algorithm A2, lines 4–5). Based on u and v, the steplength is computed (Algorithm A2, line 6). For global convergence, the steplength is modified if necessary (Algorithm A2, line 7). Then, the SQUAREM update is computed (Algorithm A2, line 8). Finally, an EM update of the SQUAREM update provides a new parameter estimate for the next iteration [13,28]. The algorithm can be run in three versions, “1”, “2”, or “3”, depending on which steplength is to be used. By default, the turboEM:::bodySquarem1 method uses steplength S3, as recommended by [13]. The implementation of Algorithm A2 in the turboEM:::bodySquarem1 method includes additional checks on the SQUAREM update [28]. For instance, if the user has specified constraints on the parameter space, the update must fall within the constraints. If the SQUAREM update does not increase the log-likelihood, the last EM update is used instead. Finally, upper and lower bounds are set on the steplength and modified dynamically to increase stability and convergence [28]. Pseudo-code for higher-order SQUAREM is not shown here.
| Algorithm A2: Pseudocode for SQUAREM () |
 |
Algorithm A3 shows pseudocode for the PEM acceleration method, consistent with the implementation of PEM in the turboEM:::bodyParaEM method [14,28]. First, an initial PEM update is computed for an initial value of the search parameter s (Algorithm A3, lines 2–4). If the log-likelihood is not increased by this PEM update, then the PEM update is disregarded and regular EM updates are performed instead (Algorithm A3, lines 5–9). If the log-likelihood does increase, further PEM updates are performed for increasing values of s, until the log-likelihood no longer increases (Algorithm A3, lines 11–18). The last PEM update for which the log-likelihood increased is retained, and two regular EM updates are performed on this PEM update to create the next member of the parameter estimation sequence (Algorithm A3, lines 19–22). According to [14], these two EM updates performed on the final PEM update stabilize the algorithm. Finally, the procedure is repeated until convergence.
| Algorithm A3: Pseudocode for PEM |
 |
Appendix B
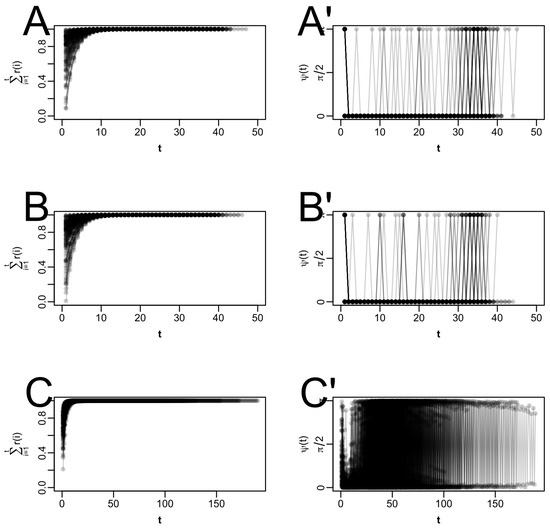
Figure A1.
Properties of F for conditions 1–3 (i.e., with nine items), with starting values 0 and 1 for all difficulties and all discriminations, respectively. For illustrative purposes, only the parameter spaces of item 1 are shown here. Note that the colors are transparent, so darker colors indicate that more trajectories pass through the same spot. For each trajectory, the cumulative relative steplength ((A) for condition 1 (1PL), (B) for condition 2 (1PL with fixed variance), (C) for condition 3 (2PL)) and the angle between successive EM updates ((A′) for condition 1, (B′) for condition 2, (C′) for condition 3) are plotted as a function of the iteration index, t.
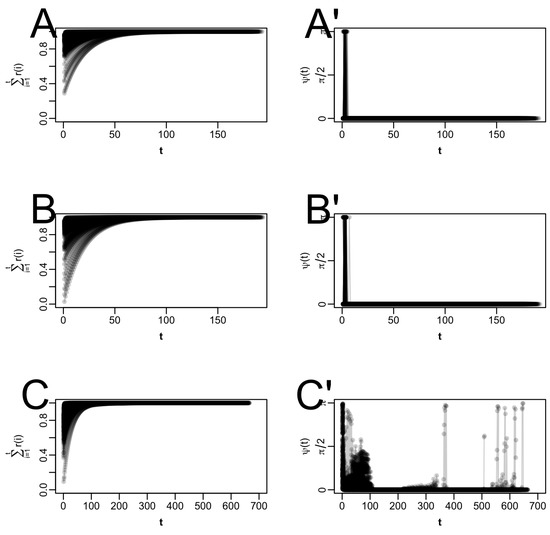
Figure A2.
Properties of F for conditions 4–6 (i.e., with 100 items), with starting values 0 and 1 for all difficulties and all discriminations, respectively. For illustrative purposes, only the parameter spaces of item 1 are shown here. Note that the colors are transparent, so darker colors indicate that more trajectories pass through the same spot. For each trajectory, the cumulative relative steplength ((A) for condition 4 (1PL), (B) for condition 5 (1PL with fixed variance), (C) for condition 6 (2PL)) and the angle between successive EM updates ((A′) for condition 4, (B′) for condition 5, (C′) for condition 6) are plotted as a function of the iteration index, t.
Appendix C
In this appendix, we provide the simulation results for a setting with persons instead of the N = 10,000 setting shown in the results section.

Table A1.
EM acceleration results for a sample of for conditions 1, 2, and 3 (all with nine items), with starting values as provided by mirt. The numbers shown represent a rounded average over 100 simulation trials. : Average number of iterations from the starting value to the fixed point; Fevals: Average number of F evaluations; Levals: Average number of log-likelihood evaluations; Conv.: Fraction of converging runs; CPU: Average CPU time in milliseconds; Rel. time: Relative computing time as compared to standard EM.
Table A1.
EM acceleration results for a sample of for conditions 1, 2, and 3 (all with nine items), with starting values as provided by mirt. The numbers shown represent a rounded average over 100 simulation trials. : Average number of iterations from the starting value to the fixed point; Fevals: Average number of F evaluations; Levals: Average number of log-likelihood evaluations; Conv.: Fraction of converging runs; CPU: Average CPU time in milliseconds; Rel. time: Relative computing time as compared to standard EM.
| Condition 1: 1PL, 9 Items | |||||||
|---|---|---|---|---|---|---|---|
| Method | Fevals | Levals | Conv. | CPU (ms) | Rel. Time | ||
| EM | 29 | 29 | 1 | 1.00 | 4.58 | 1.00 | |
| QN () | 14 | 17 | 15 | 1.00 | 9.64 | 2.10 | |
| QN () | 14 | 18 | 14 | 1.00 | 5.61 | 1.22 | |
| QN () | 13 | 18 | 13 | 1.00 | 7.03 | 1.53 | |
| QN () | 13 | 19 | 13 | 1.00 | 5.17 | 1.13 | |
| SQUAREM () | 15 | 26 | 16 | 1.00 | 11.48 | 2.51 | |
| SQUAREM () | 8 | 38 | 7 | 1.00 | 5.35 | 1.17 | |
| SQUAREM () | 6 | 37 | 5 | 1.00 | 6.48 | 1.41 | |
| SQUAREM () | 5 | 39 | 4 | 1.00 | 5.70 | 1.24 | |
| PEM | 10 | 30 | 22 | 1.00 | 5.27 | 1.15 | |
| Condition 2: 1PL (fixed var.), 9 Items | |||||||
| Method | Fevals | Levals | Conv. | CPU (ms) | Rel. Time | ||
| EM | 21 | 21 | 1 | 1.00 | 1.86 | 1.00 | |
| QN () | 8 | 12 | 17 | 1.00 | 2.72 | 1.46 | |
| QN () | 6 | 10 | 13 | 1.00 | 3.20 | 1.72 | |
| QN () | 5 | 10 | 10 | 1.00 | 1.86 | 1.00 | |
| QN () | 4 | 10 | 9 | 1.00 | 2.34 | 1.26 | |
| SQUAREM () | 10 | 11 | 11 | 1.00 | 2.55 | 1.37 | |
| SQUAREM () | 4 | 20 | 5 | 1.00 | 2.33 | 1.25 | |
| SQUAREM () | 3 | 22 | 4 | 1.00 | 2.96 | 1.59 | |
| SQUAREM () | 3 | 25 | 4 | 1.00 | 2.61 | 1.40 | |
| PEM | 5 | 21 | 12 | 1.00 | 2.61 | 1.40 | |
| Condition 3: 2PL, 9 Items | |||||||
| Method | Fevals | Levals | Conv. | CPU (ms) | Rel. Time | ||
| EM | 170 | 170 | 1 | 1.00 | 15.88 | 1.00 | |
| QN () | 92 | 95 | 183 | 1.00 | 30.86 | 1.94 | |
| QN () | 85 | 89 | 170 | 1.00 | 26.59 | 1.67 | |
| QN () | 71 | 76 | 142 | 1.00 | 21.63 | 1.36 | |
| QN () | 65 | 71 | 130 | 1.00 | 18.83 | 1.19 | |
| SQUAREM () | 86 | 109 | 87 | 1.00 | 22.63 | 1.43 | |
| SQUAREM () | 25 | 128 | 26 | 1.00 | 12.68 | 0.80 | |
| SQUAREM () | 19 | 137 | 20 | 1.00 | 12.08 | 0.76 | |
| SQUAREM () | 13 | 118 | 14 | 1.00 | 10.45 | 0.66 | |
| PEM | 27 | 64 | 99 | 1.00 | 11.71 | 0.74 |

Table A2.
EM acceleration results for a sample of for conditions 4, 5, and 6 (all with 100 items), with starting values as provided by mirt. The numbers shown represent a rounded average over 100 simulation trials. : Average number of iterations from the starting value to the fixed point; Fevals: Average number of F evaluations; Levals: Average number of log-likelihood evaluations; Conv.: Fraction of converging runs; CPU: Average CPU time in milliseconds; Rel. time: Relative computing time as compared to standard EM.
Table A2.
EM acceleration results for a sample of for conditions 4, 5, and 6 (all with 100 items), with starting values as provided by mirt. The numbers shown represent a rounded average over 100 simulation trials. : Average number of iterations from the starting value to the fixed point; Fevals: Average number of F evaluations; Levals: Average number of log-likelihood evaluations; Conv.: Fraction of converging runs; CPU: Average CPU time in milliseconds; Rel. time: Relative computing time as compared to standard EM.
| Condition 4: 1PL, 100 Items | |||||||
|---|---|---|---|---|---|---|---|
| Method | Fevals | Levals | Conv. | CPU (ms) | Rel. Time | ||
| EM | 77 | 77 | 1 | 1.00 | 31.41 | 1.00 | |
| QN () | 39 | 42 | 39 | 1.00 | 38.07 | 1.21 | |
| QN () | 38 | 42 | 38 | 1.00 | 38.35 | 1.22 | |
| QN () | 38 | 43 | 38 | 1.00 | 37.47 | 1.19 | |
| QN () | 37 | 43 | 37 | 1.00 | 36.93 | 1.18 | |
| SQUAREM () | 39 | 76 | 40 | 1.00 | 50.72 | 1.61 | |
| SQUAREM () | 20 | 99 | 20 | 1.00 | 38.49 | 1.23 | |
| SQUAREM () | 14 | 93 | 13 | 0.91 | 37.55 | 1.20 | |
| SQUAREM () | 11 | 90 | 10 | 0.89 | 34.13 | 1.09 | |
| PEM | 34 | 79 | 70 | 1.00 | 44.10 | 1.40 | |
| Condition 5: 1PL (fixed var.), 100 Items | |||||||
| Method | Fevals | Levals | Conv. | CPU (ms) | Rel. Time | ||
| EM | 131 | 131 | 1 | 1.00 | 42.85 | 1.00 | |
| QN () | 52 | 55 | 104 | 1.00 | 59.80 | 1.40 | |
| QN () | 34 | 38 | 69 | 1.00 | 41.83 | 0.98 | |
| QN () | 20 | 25 | 39 | 1.00 | 24.99 | 0.58 | |
| QN () | 10 | 16 | 20 | 1.00 | 14.41 | 0.34 | |
| SQUAREM () | 44 | 71 | 45 | 1.00 | 46.38 | 1.08 | |
| SQUAREM () | 7 | 38 | 8 | 1.00 | 17.12 | 0.40 | |
| SQUAREM () | 6 | 43 | 7 | 1.00 | 17.45 | 0.41 | |
| SQUAREM () | 6 | 52 | 7 | 1.00 | 15.69 | 0.37 | |
| PEM | 18 | 45 | 66 | 1.00 | 32.42 | 0.76 | |
| Condition 6: 2PL, 100 Items | |||||||
| Method | Fevals | Levals | Conv. | CPU (ms) | Rel. Time | ||
| EM | 283 | 283 | 1 | 1.00 | 103.86 | 1.00 | |
| QN () | 127 | 130 | 254 | 1.00 | 155.51 | 1.50 | |
| QN () | 113 | 117 | 226 | 1.00 | 139.85 | 1.35 | |
| QN () | 111 | 116 | 222 | 1.00 | 137.81 | 1.33 | |
| QN () | 100 | 106 | 200 | 1.00 | 125.73 | 1.21 | |
| SQUAREM () | 111 | 153 | 112 | 1.00 | 118.03 | 1.14 | |
| SQUAREM () | 19 | 98 | 20 | 1.00 | 44.41 | 0.43 | |
| SQUAREM () | 14 | 96 | 15 | 1.00 | 42.88 | 0.41 | |
| SQUAREM () | 12 | 111 | 13 | 1.00 | 47.56 | 0.46 | |
| PEM | 70 | 151 | 216 | 1.00 | 108.00 | 1.04 |

Table A3.
EM acceleration results for a sample of for conditions 1, 2, and 3 (all with nine items), with starting values 0 and 1 for all difficulties and discriminations, respectively. The numbers shown represent a rounded average over 100 simulation trials. : Average number of iterations from the starting value to the fixed point; Fevals: Average number of F evaluations; Levals: Average number of log-likelihood evaluations; Conv.: Fraction of converging runs; CPU: Average CPU time in milliseconds; Rel. time: Relative computing time as compared to standard EM.
Table A3.
EM acceleration results for a sample of for conditions 1, 2, and 3 (all with nine items), with starting values 0 and 1 for all difficulties and discriminations, respectively. The numbers shown represent a rounded average over 100 simulation trials. : Average number of iterations from the starting value to the fixed point; Fevals: Average number of F evaluations; Levals: Average number of log-likelihood evaluations; Conv.: Fraction of converging runs; CPU: Average CPU time in milliseconds; Rel. time: Relative computing time as compared to standard EM.
| Condition 1: 1PL, 9 Items | |||||||
|---|---|---|---|---|---|---|---|
| Method | Fevals | Levals | Conv. | CPU (ms) | Rel. Time | ||
| EM | 32 | 32 | 1 | 1.00 | 3.09 | 1.00 | |
| QN () | 15 | 18 | 16 | 1.00 | 4.03 | 1.30 | |
| QN () | 15 | 19 | 15 | 1.00 | 4.02 | 1.30 | |
| QN () | 14 | 19 | 15 | 1.00 | 4.74 | 1.53 | |
| QN () | 14 | 20 | 14 | 1.00 | 4.00 | 1.29 | |
| SQUAREM () | 16 | 29 | 17 | 1.00 | 5.99 | 1.94 | |
| SQUAREM () | 8 | 40 | 8 | 1.00 | 4.65 | 1.50 | |
| SQUAREM () | 6 | 40 | 6 | 1.00 | 4.63 | 1.50 | |
| SQUAREM () | 5 | 40 | 5 | 1.00 | 4.54 | 1.47 | |
| PEM | 11 | 32 | 24 | 1.00 | 5.18 | 1.68 | |
| Condition 2: 1PL (fixed var.), 9 Items | |||||||
| Method | Fevals | Levals | Conv. | CPU (ms) | Rel. Time | ||
| EM | 30 | 30 | 1 | 1.00 | 2.75 | 1.00 | |
| QN () | 10 | 13 | 20 | 1.00 | 3.13 | 1.14 | |
| QN () | 8 | 12 | 15 | 1.00 | 2.31 | 0.84 | |
| QN () | 7 | 12 | 14 | 1.00 | 2.47 | 0.90 | |
| QN () | 7 | 13 | 14 | 1.00 | 2.76 | 1.00 | |
| SQUAREM () | 12 | 13 | 12 | 1.00 | 3.41 | 1.24 | |
| SQUAREM () | 4 | 23 | 5 | 1.00 | 2.56 | 0.93 | |
| SQUAREM () | 4 | 26 | 5 | 1.00 | 2.26 | 0.82 | |
| SQUAREM () | 3 | 29 | 4 | 1.00 | 2.81 | 1.02 | |
| PEM | 9 | 29 | 26 | 1.00 | 4.60 | 1.67 | |
| Condition 3: 2PL, 9 Items | |||||||
| Method | Fevals | Levals | Conv. | CPU (ms) | Rel. Time | ||
| EM | 176 | 176 | 1 | 1.00 | 17.04 | 1.00 | |
| QN () | 104 | 107 | 207 | 1.00 | 33.68 | 1.98 | |
| QN () | 92 | 96 | 184 | 1.00 | 30.69 | 1.80 | |
| QN () | 82 | 87 | 164 | 1.00 | 22.96 | 1.35 | |
| QN () | 70 | 76 | 139 | 1.00 | 19.65 | 1.15 | |
| SQUAREM () | 95 | 113 | 96 | 1.00 | 22.92 | 1.35 | |
| SQUAREM () | 39 | 198 | 40 | 1.00 | 16.85 | 0.99 | |
| SQUAREM () | 34 | 240 | 35 | 1.00 | 20.63 | 1.21 | |
| SQUAREM () | 24 | 221 | 25 | 1.00 | 17.99 | 1.06 | |
| PEM | 33 | 75 | 134 | 1.00 | 14.57 | 0.86 |

Table A4.
EM acceleration results for a sample of for conditions 4, 5, and 6 (all with 100 items), with starting values 0 and 1 for all difficulties and discriminations, respectively. The numbers shown represent a rounded average over 100 simulation trials. : Average number of iterations from the starting value to the fixed point; Fevals: Average number of F evaluations; Levals: Average number of log-likelihood evaluations; Conv.: Fraction of converging runs; CPU: Average CPU time in milliseconds; Rel. time: Relative computing time as compared to standard EM.
Table A4.
EM acceleration results for a sample of for conditions 4, 5, and 6 (all with 100 items), with starting values 0 and 1 for all difficulties and discriminations, respectively. The numbers shown represent a rounded average over 100 simulation trials. : Average number of iterations from the starting value to the fixed point; Fevals: Average number of F evaluations; Levals: Average number of log-likelihood evaluations; Conv.: Fraction of converging runs; CPU: Average CPU time in milliseconds; Rel. time: Relative computing time as compared to standard EM.
| Condition 4: 1PL, 100 Items | |||||||
|---|---|---|---|---|---|---|---|
| Method | Fevals | Levals | Conv. | CPU (ms) | Rel. Time | ||
| EM | 126 | 126 | 1 | 1.00 | 47.97 | 1.00 | |
| QN () | 63 | 66 | 63 | 1.00 | 69.60 | 1.45 | |
| QN () | 63 | 67 | 63 | 1.00 | 69.55 | 1.45 | |
| QN () | 62 | 67 | 62 | 1.00 | 69.06 | 1.44 | |
| QN () | 62 | 68 | 62 | 1.00 | 67.81 | 1.41 | |
| SQUAREM () | 64 | 125 | 65 | 1.00 | 92.78 | 1.93 | |
| SQUAREM () | 32 | 158 | 32 | 0.96 | 74.39 | 1.55 | |
| SQUAREM () | 21 | 146 | 21 | 0.85 | 66.58 | 1.39 | |
| SQUAREM () | 16 | 143 | 16 | 0.77 | 64.01 | 1.33 | |
| PEM | 59 | 127 | 118 | 1.00 | 82.71 | 1.72 | |
| Condition 5: 1PL (fixed var.), 100 Items | |||||||
| Method | Fevals | Levals | Conv. | CPU (ms) | Rel. Time | ||
| EM | 187 | 187 | 1 | 1.00 | 65.00 | 1.00 | |
| QN () | 56 | 59 | 112 | 1.00 | 71.80 | 1.10 | |
| QN () | 42 | 46 | 83 | 1.00 | 55.62 | 0.86 | |
| QN () | 30 | 35 | 60 | 1.00 | 43.05 | 0.66 | |
| QN () | 22 | 28 | 45 | 1.00 | 34.12 | 0.52 | |
| SQUAREM () | 54 | 88 | 55 | 1.00 | 70.65 | 1.09 | |
| SQUAREM () | 10 | 49 | 11 | 1.00 | 23.65 | 0.36 | |
| SQUAREM () | 8 | 54 | 9 | 1.00 | 25.63 | 0.39 | |
| SQUAREM () | 7 | 62 | 8 | 1.00 | 29.35 | 0.45 | |
| PEM | 19 | 48 | 77 | 1.00 | 41.76 | 0.64 | |
| Condition 6: 2PL, 100 Items | |||||||
| Method | Fevals | Levals | Conv. | CPU (ms) | Rel. Time | ||
| EM | 344 | 344 | 1 | 1.00 | 122.69 | 1.00 | |
| QN () | 136 | 139 | 271 | 1.00 | 180.54 | 1.47 | |
| QN () | 113 | 117 | 226 | 1.00 | 148.52 | 1.21 | |
| QN () | 109 | 114 | 218 | 1.00 | 147.79 | 1.20 | |
| QN () | 99 | 105 | 199 | 1.00 | 128.62 | 1.05 | |
| SQUAREM () | 122 | 178 | 123 | 1.00 | 144.51 | 1.18 | |
| SQUAREM () | 20 | 103 | 21 | 1.00 | 50.94 | 0.42 | |
| SQUAREM () | 17 | 117 | 18 | 1.00 | 53.58 | 0.44 | |
| SQUAREM () | 14 | 124 | 15 | 1.00 | 53.24 | 0.43 | |
| PEM | 66 | 141 | 221 | 1.00 | 115.04 | 0.94 |
Appendix D
In this appendix, we provide the simulation results for a setting with persons instead of the N = 10,000 setting shown in the results section.

Table A5.
EM acceleration results for a sample of for conditions 1, 2, and 3 (all with nine items), with starting values as provided by mirt. The numbers shown represent a rounded average over 100 simulation trials. : Average number of iterations from the starting value to the fixed point; Fevals: Average number of F evaluations; Levals: Average number of log-likelihood evaluations; Conv.: Fraction of converging runs; CPU: Average CPU time in milliseconds; Rel. time: Relative computing time as compared to standard EM.
Table A5.
EM acceleration results for a sample of for conditions 1, 2, and 3 (all with nine items), with starting values as provided by mirt. The numbers shown represent a rounded average over 100 simulation trials. : Average number of iterations from the starting value to the fixed point; Fevals: Average number of F evaluations; Levals: Average number of log-likelihood evaluations; Conv.: Fraction of converging runs; CPU: Average CPU time in milliseconds; Rel. time: Relative computing time as compared to standard EM.
| Condition 1: 1PL, 9 Items | |||||||
|---|---|---|---|---|---|---|---|
| Method | Fevals | Levals | Conv. | CPU (ms) | Rel. Time | ||
| EM | 30 | 30 | 1 | 1.00 | 25.91 | 1.00 | |
| QN () | 14 | 17 | 15 | 1.00 | 24.67 | 0.95 | |
| QN () | 14 | 18 | 14 | 1.00 | 18.00 | 0.69 | |
| QN () | 13 | 18 | 14 | 1.00 | 18.32 | 0.71 | |
| QN () | 13 | 19 | 13 | 1.00 | 25.11 | 0.97 | |
| SQUAREM () | 15 | 27 | 16 | 1.00 | 21.41 | 0.83 | |
| SQUAREM () | 8 | 38 | 7 | 1.00 | 15.28 | 0.59 | |
| SQUAREM () | 6 | 38 | 5 | 1.00 | 13.87 | 0.54 | |
| SQUAREM () | 5 | 38 | 4 | 1.00 | 15.83 | 0.61 | |
| PEM | 10 | 30 | 22 | 1.00 | 16.21 | 0.63 | |
| Condition 2: 1PL (fixed var.), 9 Items | |||||||
| Method | Fevals | Levals | Conv. | CPU (ms) | Rel. Time | ||
| EM | 22 | 22 | 1 | 1.00 | 7.75 | 1.00 | |
| QN () | 8 | 11 | 17 | 1.00 | 21.01 | 2.71 | |
| QN () | 7 | 11 | 14 | 1.00 | 9.84 | 1.27 | |
| QN () | 5 | 10 | 10 | 1.00 | 9.39 | 1.21 | |
| QN () | 4 | 10 | 8 | 1.00 | 6.72 | 0.87 | |
| SQUAREM () | 10 | 11 | 11 | 1.00 | 13.45 | 1.74 | |
| SQUAREM () | 4 | 21 | 5 | 1.00 | 11.58 | 1.49 | |
| SQUAREM () | 3 | 22 | 4 | 1.00 | 9.61 | 1.24 | |
| SQUAREM () | 3 | 25 | 4 | 1.00 | 8.75 | 1.13 | |
| PEM | 5 | 21 | 13 | 1.00 | 12.11 | 1.56 | |
| Condition 3: 2PL, 9 Items | |||||||
| Method | Fevals | Levals | Conv. | CPU (ms) | Rel. Time | ||
| EM | 74 | 74 | 1 | 1.00 | 25.08 | 1.00 | |
| QN () | 34 | 37 | 68 | 1.00 | 35.03 | 1.40 | |
| QN () | 29 | 33 | 58 | 1.00 | 29.94 | 1.19 | |
| QN () | 25 | 30 | 51 | 1.00 | 23.82 | 0.95 | |
| QN () | 22 | 28 | 44 | 1.00 | 21.82 | 0.87 | |
| SQUAREM () | 31 | 41 | 32 | 1.00 | 28.81 | 1.15 | |
| SQUAREM () | 11 | 56 | 12 | 1.00 | 16.84 | 0.67 | |
| SQUAREM () | 8 | 56 | 9 | 1.00 | 14.24 | 0.57 | |
| SQUAREM () | 7 | 62 | 8 | 1.00 | 15.79 | 0.63 | |
| PEM | 19 | 48 | 63 | 1.00 | 25.16 | 1.00 |

Table A6.
EM acceleration results for a sample of for conditions 4, 5, and 6 (all with 100 items), with starting values as provided by mirt. The numbers shown represent a rounded average over 100 simulation trials. : Average number of iterations from the starting value to the fixed point; Fevals: Average number of F evaluations; Levals: Average number of log-likelihood evaluations; Conv.: Fraction of converging runs; CPU: Average CPU time in milliseconds; Rel. time: Relative computing time as compared to standard EM.
Table A6.
EM acceleration results for a sample of for conditions 4, 5, and 6 (all with 100 items), with starting values as provided by mirt. The numbers shown represent a rounded average over 100 simulation trials. : Average number of iterations from the starting value to the fixed point; Fevals: Average number of F evaluations; Levals: Average number of log-likelihood evaluations; Conv.: Fraction of converging runs; CPU: Average CPU time in milliseconds; Rel. time: Relative computing time as compared to standard EM.
| Condition 4: 1PL, 100 Items | |||||||
|---|---|---|---|---|---|---|---|
| Method | Fevals | Levals | Conv. | CPU (ms) | Rel. Time | ||
| EM | 81 | 81 | 1 | 1.00 | 112.03 | 1.00 | |
| QN () | 40 | 44 | 40 | 1.00 | 151.52 | 1.35 | |
| QN () | 40 | 44 | 40 | 1.00 | 154.62 | 1.38 | |
| QN () | 40 | 44 | 40 | 1.00 | 137.46 | 1.23 | |
| QN () | 39 | 45 | 39 | 1.00 | 135.70 | 1.21 | |
| SQUAREM () | 41 | 80 | 42 | 1.00 | 189.39 | 1.69 | |
| SQUAREM () | 21 | 103 | 21 | 1.00 | 151.86 | 1.36 | |
| SQUAREM () | 14 | 98 | 14 | 1.00 | 126.50 | 1.13 | |
| SQUAREM () | 11 | 96 | 11 | 1.00 | 151.89 | 1.36 | |
| PEM | 36 | 82 | 73 | 1.00 | 191.69 | 1.71 | |
| Condition 5: 1PL (fixed var.), 100 Items | |||||||
| Method | Fevals | Levals | Conv. | CPU (ms) | Rel. Time | ||
| EM | 121 | 121 | 1 | 1.00 | 131.40 | 1.00 | |
| QN () | 50 | 53 | 100 | 1.00 | 200.08 | 1.52 | |
| QN () | 34 | 38 | 67 | 1.00 | 122.34 | 0.93 | |
| QN () | 20 | 25 | 40 | 1.00 | 77.66 | 0.59 | |
| QN () | 8 | 14 | 17 | 1.00 | 37.60 | 0.29 | |
| SQUAREM () | 42 | 67 | 43 | 1.00 | 142.42 | 1.08 | |
| SQUAREM () | 6 | 30 | 7 | 1.00 | 33.39 | 0.25 | |
| SQUAREM () | 5 | 38 | 6 | 1.00 | 45.28 | 0.34 | |
| SQUAREM () | 5 | 45 | 6 | 1.00 | 55.58 | 0.42 | |
| PEM | 16 | 43 | 64 | 1.00 | 110.85 | 0.84 | |
| Condition 6: 2PL, 100 Items | |||||||
| Method | Fevals | Levals | Conv. | CPU (ms) | Rel. Time | ||
| EM | 245 | 245 | 1 | 1.00 | 249.30 | 1.00 | |
| QN () | 106 | 109 | 212 | 1.00 | 386.26 | 1.55 | |
| QN () | 101 | 105 | 203 | 1.00 | 362.95 | 1.46 | |
| QN () | 96 | 101 | 192 | 1.00 | 355.50 | 1.43 | |
| QN () | 87 | 93 | 173 | 1.00 | 367.72 | 1.48 | |
| SQUAREM () | 90 | 143 | 91 | 1.00 | 344.84 | 1.38 | |
| SQUAREM () | 18 | 91 | 19 | 1.00 | 129.34 | 0.52 | |
| SQUAREM () | 14 | 99 | 15 | 1.00 | 123.45 | 0.50 | |
| SQUAREM () | 12 | 107 | 13 | 1.00 | 130.49 | 0.52 | |
| PEM | 51 | 112 | 184 | 1.00 | 295.09 | 1.18 |

Table A7.
EM acceleration results for a sample of for conditions 1, 2, and 3 (all with nine items), with starting values 0 and 1 for all difficulties and discriminations, respectively. The numbers shown represent a rounded average over 100 simulation trials. : Average number of iterations from the starting value to the fixed point; Fevals: Average number of F evaluations; Levals: Average number of log-likelihood evaluations; Conv.: Fraction of converging runs; CPU: Average CPU time in milliseconds; Rel. time: Relative computing time as compared to standard EM.
Table A7.
EM acceleration results for a sample of for conditions 1, 2, and 3 (all with nine items), with starting values 0 and 1 for all difficulties and discriminations, respectively. The numbers shown represent a rounded average over 100 simulation trials. : Average number of iterations from the starting value to the fixed point; Fevals: Average number of F evaluations; Levals: Average number of log-likelihood evaluations; Conv.: Fraction of converging runs; CPU: Average CPU time in milliseconds; Rel. time: Relative computing time as compared to standard EM.
| Condition 1: 1PL, 9 Items | |||||||
|---|---|---|---|---|---|---|---|
| Method | Fevals | Levals | Conv. | CPU (ms) | Rel. Time | ||
| EM | 33 | 33 | 1 | 1.00 | 18.44 | 1.00 | |
| QN () | 16 | 19 | 16 | 1.00 | 18.24 | 0.99 | |
| QN () | 16 | 20 | 16 | 1.00 | 14.44 | 0.78 | |
| QN () | 15 | 20 | 15 | 1.00 | 17.11 | 0.93 | |
| QN () | 15 | 21 | 15 | 1.00 | 13.95 | 0.76 | |
| SQUAREM () | 17 | 31 | 18 | 1.00 | 19.44 | 1.05 | |
| SQUAREM () | 9 | 42 | 8 | 1.00 | 14.02 | 0.76 | |
| SQUAREM () | 6 | 42 | 6 | 1.00 | 13.56 | 0.74 | |
| SQUAREM () | 5 | 42 | 5 | 1.00 | 11.83 | 0.64 | |
| PEM | 12 | 34 | 26 | 1.00 | 19.53 | 1.06 | |
| Condition 2: 1PL (fixed var.), 9 Items | |||||||
| Method | Fevals | Levals | Conv. | CPU (ms) | Rel. Time | ||
| EM | 29 | 29 | 1 | 1.00 | 11.22 | 1.00 | |
| QN () | 10 | 13 | 20 | 1.00 | 14.18 | 1.26 | |
| QN () | 8 | 12 | 15 | 1.00 | 10.56 | 0.94 | |
| QN () | 7 | 12 | 14 | 1.00 | 10.16 | 0.91 | |
| QN () | 7 | 13 | 15 | 1.00 | 9.19 | 0.82 | |
| SQUAREM () | 12 | 13 | 13 | 1.00 | 9.95 | 0.89 | |
| SQUAREM () | 4 | 22 | 5 | 1.00 | 8.83 | 0.79 | |
| SQUAREM () | 3 | 25 | 4 | 1.00 | 8.15 | 0.73 | |
| SQUAREM () | 3 | 29 | 4 | 1.00 | 9.39 | 0.84 | |
| PEM | 9 | 28 | 26 | 1.00 | 13.52 | 1.20 | |
| Condition 3: 2PL, 9 Items | |||||||
| Method | Fevals | Levals | Conv. | CPU (ms) | Rel. Time | ||
| EM | 81 | 81 | 1 | 1.00 | 25.85 | 1.00 | |
| QN () | 37 | 40 | 74 | 1.00 | 37.47 | 1.45 | |
| QN () | 32 | 36 | 63 | 1.00 | 34.69 | 1.34 | |
| QN () | 28 | 33 | 55 | 1.00 | 31.63 | 1.22 | |
| QN () | 24 | 30 | 49 | 1.00 | 26.66 | 1.03 | |
| SQUAREM () | 34 | 44 | 35 | 1.00 | 33.74 | 1.31 | |
| SQUAREM () | 12 | 60 | 13 | 1.00 | 16.61 | 0.64 | |
| SQUAREM () | 9 | 61 | 10 | 1.00 | 17.71 | 0.69 | |
| SQUAREM () | 7 | 68 | 8 | 1.00 | 21.52 | 0.83 | |
| PEM | 21 | 52 | 68 | 1.00 | 27.97 | 1.08 |

Table A8.
EM acceleration results for a sample of for conditions 4, 5, and 6 (all with 100 items), with starting values 0 and 1 for all difficulties and discriminations, respectively. The numbers shown represent a rounded average over 100 simulation trials. : Average number of iterations from the starting value to the fixed point; Fevals: Average number of F evaluations; Levals: Average number of log-likelihood evaluations; Conv.: Fraction of converging runs; CPU: Average CPU time in milliseconds; Rel. time: Relative computing time as compared to standard EM.
Table A8.
EM acceleration results for a sample of for conditions 4, 5, and 6 (all with 100 items), with starting values 0 and 1 for all difficulties and discriminations, respectively. The numbers shown represent a rounded average over 100 simulation trials. : Average number of iterations from the starting value to the fixed point; Fevals: Average number of F evaluations; Levals: Average number of log-likelihood evaluations; Conv.: Fraction of converging runs; CPU: Average CPU time in milliseconds; Rel. time: Relative computing time as compared to standard EM.
| Condition 4: 1PL, 100 Items | |||||||
|---|---|---|---|---|---|---|---|
| Method | Fevals | Levals | Conv. | CPU (ms) | Rel. Time | ||
| EM | 140 | 140 | 1 | 1.00 | 167.68 | 1.00 | |
| QN () | 70 | 73 | 70 | 1.00 | 199.63 | 1.19 | |
| QN () | 70 | 74 | 70 | 1.00 | 211.01 | 1.26 | |
| QN () | 69 | 74 | 69 | 1.00 | 200.21 | 1.19 | |
| QN () | 69 | 75 | 69 | 1.00 | 209.90 | 1.25 | |
| SQUAREM () | 71 | 139 | 72 | 1.00 | 286.52 | 1.71 | |
| SQUAREM () | 36 | 177 | 35 | 0.99 | 209.01 | 1.25 | |
| SQUAREM () | 24 | 166 | 24 | 0.94 | 190.41 | 1.14 | |
| SQUAREM () | 18 | 160 | 18 | 0.82 | 197.89 | 1.18 | |
| PEM | 66 | 142 | 133 | 1.00 | 287.87 | 1.72 | |
| Condition 5: 1PL (fixed var.), 100 Items | |||||||
| Method | Fevals | Levals | Conv. | CPU (ms) | Rel. Time | ||
| EM | 188 | 188 | 1 | 1.00 | 219.15 | 1.00 | |
| QN () | 58 | 61 | 117 | 1.00 | 214.54 | 0.98 | |
| QN () | 39 | 43 | 78 | 1.00 | 139.70 | 0.64 | |
| QN () | 30 | 35 | 60 | 1.00 | 112.24 | 0.51 | |
| QN () | 22 | 28 | 44 | 1.00 | 82.50 | 0.38 | |
| SQUAREM () | 54 | 90 | 55 | 1.00 | 181.50 | 0.83 | |
| SQUAREM () | 9 | 47 | 10 | 1.00 | 54.92 | 0.25 | |
| SQUAREM () | 7 | 53 | 8 | 1.00 | 58.67 | 0.27 | |
| SQUAREM () | 7 | 67 | 8 | 1.00 | 85.37 | 0.39 | |
| PEM | 20 | 51 | 80 | 1.00 | 166.40 | 0.76 | |
| Condition 6: 2PL, 100 Items | |||||||
| Method | Fevals | Levals | Conv. | CPU (ms) | Rel. Time | ||
| EM | 304 | 304 | 1 | 1.00 | 300.58 | 1.00 | |
| QN () | 113 | 116 | 226 | 1.00 | 397.73 | 1.32 | |
| QN () | 103 | 107 | 205 | 1.00 | 365.66 | 1.22 | |
| QN () | 96 | 101 | 192 | 1.00 | 328.40 | 1.09 | |
| QN () | 88 | 94 | 177 | 1.00 | 328.62 | 1.09 | |
| SQUAREM () | 100 | 163 | 101 | 1.00 | 382.44 | 1.27 | |
| SQUAREM () | 19 | 94 | 20 | 1.00 | 140.33 | 0.47 | |
| SQUAREM () | 15 | 105 | 16 | 1.00 | 144.42 | 0.48 | |
| SQUAREM () | 13 | 117 | 14 | 1.00 | 147.19 | 0.49 | |
| PEM | 53 | 116 | 189 | 1.00 | 337.60 | 1.12 |
Appendix E
In this appendix, we wanted to give a brief impression of how far our results for IRT—in particular, 1PL and 2PL—models are likely to generalize to other model classes. To this end, we briefly examined the accelerators’ performance in the context of the Maximum Likelihood (ML) estimation for Gaussian mixture models (GMM). A Gaussian mixture model describes an observable random variable X with a multimodal distribution generated by the sum of K subpopulations of X. Each subpopulation is produced by an independent random variable , which follows a multivariate (d-dimensional) normal distribution with expected value and variance . A latent, multinomial random variable Z determines which subpopulation a given value of X comes from. In other words, X can be written as [9]
Here, is an indicator function, which equals 1 if and 0 otherwise. For a given subpopulation k, X therefore follows a multivariate normal distribution, i.e., the conditional probability density function of X given is
for with and [9]. Because Z is a multinomial variable, the probability distribution of Z is given by , with . The marginal log-likelihood for the GMM is given by [9]:
Assuming that the GMM is a widely known model and its estimation with the EM algorithm is a standard application of the EM algorithm, we are not going to go into more detail here with the model description or the EM algorithm for this model, but instead refer the interested reader to [9]. In the following, we are going to describe a brief simulation aimed at garnering an impression of how the accelerators behave in a different model class. To reduce complexity in this brief additional simulation comprising four different settings, only two subpopulations are considered (), where is the probability of being in the first subpopulation, and . To reduce complexity further, the first three settings deal only with one dimension (), whereas the fourth setting studies the effect of increasing the number of dimensions. During the maximization step, the optimization of is independent of all other parameters (for ), and the optimizations of the parameters of the subpopulations are independent of each other, although of course, the optimization depends on the membership probabilities calculated during the expectation step, which depend on all parameters. Still, to study the properties of the EM algorithm, it is illustrative to vary only the parameters of one subpopulation. The first subpopulation shall be distributed as and the second subpopulation as . Then, three simple cases are studied that are illustrative in their simplicity, but still also relevant in the sense that many one-dimensional datasets can be transformed in such a way that they fall into one of these categories. Furthermore, to study the effect of increasing the dimensions of , a fourth setting is examined:
- Setting 1.
- Let be known, and variances be equal . In this case, acceleration of the EM algorithm for the estimation of proportions is examined. Because can be optimized independently of all other parameters, all other parameters are kept constant.
- Setting 2.
- Let be known, and variances be equal . In this case, acceleration of the EM algorithm for the estimation of location and equal variance in two subpopulations is investigated. Because is independent of the parameters of the second subpopulation, its estimation is no longer of interest, and it is kept constant.
- Setting 3.
- Let be known . In this case, acceleration of the EM algorithm for the estimation of location and variance of one subpopulation is analyzed. Because , and are independent of the parameters of the second subpopulation, their estimation is no longer of interest.
- Setting 4.
- Let be known, and and be unknown . By increasing the dimension of X (), the dimension of is increased to . This case addresses the question of how this increase in dimensions affects the acceleration of the EM algorithm.
To ensure comparability between the four settings in this brief additional simulation, a single Gaussian mixture dataset is simulated. The simulated dataset is shown in Figure A3. The total number of observations is N = 100,000 (as in the main simulations of this work, this is to examine a large-assessment setting; as we have also seen in the main simulations, results may be different in smaller samples). For (Settings 1–3), the dataset is characterized by the real parameter values of , , , , and . For (Setting 4), the same data are used for the first dimension, but additional dimensions are simulated with the real parameter values and (not shown).
Figure A3.
Simulated Gaussian mixture model (GMM) dataset in one dimension () with two subpopulations (). Blue: the first subpopulation. Red: the second subpopulation. The dataset is simulated in R with the rnorm function and parameter values , , , , and . The total number of observations in the dataset is .
In the following, we are going to present the results obtained from this brief simulation, in which we compared the acceleration methods described in the main text in the four settings outlined above. The implementation of the simulation in R is similar to what we have described in the main text for the IRT simulation, and thus will not be reiterated here. For this brief simulation, which was mostly intended as an illustration of the accelerators’ behavior in model classes other than (logistic) IRT models, we only ran 16 trials in each setting, which were characterized by 16 different starting values for (ranging from 0.05 to 0.95 in equidistanced steps for the first setting), as well as by 16 different pairs of starting values for and or (ranging from 0 to 6 for , and 0.1 to 3 for ) for the second and third setting, respectively. The starting values and in setting 4 were the same as in setting 3; the starting values for are set to zero.
For the most simple setting, setting 1, in which we only estimate one parameter, only the first-order variants of SQUAREM and QN are studied. For PEM, only three initial EM updates that do not count towards the total number of iterations were performed. In line with the main simulations of this work, default tuning parameters were used (otherwise). As convergence criterion, was used because it does not require additional evaluations of the log-likelihood. The results, averaged for the 16 runs, are shown in Table A9. All three methods studied (QN (), SQUAREM (), and PEM) converge to the fixed point in all 16 runs (Table A9). The total number of iterations required to reach the fixed point is reduced three- to four-fold on average in all three methods studied compared to standard EM, from 11 to 3 (QN) or 4 (SQUAREM and PEM; Table A9). However, since the acceleration methods do require at least two evaluations of F per iteration, the total number of F evaluations is only reduced by less than half in QN and SQUAREM (from 11 to 6 or 7) and not greatly reduced with PEM (from 11 to 10), which has to perform three additional EM updates to obtain initial points for the Bezier parabola before it can start. As expected, the number of log-likelihood evaluations is larger for the accelerated methods than for EM, increasing the acceleration cost. However, even so, the CPU time spent on QN and SQUAREM is greatly reduced (Table A9). For PEM, which has the highest number of log-likelihood evaluations due to exploration of the parameter space, the CPU time actually increases compared to EM. However, perhaps in this example, there is not much scope for PEM to show its full power because even the standard EM algorithm only requires 11 steps for completion.

Table A9.
EM acceleration results for GMM setting 1 based on runs performed in R with the package turboEM, with the sixteen different starting values, and with as the convergence criterion. The numbers shown represent a rounded average over the sixteen runs. MLE: Maximum likelihood estimate (fixed point); : Average number of iterations from the starting value to the fixed point; Fevals: Average number of F evaluations; Levals: Average number of log-likelihood evaluations; Conv.: Fraction of converging runs; CPU: Average CPU time in milliseconds; Rel. Time: Computing time relative to standard EM.
Table A9.
EM acceleration results for GMM setting 1 based on runs performed in R with the package turboEM, with the sixteen different starting values, and with as the convergence criterion. The numbers shown represent a rounded average over the sixteen runs. MLE: Maximum likelihood estimate (fixed point); : Average number of iterations from the starting value to the fixed point; Fevals: Average number of F evaluations; Levals: Average number of log-likelihood evaluations; Conv.: Fraction of converging runs; CPU: Average CPU time in milliseconds; Rel. Time: Computing time relative to standard EM.
| Method | MLE () | Fevals | Levals | Conv. | CPU (ms) | Rel. Time | ||
|---|---|---|---|---|---|---|---|---|
| EM | (0.7496) | 11 | 11 | 1 | 1.00 | 11.62 | 1.00 | |
| QN () | (0.7496) | 3 | 6 | 6 | 1.00 | 8.69 | 0.75 | |
| SQUAREM () | (0.7496) | 4 | 7 | 5 | 1.00 | 10.38 | 0.89 | |
| PEM | (0.7496) | 4 | 10 | 14 | 1.00 | 14.81 | 1.27 |
The average EM acceleration results across the 16 different starting values for the second setting are shown in Table A10. Because is two-dimensional, higher-order QN () and SQUAREM () can now be analyzed in addition to QN (), SQUAREM () and PEM. All algorithms converge in all trials. Like in Case 1, there is an almost four-fold reduction in the total number of iterations needed to reach the fixed point (from 22 on average to 6 on average; Table A10). Again, all acceleration methods behave fairly similarly; there is also no great difference between QN () and QN (). SQUAREM () and PEM require a large number of F evaluations (20 and 15, respectively), which is close to standard EM (22; Table A10). However, in terms of CPU time, SQUAREM () still performs second best, with SQUAREM () performing the best (Table A10).
Setting 3 loosens the assumption of the variance being equal in the two subpopulations, leading us to estimate and in the second subpopulation, while we assume the remaining parameters to be known. In this setting, EM acceleration is performed with the same techniques as for the second setting. All runs converge, and the number of iterations required to reach the fixed point is reduced five-fold or more by the accelerators (Table A11). Of the five acceleration methods studied (QN (), QN (), SQUAREM (), SQUAREM (), and PEM), the second-order QN as well as the two SQUAREM methods perform best in terms of CPU time (Table A11).

Table A10.
EM acceleration results for GMM setting 2 based on runs performed in R with the package turboEM, with the sixteen different starting values, and with as the convergence criterion. The numbers shown represent a rounded average over the sixteen runs. MLEs: Maximum likelihood estimates (fixed point); : Average number of iterations from the starting value to the fixed point; Fevals: Average number of F evaluations; Levals: Average number of log-likelihood evaluations; Conv.: Fraction of converging runs; CPU: Average CPU time in milliseconds; Rel. Time: Computing time relative to standard EM.
Table A10.
EM acceleration results for GMM setting 2 based on runs performed in R with the package turboEM, with the sixteen different starting values, and with as the convergence criterion. The numbers shown represent a rounded average over the sixteen runs. MLEs: Maximum likelihood estimates (fixed point); : Average number of iterations from the starting value to the fixed point; Fevals: Average number of F evaluations; Levals: Average number of log-likelihood evaluations; Conv.: Fraction of converging runs; CPU: Average CPU time in milliseconds; Rel. Time: Computing time relative to standard EM.
| Method | MLEs () | Fevals | Levals | Conv. | CPU (ms) | Rel. Time | ||
|---|---|---|---|---|---|---|---|---|
| EM | (2.9963, 1.0009) | 22 | 22 | 1 | 1.00 | 36.81 | 1.00 | |
| QN () | (2.9963, 1.0009) | 6 | 9 | 12 | 1.00 | 31.69 | 0.86 | |
| QN () | (2.9963, 1.0009) | 6 | 10 | 12 | 1.00 | 34.50 | 0.94 | |
| SQUAREM () | (2.9963, 1.0009) | 6 | 10 | 6 | 1.00 | 29.00 | 0.79 | |
| SQUAREM () | (2.9963, 1.0009) | 4 | 20 | 5 | 1.00 | 35.25 | 0.96 | |
| PEM | (2.9963, 1.0009) | 6 | 15 | 29 | 1.00 | 36.44 | 0.99 |

Table A11.
EM acceleration results for GMM setting 3 based on runs performed in R with the package turboEM, with the sixteen different starting values, and with as the convergence criterion. The numbers shown represent a rounded average over the sixteen runs. MLEs: Maximum likelihood estimates (fixed point); : Average number of iterations from the starting value to the fixed point; Fevals: Average number of F evaluations; Levals: Average number of log-likelihood evaluations; Conv.: Fraction of converging runs; CPU: Average CPU time in milliseconds; Rel. Time: Computing time relative to standard EM.
Table A11.
EM acceleration results for GMM setting 3 based on runs performed in R with the package turboEM, with the sixteen different starting values, and with as the convergence criterion. The numbers shown represent a rounded average over the sixteen runs. MLEs: Maximum likelihood estimates (fixed point); : Average number of iterations from the starting value to the fixed point; Fevals: Average number of F evaluations; Levals: Average number of log-likelihood evaluations; Conv.: Fraction of converging runs; CPU: Average CPU time in milliseconds; Rel. Time: Computing time relative to standard EM.
| Method | MLEs () | Fevals | Levals | Conv. | CPU (ms) | Rel. Time | ||
|---|---|---|---|---|---|---|---|---|
| EM | (2.9979, 0.9953) | 40 | 40 | 1 | 1.00 | 53.88 | 1.00 | |
| QN () | (2.9979, 0.9953) | 8 | 12 | 17 | 1.00 | 36.44 | 0.67 | |
| QN () | (2.9979, 0.9953) | 6 | 10 | 13 | 1.00 | 27.75 | 0.52 | |
| SQUAREM () | (2.9979, 0.9953) | 7 | 12 | 8 | 1.00 | 26.25 | 0.49 | |
| SQUAREM () | (2.9979, 0.9953) | 4 | 22 | 5 | 1.00 | 25.94 | 0.48 | |
| PEM | (2.9979, 0.9953) | 8 | 19 | 42 | 1.00 | 43.50 | 0.81 |
Finally, in setting 4, we increased the number of dimensions of X from to . Like in setting 3, the parameters of the first subpopulation are considered known. In higher dimensions, these parameters are , , and . The parameters of the second subpopulation are to be estimated: , and . The unknown parameter vector is therefore given by —it has dimensions. In this setting, it takes fewer iterations to reach the fixed point (even with just standard EM), as few as half of those required in setting 3. The reason for faster convergence may be that more data are available to estimate . As is 11-dimensional, even higher orders of QN (q > 2) and SQUAREM (k > 2) methods can be studied (Table A12). As in the other three cases, QN, SQUAREM, and PEM accelerate the EM algorithm four- to five-fold in terms of number of iterations (Table A12). However, it is worth noting that SQUAREM () and SQUAREM () actually use a higher number of F evaluations than the standard EM algorithm, and so do not improve on it for those scores (Table A12). PEM hardly accelerates the EM algorithm, while the higher-order SQUAREM methods actually decelerate it. Overall, acceleration in terms of CPU time is not very strong in terms of magnitude, with a maximum reduction of about 20% for QN () (Table A12).
Overall, the GMM analysis shows that all three acceleration techniques—QN, SQUAREM, and PEM-work well for Gaussian mixture models (Table A9, Table A10, Table A11, Table A12). The four- to five-fold decrease in the number of iterations is consistent with what has been observed in previous studies for other models [10,12,13,14]. In the context of Gaussian mixture models, PEM is consistently more expensive in terms of the number of evaluations of F and the log-likelihood, and also in terms of CPU time. However, in all four cases, even the high-dimensional one, the fixed point is reached relatively quickly. Perhaps differences in the three acceleration methods will become more apparent in contexts where the standard EM algorithm requires a much higher number of iterations to reach the fixed point. This leads us to the recommendation we have formulated in our discussion of studying the accelerators discussed in this work in the context of other, more complex model classes.

Table A12.
EM acceleration results for GMM setting 4 () based on runs performed in R with the package turboEM, with the sixteen different starting values, and with as the convergence criterion. The numbers shown represent a rounded average over the sixteen runs. For comparison with setting 3, only the maximum likelihood estimates for and are shown. MLEs: Maximum likelihood estimates (fixed point); : Average number of iterations from the starting value to the fixed point; Fevals: Average number of F evaluations; Levals: Average number of log-likelihood evaluations; Conv.: Fraction of converging runs; CPU: Average CPU time in milliseconds; Rel. Time: Computing time relative to standard EM.
Table A12.
EM acceleration results for GMM setting 4 () based on runs performed in R with the package turboEM, with the sixteen different starting values, and with as the convergence criterion. The numbers shown represent a rounded average over the sixteen runs. For comparison with setting 3, only the maximum likelihood estimates for and are shown. MLEs: Maximum likelihood estimates (fixed point); : Average number of iterations from the starting value to the fixed point; Fevals: Average number of F evaluations; Levals: Average number of log-likelihood evaluations; Conv.: Fraction of converging runs; CPU: Average CPU time in milliseconds; Rel. Time: Computing time relative to standard EM.
| Method | MLEs () | Fevals | Levals | Conv. | CPU (ms) | Rel. Time | ||
|---|---|---|---|---|---|---|---|---|
| EM | (2.9971, 0.998) | 19 | 19 | 1 | 1.00 | 570.69 | 1.00 | |
| QN () | (2.9971, 0.998) | 6 | 9 | 12 | 1.00 | 497.69 | 0.87 | |
| QN () | (2.9971, 0.998) | 5 | 9 | 10 | 1.00 | 490.75 | 0.86 | |
| QN () | (2.9971, 0.998) | 4 | 10 | 9 | 1.00 | 488.19 | 0.86 | |
| QN () | (2.9971, 0.998) | 4 | 10 | 7 | 1.00 | 459.75 | 0.81 | |
| SQUAREM () | (2.9971, 0.998) | 5 | 10 | 6 | 1.00 | 502.94 | 0.88 | |
| SQUAREM () | (2.9971, 0.998) | 3 | 17 | 4 | 1.00 | 543.50 | 0.95 | |
| SQUAREM () | (2.9971, 0.998) | 3 | 21 | 4 | 1.00 | 663.12 | 1.16 | |
| SQUAREM () | (2.9971, 0.998) | 2 | 22 | 3 | 1.00 | 675.44 | 1.18 | |
| PEM | (2.9971, 0.998) | 6 | 15 | 25 | 1.00 | 623.56 | 1.09 |
References
- Lee, C.S.; Huggins, A.C.; Therriault, D.J. A measure of creativity or intelligence? Examining internal and external structure validity evidence of the Remote Associates Test. Psychol. Aesthet. Creat. Arts 2014, 8, 446–460. [Google Scholar] [CrossRef]
- Chermahini, S.A.; Hickendorff, M.; Hommel, B. Development and validity of a Dutch version of the Remote Associates Task: An item-response theory approach. Think. Ski. Creat. 2012, 7, 177–186. [Google Scholar] [CrossRef]
- Berezner, A.; Adams, R.J. Implementation of Large-Scale Education Assessments; Chapter Why Large-Scale Assessments Use Scaling and Item Response Theory; Wiley Online Library: Hoboken, NJ, USA, 2017; pp. 323–356. [Google Scholar]
- Von Davier, M.; Sinharay, S. Handbook of International Large-Scale Assessment: Background, Technical Issues, and Methods of Data Analysis; Chapter Analytics in International Large-Scale Assessments: Item Response Theory and Population Models; CRC Press: Boca Raton, FL, USA, 2014; pp. 155–174. [Google Scholar]
- Dempster, A.P.; Laird, N.M.; Rubin, D.B. Maximum Likelihood from Incomplete Data via the EM Algorithm. J. R. Stat. Soc. Ser. 1977, 39, 1–38. [Google Scholar]
- Bock, R.D.; Aitkin, M. Marginal maximum likelihood estimation of item parameters: Application of an EM algorithm. Psychometrika 1981, 46, 443–459. [Google Scholar] [CrossRef]
- McLachlan, G.J.; Krishnan, T. The EM Algorithm and Extensions, 2nd ed.; Wiley-Interscience: Hoboken, NJ, USA, 2008. [Google Scholar]
- Baker, F.B.; Kim, S.H. Item Response Theory; Marcel Dekker, Inc.: New York City, NY, USA, 2004. [Google Scholar]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning, 1st ed.; Chapter 8.5 the EM Algorithm; Springer: Berlin, Germany, 2001; pp. 236–243. [Google Scholar]
- Zhou, H.; Alexander, D.; Lange, K. A quasi-Newton acceleration for highdimensional optimization algorithms. Stat. Comput. 2011, 21, 261–273. [Google Scholar] [CrossRef] [PubMed]
- Varadhan, R.; Roland, C. Squared Extrapolation Methods (Squarem): A New Class of Simple and Efficient Numerical Schemes for Accelerating the Convergence of the EM Algorithm; Working Papers; Department of Biostatistics, Johns Hopkins University: Baltimore, MD, USA, 2004. [Google Scholar]
- Roland, C.; Varadhan, R.; Frangakis, C. Squared polynomial extrapolation methods with cycling: An application to the positron emission tomography problem. Numer. Algorithms 2007, 44, 159–172. [Google Scholar] [CrossRef]
- Varadhan, R.; Roland, C. Simple and Globally Convergent Methods for Accelerating the Convergence of Any EM Algorithm. Scand. J. Stat. 2008, 35, 335–3531. [Google Scholar] [CrossRef]
- Berlinet, A.; Roland, C. Parabolic acceleration of the EM algorithm. Stat. Comput. 2009, 19, 35–47. [Google Scholar] [CrossRef]
- Bartolucci, F.; Forcina, A.; Stanghellini, E. A Comparison of Recent EM Accelerators within Item Response Theory; COMPSTAT; Springer: Berlin, Germany, 1998; pp. 173–178. [Google Scholar]
- Embretson, S.E. Item Response Theory for Psychologists, 1st ed.; Multivariate Applications Series; Psychology Press:: London, UK, 2000. [Google Scholar]
- Chalmers, R.P. mirt: A Multidimensional Item Response Theory Package for the R Environment. J. Stat. Softw. 2012, 48, 1–29. [Google Scholar] [CrossRef]
- Mislevy, R.J.; Bock, R.D. Implementation of the EM Algorithm in the Estimation of Item Parameters: The BILOG Computer Program; ERIC: Wayzata, MN, USA, 1982. [Google Scholar]
- Meng, X.L.; Van Dyk, D. The EM Algorithm—An Old Folk-song Sung to a Fast New Tune. J. R. Stat. Soc. Ser. 1997, 59, 511–567. [Google Scholar] [CrossRef]
- Liu, C.; Rubin, D.B.; Wu, Y.N. Parameter expansion to accelerate EM: The PX-EM algorithm. Biometrika 1998, 85, 755–770. [Google Scholar] [CrossRef]
- Meng, X.L.; Rubin, D.B. Maximum likelihood estimation via the ECM algorithm: A general framework. Biometrika 1993, 80, 267–278. [Google Scholar] [CrossRef]
- Liu, C.; Rubin, D.B. The ECME Algorithm: A Simple Extension of EM and ECM with Faster Monotone Convergence. Biometrika 1994, 81, 633–648. [Google Scholar] [CrossRef]
- Lange, K. A Quasi-Newton Acceleration of the EM Algorithm. Stat. Sin. 1995, 5, 1–18. [Google Scholar]
- Jamshidian, M.; Jennrich, R.I. Acceleration of the EM Algorithm by Using Quasi-Newton Methods. J. R. Stat. Soc. Ser. (Methodol.) 1997, 59, 569–587. [Google Scholar] [CrossRef]
- Jamshidian, M.; Jennrich, R.I. Conjugate Gradient Acceleration of the EM Algorithm. J. Am. Stat. Assoc. 1993, 88, 221–228. [Google Scholar]
- Louis, T.A. Finding the Observed Information Matrix when Using the EM Algorithm. J. R. Stat. Soc. Ser. (Methodol.) 1982, 44, 226–233. [Google Scholar]
- Wu, C.F.J. On the Convergence Properties of the EM Algorithm. Ann. Stat. 1983, 11, 95–103. [Google Scholar] [CrossRef]
- Bobb, J.F.; Varadhan, R. turboEM: A Suite of Convergence Acceleration Schemes for EM, MM and Other Fixed-Point Algorithms, R Package Version 2018.1; 2018. Available online: https://cran.r-project.org/web/packages/turboEM/index.html (accessed on 8 November 2020).
- Kriegel, H.P.; Schubert, E.; Zimek, A. The (black) art of runtime evaluation: Are we comparing algorithms or implementations? Knowl. Inf. Syst. 2017, 52, 341–378. [Google Scholar] [CrossRef]
- Paek, I.; Cai, L. A comparison of item parameter standard error estimation procedures for unidimensional and multidimensional item response theory modeling. Educ. Psychol. Meas. 2014, 74, 58–76. [Google Scholar] [CrossRef]
- Stone, C.A. Recovery of marginal maximum likelihood estimates in the two-parameter logistic response model: An evaluation of MULTILOG. Appl. Psychol. Meas. 1992, 16, 1–16. [Google Scholar] [CrossRef]
- Nader, I.W.; Tran, U.S.; Formann, A.K. Sensitivity to initial values in full non-parametric maximum-likelihood estimation of the two-parameter logistic model. Br. J. Math. Stat. Psychol. 2011, 64, 320–336. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).