A Meta-Analysis of Spearman’s Hypothesis Tested on Latin-American Hispanics, Including a New Way to Correct for Imperfectly Measuring the Construct of g
Abstract
:1. Introduction
2. Methods
2.1. Meta-Analysis
2.2. Rules for Inclusion
2.3. Searching and Screening Studies
2.4. g Loadings
2.5. Calculating Glass’ d
2.6. Studies Supplying Multiple Effect Sizes
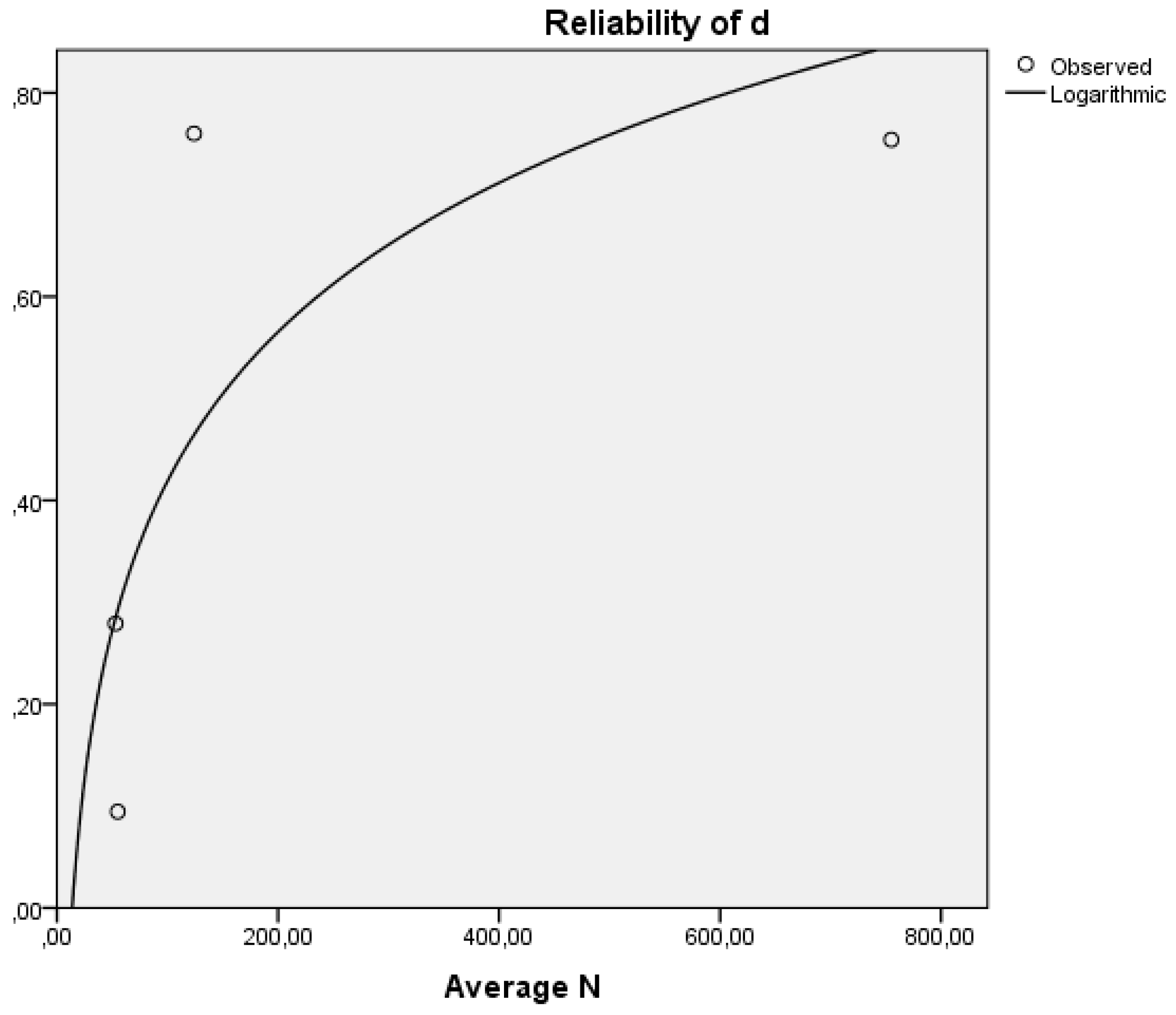
2.7. Correcting for Sampling Error, Reliability of the g Vector, and Reliability of the Glass’ d Vector
2.8. Correction for Restriction of Range in g Loadings
2.9. Correction for Deviation from Perfect Construct Validity
2.9.1. Research Participants
2.9.2. Psychometric Variables
- Closure; the child is given very incomplete pictures and has to figure out the complete picture. According to Carroll’s [47] taxonomy, this subtest is a measure of Closure Speed at stratum I, which makes this subtest a measure of Broad Visual Perception at stratum II.
- Exclusion; out of four abstract figures the child has to select the one that is different from the other three. The child has to detect the necessary rule to solve the task. This subtest measures Induction at stratum I, which makes it a measure of Fluid Intelligence at stratum II.
- Memory Span; the child has to memorize figures put on cards and the sequence in which they are presented. After five seconds the card is turned and the child has to reproduce the figures in the right sequence using blocks on which the figures are printed. The subtest contains a series with concrete figures and a series with abstract figures. Both series measure (Visual) Memory Span at stratum I. Both series fall under General Memory and Learning at stratum II.
- Verbal Meaning; words are presented to the child in an auditory fashion and from four figures the child has to choose the one which resembles the word it has just heard. This subtest measures Lexical Knowledge at stratum I and is a measure of Crystallized Intelligence at stratum II.
- Mazes; the child has to go through a maze with a stick as fast as they can. Because of the speed factor this subtest is a measure of Spatial Scanning at stratum I, which falls under Broad Visual Perception at stratum II.
- Analogies; the child has to complete verbal analogies that are stated as follows: A:B is like C: … (there are four options to choose from). The constructors of this subtest tried to avoid measuring Lexical Knowledge, by including only those words that are highly frequently used in ordinary life. All words in the analogy items are accompanied by illustrations, so as to reduce the verbal aspect of the task to a minimum. This subtest is a measure of Induction at stratum I which makes it a measure of Fluid Intelligence at stratum II.
- Quantity; in this multiple-choice test the child has to make comparisons between pictures, differing in volume, length, weight, and surface. This subtest is a measure of Quantitative Reasoning at stratum I, which measures Fluid Intelligence at stratum II.
- Disks; the child has to use pins to put disks with two, three, or four holes on a board as fast as possible until three layers of disks are on the board. This subtest is a measure of Spatial Relations at stratum I, which measures Broad Visual Perception at stratum II.
- Learning Names; the child has to memorize the names of different butterflies and cats using pictures presented on cardboard. This subtest measures Associative Memory at stratum I, which makes it a measure of General Memory and Learning at stratum II.
- Hidden Figures; the child has to discover which of six figures is hidden in a complex drawing. This subtest is a measure of Flexibility of Closure at stratum I, which makes it a measure of Broad Visual Perception at stratum II.
- Idea Production; the child has to name as many words, objects, or situations as possible that can be associated with a broad category within a certain time span, for example: “What can you eat?” This subtest is a measure of Ideational Fluency at stratum I, which is a measure of Broad Retrieval Ability at stratum II.
- Storytelling; the child has to tell as much as possible about a picture on a board and what could happen to the persons or objects in the picture. The total score is composed of both quantitative measures (number of words, number of relations, did or did not the child tell a plot, etc.) and qualitative measures (did the child grasp the central meaning of the story). This subtest consists of different elements and measures at stratum I: Naming Facility and Ideational Fluency, Sequential Reasoning, and to some extent Communication Ability. These stratum-I abilities are measures of Broad Retrieval Ability, Fluid Intelligence, and Crystallized Intelligence, respectively, at stratum II.
- Information; the child has to verbally answer all kinds of general questions, some of which have several possible correct answers. This subtest measures General Information, which is a measure of Crystallized Intelligence at stratum II.
- Picture Completion; the child has to find out which essential part of a picture is missing, within a given time. This subtest measures Closure Speed at stratum I, which makes it a measure of Broad Visual Perception at stratum II.
- Similarities; the child has to find a similarity between two objects or concepts. There are several correct answers. This subtest is a measure of Induction at stratum I, which makes it a measure of Fluid Intelligence at stratum II.
- Picture Arrangement; the child has to order a series of pictures in such a way that the pictures form a comprehensive story within a given time. This subtest is a measure of General Sequential Reasoning at stratum I, which makes it a measure of Fluid Intelligence at stratum II.
- Arithmetic; the child has to solve arithmetic problems. These arithmetic problems are verbally presented: Four boys have 72 fish. They divided the fish, and everybody gets the same amount. How many fish does each boy get? This subtest is a measure of Crystallized Intelligence at stratum II.
- Block Design; using blocks, the child has to replicate a pattern presented on a card. This subtest is a measure of Visualization at stratum I, which measures Broad Visual Perception at stratum II.
- Vocabulary; the child has to give the meaning of a presented word. This subtest measures Lexical Knowledge at stratum I, which makes it a measure of Crystallized Intelligence at stratum II.
- Object Assembly; the child has to put different pieces of cardboard together to copy a given figure within a given time. This subtest is a measure of Visualization at stratum I, which makes it a measure of Broad Visual Perception at stratum II.
- Comprehension; the child has to answer different questions in which they have to give their insight and judgment about everyday-life issues. This subtest measures General Knowledge, which is a measure of Crystallized Intelligence at stratum II and is a measure of General Sequential Reasoning at stratum I, which is a measure of Fluid Intelligence at stratum II.
- Coding; the child has to put a sign in a series of figures (code A) or under a series of numbers (code B). The sign belonging to the figure of number that was presented to the child earlier. This subtest is a measure of Visual Memory as stratum I, which falls under General Memory and Learning at stratum II.
- Digit Span; the child has to repeat a series of numbers in the sequence presented to them auditorily (Forward Digit Span) or in reverse order starting with the last number they heard back to the first number (Backward Digit Span). This subtest is a measure of Memory Span at stratum I, which makes it a measure of General Memory and Learning at stratum II.
- Mazes; the child has to trace the way out of a maze presented on paper with a pencil within a given time. The child is not allowed to enter a dead end. This subtest is a measure of Spatial Scanning at stratum I, which falls under Broad Visual Perception at stratum II.
2.9.3. g Loadings
2.9.4. Computation of g Scores and “True” g Scores
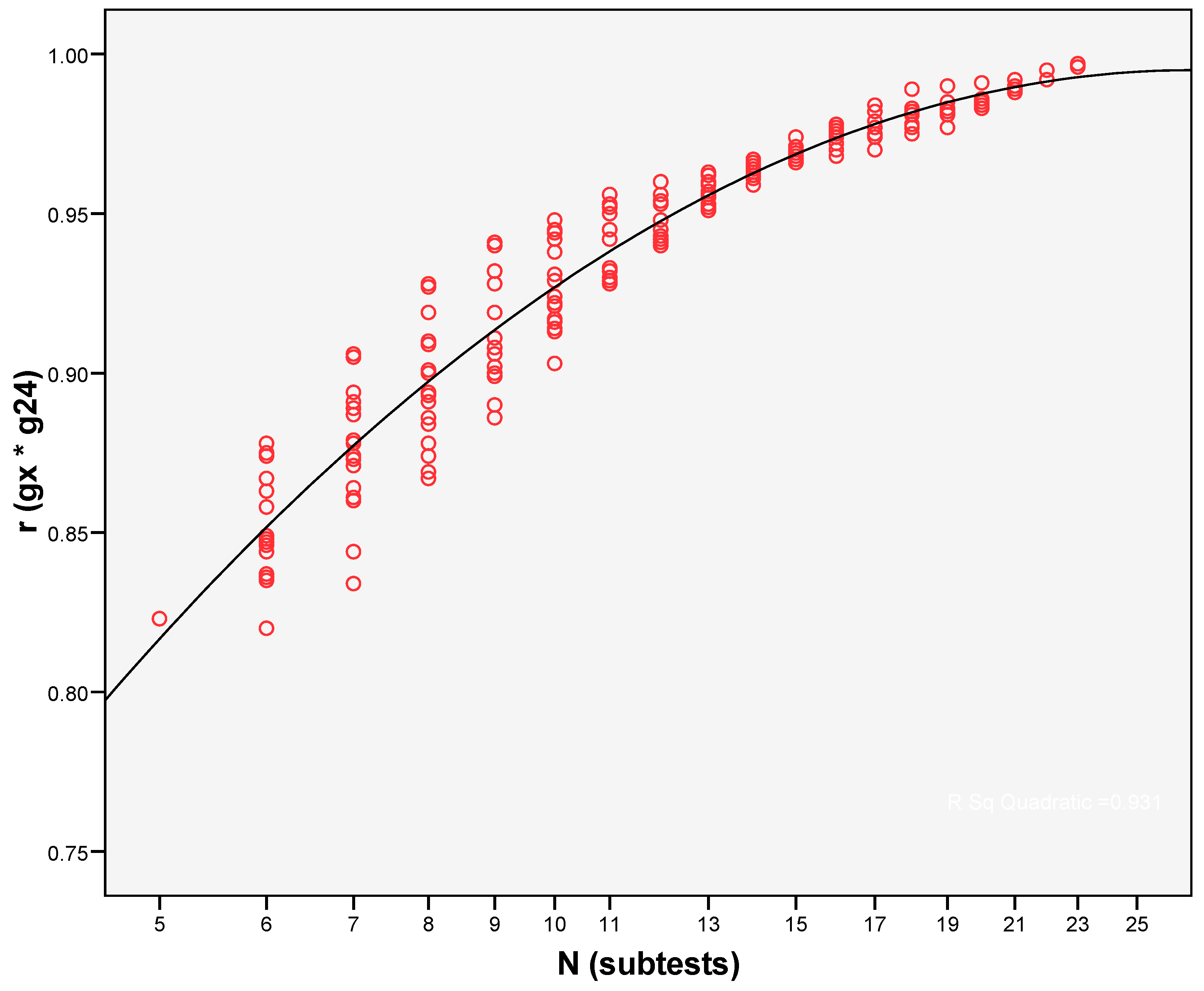
2.9.5. Combinations of Subtests
2.9.6. Correlations of g Scores and “True” g Scores
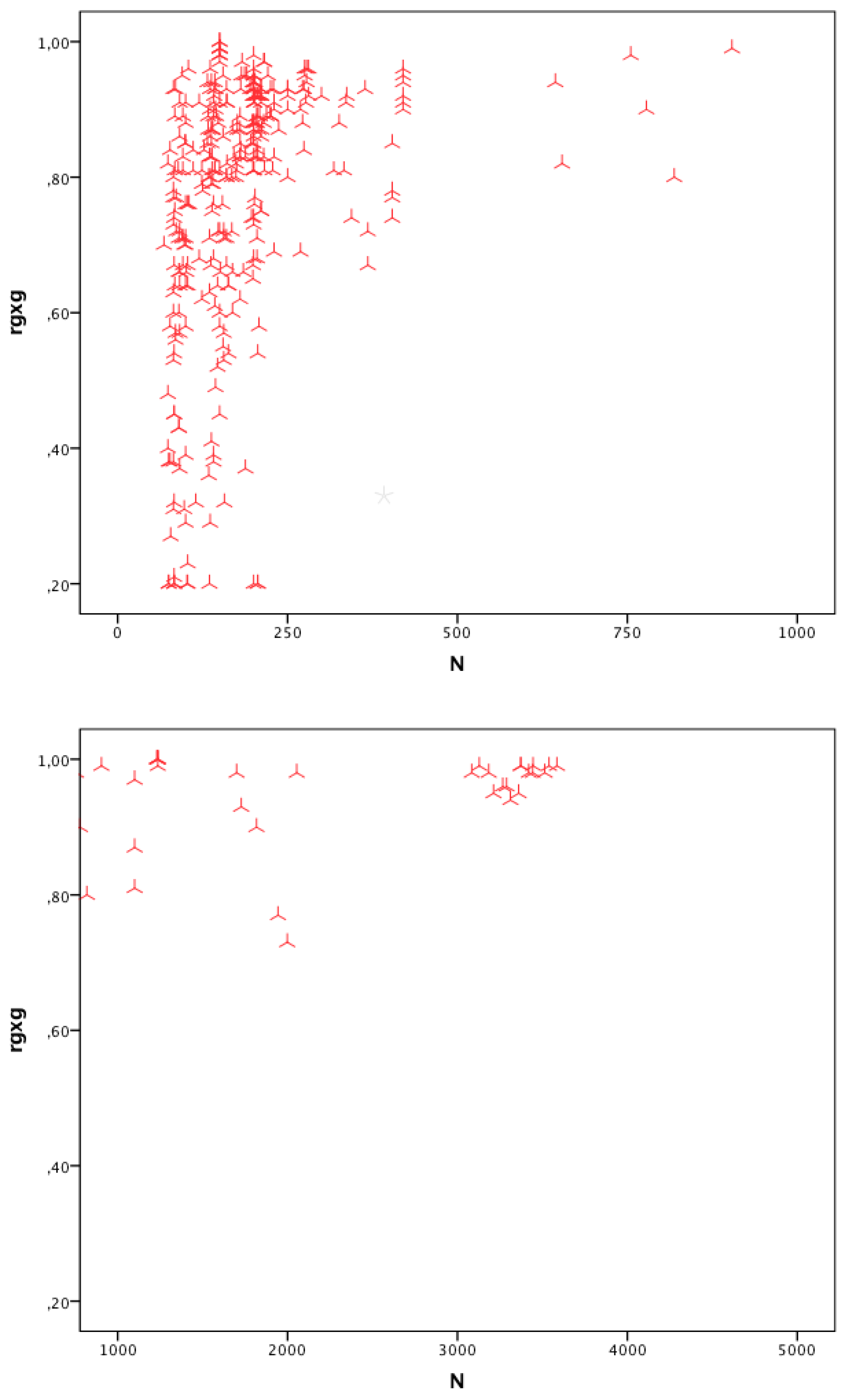
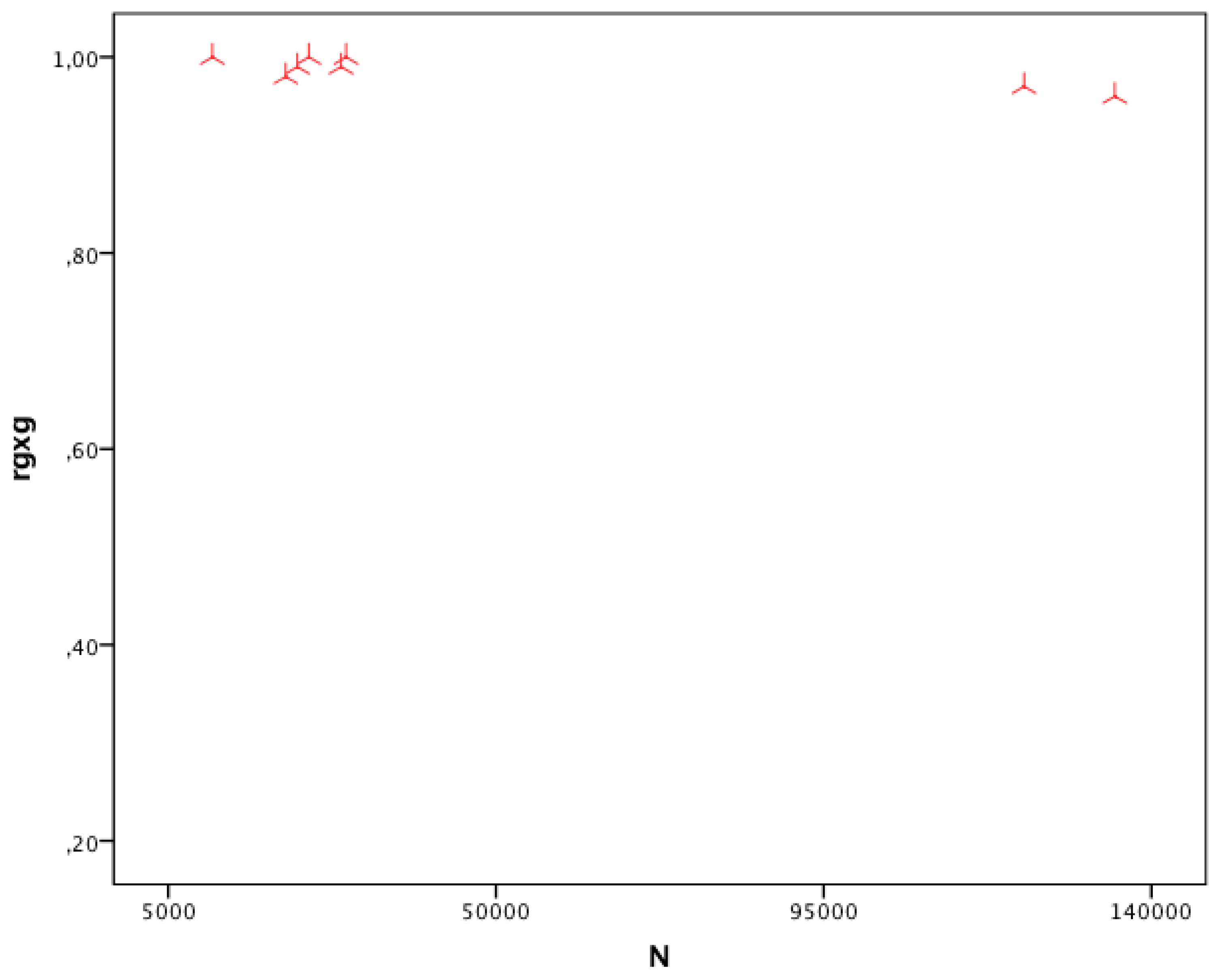
2.9.7. Scatter Plot
2.9.8. Computation of the Correction Value
3. Results
4. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- U.S. Department of Commerce, Economics and Statistics Administration, U.S. Census Bureau. The Hispanic Population: 2010: 2010 Census Briefs (Publication No. C2010BR-04). 2011. Available online: http://www.census.gov/prod/cen2010/briefs/c2010br-04.pdf (accessed on 15 January 2019).
- U.S. Census Bureau, National Advisory Committee on Racial, Ethnic and Other Populations. 2020 Census: Race and Hispanic Origin Research Working Group: Final Report. 2014. Available online: https://www2.census.gov/cac/nac/reports/2014-06-10_RHO_wg-report.pdf (accessed on 15 January 2019).
- CIA Factbook. The World Factbook. 2015. Available online: https://www.cia.gov/library/publications/the-world-factbook/geos/us.html (accessed on 15 January 2019).
- Lynn, R.; Vanhanen, T. IQ and the Wealth of Nations; Praeger: London, UK, 2002. [Google Scholar]
- Kena, G.; Aud, S.; Johnson, F.; Wang, X.; Zhang, J.; Rathbun, A.; Wilkinson-Flicker, S.; Kristapovich, P. The Condition of Education 2014 (NCES 2014-083); U.S. Department of Education, National Center for Education Statistics: Washington, DC, USA, 2014. Available online: http://nces.ed.gov/pubsearch (accessed on 15 January 2019).
- Ryan, C.L.; Siebens, J. Educational Attainment in the United States: 2009; US Census Bureau: Washington, DC, USA, 2012.
- Brown, A.; Patten, E. Statistical Portrait of Hispanics in the United States, 2012; Pew Hispanic Center: Washington, DC, USA, 2014.
- Lynn, R. Racial and ethnic differences in intelligence in the United States on the Differential Ability Scale. Personal. Individ. Differ. 1996, 20, 271–273. [Google Scholar] [CrossRef]
- Roth, P.L.; Bevier, C.A.; Bobko, P.; Switzer, F.S.; Tyler, P. Ethnic group differences in cognitive ability in employment and educational settings: A meta-analysis. Pers. Psychol. 2001, 54, 297–330. [Google Scholar] [CrossRef]
- Jensen, A.R. The g Factor: The Science of Mental Ability; Praeger: Westport, CT, USA, 1998. [Google Scholar]
- Rushton, J.P.; Jensen, A.R. Thirty years of research on race differences in cognitive ability. Psychol. Publ. Pol. Law 2005, 11, 235–294. [Google Scholar] [CrossRef]
- te Nijenhuis, J.; van den Hoek, M.; Armstrong, E. Spearman’s hypothesis and Amerindians: A meta-analysis. Intelligence 2015, 50, 87–92. [Google Scholar] [CrossRef]
- te Nijenhuis, J.; David, H.; Metzen, D.; Armstrong, E.L. Spearman’s hypothesis tested on European Jews vs non-Jewish Whites and vs Oriental Jews: Two meta-analyses. Intelligence 2014, 44, 15–18. [Google Scholar] [CrossRef]
- Hartmann, P.; Kruuse, N.H.S.; Nyborg, H. Testing the cross-racial generality of Spearman’s hypothesis in two samples. Intelligence 2007, 35, 47–57. [Google Scholar] [CrossRef]
- Kane, H. Race differences on the UNIT: Evidence from multi-sample confirmatory analysis. Mank. Q. 2008, 48, 283–298. [Google Scholar]
- Dalliard. Spearman’s Hypothesis and Racial Differences on the DAS-II. Humanvarieties.com. 2013. Available online: http://humanvarieties.org/2013/12/08/spearmans-hypothesis-and-racial-differences-on-the-das-ii/ (accessed on 15 January 2019).
- Ganzach, Y. Another look at the Spearman’s hypothesis and relationship between Digit Span and General Mental Ability. Learn. Individ. Differ. 2016, 45, 128–132. [Google Scholar] [CrossRef]
- Ganzach, Y. On general mental ability, digit span and Spearman’s hypothesis. Learn. Individ. Differ. 2016, 45, 135–136. [Google Scholar] [CrossRef]
- Jensen, A.R.; Figueroa, R.A. Forward and backward digit span interaction with race and IQ. Predicitons form Jensen’s theory. J. Educ. Psychol. 1975, 67, 882–893. [Google Scholar] [CrossRef]
- Ashton, M.C.; Lee, K. Problems with the method of correlated vectors. Intelligence 2005, 33, 431–444. [Google Scholar] [CrossRef]
- Dolan, C.V. Investigating Spearman’s hypothesis by means of multi-group confirmatory factor analysis. Multivar. Behav. Res. 2000, 35, 21–50. [Google Scholar] [CrossRef] [PubMed]
- Hunt, E. Human Intelligence; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Woodley, M.A.; te Nijenhuis, J.; Must, O.; Must, A. Controlling for increased guessing enhances the independence of the Flynn effect from g: The return of the Brand effect. Intelligence 2014, 43, 27–34. [Google Scholar] [CrossRef]
- te Nijenhuis, J.; van den Hoek, M. Spearman’s hypothesis tested on Black adults: A meta-analysis. J. Intell. 2016, 4, 6. [Google Scholar] [CrossRef]
- Te Nijenhuis, J.; Choi, Y.Y.; van den Hoek, M.; Valueva, E.; Lee, K.H. Spearman’s hypothesis tested comparing Korean young adults with various other groups of young adults on the items of the Advanced Progressive Matrices. J. Biosoc. Sci. 2019, in press. [Google Scholar]
- Wicherts, J.M. Ignoring psychometric problems in the study of group differences in cognitive test performance. J. Biosoc. Sci. 2018, 50, 868–869. [Google Scholar] [CrossRef]
- te Nijenhuis, J.; van den Hoek, M. Analysing group differences in intelligence using the psychometric meta-analytic-method of correlated vectors hybrid model: A reply to Wicherts (2018) attacking a strawman. J. Biosoc. Sci. 2018, 50, 870–871. [Google Scholar] [CrossRef]
- Jensen, A.R. Spearman’s hypothesis tested with chronometric information-processing tasks. Intelligence 1993, 17, 47–77. [Google Scholar] [CrossRef]
- Schmidt, F.L.; Hunter, J.E. Methods of Meta-Analysis: Correcting Error and Bias in Research Findings, 3rd ed.; Sage: Thousand Oaks, CA, USA, 2015. [Google Scholar]
- Schmidt, F.L.; Le, H. Software for the Hunter-Schmidt Meta-Analysis Methods; University of Iowa, Department of Management and Organization: Iowa City, IQ, USA, 2004. [Google Scholar]
- Jensen, A.R. The nature of the black-white difference on various psychometric tests. Spearman’s hypothesis. Behav. Brain Sci. 1985, 8, 193–263. [Google Scholar] [CrossRef]
- te Nijenhuis, J.; van Vianen, A.E.M.; van der Flier, H. Score gains on g-loaded tests: No g. Intelligence 2007, 35, 283–300. [Google Scholar] [CrossRef]
- te Nijenhuis, J.; Jongeneel-Grimen, B.; Kirkegaard, E.O. Are Headstart gains on the g factor? A meta-analysis. Intelligence 2014, 46, 209–215. [Google Scholar] [CrossRef]
- te Nijenhuis, J.; Jongeneel-Grimen, B.; Armstrong, E.L. Are adoption gains on the g factor? A meta-analysis. Personal. Individ. Differ. 2015, 73, 56–60. [Google Scholar] [CrossRef]
- te Nijenhuis, J.; van den Hoek, M.; Willigers, D. Testing Spearman’s hypothesis with alternative intelligence tests: A meta-analysis. Mank. Q. 2017, 57, 687–705. [Google Scholar]
- te Nijenhuis, J.; van der Flier, H. Is the Flynn effect on g?: A meta-analysis. Intelligence 2013, 41, 802–807. [Google Scholar]
- Flynn, J.R.; te Nijenhuis, J.; Metzen, D. The g beyond Spearman’s g: Flynn’s paradoxes resolved using four exploratory meta-analyses. Intelligence 2014, 44, 1–10. [Google Scholar] [CrossRef]
- Sternberg, R.J.; The Rainbow Project Collaborators. The Rainbow Project: Enhancing the SAT through assessments of analytical, practical, and creative skills. Intelligence 2006, 34, 321–350. [Google Scholar] [CrossRef]
- Lynn, R. Race Differences in Intelligence: An Evolutionary Analysis; Washington Summit Books: Atlanta, GA, USA, 2006. [Google Scholar]
- Glass, G.V.; McGaw, B.; Smith, M.L. Meta-Analysis in Social Research; Sage: London, UK, 1981. [Google Scholar]
- Grissom, R.J.; Kim, J.J. Effect Sizes for Research: Univariate and Multivariate Applications, 2nd ed.; Routledge: New York, NY, USA, 2012. [Google Scholar]
- Kaufman, A.S.; McLean, J.E.; Kaufman, J.C. The fluid and crystallized abilities of white, black, and Hispanic adolescents and adults, both with and without an education covariate. J. Clin. Psychol. 1995, 51, 636–647. [Google Scholar] [CrossRef]
- Flemmer, D.D.; Roid, G.H. Nonverbal intellectual assessment of Hispanic and speech-impaired adolescents. Psychol. Rep. 1997, 80, 1115–1122. [Google Scholar] [CrossRef]
- Hunter, J.E.; Schmidt, F.L. Methods of Meta-Analysis: Correcting Error and Bias in Research Findings, 2nd ed.; Sage: Thousand Oaks, CA, USA, 2004. [Google Scholar]
- Flynn, J.R. Intelligence and Human Progress: The Story of What was Hidden in our Genes; Academic Press: Oxford, UK, 2013. [Google Scholar]
- Bleichrodt, N.; Resing, W.C.M.; Drenth, P.J.D.; Zaal, J.N. Intelligentiemeting Bij Kinderen [The Measurement of Children’s Intelligence]; Swets: Lisse, The Netherlands, 1987. [Google Scholar]
- Carroll, J.B. Human Cognitive Abilities; Cambridge University Press: Cambridge, UK, 1993. [Google Scholar]
- van Haasen, P.P.; de Bruyn, E.E.J.; Pijl, Y.J.; Poortinga, Y.H.; Lutje-Spelberg, H.C.; Vandersteene, G.; Coetsier, P.; Spoelders-Claes, R.; Stinissen, J. Wechsler Intelligence Scale for Children-Revised, Dutch Version; Swets: Lisse, The Netherlands, 1986. [Google Scholar]
- Carretta, T.R. Group differences on US Air Force pilot selection tests. Int. J. Sel. Assess. 1997, 5, 115–127. [Google Scholar] [CrossRef]
- Reynolds, C.R.; Willson, V.L.; Ramsey, M. Intellectual differences among Mexican Americans, Papagos and Whites, independent of g. Personal. Individ. Differ. 1999, 27, 1181–1187. [Google Scholar] [CrossRef]
- Valencia, R.R.; Rankin, R.J. Factor Analysis of the K–ABC for groups of Anglo and Mexican American children. J. Educ. Meas. 1986, 23, 209–219. [Google Scholar] [CrossRef]
- Snyder, B.J. WISC-R Performance Patterns of Referred Anglo, Hispanic, and American Indian Children. Ph.D. Thesis, University of Arizona, Tucson, AZ, USA, 1991. [Google Scholar]
- Taylor, R.L.; Richards, S.B. Patterns of intellectual differences of Black, Hispanic, and White children. Psychol. Sch. 1991, 28, 5–9. [Google Scholar] [CrossRef]
- Sandoval, J. The WISC-R and internal evidence of test bias with minority groups. J. Consult. Clin. Psychol. 1979, 47, 919–927. [Google Scholar] [CrossRef]
- Dean, R.S. Distinguishing patterns for Mexican-American children on the WISC-R. J. Clin. Psychol. 1979, 35, 790–794. [Google Scholar] [CrossRef]
- Naglieri, J.A.; Rojahn, J.; Matto, H.C. Hispanic and non-Hispanic children’s performance on PASS cognitive processes and achievement. Intelligence 2007, 35, 568–579. [Google Scholar] [CrossRef]
- Kline, R.B. Principles and Practice of Structural Equation Modeling, 3rd ed.; Guilford: New York, NY, USA, 2011. [Google Scholar]
- Rodgers, R.; Hunter, J.E. The methodological war of the “Hardheads” versus the “softheads”. J. Appl. Behav. Sci. 1996, 32, 189–208. [Google Scholar] [CrossRef]
- te Nijenhuis, J.; Willigers, D.; Dragt, J.; van der Flier, H. The effects of language bias and cultural bias estimated using the method of correlated vectors on a large database of IQ comparisons between native Dutch and ethnic minority immigrants from non-Western countries. Intelligence 2016, 54, 117–135. [Google Scholar] [CrossRef]
- Schmidt, F.L.; Hunter, J.E. The validity and utility of selection methods in personnel psychology: Practical and theoretical implications of 85 years of research findings. Psychol. Bull. 1998, 124, 262–274. [Google Scholar] [CrossRef]
- te Nijenhuis, J.; Bakhiet, S.F.; van den Hoek, M.; Repko, J.; Allik, J.; Žebec, M.S.; Sukhanovskiy, V.; Abduljabbar, A.S. Spearman’s hypothesis tested comparing Sudanese children and adolescents with various other groups of children and adolescents on the items of the Standard Progressive Matrices. Intelligence 2016, 56, 46–57. [Google Scholar] [CrossRef]
- Schmidt, F.L. What do data really mean?: Research findings, meta-analysis, and cumulative knowledge in psychology. Am. Psychol. 1992, 47, 1173–1181. [Google Scholar] [CrossRef]
| Subtest | g | |
|---|---|---|
| Dutch names | English names | |
| Rakit | ||
| Figuur Herkennen | Figure Recognition | 0.53 |
| Exclusie | Exclusion | 0.47 |
| Geheugenspan | Memory Span | 0.56 |
| Woordbetekenis | Verbal Meaning | 0.39 |
| Doolhoven | Mazes | 0.61 |
| Analogieën | Analogies | 0.63 |
| Kwantiteit | Quantity | 0.51 |
| Schijven | Disks | 0.49 |
| Namen Leren | Learning Names | 0.62 |
| Verborgen figuren | Hidden Figures | 0.20 |
| Ideeënproduktie | Idea Production | 0.25 |
| Vertelplaat | Storytelling | 0.58 |
| WISC-R | ||
| Informatie | Information | 0.61 |
| Onvolledige tekeningen | Picture Completion | 0.52 |
| Overeenkomsten | Similarities | 0.57 |
| Plaatjes ordenen | Picture Arrangement | 0.70 |
| Rekenen | Arithmetic | 0.64 |
| Blokpatronen | Block Design | 0.56 |
| Woordenschat | Vocabulary | 0.43 |
| Figuurleggen | Object Assembly | 0.27 |
| Begrijpen | Comprehension | 0.35 |
| Substitutie | Coding | 0.44 |
| Cijferreeksen | Digit Span | 0.44 |
| Doolhoven | Mazes | 0.53 |
| Study | Group | Test Battery | r | Nsubtests | NWhite | NHispanic | Nharmonic | Ng | rgg | rdd | u | Mean Age (Range) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Carretta (1997) [49] | Hispanic | AFOQT | 0.36 | 16 | 212,238 | 12,647 | 47,743 | 212,238 | 1.00 | 1.00 | 0.68 | 21 (18–27) |
| Reynolds, Willson, & Ramsey (1999) [50] | Mexican-American | WISC-R | 0.77 | 12 | 2200 | 223 | 810 | 2200 | 0.98 | 0.87 | 0.77 | 10.12 (6–16) |
| Valencia & Rankin (1986) [51] | Mexican-American | K-ABC | 0.70 | 13 | 100 | 100 | 200 | 1500 | 0.96 | 0.57 | 0.64 | 11 (10–12.5) |
| Hartmann, Kruuse, & Nyborg (2007) [14] | Hispanic | Various tests | 0.71 | 16 | 3556 | 181 | 689 | 3556 | 0.98 | 0.84 | 0.99 | 19.9 (17–25) |
| Hartmann, Kruuse, & Nyborg (2007) [14] | Hispanic | ASVAB | 0.74 | 10 | 6947 | 1704 | 5473 | 6947 | 0.99 | 1.00 | 0.59 | 19.6 (15–24) |
| Snyder 2 (1991) [52] | Hispanic | WISC-R | 0.81 | 11 | 64 | 64 | 128 | 1800 | 0.96 | 0.45 | 0.68 | 10.5 1 (6.5–14.5) |
| Dalliard (2013) [16] | Hispanic | DAS-II | 0.70 | 13 | 864 | 432 | 1152 | 2952 | 0.98 | 1.00 | 0.73 | (5–17) |
| Taylor & Richards (1991) [53] | Hispanic | WISC-R | 0.72 | 10 | 1200 | 100 | 369 | 1200 | 0.96 | 0.70 | 0.56 | 8.3 (6–11) |
| Sandoval (1979) [54] | Mexican-American/Hispanic | WISC-R | 0.55 | 10 | 351 | 349 | 700 | 1200 | 0.96 | 0.85 | 0.50 | 8 (5–11) |
| Kaufman, McLean & Kaufman (1995) [42] | Hispanic | KAIT | 0.56 | 8 | 1535 | 138 | 502 | 1535 | 0.96 | 0.75 | 0.45 | 11–94 |
| Dean2 (1979) [55] | Mexican-American | WISC-R | 0.75 | 10 | 60 | 60 | 120 | 2200 | 0.98 | 0.44 | 0.68 | 10 |
| Naglieri, Rojahn, & Matto (2007) [56] | Hispanic | CAS | −0.47 | 12 | 1956 | 244 | 868 | 155 | 0.78 | 0.92 | 0.82 | 8.3 (5–17) |
| Kane (2007) [15] | Hispanic | UNIT | 0.42 | 6 | 77 | 77 | 154 | 77 | 0.48 | 0.50 | 1.07 | 10.5 |
| Flemmer & Roid (1997) [43] | Hispanic | Leiter-R | 0.28 | 7 | 258 | 62 | 181 | 410 | 0.88 | 0.54 | 0.31 | 11–21 |
| Studies Included | K | Total N | r | SDr | rho-4 | SDrho-4 | rho-5 | %VE | 80% CI |
|---|---|---|---|---|---|---|---|---|---|
| All studies | 14 | 154 | 0.55 | 0.333 | 0.75 | 0.368 | 0.80 | 24.3 | 0.27–1.22 |
| All studies minus outlier | 13 | 142 | 0.63 | 0.158 | 0.86 | 0 | 0.91 | 199.7 | 0.86–0.86 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
te Nijenhuis, J.; van den Hoek, M.; Dragt, J. A Meta-Analysis of Spearman’s Hypothesis Tested on Latin-American Hispanics, Including a New Way to Correct for Imperfectly Measuring the Construct of g. Psych 2019, 1, 101-122. https://doi.org/10.3390/psych1010008
te Nijenhuis J, van den Hoek M, Dragt J. A Meta-Analysis of Spearman’s Hypothesis Tested on Latin-American Hispanics, Including a New Way to Correct for Imperfectly Measuring the Construct of g. Psych. 2019; 1(1):101-122. https://doi.org/10.3390/psych1010008
Chicago/Turabian Stylete Nijenhuis, Jan, Michael van den Hoek, and Joep Dragt. 2019. "A Meta-Analysis of Spearman’s Hypothesis Tested on Latin-American Hispanics, Including a New Way to Correct for Imperfectly Measuring the Construct of g" Psych 1, no. 1: 101-122. https://doi.org/10.3390/psych1010008
APA Stylete Nijenhuis, J., van den Hoek, M., & Dragt, J. (2019). A Meta-Analysis of Spearman’s Hypothesis Tested on Latin-American Hispanics, Including a New Way to Correct for Imperfectly Measuring the Construct of g. Psych, 1(1), 101-122. https://doi.org/10.3390/psych1010008





