Fundamental Vibrational Frequencies and Spectroscopic Constants for Additional Tautomers and Conformers of NH₂CHCO

Abstract

The creation of larger prebiotic molecules in astronomical regions may require aminoketene (NH₂CHCO) as an intermediate, and the two conformers of this molecule exhibit infrared vibrational frequencies with intensities larger even than the antisymmetric stretch in CO₂. While the present quantum chemically computed frequencies of these fundamentals of ∼4.7 μm are in the same spectroscopic region as features from functionalized polycyclic aromatic hydrocarbons, they provide clear markers for what James Webb Space Telescope IR observations may be able to distinguish. Additionally, the IR and radioastronomical spectral characterization of two additional 2-iminoacetaldehyde, HN=CHC(=O)H, conformers are also computed as are the same data for a new carbene isomer (NH₂CC(=O)H). All conformers of aminoketene and 2-iminoacetaldehyde exhibit dipole moments of more than 2.0 D, if not greater than 4.0 D, implying that they would be notable targets for radioastronomical searches. Additionally, the 2-iminoacetaldehyde conformers have a notable mid-IR C=O stretch around 1735 cm⁻¹ slightly below the same fundamental in formaldehyde. This quantum chemical study is providing a more complete set of reference data for the potential observation of these tautomers and conformers of NH₂CHCO in the laboratory or even in space.

1. Introduction

Chemical complexity leading to the molecular origins of life relies upon the creation of molecules containing the elements carbon, hydrogen, oxygen, and nitrogen. While many such molecules are known towards various astronomical sources [1,2], their complexity has grown over the recent few years. Notably, ethanolamine (NH₂CH₂CH₂OH) has been observed towards the G+0.693 molecular cloud [3]. The proposed reaction pathway for the creation of this complicated, highly-saturated, pre-biotic molecule involves the formation of a NH₂CHCO structure (aminoketene) from smaller, known interstellar molecules which themselves contain fewer than five atoms. The formation of NH₂CHCO could utilize HNCCO + 2H, NH₂CH + CO, and NH₃ + C + CO [3,4] and may occur in shocked regions [5] where solid-phase formation supported by laboratory experiments [6,7] could then lead to gas-phase desorption and possible detection. Hence, if the formation of ethanolamine proceeds in this way, the aminoketene intermediate should be detectable in the same astronomical regions, as well. In order to potentially observe this intermediate, or any other molecule for that matter, the spectroscopic reference data for the desired compound must be on hand for comparison whether to radioastronomical observation through observatories like the IRAM 30 m telescope, the Yebes 40 m telescope, or even the Atacama Large Millimeter Array (ALMA) or through infrared observation via the James Webb Space Telescope (JWST) or any of its potential successors, e.g., the Habitable Worlds Observatory (HWO).

Previous work has shown that the $C_s$ aminoketene structure is not the lowest energy arrangement of the NCCO connectivity with three additional hydrogen atoms among the possible isomers [4,8,9]. This actually belongs to a formyl-imine structure, 2-iminoacetaldehyde or HN=CHC(=O)H, which itself exhibits four conformers all within 0.25 eV relative energy of one another [4,8]. The NH₂CHCO isomer actually lies 0.36 eV above the formyl-imine minimum, and it has two conformers: the lower-energy with the amine hydrogens pointing equatorially away from the C=C=O portion of the molecule as well another conformer where the amine hydrogens are axial pointing more towards the portion of the molecule containing the heavy atoms. There are other cyclic and even zwitterionic isomers, but those are higher in energy and exhibit strain or other destabilizing factors. While the previous work has already provided high-level quantum chemical predictions for the fundamental vibrational frequencies and the rotational constants for the two lowest formyl-imine isomers as well as the equatorial aminoketene [4,8], the small energy gaps between isomers and the kinetic nature of gas-phase astrochemical reactions implies that the other conformers/isomers may also be present.

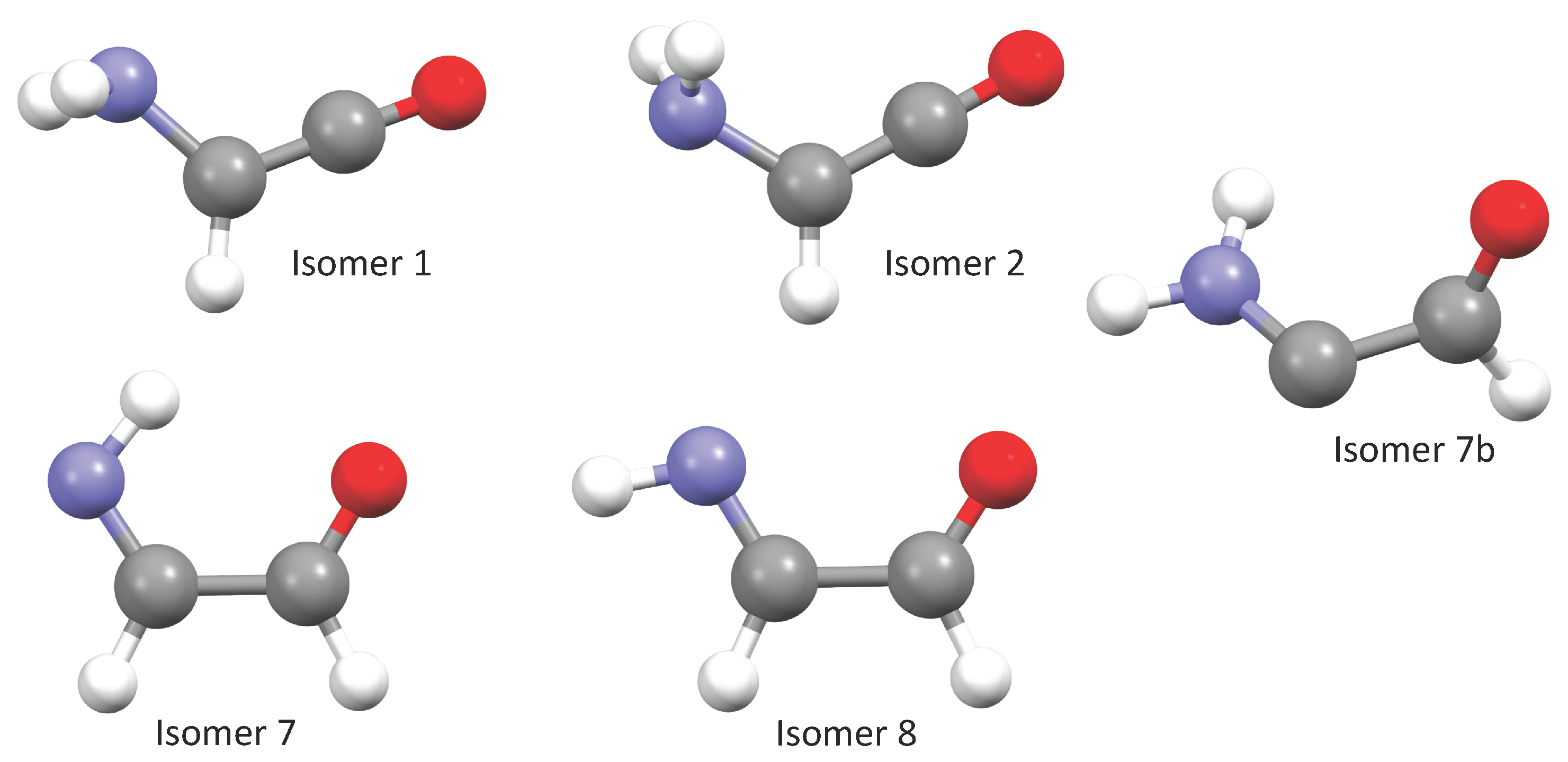
As mentioned, we have previously investigated 14 tautomers and conformers of NH₂CHCO [4]. A full depiction of them can be found in Figure 1 of Ref. [8]. Following a re-evaluation of the energetic properties across the entire isomeric family, a corrigendum has been published (see Figure 1 of [8]) confirming that isomer 10 ($anti$-(E)-2-iminoacetaldehyde) remains the lowest-energy structure, followed by its conformers 9, 7, and 8 ($anti$-(Z)-2-iminoacetaldehyde, $syn$-2-(Z)-iminoacetaldehyde, and $syn$-(E)-2-iminoacetaldehyde, respectively). In that study, isomer 8 is conclusively shown to be a local minimum at the CCSD(T)-F12b/cc-pVTZ-F12 level of theory [8]. Additionally, isomer 1 and its conformer, isomer 2, are verified to constitute the next-lowest energy set within the series. Isomers 5, 6, 11, and 12 were initially considered local minima (Figure 1 of [4]); however, further analysis has revealed that they dissociate into van der Waals complexes of methanimine HN=CH₂ and carbon monoxide. Consequently, these structures should not be classified as tautomers and conformers of NH₂CHCO and should have been excluded from Table 1 of [8] and are excluded from the present study, as well. Isomer 3 remains a second-order saddle point, but the relative energy reported represents the most accurate value to date. Isomer 4 does not correspond to a local minimum and instead reverts to isomer 1 or 2 upon geometry optimization, depending on the initial structural guess. Similarly, isomer 14 relaxes to isomer 13; thus, both are excluded from further consideration.

While the previous study presents accurate spectroscopic data for the lowest-energy isomer and the NH₂CHCO isomer hypothesized to be involved in ethanolamine synthesis, we now extend the spectral characterization to additional structures depicted in Figure 1 in this work. Specifically, conformers of the $syn$-(Z)- and $syn$-(E)-2-iminoacetaldehyde (HN=CHC(=O)H; isomers 7 and 8), which represent conformers of the global minimum and lie within 0.250 eV (2000 cm⁻¹) of the lowest-energy tautomer or conformer of aminoketene, may contribute to the overall vibrational and/or rotational spectra of this system. Furthermore, the two lower-energy, $anti$ isomers have been observed in condensed-phase experiments [10] as well as studied computationally [11], and similar diiminoethene conformers have been explored via quantum chemistry with a similar approach as that used here [12]. Consequently, the spectral properties of the higher-energy $syn$-2-iminoacetaldehyde isomers (isomers 7 and 8, as defined in [8] and depicted in Figure 1) are computed herein. While theoretically computed spectroscopic data exist for isomers 7 and 8 [13], the present work aims to provide these at a higher level. Furthermore, new spectral data for isomer 2, as well as updated spectroscopic parameters for isomer 1, the lowest-energy conformation of aminoketene are also presented. Finally, the spectral characteristics of a previously uncharacterized aminoketene tautomer/conformer (7b) are reported in this work. Additionally, our previous work does not provide the intensities for the aminoketene fundamental frequencies, and that is addressed in this work. The revised relative energies presented in this study enhance our ability to model the interconversion and interactions of these molecular species in various environments, including diverse astrophysical regions. As such, several knowledge gaps are present for a more complete characterization of the tautomers and conformers of NH₂CHCO, and this work will provide such.

As done in the previous work, the anharmonic spectroscopic data reported herein will rely upon quartic force fields (QFFs) [14,15,16,17,18,19] computed with explicitly correlated coupled-cluster theory within the F12 formalism [20,21,22]. The use of core electron correlation (“cC”) and scalar relativity (“R”) [23] adds to the accuracy of the explicit correlation which, itself, better approximates the complete basis set limit for a smaller basis set size [24,25,26,27,28,29]. As such, the so-called “F12-TcCR” QFF (so named for the F12-based energy with a “T” triple-$\zeta$ basis set along with the “cC” and “R” terms) has been shown to provide accuracies for B and C spectroscopic constants to better than 0.1% of experiment and fundamental vibrational frequencies within 0.7%, often within 1.0 cm⁻¹ [30,31]. Furthermore, rotational constants for related nitrogen-containing hydrocarbons have been predicted to within 10 MHz of experiment for numerous molecules [32,33,34]. and the rotational constants and fundamental vibrational frequencies of other prebiotic species of astrochemical and astrobiological significance have also been provided [35,36,37,38,39]. Hence, this work will utilize this same quantum chemical approach to increase the spectroscopic reference data available for the aminoketene conformers and tautomers. These data will provide for a more complete laboratory experimental exploration of these isomers and will inform where and to what extent these isomers and conformers will be detectable with current, archival, and future multi-messenger observations [40,41].

2. Results & Discussion

2.1. Fundamental Vibrational Frequencies

As isomers 1 and 2 represent the conformers of the isomer believed to play a role in the formation of ethanolamine potentially in shocked regions, their comparison begins the discussion of the fundamental vibrational frequencies from

Table 1. The F12-TcCR fundamental vibrational frequencies (in cm⁻¹) and B3LYP/6-311+G(d,p) intensities (I; in km mol⁻¹) of aminoketene isomer 1.

Mode	Sym.	Harmonic a	Anharmonic a	I	B3LYP b
1	$a^{″}$	3611.4	3435.8	8	3600.2
2	$a^{\prime }$	3530.4	3374.7	1	3519.1
3	$a^{\prime }$	3171.4	3036.0	19	3159.4
4	$a^{\prime }$	2192.3	2143.4	598	2187.4
5	$a^{\prime }$	1671.2	1622.0	23	1652.7
6	$a^{\prime }$	1437.7	1402.3	3	1380.7
7	$a^{″}$	1224.1	1188.4	10	1208.0
8	$a^{\prime }$	1182.0	1154.4	10	1191.9
9	$a^{\prime }$	1033.8	1006.7	3	1046.8
10	$a^{\prime }$	821.2	748.2	7	706.4
11	$a^{\prime }$	656.4	641.3	116	667.7
12	$a^{″}$	599.0	582.3	42	600.3
13	$a^{″}$	531.5	537.9	29	559.4
14	$a^{\prime }$	254.9	249.8	4	207.4
15	$a^{″}$	218.2	216.9	30	157.2

^a From [4]. ^b B3LYP/6-311+G(d,p) anharmonic frequencies.

and

Table 2. The F12-TcCR fundamental vibrational frequencies (in cm⁻¹) and B3LYP/6-311+G(d,p) intensities (in km mol⁻¹) of aminoketene isomer 2.

Mode	Sym.	Harmonic	Anharmonic	I	B3LYP a
1	$a^{″}$	3625.1	3442.5	8	3584.4
2	$a^{\prime }$	3537.6	3382.5	1	3511.2
3	$a^{\prime }$	3210.8	3079.9	20	3113.8
4	$a^{\prime }$	2173.3	2128.4	596	2208.3
5	$a^{\prime }$	1664.6	1621.5	22	1660.4
6	$a^{\prime }$	1392.8	1392.7	3	1420.5
7	$a^{″}$	1213.0	1160.9	1	1205.2
8	$a^{\prime }$	1212.3	1193.0	10	1179.8
9	$a^{\prime }$	1057.3	1023.8	3	1026.8
10	$a^{\prime }$	757.0	753.0	3	770.2
11	$a^{\prime }$	679.5	673.0	123	650.9
12	$a^{″}$	586.4	257.6	43	607.6
13	$a^{″}$	536.1	446.8	26	553.8
14	$a^{\prime }$	210.9	219.6	5	254.5
15	$a^{″}$	154.0	–	30	212.7

^a B3LYP/6-311+G(d,p) anharmonic frequencies.

. As expected and at first glance, they exhibit notably similar fundamental vibrational frequencies and corresponding intensities. Most significantly, however, are the exceptionally intense ${\nu }_4$ $a^{\prime }$ fundamental frequencies at 2143.4 cm⁻¹ and 2128.4 cm⁻¹ for isomer 1 and 2, respectively. Their respective intensities of 598 km mol⁻¹ and 596 km mol⁻¹ are far larger than most organic molecules exhibit, and, in fact, are more than 50% larger than even the antisymmetric stretch in carbon dioxide. These fundamentals both arise from the “antisymmetric” central carbon shuttling motion in the C=C=O portion of each isomer, again, similar to the antisymmetric stretch in CO₂, and these strong intensities have been previously documented quantum chemically [42]. Additionally, they fall in the range of 4.6 μm to 4.7 μm, an IR observational region where the majority of the observed features have recently been attributed to CN and/or CD stretches within polycyclic aromatic hydrocarbons (PAHs) or CN-PAHs [43,44,45]. Hence, these molecules are exhibiting exceptional intensities in regions of current interest for explaining portions of JWST observations.

Another intense fundamental is also present for both aminoketene isomers at 748.2 cm⁻¹ and 753.0 cm⁻¹, again respective of isomers 1 and 2. This ${\nu }_{10}$ $a^{\prime }$ fundamental represents the umbrella inversion motion of the amine group akin to the same motion in ammonia and would be observed at 13.3 μm. Besides these sets, the fundamental frequencies exhibit in large part either small intensities or fundamental frequencies below what JWST could observe. Additionally, the isomer 2 fundamentals below 600 cm⁻¹ are producing questionable anharmonicities. QFFs are known to exhibit such poor descriptions for quasi-degenerate conformers [46], but the use of normal coordinates from pbqff helps to minimize such improper descriptions [47,48] where they appear to influence only the low-frequency fundamentals for isomer 2. Additional considerations for a Hamiltonian employing hindered rotation would potentially also improve the descriptions of these likely, large-amplitude motions. However, the instruments onboard JWST do not perform well at frequencies of less than 400 cm⁻¹ (25 μm) and do not operate below 333 cm⁻¹ (30 μm) at all, making any such fundamental vibrational frequencies not relevant for application to this mission data. Their treatment is left for future work for other applications. Beyond this, the current methods are unable to fully quantify the contribution of the Darling-Denison resonances between modes 7 and 8 of isomer 2. An analysis similar to that of [49] would quantify this, but the contributions that these fundamentals would have on the overall spectrum is likely small due to the low intensities computed.

The $syn$-2-iminoacetaldehyde conformers (isomers 7 and 8) also share similarities between themselves for the fundamental vibrational frequencies and corresponding intensities as shown in

Table 3. The F12-TcCR fundamental vibrational frequencies (in cm⁻¹) and B3LYP/6-311+G(d,p) intensities (in km mol⁻¹) of $syn$-(Z)-2-iminoacetaldehyde isomer 7.

Mode	Sym.	Harmonic	Anharmonic	I	B3LYP a
1	$a^{\prime }$	3396.0	3224.2	2	3380.2
2	$a^{\prime }$	3134.7	2971.5	32	3092.0
3	$a^{\prime }$	2979.0	2844.4	76	2922.8
4	$a^{\prime }$	1774.0	1739.7	95	1793.7
5	$a^{\prime }$	1664.2	1620.7	27	1679.5
6	$a^{\prime }$	1437.9	1408.0	5	1424.5
7	$a^{\prime }$	1395.3	1365.5	13	1387.7
8	$a^{\prime }$	1239.5	1211.8	70	1238.7
9	$a^{″}$	1152.7	1106.4	65	1157.4
10	$a^{″}$	1031.4	1004.2	1	1041.1
11	$a^{\prime }$	899.6	867.1	34	872.8
12	$a^{\prime }$	781.3	800.3	17	777.9
13	$a^{″}$	678.1	643.5	15	676.6
14	$a^{\prime }$	301.4	291.3	17	295.8
15	$a^{″}$	181.1	56.0	12	183.8

^a B3LYP/6-311+G(d,p) anharmonic frequencies.

and

Table 4. The F12-TcCR fundamental vibrational frequencies (in cm⁻¹) and B3LYP/6-311+G(d,p) intensities (in km mol⁻¹) of $syn$-(E)-2-iminoacetaldehyde (isomer 8).

Mode	Sym.	Harmonic	Anharmonic	I	B3LYP a
1	$a^{\prime }$	3471.3	3315.0	1	3450.4
2	$a^{\prime }$	3061.8	2932.2	61	3009.3
3	$a^{\prime }$	2943.1	2751.1	67	2883.3
4	$a^{\prime }$	1788.4	1769.1	105	1811.7
5	$a^{\prime }$	1677.0	1666.5	21	1691.3
6	$a^{\prime }$	1436.2	1451.9	22	1429.4
7	$a^{\prime }$	1395.3	1405.0	1	1395.7
8	$a^{\prime }$	1210.0	1195.3	54	1206.8
9	$a^{″}$	1115.7	1112.7	6	1127.3
10	$a^{″}$	1026.0	1049.7	9	1039.3
11	$a^{\prime }$	903.5	907.7	38	879.2
12	$a^{\prime }$	767.8	803.7	45	765.5
13	$a^{″}$	636.3	647.6	46	636.1
14	$a^{\prime }$	295.1	417.5	1	297.0
15	$a^{″}$	27.6	–	3	68.3

^a B3LYP/6-311+G(d,p) anharmonic frequencies.

. The ${\nu }_3$ $a^{\prime }$ fundamental at 2844.4 cm⁻¹ and 2751.1 cm⁻¹, isomers 7 & 8 respectively, also has relatively large organic intensities above 70 km mol⁻¹, but these are still nowhere near what isomers 1 and 2 exhibit. This ${\nu }_3$ intensity here for isomers 7 and 8 originates from the CH stretch on the formyl moiety, but the NH stretch has nearly no intensity in either isomer with the other CH stretch intensity in between these two. The ${\nu }_4$ C=O stretch just below 1800 cm⁻¹ in both isomers also exhibits a notable intensity, but the ${\nu }_5$ N=H stretch is not as intense. The ${\nu }_8$ in-plane hydrogen bending at 1211.8 cm⁻¹ for isomer 7 (Table 3) exhibits an intensity of nearly 100 km mol⁻¹, but this drops off to roughly half this much in isomer 8. This drop occurs between isomers due to the intramolecular hydrogen bonding present in isomer 7 that is not present in isomer 8.

The lowest-frequency anharmonic fundamentals of both $syn$-2-iminoacetaldehyde conformers (isomers 7 and 8) also struggle within the QFF/VPT2 framework, but their anharmonicities should be within the accuracy of the method where the harmonic fundamental frequencies are sufficient approximations for the fundamental frequencies. Again, these frequencies are below the JWST observeable range, but the harmonic frequencies computed here should be sufficient for other applications. The B3LYP/6-311+G(d,p) anharmonic frequencies are able to provide an additional estimate for these low-frequency modes.

One final set of fundamental vibrational frequencies is provided here for a new isomer. This isomer was discovered when an attempted geometry optimization of isomer 7 went awry leading us to call this isomer 7b. Its fundamental frequencies are shown in

Table 5. The F12-TcCR fundamental vibrational frequencies (in cm⁻¹) and B3LYP/6-311+G(d,p) intensities (in km mol⁻¹) of 7b.

Mode	Sym.	Harmonic	Anharmonic	I	B3LYP a
1	a	3603.9	3422.4	22	3543.8
2	a	3433.0	3221.6	16	3376.9
3	a	2927.4	2694.8	64	2843.4
4	a	1713.7	1680.3	14	1710.6
5	a	1692.9	1697.0	232	1690.2
6	a	1539.3	1510.2	9	1559.9
7	a	1393.0	1377.2	4	1381.6
8	a	1217.6	1191.5	10	1212.5
9	a	1010.2	991.4	24	999.7
10	a	959.3	957.2	45	952.0
11	a	829.4	828.0	31	820.6
12	a	796.4	787.1	119	810.3
13	a	437.2	484.9	29	429.0
14	a	381.6	425.7	33	367.6
15	a	115.2	189.1	26	147.7

^a B3LYP/6-311+G(d,p) anharmonic frequencies.

and structure in Figure 1. This $C_1$, carbene molecule lies 1.33 eV above isomer 7 which puts it 1.42 eV above the lowest-energy isomer (isomer 10) from [8]. While this energy and the highly-reactive nature of the carbene imply that such a molecule is likely short-lived in any environment in which it may briefly exist, the spectral features still may provide insights into the evolution of the NCCO molecular connectivity in that if this isomer is observable, chemistry different from the formation ethanolamine is likely taking place. Isomer 7b exhibits a number of large intensity fundamentals in Table 5 with ${\nu }_3$, ${\nu }_5$, and ${\nu }_{12}$ all exhibiting intensities of ∼70 km mol⁻¹ or greater with two above 115 km mol⁻¹. The ${\nu }_4$ and ${\nu }_5$ C=O and C-N stretches at 1680.3 cm⁻¹ and 1697 cm⁻¹, respectively, imply that these features will likely combine together in some observations, especially at low resolution (potentially in archival data form older IR observatories like the Kuiper Airborne Observatory or the Spitzer Space Telescope), to generate a large feature in their lower-resolution IR spectra. Again, the anharmonic fundamental frequencies below 500 cm⁻¹ are of questionable quality, but these harmonics and the rest of the anharmonic fundamentals should be good predictions of vibrational behavior for this molecule.

2.2. Spectroscopic Constants

The A, B, and C rotational constants for each of the isomers unique to this work are given in

Table A1. The F12-TcCR rotational constants (in cm⁻¹) for the tautomers and conformers of NH₂CHCO.

Vib.	Isomer 2			Isomer 7			Isomer 8			Isomer 7b
State	A	B	C	A	B	C	A	B	C	A	B	C
0	1.3629509	0.1564255	0.1433041	0.7982917	0.2160520	0.1699816	0.8679701	0.2018905	0.1654165	1.0048315	0.1849222	0.1679052
1	1.3590094	0.1563680	0.1432120	0.7973042	0.2161697	0.1700128	0.8671622	0.2017716	0.1653131	1.0084002	0.1843525	0.1676343
2	1.3579747	0.1563555	0.1432253	0.7981337	0.2154747	0.1696303	0.8677828	0.2013875	0.1650946	0.9970994	0.1857703	0.1682240
3	1.3772180	0.1556337	0.1428176	0.7986017	0.2153799	0.1695969	0.8681743	0.2014409	0.1651462	1.0283836	0.1816024	0.1665233
4	1.3594890	0.1556400	0.1426105	0.7948480	0.2159468	0.1697604	0.8641257	0.2017046	0.1651558	1.0000290	0.1849677	0.1676992
5	1.3591170	0.1563850	0.1433174	0.7942485	0.2158545	0.1696747	0.8632939	0.2017142	0.1651020	0.9968289	0.1856149	0.1680231
6	1.3486644	0.1566485	0.1432260	0.7984735	0.2161584	0.1697819	0.8674469	0.2022396	0.1653654	0.9905204	0.1859057	0.1681927
7	1.4872806	0.1569801	0.1432941	0.7976619	0.2165681	0.1699849	0.8670468	0.2023804	0.1654288	1.0062175	0.1847629	0.1678530
8	1.2193176	0.1563644	0.1434498	0.8049232	0.2159964	0.1698007	0.8811927	0.2022305	0.1654386	1.0084480	0.1846934	0.1676515
9	1.3751164	0.1556949	0.1427539	0.7902159	0.2159143	0.1699246	0.8522102	0.2017805	0.1654427	1.0113896	0.1837456	0.1673406
10	1.3671396	0.1565262	0.1434222	0.7968237	0.2158027	0.1700387	0.8664768	0.2017843	0.1655069	1.0023347	0.1844507	0.1674099
11	1.3795352	0.1562589	0.1431526	0.7986630	0.2149380	0.1691413	0.8688271	0.2007825	0.1646034	1.0098699	0.1837699	0.1672491
12	1.3614459	0.1559866	0.1431955	0.7996714	0.2158890	0.1697064	0.8671591	0.2019031	0.1652437	1.0000525	0.1848609	0.1678934
13	1.3577394	0.1564494	0.1434554	0.7966941	0.2155632	0.1699333	0.8671115	0.2014987	0.1653850	1.0211571	0.1834660	0.1673613
14	1.3791663	0.1571186	0.1435859	0.8044780	0.2149457	0.1692348	0.8735755	0.2018280	0.1650911	1.0180646	0.1828524	0.1672123
15	1.3893752	0.1557369	0.1428035	0.8015797	0.2146601	0.1698974	0.8913232	0.1964369	0.1667708	1.0057230	0.1871574	0.1686394

. The numbers in column 1 correspond to the fundamental vibrational state that exhibits those specific rotational constants; the “0” is for the pure rotational constants. For isomer 2, the $R_{\alpha }$ zero-point corrected A₀, B₀, and C₀ constants (given as row “0”) of 1.3629509 cm⁻¹, 0.1564255 cm⁻¹, and 0.1433041 cm⁻¹ make this molecule near-prolate and translate into 40860 MHz, 4689 MHz, and 4296 MHz as given in

Table 6. The F12-TcCR rotational constants (in MHz) for the aminoketene tautomers and conformers.

Vib.	Isomer 2			Isomer 7			Isomer 8			Isomer 7b
State	A	B	C	A	B	C	A	B	C	A	B	C
0	40,860.2400	4689.5185	4296.1488	23,932.1831	6477.0760	5095.9202	26,021.0890	6052.5249	4959.0619	30,124.0905	5543.8281	5033.6713
1	40,742.0768	4687.7947	4293.3877	23,902.5786	6480.6046	5096.8555	25,996.8687	6048.9604	4955.9621	30,231.0775	5526.7489	5025.5499
2	40,711.0573	4687.4200	4293.7865	23,927.4464	6459.7690	5085.3885	26,015.4739	6037.4454	4949.4116	29,892.2880	5569.2535	5043.2286
3	41,287.9569	4665.7809	4281.5639	23,941.4767	6456.9270	5084.3872	26,027.2107	6039.0463	4950.9585	30,830.1647	5444.3030	4992.2429
4	40,756.4549	4665.9698	4275.3552	23,828.9436	6473.9222	5089.2888	25,905.8368	6046.9518	4951.2463	29,980.1152	5545.1921	5027.4955
5	40,745.3026	4688.3044	4296.5476	23,810.9710	6471.1551	5086.7195	25,880.9000	6047.2396	4949.6334	29,884.1786	5564.5947	5037.2058
6	40,431.9415	4696.2039	4293.8075	23,937.6333	6480.2658	5089.9333	26,005.4038	6062.9907	4957.5300	29,695.0545	5573.3127	5042.2903
7	44,587.5507	4706.1450	4295.8490	23,913.3022	6492.5483	5096.0191	25,993.4091	6067.2118	4959.4307	30,165.6418	5539.0524	5032.1063
8	36,554.2220	4687.6868	4300.5168	24,130.9905	6475.4092	5090.4969	26,417.4926	6062.7179	4959.7245	30,232.5105	5536.9688	5026.0655
9	41,224.9526	4667.6157	4279.6543	23,690.0767	6472.9479	5094.2114	25,548.6191	6049.2272	4959.8474	30,320.6974	5508.5545	5016.7450
10	40,985.8141	4692.5374	4299.6894	23,888.1736	6469.6022	5097.6320	25,976.3210	6049.3411	4961.7720	30,049.2383	5529.6929	5018.8225
11	41,357.4249	4684.5240	4291.6070	23,943.3144	6443.6791	5070.7286	26,046.7812	6019.3079	4934.6858	30,275.1380	5509.2830	5014.0019
12	40,815.1213	4676.3606	4292.8931	23,973.5455	6472.1894	5087.6699	25,996.7758	6052.9027	4953.8815	29,980.8197	5541.9904	5033.3175
13	40,704.0032	4690.2350	4300.6847	23,884.2883	6462.4222	5094.4722	25,995.3488	6040.7791	4958.1176	30,613.5197	5500.1723	5017.3656
14	41,346.3655	4710.2971	4304.5970	24,117.6437	6443.9100	5073.5317	26,189.1346	6050.6512	4949.3067	30,520.8089	5481.7770	5012.8986
15	41,652.4206	4668.8748	4281.1412	24,030.7549	6435.3479	5093.3959	26,721.1973	5889.0301	4999.6628	30,150.8170	5610.8377	5055.6820

. Additionally, the isomer 2 B and C rotational constants are 52 MHz and 10 MHz greater than their counterparts in isomer 1 [4], again confirming that they will have similar rotational spectra even though the A constant is more than 3000 MHz smaller here in isomer 2. However, isomers 1 and 2 have nearly the same dipole moment at 2.65 D (

Table 7. The Watson A-reduced F12-TcCR quartic and sextic spectroscopic constants (in MHz and B3LYP/6-311+G(d,p) dipole moments (in D) for the aminoketene isomers.

Constant	Isomer 2	Isomer 7	Isomer 8	Isomer 7b
${\Delta }_J$	0.0031	0.0057	0.0051	0.0144
${\Delta }_K$	2.2024	0.0956	0.1142	1.5656
${\Delta }_{JK}$	−0.1079	−0.0289	0.0023	−0.2345
${\delta }_J$	0.0007	0.0016	0.0014	0.0045
${\delta }_k$	0.0018	0.0116	0.0126	−0.1116
${\Phi }_J$	1.280 × ${10}^{-8}$	1.405 × ${10}^{-10}$	−8.193 × ${10}^{-7}$	2.717 × ${10}^{-7}$
${\Phi }_K$	3.822 × ${10}^{-4}$	2.745 × ${10}^{-6}$	−8.010 × ${10}^{-4}$	2.611 × ${10}^{-4}$
${\Phi }_{JK}$	−2.131 × ${10}^{-7}$	1.658 × ${10}^{-7}$	−8.178 × ${10}^{-6}$	−1.426× ${10}^{-6}$
${\Phi }_{KJ}$	−1.161 × ${10}^{-5}$	−1.329 × ${10}^{-6}$	−6.598 × ${10}^{-5}$	−2.837 × ${10}^{-5}$
${\varphi }_J$	4.536 × ${10}^{-9}$	7.207 × ${10}^{-7}$	−4.098 × ${10}^{-7}$	1.253 × ${10}^{-7}$
${\varphi }_{JK}$	4.116 × ${10}^{-7}$	−2.816 × ${10}^{-9}$	−1.622 × ${10}^{-5}$	1.448 × ${10}^{-6}$
${\varphi }_k$	1.113 × ${10}^{-5}$	7.939 × ${10}^{-7}$	1.302 × ${10}^{-5}$	1.232 × ${10}^{-4}$
$\mu$	2.65	2.22	4.22	4.83
${\mu }_x$	−1.41	2.18	0.00	−0.64
${\mu }_y$	0.00	0.00	−3.56	2.12
${\mu }_z$	−2.25	0.40	−2.26	−4.29

and

Table A2. The Watson A-reduced F12-TcCR spectroscopic constants (in cm⁻¹) and B3LYP/6-311+G(d,p) dipole moments (in D) for the aminoketene isomers.

Constant	Isomer 2	Isomer 7	Isomer 8	Isomer 7b
${\Delta }_J$	0.000000102706	0.000000190916	0.000000169972	0.000000481225
${\Delta }_K$	0.000073463780	0.000003187355	0.000003809995	0.000052224135
${\Delta }_{JK}$	−0.000003598161	−0.000000964165	0.000000077775	−0.000007822597
${\delta }_J$	0.000000022097	0.000000053488	0.000000045609	0.000000148854
${\delta }_k$	0.000000060007	0.000000385453	0.000000421895	−0.000003723975
${\Phi }_J$	4.271 × ${10}^{-13}$	4.687 × ${10}^{-15}$	−2.733 × ${10}^{-11}$	9.064 × ${10}^{-12}$
${\Phi }_K$	1.275 × ${10}^{-8}$	9.158 × ${10}^{-11}$	−2.672 × ${10}^{-8}$	8.709 × ${10}^{-9}$
${\Phi }_{JK}$	−7.108 × ${10}^{-12}$	5.529 × ${10}^{-12}$	−2.728 × ${10}^{-10}$	−4.758 × ${10}^{-11}$
${\Phi }_{KJ}$	−3.874 × ${10}^{-10}$	−4.433 × ${10}^{-11}$	−2.201 × ${10}^{-9}$	−9.462 × ${10}^{-10}$
${\varphi }_J$	1.513 × ${10}^{-13}$	2.404 × ${10}^{-14}$	−1.367 × ${10}^{-11}$	4.180 × ${10}^{-12}$
${\varphi }_{JK}$	1.373 × ${10}^{-11}$	−9.394 × ${10}^{-14}$	−5.411 × ${10}^{-10}$	4.831 × ${10}^{-11}$
${\varphi }_k$	3.714 × ${10}^{-10}$	2.648 × ${10}^{-11}$	4.342 × ${10}^{-10}$	4.111 × ${10}^{-9}$
$\mu$	2.65	2.22	4.22	4.83
${\mu }_x$	−1.41	2.18	0.00	−0.64
${\mu }_y$	0.00	0.00	−3.56	2.12
${\mu }_z$	−2.25	0.40	−2.26	−4.29

) which is expected for similar isomers with a simple shift in the positions of the hydrogen atoms. Such close correlation of dipole moments implies that the intensity of the rotational signal will not decrease if the higher energy conformer is populated.

Similarly, the rotational constants of isomers 7 and 8 show that these are also near-prolate molecules, but to a lesser degree than isomers 1 and 2. The rotational constants of isomers 7 and 8 mirror one another as shown in Table 6 and Table A1; the quartic and sextic distortion constants are reported in Table 7 and Table A2. However, the dipole moment of $syn$-(E)-2-iminoacetaldehyde (isomer 8) at 4.22 D is nearly double that of isomer 7 at 2.22 D. Hence, in warmer regions (assuming thermal equilibrium in those regions) isomer 8 may likely be more readily observed than isomer 7 even though the former is 0.15 eV higher in relative energy [8]. Such a case has already been noted for two conformers of carbonic acid, where the higher-energy but higher-dipole $cis$-$trans$ form has been observed while the $cis$-$cis$ has not [50]. Differently here, though, both isomers are notably polar, implying both isomers, as well as isomers 9 and 10 computed previously [4], may all produce observable signal in any environment wherever the HN=CHC(=O)H molecule is synthesized.

Isomer 7b also exhibits a dipole moment of nearly 5 D and has similar spectroscopic constants as the 2-iminoacetaldehyde isomer constants. However, this molecule has its own unique spectroscopic signatures that will allow it to be distinguished in any observations of this molecule, especially in any potential high-resolution laboratory experiments. Finally, while the rotational constants for states ${\nu }_{13}-{\nu }_{15}$ of each isomer are given in Table 6 for completeness, the questionable behavior of the corresponding vibrational frequencies for these states likely implies that these estimates are not as accurate as the rotational constants for the higher frequency states and, especially, the zero-point.

3. Observational and Spectroscopic Considerations

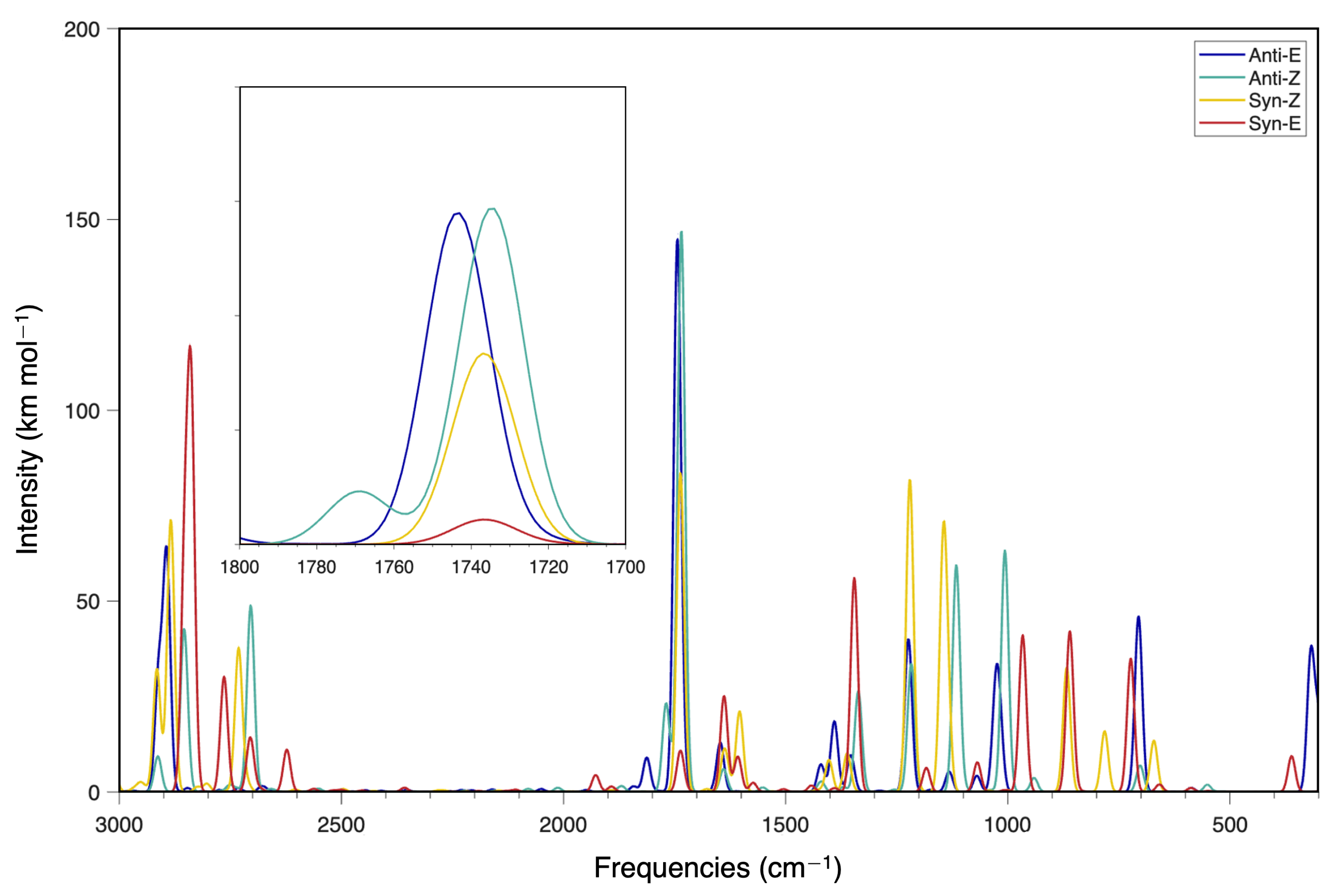
2-iminoacetaldehyde is one of the simplest prebiotic molecules yet to be observed in the ISM or other astronomical regions. Its family of conformers exhibits strong IR absorption in the range of 1720 cm⁻¹ to 1780 cm⁻¹ and notable dipole moments for all four conformers (isomers 7–10). Case in point, Figure 2 displays the F12-TcCR QFF spectra for all four conformers. Clearly, the region from 1700 cm⁻¹ to 1800 cm⁻¹ (given as an inset) produces the most intense features as the ${\nu }_4$ C=O stretch fundamental carries the largest intensity. The three lowest-energy conformers all cluster together in this region with the highest energy $syn$-(E) conformer showcasing a blue-shifted fundamental in this region. The C=O stretch of formaldehyde also lies in this region at 1746.1 cm⁻¹ [51], but F12-TcCR computations shift this frequency of H₂CO up to 1752.0 cm⁻¹ [30]. Hence, the C=O stretches of the 2-iminoacetaldehyde conformers computationally predicted to lie in the region of 1735 cm⁻¹ should still be distinct from the C=O stretch of the more common formaldehyde molecule.

Additionally, Figure 2 highlights that population of the first three conformational levels will not shift the frequency of this molecule as the higher energy conformers become populated at higher temperatures. Purely thermodynamically, the $anti$-(E) conformer should be the dominant form observed in the cold ISM. From the relative energies of Ref. [8], temperatures would have to surpass 115 K before a meager 1% of the population would convert from $anti$-(E) to $anti$-(Z) (isomer 9 to isomer 10) and more than 170 K before $syn$-(Z) would provide a notable contribution to the population of 2-iminoacetaldehyde. The highest energy $syn$-(E) (isomer 8) conformer would require more than 500 K before its population is ever greater than 1%. Hence, the $anti$-(E) should be the primary target for observation in colder regions, but all conformers may contribute to the observed IR or JWST spectra in warmer regions if they are present.

Even with these considerations, the possible unique detection of 2-iminoacetaldehyde will likely arise from radioastronomy due to the nature of emission rotational spectroscopy and from the 2.0+ D dipole moments of the conformers of this molecular family. While the rotational constants and the fundamental vibrational frequencies of the two $anti$-2-iminoacetaldehyde conformers have been computationally explored previously [4,8], this present work is expanding that to the $syn$-2-iminoacetaldehyde (Z) and (E) pair. The $anti$ conformers are both very much of near-prolate character with $\kappa$ values of −0.98. Due to their similarities, high resolution rotational spectroscopy would be required to separate the rotational spectra of the $anti$ conformers. Most notably, the differences in the $B_0$ constants are less than 4.0 MHz while this grows to more than 15 MHz in the $C_0$ constants [4] However, the dipole moments and rotational constants of the $syn$ conformers are notably separated from each other and from the two $anti$ conformers. Hence, they will produce other lines in the spectra as these higher-energy conformers are populated at higher temperatures. Regardless, the small number of heavy atoms (4) puts this molecule in the range of known prebiotic complex organic molecules [1,2,52]. In addition to ethanolamine, the conformers of 2-iminoacetaldehyde exhibit nearly the same skeletal structure as glycine in the N-C-C-O connectivity, missing only an additional oxygen atom bonded to the aldehyde carbon and a couple of ubiquitous hydrogen atoms.

This connectivity is maintained for the aminoketene conformers (isomers 1 and 2). Only the positions of the hydrogen atoms change. While the conformers of 2-iminoacetaldehyde are the lowest energy isomers, the NH₂CHCO conformers could still be the first of these isomers synthesized in astronomical environments potentially in shocked regions [3,5]. As such, the spectroscopic constants provided in this work are vital for understanding the possible populations of these isomers astrophysically. Like isomers 9 and 10, the spectroscopic constants of isomers 1 and 2 differ by less than 50 MHz for the B constant and less than 10 MHz for the C constant. As such, the rotational signals of the two NH₂CHCO conformers may combine with lower-resolution laboratory characterization or possible astronomical observation. Hence, shifts in population between the aminoketene isomers would not greatly change the observations.

While laboratory work would need to conclusively determine the rotational constants for any of these isomers, the present work should be providing rotational constants to within 10 MHz or less of experiment [30,34], greatly reducing the need to comb the spectra significantly in order to make attributions. Finally, the ratio of aminoketene to 2-iminoacetaldehyde would also provide insights into the nature of the formation of these molecules themselves, and it would also be able to give a clue as to the evolution of relatively simple prebiotic molecules.

4. Computational Details

The QFFs producing the anharmonic spectral data in this work begin with tightly converged F12 coupled cluster singles, doubles, and perturbative triples [CCSD(T)-F12b] [20,21,53] geometry optimizations employing the cc-pCVTZ-F12 basis set [54,55,56]. The optimizations and all electronic structure computations in this work (unless otherwise noted) make use of the Molpro2024.1 quantum chemistry program [57,58]. After the geometries are optimized, the pbqff program [47,59] constructs normal coordinates, executes displacements of 0.005 Å to construct the actual QFF, computes the F12-TcCR energies, sets up the Fermi resonances [60], and runs the second-order rotational and vibrational perturbation theory (VPT2) computations [61,62,63,64] in order to produce the rotational constants and vibrational frequencies. The dipole moments and fully anharmonic fundamental frequency intensities are computed with B3LYP/6-311+G(d,p) within Gaussian16 [65,66,67,68,69]. Such intensities are known to be sufficiently accurate as compared to higher-level methods and require orders of magnitude less complexity and computational time [70,71,72]. The spectra of the 2-iminoacetaldehyde conformers are produced with these intensities and F12-TcCR frequencies utilizing an artificial full-width at half-max of 15.0 cm⁻¹. The full sets of geometries and resonances are included in the Appendix A, Appendix B and Appendix C.

5. Conclusions

A more complete spectral picture of the tautomers and conformers of NH₂CHCO is produced in this work, notably showcasing that the two aminoketene conformers have strong IR features in the range of 4.6–4.7 μm (2125–2150 cm⁻¹) potentially in competition with functionalized PAHs in astronomical observations where C≡N stretches have been reported recently [45]. Hence, these two molecules are also notable targets for their IR features as well as their radioastronomical (rotational) signatures. Since the slightly lower-energy equatorial conformer (isomer 1) has a nearly identical dipole moment as the axial conformer (isomer 2), either can be observed rotationally and would likely be observed in similar amounts. Detection of either would help to add evidence for this molecule’s role in the interstellar formation of the known prebiotic molecule ethanolamine.

The 2-iminoacetaldehyde conformers from this and previous work [4] all exhibit notable dipole moments of at least 2.0 D if not greater than 4.0 D. Their IR fundamental vibrational frequencies are also populated with intense ${\nu }_4$ C=O stretch fundamentals enabling their observation at frequencies in the range of 1700 cm⁻¹ to 1800 cm⁻¹. The presently examined $syn$-(Z) and $syn$-(E) conformers of 2-iminoacetaldehyde or even the lower-energy $anti$-(E) and $anti$-(Z) conformers are likely not part of the synthesis of ethanolamine. They would be required to migrate a hydrogen atom to create the amine group. However, they may have other roles to play astrochemically given their notable mid-IR intensities, and these data provide the necessary references for their potential observation.

Finally, a new isomer, isomer 7b NH₂CCOH, is also shown to be a local minimum in this work despite being a carbene. While much higher in energy that most of the rest of the isomers examined this and the previous work, it could still form from other chemical reactions. Hence, its spectral data are produced in this work, as well.